Abstract
Let E and be elliptic curves over with complex multiplication by the ring of integers of an imaginary quadratic field K and let be the minimal desingularisation of the quotient of by the action of . We study the Brauer groups of such surfaces Y and use them to furnish new examples of transcendental Brauer–Manin obstructions to weak approximation.
Mathematics Subject Classification: Primary: 14G05, Secondary: 14F22, 11G05, 14J28
Introduction
Let k be a number field and let denote the adèles of k. Let X/k be a smooth, projective, geometrically irreducible algebraic variety, let denote its base change to an algebraic closure of k, and let denote the Brauer group of X. For v a place of k and , functoriality yields an evaluation map
The Hasse invariant is an isomorphism for v finite, and has image for v real and zero for v complex. In [17], Manin defined what became known as the Brauer–Manin pairing
| 1 |
where the sum is over all places v of k. For , the subset of consisting of all elements that are orthogonal to B under the pairing (1) is denoted . The Brauer–Manin set is . Global class field theory (the Albert–Brauer–Hasse–Noether Theorem), and continuity of evaluation maps, shows that contains the closure of X(k) in with respect to the product of the v-adic topologies. This shows that, in some cases, the emptiness of X(k) despite X having points in all completions can be explained by the emptiness of . This is known as a Brauer–Manin obstruction to the Hasse principle. In cases where X(k) is non-empty, one would like to understand more about the rational points on X: for example, does weak approximation hold, i.e. is X(k) dense in ? If is not equal to for some , we say that B obstructs weak approximation on X.
Manin’s work initiated a great deal of activity, see [29] for a recent summary. Initially, most research focused on the algebraic part of the Brauer group, which by definition is , and the more mysterious transcendental part was rarely computed. In [12, 14], the authors computed the odd order torsion in the transcendental Brauer groups of diagonal quartic surfaces by relating these surfaces to Kummer surfaces of products of elliptic curves over with complex multiplication by . In [12, 13], Ieronymou and Skorobogatov went on to study the evaluation maps for these elements of odd order and thus gave new examples of Brauer–Manin obstructions to weak approximation coming from transcendental Brauer group elements.
In this paper, we replace by the ring of integers of an imaginary quadratic field K and study Brauer groups and Brauer–Manin obstructions to weak approximation for Kummer surfaces of products of elliptic curves over with complex multiplication by . Note that the assumption that is the endomorphism ring of an elliptic curve over implies that K is an imaginary quadratic field of class number one (see e.g. [25, Theorem II.4.1]), but this is the only restriction on K. Moreover, our assumptions also imply that the elliptic curves E and are geometrically isomorphic, see e.g. [25, Proposition II.2.1].
Theorem 1.1
Let K be an imaginary quadratic field and let for elliptic curves over with . Suppose that contains an element of order . Then and .
Remark 1.2
Similar results can be obtained in the more general setting where the elliptic curves can have CM by non-maximal orders in , see Remark 3.2 below.
In Theorem 1.1 and throughout the paper, we write to mean the minimal desingularisation of the quotient of by the action of , which sends (P, Q) to . Such Kummer surfaces are examples of so-called singular K3 surfaces, which are defined to be K3 surfaces of maximal Picard rank.
The cases of Theorem 1.1 where K is or follow from work of Valloni on Brauer groups of principal K3 surfaces with CM in [28]. In the case where , the odd order torsion in the Brauer group was computed by Ieronymou–Skorobogatov–Zarhin [14] and Ieronymou–Skorobogatov [12] in their study of Brauer groups of diagonal quartic surfaces. In particular, [12, Theorem 1.1] also applies to the Kummer surface where has affine equation for . It shows that
| 2 |
Our next result handles all cases where .
Theorem 1.3
Let K be an imaginary quadratic field with and let for elliptic curves over with . Suppose that contains an element of odd order. Then
;
;
- Y is the minimal desingularisation of the projective surface with affine equation where
The remaining, and most interesting, case is . Any elliptic curve E over with has an affine equation of the form for some . Let and let . Then can contain transcendental elements of odd order n for . Cases involving elements of order divisible by 3 require a more delicate analysis, essentially because 3 ramifies in the CM field , and will be explored in future work. For elements of order 5 or 7, we have the following:
Theorem 1.4
For , let be the elliptic curve over with affine equation . Let and let . Let and let . Then
Furthermore, if then
The reason for the focus on odd order torsion in is a result of Skorobogatov and Zarhin (Theorem 2.1 below), which shows that odd order torsion in descends to the transcendental Brauer group of . This means that one can transfer many calculations concerning transcendental Brauer classes to the realm of abelian varieties. In particular, the method of Skorobogatov and Zarhin described in Sect. 2.2 enables one to compute Brauer–Manin pairings for transcendental Brauer group elements of odd order without the need to find explicit Azumaya algebras representing them.
However, it is important that we consider Kummer surfaces and not just abelian surfaces, for the following reason. For torsors under abelian varieties over number fields, any Brauer–Manin obstruction to the Hasse principle or weak approximation can already be explained by an algebraic element in the Brauer group, see [8, 17]. In contrast, for K3 surfaces, it can happen that the algebraic part of the Brauer group consists only of constant elements (and so does not contribute to any Brauer–Manin obstruction), while there is an obstruction coming from a transcendental element in the Brauer group. Examples of this phenomenon were given in [11, 19, 21]. Our next two results yield a new source of examples.
Theorem 1.5
Let K be an imaginary quadratic field and let for elliptic curves over with . Let be an odd prime and if assume that . Suppose that . Then the evaluation map is surjective and hence
i.e. obstructs weak approximation on Y.
Theorem 1.6
Reinstate the notation and assumptions of Theorem 1.4. Suppose that and . Then
and hence the failure of weak approximation in Theorem 1.5 cannot be explained by any algebraic element in the Brauer group of Y.
Remark 1.7
In Theorem 6.1 we prove a complement to Theorem 1.5, showing in many cases that the evaluation maps for places are constant, cf. [12, Theorem 1.2(i)].
Creutz and Viray showed in [9, Theorem 1.7] that if there is a Brauer–Manin obstruction to the Hasse principle on a Kummer variety, then there is an obstruction coming from an element in the 2-primary part of the Brauer group. It was already known (see e.g. [21]) that the analogous statement for Brauer–Manin obstructions to weak approximation does not hold. Theorem 1.6 gives further illustration of this fact, generalising the example given in [21, Theorem 1.3]. We note that the statement of [21, Theorem 1.3] needs correcting: for , the evaluation map is constant, but not necessarily zero, for all . However, any such does give an obstruction to weak approximation and there is a choice of for which the theorem holds as stated – one takes , where the notation is as in the proof of Theorem 6.1. This choice of should be in force throughout [21, Sect. 5], yielding corrections to the statements of [21, Proposition 5.1, Theorems 5.2, 5.3], see [22].
In the same way that Ieronymou, Skorobogatov and Zarhin used Kummer surfaces of products of elliptic curves with CM by to study Brauer groups and Brauer–Manin obstructions on diagonal quartic surfaces in [12–14], the results of this paper could be applied to the study of other families of quartic surfaces, e.g. those of the form with , in other words the family of surfaces geometrically isomorphic to Schur’s quartic surface. Note that these surfaces contain lines given by so any Brauer–Manin obstructions arising would be obstructions to weak approximation.
Outline of the paper
We begin by gathering some preliminary results on transcendental elements of Brauer groups and their evaluations at local points in Sect. 2. In Sect. 3, for K an imaginary quadratic field with , we compute transcendental Brauer groups of products of elliptic curves over with CM by and prove Theorem 1.1. In Sect. 4 we perform the same calculation in the case where and prove Theorem 1.4. In Sect. 5 we compute the algebraic part of the Brauer group for each of the Kummer surfaces under consideration and prove Theorem 1.6. Combining the results for the transcendental and algebraic parts of the Brauer group allows us to prove Theorem 1.3. In Sect. 6 we consider the evaluation of a Brauer group element of prime order at p-adic points with and show in many cases that these evaluation maps are constant, providing a complement to Theorem 1.5. Section 7 is devoted to the proof of Theorem 1.5.
Notation
If A is an abelian group and n a positive integer, then and A/n denote the kernel and cokernel, respectively, of multiplication by n on A. If is prime, then denotes the -power torsion subgroup of A.
If k is a field of characteristic zero, then denotes an algebraic closure of k and denotes the absolute Galois group . If X is an algebraic variety over k and l/k is a field extension then denotes the base change . The base change is denoted by .
The Brauer group of X/k is denoted by and its algebraic part is denoted by . The quotient is called the transcendental part of , or the transcendental Brauer group of X.
For an elliptic curve E/k we denote by the full ring of endomorphisms defined over .
Preliminaries
Transcendental Brauer groups
The following result of Skorobogatov and Zarhin allows us to move between the transcendental Brauer group of an abelian surface and that of the associated Kummer surface.
Theorem 2.1
([26, Theorem 2.4]) Let A be an abelian surface, let and let . There is a natural embedding
| 3 |
which is an isomorphism if n is odd. The subgroups of elements of odd order of the transcendental Brauer groups and are isomorphic.
To calculate the transcendental part of the Brauer group for products of elliptic curves, we use another result of Skorobogatov and Zarhin.
Proposition 2.2
([26, Proposition 3.3]) Let E and be elliptic curves over a field k of characteristic zero. For , we have a canonical isomorphism of abelian groups
When the elliptic curves have complex multiplication, we can say more.
Definition 2.3
Let k be a field of characteristic zero and let be elliptic curves over k with and for an imaginary quadratic field K. For , we define -submodules of , as follows:
where denotes the complex conjugate of .
The following lemma and corollary are slight generalisations of some results from [12, §3].
Lemma 2.4
Let k be a field of characteristic zero. Let be squarefree and let . Let be elliptic curves over k with and . For all coprime to 2d, we have equalities of -modules
| 4 |
and
| 5 |
Proof
First suppose that n is coprime to 2d. Then multiplication by is invertible on and and we have
Since n is odd, we can write any as
and thus prove (4).
The case and n coprime to 3 is similar except that we consider conjugation by instead of . Since , we have
where . But if then , which implies that and hence , as n is coprime to 3. Therefore, . Now observe that and to complete the proof of (4).
For (5), view and as -modules via the action of on the second factor in each case, so that sends an endomorphism to . Since , the elliptic curve is a twist of E by an element in . Thus, the -modules and are twists of and , respectively, by the same element of , acting on the second factor. Therefore, it is enough to prove that . Since , it is clear that . Equality follows from the fact that both are isomorphic to as abelian groups.
Corollary 2.5
Under the assumptions of Lemma 2.4, we have a canonical isomorphism of abelian groups
Proof
Follows immediately from Proposition 2.2 and Lemma 2.4.
In order to use Proposition 2.2 to calculate the whole of the transcendental part of the Brauer group, we will need the following material from [21].
Definition 2.6
Fix a number field L, an imaginary quadratic field K and a prime number . Define to be the largest integer t such that the ring class field corresponding to the order embeds into KL.
Theorem 2.7
Let L be a number field and let E/L be an elliptic curve such that for an imaginary quadratic field K. Then for all prime numbers ,
Proof
This is an immediate consequence of [21, Proposition 2.2, Theorems 2.5 and 2.9].
To aid us in our applications of Theorem 2.7, we will need the following well-known formula for the degree of a ring class field (see [7, Theorem 7.24], for example). Let K be an imaginary quadratic field with discriminant and class number , let and let be the order of conductor c in . Then
| 6 |
The symbol denotes the Legendre symbol for odd primes. For the prime 2, the Legendre symbol is replaced by the Kronecker symbol , with
Evaluation maps
Let k be a number field. Let be squarefree and let . Let be elliptic curves over k with and and let . Let be coprime to 2d and let . For the reader’s convenience, following [12, §5.1], [26, §3], we summarise here the construction of an element of from , and describe its evaluation at a p-adic point of Y in terms of a cup-product map.
Multiplication by n on E turns E into an E-torsor with structure group . Denote this torsor by and let denote its class in . Similarly, let denote considered as an -torsor with structure group , and let denote its class in . The homomorphism gives rise to the -torsor with structure group , with class .
Composing the cup-product map with the Weil pairing yields a pairing
| 7 |
Let and be the natural projection maps. The pullbacks and are -torsors with structure group ; let denote the pairing of their classes in via (7). By [26, Lemma 3.1, Proposition 3.3], the natural map
sends to . Let denote the involution on induced by on . The proof of [26, Theorem 2.4] identifies with the subgroup of consisting of elements fixed by . By the functoriality and bilinearity of the cup product, we find that . Let be the element of corresponding to .
Note that if we take quadratic twists of E and by the same element then there is a natural isomorphism . Applying the construction described above to the homomorphism of -modules coming from , we obtain an element of the Brauer group of that is identified with under the isomorphism .
Let F be a field containing k (e.g. F could be the completion of k at some place v of k). Let , let and let denote the corresponding point on the Kummer surface. Then
Let denote the image of P under the natural map and let denote the image of Q under the natural map . The cup product and the Weil pairing give a pairing
| 8 |
Now the construction of and the functoriality of the cup product show that
| 9 |
This description of the evaluation map, due to Skorobogatov and Zarhin in [26], is very powerful because it enables one to evaluate transcendental elements of at local points (and thus compute the Brauer–Manin pairing) without the need to obtain explicit Azumaya algebras representing these elements of the Brauer group.
Lemma 2.8
Let k be a number field and let be its completion at a place v. Let be squarefree and let . Let be elliptic curves over k with and and let . Let be coprime to 2d and let . Let be constructed from as described above. If the evaluation map
is constant then it is zero.
Proof
Let (so that ) and let . If is constant then and (9) gives
Hence , which suffices to prove the lemma.
CM by with : transcendental Brauer groups
If for an imaginary quadratic field K with (i.e. K is not or ), then the only twists of E are quadratic twists. Theorem 3.1 below shows that in this case the transcendental part of the Brauer group of has exponent at most 6, where denotes a quadratic twist of E. The theorem is stated for elliptic curves over K, but the conclusion also holds for elliptic curves over , by definition of the transcendental part of the Brauer group (cf. (10) below).
Theorem 3.1
Let K be an imaginary quadratic field with . Let E/K be an elliptic curve with , let be a quadratic twist of E and let .
-
(i)
If then T is killed by 6.
-
(ii)
If then T is killed by 4.
-
(iii)
If then T is killed by 3.
-
(iv)
In all other cases, .
Proof
Let be the quadratic twist of E by some and let . Write . Observe that is isomorphic to over L and by definition we have
| 10 |
Applying [21, Theorem 1.1 and Proposition 2.2], we see that for any prime number ,
| 11 |
where is the largest integer t such that the ring class field corresponding to the order embeds into L. Bounds on are easily obtained by noting that if embeds into L then divides . Furthermore, we can use the formula (6) to calculate , noting that the theory of complex multiplication shows that , since the Hilbert class field is equal to K(j(E)) and E is defined over K. In this way, we find that for all . For , we find that , and unless K is an imaginary quadratic field of class number one with , i.e. unless . Similarly, we find that unless , and furthermore if and if .
Proof of Theorem 1.1
As noted in the introduction, the assumptions of Theorem 1.1 imply that the CM field K has class number one and the elliptic curves E and are geometrically isomorphic. If , then this means that is a quadratic twist of E and the result follows from Theorems 3.1 and 2.1. The remaining cases, where , follow from [28, Examples 1 and 2, pp. 48–51] and Theorem 2.1.
Remark 3.2
If we relax the assumptions of Theorem 1.1 to allow E and to have CM by orders and in of conductors and , respectively, we can obtain similar results using the existence of isogenies of degrees and from E and , respectively, to elliptic curves with CM by . Since (see e.g. [7, Theorem 11.1]), the formula (6) shows that and . Bounds on the order of a non-trivial class in the transcendental Brauer group then follow from [2, Theorem 5.13] and Theorem 2.1.
Thus, in the setting of Theorem 3.1, an element of odd order in has order dividing 3. In Sect. 4, we will see that the situation is more interesting in the case of elliptic curves with complex multiplication by , where sextic twists can occur. But first we will investigate the cases in Theorem 3.1 where non-trivial elements of odd order can occur in the transcendental part of the Brauer group, namely when . Elements of odd order are of particular interest to us because Theorem 2.1 shows that they descend to the transcendental part of the Brauer group of the relevant Kummer surface, where there is a chance they may give obstructions to weak approximation that cannot be explained by any algebraic element in the Brauer group.
Lemma 3.3
Let , let , let E/F be an elliptic curve such that and let . Then
Proof
Let . Since is torsion (see [5, Lemma 3.5.3]),
Let and let . Then (10), (11) and the fact that (see the proof of Theorem 3.1) give
| 12 |
Hence, where and . Applying corestriction yields
where and , by [4, Lemme 1.4]. Since [L : F] is coprime to 3, we can invert [L : F] modulo the order of to see that the class of in lies in .
Proposition 3.4
Let , let E/K be an elliptic curve with CM by , let and let denote the quadratic twist of E by a. Suppose that contains an element of order 3. Then and hence .
Proof
The proof of Theorem 3.1 shows that if the 3-primary part of is non-trivial (so necessarily ) then . It is easily checked that .
Theorem 3.5
Let , let and let E/F be an elliptic curve such that . Furthermore, let . Then
Remark 3.6
In Theorem 3.5, if then one may assume since multiplying a by an element of does not change . Likewise, if then one may assume if , and if . Proposition 3.4 shows that these are the only quadratic twists for which contains non-trivial elements of odd order.
Proof of Theorem 3.5
We begin by computing . Since K has class number one, the theory of complex multiplication shows that any two elliptic curves over F with CM by are geometrically isomorphic and hence quadratic twists of each other, in this case. Therefore, we can select a chosen elliptic curve with CM by and write for some . Thus, and . Now acts on by conjugation and the two quadratic twists by cancel each other out so that as a -module. Furthermore, the -module is the quadratic twist of by the quadratic character corresponding to . In other words, we identify with the group equipped with an action of such that sends to .
: We take to be the elliptic curve with affine equation , which has complex multiplication by by [25, Proposition II.2.3.1(ii)]. One computes that and . This can be done by calculating the 3-torsion points of and using the fact that the -module is the quadratic twist of by the quadratic character corresponding to . Alternatively, for an explicit computation of the -modules for , see the proof of [1, Lemma 2.3.3].
Now Lemma 3.3 and Corollary 2.5 show that
By Theorem 3.1(i), it only remains to show that the 2-primary part of is trivial. Write and . By (10), (11) and the computation of n(2) in the proof of Theorem 3.1, it is enough to show that . Now Proposition 2.2 shows that
One computes that this quotient is trivial. As before, one can take and compute the 2-torsion explicitly. For the details, see the proof of [1, Lemma 2.3.6].
: We take to be the elliptic curve with LMFDB label 121.b2, which has affine equation . This is the modular curve . It has complex multiplication by by [27]. One computes that and . Explicit calculations can be found in the proof of [1, Theorem 2.4.1]. Now Theorem 3.1(ii), Lemma 3.3 and Corollary 2.5 show that
CM by : transcendental Brauer groups
Throughout this section, for , let denote the elliptic curve over with affine equation
The curve has complex multiplication by , where denotes a primitive 3rd root of unity. Multiplication by sends
The curve is the sextic twist of by the class of in . Since has class number one, any elliptic curve over with complex multiplication by is of the form for some .
In this section, we study the transcendental Brauer groups of and for .
Lemma 4.1
Let . For every prime number ,
For ,
For ,
Proof
Let and let . By definition of , we have an injection
Since Y is a K3 surface with CM by , we can apply [28, Example 2, pp. 50–51] to Y to see that, for all primes , and hence . Since is a torsion group, . The first statement now follows easily from Theorem 2.1.
Let so that . By definition,
| 13 |
for all . By Theorem 2.7, for any prime number ,
| 14 |
where is as defined in Definition 2.6.
Observe that . By (6), we have and , whence . This, together with (13) and (14), proves the statement for .
Now suppose that . By (6), , so . Our discussion above shows that
| 15 |
Now an argument using restriction and corestriction similar to the one used in the proof of Lemma 3.3 shows that .
In this paper, we will focus on the cases with CM by where the transcendental part of the Brauer group contains an element of order 5 or 7. The other cases will be discussed in future work.
Lemma 4.2
Let and let . Let and suppose that . Then (3) yields an isomorphism
Proof
This follows from [28, Example 2, pp. 50–51] and Lemma 4.1.
We now calculate for , using Corollary 2.5. To compute for , we will use Eisenstein’s sextic reciprocity law, as stated in [16, Theorem 7.10].
Definition 4.3
An element is called E-primary if and
Let N denote the norm map . Recall the definition of the sextic residue symbol: for with prime, is the unique 6th root of unity satisfying
Theorem 4.4
(Eisenstein) If are E-primary and relatively prime, then
Definition 4.5
Let and let be the isomorphism defined over given by .
We use to denote .
Proposition 4.6
View and as subgroups of , so that the set difference is defined.
-
(i)If then, for , abusing notation and viewing as an element of ,
Otherwise, . -
(ii)If then, for , abusing notation and viewing as an element of ,
Otherwise, .
Proof
Multiplying by 6th powers if necessary, we may assume that . By Corollary 2.5 it suffices to compute for . Let . First, we will show that
To prove this claim, we will determine the action of on via a study of the actions of Frobenius elements for sufficiently many primes in . The action of factors through . Let be an E-primary prime that is coprime to and unramified in . The prime ideals generated by such comprise all but finitely many prime ideals of , as every prime ideal of that is coprime to 6 has an E-primary generator. Furthermore, Chebotarev’s density theorem shows that is generated by Frobenius elements associated to such primes . We require to be E-primary so that we can apply sextic reciprocity later on in the proof. In particular, we have .
For , let be the Grössencharakter attached to . We write for the image under of the idèle with entry at the place and entry 1 at every other place. Then acts on as multiplication by , see [15, Corollary 4.1.3], for example. By [25, Example II.10.6],
| 16 |
The here comes from the fact that [25, Example II.10.6] is stated for primes that are congruent to , whereas our E-primary prime maybe congruent to either 1 or . In any case, the in (16) is independent of a and is therefore of no consequence for the action on by conjugation, as the for the actions on and cancel out. Thus, for , we have
| 17 |
For , sextic reciprocity gives
Furthermore, , whereby . Substituting this into (17) gives
| 18 |
for all E-primary primes that are coprime to 30cd and unramified in . Since is invertible modulo 5 for all , we deduce that if and only if either or for all E-primary primes that are coprime to 30cd and unramified in . The latter condition holds if and only if (see [20, Theorem 9.1.11]). Hence, if then , whereby (18) shows that , as required.
For , factorise 7 in as with . Then and are both E-primary and sextic reciprocity gives
| 19 |
Taking complex conjugates and then inverting both sides of (19) gives and hence . Substituting this into (17) gives
| 20 |
for all E-primary primes that are coprime to 42cd and unramified in . As before, we deduce that if then and , completing the proof of our claim.
To complete the proof of Proposition 4.6, it remains to compute for in the case where . It is easy to see that the conditions on cd ensure that and hence there exists some . Now observe that
Indeed, it is clear that and both are isomorphic to as abelian groups.
Furthermore, since the image of generates , an element of is fixed by the action of if and only if it commutes with . Therefore, , as claimed.
Proof of Theorem 1.4
This now follows from Theorem 2.1, Proposition 4.6 and Lemma 4.2.
Algebraic Brauer groups
Let E and be elliptic curves over and let . Since , the Hochschild–Serre spectral sequence gives a short exact sequence
| 21 |
Since Y is a K3 surface, . Furthermore, [26, Proposition 1.4(i)] gives a short exact sequence
| 22 |
where and are permutation modules and hence . Therefore, the long exact sequence of Galois cohomology attached to (22) can be combined with (21) to yield
| 23 |
Now suppose that for an imaginary quadratic field K and suppose that there exists a finite extension L/K such that is Galois and . Then inflation-restriction gives an exact sequence
| 24 |
where we view as a twist of defined over L. But then . Thus, (24) gives a canonical isomorphism from to . Plugging this into (23) gives
| 25 |
Theorem 5.1
Let be squarefree so that is an imaginary quadratic field. Let be an elliptic curve with , let be the quadratic twist of E by and let . Then
Proof
Let . Then (25) gives
where the -module is the twist of by the quadratic character corresponding to .
If then is cyclic and a Tate cohomology calculation gives
If then letting , and , inflation-restriction gives an exact sequence
Since M is the twist of by the character corresponding to , the generator of N acts as multiplication by on M, whereby and the inflation-restriction sequence yields an isomorphism from to . Now a Tate cohomology calculation gives . One checks that
We now have all the necessary ingredients for the proof of Theorem 1.3.
Proof of Theorem 1.3
By Theorem 5.1, contains no elements of odd order. Therefore, the assumption that contains an element of odd order implies that . Therefore, by Theorems 2.1 and 3.1, contains an element of order 3 and , proving (1). Hence, with , by Proposition 3.4. Now (2) follows from Theorems 2.1 and 3.5, and (3) follows from Theorem 5.1. To prove (4), note that K has class number one and therefore E is a quadratic twist of any chosen elliptic curve with . We take with affine equation , where f(x) is as stated in Theorem 1.3. Thus, E has equation for some and is the minimal desingularisation of the projective surface with affine equation . Replacing u by and computing completes the proof.
Theorem 5.2
For , let be the elliptic curve with affine equation . Let , let and let . We have
Proof
If then is a quadratic twist of and the result follows from Theorem 5.1. So henceforth we may assume that .
Let be the isomorphism defined over given by , whereby
so (25) gives
| 26 |
where . It remains to calculate .
Inflation-restriction gives an exact sequence
| 27 |
Since , the Galois group acts non-trivially on and therefore on , and we have . Thus, (27) yields
| 28 |
Since is cyclic, we can use Tate cohomology to compute .
First suppose that . Then we can choose a generator of that sends to . Therefore,
| 29 |
The first isomorphism in (29) is induced by sending a 1-cocycle to its value at . Let be the 1-cocycle sending to . To determine whether is trivial or isomorphic to , we just have to check whether the class of f in is fixed by the action of . Let be such that its image in is non-trivial. Then and the 1-cocycle property gives
Therefore,
| 30 |
by definition of the action of on in terms of its actions on and on .
If then we may assume that acts trivially on , whereby (30) gives . Hence, and f are not cohomologous (as can be seen using (29), for example). Therefore, and (26) and (28) give
On the other hand, if then and in fact . In this case we may assume that and hence . Therefore, (30) gives and hence is cohomologous to f (as can be seen using (29), for example). Therefore, and the result follows from (26) and (28).
Finally, suppose that . Then we can choose a generator of that sends to . Therefore,
Proof of Theorem 1.6
We have for some and so
Suppose for contradiction that . Then and hence , which is evidently not the case. Furthermore, if and only if c/d lies in , if and only if . Now the result follows from Theorem 5.2.
For completeness, we also include the calculation of the algebraic part of the Brauer group in the case of CM by .
Theorem 5.3
For , let be the elliptic curve with affine equation . Let , let and let . We have
Proof
The proof is very similar to that of Theorem 5.2 so we shall be brief. Given Theorem 5.1, our concern is the case . Let be the isomorphism defined over given by , whereby
where . Inflation-restriction gives
Constant evaluation maps
In this section, we prove the following analogue of [12, Theorem 1.2(i)].
Theorem 6.1
Let be an imaginary quadratic field and let for elliptic curves over with . Let be an odd prime and if assume that . Suppose that and let be a place of . Then the evaluation map is constant.
The statement for odd primes of good reduction for Y follows immediately from [3, Theorem D, Remark 1.6.2], and in the remaining cases the proof boils down to showing -divisibility for the sets of local points of certain elliptic curves with bad reduction. We will need the following elementary lemmas.
Lemma 6.2
Let K be an imaginary quadratic field and let for elliptic curves over with . Let be an odd prime and if assume that . Suppose that . Then , K is one of and
| 31 |
Furthermore, if is non-zero then it is an isomorphism.
Proof
Suppose for contradiction that . Then Theorems 5.1, 5.2 and 5.3 show that and , contradicting our assumptions. Consequently, and Theorem 1.1 shows that and . Since is odd, Theorem 1.3 shows that .
For , (31) follows from Theorems 5.2, 2.1 and Proposition 4.6. For , (31) follows from (2) and [12, Sect. 4]. For K equal to or , (31) follows from Theorems 1.3, 2.1 and Corollary 2.5 (note that must equal 3 in this case).
Now let . We claim that is an isomorphism. For , this follows from the explicit generator given in Proposition 4.6. For , it is proved in [12, Sect. 5.1], and we adapt the argument therein for K equal to or , observing that 3 splits in as and we can write but neither factor is a -submodule of and therefore neither factor can be the kernel of . Thus, the restrictions of to and are isomorphisms and . Hence, is an isomorphism.
Lemma 6.3
Let be an elliptic curve with . Then 2 is a prime of bad reduction for E. Furthermore, if is a prime of bad reduction for E then is 3-divisible.
Proof
Since has class number one, E is a quadratic twist of by some squarefree . Hence E has an affine equation . One checks that this equation is minimal and that 2 is a prime of bad reduction. Running Tate’s algorithm (see [25, IV.9], for example) shows that if p is a prime of bad reduction for E then the reduction type is additive and the Tamagawa number is either 2 or 4, so it suffices to show that is 3-divisible. This follows from the description of given in [23, Theorem 1].
Remark 6.4
The analogue of Lemma 6.3 for elliptic curves with complex multiplication by is false. For example, the elliptic curve with LMFDB label 121.b2, which has affine equation , has good (supersingular) reduction at 2 and , so is not 3-divisible. This is why was excluded from Theorem 6.1; further investigation would be needed to determine whether the statement still holds in that case.
Lemma 6.5
Let p and be distinct primes with . Let , let denote the elliptic curve with affine equation and if p is odd suppose that has bad reduction. Then is -divisible.
Proof
First suppose that has bad reduction. An examination of Tate’s algorithm (see [25, IV.9], for example) shows that has additive reduction at p and the Tamagawa number is at most 4. In particular, the Tamagawa number is coprime to and thus the claim is proved once we have shown that is -divisible. The -divisibility of follows from the description of this group given in [23, Theorem 1].
Now suppose that and has good reduction. Tate’s algorithm shows that this can only happen if and has a minimal Weierstrass equation of the form for some . The standard filtration on the points of is
where denotes the kernel of the reduction map. The theory of formal groups (see [24, IV, VII], for example) shows that , which is -divisible, and . Therefore, is -divisible. Finally, , whence it follows that is -divisible, as required.
Proof of Theorem 6.1
The statement for the infinite place is clear, since has trivial -torsion. The statement for odd primes of good reduction for Y follows from [3, Theorem D, Remark 1.6.2].
If then there is nothing to prove, so henceforth we will assume that . Thus, by Lemma 6.2, K is one of and .
For , we have by (2). For , Theorem 1.3 shows that and . For , we are assuming that , and Theorem 1.4 gives . So from now on let be a finite prime and if p is odd assume that Y has bad reduction at p. Our task is to show that is constant.
Let and let be the element of constructed from as in Sect. 2.2. By construction, and Lemma 6.2, generates . Therefore, it suffices to prove that is the zero map.
Let E and have affine equations and , respectively. Then Y is the minimal desingularisation of the projective surface with affine equation
| 32 |
Note that if E and are both replaced by their quadratic twists by some , with affine equations and , respectively, then the resulting Kummer surface has affine equation
and the map gives an isomorphism back to the original model, showing that the Kummer surface remains the same.
We adapt the arguments given in [12, Sect. 5] to our setting. Since the evaluation map is locally constant, it is enough to show that it is zero on all -points satisfying (32). Let . Again by local constancy, we are free to use the implicit function theorem to replace R by a point satisfying (32), sufficiently close to R, such that and . Now gives rise to points and . Note that is the minimal desingularisation of the projective surface with affine equation and the map gives a -isomorphism from to Y that sends the point corresponding to to . Let denote the isomorphism coming from . Now (9) shows that
| 33 |
where is the image of P under and is the image of Q under . The maps denoted by factor through the quotients and , respectively.
Recall that p is either equal to 2 or a prime of bad reduction for Y. By [18, Lemma 4.2], odd primes of good reduction for an abelian surface are primes of good reduction for the corresponding Kummer surface. Therefore, switching and if necessary, if p is odd then we may assume that p is a prime of bad reduction for . Now Lemmas 6.3, 6.5 and [12, Sect. 5.2] show that and hence (33) shows that , as required.
Surjective evaluation maps
In this section, we prove Theorem 1.5. The notation and assumptions of that theorem will be in force throughout this section. Furthermore, henceforth let be a non-zero element of .
Proposition 7.1
To prove Theorem 1.5, it suffices to prove the existence of and such that
where is the image of P under and is the image of Q under .
Proof
Lemma 6.2 shows that is an isomorphism. Let be the element constructed from as in Sect. 2.2. By construction, and Lemma 6.2, generates . Therefore, it suffices to prove Theorem 1.5 with . By continuity, we may assume that P and Q are not 2-torsion points (replacing them with nearby points if necessary). Let denote the point of Y coming from (P, Q). Then (9) shows that
Furthermore, for all such that , we have
Therefore, taking scalar multiples of P gives the desired surjectivity. (Again, we can always substitute a sufficiently close point to avoid any issues with 2-torsion points.)
Finally, it is well known and easy to verify that having a non-constant evaluation map implies the existence of an adelic point on Y that does not pair to zero with under the Brauer–Manin pairing (1).
Therefore, our task is to find and such that , as in Proposition 7.1. We begin by treating the easier case where the order of our Brauer group element splits in the CM field K.
The case of split in
This section mimics [12, §5.3]. Let be an odd prime number that splits in , so for some . This splitting will allow us to replace the cup-product pairing that gives the evaluation map (see (9)) with a non-degenerate pairing (see (35) below). The proof of Theorem 1.5 in this setting will then come down to showing that the images of and in and , respectively, are sufficiently large.
Choose an embedding of K into such that is a uniformiser of and . Now as -modules and therefore . Since the restriction of the skew-symmetric Weil pairing to each of the one-dimensional -subspaces and is trivial, each of the subspaces and is isotropic for the pairing
described in (8). By the non-degeneracy of the cup product, these subspaces are maximal isotropic subspaces of , each of dimension . Thus, (8) induces a non-degenerate pairing
| 34 |
Recall that we have
Then where is an isomorphism of -modules and is an isomorphism of -modules . Consequently, the induced isomorphism is a sum of and . In conclusion, (34) together with induces a non-degenerate pairing
| 35 |
We will use the non-degeneracy of the pairing (35) to prove Theorem 1.5 via Proposition 7.1 in the case where splits in . For this to work, we will need to show that the images of and in and , respectively, are sufficiently large. We will frequently use that and are both maximal isotropic subspaces of . Moreover,
and .
We need to treat four cases as delineated in Lemma 6.2: the CM field K is one of .
We begin with the case . In this case, Theorem 1.3 shows that and where is the elliptic curve with affine equation , and denotes the quadratic twist of E by a.
Proposition 7.2
Let have affine equation and let denote its quadratic twist by . Choose an embedding of in such that , whereby is a uniformiser for and . Then
and for we have and
Proof
First, we prove the statement for E. This elliptic curve has good reduction at 3 and we have
Let denote the formal group associated to E. We have isomorphisms of topological groups
| 36 |
where denotes the formal logarithm, which is given by a power series for some , see [24, Proposition IV.5.5]. These isomorphisms respect the action of . This means that acts as a multiplication by a unit in and acts as multiplication by a uniformiser and hence
| 37 |
Now one checks that induces an automorphism of . Thus,
| 38 |
and
by (37). Furthermore, (38) gives
since acts as an automorphism on by our discussion above. Therefore,
Now we deal with for . In fact, since , and are isomorphic over and we may take in what follows. The elliptic curve has additive reduction at 3 and the Tamagawa number is 2, so we can replace by in our calculations. As above, we find that
| 39 |
and
| 40 |
Furthermore, and acts as the identity on , whereby
| 41 |
and hence
by (40). Moreover, (41) and (39) give
Now [23, Theorem 1] shows that and hence
Now since , and and are both maximal isotropic subspaces of , they must be equal.
Corollary 7.3
Let have affine equation and let denote its quadratic twist by . Then for , there exist and such that is non-zero.
Proof
This follows from the non-degeneracy of (35), with and , and Proposition 7.2.
Next, we treat the case where . In this case, Theorem 1.3 shows that and where has affine equation , and denotes the quadratic twist of E by a. A minimal Weierstrass equation for E is given by , see [27].
Proposition 7.4
Let have affine equation and let denote its quadratic twist by . Choose an embedding of in such that , whereby is a uniformiser for and . Then for we have and
Proof
Standard calculations similar to those in the proof of Proposition 7.2 show that
Now since and both are maximal isotropic subspaces of , they must be equal. This completes the proof of the statement for E.
Now we deal with for . Since , it suffices to take . Using [6, §4.3] and Tate’s algorithm, we find that . Moreover, the isomorphism (36) respects complex multiplication. Therefore,
By [23, Definition 10 and Proposition 11], the map extends to an isomorphism of topological groups . Furthermore, [23, Proposition 18] gives an isomorphism of topological groups extending the isomorphism given by the formal logarithm. Transporting the action of complex multiplication by along these isomorphisms gives an endomorphism of that coincides with multiplication by on . But this endomorphism must then be multiplication by . The same argument applies to and hence we have
| 42 |
The usual argument about maximal isotropic subspaces of completes the proof.
Corollary 7.5
Let have affine equation and let denote its quadratic twist by . Then for , there exist and such that is non-zero.
Proof
This follows from the non-degeneracy of (35), with and , and Proposition 7.4.
Now we treat the case where . By Lemma 6.2, we have . In this section, our focus is on the case where splits in , so we take . For , let denote the ellliptic curve over with affine equation . Now Theorems 1.4 and 5.2 give where satisfy .
Proposition 7.6
For any , let E be the elliptic curve with affine equation . Choose an embedding of in such that , whereby is a uniformiser for and .
- If then and
If then
- In all other cases, and
Proof
Recall that and are both maximal isotropic subspaces of , and . Therefore, in cases where we show that , it will follow that this group is also equal to .
Since the -isomorphism class of only depends on the class of a in , we may assume that . The reduction type of is either good or additive. The Tamagawa number is coprime to 7, so we can replace by in our calculations. Standard calculations give
| 43 |
If , then [23, Proposition 18] shows that the extension is split. Computing the action of on shows that it coincides with multiplication by 2. Therefore, and . When combined with (43), this proves part (1) of the proposition.
In the case where has additive reduction and , we use [23, Definition 10, Propositions 11 and 18] to obtain an isomorphism respecting the action of , and hence show that and , proving the proposition in this case.
Now suppose that has good reduction so . Elementary calculations show that is coprime to 7, unless when . Thus, (43) proves the proposition for .
Our final task is to prove part (2). Taking , we have
and multiplication by sends (x, y) to (2x, y), which coincides with multiplication by 4 on . Therefore, and hence . By (43), this containment is an equality and hence
Moreover, and hence
whereby (43) gives
Corollary 7.7
For , let denote the ellliptic curve over with affine equation . Let satisfy . Then there exist and such that is non-zero.
Proof
First note that the relation implies that if and only if . Suppose that . Then and the result follows from the non-degeneracy of (35), with and , and Proposition 7.6(1) and (2). The proof in the case where follows by symmetry in c and d. In the remaining case, where c and d are in neither nor , the result follows from the non-degeneracy of (35) and Proposition 7.6(3).
The remaining case is where and (2) together with the splitting condition gives and where satisfy and is the elliptic curve with affine equation . This case was tackled by Ieronymou and Skorobogatov in [12], en route to their treatment of diagonal quartic surfaces. In particular, [12, Proposition 5.7 and Corollary 5.8] shows that if and are not in then there exist and such that is non-zero. If or is in then replace and by and , respectively. Now the relation implies that and are not in and one can apply [12, Proposition 5.7 and Corollary 5.8] as before. The Kummer surface Y is unchanged when we replace and by and , respectively, because this simply amounts to replacing each of and by their quadratic twists by . We have seen previously (in the proof of Theorem 6.1) that this does not change the Kummer surface.
At this stage, thanks to Proposition 7.1, Corollaries 7.3, 7.5, 7.7 and the above discussion for and , we have proved Theorem 1.5 in all cases where splits in K.
The case of inert in
This is the hardest case. We will follow the work of Ieronymou and Skorobogatov in [13] and use a result of Harpaz and Skorobogatov (Proposition 7.10 below) to reduce the proof of Theorem 1.5 in this case to the task of showing that the function fields of torsors associated to certain elements of are not isomorphic. We will avoid difficult calculations with these totally wildly ramified extensions of degree 25 by using quadratic twists to obtain function fields with distinct discriminants.
By Lemma 6.2 and our assumptions in the statement of Theorem 1.5 that is odd, and if then , we have excluded all cases where ramifies in . For , the evaluations at 3-adic points of Brauer group elements of orders 3 and 9 will be studied in future work.
By Lemma 6.2 and Theorems 1.3, 1.4 and (2), the only cases where the order of our Brauer group element is inert in the CM field K are when and , and when and .
The case where and was tackled by Ieronymou and Skorobogatov in [13]. In this case, (2) gives where satisfy and is the elliptic curve with affine equation . By [13, Proposition 2.2], if the 3-adic valuations of and are both non-zero modulo 4, then there exist and such that . If the 3-adic valuation of or is zero modulo 4, then we can replace and by and , respectively, which does not change the Kummer surface Y, and then apply [13, Proposition 2.2]. Now applying Proposition 7.1 completes the proof of Theorem 1.5 in this case.
Note the qualitative difference in behaviour between the Kummer surfaces Y and the closely related diagonal quartic surfaces studied by Ieronymou and Skorobogatov. In [13, Theorem 2.3], the authors show that for some diagonal quartic surfaces, a Brauer group element of order 3 has constant evaluation on 3-adic points, while for others it attains all three possible values.
The remainder of this section is devoted to proving the last remaining case of Theorem 1.5, wherein and . Henceforth, for , we use to denote the elliptic curve over with affine equation . Theorems 1.4 and 5.2 give where satisfy . The work below should be compared to [13].
We begin by showing that the image of in is a one-dimensional vector space over .
Lemma 7.8
Let . Then as abelian groups.
Proof
An inspection of Tate’s algorithm shows that has either good or additive reduction and in all cases the Tamagawa number is coprime to 5. So it is enough to show that . In the case of additive reduction, this follows from [23, Theorem 1]. Now suppose that has good reduction. Then we compute , so it suffices to show that . The theory of formal groups gives .
Proposition 7.9
Let be such that . Let P and Q generate and , and let and denote their images in and , respectively. To prove Theorem 1.5 for and , it suffices to show that is not a scalar multiple of .
Proof
This follows from Proposition 7.1, Lemma 7.8 and the fact that the image of in is a maximal isotropic subspace for the pairing (8).
To prove that is not a scalar multiple of (with the notation of Proposition 7.9), we wish to apply the following special case of a result of Harpaz and Skorobogatov.
Proposition 7.10
([10, Corollary 3.7]) Let k be a field of characteristic zero and let M be a finite simple -module, identified with the group of -points of a finite étale commutative group k-scheme . Let K be the smallest extension of k such that acts trivially on M, let and suppose that . Let be non-zero. Then the associated torsors and for are integral k-schemes. Furthermore, the following conditions are equivalent:
there exists such that ;
;
and are isomorphic as abstract k-schemes.
Lemmas 7.11 and 7.12 below are used to show that the hypotheses relevant for our application of Proposition 7.10 are satisfied.
Lemma 7.11
Let and let G and H be the images of and in , respectively. Then [G : H] divides 3.
Proof
We adapt the strategy of the proof of [13, Lemma 2.1]. Multiplying by a 6th power, we may assume that . Let , so . For any E-primary prime that is coprime to and unramified in , the action of on is given by multiplication by (the reduction modulo 5 of)
| 44 |
see [25, Example II.10.6]. Thus, the action of on factors through a homomorphism to .
Let be the fixed field of the kernel of the action of on . The natural map restricts to a surjective homomorphism with kernel . By Lemma 2.4, . Therefore, .
The proof of Proposition 4.6 shows that acts on as left-multiplication by . By the definition of the sextic residue symbol and the fact that these Frobenius elements generate , this means that the action of on is given by the sextic character attached to , which sends to . Therefore, .
Now fix an inclusion . Let , so . Let be the fixed field of the kernel of the action of on . Write for and use that every unit in is a cube to see that . Therefore, is either 2 or 6 depending on whether . Thus, has index dividing 3 in . To complete the proof, it remains to show that .
Consider the restriction of to . This is a cyclic group of order dividing , which contains as its unique subgroup of order 4, and is the quotient by . It suffices to show that . We have
Therefore, divides (whereby has even order) and . Since is a subgroup of the cyclic group of order dividing 24, we can now conclude that unless has order 6. Suppose for contradiction that . Then and , a contradiction.
Lemma 7.12
Let and let H denote the image of in . Then
;
is a simple -module;
.
Proof
Multiplying by a 6th power in , we may assume that . Let G denote the image of in . Recall from the proof of Lemma 7.11 that the action of on factors through a homomorphism to . Therefore, G has order dividing . Now (1) is immediate since is a finite group of order coprime to 5 and is killed by |H| and by 5.
The strategy of the rest of the proof is to use Lemma 7.11 to move from the action of on to that of , and from there to the action of , where we have the explicit action of Frobenius elements on given by (44). Henceforth, let be an E-primary prime lying above a rational prime p that is coprime to and completely split in . Then (44) shows that the action of on is given by multiplication by the reduction modulo 5 of for some . Assume in addition that p is inert in . Then, writing , we see that if then and hence quadratic reciprocity gives , contradicting the fact that p is inert in . Therefore, Similarly, By Lemma 7.11, the image of in is contained in H. It acts on as multiplication by the reduction modulo 5 of .
Let M be a -submodule of and suppose is non-zero. We have . Since , T and form an -basis of and hence , proving (2).
For (3), Propositions 2.2 and 4.6 show that
Thus, it suffices to show that . Clearly,
so it suffices to show the reverse inclusion. Let . Then for as above, commutes with the image of in , which implies that commutes with the image of in . Therefore, commutes with the image of in . Let denote complex conjugation, which generates . Since has order 2, Lemma 7.11 shows that the image of in lies in H. Therefore, commutes with and hence with the whole image of in , as required.
For , write for the function field of the -torsor for the group -scheme corresponding to . Note that is a finite extension of .
Proposition 7.13
Let be as in Proposition 7.9. To prove Theorem 1.5 for and , it suffices to show that is not isomorphic to . In particular, it suffices to show that is not equal to .
Proof
Proposition 7.9 tells us that it suffices to show that is not a scalar multiple of . By Lemma 7.12, we can apply Proposition 7.10 to see that this is equivalent to showing that the -torsor for the group -scheme determined by is not isomorphic (as an abstract -scheme) to that determined by . For this, it suffices to show that the function fields of the torsors are not isomorphic as extensions of . Since is an isomorphism (by Lemma 6.2), it follows from the construction of the pushforward that and are isomorphic as -schemes.
Note that if we prove Theorem 1.5 with and for a given pair of rational numbers c and d, then it also holds for all multiples of c and d by elements in , since the relevant elliptic curves are isomorphic over . Hence, we can reduce to considering , since these elements represent all cosets in . For , Table 1 records a generator for and the discriminant of the function field of the torsor , which we denote by .
Table 1.
.
| a | ||
|---|---|---|
| 1 | ||
| 5 | ||
| 2 | ||
Note that in all cases .
We are now ready to prove the last remaining case of Theorem 1.5, in which for with , and .
Proof
(Completion of the proof of Theorem 1.5) Since , and , Table 1 and the preceding discussion show that , where we can take modulo .
Let . An inspection of Table 1 shows that is not equal to unless . Thus, by Proposition 7.13, we have proved Theorem 1.5 for . Now suppose that . Then so Theorem 1.5 holds for . Now recall that , so the proof of Theorem 1.5 is complete.
Acknowledgements
We are grateful to David Kurniadi Angdinata, Tudor Ciurca, Netan Dogra, Jack Shotton, Alexei Skorobogatov and Alex Torzewski for useful discussions. We thank the anonymous reviewers for their thorough reading of an earlier draft of this paper and for many insightful comments and suggestions that have significantly improved it, including pointing out an error in a previous version of Theorem 5.2. Mohamed Alaa Tawfik was supported by a University of Reading International Research Studentship and a King’s College London Faculty of Natural, Mathematical and Engineering Sciences Studentship. Rachel Newton was supported by EPSRC grant EP/S004696/1 and EP/S004696/2, and UKRI Future Leaders Fellowship MR/T041609/1 and MR/T041609/2.
Data availability
Data sharing is not applicable to this article as it has no associated datasets.
Footnotes
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
References
- 1.Alaa Tawfik, M.: Brauer–Manin obstructions for Kummer surfaces of products of CM elliptic curves. PhD Thesis, King’s College London (2024)
- 2.Balestrieri, F., Johnson, A., Newton, R.: Explicit uniform bounds for Brauer groups of singular K3 surfaces. Ann. Inst. Fourier 73(2), 567–607 (2023) [Google Scholar]
- 3.Bright, M., Newton, R.: Evaluating the wild Brauer group. Invent. Math. 234, 819–891 (2023) [Google Scholar]
- 4.Colliot-Thélène, J.-L., Skorobogatov, A.N.: Descente galoisienne sur le groupe de Brauer. J. reine angew. Math. 2013(682), 141–165 (2013) [Google Scholar]
- 5.Colliot-Thélène, J.-L., Skorobogatov, A.N.: The Brauer-Grothendieck group. Volume 71 of Ergebnisse der Mathematik und ihrer Grenzgebiete. 3. Folge. A Series of Modern Surveys in Mathematics [Results in Mathematics and Related Areas. 3rd Series. A Series of Modern Surveys in Mathematics]. Springer, Cham (2021)
- 6.Connell, I.: Elliptic Curve Handbook. Preprint https://webs.ucm.es/BUCM/mat/doc8354.pdf
-
7.Cox, D.A.: Primes of the form
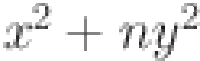 . Fermat, Class Field Theory, and Complex Multiplication. Wiley, New York (1989) [Google Scholar]
. Fermat, Class Field Theory, and Complex Multiplication. Wiley, New York (1989) [Google Scholar] - 8.Creutz, B.M.: There are no transcendental Brauer-Manin obstructions on abelian varieties. Int. Math. Res. Not. 9, 2684–2697 (2020) [Google Scholar]
- 9.Creutz, B., Viray, B.: Degree and the Brauer-Manin obstruction. Appendix by A. Skorobogatov. Algebra Number Theory 12(10), 2445–2470 (2018) [Google Scholar]
- 10.Harpaz, Y., Skorobogatov, A.: Hasse principle for Kummer varieties. Algebra Number Theory 10(4), 813–841 (2016) [Google Scholar]
- 11.Ieronymou, E.: Diagonal quartic surfaces and transcendental elements of the Brauer group. J. Inst. Math. Jussieu 4(9), 769–798 (2010) [Google Scholar]
- 12.Ieronymou, E., Skorobogatov, A.N.: Odd order Brauer-Manin obstruction on diagonal quartic surfaces. Adv. Math. 270, 181–205 (2015) [Google Scholar]
- 13.Ieronymou, E., Skorobogatov, A.N.: Corrigendum to “Odd order Brauer-Manin obstruction on diagonal quartic surfaces’’. Adv. Math. 307, 1372–1377 (2017) [Google Scholar]
- 14.Ieronymou, E., Skorobogatov, A.N., Zarhin, Y.G.: On the Brauer group of diagonal quartic surfaces. (With an appendix by Sir Peter Swinnerton-Dyer.). J. Lond. Math. Soc. 83, 659–672 (2011) [Google Scholar]
- 15.Lang, S.: Complex Multiplication. Grundlehren Math. Wiss., vol. 255. Springer, New York (1983) [Google Scholar]
- 16.Lemmermeyer, F.: Reciprocity Laws: From Euler to Eisenstein. Springer Monographs in Mathematics. Springer, Berlin, Heidelberg (2000)
- 17.Manin, Y.: Le groupe de Brauer–Grothendieck en géométrie diophantienne. In: Actes du Congrès International Mathématiciens (Nice, 1970), vol. 1, pp. 401–411. Gauthier-Villars, Paris (1971)
- 18.Matsumoto, Y.: On good reduction of some K3 surfaces related to abelian surfaces. Tohoku Math J. 67, 83–104 (2015) [Google Scholar]
- 19.McKinnie, K., Sawon, J., Tanimoto, S., Várilly-Alvarado, A.: Brauer groups on K3 surfaces and arithmetic applications. In: Auel, A., Hassett, B., Várilly-Alvarado, A., Viray, B. (eds.) Brauer Groups and Obstruction Problems. Progr. Math., vol. 320. Birkhäuser, Cham (2017) [Google Scholar]
- 20.Neukirch, J., Schmidt, A., Wingberg, K.: Cohomology of Number Fields. Grundlehren der Mathematischen Wissenschaften, vol. 323, 2nd edn. Springer, Berlin, Heidelberg (2008)
- 21.Newton, R.: Transcendental Brauer groups of products of CM elliptic curves. J. Lond. Math. Soc. 93(2), 397–419 (2016) [Google Scholar]
- 22.Newton, R.: Corrigendum: Transcendental Brauer groups of products of CM elliptic curves. J. Lond. Math. Soc. 110, e12953 (2024). 10.1112/jlms.12953 [Google Scholar]
-
23.Pannekoek, R.: On
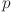 -torsion of
-torsion of 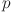 -adic elliptic curves with additive reduction. arXiv:1211.5833v2
-adic elliptic curves with additive reduction. arXiv:1211.5833v2
- 24.Silverman, J.H.: The Arithmetic of Elliptic Curves. Graduate Texts in Mathematics, vol. 106, 2nd edn. Springer, New York (1986) [Google Scholar]
- 25.Silverman, J.H.: Advanced Topics in the Arithmetic of Elliptic Curves. Graduate Texts in Mathematics, Springer, New York (1994) [Google Scholar]
- 26.Skorobogatov, A.N., Zarhin, Yu.G.: The Brauer group of Kummer surfaces and torsion of elliptic curves. J. reine angew. Math. 666, 115–140 (2012) [Google Scholar]
- 27.The LMFDB Collaboration. The L-functions and modular forms database (2023). https://www.lmfdb.org. Accessed 16 Aug 2023
- 28.Valloni, D.: Complex multiplication and Brauer groups of K3 surfaces. Adv. Math. 385, 107772 (2021) [Google Scholar]
- 29.Wittenberg, O.: Rational points and zero-cycles on rationally connected varieties over number fields. In: Algebraic Geometry: Salt Lake City 2015, Part 2. In: Proceedings of Symposia in Pure Mathematics vol. 97, 597–635, American Mathematical Society, Providence (2018)
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
Data sharing is not applicable to this article as it has no associated datasets.


