Coexistence of the Radial-Guided Mode and WGM in Azimuthal-Grating-Integrated Microring Lasers

Abstract

Whispering-gallery mode (WGM) resonators, renowned for their high Q-factors and narrow line widths, are widely utilized in integrated photonics. Integrating diffraction gratings onto WGM cavities has gained significant attention because these gratings function as azimuthal refractive index modulators, enabling single-mode WGM emissions and supporting beams with orbital angular momentum (OAM). The introduction of curved grating structures facilitates guided mode resonances by coupling high-order diffracted waves with leaking modes from the waveguide. These gratings act as wavelength-selective mirrors and support concentric circular radial-guided modes. This study investigates the coexistence and interaction between OAM-carrying WGMs and radial-guided modes with Bessel beam characteristics in an active cladding grating-integrated microring laser. These phenomena are examined through both three-dimensional simulations and experiments. The active layer enhances the radial-guided modes at the microring’s center, where cylindrical waves from the active cladding produce strong guided mode resonance at specific wavelengths corresponding to radial modes. Additionally, general WGMs are formed and confined within the microring. The effects of grating depth and microring size on radial-guided mode resonance are evaluated through two-dimensional simulations and experiments. These insights pave the way for integrating functional lasers into photonic circuits and advancing technologies for topological optical vortex emission and manipulation.

1. Introduction

Optical microcavities are fundamental components in the field of photonics, designed to confine light and induce feedback and resonance at the micrometer scale.¹ These cavities are deployed in both active and passive configurations, addressing a variety of applications across the photonics spectrum. Specifically, passive microcavities, recognized for their high quality factors (Q factors) are critical in wavelength selective filtering for optical communications^2,3 and evanescent-field coupling-based optical sensing.^4,5 Their significance is further underscored by their high sensitivity, attributed to superior energy confinement, which renders them indispensable in photonic integrated circuits.^6,7 In contrast to passive configurations, active microcavities utilize diverse gain materials to modulate spontaneous light-emission rates⁸⁻¹⁰ and support the development of multifunctional, integrable lasers.^11,12

Among the various configurations of optical microcavities, whispering-gallery mode (WGM) microcavities stand out. These include microrings,¹³ microspheres,¹⁴ and microdisks,¹⁵ which exploit rotational symmetry to optimize feedback via total internal reflection.¹⁶ A notable advancement in this area is the strategic integration of azimuthal gratings to these microcavities, enhancing their functionality by enabling single-mode operations through refractive index modulation in the angular direction as a micro gear structure^17,18 and supporting unidirectional vertical laser emissions.¹⁹ Such advancements are crucial because they facilitate the generation of beams carrying high orbital angular momentum (OAM),²⁰⁻²² for advancing applications in optical manipulation,²³ imaging,²⁴ optical communication,²⁵ and microscopy,²⁶ thereby demonstrating the significant potential of grating-integrated microring resonators in expanding the functionality and application scope of WGM microcavities.

Moreover, gratings in Fabry–Pérot lasers typically provide maximum gain only for modes near the grating’s Bragg wavelength.²⁷ Similarly, an azimuthal grating integrated into a microring can function as a curved Bragg grating when the microring’s size is much larger than the grating period.²⁸ The use of curved Bragg gratings (CBGs) as diffraction gratings around the ring has been studied, offering new possibilities in photonic applications.²⁹⁻³¹ These CBGs are meticulously engineered to alter the direction of light propagation and simultaneously optimize the optical response. This engineering precision enables the guided mode resonance (GMR) phenomenon, which occurs when waveguide modes align with grating parameters, resulting in intense coupling during grating diffraction. GMR is applied in various technological domains, including the design of filters³² and biosensors.³³ Within these CBGs, novel coupled modes emerge when incident plane waves interact with the leaky modes generated by the WGM under the influence of GMR, creating what are termed radial-guided modes. To illustrate, finite-difference time-domain (FDTD) simulations have shown that CBGs with consistent local curvature can exhibit the GMR effect for concentric circular waves,³⁴ enabling CBGs to produce concentric circular radial magnetic fields through the simultaneous presence of WGMs and GMR modes.³⁵ Despite the promising simulations, the presence and interaction of WGM and radial-guided modes within grating-integrated microring lasers have not yet been experimentally validated.

Azimuthal grating-integrated microrings are widely used in OAM emitters within the semiconductor and photonic crystals,³⁶⁻³⁸ where they leverage grating modulation to produce OAM-carrying beams. However, GMR can also occur in these structures, potentially affecting the modes in complex ways. Controlling and utilizing these GMRs is crucial for optimizing microring laser design and applications. While previous research has investigated GMR in microring cavities using FDTD simulations, a comprehensive study that generalizes GMR modes, WGMs, and the OAM they carry is still lacking. In this study, we investigate the mode generation mechanism in active cladding grating-integrated microrings using both three-dimensional simulations and experimental validation. Our findings reveal the coexistence of OAM-carrying WGMs and radial-guided modes with Bessel beam characteristics. We provide a generalized description of the wave functions for all fields using the Bessel equation. The active layer serves to enhance radial-guided modes, with the radial-guided mode wavelength being governed by the GMR wavelength, which is determined by the grating period. Furthermore, we analyze the modulation effect of grating depth and microring size on radial-guided mode resonance through two-dimensional simulations and experiments. These simulation results are corroborated by experimental demonstrations. Ultimately, this approach, leveraging straightforward nanofabrication techniques, holds significant promise for the development of multifunctional lasers capable of emitting in free space, combining OAM-carrying WGMs and radial-guided modes with gradient fields.

2. Coexistence of the Radial-Guided Mode and WGM in Active Cladding Microring Lasers

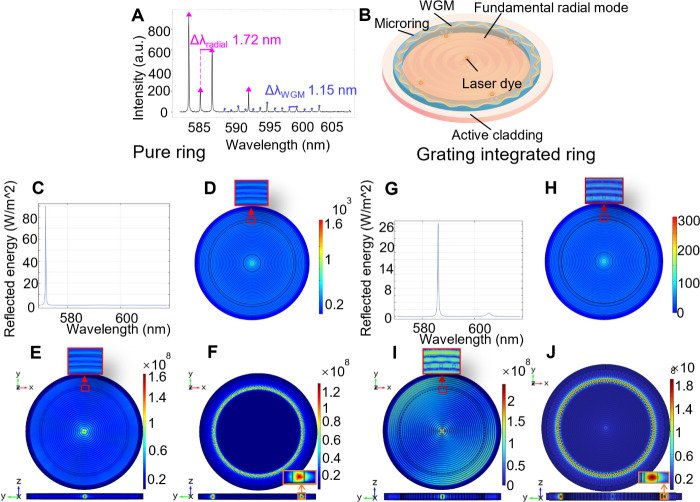
In our study, an active cladding, spin-coated on the upper side of Si₃N₄ microrings, was introduced to enhance all possible modes. A photoluminescence experiment was conducted to investigate the lasing modes in the active cladding laser. Figure 1A shows the lasing spectrum (wavelength λ vs intensity I) of an active cladding microring with R = 25 μm. The spectrum includes two groups of modes with free spectral ranges (FSR) of 1.72 and 1.15 nm, respectively. Details of the sample fabrication process and the experimental setup are provided in Figures S2 and S3, respectively.

Figure 1.

(A) Spectrum of the active cladding microring laser with R = 25 μm, showing radial modes (magenta triangle), WGMs (blue dot). (B) Schematic of the coexistence of radial modes and WGMs. (C)–(J) Simulation results on active cladding microring, where (C)–(F) for pure ring: (C) dependence of reflectivity on wavelength, (D) intensity distribution of the light source formed by the active layer in the xy-plane at 572.25 nm, (E) intensity distribution of fundamental radial mode at 572.51 nm, and (F) intensity distribution of WGM at 602.25 nm. And (G)–(J) for grating integrated ring: (G) dependence of reflectivity on wavelength, (H) intensity distribution of the light source formed by the active layer in the xy-plane at 587.92 nm, (I) intensity distribution of fundamental radial mode at 587.79 nm, and (J) intensity distribution of WGM at 602.24 nm.

Next, simulations on the active cladding microring laser are performed to better understand the mechanism of mode generation.

Typically, in a cylindrical microcavity, a light source can be formed by the oscillation of a cylindrical wave described by a Bessel function. When the excitation light is focused onto the active cladding through the microscope objective, a bulk light source is formed in the microdisk-type active layer. The photoluminescence of the active layer exhibits isotropic fluorescence, which is reflected and guided by the microcavity to form a laser pattern. Under appropriate refractive index contrast and microring shape, these reflected light waves form stable interference patterns at the cavity.

To simulate the body light source from the active layer, the 3D finite element method using the frequency domain solver in COMSOL Multiphysics was employed. In the simulation, the microring had a radius of 5 μm, a ring width of 300 nm, a thickness of 300 nm, and a refractive index n₁ of 2.04. The active layer had a complex refractive index n₂ of 1.76–0.1i, where the imaginary part being negative indicates that the material has gain properties, meaning light is amplified within the material. A uniform background electric field of E₀ = 1 was used as the excitation field and calculated the excited field under a wavelength range of 571–618 nm. The cylindrical waves continuously radiate outward and are reflected by the inner wall, producing resonance at specific wavelengths, resulting in an intensity peak at the center. A receiving boundary was set at a radius of 1 μm to calculate the time-averaged Poynting vector toward the center, thus assessing the reflected energy from the microring’s inner wall, indicating a GMR mode near the wavelength. Figure 1C shows the reflectance of the inner sidewall of the microring, which peaks at a wavelength of 572.25 nm. At the peak wavelength of 572.25 nm, the intensity distribution of the light source formed by the active layer in the xy-plane is shown in Figure 1D, where the intensity peak at the center is the strongest among all wavelengths.

Next, the cavity eigenmodes around 600 nm were simulated. The eigenmode at 572.51 nm is shown in Figure 1E, with the highest intensity among all the radial modes. This mode is formed by the interference of divergent and convergent waves, with a wavefront shape corresponding to the curvature of the microring’s inner wall, similar to the standing wave mode in a Fabry–Pérot cavity. The wave function of the radial mode can be expressed as

1

Under typical conditions, the dominant radial mode can be estimated using the effective refractive index n_eff, boundary conditions R, and the gain wavelength range of the active material. The leading radial mode is determined by identifying the azimuthal order that satisfies J_m(k_rR) = 0. In microrings with small radii, radial modes are primarily governed by the solutions to low-order Bessel functions. Simulation results, as shown in Figure 1E, indicate that in a 5 μm structure, the dominant radial mode exhibits no phase change in the azimuthal direction and can be predominantly described by the zero-order Bessel function J₀(k_rR) = 0. It can also be reduced to the propagation of wave vectors, where the propagation of radial wave vectors still satisfies the generation of conventional standing wave modes. The radial wave vector k_r is given by 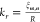where ξ_m,n are the solutions of J_m(k_rR) = 0, and m = 0 or 1. Additionally, for a given microring, the wave vector is related to the standing wave condition as 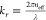. Rearranging, we get: ξ_m,nλ = 2πn_eff. For integer n, this can be written as 2Rn_eff = nλ, which is also the standing wave condition in a cavity length with 2R. The FSR of the fundamental modes is

2

The conventional microdisk cavity is typically surrounded by materials with a lower refractive index, while the microring around microdisk-shaped active cladding has a higher refractive index. This configuration enhances the radial mode’s quality factor by reducing energy dissipation thus promoting stable lasing modes. In the low-refractive-index region, some light undergoes total internal reflection, but this is insufficient to form stable WGMs. When light enters the high-refractive-index microring, it experiences stronger confinement through effective total internal reflection, allowing WGMs to form with higher quality factors. As the structure’s size increases, higher-order radial and azimuthal modes are likely to appear due to the increased mode complexity.

When the light wave propagates in a high n_eff microring, the radially propagating wavevector k_r is gradually transformed into an angularly propagating wavevector k_ϕ after many reflections. Each reflection reduces the radial component k_r as the light path adjusts to maximize its length within the ring.³⁹ Consequently, the energy of the radial mode is converted into the energy of the angular mode, forming a WGM, as shown in Figure 1F. The wave travels in the circumferential direction, undergoing total internal reflection along the outer sidewall, with the field being radially confined. This primarily results in standing waves forming in the angular direction. The angular mode number m represents the number of wavelengths around the circumference and corresponds to the order of the Bessel function. 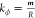The angular phase transition translates into an angular wave vector , representing the propagation constant in the circumferential direction. In the radial direction, only one node exists, corresponding to the first zero of this type of Bessel function. The radial wave vector 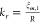. The wave function of the WGM can be expressed as

3

The angular wave vector 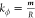also satisfies 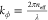as a propagating constant. For integer m, it satisfies 2Rn_eff = mλ, and the FSR of the WGMs is expressed as

4

As for the grating integrated ring, when the microring size is relatively large (i.e., the curvature is much larger than the grating period, with the number of grating elements around the microring exceeding 50,^28,34 the coupled mode theory (CMT) for grating structure can be used to simplify the calculation on how the grating parameter influence the GMR mode. However, it is necessary to quantitatively evaluate and compensate for the bending loss for diffraction waves propagating on the grating. For the microring and grating, the bending loss coefficient of a curved waveguide can be simplified and evaluated by α = A e^(−B/R),⁴⁰ where A and B depend on the material properties. The wavelength of the GMR considering the bending loss is expressed as

5

For the grating-integrated microring laser, the grating period Λ is 351.38 nm (determined by the number of grating elements M). The grating duty cycle σ is 0.25, with a grating depth d_g of 80 nm, and the ring size parameters are the same as those of the previously simulated microring model.

Figure 1G shows the reflectance of the inner sidewall of the microring, which peaks at a wavelength of 587.92 nm. Figure 1H shows the intensity distribution in the xy-plane at peak wavelength in Figure 1 G. The fundamental radial mode appears at 587.79 nm, as shown in Figure 1I. The mode profile is similar to that of the microring without a grating, but the wavelength with the highest reflection is shifted due to the influence of the gratings, comparing Figure 1C and G. When n_eff is simplified by the refractive index of the Si₃N₄ waveguide, λ_GMR can be roughly estimated to be 587.78 nm as the bending loss coefficient α ≈ 0.18 for Si₃N₄ waveguide in a π rad bending.⁴¹ The estimation result is similar to the simulation results in Figure 1I.

This demonstrates that the secondary spherical wave interference of azimuthal gratings can be simplified to GMR on a curved grating and that grating-integrated microring lasers form the underlying radial mode at λ_GMR. At this wavelength, the curved grating achieves the highest reflectivity, consistent with the wavelength of the radial mode in Figure 1I. Under this condition, the radial mode due to guided wave resonance from the grating is called the radial-guided mode.

Additionally, WGMs also formed in the grating-integrated microring, as shown in Figure 1J. The WGM can be described by the wave function:

6

The grating azimuthal mode number m equals the number of grating elements M, ensuring that there is no phase shift between the WGM standing wave propagating in the angular direction and the grating. The scattered field forms a concentric circle pattern, with all standing-wave peaks confined within the grating elements, minimizing scattering loss due to phase shifts. Consequently, the WGM mode with m = M has the highest quality factor.^17,18 Additionally, the mode profile in the yz-plane, highlighted in orange in Figure 1(F,I), indicates that the WGM is formed through total internal reflection along the outer side of the ring, rather than alternating reflections at the inner and outer sidewalls. The intensity of the mode is stronger on the outer side of the ring, while only an evanescent field is present on the inner side. In this study, a smaller ring width can effectively suppress higher-order modes because it is difficult to form standing waves in the radial direction inside the microring. The details of the formula derivations are provided in the “Theoretical Details on Mode Generation Mechanism” section in the Supporting Information, along with a simulation of the OAM carried by the WGM, which is included in Figure S1.

Come back to the experiment results of spectra of active cladding microring (without grating) in Figure 1A. Referring to eq 4, the FSR (Δλ) for the WGM is 1.13 nm where n_eff is calculated with n₁ for estimation. The theoretical FSR value for the WGM is in close agreement with the measured value of 1.15 nm in Figure 1A. By contrast, referring to eq 2, the FSR value of a fundamental radial mode is 1.78 nm. where n_eff is calculated with n₂ for estimation. The theoretical value of the FSR for such a radial mode is in close agreement with the measured value of 1.72 nm in Figure 1A. Meanwhile, the fundamental radial modes with solutions of J_0,1(k_rR) = 0 in the range of 583 to 595 nm is 583.74, 587.64, and 591.6 nm for J₀(k_rR) = 0, and 585.69, 589.61, 593.59 nm for J₁(k_rR) = 0. The experimental results corroborate our discussion of radial modes in the simulation section. Even modes described by zero-order Bessel functions have higher intensity, while odd modes described by first-order Bessel functions have slightly weaker intensity. Higher-order radial modes may also appear but are weaker due to a smaller Q-factor. The schematic of the mode profile of radial modes and WGMs is shown in Figure 1B, where radial modes, benefiting from gain, generally exhibit higher intensity. Thus, spectral analysis typically distinguishes WGMs by smaller FSRs and lower intensities (blue dots), while modes with larger FSRs and higher intensities are radial modes (magenta triangles).

For the gain range determined by the active material (pyrromethene 597) between 580 and 610 nm, if analyzed purely according to resonance, multiradial modes and multi-WGMs should be uniformly distributed across the entire range according to the FSR. However, in the experimental spectrum result in Figure 1A, the wavelengths of the radial modes appear in a shorter range. We attribute this to the consideration of reabsorption effects. As the radial modes experience preferential gain at the shorter wavelength due to gain saturation effects, higher energy photons are more likely to induce saturation.

In conclusion, the coexistence of radial-guided modes and WGMs in active cladding microring lasers has been demonstrated through photoluminescence experiments and 3D frequency-domain simulations. In the following section, we discuss the results of grating-integrated microrings with varying parameters to explore mode control in these structures.

3. Control of the Mode in a Grating-Integrated Microring

After confirming the possibility of the coexistence of the radial modes and WGMs in an active cladding microring laser, we explored whether the gratings period, grating depth, and ring size influence the modes experimentally. Grating modifications are determined by the period Λ and are further influenced by its depth d_g. The duty cycle σ that is defined as the ratio of the grating peak (l_g) to the entire period Λ, and the ring radius is R. The grating was meticulously designed to ensure that the guided mode resonance (λ_GMR) was within the central emission range (580–600 nm) of the active material. The duty cycle σ was fixed at 0.2. Scanning electron micrography images of the grating-integrated microring laser are shown in Figure 2A,B). These images highlight the structural details of the gratings postfabrication. It should be noted that some polymer residues are visible due to the cladding removal process after spin-coating, which does not affect the integrity of the grating structure. Figure 2c exhibits a schematic of the active cladding azimuthal grating integrated microring mode distribution profile for inferred from simulation theory, where the radial guided mode is formed due to the grating’s GMR and oscillates in the central region of the microring, while the WGMs oscillate within the microring cavity.

Figure 2.

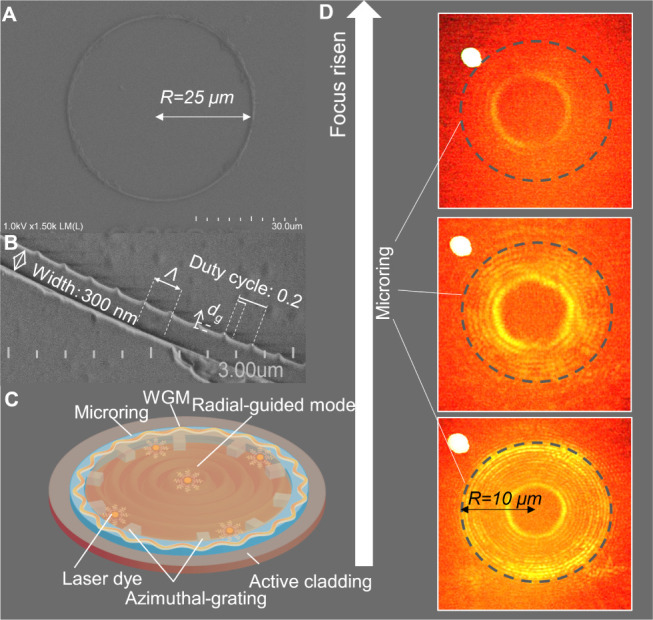
Effect of the grating. (A, B) SEM image of the grating-integrated microring with R = 25 μm: (A) total image of microring, and (B) the grating structure with depth d_g = −85 nm, period Λ = 294.16 nm, and duty cycle σ = 0.2. (C) Schematic of the effect of the grating on the radial waveguide mode and the WGM. (D) Excitation image with R = 10 μm and d_g = −25 nm with focus risen in z-axis.

Excitation images of the active cladding grating integrated microring with R = 10 μm and d_g = −25 nm with microscope focus plane risen in z-axis are shown in Figure 2D. The white spots in the upper left of the images are due to damage to the camera, which does not affect the sample light field. The simulation results indicate that for an R = 5 μm microring, the fundamental radial-guided mode can be accurately described by a zero-order Bessel beam. However, due to practical issues such as grating and microring fabrication errors, increased microring dimensions, nonuniform spin-coating of the active layer, and dye fluorescence instability, higher-order radial modes are eventually excited in an R = 10 μm microring. These modes manifest as stable concentric rings within the microring, with the innermost ring exhibiting the highest intensity. The axial extent of the beam changes with energy concentration shifting from various rings to the central region, creating an optical singularity with zero intensity. As the focal plane rises, the charge-coupled device camera can continuously capture this inner ring. Although these modes extend and attenuate along the z-axis, the inner ring maintains its intensity, resulting in a Gaussian intensity distribution in the axial plane (excluding the central region, where interference from higher-order azimuthal modes creates a singularity). The sustained energy of the central ring indicates that, despite some diffusion due to material reabsorption, the beam excited by the radial- guide mode retains the nondiffracting and conical propagation characteristics of a Bessel beam.⁴² These excitation images confirm that GMR can produce integrable Bessel beams within the microring size, although controlling the azimuthal order remains a challenge.

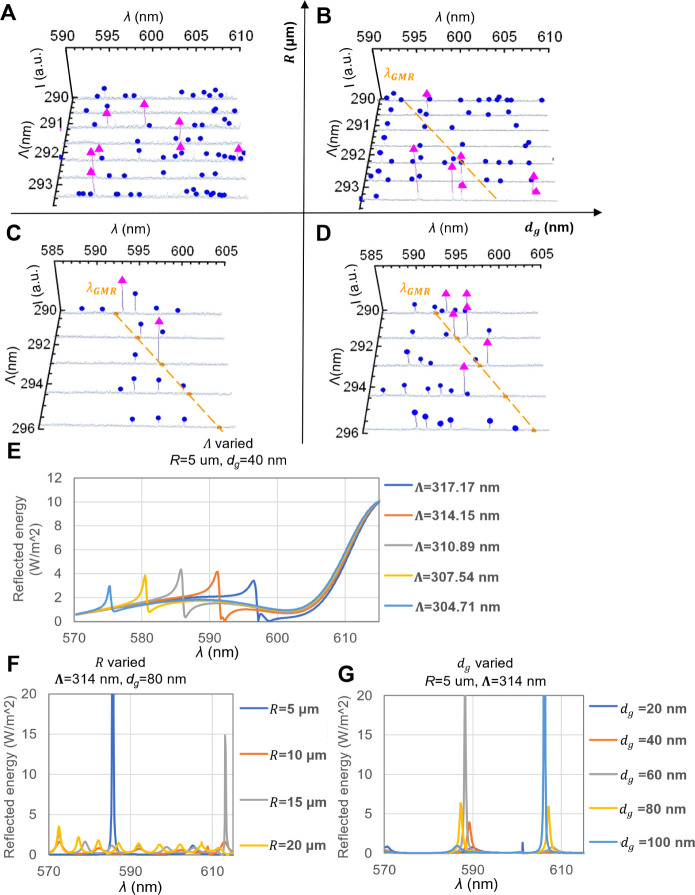
To examine the typical behavior of WGMs and radial-guided modes under different structural parameters—specifically, grating period, grating depth, and microring radius— we conducted photoluminescence excitation experiments to measure the spectra, and the results are shown in Figure 3A–D. Furthermore, 2D simulations were also employed. In this 2D model, which does not account for thickness, all dimensional parameters, except the variables of interest, are identical to those in the 3D model. The y-axis in simulation results, which depict the reflected energy at the inner wall versus wavelength that indicates the GMR wavelength, are shown in Figure 3E,F, with the grating period Λ, microring radius R, and grating depth d_g as the scanning parameters.

Figure 3.

(A)–(D) Spectra of grating-integrated microring lasers: (A) R = 40 μm, d_g = −25 nm; (B) R = 40 μm, d_g = −85 nm; (C) R = 10 μm, d_g = −25 nm; (D) R = 10 μm, d_g = −85 nm. Radial modes: magenta triangles; WGMs: blue dots; λ_GMR: orange dashed lines. (E)–(G) Simulation results on radial guide mode with different parameters: (E) Λ varied, R = 5 μm, d_g = 40 nm, (F) R varied, Λ = 314 nm, d_g = 80 nm, and (G) d_g varied, R = 5 μm, Λ = 314 nm.

Figure 3A–D show the spectral results for different grating periods Λ, where the x-axis is λ, the y-axis is Λ, and the z-axis is the mode intensities. Each plot has a different combination of R and d_g. We attribute the stronger modes to radial modes, labeled with magenta triangles, and the less intense modes with FSRs that meet the theoretical value of Δλ_WGM to the WGMs, labeled with blue distant points. The λ_GMR labeled with an orange dash line is calculated with eq 5, the bending loss coefficient is roughly estimated by 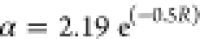. Figure 3E shows the reflected energy at the inner wall with Λ varied. It shows a clear dependence of the radial-guidedmode wavelength on Λ, confirming eq 5, which predicts oscillations of the radial-guided mode at the λ_GMRFigure 3F shows the results with R varied. Figure 3G shows the results with d_g varied.

In configurations with a large R and either a small or large d_g (Figure 3A,B), radial modes and WGMs tend to oscillate independently. With a small d_g, this independence results in isolated mode behavior without observable coupling, leading to the presence of higher-order radial modes that do not depend on λ_GMR. Conversely, with a large d_g, enhanced grating diffraction strongly influences the radial modes under intense GMR conditions, causing mode wavelengths to show a certain dependence on λ_GMR due to the strong feedback. This can be discussed with the simulation results shown in Figure 3G, where d_g is varied. At a d_g = 20 nm (the dark blue line), the radial-guided mode exhibits a single peak at the λ_GMR. However, as d_g increases, a stopband centered around the λ_GMR forms, with radial modes oscillating on the side of the stopband. This phenomenon can be explained by the CMT of grating structure.²⁷ When light propagates along the direction of the grating distribution under Bragg conditions, coherent interference between reflected and incident light waves results in a strong interference effect. Due to the same phase change of reflected and incident light, this interference effect leads to strong reflection over a certain wavelength range, preventing GMR and forming a bandgap centered around λ_GMR. The feedback coefficient K describes the strength of coupling within the grating, quantifying the ability of the grating to couple forward and backward propagating waves. Specifically, K is mainly determined by the d_g, and can be expressed in⁴³

7

A larger d_g leads to a greater feedback coefficient, which enhances the grating’s modulation effect, causing the spectra to show a stronger dependence on λ_GMR.

Furthermore, when R is small and d_g is large (Figure 3D, fundamental radial-guided modes appear along λ_GMR, but WGMs are not significantly affected by these changes. When both R and d_g were large (Figure 3B), enhanced grating diffraction strongly influenced the radial modes under intense GMR conditions. Even higher-order radial-guided modes emerge, with their wavelengths showing some dependence on λ_GMR due to the strong feedback coefficient. This is evident in the simulation results in Figure 3F. As R increased from 5 to 20 μm, the number of GMR wavelengths in the range of 570 to 610 nm increased from 1 to 9, indicating the generation of higher-order angular radial modes. Both experimental and simulation results show that as R increases, the angular order of radial-guided modes also increases, supporting the energy distribution within the larger structure and leading to the emergence of higher-order angular modes and mode competition within the gain spectrum.

Conversely, with small values for both R and d_g (Figure 3C), the spectrum is dominated by WGMs. The azimuthal phase match of the grating-element position allows specific WGMs to be selected, as described in previous studies.^17,18 An optimal Q factor was achieved only when the WGM azimuthal mode order m matched the grating-element number M. For a WGM with a refractive index of 2.04, a wavelength of 596 nm, and a ring radius of 10 μm, the theoretical m is 214. However, since n_eff is affected by scattering, the practical m for wavelengths around 596 nm should be less than the theoretical value. This is evidenced by only two modes being observed in the excitation spectra for devices with grating periods between 291 and 293 nm, indicating that the grating’s influence on the evanescent field affects the mode Q-factor, enabling the selection of azimuthal modes closest to M from multimode competition. Additionally, the scattered light field of the WGM corresponds to a radial mode described by the first-order Bessel function, allowing strong coupling with the first-order fundamental radial mode due to similar intensity profiles. Concurrently, the radial-guided mode is modulated by the grating and resonates at λ_GMR, resulting in strong coupling and quasi-single-mode emission at 596 nm near λ_GMR.

In summary, precise control over radial-guiding modes and WGMs, including their coupling, is achievable at specific grating periods, particularly in smaller microring and larger grating depth configurations.

4. Conclusions

This study demonstrates the coexistence of WGMs and radial-guided modes within a grating-integrated microring laser with active cladding. Utilizing a Si₃N₄ microring structure incorporating an organic active layer, we observed that the fluorescence from the active layer was reflected and guided by the microring, forming cylindrical waves with both radial and angular propagation, leading to the coexistence of WGMs and radial-guided modes. Both experimental and simulation results confirm radial-guided mode lasing at the GMR wavelength, which is determined by the grating period. Additionally, the grating depth and ring radius influence the grating’s modulation effect on the radial-guided mode. The WGM can be effectively controlled with a well-designed period, particularly when the number of grating elements M closely matches the azimuthal mode order m.

This study explores the various modes that occur when integrating azimuthal gratings on microrings—commonly used in OAM-emitters—and their generation mechanisms, as well as methods for controlling these modes. The findings highlight the potential for fabricating innovative hybrid light sources for applications in laser displays, biosensor networks, and tunable multi-OAM emitters. Current challenges such as dye degradation in the active cladding and variable cladding thickness limit precise wavelength control and accurate single-mode emission. Future work will focus on breaking the symmetry of the cavity to achieve chiral OAM emission and improving the stability and uniformity of the active cladding.

Data Availability Statement

The data is available from the corresponding author upon reasonable request.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsphotonics.4c00956.

• Theoretical details on the mode generation mechanism, simulation results of the OAM carried by the WGM, the sample fabrication process, and the experimental details (PDF)

Author Contributions

H.Y. contributed to conceptualization. A.A., A.E., A.S., C.S., Y.Y., and H.Y. contributed to methodology. J.C. and A.N. contributed to investigation. Y.O. contributed to theoretical discussion. N.T., H.T., and Y.M. contributed to formal analysis. J.C. contributed to visualization. H.Y. contributed to supervision. J.C. contributed to writing—original draft. All authors contributed to writing—review and editing.

This study was funded by JST-CREST grant JPMJCR20T4, Grant-in-Aid for Scientific Research JP19KK0379, JST-SPRING grant JPMJSP2136, Ministry for Culture and Science of North Rhine-Westphalia grant 421-8.03.03.02-130428 (CS), and European Union (HORIZON EUROPE Marie Sklodowska-Curie Actions) grant 101064466.

The authors declare no competing financial interest.