Abstract
In this paper, we present a semi-supervised deep learning approach to accurately recover high-resolution (HR) CT images from low-resolution (LR) counterparts. Specifically, with the generative adversarial network (GAN) as the building block, we enforce the cycle-consistency in terms of the Wasserstein distance to establish a nonlinear end-to-end mapping from noisy LR input images to denoised and deblurred HR outputs. We also include the joint constraints in the loss function to facilitate structural preservation. In this process, we incorporate deep convolutional neural network (CNN), residual learning, and network in network techniques for feature extraction and restoration. In contrast to the current trend of increasing network depth and complexity to boost the imaging performance, we apply a parallel 1 × 1 CNN to compress the output of the hidden layer and optimize the number of layers and the number of filters for each convolutional layer. The quantitative and qualitative evaluative results demonstrate that our proposed model is accurate, efficient and robust for super-resolution (SR) image restoration from noisy LR input images. In particular, we validate our composite SR networks on three large-scale CT datasets, and obtain promising results as compared to the other state-of-the-art methods.
Keywords: Computed tomography (CT), super-resolution, noise reduction, deep learning, adversarial learning, residual learning
I. INTRODUCTION
X-RAY computed tomography (CT) is one of the most popular medical imaging methods for screening, diagnosis, and image-guided intervention [1]. Potentially, high-resolution (HR) CT (HRCT) imaging may enhance the fidelity of radiomic features as well. Therefore, super-resolution (SR) methods in the CT field are receiving a major attention [2]. The image resolution of a CT imaging system is constrained by x-ray focal spot size, detector element pitch, reconstruction algorithms, and other factors. While physiological and pathological units in human bodies are on an order of 10 microns, the in-plane and through-plane resolution of clinical CT systems are on an order of submillimeter or 1 mm [2]. Even though the modern CT imaging and visualization software can generate any small voxels, the intrinsic resolution is still far lower than what is ideal in important applications such as early tumor characterization and coronary artery analysis [3]. Consequently, producing HRCT images at a minimum radiation dose level is highly desirable in the CT field.
In general, there are two strategies for improving CT image resolution: (1) hardware-oriented and (2) computational. First, more sophisticated hardware components can be used, including an x-ray tube with a fine focal spot size, detector elements of small pitch, and better mechanical precision for CT scanning. These hardware-oriented methods are generally expensive, increase CT system costs and radiation dose, and compromise imaging speeds. Especially, it is well known that high radiation dosage in a patient could induce genetic damages and cancerous diseases [4]–[6]. As a result, the second type of methods for resolution improvement [7]–[11] is more attractive, which is to obtain HRCT images from LRCT images. This computational deblurring job is a major challenge, representing a seriously ill-posed inverse problem [2], [12]. Our neural network approach proposed in this paper is computational, utilizing advanced network architectures. More details are as follows.
To improve the signal-to-noise ratio and image resolution, various algorithms were proposed. These algorithms can be broadly categorized into the following classes: (1) Model-based reconstruction methods [13]–[17]: These techniques explicitly model the image degradation process and regularize the reconstruction according to the characteristics of projection data. These algorithms promise an optimal image quality under the assumption that model-based priors can be effectively imposed; and (2) Learning-based (before deep learning) SR methods [18]–[20]: These methods learn a nonlinear mapping from a training dataset consisting of paired LR and HR images to recover missing high-frequency details. Especially, sparse representation-based approaches have attracted an increasing interest since it exhibits strong robustness in preserving image features, suppressing noise and artifacts. Dong et al. [20] applied adaptive sparse domain selection and adaptive regularization to obtain excellent SR results in terms of both visual perceptions and PSNR. Zhang et al. [19] proposed a patch-based technique for SR enhancements of 4D-CT images. These results demonstrate that learning-based SR methods can greatly enhance overall image quality but outcomes may still lose image subtleties and yield blocky appearance.
Recently, deep learning (DL) has been instrumental for computer vision tasks [21], [22]. Hierarchical features and representations derived from a convolutional neural network (CNN) are leveraged to enhance the discriminative capacity of visual quality, thus people have started developing SR models for natural images [23]–[27]. The key to the success of DL-based methods is its independence from explicit imaging models and backup by big domain-specific data. The image quality is optimized by learning features in an end-to-end manner. More importantly, once a CNN-based SR model is trained, achieving SR is a purely feed-forward propagation, which demands a very low computational overhead.
In the medical imaging field, DL is an emerging approach which has exhibited a great potential [28]–[30]. For several imaging modalities, DL-based SR methods were successfully developed [31]–[38]. Chen et al. [31] proposed a deep densely connected super-resolution network to reconstruct HR brain magnetic resonance (MR) images. More recently, Yu et al. [32] developed two advanced CNN-based models with a skip connection to promote high-frequency textures which are then fused with up-sampled images to produce SR images.
Very recently, adversarial learning [39], [40] has become increasingly popular, which enables CNNs to learn feature representations from complex data distributions, with unprecedented successes. Adversarial learning is performed based on a generative adversarial network (GAN), defined as a mini-max game in which two competing players are a generator and a discriminator . In the game, is trained to learn a mapping from source images in a source domain to target images in the target domain . On the other hand, distinguishes the generated images and the target images with a binary label. Once well trained, GAN is able to model a high-dimensional distribution of target images. Wolterink et al. [41] proposed an unsupervised conditional GAN to optimize the nonlinear mapping, successfully enhancing the overall image quality. Also, Mardani et al. [38] adopted a Compressed Sensing (CS) based MRI reconstruction method into the GAN-based network termed GANCS to reconstruct high-quality MR images. Also, in order to ensure data consistency in the learned manifold domain, a least-square penalty was applied to the training process.
However, there are still several major limitations in the DL-based SR imaging. First, existing supervised DL-based algorithms cannot address blind SR tasks without LR-HR pairs. In clinical practice, a limited number of LR and HR CT image pairs makes the supervised learning methods impractical since it is infeasible to ask patients to take multiple CT scans with additional radiation doses for paired CT images. Thus, it is essential to resort to semi-supervised learning. Second, utilizing the adversarial strategy can push the generator to learn an inter-domain mapping and produce compelling target images [42] but there is a potential risk that the network may yield features that are not exhibited in target images due to the degeneracy of the mapping. Since the optimal is capable of translating to distributed identically to , the GAN network cannot ensure that the noisy input and predicted output are paired in a meaningful way - there exist many mappings that may yield the same distribution over . Consequently, the mapping is highly under-constrained. Furthermore, it is undesirable to optimize the adversarial objective in isolation: the model collapse problem may occur to map all inputs to the same output image [40], [43], [44]. To address this issue, Cycle-consistent GANs (cycleGAN) was designed to improve the performance of generic GAN, and utilized for SR imaging [27]. Third, other limitations of GANs were also pointed out in [45]–[48]. How to steer a GAN learning process is not easy since G may collapse into a narrow distribution which cannot represent diverse samples from a real data distribution. Also, there is no interpretable metric for training progress. Fourth, as the number of layers increases, deep neural networks can derive a hierarchy of increasingly more complex and more abstract features. Frequently, to improve the SR imaging capability of a network, complex networks are often tried with hundreds of millions of parameters. However, given the associated computational overheads, they are hard to use in real-world applications. Fifth, local feature parts in the CT image have different scales. This feature hierarchy can provide more information to reconstruct images, but most DL-based methods [24], [25] neglect to use hierarchical features. Finally, the distance between and is commonly used for the loss function to guide the training process of the network. However, the output optimized by the norm may suffer from over-smoothing as discussed in [49], [50], since the distance means to maximize the peak signal-to-noise rate (PSNR) [23].
Motivated by the aforementioned drawbacks, in this study we made major efforts in the following aspects. First, we present a novel residual CNN-based network in the CycleGAN framework to preserve high-resolution anatomical details with no task-specific regularization. Specially, we utilize the cycle-consistency constraint to enforce a strong across-domain consistency between and . Second, to address the training problem of GANs [40], [46], we use the Wasserstein distance or “Earth Moving” distance (EM distance) instead of the Jensen-Shannon (JS) divergence. Third, inspired by the recent work [51], we optimize the network according to several fundamental designing principles to alleviate computational overheads [52]–[54], which also helps prevent the network from over-fitting. Fourth, we cascade multiple layers to learn highly interpretable and disentangled hierarchical features. Moreover, we enable the information flow across skip-connected layers to prevent gradient vanishing [52]. Finally, we employ the norm instead of norm to refine deblurring, and we propose to use a jointly constrained total variation-based regularization as well, which leverages the prior information to reduce noise with a minimal loss in spatial resolution or anatomical information. Extensive experiments with three real datasets demonstrate that our proposed composite network can achieve an excellent CT SR imaging performance comparable to or better than that of the state-of-the-art methods [23]–[26], [55].
II. METHODS
Let us first review the SR problems in the medical imaging field. Then, we introduce the proposed adversarial nets framework and also present our SR imaging network architecture. Finally, we describe the optimization process.
A. Problem Statement
Let be an input LR image and a matrix an output HR image, the conventional formulation of the ill-posed linear SR problem [18] can be formulated as
| (1) |
where denote the down-sampling and blurring system matrices, and the noise and other factors. Note that in practice, both the system matrix and not-modeled factors can be non-linear, instead of being linear (i.e., neither scalable nor additive).
Our goal is to computationally improve noisy LRCT images obtained under a low-dose CT (LDCT) protocol to HRCT images. The main challenges in recovering HRCT images can be listed as follows. First, LRCT images contain different or more complex spatial variations, correlations and statistical properties than natural images, which limit the SR imaging performance of the traditional methods. Second, the noise in raw projection data is introduced to the image domain during the reconstruction process, resulting in unique noise and artifact patterns. This creates difficulties for algorithms to produce high image quality results. Finally, since the sampling and degradation operations are coupled and ill-posed, SR tasks cannot be performed beyond a marginal degree using the traditional methods, which cannot effectively restore some fine features and suffer from the risk of producing a blurry appearance and new artifacts. To address these limitations, here we develop an advanced neural network by composing a number of non-linear SR functional blocks for SR CT (SRCT) imaging along with the residual module to learn high-frequency details. Then, we perform adversarial learning in a cyclic manner to generate perceptually and quantitatively superior SRCT images.
B. Deep Cycle-Consistent Adversarial SRCT Model
1). Cycle-Consistent Adversarial Model:
Current DL-based algorithms use feed-forward CNNs to learn non-linear mappings parametrized by , which can be written as:
| (2) |
In order to obtain a decent , a suitable loss function must be specified to encourage to generate a SR image based on the training samples so that
| (3) |
where are paired LRCT and HRCT images for training. To address the limitations mentioned in II-A, our cyclic SRCT model is shown in Fig. 1. The proposed model includes two generative mappings and given training samples and . The two mappings and are jointly trained to produce synthesized images in a way that confuse the adversarial discriminators and respectively, which intend to identify whether the output of each generative mapping is real or artificial. i.e., given an LRCT image , attempts to generate a synthesized image highly similar to a real image so as to fool . In a similar way, attempts to discriminate between a reconstructed from and a real . The key idea is that the generators and discriminators are jointly/alternatively trained to improve their performance metrics synergistically. Thus, we have the following optimization problem:
| (4) |
Fig. 1.
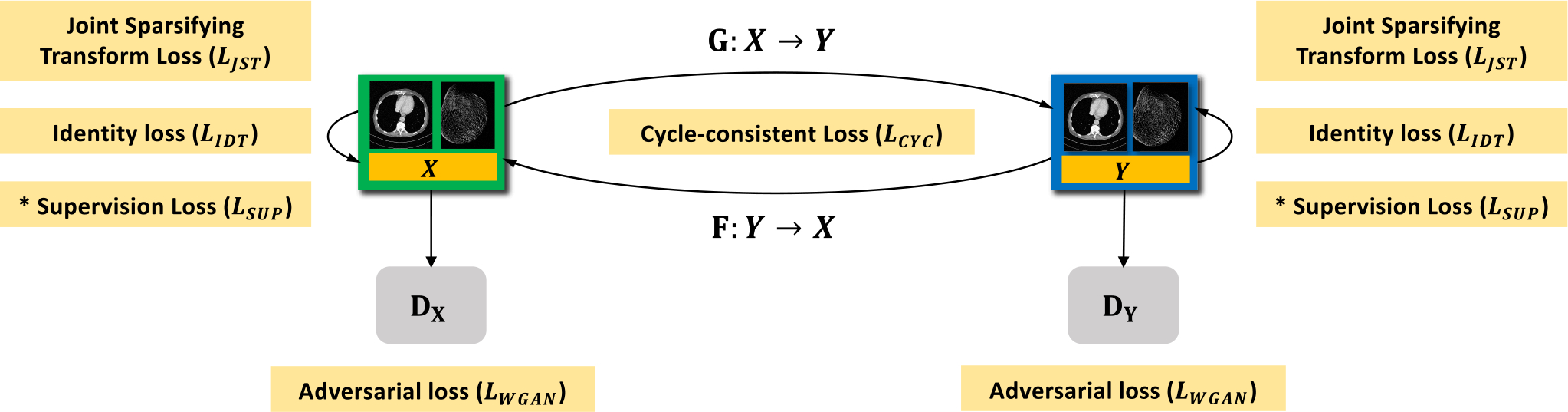
Proposed GAN framework for SR CT imaging. Our approach uses two generators and , and the corresponding adversarial discriminators and respectively, where denotes a LR CT image and is the HR CT counterpart. To regularize the training and deblurring processes, we utilize the generator-adversarial loss (adv), cycle-consistency loss (cyc), identity loss (idt), and joint sparsifying transform loss (jst) synergistically. In the supervised/semi-supervised mode, we also apply a supervision loss (sup) on and . For brevity, we denote and as and respectively. * denotes that the loss is only trained in the supervised fashion.
To enforce the mappings between the source and target domains and regularize the training procedure, our proposed network combines four types of loss functions: adversarial loss (adv); cycle-consistency loss (cyc); identity loss (idt); joint sparsifying transform loss (jst).
2). Adversarial Loss:
For marginal matching [39], we employ adversarial losses to urge the generated images to obey the empirical distributions in the source and target domains. To improve the training quality, we apply the Wasserstein distance with gradient penalty [56] instead of the negative log-likelihood used in [39]. Thus, we have the adversarial objective with respect to :
| (5) |
where denotes the expectation operator; the first two terms are in terms of the Wasserstein estimation, and the third term penalizes the deviation of the gradient norm of its input relative to one, is uniformly sampled along straight lines for pairs of and , and is a regularization parameter. A similar adversarial loss is defined for marginal matching in the reverse direction.
3). Cycle Consistency Loss:
Adversarial training is for marginal matching [39], [40]. However, in these earlier studies [43], [57], it was found that using adversarial losses alone cannot ensure the learned function can transform a source input successfully to a target output. To promote the consistency between and , the cycle-consistency loss can be express as:
| (6) |
where denotes the norm. Since the cycle consistency loss encourages and , they are referred to as forward cycle consistency and backward cycle consistency respectively. The domain adaptation mapping refers to the cycle-reconstruction mapping. In effect, it imposes shared-latent space constraints to encourage the source content to be preserved during the cycle-reconstruction mapping. In other words, the cycle consistency enforces latent codes deviating from the prior distribution in the cycle-reconstruction mapping. Additionally, the cycle consistency can help prevent the degeneracy in adversarial learning [58].
4). Identity Loss:
Since an HR image should be a refined version of the LR counterpart, it is necessary to use the identity loss to regularize the training procedure [43], [44]. Compared with the loss, the loss does not over-penalize large differences or tolerate small errors between estimated and target images. Thus, the loss is preferred to alleviate the limitations of the loss in this context. Additionally, the loss enjoys the same fast convergence speed as that of the loss. The loss is formulated as follows:
| (7) |
We follow the same training baseline as in [44]; i.e., in the bi-directional mapping, the size of (or ) is the same as that of (or ).
5). Joint Sparsifying Transform Loss:
The total variation (TV) has demonstrated the state-of-the-art performance in promoting image sparsity and reducing noise in piecewise-constant images [59], [60]. To express image sparsity, we formulate a nonlinear TV-based loss with the joint constraints as follows:
| (8) |
where is a scaling factor. Intuitively, the above constrained minimization combines two components: the first component is used for sparsifying reconstructed images and alleviating conspicuous artifacts, and the second helps preserve anatomical characteristics by minimizing the difference image . Essentially, these two components require a joint minimization under the bidirectional constraints. In this paper, the control parameter was set to 0.5. In the case of , the is regarded as the conventional TV loss.
6). Overall Objective Function:
In the training process, our proposed network is fine-tuned in an end-to-end manner to minimize the following overall objective function:
| (9) |
where , and are parameters for balancing among different penalties. We call this modified cycleGAN as the GAN-CIRCLE as summarized in the title of this paper.
7). Supervised Learning With GAN-CIRCLE:
In the case where we have access to paired dataset, we can render SRCT problems to train our model in a supervised fashion. Given the training paired data from the true joint, i.e., , we can define a supervision loss as follows:
| (10) |
C. Network Architecture
Although more layers and larger model size usually result in the performance gain, for real application we designed a lightweight model to validate the effectiveness of GAN-CIRCLE. The full architecture and details of GAN-CIRCLE are provided in the supplementary material.
III. EXPERIMENTS AND RESULTS
We discuss our experiments in this section. We first introduce the datasets we utilize and then describe the implementation details and parameter settings in our proposed methods. We also compare our proposed algorithms with the state-of-the-art SR methods quantitatively and qualitatively. We further evaluate our results in reference to the state-of-the-art, and demonstrate the robustness of our methods in the real SR scenarios. Then, we present the detailed diagnostic quality assessments from expert radiologists. Next, we progressively modify some of key elements to investigate the best trade-off between performance and speed, and evaluate the relations between performance and parameters. Finally, we further illustrate the effect of the filter size, of the number of layers, and of the training patch size with respect to the training and testing datasets. Note that we use the default parameters of all the evaluated methods. The source code is released at https://github.com/charlesyou999648/GAN-CIRCLE.
A. Training Datasets
In this study, we used two high-quality sets of training images to demonstrate the fidelity and robustness of the proposed GAN-CIRCLE. As shown in Figs. 2–5, these two datasets are of very different characteristics. Note the descriptions of detailed data preprocessing are provided in the supplementary material.
Fig. 2.
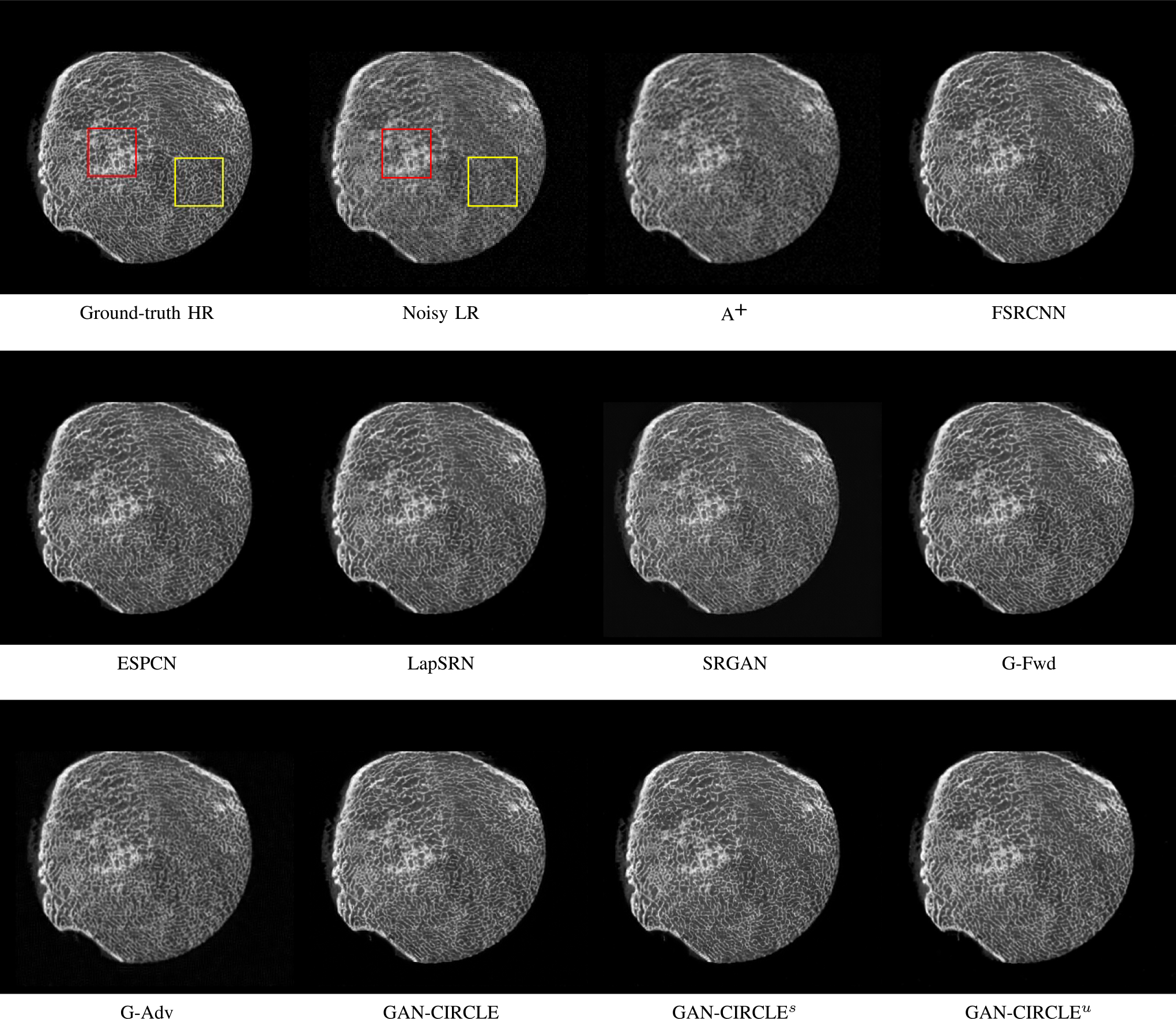
Visual comparison of SRCT Case 1 from the Tibia dataset. The restored bony structures are shown in the red and yellow boxes in Fig. 3. The display window is [−900, 2000] HU.
Fig. 5.

Visual comparison of SRCT Case 2 from the abdominal dataset. The display window is [−160, 240] HU. The restored anatomical features are shown in the red and yellow boxes. (Zoomed for visual clarity).
1). Tibia Dataset:
This micro-CT image dataset reflects twenty-five fresh-frozen cadaveric ankle specimens which were removed at mid-tibia from 17 body donors (mean age at death ± SD: 79.6 ± 13.2 Y; 9 female). After the soft tissue were removed and the tibia was dislocated from the ankle joint, each specimen was scanned on a Siemens microCAT II (Preclinical Solutions, Knoxville, TN, USA) in the cone beam imaging geometry. The micro-CT parameters are briefly summarized as follows: a tube voltage 100 kV, a tube current 200 mAs, 720 projections over a range of 220 degrees, an exposure time of 1.0 sec per projection, and the filter backprojection (FBP) method was utilized to produce 28.8 μm isotropic voxels. Since CT images are not isotropic in each direction, for convenience of our previous analysis [61], we convert micro-CT images to 150 μm using a windowed sync interpolation method. In this study, the micro-CT images we utilized as HR images were prepared at 150 μm voxel size, as the target for SR imaging based of the corresponding LR images at 300 μm voxel size. The full description is in [61]. We target 1X resolution improvement.
2). Abdominal Dataset:
This clinical dataset is authorized by Mayo Clinic for 2016 NIH-AAPM-Mayo Clinic Low Dose CT Grand Challenge. The dataset contains 5, 936 full dose CT images from 10 patients with the reconstruction interval and slice thickness of 0.8 mm and 1.0 mm respectively. The original CT images were generated by multidetector row CT (MDCT) with the image size of 512 × 512. The projection data is from 2, 304 views per scan. The HR images, with voxel size 0.74 × 0.74 × 0.80 mm3, were reconstructed using the FBP method from all 2, 304 projection views. More detailed information of the dataset is given in [62].
B. Performance Comparison
In this study, we compared the proposed GAN-CIRCLE with the state-of-the-art methods: adjusted anchored neighborhood regression A+ [55], FSRCNN [24], ESPCN [26], LapSRN [25], and SRGAN [23]. For clarity, we categorized the methods into the following classes: the interpolation-based, dictionary-based, PSNR-oriented, and GAN-based methods. Especially, we trained the publicly available FSRCNN, ESPCN, LapSRN, and SRGAN with our paired LR and HR images. To demonstrate the effectiveness of the DL-based methods, we first denoised the input LR images and then super-resolved the denoised CT image using the typical method A+. BM3D [63] is one of the classic image domain denoising algorithms, which is efficient and powerful. Thus, we preprocessed the noisy LRCT images with BMD3, and then super-solved the denoised images by A+.
We evaluated three variations of the proposed method: (1) G-Forward (G-Fwd), which is the forward generator of GAN-CIRCLE, (2) G-Adversarial (G-Adv), which uses the adversarial learning strategy, and (3) the full-fledged GAN-CIRCLE. To emphasize the effectiveness of the GAN-CIRCLE structure, we first trained the three models using the supervised learning strategy, and then trained our proposed GAN-CIRCLE in the semi-supervised scenario (GAN-CIRCLEs), and finally implement GAN-CIRCLE in the unsupervised manner (GAN-CIRCLEu). In the semi-supervised settings, two datasets were created separately by randomly splitting the dataset into the paired and unpaired dataset with respect to three variants: 100%, 50%, and 0% paired. To better evaluate the performance of each method, we use the same size of the dataset for training and testing.
We validated the SR performance in terms of three widely-used image quality metrics: Peak signal-to-noise ratio (PSNR), Structural Similarity (SSIM) [64], and Information Fidelity Criterion (IFC) [65]. Through extensive experiments, we compared all the above-mentioned methods on the two benchmark datasets described in Section III-A. Due to the space limit, we present network architecture details, and the implementation details are presented in the supplementary material.
C. Experimental Results With the Tibia Dataset
We evaluated the proposed algorithms against the state-of-the-art algorithms on the tibia dataset. We present typical results in Fig. 2. It can be seen that our proposed GAN-CIRCLE recovers more fine subtle details and captures more anatomical information in Fig. 3. It is worth mentioning that Fig. 2 shows that there are severe distortions of the original images but SRGAN generates compelling results in Figs. 5–8, which indicate VGG network is a task-specific network which can generate images with excellent image quality. We argue that the possible reason is that the VGG network [66] is a pre-trained CNN-based network based on natural images with structural characteristic correlated with the content of medical images [67]. Fig. 3 shows that the proposed GAN-CIRCLEs can predict images with sharper boundaries and richer textures than GAN-CIRCLEu which learns additional anatomical information from the unpaired samples. The difference images are shown in the Figs. 4. The difference images were generated by subtracting the generated image from the reference image. We compared our method with adjusted anchored neighborhood regression A+ [55], FSRCNN [24], ESPCN [26], LapSRN [25], SRGAN [23], G-Forward (G-Fwd), G-Adversarial (G-Adv). The quantitative results are in Table I. The results demonstrate that the G-Forward achieves the highest scores using the evaluation metrics, PSNR and SSIM, which outperforms all other methods. However, it has been pointed out in [68], [69] that high PSNR and SSIM values cannot guarantee a visually favorable result. Non-GAN based methods (FSRCNN, ESPCN, LapSRN) may fail to recover some fine structure for diagnostic evaluation, such as shown by zoomed boxes in Fig. 3. Quantitatively, GAN-CIRCLE achieves the second best values in terms of SSIM and IFC. It has been pointed out in [70] that IFC value is correlated well with the human perception of SR images. Our GAN-CIRCLEs obtained comparable results qualitatively and quantitatively. Table I shows that the proposed semi-supervised method performs similarly compared to the fully supervised methods on the tibia dataset. In general, our proposed GAN-CIRCLE can generate more pleasant results with sharper image contents.
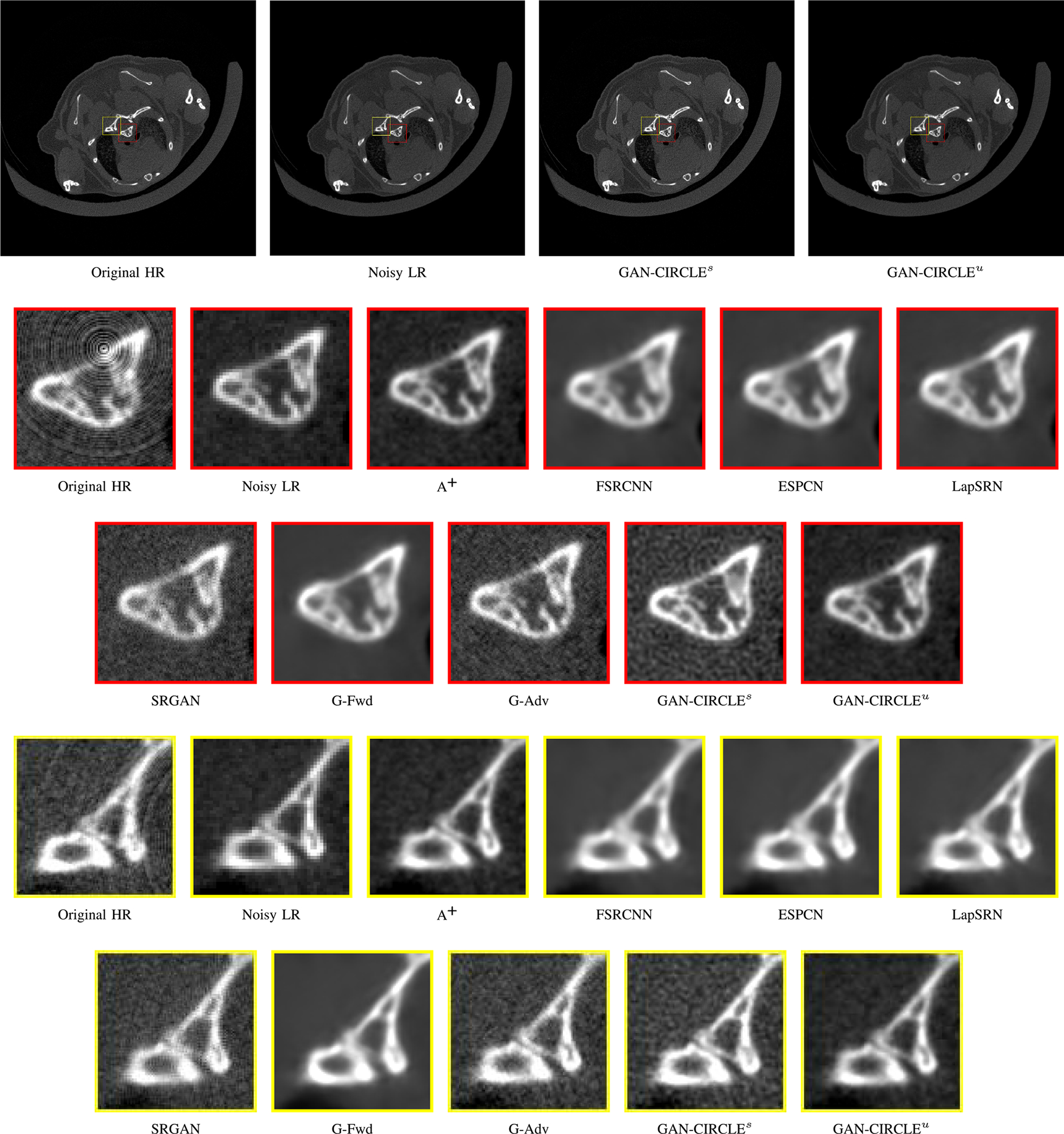
Fig. 3.

Zoomed regions of interest (ROIs) marked by the red rectangle in Fig. 2. The restored image with GAN-CIRCLE reveals subtle structures better than the other variations of the proposed neural network, especially in the marked regions. The display window is [−900, 2000] HU.
Fig. 8.
Visual comparison of SRCT Case 4 from the real dataset. The display window is [139, 1913] HU. The restored bony structures are shown in the red and yellow boxes. (Zoomed for visual clarity).
Fig. 4.

Absolute difference images relative to the original HR image from the Tibia dataset. The display window is [0, 900] HU.
TABLE I.
Quantitative Evaluation of State-of-the-Art SR Algorithms. Red and Blue Indicate the Best and the Second Best Performance, Respectively
| Tibia Case | Abdominal Case | Real Case 1 | Real Case 2 | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PSNR | SSIM | IFC | PSNR | SSIM | IFC | PSNR | SSIM | IFC | PSNR | SSIM | IFC | |
|
|
|
|
|
|||||||||
| A+ | 26.496 | 0.696 | 3.028 | 28.154 | 0.589 | 1.899 | 27.877 | 0.804 | 0.249 | 27.037 | 0.778 | 0.236 |
| FSRCNN | 28.360 | 0.923 | 3.533 | 30.950 | 0.924 | 2.285 | 35.384 | 0.830 | 0.265 | 33.643 | 0.805 | 0.237 |
| ESPCN | 28.361 | 0.921 | 3.520 | 30.507 | 0.923 | 2.252 | 35.378 | 0.830 | 0.278 | 33.689 | 0.805 | 0.245 |
| LapSRN | 28.486 | 0.923 | 3.533 | 30.985 | 0.925 | 2.299 | 35.372 | 0.830 | 0.277 | 33.711 | 0.805 | 0.244 |
| SRGAN | 21.924 | 0.389 | 1.620 | 28.550 | 0.871 | 1.925 | 33.002 | 0.737 | 0.232 | 31.775 | 0.701 | 0.220 |
| G-Fwd | 28.649 | 0.931 | 3.618 | 31.282 | 0.925 | 2.348 | 35.227 | 0.829 | 0.276 | 33.589 | 0.803 | 0.236 |
| G-Adv | 26.945 | 0.676 | 2.999 | 26.930 | 0.889 | 1.765 | 32.518 | 0.725 | 0.199 | 31.712 | 0.700 | 0.210 |
| GAN-CIRCLE | 27.742 | 0.895 | 3.944 | 30.720 | 0.924 | 2.435 | - | - | - | - | - | - |
| GAN-CIRCLEs | 28.402 | 0.907 | 3.943 | 29.988 | 0.902 | 2.367 | 33.194 | 0.829 | 0.285 | 31.252 | 0.804 | 0.245 |
| GAN-CIRCLEu | 27.255 | 0.891 | 2.713 | 28.439 | 0.894 | 2.019 | 32.138 | 0.824 | 0.283 | 30.641 | 0.796 | 0.232 |
D. Experimental Results on the Abdominal Dataset
We further compared the above-mentioned algorithms on the abdominal benchmark dataset. A similar trend can be observed on this dataset. Our proposed GAN-CIRCLE can preserve better anatomical informations and more clearly visualize the portal vein as shown in Fig. 5. These results demonstrate that PSNR-oriented methods (FSRCNN, ESPCN, LapSRN) can significantly suppress the noise and artifacts. However, it suffers from low image quality as judged by the human observer since it assumes that the impact of noise is independent of local image features, while the sensitivity of the Human Visual System (HVS) to noise depends on local contrast, intensity and structural variations. Fig. 5 displays the LRCT images processed by GAN-based methods (SRGAN, G-Adv, GAN-CIRCLE, GAN-CIRCLEs, and GAN-CIRCLEu) with improved structural identification. It can also observed that the GAN-based models also introduce strong noise into results. For example, there exist tiny artifacts on the results of GAN-CIRCLEu. As the SR results shown in Fig. 5, our proposed approaches (GAN-CIRCLE, GAN-CIRCLEs) are capable of retaining high-frequency details to reconstruct more realistic images with relatively lower noise compared with the other GAN-based methods (G-Adv, SRGAN). In the Figs. 6, we showed the difference images by subtracting the generated image from the reference image. We compared our method with adjusted anchored neighborhood regression A+ [55], FSRCNN [24], ESPCN [26], LapSRN [25], SRGAN [23], G-Forward (G-Fwd), G-Adversarial (G-Adv). Table I show that G-Fwd achieves the best performance in PSNR. Our proposed methods GAN-CIRCLE and GAN-CIRCLEs both obtain the pleasing results in terms of SSIM and IFC. In other words, the results show that the proposed GAN-CIRCLE and GAN-CIRCLEs generate more visually pleasant results with sharper edges on the abdominal dataset than the competing state-of-the-art methods.
Fig. 6.

Absolute difference images relative to the original HR image from the abdominal dataset. The display window is [100, 280] HU.
E. Super-Resolving Clinical Images
We analyzed the performance of the SR methods in the simulated SRCT scenarios in Sections III-C and III-D. These experimental results show that the DL-based methods are very effective in addressing the ill-posed SRCT problems with two significant features. First, SRCT aims at recovering a HRCT image from a LRCT images under a low-dose protocol. Second, most DL-based methods assume the paired LRCT images and HRCT images are matched, an assumption which is likely to be violated in clinical practice. In other words, the above-evaluated datasets were simulated, and thus the fully supervised algorithms can easily cope with SRCT tasks, with exactly matched training samples. Our further goal is to derive the semi-supervised scheme to handle unmatched/unpaired data with a relative lack of matched/paired data to address real SRCT tasks. In this subsection, we demonstrate a strong capability of the proposed methods in the real applications using a small amount of mismatched paired LRCT and HRCT images as well as a high flexibility of adapting to various noise distributions.
1). Practical SRCT Implementation Details:
We first obtained 3 LRCT and HRCT image pairs using a deceased mouse on the same scanner with two scanning protocols. The micro-CT parameters are as follows: X-ray source circular scanning, 60 kVp, 134 mAs, 720 projections over a range of 360 degrees, exposure 50 ms per projection, and the micro-CT images were reconstructed using the Feldkamp-Davis-Kress (FDK) algorithm [71] in practice: HRCT image size 1450 × 1450, 600 slices at 24 μm isotropic voxel size, and the LRCT image size 725 × 725, 300 slices at 48 μm isotropic voxel size. Then, we compared with the state-of-the-art super-resolution methods. Since the real data are unmatched, we accordingly evaluated our proposed GAN-CIRCLEs and GAN-CIRCLEu networks for 1X resolution improvement.
2). Comparison With the State-of-the-Art Methods:
The quantitative results were summarized for all the involved methods in Table I. The PSNR-oriented approaches, such as FSRCNN, ESPCN, LapSRN, and our G-Fwd, yield higher PSNR and SSIM values than the GAN-based methods. It is not surprising that the PSNR-oriented methods obtained favorable PSNR values since their goal is to minimize per-pixel distance to the ground truth. However, our GAN-CIRCLEs and GAN-CIRCLEu achieved the highest IFC among all the SR methods. Our method GAN-CIRCLEs obtained the second best results in term of SSIM. The visual comparisons are given in Figs. 7 and 8. To demonstrate the robustness of our methods, we examined anatomical features in the lung regions and the bone structures of the mice, as shown in Figs. 7 and 8 respectively. It is observed that the GAN-based approaches performed favorably over the PSNR-oriented methods in term of perceptual quality as illustrated in Figs. 7 and 8. Fig. 7 confirms that the PSNR-oriented methods produced blurry results especially in the lung regions, while the GAN-based methods restored anatomical contents satisfactorily. In Fig. 8, it is notable that our methods GAN-CIRCLEs and GAN-CIRCLEu performed better than the other methods in terms of recovering structural information and preserving edges. These SR results demonstrate that our proposed methods can provide better visualization of bone and lung microarchitecture with sharp edge and rich texture.
Fig. 7.
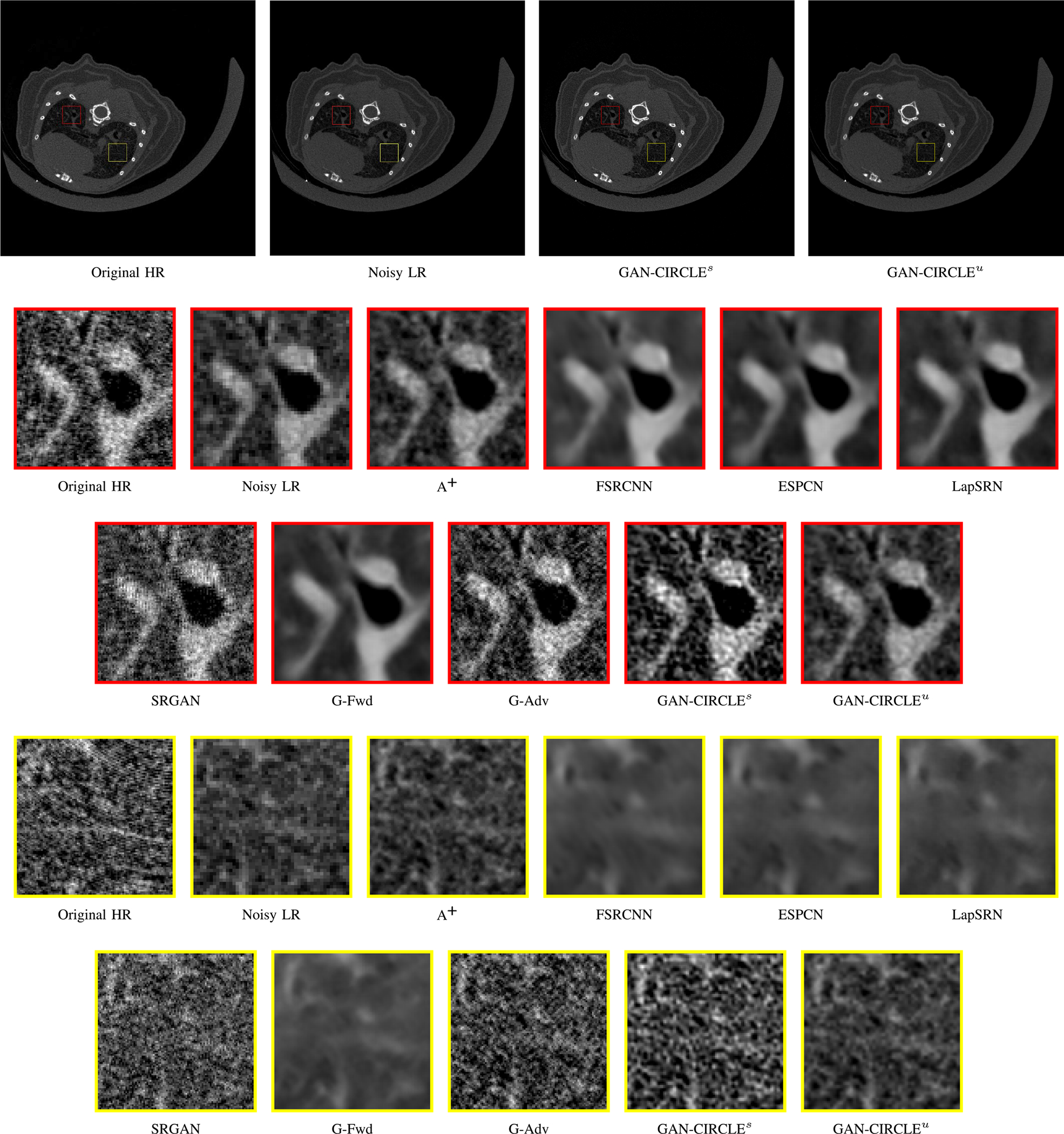
Visual comparison of SRCT Case 3 from the real dataset. The display window is [139, 1913] HU. The restored anatomical features are shown in the red and yellow boxes. (Zoomed for visual clarity).
F. Diagnostic Quality Assessment
We invited three board-certified radiologists with mean clinical CT experience of 12.3 years to perform independent qualitative image analysis on 10 sets of images from two benchmark dataset (Tibia and Abdominal Dataset). Each set includes the same image slice but generated using different methods. We label HRCT and LRCT images in each set as reference. The 10 sets of images from two datasets were randomized and deidentified so that the radiologists were blind to the post-processing algorithms. Image sharpness, image noise, contrast resolution, diagnostic acceptability, and overall image quality were graded on a scale from 1 (worst) to 5 (best). A score of 1 refers to a ‘non-diagnostic’ image, while a score of 5 means an ‘excellent’ diagnostic image quality. The mean scores with their standard deviation are presented in Table III. The radiologists confirmed that GAN-based methods (G-Adv, SRGAN, GAN-CIRCLE, GAN-CIRCLEs and GAN-CIRCLEu) provide sharper images with better texture details, while PSNR-oriented algorithms (FSRCNN, ESPCN, LapSRN, G-Fwd) give the higher noise suppression scores. Table III shows that our proposed GAN-CIRCLE and GAN-CIRCLEs achieve comparable results, while outperforming the other methods in terms of image sharpness, contrast resolution, diagnostic acceptability, and overall image quality.
TABLE III.
Diagnostic Quality Assessment in Terms of Subjective Quality Scores for Different Algorithms (Mean±Stds). Red and Blue Indicate the Best and the Second Best Performance, Respectively
| Tibia Dataset | Abdominal Dataset | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Image Sharpness | Image Noise | Contrast Resolution | Diagnostic Acceptance | Overall Quality | Image Sharpness | Image Noise | Contrast Resolution | Diagnostic Acceptance | Overall Quality | |
|
|
||||||||||
| A+ | 2.34±0.47 | 2.54±0.68 | 2.52±0.67 | 1.98±0.59 | 2.37±0.97 | 2.74±0.75 | 3.07±0.96 | 2.61±0.69 | 2.35±0.57 | 2.74±0.71 |
| FSRCNN | 2.85±0.94 | 3.16±0.57 | 2.54±0.96 | 2.77±0.69 | 3.27±0.76 | 3.07±0.89 | 3.55±0.50 | 2.94±0.78 | 2.92±0.58 | 3.09±0.53 |
| ESPCN | 2.82±0.86 | 3.18±0.51 | 2.58±0.46 | 2.95±0.46 | 3.49±0.66 | 2.95±1.43 | 3.39±0.80 | 2.85±0.63 | 2.76±0.83 | 3.06±0.85 |
| LapSRN | 2.91±0.88 | 3.49±0.70 | 2.69±0.56 | 3.01±0.78 | 3.63±0.61 | 3.01±0.56 | 3.58±0.81 | 2.83±0.71 | 3.25±0.92 | 3.11±0.78 |
| SRGAN | 1.94±0.37 | 2.71 ±0.23 | 1.91±0.71 | 1.75±0.83 | 1.93±1.01 | 3.35±0.97 | 3.23±1.01 | 3.27±0.92 | 3.46±1.11 | 3.41 ±0.94 |
| G-Fwd | 2.99±0.42 | 3.59±0.57 | 3.07±0.91 | 3.45 ±1.02 | 3.70±0.71 | 3.25±0.94 | 3.53±0.70 | 2.95±0.57 | 3.38±0.93 | 3.09±0.55 |
| G-Adv | 2.89±0.86 | 3.13Ü.02 | 3.02±0.58 | 3.29±0.69 | 3.62±0.67 | 3.45±1.12 | 3.34±0.81 | 3.31±0.86 | 3.48±0.77 | 3.32±0.82 |
| GAN-CIRCLE | 3.12±0.73 | 3.40±0.43 | 3.17Ì0.46 | 3.6Ü0.36 | 3.79±0.72 | 3.59±0.41 | 3.41 ±0.42 | 3.51 ±0.66 | 3.64±0.54 | 3.62±0.41 |
| GAN-CIRCLEs | 3.02±0.78 | 3.14±0.68 | 3.12±0.88 | 3.47±0.67 | 3.71±0.76 | 3.48±0.81 | 3.29±0.80 | 3.42±0.78 | 3.57±0.68 | 3.51 ±0.46 |
| GAN-CIRCLEu | 2.91±0.82 | 3.32±0.89 | 3.08±0.94 | 3.32±0.48 | 3.57±0.52 | 3.46±0.73 | 3.39±1.04 | 3.39±0.50 | 3.54±0.53 | 3.34±1.01 |
G. Model and Performance Trade-Offs
1). Filter Size:
Here we compared the GAN-CIRCLE network sensitivities with respect to different filter sizes. First, we fixed the filter size of the reconstruction network and enlarged the filter size of the feature extraction network to 5×5 and 7×7 respectively. Note that all the other settings remained the same as that in Supplementary Material Section I–B. The average PSNR with the filter size 3 × 3 is slightly higher than that with the filter size 5 × 5 and 7 × 7 shown in Fig. 9a. In general, the reasonably larger filter size could help capture larger structural features, leading to a performance gain [72]. In the case of the Tibia dataset, utilizing filter size 3 × 3 is sufficient to grasp small structural information. Considering the tiny structural texture with small pixel size in the case of bone images, the filter size 3 × 3 is already good enough.
Fig. 9.
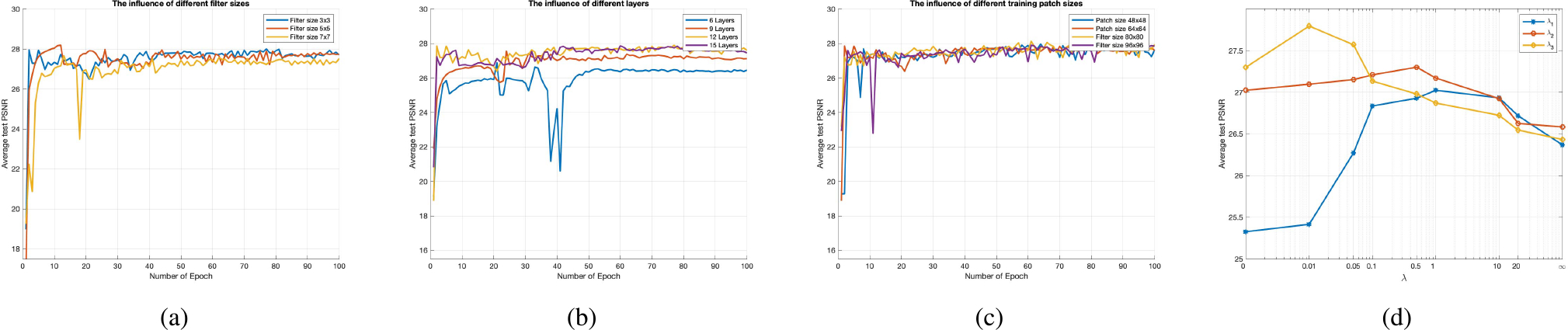
The test convergence curve of GAN-CIRCLE on the Tibia dataset. (a) The influence of different filter sizes, (b) The influence of different layers, (c) The influence of different training patch sizes, and (d) Average PSNR results over GAN-CIRCLE on the Tibia dataset with respect to the parameters λ1, λ2, λ3. Note that the parameter λ = 0 (λ = ∞) indicates that the SR model was only optimized with respect to the corresponding loss.
2). Number of Layers:
Recent studies reported in [72], [73] suggest that training a network could benefit from increasing the network depth moderately. Here we evaluated different network depths by adjusting the number of non-linear mapping layers in the feature extraction network to 6, 9, 12, 15 layers respectively in the case of the Tibia dataset. Note that all the other settings remained the same as that in Supplementary Material Section I–B, and our proposed GAN-CIRCLE used the twelve-layer network. It can be seen in Fig. 9b that the twelve-layer network is superior to the six-layer and nine-layer networks, respectively. Furthermore, it is found that deeper networks cannot always do better. Specifically, the performance of the fifteen-layer network did not outperform the twelve-layer network. The observation that “deeper” does not mean “better” was also reported in [74], [75]. Therefore, we have selected the twelve-layer networks in this study.
3). Training Patch Size:
In general, the benefit of training a CNN-based network with patches is two-fold. First, a properly truncated receptive field can reduce the complexity of the network while still capturing the richness of local anatomical information [66], [76], [77]. Second, the use of patches significantly increases the number of training samples [41], [77]. Here we respectively experimented with patch sizes 48 × 48, 64×64, 80×80, and 96×96 respectively on the Tibia dataset. The results are shown in Fig. 9c. It is observed that large training patch sizes do not show any improvement in term of the average PSNR. As a trade-off, we used the patch size 64 × 64 in our investigation.
IV. DISCUSSIONS
SR imaging promises multiple benefits in medical applications; i.e., depicting bony details, lung structures, and implanted stents, and potentially enhancing radiomics analysis. As a result, X-ray computed tomography can provide compelling practical benefit in biological evaluation.
High resolution micro-CT is well-suited for bone imaging. Osteoporosis, characterized by reduced bone density and structural degeneration of bone, greatly diminishes bone strength and increases the risk of fracture [78]. Histologic studies have convincingly demonstrated that bone micro-structural properties are strong determinants of bone strength and fracture risk [79]–[81]. Modern whole-body CT technologies, benefitted with high spatial resolution, ultra-high speed scanning, relatively-low dose radiation, and large scan length, allows quantitative characterization of bone micro-structure [61]. However, the state-of-the-art CT imaging technologies only allow the spatial resolution comparable or slightly higher than human trabecular bone thickness (100 − 200 μm6 [82]) leading to fuzzy representations of individual trabecular bone micro-structure with significant partial volume effects that add significant errors in measurements and interpretations. The spatial resolution improvements in bone micro-structural representation will largely reduce such errors and improve the generalizability of bone micro-structural measures from multi-vendor CT scanners by homogenizing spatial resolution.
Besides revealing micro-architecture, CT scans of the abdomen and pelvis are diagnostic imaging tests used to help detect diseases of the small bowel and colon, kidney stone, and other internal organs, and are often used to determine the cause of unexplained symptoms. With rising concerns over increased lifetime risk of cancer by radiation dose associated with CT, several studies have assessed manipulation of scanning parameters and newer technologic developments as well as the adoption of advanced reconstruction techniques for radiation dose reduction [83]–[85]. However, in practice, the physical constraints of system hardware components and radiation dose considerations constrain the imaging performance, and computational means are necessary to optimize image resolution. For the same reason, high-quality/high-dose CT images are not often available, which means that there are often not enough paired data to train a hierarchical deep generative model.
Our results have suggested an interesting topic on how to utilize unpaired data so that the imaging performance could be improved. In this regard, the use of the adversarial learning as the regularization term for SR imaging is a new mechanism to capture anatomical information. In this work, we have confirmed the following expected performance order: GAN-CIRCLE > GAN-CIRCLEs > GAN-CIRCLEu, and even in the unsupervised context we still have decent deblurring effects. Our proposed semi-supervised learning method has achieved the compelling results with abdominal and mouse datasets. Specifically, as listed in Tables I, II, and III, the proposed semi-supervised methods achieved promising quantitative results. However, it should be noted that the existing GAN-based methods introduce additional noise to the results, as seen in Section III-C and III-D. To cope with this limitation, we have incorporated the cycle-consistency so that the network can learn a complex deterministic mapping to improve image quality. The enforcement of identity and supervision allows the model to master more latent structural information to improve image resolution. Also, we have used the Wasserstein distance to stabilize the GAN training process. Moreover, typical prior studies used complex inference to learn a hierarchy of latent variables for HR imaging, which is hard to be utilized in medical applications. Thus, we have designed an efficient CNN-based network with skip-connection and network in network techniques. In the feature extraction network, we have optimized the network structures and reduced the computational complexity by applying a small amount of filters in each Conv layer and utilizing the ensemble learning model. Both local and global features are cascaded through skip connections before being fed into the restoration/reconstruction network.
TABLE II.
Statistical Properties of the Images in Figs. 2, 5, 7, and 8. Red and Blue Indicate the Best and the Second Best Performance, Respectively
| Tibia Case | Abdominal Case | Real Case 1 | Real Case 2 | |||||
|---|---|---|---|---|---|---|---|---|
| Mean | SDs | Mean | SDs | Mean | SDs | Mean | SDs | |
|
|
|
|
|
|||||
| HRCT | −321.571 | 676.683 | 125.427 | 176.351 | 485.584 | 305.261 | 484.394 | 332.121 |
| LRCT | −310.300 | 648.118 | 129.262 | 172.767 | 308.147 | 288.917 | 308.789 | 314.800 |
| A+ | −316.080 | 637.457 | 128.724 | 170.591 | 301.891 | 288.222 | 302.525 | 313.994 |
| FSRCNN | −333.806 | 657.914 | 125.102 | 174.567 | 480.237 | 291.184 | 481.097 | 318.084 |
| ESPCN | −330.660 | 660.538 | 125.500 | 174.771 | 482.686 | 291.445 | 483.427 | 317.809 |
| LapSRN | −322.968 | 667.776 | 125.397 | 174.883 | 483.903 | 292.359 | 484.605 | 319.162 |
| SRGAN | −255.065 | 628.754 | 122.264 | 167.347 | 469.796 | 296.98 | 469.641 | 321.566 |
| G-Fwd | −323.492 | 670.247 | 125.130 | 174.607 | 484.833 | 292.336 | 485.426 | 319.307 |
| G-Adv | −314.155 | 643.952 | 123.992 | 173.391 | 471.312 | 302.897 | 471.853 | 328.565 |
| GAN-CIRCLE | −320.519 | 676.526 | 125.330 | 175.607 | - | - | - | - |
| GAN-CIRCLEs | −320.417 | 680.264 | 125.304 | 175.389 | 472.359 | 304.110 | 473.182 | 330.182 |
| GAN-CIRCLEu | −316.080 | 681.024 | 125.961 | 176.120 | 467.897 | 288.376 | 308.538 | 334.277 |
Although our model has achieved compelling results, there still exist some limitations. First, the proposed GAN-CIRCLE requires much longer training time than other standard GAN-based methods, which generally requires 1–2 days. Future work in this aspect should consider more principled ways of designing more efficient architectures that allow for learning more complex structural features with less complex networks at less computational cost and lower model complexity. Second, although our proposed model can generate more plausible details and better anatomical details, all subtle structures may not be always faithfully recovered. It has been also observed that the recent literature [86] mentions that the Wasserstein distance may yield the biased sample gradients, is subject to the risk of incorrect minimum, and not well suitable for stochastic gradient descent searching. In the future, experiments with the variants of GANs are highly recommended. Finally, we notice that the network with the adversarial training can generate more realistic images. However, the restored images cannot be uniformly consistent to the original high-resolution images. Also, the recent literature [87]demonstrates that CycleGAN model learn to hide reconstruction details in imperceptible noise (high-frequency signal). This could theoretically be avoided by strictly enforcing the latent space assumption with added losses. It is also mentioned that the cycle-consistency loss may make the CycleGAN network vulnerable to adversarial attacks. Increasing the domain entropy with additional hidden variables is recommended. To make further progress, we may also undertake efforts to add more constraints such as the sinogram consistence and the low-dimensional manifold constraint to decipher the relationship between noise, blurry appearances of images and the ground truth, and even develop an adaptive and/or task-specific loss function.
V. CONCLUSIONS
In this paper, we have established a cycle Wasserstein regression adversarial training framework for CT SR imaging. Aided by unpaired data, our approach learns complex structured features more effectively with a limited amount of paired data. At a low computational cost, the proposed network G-Forward can achieve the significant SR gain. In general, the proposed GAN-CIRCLE has produced promising results in terms of preserving anatomical information and suppressing image noise in a purely supervised and semi-supervised learning fashion. Visual evaluations by the expert radiologists confirm that our proposed GAN-CIRCLE networks have brought superior diagnostic quality, which is consistent with systematic quantitative evaluations in terms of traditional image quality measures.
Supplementary Material
ACKNOWLEDGMENT
The authors would like to thank the NVIDIA Corporation for the donation of the TITAN XP GPU to Dr. Ge Wang’s laboratory, which was used for this study. The authors would like to thank Dr. Shouhua Luo (Southeast University, China) for providing small animal data collected on an in vivo micro-CT system.
Footnotes
This paper has supplementary downloadable material available at http://ieeexplore.ieee.org., provided by the author.
Color versions of one or more of the figures in this paper are available online at http://ieeexplore.ieee.org.
Contributor Information
Chenyu You, Departments of Bioengineering and Electrical Engineering, Stanford University, Stanford, CA 94305 USA.
Guang Li, Department of Biomedical Engineering, Rensselaer Polytechnic Institute, Troy, NY 12180 USA.
Yi Zhang, College of Computer Science, Sichuan University, Chengdu 610065, China.
Xiaoliu Zhang, Department of Electrical and Computer Engineering, University of Iowa, Iowa City, IA 52246 USA.
Hongming Shan, Department of Biomedical Engineering, Rensselaer Polytechnic Institute, Troy, NY 12180 USA.
Mengzhou Li, Department of Biomedical Engineering, Rensselaer Polytechnic Institute, Troy, NY 12180 USA.
Shenghong Ju, Jiangsu Key Laboratory of Molecular and Functional Imaging, Department of Radiology, Zhongda Hospital, Medical School, Southeast University, Nanjing 210009, China.
Zhen Zhao, Jiangsu Key Laboratory of Molecular and Functional Imaging, Department of Radiology, Zhongda Hospital, Medical School, Southeast University, Nanjing 210009, China.
Zhuiyang Zhang, Department of Radiology, Wuxi No.2 People’s Hospital, Wuxi 214000, China.
Wenxiang Cong, Department of Biomedical Engineering, Rensselaer Polytechnic Institute, Troy, NY 12180 USA.
Michael W. Vannier, Department of Radiology, University of Chicago, Chicago, IL 60637 USA..
Punam K. Saha, Department of Electrical and Computer Engineering and Radiology, University of Iowa, Iowa City, IA 52246 USA.
Eric A. Hoffman, Department of Radiology and Biomedical Engineering, University of Iowa, Iowa City, IA 52246 USA.
Ge Wang, Department of Biomedical Engineering, Rensselaer Polytechnic Institute, Troy, NY 12180 USA.
REFERENCES
- [1].Brenner DJ, Elliston CD, Hall EJ, and Berdon WE, “Estimated risks of radiation-induced fatal cancer from pediatric CT,” AJR Amer. J. Roentgenol, vol. 176, no. 2, pp. 289–296, Feb. 2001. [DOI] [PubMed] [Google Scholar]
- [2].Greenspan H, “Super-resolution in medical imaging,” Comput. J, vol. 52, no. 1, pp. 43–63, 2008. [Google Scholar]
- [3].Hassan A, Nazir SA, and Alkadhi H, “Technical challenges of coronary CT angiography: Today and tomorrow,” Eur. J. Radiol, vol. 79, no. 2, pp. 161–171, 2011. [DOI] [PubMed] [Google Scholar]
- [4].Brenner DJ and Hall EJ, “Computed tomography—An increasing source of radiation exposure,” Eng. J. Med, vol. 357, no. 22, pp. 2277–2284, 2007. [DOI] [PubMed] [Google Scholar]
- [5].de González AB and Darby S, “Risk of cancer from diagnostic X-rays: Estimates for the U.K. and 14 other countries,” Lancet, vol. 363, no. 9406, pp. 345–351, Jan. 2004. [DOI] [PubMed] [Google Scholar]
- [6].Li G et al. , “A novel calibration method incorporating nonlinear optimization and ball-bearing markers for cone-beam CT with a parameterized trajectory,” Med. Phys, vol. 46, no. 1, pp. 152–164, 2019. [DOI] [PubMed] [Google Scholar]
- [7].La Rivière PJ, Bian J, and Vargas PA, “Penalized-likelihood sinogram restoration for computed tomography,” IEEE Trans. Med. Imag, vol. 25, no. 8, pp. 1022–1036, Aug. 2006. [DOI] [PubMed] [Google Scholar]
- [8].Wang G, Snyder DL, O’Sullivan JA, and Vannier MW, “Iterative deblurring for CT metal artifact reduction,” IEEE Trans. Med. Imag, vol. 15, no. 5, pp. 651–664, Oct. 1996. [DOI] [PubMed] [Google Scholar]
- [9].Wang G, Vannier MW, Skinner MW, Cavalcanti MGP, and Harding GW, “Spiral CT image deblurring for cochlear implantation,” IEEE Trans. Med. Imag, vol. 17, no. 2, pp. 251–262, Apr. 1998. [DOI] [PubMed] [Google Scholar]
- [10].Robertson DD, Yuan J, Wang G, and Vannier MW, “Total hip prosthesis metal-artifact suppression using iterative deblurring reconstruction,” J. Comput. Assist. Tomogr, vol. 21, no. 2, pp. 293–298, 1997. [DOI] [PubMed] [Google Scholar]
- [11].Jiang M, Wang G, Skinner MW, Rubinstein JT, and Vannier MW, “Blind deblurring of spiral CT images,” IEEE Trans. Med. Imag, vol. 22, no. 7, pp. 837–845, Jul. 2003. [DOI] [PubMed] [Google Scholar]
- [12].Tian J and Ma K-K, “A survey on super-resolution imaging,” Signal, Image Video Process, vol. 5, no. 3, pp. 329–342, 2011. [Google Scholar]
- [13].Zhang R, Thibault J-B, Bouman C, Sauer KD, and Hsieh J, “Model-based iterative reconstruction for dual-energy X-ray CT using a joint quadratic likelihood model,” IEEE Trans. Med. Imag, vol. 33, no. 1, pp. 117–134, Jan. 2014. [DOI] [PubMed] [Google Scholar]
- [14].Bouman CA and Sauer K, “A unified approach to statistical tomography using coordinate descent optimization,” IEEE Trans. Image Process, vol. 5, no. 3, pp. 480–492, Mar. 1996. [DOI] [PubMed] [Google Scholar]
- [15].Yu Z, Thibault JB, Bouman CA, Sauer KD, and Hsieh J, “Fast model-based X-ray CT reconstruction using spatially nonhomogeneous ICD optimization,” IEEE Trans. Image Process, vol. 20, no. 1, pp. 161–175, Jan. 2011. [DOI] [PubMed] [Google Scholar]
- [16].Sauer K and Bouman C, “A local update strategy for iterative reconstruction from projections,” IEEE Trans. Signal Process, vol. 41, no. 2, pp. 534–548, Feb. 1993. [Google Scholar]
- [17].Thibault J-B, Sauer KD, Bouman CA, and Hsieh J, “A three-dimensional statistical approach to improved image quality for multislice helical CT,” Med. Phys, vol. 34, no. 11, pp. 4526–4544, 2007. [DOI] [PubMed] [Google Scholar]
- [18].Yang J, Wright J, Huang TS, and Ma Y, “Image super-resolution via sparse representation,” IEEE Trans. Image Process, vol. 19, no. 11, pp. 2861–2873, Nov. 2010. [DOI] [PubMed] [Google Scholar]
- [19].Zhang Y et al. , “Reconstruction of super-resolution lung 4D-CT using patch-based sparse representation,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit. (CVPR), Jun. 2012, pp. 925–931. [Google Scholar]
- [20].Dong W, Zhang L, Shi G, and Wu X, “Image deblurring and super-resolution by adaptive sparse domain selection and adaptive regularization,” IEEE Trans. Image Process, vol. 20, no. 7, pp. 1838–1857, Jul. 2011. [DOI] [PubMed] [Google Scholar]
- [21].LeCun Y, Bottou L, Bengio Y, and Haffner P, “Gradient-based learning applied to document recognition,” Proc. IEEE, vol. 86, no. 11, pp. 2278–2324, Nov. 1998. [Google Scholar]
- [22].LeCun Y, Bengio Y, and Hinton G, “Deep learning,” Nature, vol. 521, no. 7553, p. 436, 2015. [DOI] [PubMed] [Google Scholar]
- [23].Ledig C et al. , “Photo-realistic single image super-resolution using a generative adversarial network,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit. (CVPR), Jul. 2017, vol. 2, no. 3, pp. 4681–4690. [Google Scholar]
- [24].Dong C, Loy CC, and Tang X, “Accelerating the super-resolution convolutional neural network,” in Proc. Eur. Conf. Comput. Vis. (ECCV), 2016, pp. 391–407. [Google Scholar]
- [25].Lai W-S, Huang J-B, Ahuja N, and Yang M-H, “Deep laplacian pyramid networks for fast and accurate super-resolution,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit. (CVPR), Jul. 2017, pp. 624–632. [Google Scholar]
- [26].Shi W et al. , “Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit. (CVPR), Jun. 2016, pp. 1874–1883. [Google Scholar]
- [27].Yuan Y, Liu S, Zhang J, Zhang Y, Dong C, and Lin L, “Unsupervised image super-resolution using cycle-in-cycle generative adversarial networks,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit. (CVPR), Jun. 2018, pp. 701–710. [Google Scholar]
- [28].Wang G, Kalra M, and Orton CG, “Machine learning will transform radiology significantly within the next 5 years,” Med. Phys, vol. 44, no. 6, pp. 2041–2044, 2017. [DOI] [PubMed] [Google Scholar]
- [29].Wang G, “A perspective on deep imaging,” IEEE Access, vol. 4, pp. 8914–8924, 2016. [Google Scholar]
- [30].Wang G, Ye JC, Mueller K, and Fessler JA, “Image reconstruction is a new frontier of machine learning,” IEEE Trans. Med. Imag, vol. 37, no. 6, pp. 1289–1296, Jun. 2018. [DOI] [PubMed] [Google Scholar]
- [31].Chen Y, Shi F, Christodoulou AG, Zhou Z, Xie Y, and Li D, “Efficient and accurate MRI super-resolution using a generative adversarial network and 3D multi-level densely connected network,” CoRR, Mar. 2018. [Google Scholar]
- [32].Yu H et al. , “Computed tomography super-resolution using convolutional neural networks,” in Proc. IEEE Int. Conf. Image Process, Sep. 2017, pp. 3944–3948. [Google Scholar]
- [33].Park J, Hwang D, Kim KY, Kang SK, Kim YK, and Lee JS, “Computed tomography super-resolution using deep convolutional neural network,” Phys. Med. Biol, vol. 63, no. 14, 2018, Art. no. 145011. [DOI] [PubMed] [Google Scholar]
- [34].Adler J and Öktem O, “Learned primal-dual reconstruction,” IEEE Trans. Med. Imag, vol. 37, no. 6, pp. 1322–1332, Jun. 2018. [DOI] [PubMed] [Google Scholar]
- [35].You C, Yang L, Zhang Y, Liphardt J, and Wang G, “Low-dose CT via deep cnn with skip connection and network in network,” CoRR, Nov. 2018. [Google Scholar]
- [36].Lyu Q, You C, Shan H, and Wang G, “Super-resolution MRI through deep learning,” CoRR, Oct. 2018. [Google Scholar]
- [37].Hammernik K et al. , “Learning a variational network for reconstruction of accelerated MRI data,” Magn. Reson. Med, vol. 79, no. 6, pp. 3055–3071, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [38].Mardani M et al. , “Deep generative adversarial neural Networks for compressive sensing MRI,” IEEE Trans. Med. Imag, vol. 38, no. 1, pp. 167–179, Jan. 2019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [39].Goodfellow I et al. , “Generative adversarial nets,” in Proc. Adv. Neural Inf. Process. Syst, 2014, pp. 2672–2680. [Google Scholar]
- [40].Goodfellow I, “NIPS 2016 tutorial: Generative adversarial networks,” CoRR, Dec. 2016. [Google Scholar]
- [41].Wolterink JM, Leiner T, Viergever MA, and Išgum I, “Generative adversarial networks for noise reduction in low-dose CT,” IEEE Trans. Med. Imag, vol. 36, no. 12, pp. 2536–2545, Dec. 2017. [DOI] [PubMed] [Google Scholar]
- [42].Nie D et al. , “Medical image synthesis with deep convolutional adversarial networks,” IEEE Trans. Biomed. Eng, vol. 65, no. 12, pp. 2720–2730, Dec. 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [43].Zhu J-Y, Park T, Isola P, and Efros AA, “Unpaired image-to-image translation using cycle-consistent adversarial networks,” in Proc. IEEE Int. Conf. Comput. Vis. (ICCV), Oct. 2017, pp. 2223–2232. [Google Scholar]
- [44].Kang E, Koo HJ, Yang DH, Seo JB, and Ye JC, “Cycle consistent adversarial denoising network for multiphase coronary CT angiography,” CoRR, Jun. 2018. [DOI] [PubMed] [Google Scholar]
- [45].Radford A, Metz L, and Chintala S, “Unsupervised representation learning with deep convolutional generative adversarial networks,” in Proc. Int. Conf. Learn. Represent. (ICLR), 2016, pp. 1–16. [Google Scholar]
- [46].Arjovsky M, Chintala S, and Bottou L, “Wasserstein generative adversarial networks,” in Proc. Int. Conf. Mach. Learn. (ICML), 2017, pp. 214–223. [Google Scholar]
- [47].Mao X, Li Q, Xie H, Lau RYK, Wang Z, and Smolley SP, “Least squares generative adversarial networks,” in Proc. IEEE Int. Conf. Comp. Vis. (ICCV), Oct. 2017, pp. 2794–2802. [Google Scholar]
- [48].Grewal K, Hjelm RD, and Bengio Y, “Variance regularizing adversarial learning,” CoRR, Jul. 2017. [Google Scholar]
- [49].Zhao H, Gallo O, Frosio I, and Kautz J, “Loss functions for image restoration with neural networks,” IEEE Trans. Comput. Imag, vol. 3, no. 1, pp. 47–57, Mar. 2017. [Google Scholar]
- [50].You C et al. , “Structurally-sensitive multi-scale deep neural network for low-dose CT denoising,” IEEE Access, vol. 6, pp. 41839–41855, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [51].Yamanaka J, Kuwashima S, and Kurita T, “Fast and accurate image super resolution by deep CNN with skip connection and network in network,” in Proc. 24th Int. Conf. Neural Inf. Process. (ICONIP). Guangzhou, China: Springer, Nov. 2017, pp. 217–225. [Google Scholar]
- [52].He K, Zhang X, Ren S, and Sun J, “Deep residual learning for image recognition,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit. (CVPR), Jun. 2016, pp. 770–778. [Google Scholar]
- [53].Huang G, Liu Z, Weinberger KQ, and van der Maaten L, “Densely connected convolutional networks,” in Proc. IEEE CVPR, Jun. 2017, vol. 1, no. 2, p. 3. [Google Scholar]
- [54].Srivastava N, Hinton G, Krizhevsky A, Sutskever I, and Salakhutdinov R, “Dropout: A simple way to prevent neural networks from overfitting,” J. Mach. Learn. Res, vol. 15, no. 1, pp. 1929–1958, 2014. [Google Scholar]
- [55].Timofte R, De Smet V, and Van Gool L, “A+: Adjusted anchored neighborhood regression for fast super-resolution,” in Proc. Asian Conf. Comput. Vis. Singapore: Springer, 2014, pp. 111–126. [Google Scholar]
- [56].Gulrajani I, Ahmed F, Arjovsky M, Dumoulin V, and Courville AC, “Improved training of wasserstein GANs,” in Proc. Adv. Neural Inf. Process. Syst, 2017, pp. 5769–5779. [Google Scholar]
- [57].Tzeng E, Hoffman J, Darrell T, and Saenko K, “Adversarial discriminative domain adaptation,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit. (CVPR), Jul. 2017, pp. 7167–7176. [Google Scholar]
- [58].Li C et al. , “Alice: Towards understanding adversarial learning for joint distribution matching,” in Proc. Adv. Neural Inf. Process. Syst, 2017, pp. 5495–5503. [Google Scholar]
- [59].Sidky EY and Pan X, “Image reconstruction in circular cone-beam computed tomography by constrained, total-variation minimization,” Phys. Med. Biol, vol. 53, no. 17, p. 4777, Sep. 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [60].Chen G-H, Tang J, and Leng S, “Prior image constrained compressed sensing (PICCS): A method to accurately reconstruct dynamic CT images from highly undersampled projection data sets,” Med. Phys, vol. 35, no. 2, pp. 660–663, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [61].Chen C et al. , “Quantitative imaging of peripheral trabecular bone microarchitecture using MDCT,” Med. Phys, vol. 45, no. 1, pp. 236–249, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [62].AAPM. (2017). Low Dose CT Grand Challenge. [Online]. Available: http://www.aapm.org/GrandChallenge/LowDoseCT/#
- [63].Feruglio PF, Vinegoni C, Gros J, Sbarbati A, and Weissleder R, “Block matching 3D random noise filtering for absorption optical projection tomography,” Phys. Med. Biol, vol. 55, no. 18, p. 5401, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [64].Wang Z, Bovik AC, Sheikh HR, and Simoncelli EP, “Image quality assessment: From error visibility to structural similarity,” IEEE Trans. Image Process, vol. 13, no. 4, pp. 600–612, Apr. 2004. [DOI] [PubMed] [Google Scholar]
- [65].Sheikh HR, Bovik AC, and de Veciana G, “An information fidelity criterion for image quality assessment using natural scene statistics,” IEEE Trans. Image Process, vol. 14, no. 12, pp. 2117–2128, Dec. 2005. [DOI] [PubMed] [Google Scholar]
- [66].Simonyan K and Zisserman A, “Very deep convolutional networks for large-scale image recognition,” in Proc. Int. Conf. Learn. Represent. (ICLR), 2015, pp. 1–14. [Google Scholar]
- [67].Shen D, Wu G, and Suk H, “Deep learning in medical image analysis,” Annu. Rev. Biomed. Eng, vol. 19, pp. 221–248, Jun. 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [68].Yang Q et al. , “Low-dose CT image denoising using a generative adversarial network with Wasserstein distance and perceptual loss,” IEEE Trans. Med. Imag, vol. 37, no. 6, pp. 1348–1357, Jun. 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [69].Shan H et al. , “3-D convolutional encoder-decoder network for low-dose CT via transfer learning from a 2-D trained network,” IEEE Trans. Med. Imag, vol. 37, no. 6, pp. 1522–1534, Jun. 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [70].Yang C-Y, Ma C, and Yang M-H, “Single-image super-resolution: A benchmark,” in Proc. Eur. Conf. Comput. Vis. (ECCV), 2014, pp. 372–386. [Google Scholar]
- [71].Feldkamp LA, Davis LC, and Kress JW, “Practical cone-beam algorithm,” J. Opt. Soc. Amer. A, Opt. Image Sci, vol. 1, no. 6, pp. 612–619, 1984. [Google Scholar]
- [72].He K and Sun J, “Convolutional neural networks at constrained time cost,” in Proc. IEEE Conf. Comput. Vis. Pattern Recognit. (CVPR), Jun. 2015, pp. 5353–5360. [Google Scholar]
- [73].Wang X et al. , “ESRGAN: Enhanced super-resolution generative adversarial networks,” in Proc. Eur. Conf. Comput. Vis. Workshops (ECCVW), Sep. 2018, pp. 1–16. [Google Scholar]
- [74].Glasner D, Bagon S, and Irani M, “Super-resolution from a single image,” in Proc. IEEE Int. Conf. Comput. Vis. (ICCV), Sep./Oct. 2009, pp. 349–356. [Google Scholar]
- [75].Dong C, Loy CC, He K, and Tang X, “Image super-resolution using deep convolutional networks,” IEEE Trans. Pattern Anal. Mach. Intell, vol. 38, no. 2, pp. 295–307, Feb. 2015. [DOI] [PubMed] [Google Scholar]
- [76].Johnson J, Alahi A, and Fei-Fei L, “Perceptual losses for real-time style transfer and super-resolution,” in Proc. Eur. Conf. Comput. Vis. (ECCV), 2016, pp. 697–711. [Google Scholar]
- [77].Hamwood J, Alonso-Caneiro D, Read SA, Vincent SJ, and Collins MJ, “Effect of patch size and network architecture on a convolutional neural network approach for automatic segmentation of OCT retinal layers,” Biomed. Opt. Express, vol. 9, no. 7, pp. 3049–3066, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [78].Cummings SR and Melton LJ, “Epidemiology and outcomes of osteoporotic fractures,” Lancet, vol. 359, no. 9319, pp. 1761–1767, 2002. [DOI] [PubMed] [Google Scholar]
- [79].Kleerekoper M, Villanueva AR, Stanciu J, Rao DS, and Parfitt AM, “The role of three-dimensional trabecular microstructure in the pathogenesis of vertebral compression fractures,” Calcified Tissue Int, vol. 37, no. 6, pp. 594–597, 1985. [DOI] [PubMed] [Google Scholar]
- [80].Legrand E et al. , “Trabecular bone microarchitecture, bone mineral density, and vertebral fractures in male osteoporosis,” J. Bone Mineral Res, vol. 15, no. 1, pp. 13–19, 2000. [DOI] [PubMed] [Google Scholar]
- [81].Parfitt AM, Mathews CH, Villanueva AR, Kleerekoper M, Frame B, and Rao DS, “Relationships between surface, volume, and thickness of iliac trabecular bone in aging and in osteoporosis. Implications for the microanatomic and cellular mechanisms of bone loss,” J. Clin. Invest, vol. 72, no. 4, pp. 1396–1409, 1983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [82].Ding M and Hvid I, “Quantification of age-related changes in the structure model type and trabecular thickness of human tibial cancellous bone,” Bone, vol. 26, no. 3, pp. 291–295, 2000. [DOI] [PubMed] [Google Scholar]
- [83].Kalra MK et al. , “Strategies for CT radiation dose optimization,” Radiology, vol. 230, no. 3, pp. 619–628, Mar. 2004. [DOI] [PubMed] [Google Scholar]
- [84].Prakash P et al. , “Reducing abdominal CT radiation dose with adaptive statistical iterative reconstruction technique,” Invest. Radiol, vol. 45, no. 4, pp. 202–210, 2010. [DOI] [PubMed] [Google Scholar]
- [85].Vasilescu DM et al. , “Assessment of morphometry of pulmonary acini in mouse lungs by nondestructive imaging using multiscale microcomputed tomography,” Proc. Nat. Acad. Sci. USA, vol. 109, no. 42, pp. 17105–17110, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [86].Bellemare MG et al. , “The cramer distance as a solution to biased wasserstein gradients,” CoRR, May 2017. [Google Scholar]
- [87].Chu C, Zhmoginov A, and Sandler M, “CycleGAN, a master of steganography,” CoRR, Dec. 2017. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


