Tunable band alignment and large power conversion efficiency in a two-dimensional InS/ZnIn₂S₄ heterostructure

Abstract

Heterostructures can efficiently modulate the bandgap of semiconductors and enhance the separation of photocarriers, thereby enhancing the performance of optoelectronic devices. Herein, we design an InS/ZnIn₂S₄ van der Waals (vdW) heterostructure and investigate its electronic and photovoltaic properties using first principles calculation. Compared to its individual monolayers, the InS/ZnIn₂S₄ heterostructure not only possesses a smaller band gap of 2.21 eV and superior light absorption performance in the visible short-wavelength region (<500 nm) but also forms a type-II₁ band alignment. Moreover, a large power conversion efficiency (PCE) of 10.86% is achieved. The transformation of the band alignment from type-II₁ to type-I or type-II₂ can be forced using an external electric field, and the PCE can be further increased up to 12.19% at a positive E_⊥ of 0.2 V Å⁻¹. Within a critical biaxial strain of 4%, the type-II₁ band alignment can be maintained, and a high PCE of 20.80% is achieved at a tensile strain (ε) of 4%. Our results may suggest a potential optoelectronic application direction for the InS/ZnIn₂S₄ heterostructure and offer effective means to enhance its optoelectronic device performance.

An InS/ZnIn₂S₄ heterostructure was designed, and its electronic and photovoltaic properties were systematically investigated.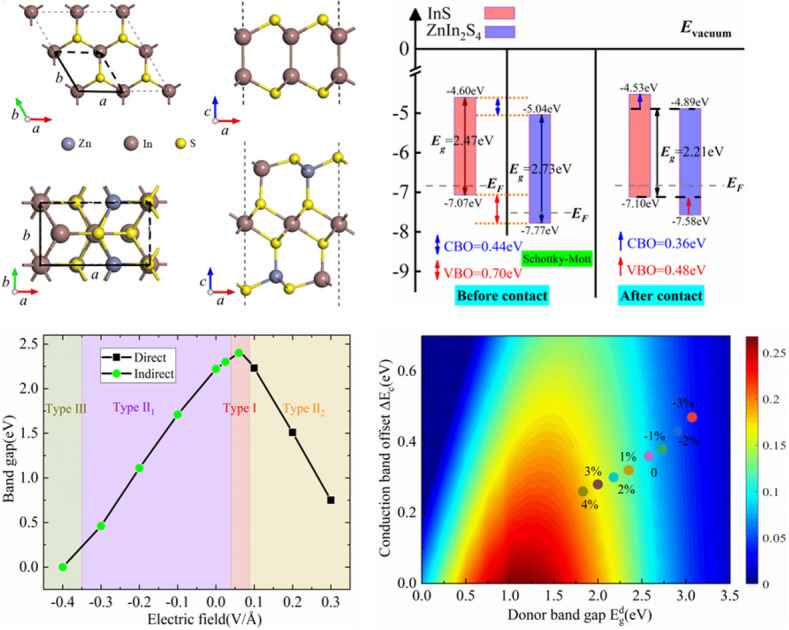

1. Introduction

Nowadays, in the face of increasing global energy shortages and environmental pollution, finding new green energy sources to replace traditional fuels has become a pressing issue, including solar energy, ocean energy, wind energy, biomass energy, and so on.¹ Solar cells made of materials with specific photovoltaic properties can directly convert solar energy into electricity, which has become the main idea of the next generation of green power generation.² Power conversion efficiency (PCE) is a metric that quantifies the efficiency with which a solar cell converts incident solar energy into useable electrical power. To enhance the PCE of solar cells, we can either employ high-quality photovoltaic materials (Si, CdSe, GaSe, and perovskite materials) with a wide spectral absorption range^3,4 or create a heterojunction using two different semiconductor materials to increase the efficiency of the separation of photogenerated electrons and holes and to prolong the life time of the carriers.^5,6 As we know, heterostructures can integrate the advantages of their individual constituent materials to overcome limitations, further enhancing their existing properties and expanding their applications.^3,4,7–11 Heterostructures with type-II band alignment are commonly utilized in photocatalytic water splitting and photovoltaic devices.^12,13

Since the emergence of graphene,¹⁴ two-dimensional (2D) materials and their heterostructures have garnered considerable attention owing to their unique physical properties and applications in novel optoelectronic devices.^{3,5,6,15–20} In recent years, solar cells constructed with 2D semiconductors heterostructures have received extensive theoretical and experimental research.^6,20–22 Using polymer stacking and chemical vapor deposition (CVD), a graphene/WS₂ heterostructure,²³ WSe₂/MoS₂ heterostructure,²⁴ WSe₂/MoSe₂ heterostructure,²⁵ and p-Si/MoS₂ heterostructure²⁶ have been successfully prepared and exhibited a photoelectric conversion efficiency ranging from 0.12% to 5.23%. Furthermore, 2D GaX/SnS₂ (X = S or Se), GaS/SnS₂, Janus Ga₂SeTe/InS, and SbI₃/BiI₃ heterostructures have been theoretically proposed for solar cells with a considerable PCE.^4,6,27 Under atom doping, compressive strain, or an electric field, their PCE can reach up to 16.47%, 23.2%, and 21.63%, respectively.

Recently, a new family of 2D binary semiconductors, metal monochalcogenides MX (M = Ga, In; X = S, Se, Te), have garnered considerable interest because of their excellent physicochemical properties.^28,29 The monolayer MX can be synthesized through mechanical exfoliation methods^30,31 and vapor phase transport approach.^32,33 MX monolayers have an indirect bandgap between 2.0 eV and 4.0 eV, and their band structure and optical absorption spectrum can be effectively modulated by layer thickness^34,35 and nanofabrication.³⁶ The InS monolayer and its heterostructure InS/InSe have been widely studied, possessing a PCE of 13.7%.³⁷ Besides the binary metal monochalcogenides MX, the ternary metal chalcogenide semiconductor ZnIn₂X₄ (X = S, Se, Te) has also garnered significant interest owing to its excellent light absorption performance, and remarkable thermal and chemical stability.^38,39 ZnIn₂S₄ nanosheets have now been synthesized and used for efficient photocatalytic hydrogen evolution, solar-powered CO₂ conversion and hydrogen evolution reactions.^40,41 In addition, many ZnIn₂X₄-based heterostructures have been fabricated and proposed for photodetectors, high-efficiency solar cells, and photocatalytic hydrogen evolution, such as O-SnS/I-ZnIn₂S₄,⁴² ZnIn₂S₄/ZnIn₂Se₄(ZnIn₂Se₄/ZnIn₂Te₄),⁴³ and ZnIn₂S₄/SnSe₂.⁴⁴ Considering this, one intriguing question is whether the InS/ZnIn₂S₄ heterostructure could exhibit better electronic and optical properties, potentially leading to improved photovoltaic performance.

In this paper, firstly, we theoretically design the InS/ZnIn₂S₄ heterostructure and present a detailed study of its electronic and optical properties, including electronic structure, band alignment, optical absorption coefficients and PCE. It is found that the InS/ZnIn₂S₄ heterostructure possesses an indirect bandgap of 2.21 eV, a type-II₁ band alignment, a large optical absorption coefficient, and a significant PCE of 10.86%. Next, the effects of an external field (electrical field and strain) on the band alignment and PCE of the InS/ZnIn₂S₄ heterostructure are also investigated. The band alignment transitions from type-II₁ to type-I, type-II₂ or type-III under an external electrical field, while it always stays in type-II₁ under a biaxial strain. The PCE will increase to 12.19% at an external electric field of 0.2 V Å⁻¹, and to 20.80% at a tensile strain of ε = 4%.

2. Methods

All calculations are carried out using the Vienna Ab initio Simulation Package (VASP),^45,46 employing density functional theory (DFT). The exchange-correlation effect are treated with the generalized gradient approximation (GGA) of the Perdew–Burke–Ernzerhof (PBE) functional,⁴⁷ within the projector augmented wave (PAW) framework.^48,49 A plane wave cutoff energy of 450 eV is used. Geometric relaxation is performed until the residual force on each atom is below 0.01 eV Å⁻¹. The Brillouin zone integration was sampled using 10 × 10 × 1 k-point meshes generated by the Monkhorst–Pack scheme.⁵⁰ The electronic structure is also calculated using the Heyd–Scuseria–Ernzerhorf (HSE06) hybrid functionals.⁵¹ van der Waals (vdW) interactions between layers in the heterostructure are accounted for using a DFT-D2 approach.⁵² To eliminate spurious periodic interactions, a vacuum layer of 15 Å was introduced along the direction perpendicular to the heterostructure.

The binding energy E_b is calculated to assess the energy stability of the InS/ZnIn₂S₄ heterostructure, which is defined as the following equation,E_b = E_InS/ZnIn2S4 − E_InS − E_ZnIn2S4where E_InS/ZnIn2S4 denotes the total energy of the InS/ZnIn₂S₄ heterostructure, while E_InS and E_ZnIn2S4 represent the total energies of the isolated InS and ZnIn₂S₄ monolayers, respectively.

Both the optical absorption coefficient α(ω) and PCE are also calculated to quantitatively analyze the optical properties of the InS/ZnIn₂S₄ heterostructure. The α(ω) is computed from the following equation,⁵³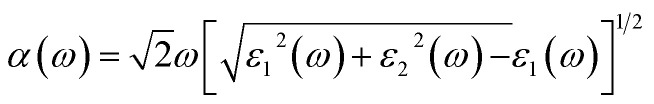where ε₂(ω) represents the imaginary part of the dielectric function, and ε₁(ω) is the real part of the dielectric function, derived from ε₂(ω) through the Kramers–Kronig transformation. The PCE is defined as follows,⁵⁴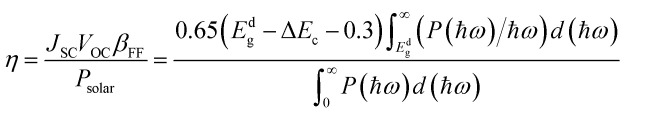where β_FF, V_OC, J_SC, and P_solar represent the band-fill factor, maximum open-circuit voltage, short-circuit current, and sum of the AM1.5 incident solar irradiation, respectively. β_FF is typically assigned a value of 0.65,⁵⁴V_OC = E^d_g − ΔE_c − 0.3, and 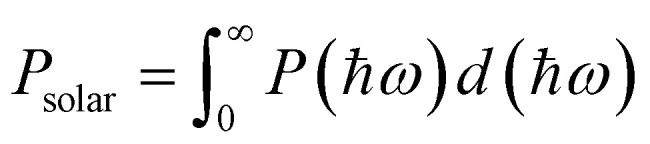. In addition, E^d_g, ΔE_c, P(hω), and hω represent the donor layer's bandgap, conduction band offset (CBO) of the heterostructure, AM1.5 solar energy flux, and photon energy, respectively.

The carrier mobility for the InS/ZnIn₂S₄ van der Waals (vdW) heterostructure can be approximated using the deformation potential model, which is expressed as,^55,56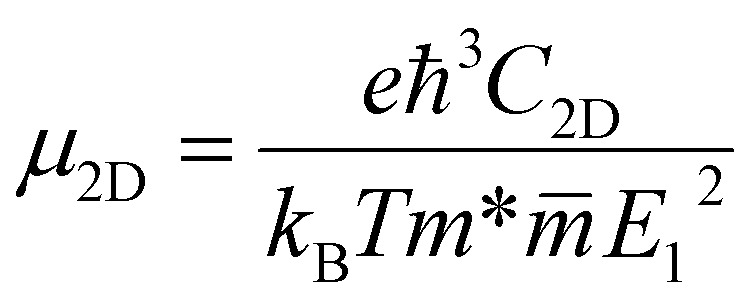where e is the electron's charge, h is the reduced Planck constant, C_2D is the elastic modulus, k_B is the Boltzmann constant, T is the temperature set to 300 K, 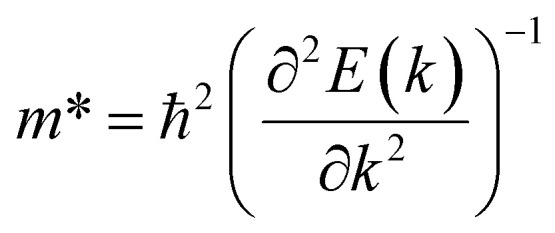is the carrier effective mass, 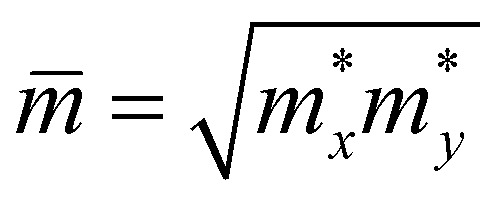is the average carrier effective mass, and 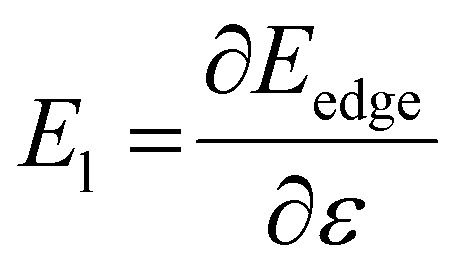is the deformation potential constant, where E_edge represents the band edge energy of the electrons and holes produced by the infinitesimal uniaxial strain ε, along the armchair and zigzag directions.

3. Results and discussion

The crystal structure and band structure of the isolated InS and ZnIn₂S₄ monolayers are displayed in Fig. S1.† The monolayer InS has a hexagonal lattice and four atomic-layer structure with a unit cell containing two In and two S atoms. The lattice constants of InS are a_InS = b_InS = 3.93 Å. The valence band maximum (VBM) is along the Γ–M line, while the conduction band minimum (CBM) is at Γ point, indicating that InS is an indirect band gap semiconductor. The band gap of InS is calculated to be 1.66 eV under the PBE functional level and 2.47 eV under the HSE06 functional level, consistent with previous reports.²⁸ The monolayer ZnIn₂S₄ forms a rectangular lattice and seven atomic-layer structure with a unit cell containing two Zn, four In and eight S atoms. The lattice constants of ZnIn₂S₄ are a_ZnIn2s4 = 6.78 Å and b_ZnIn2s4 = 3.93 Å. The CBM and VBM are both situated at the Γ point, which means that it is a direct band gap semiconductor. The calculated band gap of ZnIn₂S₄ is 1.79 eV under the PBE functional level and 2.73 eV under the HSE06 functional level, consistent with a previous study.³⁹ Moreover, for both InS and ZnIn₂S₄ monolayers, the HSE06 functional only increased the bandgap and did not change the general shape of the band structure. For all subsequent calculations, we only use the HSE06 functional.

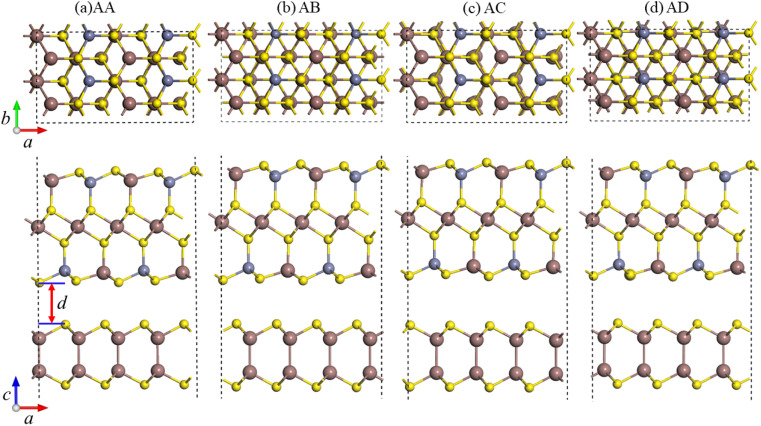
To construct a two-dimensional InS/ZnIn₂S₄ heterostructure with a small lattice mismatch,^57,58 a √3 × 1 supercell of the isolated InS monolayer and a unit cell of ZnIn₂S₄ monolayer are selected. The lattice mismatch is determined using the following formula 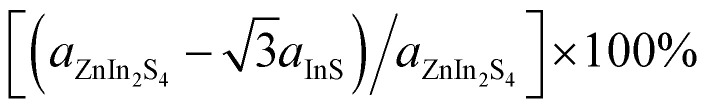for the x direction and [(b_ZnIn2S4 − b_InS)/b_ZnIn2S4] × 100% for the y direction, and the corresponding mismatch values are 0.14% and 0%, respectively. Then, to determine the energetically favorable structure of the InS/ZnIn₂S₄ heterostructures, we consider four representative heterostructures formed with different stacking configuration, specifically AA, AB, AC and AD, as shown in Fig. 1. The equilibrium structural parameters (lattice parameters a and b, interlayer distance d) and binding energy E_b of the four configurations of the InS/ZnIn₂S₄ heterostructures are listed in Table S1.† These four heterostructures have nearly identical lattice parameters of a ≈ 6.80 Å and b ≈ 3.93 Å, which closely resemble the dimensions of the unit cell of the isolated ZnIn₂S₄ (or √3 × 1 supercell of the isolated InS monolayer). The calculated interlayer distances d of the InS/ZnIn₂S₄ heterostructures with AA, AB, AC, and AD stacking are 3.71, 3.77, 4.19, and 4.03 Å, respectively. All four stacking configurations are energetically stable, as their binding energies E_b are negative.⁵⁹ The InS/ZnIn₂S₄ heterostructure with AA stacking is the most energetically favorable, since it has the smallest binding energy. To evaluate the dynamic and thermal stability of the InS/ZnIn₂S₄ heterostructure, the phonon spectrum was obtained and molecular dynamics simulations are also performed. The phonon dispersion does not have an imaginary mode, as shown in Fig. S4(a),† which indicates that the heterostructure is dynamically stable. The fluctuations of the total energy of the InS/ZnIn₂S₄ heterostructure at room temperature (300 K) as a function of time is depicted in Fig. S4(b).† The results suggest that the heterostructure is thermally stable at room temperature, since the fluctuation of the total energies is small. In addition, the AA stacking configuration has the smallest interlayer distance d. In subsequent studies, we mainly focus on the AA stacking configuration.

Fig. 1. Top and side views of the four possible stacking configurations of the InS/ZnIn₂S₄ heterostructures: (a) AA, (b) AB, (c) AC, and (d) AD. d represents the interlayer distance.

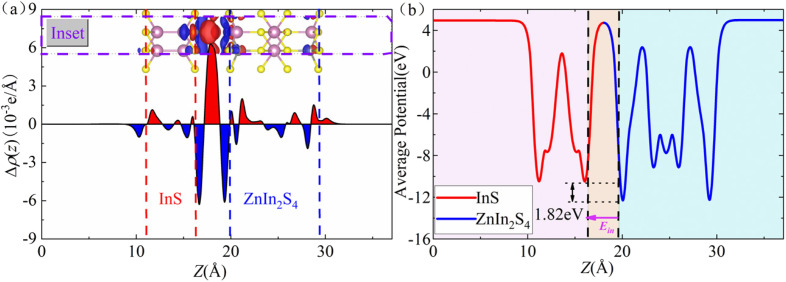
Fig. 2(a) shows the charge density difference Δρ, defined as Δρ = ρ_InS/ZnIn2S4 − ρ_InS − ρ_ZnIn2S4. Here, ρ_ZnIn2S4, ρ_InS, and ρ_ZnIn2S4 represent the charge density of the InS/ZnIn₂S₄ heterostructure, isolated InS, and isolated ZnIn₂S₄, respectively. The planar-averaged charge density difference Δρ(z), defined as 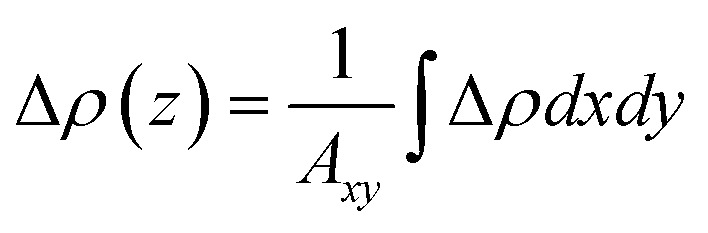, is also displayed in Fig. 2(a). Here, A_xy represents the surface area of the InS/ZnIn₂S₄ heterostructures.⁶⁰ The curves of Δρ(z) were oscillated, and the amplitude of the oscillations experiences a notable surge in proximity to the interface, indicating that charge transfer and rearrangement occur within the interfacial region of the InS/ZnIn₂S₄ heterostructure. In addition, from the three-dimensional charge density difference Δρ, we find that the electrons primarily accumulate in the vdW gap between the InS and ZnIn₂S₄ layers, while the electron-deficient regions predominantly occur around the interface S atoms of both InS layer and ZnIn₂S₄ layer. Furthermore, Bader charge analysis indicates that there is a charge transfer of about 0.004e that occurs from the ZnIn₂S₄ layer to the InS layer. This can induce a weak effective built-in electric field (E_in) at the interface that is directed from the ZnIn₂S₄ layer toward the InS layer,^61,62 as shown by the pink arrow in Fig. 2(b). Fig. 2(b) shows the planar-averaged electrostatic potential V profiles along the z-axis, from which E_in can be inferred based on the potential drop ΔV at the interface of the heterostructure. This electric field plays a crucial role in facilitating the separation of photoinduced electron–hole pairs, thereby prolonging the lifetimes of carriers in the heterostructure. In addition, we calculated the carrier mobility of the InS/ZnIn₂S₄ heterostructure. Table S4† lists the calculated carrier effective mass, the deformation potential constant, and the corresponding carrier mobilities along the zigzag and armchair directions of the InS/ZnIn₂S₄ heterostructure. It can be seen that the hole mobility of the InS/ZnIn₂S₄ heterostructure is higher than that of electrons, and the hole mobility along the armchair direction reaches 6118.01 cm² V⁻¹ s⁻¹. The high carrier mobility characteristic gives it significant advantages in photovoltaic applications.

Fig. 2. (a) The planar-averaged charge density difference Δρ(z) of the InS/ZnIn₂S₄ heterostructure (inset: three-dimensional charge density difference Δρ). Red regions indicate electron accumulation, while blue regions signify electron depletion. (b) The planar-averaged electrostatic potential of the InS/ZnIn₂S₄ heterostructure along the z-axis. The potential drop ΔV at the interface is 1.82 eV. The pink arrow indicates the direction of the built-in electric field.

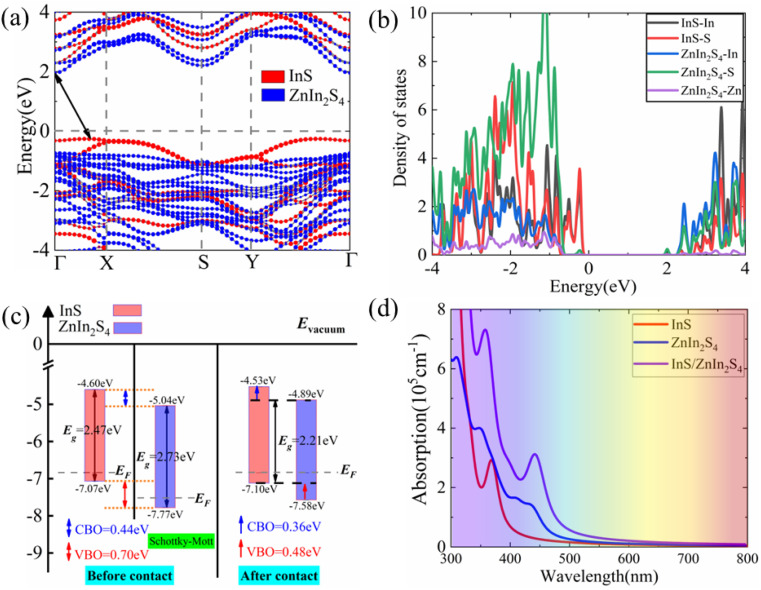
Fig. 3(a)–(c) present the projected band structure, projected density of states (DOS) and band alignment of the InS/ZnIn₂S₄ heterostructure. The heterostructure is a semiconductor with an indirect bandgap of 2.21 eV, where the CBM is at Γ point, while the VBM is along the Γ–X line, which is smaller than both InS (2.47 eV) and ZnIn₂S₄ (2.73 eV). From the projected band structure and projected DOS, we find that the CBM is derived from the ZnIn₂S₄ layer and predominantly contributed by S and In atoms in the ZnIn₂S₄ layer, while the VBM is derived from the InS layer and primarily dominated by S atoms in the InS layer. Interestingly, we find that the InS/ZnIn₂S₄ heterostructure exhibits type-II band alignment, in which the CBM and VBM of the ZnIn₂S₄ layer are lower than those of the InS layer, also denoted as type-II₁ band alignment, as illustrated in Fig. 3(c). Moreover, when the external electric field is greater than 0.1 V Å⁻¹, the CBM and VBM of the ZnIn₂S₄ layer will be higher than those of the InS layer, resulting in another type-II alignment that is different from type-II₁, defined as type-II₂, as shown in Fig. 4(a). In addition, the calculated conduction band offset (CBO) and valence band offset (VBO) are 0.36 eV and 0.48 eV, respectively, both of which are smaller than those calculated using the Schottky–Mott model.⁶³ In the ideal Schottky–Mott limit, there is no interaction between the InS and ZnIn₂S₄ layer, the CBO and VBO are 0.44 eV and 0.70 eV, respectively. The type-II band alignment will significantly improve the efficiency of the separating photoinduced electron–hole pairs at the InS/ZnIn₂S₄ heterostructure's interface, in which the InS layer can act as an electron donor, while the ZnIn₂S₄ layer acts as an electron acceptors. The absorption spectra of the InS/ZnIn₂S₄ heterostructure, as well as isolated InS and ZnIn₂S₄ monolayers, are displayed (https://www.wordhippo.com/what-is/another-word-for/display.html) in Fig. 3(d). Compared with InS and ZnIn₂S₄ monolayer, the InS/ZnIn₂S₄ heterostructure demonstrates improved light absorption in the visible short-wavelength region (approximately 300–500 nm), which is mainly due to the bandgap narrowing after the formation of the heterostructure.

Fig. 3. The projected band structure (a), projected DOS (b), band alignment (c), and absorption spectra (d) of the InS/ZnIn₂S₄ heterostructure using the vacuum energy levels as a common energy reference. E_g and E_F denote the energies of the bandgap and Fermi energy levels, respectively. The CBO and VBO are represented by blue and red arrows, respectively.

Fig. 4. The band alignments (a), band gaps (b), and charge transfer (c) of the InS/ZnIn₂S₄ heterostructure under different electric fields. (d) The η of the InS/ZnIn₂S₄ heterostructure as a function of ΔE_c and E^d_g under different electric fields.

Considering that the InS/ZnIn₂S₄ heterostructure possesses E_in, type-II band alignment, and significant absorption coefficients in the ultraviolet and visible light bands, it may exhibit high-efficiency performance in solar cells. To study the η of the InS/ZnIn₂S₄ heterostructure, we calculated the donor's bandgap (E^d_g), the ratio of the short-circuit current density to the AM1.5 solar flux (J_sc/P_solar), the conduction band offset (ΔE_c), open circuit voltage (V_oc), and η, as listed in Tables S2 and S3.† The J_sc/P_solar and V_oc of the InS/ZnIn₂S₄ heterostructure are 0.087 and 1.91 V, respectively, resulting in a η of 10.80%.

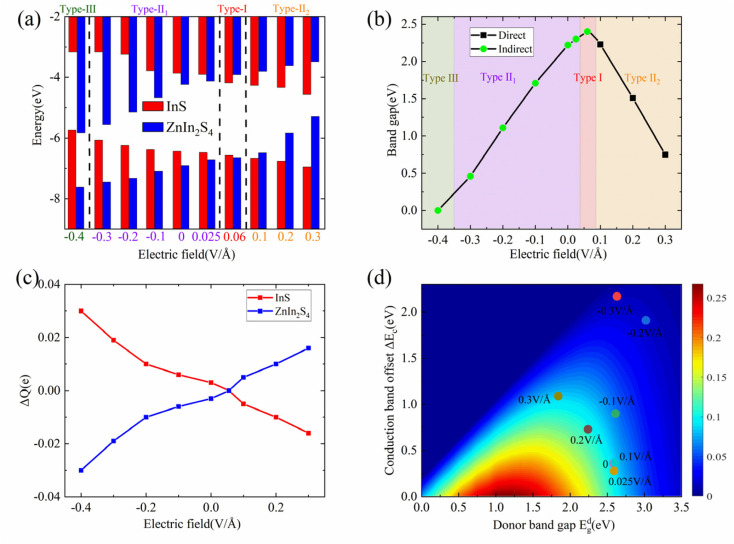
In practical applications, applying an external electric field (gate voltage) can modulate the characteristics of a given material. Here, we study the impact of a vertical electric field on the electronic band structure and band alignment of the InS/ZnIn₂S₄ heterostructure. The projected band structures and band alignments of the InS/ZnIn₂S₄ heterostructure under vertical electric fields (E_⊥) ranging from −0.4 to 0.3 V Å⁻¹ are presented in Fig. S2† and 4(a), where the direction of the positive electric field is set to point from the InS layer to ZnIn₂S₄ layer. We also calculate the interlayer charge transfer (ΔQ) of the InS/ZnIn₂S₄ heterostructure under different E_⊥, as depicted in Fig. 4(c).

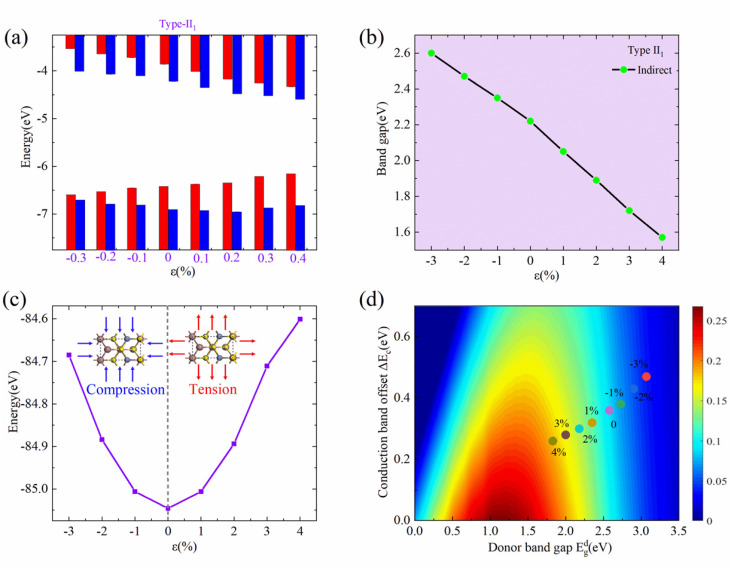
Under the positive E_⊥, the direction of E_in is opposite to that of E_⊥, and the band edge position of ZnIn₂S₄ layer will shifts upward with respect to that of the InS layer. When 0 < E_⊥ < 0.05 V Å⁻¹, the direction of the total electrical field (E_t) is the same as E_in, and there is a charge transfer from ZnIn₂S₄ to InS. The CBM and VBM of the ZnIn₂S₄ layer are both lower than those of the InS layer, and the heterostructure maintains a type-II₁ band alignment. With increasing E_⊥, the amount of ΔQ will decrease, and the CBO and VBO will both decrease. When 0.05 < E_⊥ < 0.09 V Å⁻¹, the direction of E_t is same as that for E_⊥, and there will be a charge transfer from InS to ZnIn₂S₄. The CBM of the ZnIn₂S₄ layer is higher than that of the InS layer, and the VBM of the ZnIn₂S₄ layer is lower than that of the InS layer. The heterostructure thus changes into a straddling type-I band alignment. At this point, both the CBM and VBM of the InS/ZnIn₂S₄ heterostructure are contributed by the InS layer, making it easier to form electron hole pairs during electron transitions. This makes it potentially applicable in optoelectronic devices such as light-emitting diodes and lasers. With the increase of E_⊥, the amount of ΔQ will increase, the CBO will increase, and VBO will further decrease. When 0.09 < E_⊥ < 0.3V Å⁻¹, the direction of E_t is also the same as that of E_⊥, and there will be a charge transfer from InS to ZnIn₂S₄. The CBM and VBM of the ZnIn₂S₄ layer both become higher than those of the InS layer, causing the heterostructure to transition into type-II₂ band alignment. With the increasing of E_⊥, the amount of ΔQ will increase, and the CBO and VBO will both increase.

Under a negative E_⊥, the E_in and E_⊥ have the same direction, so the direction of E_t consistently matches the E_in. There is a charge transfer (ΔQ) from ZnIn₂S₄ to InS. The band edge position of the ZnIn₂S₄ layer moves downwards relative to that of the InS layer. With the increasing of the E_⊥, the ΔQ will increase gradually, and the CBO and VBO will both increase gradually. When −0.35 < E_⊥ < 0.0V Å⁻¹, the CBM and VBM of the ZnIn₂S₄ layer both become lower than those of the InS layer, and the heterostructure can maintain a type-II₁ band alignment. When E_⊥ ≥ 0.35 V Å⁻¹, the VBM of InS becomes higher than the VBM and CBM of ZnIn₂S₄, and the band alignment of the heterostructure becomes type-III.

Moreover, the band gap size and type of the InS/ZnIn₂S₄ heterostructure are largely modulated by the electrical field, as displayed in Fig. 4(b). Under a positive E_⊥, as the E_⊥ is increasing, the band gap of the InS/ZnIn₂S₄ heterostructure will firstly increase and then decrease. Under a negative E_⊥, the band gap of the InS/ZnIn₂S₄ heterostructure will monotonically decrease with increasing E_⊥. The heterostructure can also change to a direct bandgap semiconductor when 0.09 < E_⊥ < 0.3V Å⁻¹.

Next, we attempt to explore the η of the InS/ZnIn₂S₄ heterostructure under different electric fields. As we know, to obtain a high η, a moderate E^d_g is desirable. This is because the V_oc will be enlarged and the J_sc/P_solar will be reduced by increasing E^d_g. Secondly, the ΔE_c is as low as possible to reduce the energy loss and obtain a high V_oc. The calculated E^d_g, J_sc/P_solar, ΔE_c, V_oc, and η of the heterostructure with type-II alignment under different E_⊥ are listed in Table S2.† When E_⊥ < 0, both E^d_g and ΔE_c will be enlarged, which result in J_sc/P_solar and V_oc both being reduced, so the η of the heterostructure becomes lower. When E_⊥ > 0, E^d_g will be enlarged and ΔE_c will be reduced. Subsequently, E^d_g will be reduced and ΔE_c will be enlarged, which result in J_sc/P_solar and V_oc exhibiting different varying trends. Hence, the η also exhibits a nonmonotonic variation. For E_⊥ = 0.2 V Å⁻¹ and 0.3 V Å⁻¹, the values of E^d_g are 2.24 eV and 1.84 eV, respectively, which may theoretically result in large η. However, when E_⊥ > 0.2 V Å⁻¹, the ΔE_c dramatically increases, reaching as high as 1.09 eV at E_⊥ = 0.3 V Å⁻¹. This results in a significant decrease in V_oc. The η can be increased up to 12.19% at E_⊥ = 0.2 V Å⁻¹, as shown Fig. 4(d) and Table S2.†

Strain engineering can also modulate the electronic properties and η of the semiconductor materials and their heterostructures.^17,19 Firstly, we attempt to examine the influence of biaxial strain (ε) on the electronic properties of the InS/ZnIn₂S₄ heterostructure. The biaxial strain (ε) is given by ε = (a − a₀)/a₀, where a and a₀ represent the lattice constants of the strained and unstrained heterostructure, respectively. The strength of ε ranging from −3% to 4% is considered, where a negative (positive) sign refers to compressive (tensile) strain. An increase in total energy is observed by applying a tensile or compressive strain, and the change in total energy is fitted to a quadratic curve, as depicted in Fig. 5(c). The electronic structure and band offset of the InS/ZnIn₂S₄ heterostructure under different ε are given in Fig. S3† and 5.

Fig. 5. The band alignments (a), band gaps (b), and the total energy (c) of the InS/ZnIn₂S₄ heterostructure under different biaxial strains. (d) The η of the InS/ZnIn₂S₄ heterostructure as a function of ΔE_c and E^d_g under different biaxial strains.

Under tensile strain, as the ε increases, the VBM of InS moves up and the CBM of ZnIn₂S₄ moves down, and the band gap of the InS/ZnIn₂S₄ heterostructure decreases linearly. At ε = 4%, the bandgap decreases from 2.21 eV to 1.57 eV. Under compressive strain, as the ε increases, the VBM of InS moves down and the CBM of ZnIn₂S₄ moves up, and the band gap of InS/ZnIn₂S₄ heterostructure increase linearly. At ε = −3%, the bandgap of the InS/ZnIn₂S₄ heterostructure is increased from 2.21 eV to 2.60 eV. Moreover, for −3% < ε < 4%, the InS/ZnIn₂S₄ heterostructure always maintains a type-II₁ band alignment, along with an indirect band gap. The InS/ZnIn₂S₄ heterostructure can maintain a stable Type II alignment under biaxial strain ranging from −3% to 4%, suggesting its potential as a stable candidate material for solar cells.

Next, we calculate the E^d_g, J_sc/P_solar, ΔE_c, V_oc, and η of the InS/ZnIn₂S₄ heterostructure under different ε, as summarized in Table S3.† Under tensive strain, E^d_g and ΔE_c decrease linearly with increasing strain, which result in the J_sc/P_solar being enlarged and the V_oc being reduced. Furthermore, the η values of the InS/ZnIn₂S₄ heterostructure are enlarged. When ε = 4%, a high η of 20.80% was achieved, as displayed in Fig. 5(d) and Table S3.† Under compressive strain, E^d_g and ΔE_c also increase linearly with increasing strain, which result in the J_sc/P_solar being reduced and the V_oc being increased. However, the η values of the InS/ZnIn₂S₄ heterostructure are significantly reduced. When ε = −3%, the η is reduced to 4.18%, as shown in Fig. 5(d) and Table S3.† Therefore, biaxial strain modulation could be an effective approach to increase the η.⁶⁴

4. Conclusions

In summary, we propose the two-dimensional InS/ZnIn₂S₄ heterostructure, and examine its electronic and optical characteristics using first principles calculations, focusing particularly on the band alignment and PCE. The AA stacking configuration is the most energetically favorable, possessing an indirect band gap of 2.21 eV and a large optical absorption coefficient in the short-wavelength visible region, along with a type-II₁ band alignment. Additionally, a significant η of 10.86% has been achieved. The band alignment and η of the InS/ZnIn₂S₄ heterostructure are largely modulated by applying an external electrical field or biaxial strain. The transformation of the band alignment from type-II₁ to type-I or type-II₂ can be induced by an external electric field, resulting in a further increase in η up to 12.19% at a positive E_⊥ = 0.2 V Å⁻¹. The type-II₁ band alignment remains stable within a critical biaxial strain of 4%, and a high η of 20.80% is achieved under a tensile strain of ε = 4%. This work is expected to provide new inspiration for improving solar cells with high PCE based on 2D InS/ZnIn₂S₄ heterostructures.

Data availability

The data supporting this study have been included within the article and its ESI.† Additional data will be made available on reasonable request.

Author contributions

Hui-Ying Liu: data curation (equal); formal analysis (equal); investigation (equal); writing – original draft (equal). Heng-Fu Lin: conceptualization (equal); formal analysis (equal); investigation (equal); supervision (equal); writing – review & editing (equal). Lu-Ya Xu: data curation (equal); formal analysis (equal); Ting-Ping Hou: conceptualization (equal); formal analysis (equal); investigation (equal); supervision (equal); writing – review & editing (equal). Nan-shu Liu: conceptualization (equal); formal analysis (equal); investigation (equal); supervision (equal); writing – review & editing (equal).

Conflicts of interest

The authors have no conflicts of interest.