Convergent Concordant Mode Approach for Molecular Vibrations: CMA-2

Abstract

The concordant mode approach (CMA) is a promising new scheme for dramatically increasing the system size and level of theory achievable in quantum chemical computations of molecular vibrational frequencies. Here, we achieve advances in the CMA hierarchy by computations targeting CCSD(T)/cc-pVTZ (coupled cluster singles and doubles with perturbative triples using a correlation-consistent polarized-valence triple-ζ basis set) benchmarks within the G2 molecular test set, executing a statistical analysis for 1501 frequencies from 111 compounds and then separately solving the refractory case of pyridine. First, MP2/cc-pVTZ (second-order Møller–Plesset perturbation theory with the same basis set) proves to be an excellent and preferred choice for generating the underlying (Level B) normal modes of the CMA scheme. Utilizing this Level B within the CMA-0A method reproduces the 1501 benchmark frequencies with a mean absolute error (MAE) of only 0.11 cm^–1 and an attendant standard deviation of 0.49 cm^–1. Second, a convergent CMA-2 method is constituted that allows efficient computation of higher level (Level A) frequencies to any reasonable accuracy threshold by using only Hartree–Fock (HF) and MP2 or density functional theory (DFT) data to generate ξ parameters, which select the sparse off-diagonal force field elements for explicit evaluation at Level A. When Level B = MP2/cc-pVTZ, a cutoff of ξ = 0.02 provides an average maximum absolute error per molecule of only 0.17 cm^–1 by incurring merely a 33% increase in average cost over CMA-0A. This CMA-2 method also eradicates the 4 problematic CMA-0A outliers of pyridine with even less effort (ξ = 0.04, 22% increase). Finally, the newly developed CMA procedures are shown to be highly successful when applied to 1-(1H-pyrrol-3-yl)ethanol, a new test molecule with diverse types of vibration.

1. Introduction

The force field for molecular vibrations is an indispensable tool for contemporary quantum chemistry, facilitating investigations on molecular structure, spectroscopy, and thermochemistry. Even after decades of research, transformative advances in the computation of force fields are still ongoing.¹ For highly accurate ab initio quantum chemical methods such as coupled cluster singles and doubles with perturbative triples [CCSD(T)], computing the vibrational Hessian fully analytically²⁻⁴ is possible for small systems but rapidly becomes intractable for larger molecules. Alternatively, one can numerically compute the Hessian using finite differences of analytic gradients or single-point energies, coarsely parallelizing the task. In such schemes, numerical differentiation is less resource-demanding and a necessity for theoretical methods for which analytical gradients or Hessians have not been implemented, let alone derived.

The number of single-point energies required to compute the force constants in a Hessian for a polyatomic molecule scales quadratically with the number of atoms in the molecule. Computations of CCSD(T)/cc-pVTZ quadratic force constants for systems with up to 500 basis functions and 75 vibrational degrees of freedom are still currently feasible in our laboratory, but the inherent scaling causes the full process to rapidly become intractable as the size of the system increases further. Rectilinear Cartesian displacement coordinates are often used as a basis for computing the force constants numerically; however, this set of coordinates is not optimal for describing molecular motion on inherently curvilinear potential energy surfaces. Employing intuitive curvilinear internal coordinates as a basis reduces the coupling encountered with rectilinear coordinates, and a litany of research exists on this topic.⁵⁻²¹ The Natural Internal Coordinates (NICs) of Pulay and co-workers are a trenchant choice for describing molecular vibrations.^22,23

NICs are linear combinations of chemically motivated internal coordinates, and algorithms exist for their automatic generation.²³ While NICs are a felicitous choice to represent the force field, it is difficult to know a priori which force constants are negligible. The subject of vibrational coordinate optimization for the potential energy surface beyond the harmonic approximation is well-researched.²⁴⁻²⁶ The optimal coordinates for the harmonic oscillator are the normal modes of vibration, which simultaneously diagonalize both the quadratic kinetic and potential energy matrices. Accordingly, to maximize the sparsity of the force constant matrix, the coordinates selected should target the normal mode basis.

A breakthrough solution for selecting vibrational coordinates is the recently developed Concordant Mode Approach (CMA),¹ whose protocol and notation scheme are fully specified in Section 3 below. The CMA-0A method is a highly accurate starting point centered on the computation of only diagonal force constants at the higher level theory A in a normal mode basis generated by a lower-level theory B. The remarkable accuracy of CMA-0A is demonstrated in the 1580 targeted CCSD(T)/cc-pVTZ benchmark vibrational frequencies of the G2 test set.²⁷ Utilizing NICs to represent the normal modes, out of the 1580 cases CMA-0A is successful in reducing all but three and seven frequency residuals to less than 2.5 cm^–1 for the Level B choices B3LYP/6-31G(2df,p) and CCSD(T)/cc-pVDZ, respectively. Simultaneously, CMA-0A reduces computational times by a factor of 7–10. A question not addressed in the initial study¹ is the choice of preferred Level B theory in the CMA protocol. Therefore, the first section of the present research investigates the overall performance of various Level B methods and makes some explicit recommendations.

The second section of this report focuses on the systematic convergence of the CMA methodology by an astute selection of limited off-diagonal force constants for explicit evaluation at Level A. Our introductory paper¹ formulated a CMA-1 method, where one hand-selects off-diagonal force constants, neglected in CMA-0, to eliminate frequency residuals. When a single off-diagonal force constant per molecule is introduced within CMA-1A(1)[A = CCSD(T)/cc-pVTZ, B = CCSD(T)/cc-pVDZ], all original CMA-0A outlier residuals of the G2 test set are reduced to below 1.2 cm^–1. While the aforementioned CMA-1A scheme is impressive, it is not intended to be a generally practical method, because the off-diagonal couplings were judiciously selected with full knowledge of the target Level A force constant matrix. Here we propose CMA-2, an a priori method of selecting off-diagonal force constants to manage cost and accuracy. An auxiliary force field is obtained with a method henceforth denoted as Level C at little or no additional cost in the Level B computation. In this paper, we investigate Hartree–Fock (HF) theory as Level C. The Level C force field is transformed into the Level B normal mode basis and then cast into a dimensionless matrix ξ. The matrix elements ξ_ij above a given threshold correspond to the Level A off-diagonal force constants to be explicitly computed in the CMA basis.

2. Computational Methods

The reference geometries optimized at the CCSD(T)/cc-pVTZ²⁸⁻³⁰ level of theory, their corresponding quadratic force constants, and the NICs chosen in our first CMA study¹ were also used in the present benchmark research on the G2 test set of molecules. In addition, the CCSD(T)/cc-pVDZ²⁸⁻³⁰ and B3LYP/6-31G(2df,p)³¹⁻³⁶ force constants which were previously computed¹ on top of the CCSD(T)/cc-pVTZ optimized geometries were once again employed with the caveat that symmetry was strictly enforced for all molecules, contrary to the first study where symmetry was only rigorously enforced for molecules belonging to non-Abelian symmetries. Normal modes of vibration that are the sole inhabitants of an irreducible representation will not mix with any other mode and are obtained exactly by all CMA methods. Such modes were retained in the statistical treatment of reference (1) but were omitted here in order improve measures of the efficacy of our CMA methods. For reasons discussed later in this work, pyridine is also omitted from our statistics and analyzed in greater detail in-text, reducing the number of frequencies considered in the G2 test set statistics to 1501. New force fields at the reference geometries were computed with CCSD, MP2,³⁸ density-fitted MP2 (df-MP2),^39,40 HF, and density-fitted HF (df-HF) electronic wave function methods, also complying with the full symmetry for all molecules.

As before,¹ the cc-pVXZ (X = D, T) basis sets^41,42 were employed for H and Li-F, while the corresponding cc-pV(X+d)Z basis sets⁴³ were chosen for Na-Cl in order to incorporate the flexibility of tight d-functions. For brevity, the +d designations are assumed but not listed in the basis set notations used here. The Level B quadratic force constants were computed in the NIC basis via finite differences with fourth-order accuracy, and the corresponding vibrational normal modes were computed with the GF-matrix method.⁴⁴ A displacement size of 0.01 or 0.005 in the units of the NICs was employed throughout.⁴⁴ The Level A reference force constants were transformed from the Cartesian basis to the normal mode basis of Level B to obtain the matrix F_CMA. In practical applications, the desired elements of F_CMA would be computed by finite differences of Level A energies. However, to completely eliminate numerical errors in the current benchmark research, we directly obtained CMA frequencies by zeroing out off-diagonal elements of F_CMA according to the CMA protocol being employed. The Molpro⁴⁵ program was used to compute any conventional CC, MP2, or HF energies, and the SCF and CC energy residuals were reduced to 10^–12 Hartrees upon convergence. The df-MP2 and df-HF results were computed with Psi4,⁴⁶ and the SCF energy residuals were converged to 10^–10 Hartrees in these cases. Core orbitals were frozen in all coupled cluster and MP2 computations. The optimized geometries and vibrational frequencies of the CCSD(T)/cc-pVTZ target theory, as well as the NICs employed, are compiled in the Supporting Information of this work.

3. CMA Protocol

The most general CMA protocol¹ can be summarized as follows:

• 1.Choose a complete (preferably chemically intuitive) set of nonredundant internal coordinates S.
• 2.Optimize the molecular geometry for computing the higher level theory A vibrational frequencies and for constructing the concordant modes at a lower-level of theory B, as denoted by CMA[Level A, Level B].
• 3.Solve the GF_B eigenproblem⁴⁴ after obtaining the lower-level force constants F_B. The nonorthogonal L_B eigenvector tensor yields the concordant normal modes (Q_B) according to S = L_BQ_B.
• 4.Adopt the ansatz F_A = (L^–1_B)^TF_CMA(A)L^–1_B, where F_A and F_CMA(A) are the force constants at higher level theory A in the S and Q_B basis sets, respectively. Minimally, the elements to be included in F_CMA(A) are the diagonal elements, whereas the transformation becomes exact if all elements are included.
• 5.Adopt a protocol (CMA-N) that specifies which elements of F_CMA(A) to explicitly compute via finite differences at the higher level of theory; the CMA-0, CMA-1, and CMA-2 variants discussed below are those currently available. A chosen displacement δQ_B can be mapped into a final set of Cartesian coordinates by iterative application of the linear relationship δx = uB^T_AG^–1_AL_B(δQ_B), where B_A is the customary B matrix for the S coordinates at the A reference geometry and u is a diagonal matrix of reciprocal atomic masses.^47,48
• 6.Transform the resulting F_CMA(A) to F_A, and then solve the GF_A eigenproblem to find the higher level A harmonic vibrational frequencies and corresponding normal modes.

In the CMA protocols labeled as (CMA-NA, CMA-NB), the Level B force constants are computed on top of the (Level A, Level B) optimum geometries. When necessary for clarity, the various levels of theory are appended in brackets to the end of the overarching protocol, such as CMA-0A[Level A, Level B] or CMA-2A[Level A, Level B, Level C]. All CMA variants require the diagonal elements of F_CMA(A) to be included, and the CMA-0A and CMA-0B variants include only these. In our first study,¹ CMA-0A was found to be more accurate than CMA-0B, since the underlying reference geometry is essential to the accurate prediction of second- and higher-order force constants.⁴⁷ The CMA-1(n) variant only differs from CMA-0 in that n hand-selected off-diagonal force constants are also chosen to be computed along with the diagonals. In the convergent CMA-2 method, the dimensionless matrix ξ is constructed via eq 1 from the Level C force field transformed to the Q_B normal mode basis [F_CMA(C)]:

1

In carrying out step 5 of the general protocol for the CMA-2 case, all matrix elements ξ_ij greater than a user-given threshold correspond to matrix elements of F_CMA(A) that will be explicitly computed.

4. Benchmarking Level B for CMA-0A

The CMA-0A procedure was executed for eight Level B theories, as summarized in Table 1. The deviation of the pure Level B results from the CCSD(T)/cc-pVTZ target is generally reduced by at least an order of magnitude for every summary statistic when CMA-0A is applied. The mean absolute error (MAE) is the same statistic designated as the mean absolute deviation (MAD) in our prior work;¹ MAE is used here to avoid confusion with common statistical definitions of MAD. The MAE of the CMA-0A residuals ranges from 0.11 to 1.09 cm^–1 for all Level B choices tested. The mean CMA residuals fall within a remarkably narrow range of 0.02 to 0.14 cm^–1, and the standard deviation (σ_ϵ) ranges from 0.36 to 4.93 cm^–1. The maximum absolute error (ϵ_MAX) over the entire G2 test set is between 3.4 and 11.6 cm^–1 for all CMA computations with correlated Level B theories, whereas Hartree–Fock proves to perform much more poorly in this regard. The MAEs for the zero-point vibrational energy (ZPVE) residuals (Δ) are a remarkably tight group of minuscule values across the Level B spectrum, ranging from 0.11 to 0.95 cm^–1; similarly, the standard deviation (σ_Δ) of the ZPVE Δ lies between 0.24 and 1.56 cm^–1. As observed earlier¹ a beneficial cancellation of individual frequency errors provides exceptional accuracy for the CMA-0A ZPVE values.

Table 1. Summary Statistics within the G2 Test Set^a of CMA-0A Residuals for CCSD(T)/cc-pVTZ Harmonic Vibrational Frequencies (ϵ, cm^–1) and ZPVEs (Δ, cm^–1) as Compared to the Corresponding Pure Level B Errors.

Level B		MAE ϵ	mean ϵ	ϵmaxb	σϵ	ϵMAXc	MAE Δ	mean Δ	σΔ
MP2/cc-pVTZd	pure	9.44	5.62	28.2	13.68	145	40.6	38.3	39.1
	CMA	0.11	0.02	0.54	0.49	9.3	0.12	0.12	0.24
df-MP2/cc-pVTZd,e	pure	9.00	5.19	27.2	12.55	146	37.9	35.6	32.0
	CMA	0.11	0.02	0.53	0.49	9.3	0.11	0.11	0.24
HF/cc-pVTZ	pure	56.92	54.95	94.7	34.41	251	374.4	371.5	294.7
	CMA	1.09	0.14	5.18	4.93	86.3	0.95	0.95	1.56
B3LYP/6-31G(2df,p)	pure	8.82	4.66	23.1	10.86	69	36.0	31.5	33.3
	CMA	0.16	0.04	0.59	0.36	3.4	0.27	0.27	0.32
CCSD(T)/cc-pVDZ	pure	47.54	47.12	120.0	54.46	173	319.0	318.6	244.6
	CMA	0.22	0.04	0.74	0.45	4.0	0.27	0.27	0.29
CCSD/cc-pVDZ	pure	54.34	54.05	128.2	53.55	165	365.5	365.5	267.4
	CMA	0.23	0.04	0.77	0.46	3.6	0.29	0.29	0.29
MP2/cc-pVDZd	pure	52.52	52.15	139.4	60.38	213	355.3	355.3	253.4
	CMA	0.32	0.06	1.18	0.83	11.6	0.38	0.38	0.41
HF/cc-pVDZ	pure	85.11	83.88	132.8	47.55	247	567.8	567.1	440.4
	CMA	0.72	0.12	3.45	3.02	58.4	0.81	0.81	1.17

^aThe instructive case of pyridine is omitted from these statistics and dissected in a later section, leaving 1501 frequencies in the data set.

^bAverage maximum absolute ϵ per molecule.

^cMaximum absolute ϵ over the entire data set.

^dExcluding ω₃(O₃), for which MP2 is a catastrophic failure.⁴⁹

^eExcluding ω₃(NO₂), for which df-MP2 in Psi4 does not run successfully.

For a deeper analysis, we first focus on the CMA-0A results in which a cc-pVDZ basis set was used for Level B. Both CMA-0A with B = CCSD/cc-pVDZ and B = CCSD(T)/cc-pVDZ perform very well, and there is no significant statistical difference differentiating the two. The CMA-0A MP2/cc-pVDZ statistics are almost as good as the coupled cluster results, making MP2 a promising candidate as a Level B theory which scales as N⁵ with basis set size, compared to the N⁶ and N⁷ scaling of conventional CCSD and CCSD(T), respectively. The CMA HF/cc-pVDZ results do not compare as well, displaying a standard deviation (3.02 cm^–1) and maximum absolute residual (58.4 cm^–1) that are considerably larger than the corresponding coupled cluster results. Apparently, even a minimal treatment of electron correlation in Level B is important in CMA computations targeting CCSD(T)/cc-pVTZ frequencies. Nonetheless, HF may still be an apt Level B for obtaining ZPVEs, as its MAE is only 0.81 cm^–1.

We now turn our attention to the CMA-0A results for which the larger cc-pVTZ and 6-31G(2df,p) basis sets are used. Selecting Level B = MP2/cc-pVTZ gives the best MAE (0.11 cm^–1) and mean error (+0.02 cm^–1). The conventional and density-fitted MP2 results are nearly indistinguishable, a quite promising finding because df-MP2 scales as N⁴ with basis set size, compared to the N⁵ scaling of conventional MP2. The summary statistics for the HF residuals once again show that electron correlation should be included at Level B, but not necessarily in ZPVE computations. While B3LYP/6-31G(2df,p) yields excellent CMA-0A results, this DFT method is outperformed by both MP2/cc-pVTZ and df-MP2/cc-pVTZ for the MAE ϵ, mean ϵ, ϵ_max, and ZPVE statistics. The only caveat is that MP2 and df-MP2 tend to exhibit a few larger maximum absolute residuals; for example, in six out of 1501 cases this quantity is greater than 4 cm^–1 for MP2/cc-pVTZ. Overall, the summary statistics indicate that basis set quality is more important than higher-order treatment of electron correlation in the selection of Level B. Pending further research, the key conclusion is that if one is targeting CCSD(T)/cc-pVXZ frequencies with the CMA-0A approach, then MP2/cc-pVXZ or its df-variant is the preferred Level B method.

5. Development of CMA-2A Theory

For the purpose of developing a convergent CMA-2 theory, in this section we consider a CMA outlier as any frequency residual greater than 1.5 cm^–1 in magnitude. Such outliers for CMA-0A[CCSD(T)/cc-pVTZ, MP2/cc-pVTZ] are presented in Table 2, where 16 cases are found from 9 distinct molecules out of the test set of 1501 frequencies. The size of these residuals ranges from 1.56 to 9.34 cm^–1. Pyridine presented a unique challenge to CMA-0A with four outliers at −22.61, −6.46, 4.87, and 27.60 cm^–1. Because this molecule proved to be so abnormal, it is excluded from the statistics in Table 2 and treated in greater detail below. When the vibrational modes highlighted in Table 2 are treated by CMA-1A(1) (fifth column), all absolute residuals are less than 1.2 cm^–1. In other words, the inclusion of a single off-diagonal force constant per molecule is sufficient to make all outliers disappear! This mathematical fact shows that CMA-0A is tantalizingly close to being a flawless method for this limited test set. However, finding the optimal mathematical solution without prior knowledge of the full force constant matrix remains a considerable challenge. There may be circumstances in which chemical principles can effectively guide one to choose the correct mode couplings, but the development of a generally applicable, automated approach is clearly warranted.

Table 2. Only Cases within the Set of 1501 Benchmark Frequencies with CMA-0A[CCSD(T)/cc-pVTZ, MP2/cc-pVTZ] Residuals (ϵ, cm^–1) Greater than 1.5 cm^–1 in Magnitude, Together with the Corresponding CMA-1A and CMA-2A Results That Target These Outliers.

Molecule and mode	Description	Benchmark	ϵ[CMA-0A]	ϵ[CMA-1A(1)]	ϵ[CMA-2A](n)a	ηb (%)
nitrous oxide, ω3(σ)	sym. stretch	1297.09	9.34	0.00	0.00 (1)	25
ketene, ω9(b2)	C=C=O bend	514.86	7.12	0.00	0.00 (2)	22
ketene, ω8(b2)	CH2 wag	584.48	–6.28	0.00	0.00 (2)	22
nitrous oxide, ω1(σ)	antisym. stretch	2282.57	–5.33	0.00	0.00 (1)	25
benzene, ω18(b1u)	ring def.	1158.88	4.90	0.00	0.00 (10)	36
benzene, ω17(b1u)	ring def.	1328.17	–4.29	0.00	0.00 (10)	36
spiropentane, ω4(a1)	ring breathing	1054.41	3.67	0.00	0.03 (7)	21
spiropentane, ω3(a1)	sym. CH2 wag	1076.02	–3.60	0.01	0.01 (7)	21
methyl nitrite, ω12(a)	N–O stretch	595.01	3.55	0.68	–0.12 (9)	60
nitromethane, ω4(a)	NO2 rock	1642.57	–2.87	–1.11	0.04 (13)	87
nitromethane, ω10(a)	CH3 rock	1110.76	2.71	0.12	0.12 (13)	87
n–butane, ω28(bu)	CH3 stretch	3028.05	1.81	0.00	1.81 (10)	28
n–butane, ω29(bu)	CH2 stretch	3023.91	–1.79	–0.03	–1.79 (10)	28
aziridine, ω1(a′)	CH2 rock	783.89	1.76	1.19	1.11 (12)	67
isobutane, ω3(a1)	CH stretch	3019.64	1.62	0.02	1.62 (5)	14
isobutane, ω2(a1)	CH3 sym. stretch	3024.21	–1.56	0.04	–1.56 (5)	14

^an = the number of off-diagonal elements included for the ξ = 0.020 cutoff.

^bη = number of F_CMA(A) off-diagonal elements included as a percentage of the vibrational degrees of freedom for the given molecule.

An algorithm for automatically selecting off-diagonal force constants should have a variable tolerance so that the user has ultimate control over the cost and accuracy of a convergent CMA protocol. A diagnostic can be imagined with matrix elements that correctly predict the importance of off-diagonal force constants of F_CMA(A). A simple approach would be to compute another set of force constants at a level of theory C in the Q_B normal mode basis, such that the magnitude of F_CMA(C) off-diagonal force constants mimics the ordering of the F_CMA(A) elements. Preferably, this third Level C should scale better than theory B, and the ideal circumstance would not incur any additional computational cost. If B = MP2/cc-pVXZ single-point energies are computed to target A = CCSD(T)/cc-pVXZ frequencies using CMA, then the C = HF/cc-pVXZ quadratic force field can indeed be obtained without extra cost.

With this choice, the level of theory manifestly increases in the sequence C → B → A. Because F_CMA(B) is a strictly diagonal matrix by construction, then the F_CMA(C) off-diagonal elements of greatest size directly indicate which couplings in the molecule are most sensitive to the C → B increase in level of theory. These are precisely the couplings that are expected to yield significant nonzero values for the off-diagonal elements of F_CMA(A) as a consequence of the B → A change in level of theory. In this sense, F_CMA(C) can be considered a photographic negative of F_CMA(A), although this characterization is not meant to imply that the coupling elements in these matrices are always opposite in sign. In order to translate this correspondence into a viable, universal diagnostic for identifying which parts of F_CMA(A) should be explicitly computed, the F_CMA(C) off-diagonal elements should be cast into a dimensionless form that also takes into account their size relative to the associated diagonal force constants. For this purpose we have adopted eq 1 to define the ξ_ij diagnostics for our CMA-2 theory.

For the remainder of the study, when Level B is a correlated wave function method such as CCSD or MP2 with a cc-pVXZ basis set, then Level C is chosen as HF/cc-pVXZ so that C → B → A forms a series of increasing electron correlation with a fixed basis set. When B = B3LYP/6-31G(2df,p), we have employed C = HF/6-31G(2df,p) for lack of a more transparent choice, even though extra cost is incurred because a second set of SCF orbitals must be optimized. The CMA-2A protocol that incorporates all F_CMA force constants corresponding to ξ > 0.020 is assessed in Table 2. Overall, 12 of the 16 outliers are successfully eliminated by CMA-2A (|ϵ| < 1.11 cm^–1). The remaining four residuals are hardly significant, corresponding to the (1.81, −1.79) and (1.62, −1.56) cm^–1 pairs for (ω₂₈, ω₂₉) and (ω₃, ω₂) of n-butane and isobutane, respectively. For the (n-butane, isobutane) C–H stretching modes, the ξ cutoff identified (10, 5) off-diagonal elements for explicit evaluation at Level A, but the key coupling discovered in CMA-1A(1) that eliminates these outliers escaped inclusion. The η parameter appearing in Table 2 is equal to the number of included off-diagonal F_CMA elements as a percentage of the molecular vibrational degrees of freedom that are present. This metric turns out to also be very nearly the percentage increase in computational cost in going beyond CMA-0A to CMA-2A. Demonstrating the success of CMA-2A with a ξ = 0.020 cutoff, 8 of the outliers are eliminated with η < 37%, and in the remaining instances η = 60–87%. Given that CMA-0A already reduces the cost of Level A frequency computations by 700–1000%,¹ any η value less than 100% still constitutes a rather marginal price to pay for the added certainty afforded by CMA-2A.

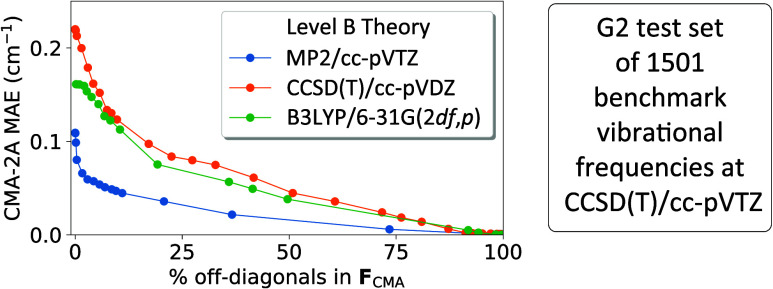
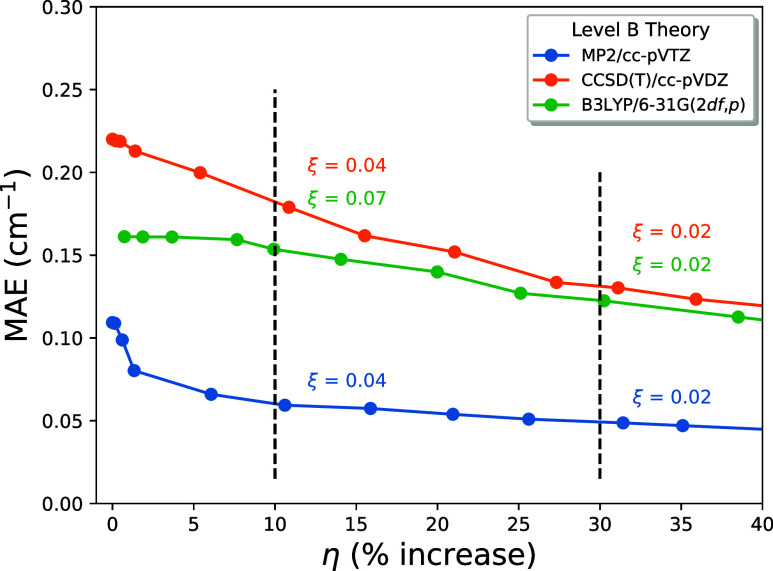
The performance of CMA-2A for the entire data set of CCSD(T)/cc-pVTZ benchmark frequencies is illustrated in Figure 1, where the MAE is plotted vs η. It is abundantly clear from the curves that MP2/cc-pVTZ (blue) is once again superior to both CCSD(T)/cc-pVDZ (orange) and B3LYP/6-31G(2df,p) (green); hence, B = MP2/cc-pVTZ is the method of choice for both CMA-0A and CMA-2A. In this case an increase in cost of only 10% is sufficient to lower the MAE to a mere 0.06 cm^–1! The corresponding blue curve has an underlying ξ = 0.040 cutoff at η = 10%, and any further reduction of ξ improves the MAE very little. In contrast, the B = CCSD(T)/cc-pVDZ curve reveals a steady MAE reduction as η ranges up to 40% and as the ξ cutoff is diminished to 0.020. While not optimal, this choice of Level B still provides excellent final results once CMA-2A is applied. Although B = B3LYP/6-31G(2df,p) achieves much success in CMA-0A, the lag in further improvement via CMA-2A is somewhat disappointing, presumably because the C → B → A series is not systematic in this circumstance.

Figure 1.

CMA-2A MAE of the 1501 CCSD(T)/cc-pVTZ benchmark frequencies plotted as a function of η, where Level C = HF and the basis set is the same as employed in Level B.

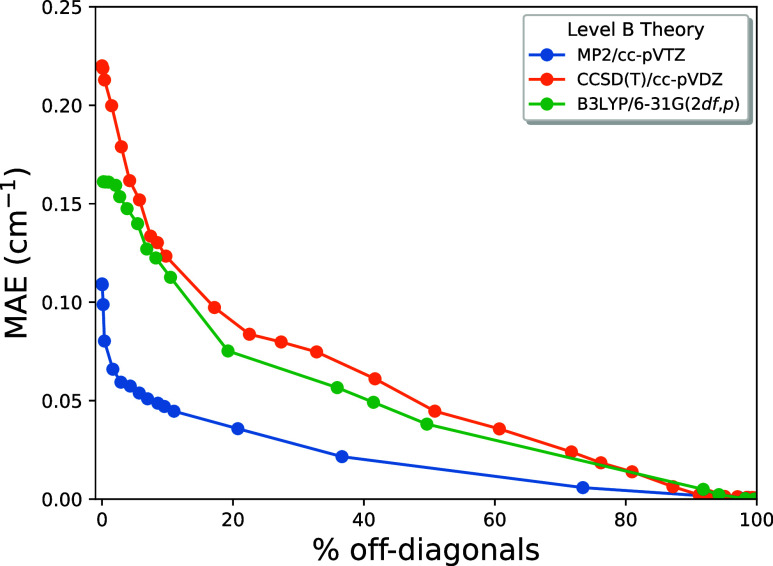
It is worth emphasizing that the maximum value of η in Figure 1 still corresponds to a very small fraction of off-diagonal elements included in F_CMA. In order to reveal the asymptotic nature of CMA-2A, the MAE over the entire data set is plotted against the percent of included nonzero F_CMA off-diagonals in Figure 2. Of course, all the MAE curves must decay to zero when 100% of the off-diagonals are explicitly computed. For all intents and purposes, this asymptotic value is reached at the 90% mark on the abscissa, regardless of the choice of Level B. The key point of Figure 2 is that CMA-2A is truly a convergent method, and the smooth and rapid decay of the blue curve for B = MP2/cc-pVTZ shows how striking the performance can be. Statistics for the overall performance of CMA-2A on the benchmark frequencies are collected in Table 3, where MAE ϵ, σ_ϵ, ϵ_max, ϵ_MAX, and η are given as the ξ cutoff ranges from 0.005 to ∞ and as Level B is varied. These data allow the CMA-2A user to make a wise choice for ξ and Level B in accord with the accuracy goals and computational costs of the chemical application at hand. A salient feature of Table 3 is that the MAE, standard deviation, and largest residual per molecule all converge much more rapidly as the ξ cutoff is made more stringent when B = MP2/cc-pVTZ as compared to B = CCSD(T)/cc-pVDZ or B3LYP/6-31G(2df,p). This observation further amplifies the conclusions from Figures 1 and 2 on the selection of Level B. Because MAE ϵ, σ_ϵ, and ϵ_max are already much less than 1 cm^–1 when no off-diagonal elements of F_CMA are accounted for (ξ cutoff = ∞), CMA-0A will be more than sufficient in a preponderance of applications. However, a very low probability remains that an isolated frequency error might occur on the order of ϵ_MAX. Informed by Table 3, the user can apply CMA-2A to eliminate this concern, while still maintaining vast savings in computing the harmonic frequencies of the molecule at higher level A. For example, application of CMA-2A with our recommended Level B = MP2/cc-pVTZ and a ξ cutoff of 0.02 yields truly outstanding accuracy while only increasing the average cost by 33% over CMA-0A. The convincing residual statistics in this case can be spelled out as follows: mean absolute error = 0.047 cm^–1, average maximum absolute residual per molecule = 0.17 cm^–1, standard deviation of residuals = 0.15 cm^–1, and global maximum absolute residual = 1.81 cm^–1.

Figure 2.

CMA-2A MAE of the 1501 CCSD(T)/cc-pVTZ benchmark frequencies plotted as a function of % nonzero off-diagonal matrix elements included in F_CMA(A).

Table 3. Metrics for CMA-2A Performance of the 1501 CCSD(T)/cc-pVTZ Benchmark Frequencies as a Function of the ξ Cutoff and the Choice of Level B^a.

	B = MP2/cc-pVTZ					B = CCSD(T)/cc-pVDZ					B = B3LYP/6-31G(2df,p)
ξ Cutoff	MAE ϵ	ϵmax	σϵ	ϵMAX	η (%)	MAE ϵ	ϵmax	σϵ	ϵMAX	η (%)	MAE ϵ	ϵmax	σϵ	ϵMAX	η (%)
∞	0.11	0.54	0.49	9.34	0	0.22	0.74	0.45	3.96	0	0.16	0.59	0.36	3.42	0
0.20	0.099	0.45	0.40	7.12	0.6	0.22	0.73	0.45	3.96	0.5	0.16	0.58	0.36	3.42	7.7
0.18	0.099	0.45	0.40	7.12	0.7	0.22	0.73	0.45	3.96	0.5	0.16	0.58	0.36	3.42	7.8
0.16	0.093	0.40	0.37	7.12	0.8	0.22	0.73	0.45	3.96	0.6	0.16	0.58	0.36	3.42	7.9
0.14	0.093	0.40	0.37	7.12	0.8	0.22	0.73	0.45	3.96	0.9	0.16	0.58	0.35	3.42	8.1
0.12	0.081	0.33	0.25	3.67	1.0	0.22	0.72	0.45	3.96	1.0	0.16	0.58	0.35	3.42	8.4
0.10	0.080	0.32	0.25	3.67	1.3	0.21	0.72	0.44	3.96	1.4	0.16	0.56	0.35	3.42	8.8
0.08	0.079	0.32	0.25	3.67	1.9	0.21	0.73	0.44	3.96	1.8	0.15	0.55	0.35	3.42	9.3
0.06	0.070	0.27	0.21	3.55	4.3	0.21	0.71	0.44	3.96	3.1	0.15	0.55	0.35	3.42	11
0.04	0.059	0.22	0.18	2.78	11	0.19	0.62	0.39	2.87	8.2	0.15	0.53	0.34	3.42	14
0.02	0.047	0.17	0.15	1.81	33	0.13	0.40	0.28	2.56	29	0.12	0.39	0.28	2.77	33
0.01	0.036	0.14	0.13	1.81	76	0.10	0.29	0.23	2.66	63	0.08	0.25	0.20	2.77	71
0.005	0.022	0.10	0.11	1.81	135	0.07	0.24	0.20	2.68	121	0.06	0.20	0.18	2.77	132

^aSee footnotes to Tables 1 and 2 for definitions of the metrics. Level C = HF with the same basis used for Level B.

6. Solution of the Pyridine Problem

The unusual behavior of pyridine in CMA applications demands that this molecule be analyzed in greater detail as an instructive, isolated benchmark species rather than as an outlier that excessively skews the statistics of the G2 test set. Pyridine is depicted in Figure 3 with atomic labeling, and corresponding NICs for our CMA analyses are defined in Table 4. The ring coordinates are constructed with the 6-fold symmetry of a regular hexagon, but the CMA frequencies would be mathematically invariant if linear combinations were made only with the C_2v symmetry of pyridine itself.

Figure 3.

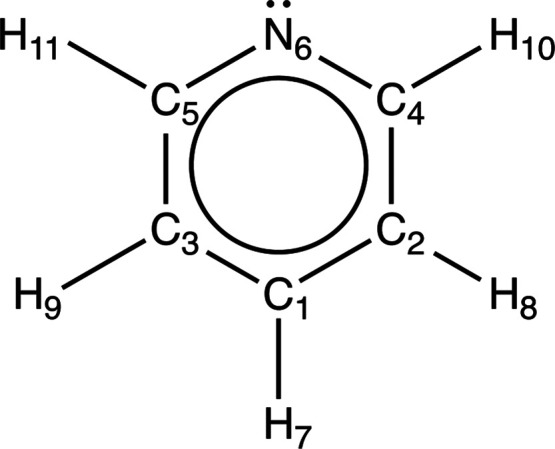
Enumerated carbon backbone of pyridine, corresponding to selected internal coordinates utilized for all CMA computations.

Table 4. Pyridine Natural Internal Coordinates for CMA Applications.

Description	Unnormalized natural internal coordinatea
ring breathing	S1(a1) = r(5,3) + r(3,1) + r(1,2) + r(2,4) + r(4,6) + r(6,5)
ring stretching def.	S2(b2) = r(5,3) – r(3,1) + r(1,2) – r(2,4) + r(4,6) – r(6,5)
ring stretching def.	S3(a1) = 2r(5,3) – r(3,1) – r(1,2) + 2r(2,4) – r(4,6) – r(6,5)
ring stretching def.	S4(b2) = 2r(5,3) + r(3,1) – r(1,2) – 2r(2,4) – r(4,6) + r(6,5)
ring stretching def.	S5(a1) = r(3,1) + r(1,2) – r(4,6) – r(6,5)
ring stretching def.	S6(b2) = r(3,1) – r(1,2) + r(4,6) – r(6,5)
sym. CH stretch	S7(a1) = r(5,11) + r(4,10)
antisym. CH stretch	S8(b2) = r(5,11) – r(4,10)
sym. CH stretch	S9(a1) = r(3,9) + r(2,8)
antisym. CH stretch	S10(b2) = r(3,9) – r(2,8)
CH stretch	S11(a1) = r(1,7)
ring stellation	S12(a1) = θ(4,6,5) – θ(6,5,3) + θ(5,3,1) – θ(3,1,2) + θ(1,2,4) – θ(2,4,6)
ring rectangulation	S13(a1) = 2θ(4,6,5) – θ(6,5,3) – θ(5,3,1) + 2θ(3,1,2) – θ(1,2,4) – θ(2,4,6)
ring shearing	S14(b2) = θ(6,5,3) – θ(5,3,1) + θ(1,2,4) – θ(2,4,6)
sym. i.p. CH rock	S15(a1) = θ(11,5,6) – θ(11,5,3) + θ(10,4,6) – θ(10,4,2)
antisym. i.p. CH rock	S16(b2) = θ(11,5,6) – θ(11,5,3) – θ(10,4,6) + θ(10,4,2)
sym. i.p. CH rock	S17(a1) = θ(9,3,5) – θ(9,3,1) + θ(8,2,4) – θ(8,2,1)
antisym. i.p. CH rock	S18(b2) = θ(9,3,5) – θ(9,3,1) – θ(8,2,4) + θ(8,2,1)
i.p. CH rock	S19(b2) = θ(7,1,2) – θ(7,1,3)
chair ring pucker	S20(b1) = τ(6,5,3,1) + τ(3,1,2,4) – τ(5,3,1,2) – τ(1,2,4,6) + τ(2,4,6,5) – τ(4,6,5,3)
boat ring pucker	S21(b1) = τ(3,1,2,4) – τ(5,3,1,2) – τ(2,4,6,5) + τ(4,6,5,3)
ring twist	S22(a2) = 2τ(6,5,3,1) – τ(5,3,1,2) – τ(3,1,2,4) + 2τ(1,2,4,6) – τ(2,4,6,5) – τ(4,6,5,3)
sym. o.o.p. CH wag	S23(b1) = γ(11,5,3,6) + γ(10,4,6,2)
antisym. o.o.p. CH wag	S24(a2) = γ(11,5,3,6) – γ(10,4,6,2)
sym. o.o.p. CH wag	S25(b1) = γ(9,3,1,5) + γ(8,2,4,1)
antisym. o.o.p. CH wag	S26(a2) = γ(9,3,1,5) – γ(8,2,4,1)
o.o.p. CH wag	S27(b1) = γ(7,1,2,3)

^ar(i,j) = i–j bond distance; θ(i,j,k) = i–j–k bond angle; τ(i,j,k,l) = dihedral angle between i–j–k and j–k–l plane; γ(i,j,k,l) = signed angle of i–j bond out of the k–j–l plane.

Comprehensive results for pyridine frequencies are listed in Table 5, where residuals for all modes with respect to the CCSD(T)/cc-pVTZ reference values are provided for seven different treatments: CMA-0A with B = CCSD(T)/cc-pVDZ, MP2/cc-pVTZ, B3LYP/6-31G(2df,p), CCSD/cc-pVTZ, and MP4/cc-pVTZ, as well as CMA-2A with B = MP2/cc-pVTZ (ξ = 0.04) and CCSD(T)/cc-pVDZ (ξ = 0.015). First we focus on the CMA-0A outlier residuals greater than 1.5 cm^–1 in magnitude that are highlighted in boldface in Table 5. With B = CCSD(T)/cc-pVDZ, five such residuals appear of modest size, (ϵ₈, ϵ₉, ϵ₁₆, ϵ₁₇, ϵ₂₅) = (−3.24, 4.61, −1.58, 2.46, 2.50) cm^–1. With B = MP2/cc-pVTZ, a clustered set of four much larger residuals crops up, (ϵ₂₂, ϵ₂₃, ϵ₂₄, ϵ₂₅) = (−6.46, −22.61, 27.60, 4.87) cm^–1, despite the fact this method is the clear overall champion for CMA applications within the G2 test set. One infers that both orbital basis set and electron correlation effects are unusually important for the normal modes of pyridine, because there is little overlap among the cases for which these two Level B methods struggle. Quite surprisingly, when B = B3LYP/6-31G(2df,p) all the CMA-0A residuals (|ϵ| < 0.8 cm^–1) are well below the outlier threshold, and thus this method happens to capture both the basis set and correlation effects present in the CCSD(T)/cc-pVTZ normal modes of pyridine. While CMA-0A with B = CCSD/cc-pVTZ generally performs better than with B = MP2/cc-pVTZ, the large outliers (ϵ₂₄, ϵ₂₅) = (−18.15, 19.79) cm^–1 still remain, the latter of which represents a considerable deterioration. This occurrence suggests that the triple-excitation effects described by the (T) correlation correction are an essential component in the physical description of the normal modes of pyridine. While MP4 is a largely defunct method in modern computational chemistry, correlation terms within this theory inspired the (T) ansatz.²⁸ It is thus compelling that the two problematic outliers for B = CCSD/cc-pVTZ are greatly diminished to (ϵ₂₄, ϵ₂₅) = (−1.56, 2.00) cm^–1 when B = MP4/cc-pVTZ is invoked.

Table 5. CMA-0A and CMA-2A Residuals (ϵ, cm^–1) for CCSD(T)/cc-pVTZ Harmonic Frequencies (ω_ref, cm^–1) of Pyridine Obtained with Various Level B Methods.

Mode	Description	ωref	ϵ[CMA-0A]					ϵ[CMA-2A]
			B = CCSD(T)/cc-pVDZ	B = MP2/cc-pVTZ	B = B3LYP/6-31G(2df,p)	B = CCSD/cc-pVTZ	B = MP4/cc-pVTZ	B = CCSD(T)/cc-pVDZa	B = MP2/cc-pVTZb
ω1(a1)	sym. CH str.	3212.85	–0.01	–0.05	–0.03	0.00	0.00	–0.01	–0.06
ω2(a1)	asym. CH str.	3187.57	–0.01	0.01	–0.08	–0.01	0.00	0.03	0.06
ω3(a1)	asym. CH str.	3169.83	0.01	0.05	0.08	0.01	0.01	–0.03	0.02
ω4(a1)	ring str. def.	1630.29	–0.47	–0.21	–0.02	–0.01	–0.06	–0.01	–0.18
ω5(a1)	sym. CH rock	1510.12	–0.48	0.10	–0.05	0.01	0.04	–0.15	0.10
ω6(a1)	asym. CH rock	1236.72	0.50	0.08	0.03	0.00	0.02	–0.02	0.08
ω7(a1)	sym. CH rock	1087.86	–0.37	–0.07	0.00	0.00	–0.06	–0.89	–0.07
ω8(a1)	ring stellation	1043.14	–3.24	0.00	–0.16	0.00	–0.02	1.06	0.00
ω9(a1)	ring breathing	1001.24	4.61	0.16	0.30	0.01	0.10	0.14	0.17
ω10(a1)	ring rectangle	603.31	0.10	0.02	0.08	0.01	0.01	0.03	0.02
ω11(a2)	asym. CH wag	995.11	–0.01	–0.51	–0.04	–0.01	–0.11	–0.01	–0.50
ω12(a2)	asym. CH wag	890.79	0.00	0.56	0.02	0.01	0.12	0.00	0.56
ω13(a2)	ring twist	378.44	0.01	0.01	0.06	0.01	0.02	0.01	0.01
ω14(b1)	asym. CH wag	996.87	–0.69	–0.41	–0.11	–0.06	–0.06	–0.15	–0.16
ω15(b1)	sym. CH wag	953.64	0.02	0.12	–0.02	0.01	0.03	0.12	0.12
ω16(b1)	ring chair	753.17	–1.58	0.02	0.03	–0.02	–0.14	0.00	–0.30
ω17(b1)	sym. CH wag	711.89	2.46	0.36	0.12	0.08	0.19	0.03	0.36
ω18(b1)	ring boat	409.22	0.21	0.01	0.03	0.00	0.00	0.03	0.01
ω19(b2)	asym. CH str.	3204.49	–0.01	–0.03	–0.02	0.00	–0.01	0.00	–0.02
ω20(b2)	asym. CH str.	3168.42	0.00	0.03	–0.04	0.00	0.01	–0.01	0.00
ω21(b2)	ring str. def.	1618.43	–0.50	–0.46	–0.01	–0.04	–0.03	–0.25	–0.48
ω22(b2)	ring str. def.	1464.66	–1.02	–6.46	–0.10	–0.17	–0.18	0.17	0.06
ω23(b2)	sym. CH wag	1379.21	–1.34	–22.61	–0.12	–0.04	–0.06	0.04	0.29
ω24(b2)	ring str. def.	1266.95	0.38	27.60	–0.37	–18.15	–1.56	–0.01	–1.05
ω25(b2)	asym. CH wag	1158.82	2.50	4.87	0.75	19.79	2.00	0.02	1.30
ω26(b2)	ring str. def.	1071.35	0.65	0.07	0.07	0.05	0.02	0.09	0.07
ω27(b2)	ring shearing	656.98	0.11	0.01	0.02	0.01	0.00	0.03	0.01

^aξ cutoff = 0.015, η = 74%, and n = 20 off-diagonals included.

^bξ cutoff = 0.04, η = 22%, and n = 6 off-diagonals included.

The outlier normal modes of pyridine are quantitatively characterized by the total energy distributions (TEDs)⁵⁰⁻⁵² provided in Table 6, where the classical vibrational energy of each mode k is decomposed into the predominant percentage contributions n attributable to the NICs S_i. When B = CCSD(T)/cc-pVDZ, all of the outliers with |ϵ| > 1.5 cm^–1 are removed by merely adding three off-diagonal force constants that couple the (ω₈, ω₉), (ω₁₆, ω₁₇), and (ω₂₄, ω₂₅) pairs, in accord with our earlier CMA-1A analysis of pyridine.¹Table 6 shows that these three pairs mostly involve strong remixing of [S₁(a₁), S₁₂(a₁)], [S₂₀(b₁), S₂₅(b₁)], and [S₂(b₂), S₁₈(b₂), S₁₉(b₂)], respectively, which Table 4 in turn identifies as the vibrations (ring breathing, ring stellation), [chair ring pucker, out-of-plane (C₂–H₈) + (C₃–H₉) wag], and [ring stretch deformation, (C₂–H₈) – (C₃–H₉) in-plane rock, (C₁–H₇) in-plane rock]. The cluster of 4 outliers for B = MP2/cc-pVTZ does not exhibit simple remixing vis-à-vis the CCSD(T)/cc-pVTZ target modes. Once again S₂(b₂), S₁₈(b₂), and S₁₉(b₂) are culprits, but now the fray is joined by an alternative ring stretching deformation S₄(b₂) and the (C₄–H₁₀) – (C₅–H₁₁) in-plane rock S₁₆(b₂). The two large outliers for B = CCSD/cc-pVTZ have similar origins as in the MP2 case, but the vibrational interactions are less intricate and mostly restricted to the [S₂(b₂), S₁₈(b₂), S₁₉(b₂)] set; accordingly, a single (ω₂₄, ω₂₅) coupling within CMA-1A(1) eliminates these outliers. Collectively, the TED analyses in Table 6 suggest that CMA-0A might generally encounter difficulties with aromatic ring vibrations that couple antisymmetric ring stretching deformations with CH in-plane rocks of the same symmetry. Indeed, our work has also found some moderate residuals up to 5 cm^–1 in size for these types of vibrations in benzene, pyrrole, and furan.

Table 6. Total Energy Distributions (TEDs) for the Outlier Modes of Pyridine at Various Levels of Theory.

Mode	Frequency (cm–1)	TEDa
CCSD(T)/cc-pVTZ
ω8(a1)	1043.14	S12(51) + S1(33) + S5(13)
ω9(a1)	1001.24	S1(65) – S12(32)
ω16(b1)	753.17	S20(68) – S25(15) – S27(13)
ω17(b1)	711.89	S20(53) + S25(27) + S27(10) + S23(9)
ω22(b2)	1464.66	S4(32) – S18(25) + S19(20) + S16(15)
ω23(b2)	1379.21	S16(67) + S18(18) – S19(13)
ω24(b2)	1266.95	S2(78) + S6(8) – S19(8) – S18(7)
ω25(b2)	1158.82	S18(36) + S19(35) + S2(20) – S6(8)
CMA-0A[CCSD(T)/cc-pVTZ, CCSD(T)/cc-pVDZ]
ω8(a1)	1039.90	S1(64) + S12(30)
ω9(a1)	1005.85	S12(61) – S1(34)
ω16(b1)	751.59	S20(46) – S25(24) – S27(20) – S23(11)
ω17(b1)	714.35	S20(75) + S25(20)
ω25(b2)	1161.32	S18(41) + S19(40) + S2(9) – S6(8)
CMA-0A[CCSD(T)/cc-pVTZ, MP2/cc-pVTZ]
ω22(b2)	1458.20	S4(29) – S18(23) + S19(17) + S16(17)
ω23(b2)	1356.60	S16(56) + S18(17) – S2(15) – S6(6)
ω24(b2)	1294.55	S2(70) – S19(13) + S16(9)
ω25(b2)	1163.69	S18(42) + S19(41) – S6(10) + S2(6)
CMA-0A[CCSD(T)/cc-pVTZ, CCSD/cc-pVTZ]
ω24(b2)	1248.80	S2(38) – S18(26) – S19(25) + S6(12)
ω25(b2)	1178.61	S2(61) + S19(18) + S18(18)

^aFor each normal mode k, the percentage n of the vibrational energy attributable to internal coordinate i is listed as S_i(n), as calculated from eq 32 of ref (50). The signs preceding these entries denote the relative phases in the normal-mode eigenvectors.

While pyridine is an abnormal case for which CMA-0A is not fully adequate for some isolated modes, this challenging test molecule is totally vanquished by CMA-2A employing either B = CCSD(T)/cc-pVDZ or B = MP2/cc-pVTZ, as shown in Table 5. With our recommended B = MP2/cc-pVTZ and a ξ cutoff of 0.04, only 6 off-diagonals are chosen, and the cost increase is merely 22%. Nevertheless, the maximum absolute residual is reduced to 1.30 cm^–1, while the MAE and standard deviation are 0.22 and 0.39 cm^–1, respectively. For B = CCSD(T)/cc-pVDZ, a ξ cutoff of 0.015 is necessary to eliminate all outliers, resulting in 20 chosen off-diagonals and a 74% increase in cost; however, in the end the statistics achieved for the residuals are even better than in the MP2/cc-pVTZ case.

7. Application to 1-(1H-Pyrrol-3-yl)ethanol

The methodological advances achieved in this study were put to the test for the vibrations of a large molecule containing several challenging motifs, including a heterocyclic aromatic ring, aromatic N–H and C–H bonds, aliphatic O–H and C–H bonds, methyl and hydroxyl internal rotations, and torsions of entire monomer groups about a central C–C bond mediated by noncovalent interactions. In particular, the CMA-0A, CMA-1A(1), and CMA-2A methods with higher level A = CCSD(T)/cc-pVTZ and lower-level B = MP2/cc-pVTZ were applied to the 1-(1H-pyrrol-3-yl)ethanol conformer shown in Figure 4. This molecule lies outside the G2 test set, and very little is known about its vibrational spectrum. Benchmark CCSD(T)/cc-pVTZ harmonic frequencies and corresponding CMA residuals are reported in Table 7. The NICs were constructed by starting with the full set of customary coordinates for the individual P = pyrrole and E = ethanol monomers. Conceptually, the hydrogens on C₅ and C₆ were then removed while keeping the bond vectors fixed, whence the entire molecule was assembled by adding the C₅–C₆ distance and the intermonomer torsion angles about this linkage. The resulting 45 NICs for 1-(1H-pyrrol-3-yl)ethanol are provided in Table 8, and the Cartesian coordinates of all atoms are given in the Supporting Information.

Figure 4.

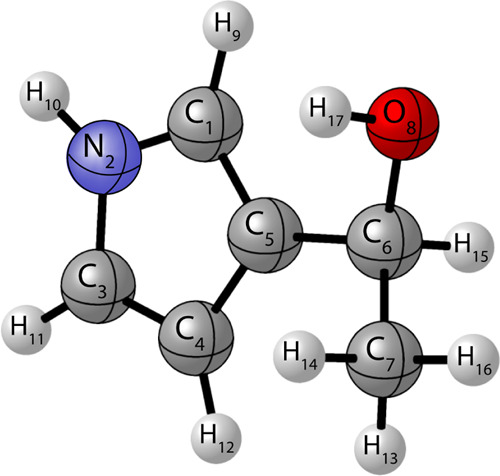
Enumerated atomic structure of 1-(1H-pyrrol-3-yl)ethanol, corresponding to selected internal coordinates utilized for all CMA computations.

Table 7. CMA-(0-2)A Residuals (ϵ, cm^–1) for CCSD(T)/cc-pVTZ Harmonic Frequencies (ω_ref, cm^–1) of 1-(1H-Pyrrol-3-yl)ethanol Obtained with B = MP2/cc-pVTZ.

			ωref	ϵ[CMA-0A]	ϵ[CMA-1A(1)]	ϵ[CMA-2A]	ϵ[CMA-2A]
		Monomera	CCSD(T)/cc-pVTZ	B = MP2/cc-pVTZ	B = MP2/cc-pVTZ	B = MP2/cc-pVTZb	B = MP2/cc-pVTZc
ω1	O–H stretch	E	3808.93	0.00	0.00	0.00	0.00
ω2	N–H stretch	P	3696.76	0.00	0.00	0.00	0.00
ω3	C1–H9 stretch	P	3276.98	0.03	0.03	0.03	0.03
ω4	C–H sym. stretch	P	3271.79	–0.01	–0.01	–0.01	–0.01
ω5	C–H antisym. stretch	P	3248.80	0.04	0.04	0.04	0.04
ω6	CH3 antisym. stretch	E	3124.60	–0.04	–0.04	–0.04	–0.04
ω7	CH3 sym. stretch	E	3108.32	–0.07	–0.07	–0.07	–0.07
ω8	C6–H15 stretch	E	3047.93	–0.00	0.00	0.00	0.00
ω9	CH3 sym. stretch	E	3031.56	0.05	0.05	0.05	0.05
ω10	ring stretching def.	P	1604.19	–0.70	–0.70	–0.25	–0.15
ω11	ring stretching def.	P	1521.94	–1.61	–1.61	–1.56	–0.11
ω12	CH3 def.	E	1498.72	–0.10	–0.10	–0.10	–0.10
ω13	CH3 scissor	E	1495.56	–0.09	–0.09	–0.09	–0.09
ω14	ring stretching def.	P	1475.70	0.61	0.61	0.76	–0.09
ω15	H15–C6–C5 wag	E	1429.80	–0.23	–0.23	–0.00	–0.02
ω16	ring stretching def.	P	1408.44	0.04	0.04	0.22	0.33
ω17	CH3 umbrella	E	1401.83	0.01	0.01	0.01	0.01
ω18	H15–C6–C5 rock	E	1365.39	0.33	0.33	0.33	0.34
ω19	C–O–H bend	E	1306.54	–0.29	–0.29	–0.29	–0.27
ω20	C1–H9 rock	P	1276.10	0.55	0.55	0.32	0.40
ω21	sym. C–H rock	P	1251.64	0.17	0.17	0.17	0.09
ω22	N–H rock	P	1156.61	0.72	0.72	0.15	0.02
ω23	C–O stretch	E	1125.73	–0.01	–0.01	–0.30	–0.36
ω24	ring breathing	P	1108.99	–0.10	–0.10	–0.10	–0.10
ω25	antisym. C–H rock	P	1088.87	0.67	0.67	0.37	0.54
ω26	CH3 rock	E	1067.33	0.48	0.47	0.48	0.23
ω27	CH3 wag	E	1034.92	0.14	0.14	0.14	0.13
ω28	ring shearing	P	958.88	0.06	0.06	0.06	0.06
ω29	ring bending	P	898.10	–0.01	–0.01	–0.01	–0.01
ω30	C6–C7 stretch	E	892.03	0.11	0.11	0.11	0.10
ω31	antisym. C–H wag	P	830.69	–0.47	–0.47	–0.21	–0.12
ω32	sym. C–H wag	P	789.78	–0.07	–0.07	–0.07	0.10
ω33	C5–C6 E wag	P ∩ E	701.34	–0.42	–0.42	–0.42	–0.03
ω34	antisym. C–H wag	P	696.28	0.52	0.52	0.29	–0.08
ω35	ring puckering	P	635.44	0.20	0.20	0.12	0.06
ω36	ring twisting	P	614.14	0.10	0.10	0.10	0.07
ω37	C7–C6–O8 bend	E	480.63	–10.90	0.04	0.04	–0.02
ω38	C5–C6 E rock	P ∩ E	457.57	–1.05	–1.05	–1.05	–1.05
ω39	N–H wag	P	442.97	13.10	1.56	1.56	1.20
ω40	C5–C6 stretch	P ∩ E	357.34	0.06	0.06	0.06	0.05
ω41	O–H torsion	E	320.88	0.04	0.04	0.04	0.04
ω42	CH3 torsion	E	261.50	0.02	0.02	0.02	0.02
ω43	C6–C5 P rock	P ∩ E	196.99	0.02	0.02	0.02	0.01
ω44	C6–C5 P wag	P ∩ E	172.27	0.04	0.04	0.04	0.02
ω45	P–E torsion	P ∩ E	47.91	0.03	0.03	0.03	0.02

^a(P, E) = (pyrrole, ethanol).

^bξ cutoff = 0.04, η = 26.7%, and n = 12 off-diagonals included.

^cξ cutoff = 0.02, η = 140.0%, and n = 63 off-diagonals included.

Table 8. 1-(1H-Pyrrol-3-yl)ethanol Natural Internal Coordinates.

Description	Monomera	Unnormalized natural internal coordinateb
ring breathing	P	S1 = r(5,4) + r(1,5) + r(4,3) + r(2,1) + r(2,3)
ring stretching def.	P	S2 = r(5,4) + B r(1,5) + B r(4,3) + A r(2,1) + A r(2,3)
ring stretching def.	P	S3 = D r(1,5) – D r(4,3) + C r(2,1) – C r(2,3)
ring stretching def.	P	S4 = r(5,4) + A r(1,5) + A r(4,3) + B r(2,1) + B r(2,3)
ring stretching def.	P	S5 = C r(1,5) – C r(4,3) – D r(2,1) + D r(2,3)
C–C stretch	P ∩ E	S6 = r(5,6)
C–C stretch	E	S7 = r(6,7)
C–O stretch	E	S8 = r(6,8)
C–H stretch	P	S9 = r(1,9)
N–H stretch	P	S10 = r(2,10)
C–H stretch	P	S11 = r(3,11)
C–H stretch	P	S12 = r(4,12)
C–H stretch	E	S13 = r(6,15)
O–H stretch	E	S14 = r(8,17)
CH3 sym. stretch	E	S15 = r(7,13) + r(7,14) + r(7,16)
CH3 sym. stretch	E	S16 = 2r(7,13) – r(7,14) – r(7,16)
CH3 antisym. stretch	E	S17 = r(7,14) – r(7,16)
ring bending	P	S18 = θ(1,2,3) + A θ(2,1,5) + A θ(2,3,4) + B θ(1,5,4) + B θ(3,4,5)
ring shearing	P	S19 = (A – B) θ(2,1,5) – (A – B) θ(2,3,4) + (1 – A) θ(1,5,4) – (1 – A) θ(3,4,5)
C6–C5 P rock	P ∩ E	S20 = θ(6,5,4) – θ(6,5,1)
C7–C6–O bend	E	S21 = θ(8,6,7)
C5–C6 E wag	P ∩ E	S22 = θ(5,6,7) + θ(5,6,8)
C5–C6 E rock	P ∩ E	S23 = θ(5,6,7) – θ(5,6,8)
C–H rock	P	S24 = θ(9,1,2) – θ(9,1,5)
N–H rock	P	S25 = θ(10,2,3) – θ(10,2,1)
C–H rock	P	S26 = θ(11,3,4) – θ(11,3,2)
C–H rock	P	S27 = θ(12,4,5) – θ(12,4,3)
C–O–H bend	E	S28 = θ(17,8,6)
H–C–C rock	E	S29 = θ(15,6,7) + θ(15,6,8)
H–C–C wag	E	S30 = θ(15,6,7) – θ(15,6,8)
CH3 umbrella	E	S31 = θ(13,7,6) + θ(14,7,6) + θ(16,7,6) – θ(14,7,16) – θ(13,7,14) – θ(13,7,16)
CH3 rock	E	S32 = 2θ(13,7,6) – θ(14,7,6) – θ(16,7,6)
CH3 wag	E	S33 = θ(14,7,6) – θ(16,7,6)
CH3 scissor	E	S34 = 2θ(14,7,16) – θ(13,7,14) – θ(13,7,16)
CH3 def.	E	S35 = θ(13,7,14) – θ(13,7,16)
ring twisting	P	S36 = τ(1,5,4,3) + B τ(4,3,2,1) + B τ(3,2,1,5) + A τ(5,4,3,2) + A τ(2,1,5,4)
ring puckering	P	S37 = (1–A) τ(4,3,2,1) – (1–A) τ(3,2,1,5) – (B–A) τ(5,4,3,2) + (B–A) τ(2,1,5,4)
CH3 torsion	E	S38 = τ(13,7,6,8) + τ(14,7,6,8) + τ(16,7,6,8)
O–H torsion	E	S39 = τ(17,8,6,7)
P–E torsion	P ∩ E	S40 = τ(1,5,6,7) + τ(1,5,6,8) + τ(4,5,6,7) + τ(4,5,6,8)
C6–C5 P wag	P ∩ E	S41 = γ(6,5,1,4)
C–H wag	P	S42 = γ(9,1,2,5)
N–H wag	P	S43 = γ(10,2,3,1)
C–H wag	P	S44 = γ(11,3,4,2)
C–H wag	P	S45 = γ(12,4,5,3)

^a(P, E) = (pyrrole, ethanol).

^b(A, B, C, D) = .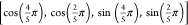

For all but two frequencies, the performance of CMA-0A is excellent, achieving a MAE and maximum absolute residual (ϵ_max) of only 0.24 and 1.61 cm^–1, respectively, for 43 of the 45 normal modes. The two prominent outliers (ϵ₃₇, ϵ₃₉) = (10.9, –13.1) cm^–1 arise from (ω₃₇, ω₃₉) = (480.6, 443.0) cm^–1, whose largest TED components occur for the (C₇–C₆–O₈ bend, N–H out-of-plane wag) coordinates. If CMA-1A(1) is applied with a single (ω₃₇, ω₃₉) coupling, then the (ϵ₃₇, ϵ₃₉) residuals are dramatically reduced to (0.04, 1.56) cm^–1. What is remarkable about this solution is that the largest contributors for the two modes occur on different monomers, so that the coupling occurs at long-range across the C₅–C₆ linkage. A likely explanation is that the coupling involves noncovalent interactions of the aromatic π cloud with the polar O–H group. In any event, the system clearly provides a rigorous test for CMA methods. When CMA-2A is invoked with ξ = 0.04 (η = 27%, n = 12 couplings), the automatic selection process indeed picks up the (ω₃₇, ω₃₉) coupling, so that the MAE becomes a mere 0.22 cm^–1 for the entire system of 45 vibrations. The residuals of largest size for CMA-2A(ξ = 0.04) are (ϵ₁₁, ϵ₃₉) = (−1.56, 1.56) cm^–1, which barely qualify as outliers by our adopted CMA-2A threshold of 1.5 cm^–1. While this level of performance is impressive, the application of CMA-2A with ξ = 0.02 (η = 140%, n = 63 couplings) removes any hint of an outlier. Specifically, the (MAE, ϵ_max) metrics for this final run are (0.15, 1.2) cm^–1.

All computations for 1-(1H-pyrrol-3-yl)ethanol were performed using 6 cores with 60 GB of memory on an Intel Xeon Gold 6130 processor in conjunction with a Luster file system. The CMA-0A, CMA-2A(ξ = 0.04), and CMA-2A(ξ = 0.02) results required a mere 4.3%, 5.6%, and 10.5%, respectively, of the CPU time for the complete CCSD(T)/cc-pVTZ harmonic frequency computation. In summary, CMA-2A gives a commanding performance for this test molecule. CMA-2A(ξ = 0.04) cuts the CPU time by a factor of 18 while evaluating all frequencies to better than 1.6 cm^–1, whereas CMA-2A(ξ = 0.02) provides additional assurance against outliers yet still cuts the original cost by almost a factor of 10.

8. Summary

The Concordant Mode Approach (CMA) is a general protocol by which harmonic vibrational frequencies at a higher level theory A can be computed using a normal mode basis generated by a lower-level theory B, with cost reductions approaching an order of magnitude for larger molecules. Our introductory study¹ on the G2 test set showed that CMA-0A can produce vibrational frequencies with at least a 99% probability of being accurate to within 1.5 cm^–1 but with a 0.2–0.4% chance of outliers greater than 2.5 cm^–1. The current research has focused on creating new CMA methods that rapidly and systematically converge to the exact Level A frequencies while also eliminating outliers. Overall, MP2/cc-pVTZ is found to be the best Level B when targeting CCSD(T)/cc-pVTZ frequencies. Our results show the importance of going beyond HF to incorporate electron correlation at Level B, but matching the quality of the Level A orbital basis set becomes paramount thereafter. Another key conclusion for Level B is that density-fitted (df) MP2 performs just as well as conventional MP2; hence, the reduced scaling of df-MP2 provides a wealth of opportunities for CMA applications on large molecules. The CMA-2A procedure developed here is demonstrated to be a robust, convergent method (Figure 2) that selects which off-diagonal force field elements to explicitly evaluate at Level A based on dimensionless ξ parameters that can be evaluated at a Level C with essentially no additional computational cost. Our current recommendation for CMA-2A applied to CCSD(T)/cc-pVXZ frequencies is to choose B = MP2/cc-pVXZ (or its df-MP2 variant) and C = HF/cc-pVXZ with ξ in the 0.02–0.04 range depending on the required certainty of the results. With ξ = 0.02 the CMA-2A residuals exhibit extremely small (MAE, σ_ϵ, ϵ_max) statistics of (0.05, 0.15, 0.17) cm^–1, and the maximum absolute discrepancy (ϵ_MAX) over the entire database is only 1.8 cm^–1, all achieved with only a 33% increase (η) in average cost over CMA-0A. Moreover, the troublesome pyridine and challenging 1-(1H-pyrrol-3-yl)ethanol vibrational problems can be fully solved by CMA-2A with the less stringent threshold ξ = 0.04, resulting in (ϵ_MAX, η) = (1.3 cm^–1, 22%) and (1.6 cm^–1, 27%) for these two molecules, respectively. The hierarchy CMA-N is now in place for N = 0, 1, 2, and the thoroughgoing success of these methods promises continuing improvements in cost and accuracy, applications to ever-larger molecules, and diversification into intermolecular vibrations. Other advances are also readily envisioned for which CMA-N can provide an ideal solution, such as the inclusion of core electron correlation and complete basis set (CBS) extrapolation in the determination of vibrational frequencies for larger molecules.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jctc.4c01240.

• CMA-2A (RMSD, ϵ_max) versus (η, percent off-diagonals in F_CMA) plots. Cartesian coordinates for the CCSD(T)/cc-pVTZ structure of 1-(1H-pyrrol-3-yl)ethanol and all molecules of the G2 test set. 1501 pure, CMA-0A, and CMA-2A frequencies at ξ = 0.02 with A = CCSD(T)/cc-pVTZ, B = [MP2/cc-pVTZ, CCSD(T)/cc-pVDZ, B3LYP/6-31G(2df,p)], and C = [HF/cc-pVTZ, HF/cc-pVDZ, HF/6-31G(2df,p)] (PDF)

The authors declare no competing financial interest.