Abstract
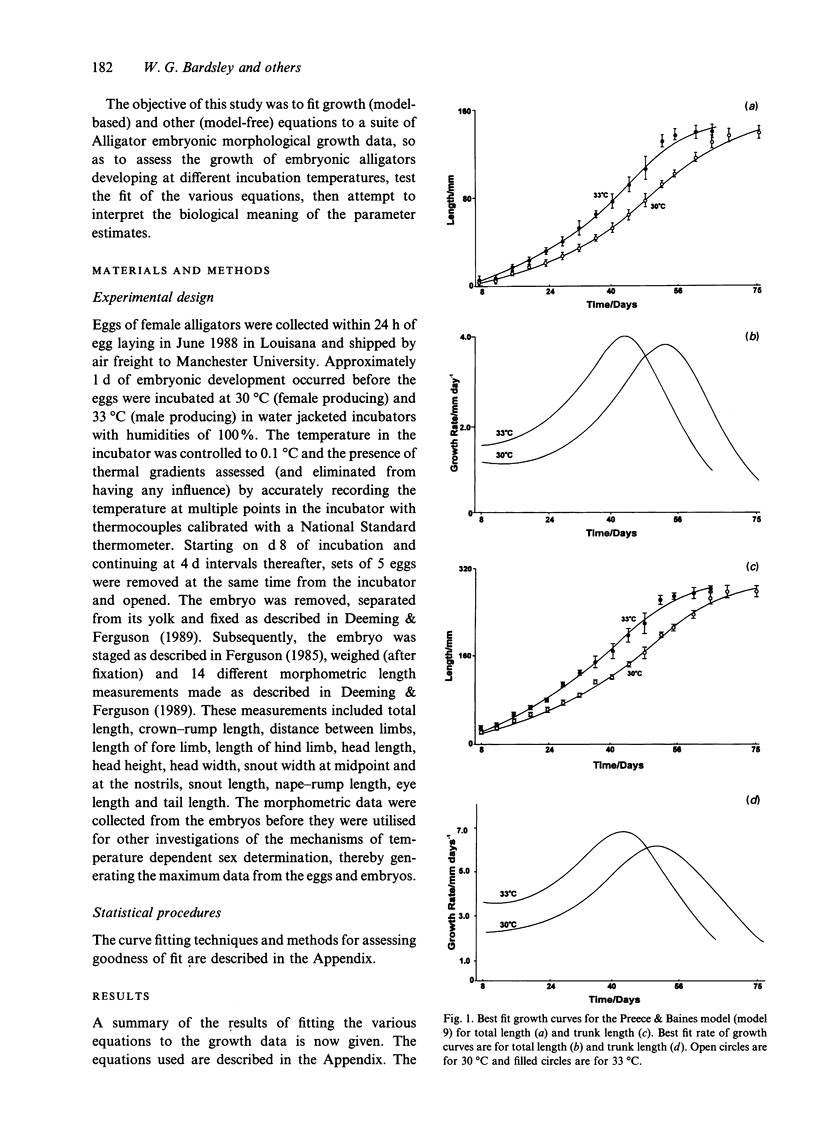
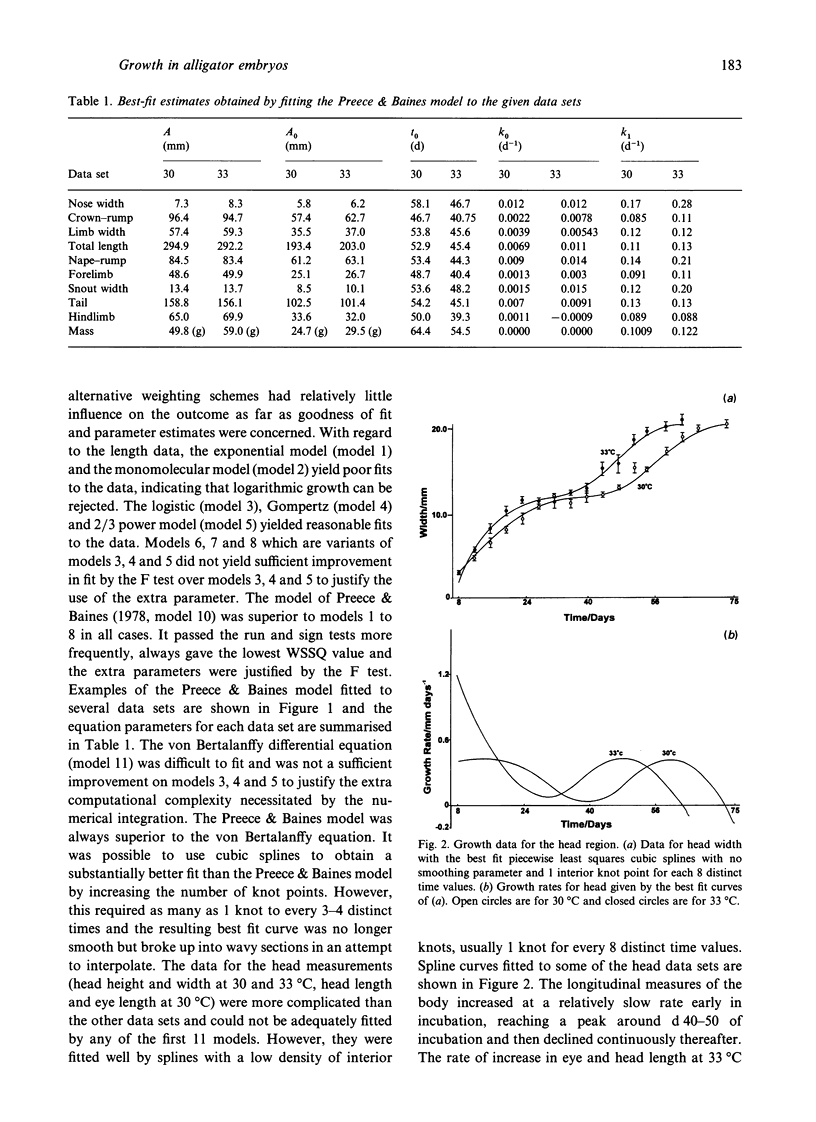
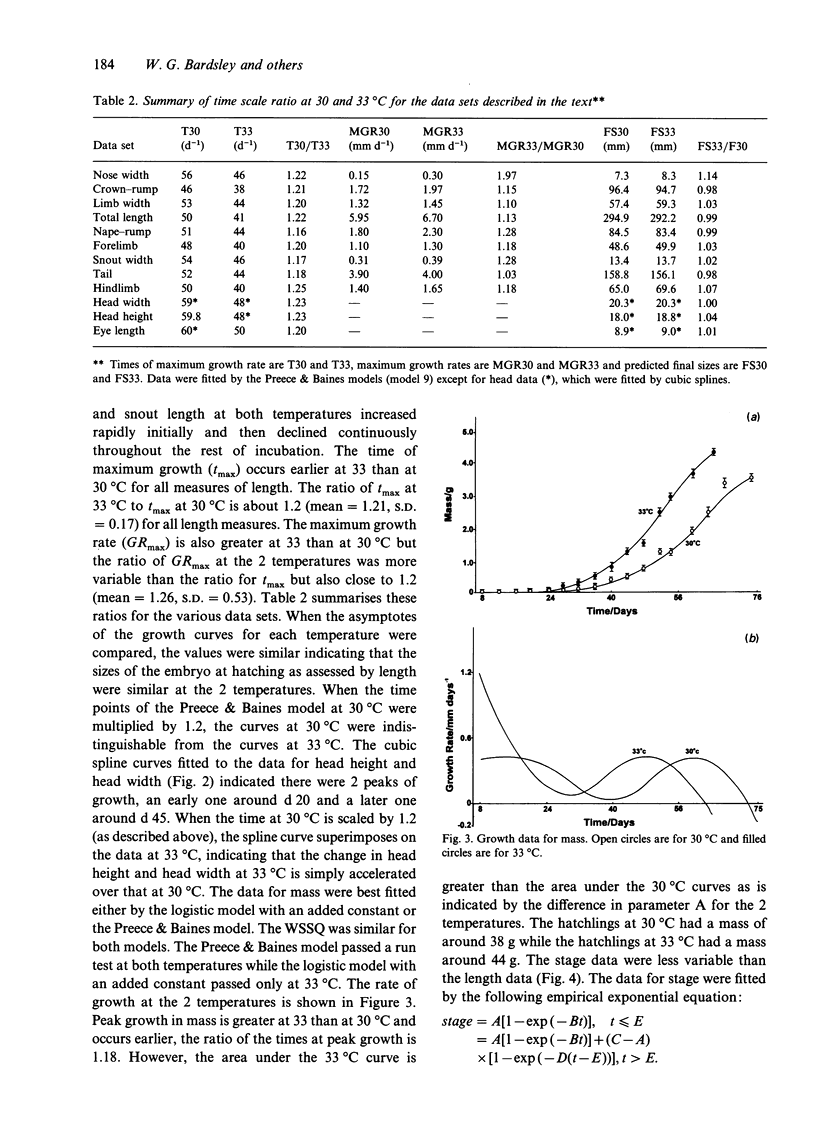
A variety of model-based (growth models) and model-free (cubic splines, exponentials) equations were fitted using weighted-nonlinear least squares regression to embryonic growth data from Alligator mississippiensis eggs incubated at 30 and 33 degrees C. Goodness of fit was estimated using a chi 2 on the sum of squared, weighted residuals, and run and sign tests on the residuals. One of the growth models used (Preece & Baines, 1978) was found to be superior to the classical growth models (exponential, monomolecular, logistic, Gompertz, von Bertalanffy) and gave an adequate fit to all longitudinal measures taken from the embryonic body and embryonic mass. However, measurements taken from the head could not be fitted by growth models but were adequately fitted by weighted least squares cubic splines. Data for the stage of development were best fitted by a sum of 2 exponentials with a transition point. Comparison of the maximum growth rates and parameter values, indicated that the growth data at 30 degrees C could be scaled to 33 degrees C to multiplying the time by a scaling factor of 1.2. This is equivalent to a Q10 of about 1.86 or, after solving the Arrhenius equation, an E++ of 46.9 kJmol-1. This may be interpreted as indicating a common rate-limiting step in development at the 2 temperatures.
Full text
PDF






Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Bardsley W. G., McGinlay P. B., Roig M. G. Conditions when statistical tests for model discrimination have high power. Some examples from pharmacokinetics, ligand binding, transient and steady-state enzyme kinetics. Biophys Chem. 1987 Apr;26(1):1–8. doi: 10.1016/0301-4622(87)80001-7. [DOI] [PubMed] [Google Scholar]
- Bardsley W. G., McGinlay P. B. The use of non-linear regression analysis and the F test for model discrimination with dose-response curves and ligand binding data. J Theor Biol. 1987 May 21;126(2):183–201. doi: 10.1016/s0022-5193(87)80228-x. [DOI] [PubMed] [Google Scholar]
- Dmi'el R. Growth and metabolism in snake embryos. J Embryol Exp Morphol. 1970 Jun;23(3):761–772. [PubMed] [Google Scholar]
- Largo R. H., Gasser T., Prader A., Stuetzle W., Huber P. J. Analysis of the adolescent growth spurt using smoothing spline functions. Ann Hum Biol. 1978 Sep;5(5):421–434. doi: 10.1080/03014467800003071. [DOI] [PubMed] [Google Scholar]
- MADERSON P. F., BELLAIRS A. D. Culture method as an aid to experiment on reptile embryos. Nature. 1962 Jul 28;195:401–402. doi: 10.1038/195401b0. [DOI] [PubMed] [Google Scholar]
- Marubini E., Resele L. F., Tanner J. M., Whitehouse R. H. The fit of Gompertz and Logistic curves to longitudinal data during adolescence on height, sitting height and biacromial diameter in boys and girls of the Harpenden Growth Study. Hum Biol. 1972 Sep;44(3):511–523. [PubMed] [Google Scholar]
- Murray J. D., Deeming D. C., Ferguson M. W. Size-dependent pigmentation-pattern formation in embryos of Alligator mississippiensis: time of initiation of pattern generation mechanism. Proc R Soc Lond B Biol Sci. 1990 Apr 23;239(1296):279–293. doi: 10.1098/rspb.1990.0017. [DOI] [PubMed] [Google Scholar]
- Preece M. A., Baines M. J. A new family of mathematical models describing the human growth curve. Ann Hum Biol. 1978 Jan;5(1):1–24. doi: 10.1080/03014467800002601. [DOI] [PubMed] [Google Scholar]


