Density-dependent flow generation in active cytoskeletal fluids

Abstract

The actomyosin cytoskeleton, a protein assembly comprising actin fibers and the myosin molecular motor, drives various cellular dynamics through contractile force generation at high densities. However, the relationship between the density dependence of the actomyosin cytoskeleton and force-controlled ordered structure remains poorly understood. In this study, we measured contraction-driven flow generation by varying the concentration of cell extracts containing the actomyosin cytoskeleton and associated nucleation factors. We observed continuous actin flow toward the center at a critical actomyosin density in cell-sized droplets. The actin flow exhibited an emergent oscillation in which the tracer advection in the bulk solution periodically changed in a stop-and-go fashion. In the vicinity of the actomyosin density where oscillatory dynamics occur, the velocity of tracer particle motion decreases with actomyosin density but exhibits superdiffusive motion. Furthermore, the increase or decrease in myosin activity causes the oscillatory flow generation to become irregular, indicating that the density-dependent flow generation of actomyosin is driven by an interplay between actin density and myosin force generation.

Introduction

The actin cytoskeletal fibers and myosin molecular motors generate force in living cells^1–4. Actin fibers, which are bundled and entangled with cross-linking proteins, confer viscoelastic properties in the intracellular space and near the plasma membrane⁵. Myosin motor proteins bind to the actin network to generate contractile forces⁶. These proteins form the actomyosin cytoskeleton, which is responsible for processes such as cytokinesis⁷, cytoplasmic fluid streaming^8,9, cell deformation¹⁰, cell motility^11,12, and organelle positioning¹³. Understanding the formation of ordered structures within this spontaneously contracting actomyosin cytoskeleton elucidates non-equilibrium mechanics in biological complexes at the cellular level^14,15 and provides insights into the development of force-generating polymer gels in biomolecular systems^16–18.

Although advances have been made in identifying proteins involved in the actomyosin cytoskeleton and their biochemical regulation, quantitative analysis of ordered pattern formation and contraction dynamics remains challenging. Because complex regulatory networks by protein signaling and the presence of organelles make the spatial homogeneity of living cells disturbed, physical analysis of simplied cytoskeletal system is one of central issue in physics and chemistry of actomyosin mechanics. This issue is addressed through a reconstituted system where the actomyosin cytoskeleton and relevant proteins are extracted and confined to cell-sized droplet compartments. These lipid membrane-covered droplets control a dense actin network and the aster-like pattern of the microtubules, which mimic the spatial distribution of cytoskeletal structures in the intracellular space^19–24. Within these confined actomyosin solution in droplets, actin fibers form a ring-like structure similar to that of the myosin contractile ring during cell division^25,26. Actin polymerization facilitates flow from the membrane to the compartment^27–29. In addition to the increased contractility of the myosin motor, the polymerization rate of actin fibers is a critical parameter in these reconstitution dynamics^30,31. Moreover, as the interaction between actin fibers and the lipid membrane becomes stronger, the resulting frictional force from actomyosin contraction facilitates the self-propelled migration of droplets confining actomyosin solution³². These studies provide valuable insights into the density of cytoskeletal and motor proteins abundant in the cytosolic space, which is essential for generating such dynamics.

High intracellular protein concentrations maintain cellular activity, and their metabolic activity loss leads to increased viscosity³³. Therefore, exploring the relationship between protein concentration and intracellular structure formation is vital for understanding the mechanisms that sustain a highly active environment. However, previous analyses of confined actomyosin systems at high concentrations of actin cytoskeleton and myosin proteins have not fully explained the mechanisms by which emergent actin flows occur in a density-dependent manner.

In this study, we experimentally examined the density dependence of actin flow generation in a reconstituted actomyosin cytoskeleton. We investigated the transition from Brownian motion to actin flow when actin density reached a critical value, as well as the effects of cell-size compartmentalization and chemical perturbation of myosin contractile activity on flow generation. This density-dependent flow of actin has implications for the higher molecular density required for cellular activity to perform functions from cytoplasmic streaming to cell migration.

Results

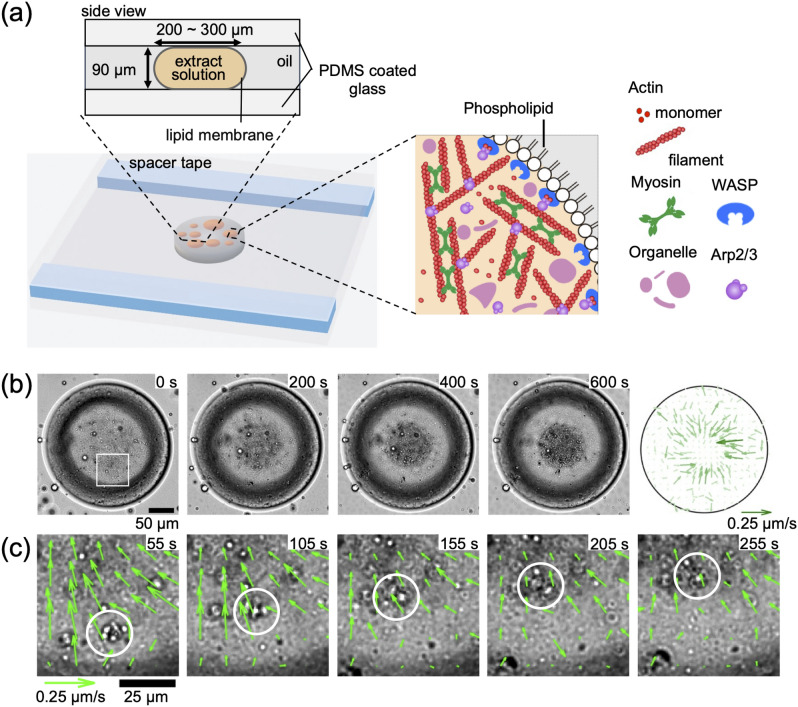
We extracted a cytosolic solution with actin, myosin, and other associated proteins such as Arp2/3 complex from Xenopus frog eggs, according to the protocol for extract extraction, keeping at least 90% of the amount of material in the cytoplasm^34,35. When myosin binds to the actin filamentous network, the actomyosin cytoskeleton is formed, which spontaneously generates contractile forces (Fig. 1a). Additionally, the Arp2/3 complex is activated by WASP family proteins at the membrane interface and then leads to the nucleation of branched actin fibers³⁶. By enclosing this extract at various densities inside emulsified extract-in-oil droplets, the actomyosin cytoskeleton is confined within the cell-sized space at the interface of the phospholipid monolayer (Fig. 1a)^28–32. We refer to this actomyosin-containing droplet as confined actomyosin solution. A chamber for microscopic observation was constructed between two polydimethylsiloxane (PDMS)-coated glass slides, held at a height of 90 μm with a spacer tape and actomyosin solution in the droplet of 150–300 μm diameter were observed with an inverted microscope (see “Methods” Section). The droplets are sandwiched between the top and bottom surfaces, with a height:diameter aspect ratio of 0.3–0.6. Although the droplet is not a perfect cylinder due to its interfacial curvature near the glass contact surface, the boundary shape appears circular from the top view (Fig. 1a). The confined actomyosin solution also contained small granular particles, which are fragments of organelles from the extract solution. These particles served as tracers to observe actomyosin cytoskeleton dynamics using time-lapse measurements (Fig. 1b). We observed granular particles flowing from the membrane boundary toward the center of the droplet, forming a spherical cluster at the center (Supplementary Movie 1)^28–31.

Fig. 1.

Flow generation of actomyosin cytoskeleton confined in a extract-in-droplet. (a) Schematic of the experimental setup. (b) Microscopic time-lapse observation of confined actomyosin solution in droplets. The number in the upper right corner of each image is the elapsed time. Scale bar: 50 μm. The figure on the right depicts the flow field of the transport of granular particles obtained using particle image velocimetry (PIV) analysis. Scale arrow is 0.25 μm s⁻¹. (c) Magnified view of the transport of the granular particle toward the center, indicating that the transport direction is consistent with the flow field obtained using PIV. Scale bar: 25 μm.

To quantitatively analyze the motion of the granular particles, we performed PIV analysis to visualize the velocity field of the flow. PIV analysis revealed that the flow toward the center of the droplet was dominant (Fig. 1b, right). The fastest flow was observed near the cluster at the droplet center. The velocity field of the flow, together with the magnified image, indicates that the granular particles moved from near the membrane boundary with a typical velocity of approximately 0.07 μm s⁻¹ at approximately 50 μm from the center of the droplet (Fig. 1c).

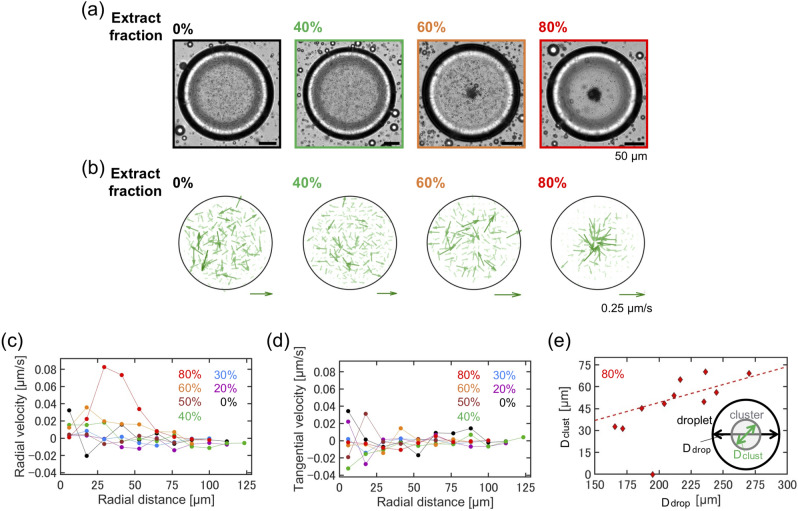
To confirm that the observed flow toward the center originated from the actomyosin cytoskeleton, we analyzed changes in the flow of particles by varying the fraction of actomyosin enclosed in the droplet by dilution. For flow analysis of the diluted extracts, we added polystyrene tracer particles with a diameter of 1.0 μm to perform PIV analysis. The volume of the actomyosin cytoskeleton was $V_{\mathit{act}}$, the volume of the buffer solution (A50 buffer) was $V_{\mathit{buf}}$, and the volume fraction of the diluted actomyosin solution was defined as $\varphi =V_{\mathit{act}}/(V_{\mathit{act}}+V_{\mathit{buf}})$. Confined actomyosin solutions were prepared using cytoplasmic extracts diluted at $\varphi$ = 0%, 20%, 30%, 40%, 50%, 60%, and 80% in solution. Extract dilution affects not only the concentration of actin, but also the concentration of myosin and other related molecules and organelles derived from the extract. The decrease of molecular components due to overall dilution may also alter the diffusion dynamics within the actomyosin solution. Figure 2 presents representative cases of $\varphi$ = 0%, 40%, 60% and 80% (Supplementary Movie 2). In confined actomyosin solutions with high dilution rates $\varphi$ = 0% and 40%, the particles were uniformly distributed, whereas in confined actomyosin solutions with $\varphi$ = 60% and 80%, the particles were transported to the center, and cluster formation was observed (Fig. 2a). PIV analysis revealed that at $\varphi$ = 0%, no clear velocity field appeared, with a disordered velocity and direction (Fig. 2b), reflecting Brownian motion. In contrast, in the droplet containing actomyosin extract with $\varphi$ = 60%, the actin flow near the cluster was slightly biased toward the center of the droplets. The actin flow at $\varphi$ = 80% was directed toward the center, with the highest velocity near the cluster (Fig. 2b).

Fig. 2.

Density dependence of actin flux inside a confining droplet. (a) Cluster formation in confined actomyosin solutions at various density fractions ($\varphi =0$%, 40%, 60%, and 80%). Scale bar: 50 μm. (b) Actin flow fields across different actomyosin density fractions. Scale arrow: 0.25 μm s⁻¹. (c) Radial velocity profile of actin flow, with radial distances measured every 11.8 μm, which corresponds to the grid size used in the PIV analysis. (d) Tangential velocity profile of actin flow. (e) Correlation between the size of the confining droplet and the cluster size. The dashed line in red ($D_{\mathit{clust}}=0.25D_{\mathit{drop}}$) is drawn by least square fitting.

We further examined the spatial profile of actin flow by decomposing the velocity into radial ($v_r$) and tangential ($v_{\theta }$) components at the same radial distances from the center and calculated the average of each component. The radial velocity of the diluted actomyosin solution ($\varphi$ = 0%, 20%, 30%, 40%) was smaller than 0.02 μm s⁻¹ (Fig. 2c). At $\varphi$ = 60%, $v_r$ increased slightly near the center, reaching a maximum at about r = 25 μm from the center (Fig. 2c). At a higher fraction $\varphi$ = 80%, $v_r$ exhibited a peak velocity within approximately $r=$33–50 μm from the center, which was 0.08 μm s⁻¹ (Fig. 2c). Conversely, $v_{\theta }$ remained below 0.02 μm s⁻¹ across all fractions $\varphi$ = 0%, 20%, 30%, 40%, 50%, 60%, and 80%, indicating an absence of rotational flow (Fig. 2d).

Actin flow toward the center drives cluster formation, where organelles and the actomyosin cytoskeleton accumulate. Consequently, we explored whether a positive correlation exists between the amount of actomyosin in the droplet and the cluster size when a sufficient fraction of actomyosin is present. Accordingly, we measured the diameters of confining droplets $D_{\mathit{drop}}$ (150–300 μm) and the clusters $D_{\mathit{clust}}$. Stable clusters formed in droplets at $\varphi$ = 60%, and a visible cluster formed at $\varphi$ = 80%, which showed a proportional increase with the droplet size (Fig. 2e). This result aligns with the mechanism whereby the actomyosin cytoskeleton and cytoplasmic contents, driven by actin flow, accumulate and enlarge the formed cluster, correlating with the increase in the droplet size.

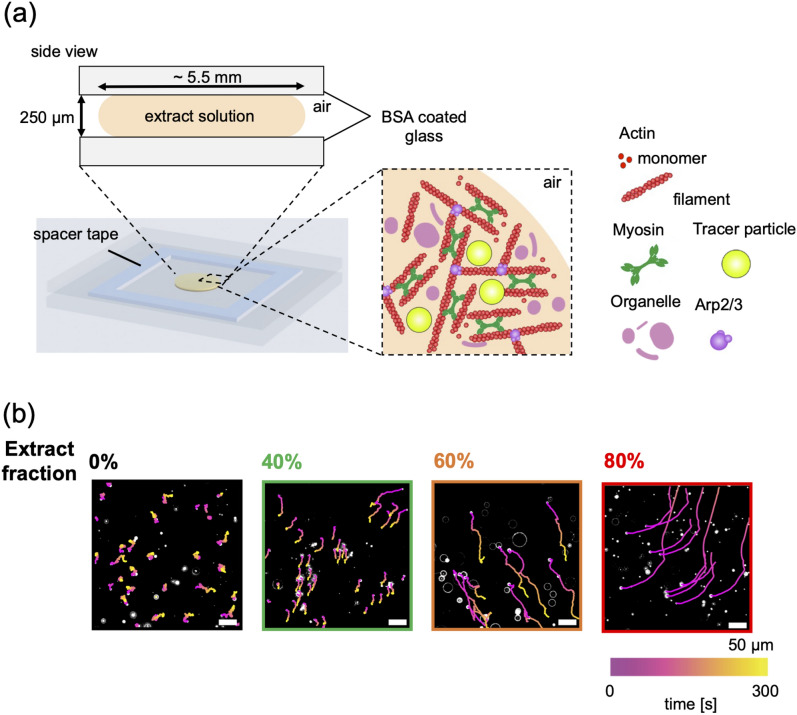
We then investigated whether the actomyosin cytoskeleton generates flow solely through spontaneous force generation. Accordingly, we investigated the density-dependent dynamics of actin flow using a bulk solution system where the diluted cytoplasmic extract was placed directly in the chamber without confinement. We prepared a bulk of the diluted actomyosin solution by dropping 6 μL of the solution onto a glass slide coated with bovine serum albumin (BSA), which prevents non-specific adsorption of myosin and actin proteins onto glass, maintaining a height of 250 μm with a spacer tape. We refer to this as the “bulk” actomyosin solution (Fig. 3a). The bulk actomyosin solution was not emulsified in oil, but was placed in a chamber of 250 μm height and 5.5 mm in diameter (Fig. 3a). Because the length scale of this bulk solution is much larger than that of the confining droplet, the confinement effect should be smaller. We note that the interface of this bulk solution is a gas-liquid interface. Actin flow in the bulk actomyosin solution was visualized by tracking fluorescent tracer particles. We recorded the motion of tracer particles at 1.0 s intervals, and trajectories were obtained from the centers of the particles in bulk solutions of different actomyosin fractions (Fig. 3b and Supplementary Movie 3). At $\varphi$ = 0%, the tracer particles moved with fluctuations characteristic of thermal Brownian motion. At higher fractions $\varphi$ =40%, 60%, and 80%, the trajectories of the tracer particles became ballistic, moving with slight changes in direction, indicating that increasing the actomyosin fraction induced a transition from diffusive to ballistic motion, driven by density-dependent actin flow.

Fig. 3.

Actin flow in bulk actomyosin solution. (a) Schematic of an experiment to visualize bulk actin flow using fluorescent tracer particles without compartmentalization in droplets. (b) Microscopic images of fluorescent tracer particles across various actomyosin cytoskeleton fractions ($\varphi =0$%, 40%, 60%, and 80%). Particle trajectories were analyzed using particle tracking (refer to “Methods” section). The color in each trajectory represents the elapsed time during tracking. Scale bar: 50 μm.

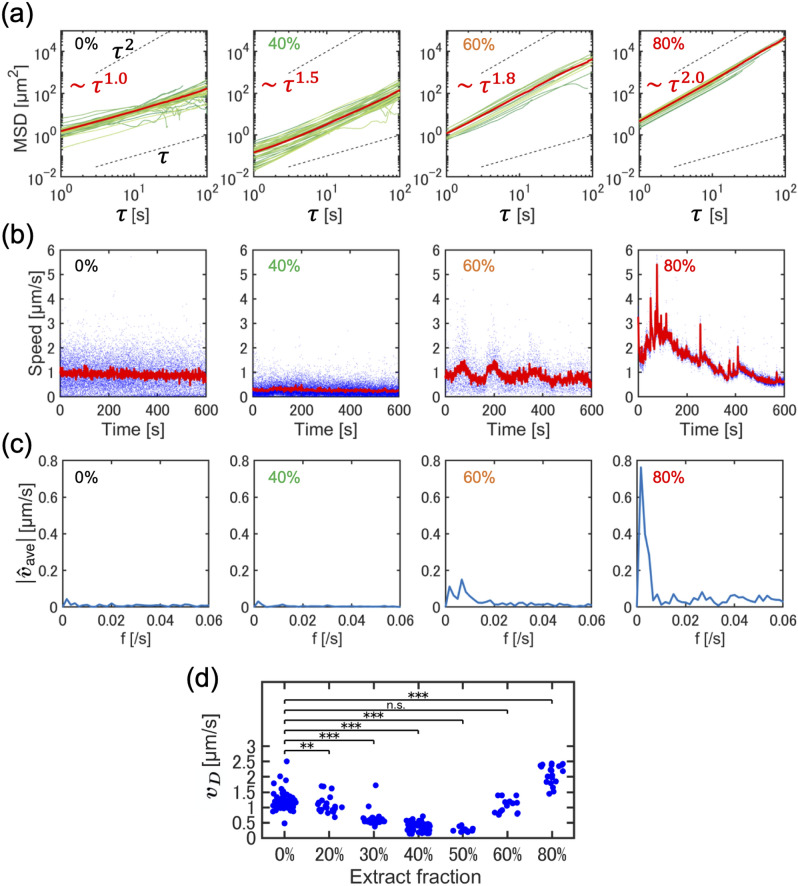
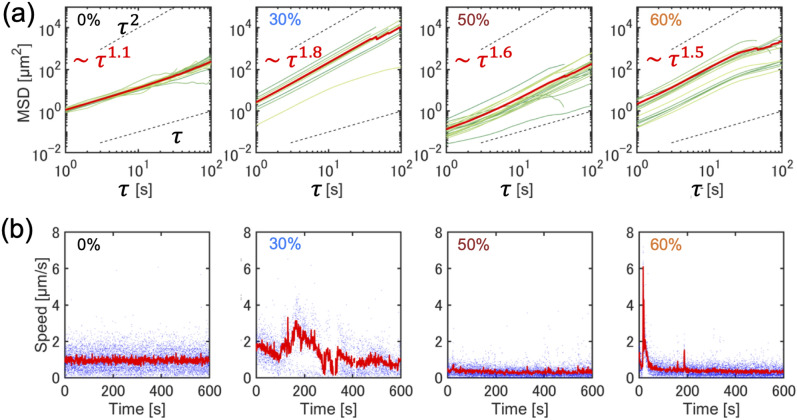
The motion of the tracer particles is further analyzed by calculating the mean squared displacement (MSD) $⟨{(\mathrm{\Delta }r(\tau ))}^2⟩$, where $\mathrm{\Delta }r(\tau )=r(t+\tau )-r(t)$ is the distance traveled in the delay time $\tau$. We fitted the MSD curve using $⟨{(\mathrm{\Delta }r(\tau ))}^2⟩\propto {\tau }^{\alpha }$ where $\alpha$ is a positive constant, allowing us to classify the dynamics of the tracer motion. When $\alpha =1$, indicating MSD $\propto {\tau }^{1.0}$, the tracer motion is simple diffusion with a randomly changing direction. At $\alpha =2$, indicating ${\tau }^{2.0}$, the tracer displacement exhibits ballistic motion, whereas at $1<\alpha <2$, the tracer motions are super-diffusive with a partially correlated change in direction. Our experimental data revealed that at $\varphi =0$% without the cytoplasmic extract, which served as the control, the MSD was proportional to ${\tau }^{1.0}$, indicating simple diffusion (Fig. 4a). For actomyosin fractions ranging from $\varphi =40$% to $\varphi =60$%, super-diffusive motion appeared at $\alpha =1.5$ and $\alpha =1.8$, respectively. Furthermore, at $\varphi =80$% the tracer motion became ballistic with $\alpha =2.0$ (Fig. 4a).

Fig. 4.

Quantitative analysis of tracer particle trajectories in actomyosin cytoskeletons in bulk conditions. (a) Mean squared displacement of tracer particles tracked at different actomyosin fractions ($\varphi =0$%, 40%, 60%, and 80%). The green line represents single particle-tracking data, and the red line represents the averaged value. (b) Time evolution of the instantaneous speed of tracer particles. The blue scatter points represent the speed of a single particle, and the red line represents the average speed over multiple particles simultaneously. (c) Fourier transform of the time evolution of the speed of tracer particles, with a peak indicating an oscillatory change in speed appearing at $\varphi$ = 60%. (d) Density dependence of the diffusion speed $v_D$ of tracer particles ($\varphi$ = 0%, 20%, 30%, 40%, 50%, 60% and 80%). Statistical analysis was performed using the Mann-Whitney U test. *** indicates significance $p<0.001$, ** indicates $p<0.01$.

Next, we investigated the transition from diffusive dynamics to persistent motion of particles under actin flow by focusing on the speed of the tracer particles. We calculated the speed of a tracer particle $v$ (t) at time t from the displacement of the particle position (Fig. 4b). We defined the mean speed $v_{\mathit{ave}}(t)$ by averaging $v$ (t) over the particle population and employed it for the following comparative analysis. For the buffer solution at $\varphi$ = 0% and the diluted actomyosin solution at $\varphi$ = 40%, $v_{\mathit{ave}}(t)$ was almost constant over time. The speed at $\varphi$ = 40% was slightly lower than that at $\varphi$ = 0%, suggesting suppressed particle displacement owing to increased viscosity with a higher fraction of the cytoplasmic extract. For the solution at $\varphi$ = 60%, $v_{\mathit{ave}}(t)$ exhibited periodic changes, increasing and decreasing with time (Fig. 4b), reflecting periodic stop-and-go motion. At a higher fraction, $\varphi$ = 80%, $v_{\mathit{ave}}(t)$ showed high initial values but then decayed with oscillatory speed fluctuations (Fig. 4b). This gradual decrease in speed is attributable to the depletion of the actomyosin cytoskeleton from the bulk solution through rapid actin flow. To confirm the periodicity of the speed, we examined the Fourier transform of $v_{\mathit{ave}}(t)-⟨v_{\mathit{ave}}⟩$ where $⟨v_{\mathit{ave}}⟩$ is the mean speed averaged over time, defined as ${\widehat{v}}_{\mathit{ave}}(f)$, and observed that the particle speed at $\varphi$ = 60% exhibited regular changes in frequency f = 0.063 ${\text{s}}^{-1}$ and period T = 1/f = 150 s (Fig. 4c). Additionally, the speed fluctuation at $\varphi$ = 80% showed several peaks in the frequency space that fluctuated over periods shorter than 150s.

Analyzing the dynamics of tracer particles among various fractions $\varphi$ is crucial; therefore, we defined the diffusion speed $v_D=\sqrt{⟨{(\mathrm{\Delta }r(\tau ))}^2⟩}/\tau$ at delay time $\tau$ = 1.0s. The diffusion velocity is the distance traveled per unit time by the particle motion. For the solutions at $\varphi$ = 20%, 30%, 40% and 50%, $v_D$ was smaller than that of normal diffusion at $\varphi$ = 0%, suggesting that even diluted fractions of actomyosin extract gradually increase the viscous friction against Brownian motion. For the solution at $\varphi$ = 60%, $v_D$ began to increase again and showed a substantial increase at $\varphi$ = 80% to 1.5 μm s⁻¹ (Fig. 4d). This suggests that as the fraction of cytoplasmic extract increased, Brownian motion was suppressed due to increased viscosity from higher overall protein concentrations. However, as the fraction of actomyosin extract further increased, tracer particles driven by actin flow moved faster than that via Brownian motion. We note that for the bulk actomyosin solution the velocity of actin flow was quantified as diffusion velocity, while the flow field analysis for the confined actomyosin solution was obtained by PIV (Figs. 1 and 2). Both provide an indication of flow velocity. However, the PIV analysis can produce small values due to averaging within the spatial window, suggesting that a direct comparison between the confined system and the bulk system is not applicable.

To further elucidate the effects of actomyosin contractility, we conducted a molecular perturbation experiment by adding calyculin A (Cal A), an inhibitor of protein phosphatase, which leads to phosphorylation of myosin to increase contractility³⁷. We repeated the particle-tracking experiment in a bulk system of diluted cytoplasmic extract solution containing 300 nmol L^−1 Cal A. The MSD of tracer particles showed that $\varphi$ = 0% exhibited behavior similar to that of simple diffusion, whereas even at a relatively low fraction $\varphi$ = 30%, it approached ballistic behavior, represented by ${\tau }^{1.8}$ (Fig. 5a). This indicates that the CalA-induced upregulation of contractile force can drive near-ballistic motion even in dilutions of cytoplasmic extracts at relatively low fractions. The speed of the tracer particles $v$ (t) at $\varphi$ = 30% increased by 2.0 μm s⁻¹ with fluctuations (Fig. 5b).

Fig. 5.

Quantitative analysis of tracer particle trajectories in chemically-perturbed actomyosin cytoskeleton solution in bulk condition. Actomyosin extract was chemically treated with 300 nM calyculin A (CalA-treated) to enhance myosin contractility. (a) Mean squared displacement of tracer particles tracked in various CalA-treated actomyosin fractions at representative $\varphi =0$%, 30%, 50%, and 60%. We note that the MSD curves at $\varphi =60$% are separated into two groups, actively transported particles and slowly transported ones. The mean MSD curve (red solid line) was acquired by averaging over actively transported particles. (b) Time evolution of the instantaneous speed of tracer particles in CalA-treated actomyosin solution.

For $\varphi$ = 50% and 60%, the slope of the MSD was smaller than that for $\varphi$ = 30% (Fig. 5a), indicating that the ballistic motion associated with actin flow was suppressed. Consistent with this result, $v$ (t) at $\varphi$ = 50% and 60% was reduced by 0.6 μm s⁻¹, comparable with that induced by thermal fluctuations (Fig. 5b). These chemical perturbation analyses suggest that actomyosin contractile force can drive ballistic tracer diffusion accompanied by actin flow; however, its strength should be maintained within a physiological range to support continuous flow.

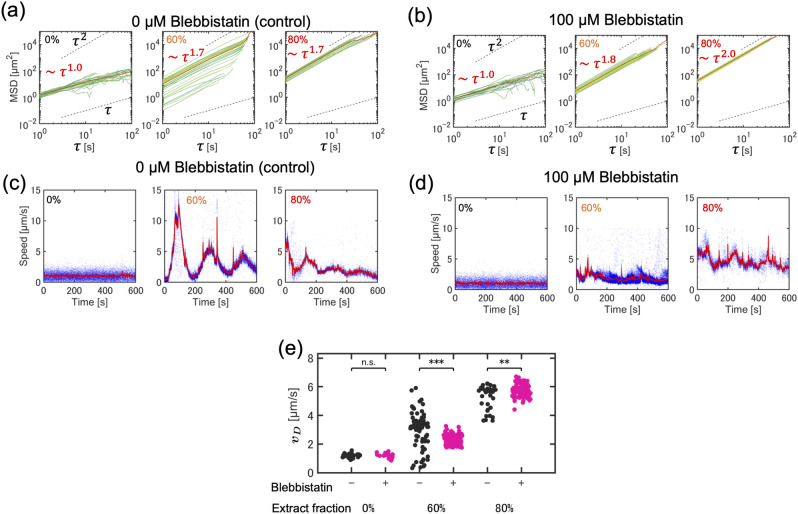
We further tested the effect of myosin contractility on the oscillatory flow of actomyosin solution by partial chemical inhibition with 100 μmol L⁻¹ blebbistatin. The actomyosin solution at $\varphi$ = 60% and 80% shows the super-diffusive motion in MSD (Fig. 6a) and the periodic change in velocity of tracer particles (Fig. 6c). In contrast, upon addition of blebbistatin, the MSD of the tracer motion is similar to the super-diffusive motion at fractions of $\varphi$ = 60% and 80% (Fig. 6b), the oscillatory tracer dynamics became disordered (Fig. 6d). The $v_D$ of the tracer particles was slightly reduced at $\varphi$ = 60% (Fig. 6e), but it should be noted that blebbistatin treatment appears to be a partial inhibition of myosin action¹⁹. If limited to such a partial inhibition of activity, the effect of chemical inhibition would be less clear as the concentration of myosin increases. We found that at a fraction of $\varphi$ = 80%, the speed of tracer particles, even under partially myosin-inhibited conditions, is almost comparable to the control condition (Fig. 6e). We also examined the effect of actin flow in confined actomyosin (fraction is $\varphi =100\%$) in the droplet by adding 100 μmol L⁻¹ blebbistatin, but the inward flow did not stop (Fig. S1). This is consistent with the result that blebbistatin has a tiny effect on the dynamics of actomyosin contraction, as seen in Fig. 6, in the high-density actomyosin.

Fig. 6.

Quantitative analysis of tracer particle trajectories in myosin-inhibited cytoskeleton solution in bulk condition. Actomyosin extract was chemically treated with 100 μmol L⁻¹ blebbistatin (Blebbistatin-treated) to reduce myosin contractility. (a and b) Mean squared displacement of tracer particles tracked in (a) the control condition and (b) blebbistatin-treated actomyosin fractions at $\varphi =0$%, 60%, and 80%. The mean MSD curve (red solid line) was acquired by averaging over actively transported particles. (c and d) Time evolution of the instantaneous speed of tracer particles in (c) the control condition and (d) blebbistatin-treated actomyosin fractions at $\varphi =0$%, 60%, and 80%. (e) Density dependence of the diffusion speed $v_D$ of tracer particles ($\varphi$ = 0%, 60% and 80%). Black: control, magenta: blebbistatin-treated. Statistical analysis was performed using the Mann-Whitney U test. *** indicates significance $p<0.001$, ** indicates $p<0.01$.

Discussion

In this study, we experimentally analyzed the occurrence of a density-dependent flow of actin. The contraction of cytoskeletal fibers is driven by the force generation of myosin molecular motor above the critical density of $\varphi =60$%, accompanied by actin flow. This occurred at comparable levels of the extract fraction in both the confined actomyosin solution and in the bulk solution. This flux oscillates near the transition point but is suppressed at higher myosin contractility levels, suggesting that instability due to actomyosin contraction is involved. In previous studies^29–31, periodic actin waves can be observed in the actomyosin solution confined within droplets when the actomyosin concentration is sufficiently high. Such actin waves originate at the boundary where nucleation factors promote actin network formation, resulting in increased actin concentration at the boundary and contraction toward the center of the droplets. Because the concentration of actomyosin used in this study was relatively low, below the threshold concentration for periodic waves, the fluid flow of confined actomyosin was steady advection. In contrast, we can find the oscillatory actin flow in the bulk actomyosin solution, without droplet confinement, at a dilute density near the transition from a uniform static state to an advective flow. Furthermore, the period of the oscillatory actin waves reported in previous studies^29–31 was approximately 60s. The period of the oscillatory actin flow in bulk solution was 150 s at $\varphi$ = 60% in bulk solution. The slightly longer cycle may be due to dilution and dilution of actin density.

When myosin activity is altered by chemical perturbation with CalA, the increased contractility of myosin results in decreased actin flux. A similar effect was found in previous work³⁸, which reported that when the addition of actin cross-linkers increases contractility, the rate of contraction of actomyosin is decreased. It has also been reported that when the actin network is at a density at which it can contract strongly, myosin force generation results in large deformations determined by the density dependence of the actin network³⁸. The periodic motion of tracer particles found in this study implies that the deformation rate of such networks becomes periodic at some critical density. To reveal such a critical actomyosin density, it may be relevant to note that there is a density at which force propagation reaches the far or percolation transition, depending on how the actin filaments are connected³⁹. Technical advances are needed to accurately measure the concentration of proteins, such as cross-linkers and the density of actin filaments in the extract solutions. Therefore, in the future, it will be clarified whether what determines this critical density is related to the binding frequency of the actin network, using a reconstruction system with purified proteins.

As actomyosin density increased, the speed of actin flow (diffusion speed of tracer particles) initially decreased. Upon reaching the critical density for flow initiation, actin flow occurred with sustained directionality. The reduction in speed at low densities may result from the actin fiber network impeding tracer particle diffusion. In contrast, the contractile force of actomyosin is insufficiently developed to overcome thermal fluctuations. This suggests that network formation of the actin filaments, associated with nucleation factors, precedes myosin contraction-driven actin flow. Furthermore, the lower value of the diffusion velocity at intermediate fractions of $\varphi =40\%$ reflects the enhanced effective viscosity, but its super-diffusive behavior suggests that there is an orientational correlation in the particle motion. We assume that the actin cytoskeleton is present in the bulk actomyosin solution, and its network increases the frictional drag, while the spontaneous contraction of the network in one direction can maintain the directional correlation in tracer motion.

The density-dependent flow of actin provides insights into biological self-organization, where cytoskeletal deformation owing to contractile force generation occurs beyond a certain concentration range. Intracellular actomyosin is not uniformly distributed but forms cortices on the plasma membrane surface, which is covered by a thin layer of the actomyosin cytoskeleton. Such localization patterns would be relevant for coexistence in the partitioning of intracellular space, providing sufficient contractility near the membrane to deform it, whereas the actin cytoskeleton restricts flow in the low-density spaces within the cytosolic space. Given the challenge of analyzing the concentration dependence of the intracellular cytoskeleton in living cells, a reconstituted system proves advantageous. Further investigation is warranted to address the development of an active gel model incorporating the density-dependent visco-elasticity of the actomyosin systems^40,41.

Materials and methods

Sample preparation

The frozen actomyosin extract was incubated on ice for 1 h prior to experimental use. TMR-LifeAct (final concentration 1.0 μmol L⁻¹) and nocodazole (final concentration 200 μmol L⁻¹) were added to the thawed extract solution and placed on ice. The extract was diluted with A50 buffer, and tracer particles (L4655 Latex beads, carboxylate-modified polystyrene, fluorescent yellow-green, solids: 0.6$\times {10}^{-2}$%) were added for flow visualization. To prepare droplets confining the actomyosin extract, 1.0 μL of this extract was injected into 10 μL of mineral oil (M5904, Sigma-Aldrich), and the mixed solution was agitated via finger tapping. The oil phase contained 1.0 ${\text{mmol}}^{-1}$ phosphatidylcholine (eggPC; Nacalai Tesque), and mechanical agitation helped form an emulsion containing extract-in-oil droplets.

To construct a sample chamber for extract-in-droplets, glass slides were coated with a silicone elastomer (polydimethylsiloxane, PDMS) (Sylgard 184; Dow Corning). The uncured PDMS was spread using a spin coater (MA-100, MIKASA). The PDMS-coated glass slides were cured at ${75}^{\circ }\text{C}$ for 1 h and then cut into three pieces on a PDMS-coated glass plate. Subsequently, 3.0 μL of the extract-in-oil emulsion was placed in the PDMS-coated glass chamber. The height of the chamber was set to 90 μm by inserting a spacer tape (Nichiban).

We also constructed a chamber using glass slides (Matsunami, S1111 and S1127) to prepare a bulk actomyosin solution. Approximately 6.0 μL of the extract was placed on a BSA-coated glass slide. The height of the chamber (i.e. spacer thickness) was 250 μm. Immediately after 1 min of plasma cleaning, 20 μL of phosphate buffer solution containing 0.1 mg/mL BSA (A2153, Sigma-Aldrich) was applied and spread near the center of the glass. After 10 min of incubation at room temperature, the BSA solution was removed, and the chamber was washed twice with phosphate buffer.

Microscopic observation

Time-lapse observation for confined actomyosin solution in droplets was performed every 5.0 s using an inverted microscope (IX73; Olympus) equipped with a 20$\times$ objective lens and an EM-CCD camera (iXon, Andor Technology). Time-lapse images of the bulk system were acquired every 1.0s using an epifluorescence microscope (IX73, Olympus) equipped with a cooled CMOS camera (Neo-5.5-CL3; Andor Technology). The temperature of the microscope stage was maintained at $20\pm 2^{\circ }\text{C}$ using a custom-made copper chamber.

Image processing

Image processing analysis was performed using custom code in MATLAB. To visualize actin flow, PIV analysis was performed using MATLAB with OpenPIV⁴², and the mean velocity field was obtained by time averaging over 110 sec. The size of interrogation window was 11.8 μm and the search window size was also 11.8 μm. Additionally, to analyze the dynamics of tracer particles in the bulk actomyosin solution, TrackMate, implemented as a plugin for Fiji/ImageJ, was used to track the fluorescent particles mixed into the actomyosin solution^43,44.

Author contributions

Y.T.M. and T. K. designed the research, T. K. performed experiment and analyzed data. T. F. contributed statistical analysis. Y. T. M. wrote the manuscript.

Data availability

The authors confirm that the data supporting the findings of this study are present within the paper and/or the Supplementary Materials.

Declarations

Competing interests

There are no conflicts of interest to declare.

Supplementary Information

The online version contains supplementary material available at 10.1038/s41598-024-82864-z.