Ultrafast Floquet engineering of Fermi-polaron resonances in charge-tunable monolayer WSe₂ devices

Abstract

Fermi polarons are emerging quasiparticles when a bosonic impurity immersed in a fermionic bath. Depending on the boson-fermion interaction strength, the Fermi-polaron resonances exhibit either attractive or repulsive interactions, which impose further experimental challenges on understanding the subtle light-driven dynamics. Here, we report the light-driven dynamics of attractive and repulsive Fermi polarons in monolayer WSe₂ devices. Time-resolved polaron resonances are probed using femtosecond below-gap Floquet engineering with tunable exciton-Fermi sea interactions. While conventional optical Stark shifts are observed in the weak interaction regime, the resonance shift of attractive polarons increases, but that of repulsive polarons decreases with increasing the Fermi-sea density. A model Hamiltonian using Chevy ansatz suggests the off-resonant pump excitation influences the free carriers that interact with excitons in an opposite valley, thereby reducing the binding energy of attractive polarons. Our findings may enable coherent Floquet engineering of Bose-Fermi mixtures in ultrafast time scales.

The authors study the light-driven dynamics of attractive and repulsive Fermi polarons in monolayer WSe₂. They show that the resonance shifts of Fermi polarons are valley-selective; the resonance shifts of attractive polarons increase with Fermi-sea density, while those of repulsive polarons decrease.

Introduction

As initially described by Landau¹ and Pekar², when electrons move in a dielectric medium, fermionic particles are dressed by lattice distortion, resulting in Bose-polaron quasiparticles³. After elaboration by Fröhlich^4,5 and Feynman^6,7, the polaron idea has successfully explained many-body exotic phenomena, for instance helium-3 in helium-4 bosonic bath⁸, formation of bipolarons⁹, and Rydberg polarons in ultracold quantum gases^10–12. A similar counterpart is a Fermi polaron, a bosonic impurity in a dressed fermionic bath. In the context of ultracold atoms, the large ratio of atomic transition energy to the fermionic particle density can be straightforwardly controlled, enabling a strong coupling regime of Bose-Fermi mixtures¹³. For solid state systems, although the significance of Fermi-polaron problems has been exemplified in studying phase transition dynamics^14–23, experimental studies on the transient Fermi-polaron problems have been barely conducted. This may be partly because of the limited availability of rigid bosonic candidates in fermion-rich solids; even when a well-characterized solid is prepared, probing the light-driven fine structures of the Fermi-polaron branches is experimentally challenging.

Atomically thin transition metal dichalcogenides (TMDs) exhibit strong exciton binding energy $\mathrm{\Delta }{E}_{\mathrm{X}}$ of around hundreds of meV due to both the reduced Coulomb screening and the large effective mass of electrons and holes. Along with the atom-like bosonic impurity of excitons, the ability to electrostatically tune the Fermi energy $E_{\mathrm{F}}$ offers a way to reach a strongly interacting regime of single mobile boson with a fluctuating Fermi sea. Indeed, steady-state optical spectroscopy has revealed that the light-generated excitons are dressed by intraband particle-hole excitations in a two-dimensional Fermi sea, resulting in the renormalized exciton spectra in the forms of attractive and repulsive Fermi polarons²⁴. Investigation of scattering channels has further revealed the electrically tunable Feshbach resonances²⁵, strongly coupled Fermi-polaron polaritons²⁴, and nonlinear polaron interactions^26,27. In principle, such strong light-matter interactions can dramatically turn the equilibrium properties into dynamical ones. However, because the energy scale of the two Fermi-polaron branches is typically of around tens of meV in monolayer TMDs, the Fermi-polaron problems using conventional above-gap optical-field driving generally involves hot-carriers mediated heat dissipation, hindering experimental observation of intrinsic Fermi-polaron spectral dynamics²⁸.

When below-gap light excitation takes place, new hybridized states (Floquet quasistates) emerge. Because the Floquet-interaction strength scales inversely with an energy detuning, the light-induced heat dissipation can be significantly suppressed, which can realize coherent photon-quasiparticle interactions such as optical Stark effects²⁹. While previous efforts have discovered various phenomena, such as ac Stark shift of $n=$1 exciton in GaAs^30–34, dynamic valley-degeneracy lifting in monolayer TMD^35–37, bandgap renormalization in black phosphorus³⁸, and ultrafast switching of optical nonlinearity in manganese phosphorus trisulfide³⁹, these studies have focused on the “isolated” excitons, and yet it is only very recent to apply the Floquet engineering into the “interacting” exciton-Fermi sea using a charge-tunable TMDs⁴⁰.

Here, we employ the ultrafast Floquet engineering into the gate-tunable monolayer WSe₂ to investigate the light-driven Fermi-polaron problems in presence of a fluctuating Fermi sea. In the polaronic phase, an exciton, regarded as a mobile impurity, experiences attractive (repulsive) interactions with the surrounding Fermi sea. These interactions produce the attractive (repulsive) polarons, as illustrated in the left of Fig. 1a. With below-gap pump excitation, a reduced interaction in Fermi polarons (right in Fig. 1a) leads to a larger resonance shift in the attractive polarons. We have developed an interacting Hamiltonian based on a contact exciton-Fermi sea interaction. Our model demonstrates that the circularly polarized below-gap optical pump results in a reduced binding energy of the attractive polarons, rendering a stronger resonance shift with increasing $E_{\mathrm{F}}$ compared to the repulsive polarons.

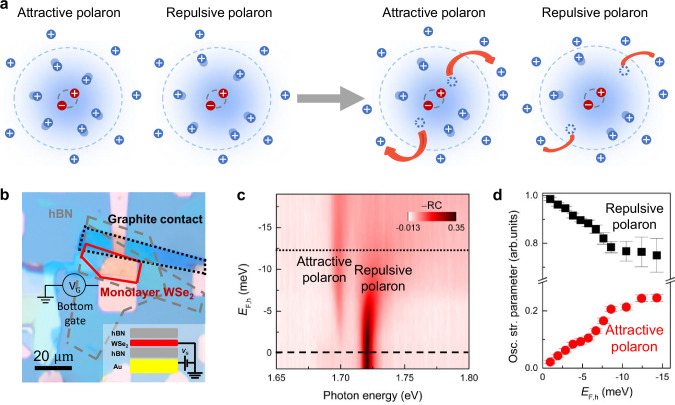
Fig. 1. Exciton-polaron interactions and optical properties in monolayer WSe₂.

a Schematic illustration of Fermi-polaron dynamics before the below-gap pump excitation (left) and after the excitation (right). The attractive interaction between excitons and holes is weakened whereas the repulsive interaction is less affected under the off-resonant pump. b An optical microscopic image of hBN-encapsulated WSe₂ device (Inset: a schematic of the device structure). c Reflectance contrast spectra as a function of the probe photon energy (bottom axis) and Fermi energy $E_{\mathrm{F},\mathrm{h}}$ (left axis). Here, RC$=\left(R-R^{\prime }\right)/R^{\prime }$, where $R$ is reflection signal from the WSe₂ monolayer sample and $R^{\prime }$ is reference spectrum from the background (hBN) nearby the sample. The dashed line ($E_{\mathrm{F},\mathrm{h}}=$ 0 meV) is the regime where an excitonic Stark effect is measured (Fig. 2a, c). The dotted line is for the hole density ($E_{\mathrm{F},\mathrm{h}}=$ −12.4 meV). Figure 2b, d are the measured data at this hole-doped density. d The oscillator strength parameters of attractive and repulsive polarons calculated from (c). Vertical error bars are obtained from the fits.

Results

Steady-state optical spectroscopy of Fermi polarons

Our experiments are performed on bottom-gated monolayer WSe₂ devices (Fig. 1b). The results from device #1 are discussed in the main text, while those from device #2 and #3 are presented in the Supplementary Note. Figure 1c shows the $E_{\mathrm{F},\mathrm{h}}$-dependent reflectance contrast (RC) spectra. We focus on the hole doped regime, i.e., increasing $E_{\mathrm{F},\mathrm{h}}$ indicates more hole doping (see Supplementary Note 1 for the detailed discussion about the Fermi polarons in the electron-doped regime). Near the charge neutrality ($E_{\mathrm{F},\mathrm{h}}\cong$ 0 meV), the RC spectra show a single exciton peak $E_{\mathrm{X}}$ near 1.72 eV. With increasing the hole doping density ($E_{\mathrm{F},\mathrm{h}}$ above −2.8 meV), the spectral resonance is shifted to the blue. Concurrently, a new resonance emerges near 1.7 eV, which is slightly redshifted compared to the exciton. The energy difference between these two resonances varies in the range of 21.7–30.6 meV at nonzero $E_{\mathrm{F},\mathrm{h}}$, which is larger than the trion binding energy $\mathrm{\Delta }{E}_{\mathrm{T}}$ (20.9 meV). These polaronic features originate from the interactions between the excitons and the Fermi sea^24,41–44 (see Supplementary Note 2 for more detailed analysis of the spectra). The $E_{\mathrm{F},\mathrm{h}}$-dependent transfer of oscillator strength from repulsive polarons to attractive polarons is summarized in Fig. 1d. The attractive polarons show redshifted resonances with an increased oscillator strength, which emerge from the increased binding energy between the excitons and the Fermi sea. Conversely, the repulsive polarons display a blueshifted feature with a reduced oscillator strength. The carrier-induced screening and Pauli blocking effects are the main contributors to the characteristics of the repulsive polarons. Similar features have also been confirmed by alternative devices (Supplementary Note 2) as well as prior reported studies^24,43,45.

Off-resonant optical dynamics of exciton-polarons

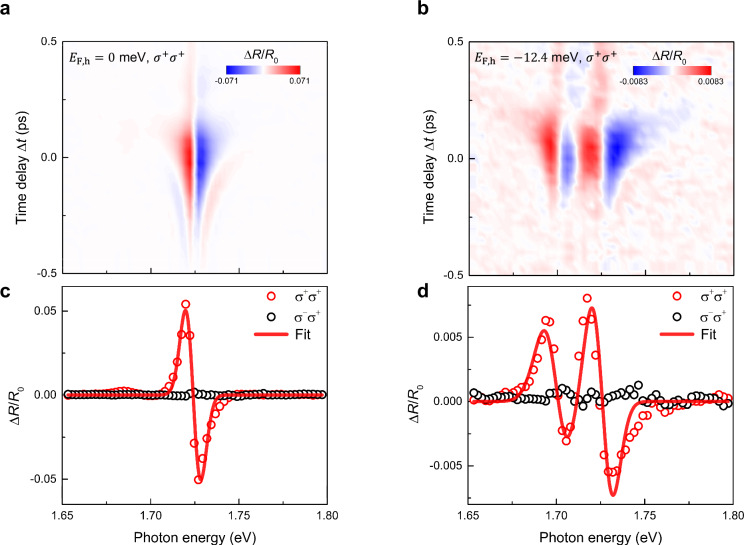
Figure 2a, b displays the two-dimensional plots corresponding to the differential reflectance spectra $\mathrm{\Delta }R/R_0$ measured using ${\sigma }^{+}$(right-circularly)-polarized probe upon excitation with ${\sigma }^{+}$-polarized pump pulses. The pump-photon energy $\hslash {\omega }_{\mathrm{pump}}$ is set below the 1s exciton to prevent any band-to-band population (a typical detuning energy ${\delta }_{\mathrm{X}}=E_{\mathrm{X}}-\hslash {\omega }_{\mathrm{pump}}$ is 171 meV) as well as below the attractive-polaron resonance. We show the two representative data: Fig. 2a is measured at $E_{\mathrm{F},\mathrm{h}}=$0 meV, i.e., charge neutral regime (see dashed line in Fig. 1c) and Fig. 2b at $E_{\mathrm{F},\mathrm{h}}=$−12.4 meV, i.e., hole-doped regime (see dotted line in Fig. 1c), respectively. The positive (negative) $\mathrm{\Delta }R/R_0$ implies a decrease (increase) in absorption. Whereas a single sign flip of $\mathrm{\Delta }R/R_0$ is seen in Fig. 2a, two clear sign flips are observed in Fig. 2b. Both $\mathrm{\Delta }R/R_0$ spectra exhibit significant spectral changes near the zero pump-probe time delay, $\mathrm{\Delta }t\cong$ 0 ps. Such instantaneous responses indicate that $\mathrm{\Delta }R/R_0$ cannot be explained by the band-to-band population changes, because such signals are measured to be lasting for many picoseconds (Supplementary Note 3 presents the data under above-gap pump excitation).

Fig. 2. Valley-selective resonance shifts of excitons and Fermi-polarons.

a A two-dimensional plot $\mathrm{\Delta }R/R_0$ when $E_{\mathrm{F},\mathrm{h}}$ is $0$ meV, i.e., the dashed line in Fig. 1c. The σ⁺-polarized pump (photon energy of 1.55 eV) is incident onto the sample and the pump-induced $\mathrm{\Delta }R/R_0$ changes are measured using with σ⁺-polarized white-light pulses. The data correspond to the conventional optical Stark effects of non-interacting excitons. b The pump-induced $\mathrm{\Delta }R/R_0$ spectra when $E_{\mathrm{F},\mathrm{h}}$ is −12.4 meV. See the dotted line in Fig. 1c. In contrast to a, two oscillatory signals are visible at 1.6981 eV and 1.7303 eV, implying the existence of two oscillator shifts. The former (latter) is attributed to the resonance blueshift due to the attractive (repulsive) Fermi polarons. Data of c and d are the spectrally-resolved $\mathrm{\Delta }R/R_0$ at zero time-delay between the pump and probe pulses. The pump and probe pulses are co-circularly polarized (open red circles). No significant $\mathrm{\Delta }R/R_0$ spectrum are observed for the cross-circularly polarized pump-probe case, i.e., ${\sigma }^{-}$-polarized pump and ${\sigma }^{+}$-polarized probe (open black circles). Solid red curves are the fit using shifted Gaussian oscillators. We have used a single Gaussian for (c) and two Gaussian oscillators model for (d). For more details on the fits, refer to the Note 4 in the Supplementary Information.

Figure 2c, d are the line cuts of $\mathrm{\Delta }R/R_0$ at $\mathrm{\Delta }t=$ 0 ps using co-circular polarization (${\sigma }^{+}$-pump and ${\sigma }^{+}$-probe, red circles) and cross-circular polarization (${\sigma }^{-}$-pump and ${\sigma }^{+}$-probe, black circles), respectively. The red solid line corresponds to the fit using one (Fig. 2c) and two Gaussian oscillators (Fig. 2d), respectively (Supplementary Note 4). The polarization-dependent $\mathrm{\Delta }R/R_0$ suggests that both signals closely resemble the valley-contrasting optical Stark effects. It is straightforward to fit using absorption derivative or integral of the change of absorption for the case of exciton-dominant $\mathrm{\Delta }R/R_0$ regime, i.e., $E_{\mathrm{F},\mathrm{h}}\cong$ 0 meV (Fig. 2c). Experiments probing excitonic and biexcitonic Stark effects also fall into this category^35,46. When $E_{\mathrm{F},\mathrm{h}}$ is nonzero (Fig. 2d), a significant transient reshaping occurs. Clearly, the dynamics does not follow a single oscillator shift, representing a strong deviation from the few-body exciton regime. This dynamics, therefore, does not represent a simple Floquet-driven “isolated” exciton picture. Based on the above aspects, one can anticipate $\mathrm{\Delta }R/R_0$ dynamics to exhibit a strong dependence of the Fermi energy.

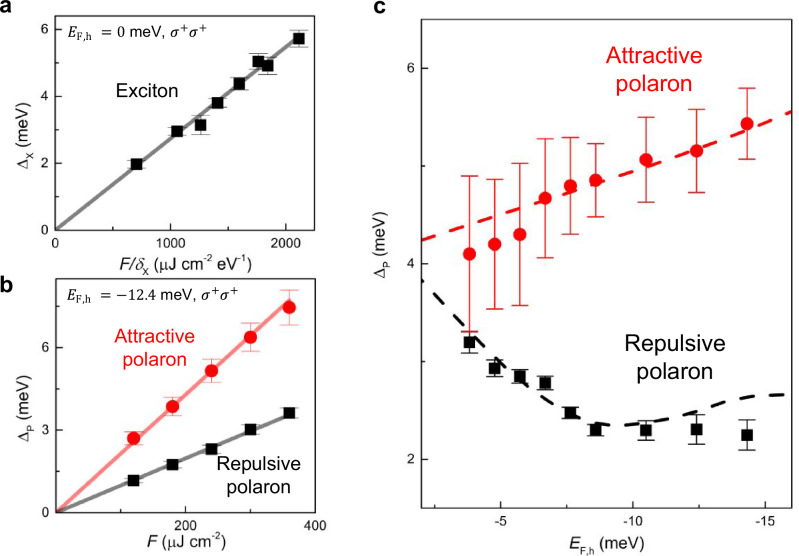
If the exciton resonance shift scales inversely with ${\delta }_{\mathrm{X}}^2$, it can be accounted for by the Coulomb repulsion between virtual excitons^47,48, which are known to be dominant when ${\delta }_{\mathrm{X}}\ll {\mathrm{\Delta }E}_{\mathrm{X}}$⁴⁹. Figure 3a is the extracted exciton-resonance shift ${\mathrm{\Delta }}_{\mathrm{X}}$ from the co-circular pump-probe spectroscopy with $\hslash {\omega }_{\mathrm{pump}}$ from 1.53 eV to 1.59 eV. Here, we vary the pump fluence F from 120 $\mathrm{\mu }\mathrm{J}{\mathrm{cm}}^{-2}$ to 360 $\mathrm{\mu }\mathrm{J}{\mathrm{cm}}^{-2}$. The gray line corresponds to a fit assuming that ${\mathrm{\Delta }}_{\mathrm{X}}$ is linearly dependent of $F/{\delta }_{\mathrm{X}}$. No higher-order quadratic dependence is found in our case. Because our ${\delta }_{\mathrm{X}}$ is in the range of 131–191 meV, which is substantially larger than the recent study (${\delta }_{\mathrm{X}}\approx$10–50 meV)⁴⁰, our experiment is different from the recent investigation of ac-Stark shifts of attractive polarons⁴⁰ (see Supplementary Note 5 for the detailed discussion about pump detuning dependence for Fermi polarons).

Fig. 3. Detuning, fluence, and Fermi energy dependence of Fermi-polaron resonance shifts.

a The optical Stark shift ${\mathrm{\Delta }}_{\mathrm{X}}$ of excitons (black squares) measured at $E_{\mathrm{F},\mathrm{h}}=$0 meV is shown as a function of $F/{\delta }_{\mathrm{X}}$. Gray line represents $F/{\delta }_{\mathrm{X}}$ dependence of ${\mathrm{\Delta }}_{\mathrm{X}}$. Because our measurement is by far off-resonant, higher-order correction including interactions between virtual excitons or polaron-polaron interactions is negligible. b The pump-fluence $F$ dependence of resonance shifts ${\mathrm{\Delta }}_{\mathrm{P}}$ for attractive polarons (red circles) and repulsive polarons (black squares) is shown. The linear dependence is clearly seen for both polarons. The data have been taken at $E_{\mathrm{F},\mathrm{h}}$ of −12.4 meV (dotted line in Fig. 1c) with $\hslash {\omega }_{\mathrm{pump}}$ of 1.55 eV. At the same $F$ (120–360 $\mu \mathrm{J}{\mathrm{cm}}^{-2}$), ${\mathrm{\Delta }}_{\mathrm{P}}$ for the attractive polarons is much larger than that of the repulsive polarons. Due to the released holes from attractive interactions with excitons due to the pump excitation, the additional blueshift occurs in the attractive polarons. c Resonance shifts of attractive polarons (red circles) and repulsive polarons (black squares) at $F$ is 240 $\mu \mathrm{J}{cm}^{-2}$ and ${\delta }_{\mathrm{X}}$ is around $171$ meV are plotted as a function of the Fermi energy: −14.3$<E_{\mathrm{F},\mathrm{h}}<$−3.8 meV. The error bars are obtained from the fits. The red and black dashed lines are theoretical calculations of the spectral function obtained from the interacting Hamiltonian using Chevy ansatz (see the main text and Supplementary Note 7 for more details). Vertical error bars in a–c are obtained from the fits.

Gate- and pump fluence-dependent dynamics of Fermi polarons

Having confirmed that the Coulomb repulsion between the virtual excitons is excluded, we show in Fig. 3b the resonance shifts ${\mathrm{\Delta }}_{\mathrm{P}}$ of both attractive polarons and repulsive polarons as a function of pump fluence $F$. Both resonance shifts exhibit a linear dependence on $F$, which is similar to the conventional excitonic Stark shifts^35,50. We find, however, that ${\mathrm{\Delta }}_{\mathrm{P}}$ for the attractive polarons is almost twice larger than the repulsive polarons. This is contradictory to the conventional atom-photon two-level model, where the resonance shift is directly proportional to the oscillator strength $f_{\mathrm{osc}}$ of the involved resonance, i.e., ${\mathrm{\Delta }}_{\mathrm{X}}\propto \left(F\cdot f_{\mathrm{osc}}\right)/{\delta }_{\mathrm{X}}$. Because $f_{\mathrm{osc}}$ of the attractive polarons is smaller than that of repulsive polarons (Fig. 1d), one expects a smaller resonance shift ${\mathrm{\Delta }}_{\mathrm{P}}$ for the attractive polarons under the same $F$ and ${\delta }_{\mathrm{X}}$. In fact, we find the standard atom-photon Floquet picture, cannot reproduce our data of Fig. 3b (see Supplementary Note 6 for details on such conventional dressed atom models). Thus, our case is different compared to the excitonic Stark effect with no Fermi-sea interactions. A central concern of our study is the ${\mathrm{\Delta }}_{\mathrm{P}}$ changes for attractive and repulsive polarons as a function of $E_{\mathrm{F},\mathrm{h}}$ (Fig. 3c). For the repulsive polarons, the ${\mathrm{\Delta }}_{\mathrm{P}}$ characteristics closely follow the excitonic properties. Thus, increasing the Fermi energy leads to a monotonically decreasing ${\mathrm{\Delta }}_{\mathrm{P}}$ feature. On the other hand, the increased ${\mathrm{\Delta }}_{\mathrm{P}}$ in the attractive polarons means that the binding energy of the attractive polarons is weakened. The below-gap optical pump generates “hot” holes from the top to the deep valence band, thereby extra holes are released from the attractive interactions with the excitons⁵¹. Such kinetics result in the reduced Coulomb binding of holes in the attractive polarons, so that ${\mathrm{\Delta }}_{\mathrm{P}}$ is blueshifted.

Discussion

Quasiparticle interactions between an exciton and the Fermi sea in Fermi polarons can be theoretically described by the Hamiltonian consisted of a bare exciton and the exciton dressed by the intraband particle-hole excitation in an opposite valley²⁴:

$$H=\sum {\omega }_{\mathrm{X}}\left(k\right)x_k^{+}{x}_k+\sum \left({\hslash k}^2/2m_{\mathrm{h}}\right)h_k^{+}{h}_k+\sum V_q\left(x_{k+q}^{+}{h}_{k^{\prime }-q}^{+}{h}_{k^{\prime }}{x}_k+h.c.\right),$$ 1

where ${\omega }_{\mathrm{X}}\left(k\right)$ is the exciton dispersion described as ${\omega }_{\mathrm{X}}\left(k\right)={\mathrm{\Delta }E}_{\mathrm{X}}+\delta \left(E_{\mathrm{F}}\right)+{\hslash k}^2/2m_{\mathrm{exc}}$, in which offset $\delta \left(E_{\mathrm{F}}\right)$ is $\beta E_{\mathrm{F}}$ with fitting parameter $\beta$ for band gap renormalization. $x_k$ ($x_k^{+}$) and $h_k$ ($h_k^{+}$) represent the annihilation (creation) operator for the exciton and the hole, respectively, and $m_{\mathrm{exc}}$ and $m_{\mathrm{h}}$ denote the effective masses of the exciton and the hole. The first and second terms describe the energies of excitons and the Fermi sea, and the third term indicates the interaction of the Fermi sea with the excitons. We also include the bandgap renormalization⁵², for which $\delta \left(E_{\mathrm{F}}\right)=0.68E_{\mathrm{F}}$ is introduced for the best fit of the RC measurements (Supplementary Note 7 for details on the polaron theory). In the presence of the finite Fermi-sea density, such interactions can be derived from the self-energy $\mathrm{\Sigma }\left(E\right)$ using Chevy Ansatz:

$$\mathrm{\Sigma }\left(E\right)={\sum }_q{\left[\frac{1}{V}-{\sum }_{k=k_F}^{\mathrm{\Omega }}\frac{1}{E+i{0}^{+}-{\omega }_{\mathrm{X}}\left(q-k\right)+ϵ\left(k\right)-ϵ\left(q\right)}\right]}^{-1},$$ 2

where $\frac{1}{V}={\sum }_{k=0}^{k_F}\frac{1}{{\mathrm{\Delta }E}_{\mathrm{P}}-{\omega }_{\mathrm{X}}\left(0\right)+{\omega }_{\mathrm{X}}\left(k\right)+ϵ\left(k\right)}$ and $0^{+}$ is the small positive imaginary for the causality of retarded Green’s function⁵³. $\mathrm{\Omega }$ denotes an ultra-violet cutoff, while $ϵ\left(k\right)$ represents the dispersion relation for holes.

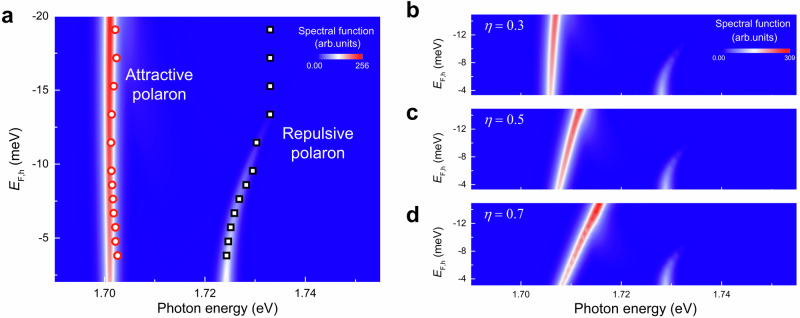
We compare the data of Fig. 3c with the theoretically derived spectrum using Eq. (2). We find that the agreement is excellent when ${\mathrm{\Delta }E}_{\mathrm{P}}=23\mathrm{meV}+1.3E_{\mathrm{F}}$ (Fig. 4a). Supposing that the below-gap excitation mainly affects ${\mathrm{\Delta }E}_{\mathrm{P}}$ of the attractive polarons, we introduce a fractional factor η to consider the reduced $\mathrm{\Delta }{E}_{\mathrm{P}}$. The spectral function is computed with η in the expression ${\mathrm{\Delta }E}_{\mathrm{P},\mathrm{pump}}=23\mathrm{meV}+1.3E_{\mathrm{F}}\left(1-\eta \right)$, where η is bounded between 0 and 1. Figure 4b–d are the calculated spectral functions at $\eta =$0.3, 0.5, and 0.7, respectively. An increased (decreased) blueshift of the attractive (repulsive) polarons is clear with increasing η. After running multiple simulations, we have found that η of 0.3 faithfully corresponds to the experimental data of Fig. 3c within the $E_{\mathrm{F},\mathrm{h}}$ range of −3.8 to −14.3 meV. It means that the photoexcited holes are released from their attractive interactions with a constant fraction η of the hole density. This 30% reduction in the Fermi-polaron binding energy cannot be associated with the fluctuating thermal energy $~4k_{B}T=$ 1.38 meV at 4 K, which remains far below the broaden linewidths of ~59.8 meV and ~9.4 meV for the repulsive and attractive polarons, respectively. Further theoretical investigations are needed to accurately determine the fractional factor η.

Fig. 4. Spectral functions of Fermi-polaron resonances.

a The calculated spectral function as a function of Fermi energy $E_{\mathrm{F},\mathrm{h}}$ is overlapped with the experimentally measured reflectance contrast without the pump excitation. The open red circles are for the attractive polarons, and the open black squares represent the repulsive polarons. Both are extracted from Fig. 1c. b–d Calculated spectral functions when different fractional factor $\eta$ is used for the polaron binding energy ${\mathrm{\Delta }E}_{\mathrm{P},\mathrm{pump}}=23\mathrm{meV}+1.3E_{\mathrm{F},\mathrm{h}}\left(1-\eta \right)$; b–d are the plots when $\eta$ is 0.3, 0.5, and 0.7, respectively. With varying $\eta$, the spectral functions show different slopes for the attractive and repulsive polaron branches as a function of $E_{\mathrm{F},\mathrm{h}}$. When a specific valley is excited with the below-gap pump, the binding energy between the excitons and the surrounding Fermi sea in an opposite valley becomes smaller than the case without the pump.

In summary, we have investigated the light-driven Fermi-polaron dynamics when a bosonic impurity strongly interacts with the resident Fermi sea. Below-gap photoexcitation is employed in the gate-tunable monolayer WSe₂. Both attractive and repulsive Fermi polarons show the valley-selective resonance shifts with a linear correlation with $F$. While the dynamical shift of the repulsive polarons exhibits a decreasing feature, that of the attractive polarons is strongly enhanced with increasing the Fermi-sea density. Such dynamics are found not to be explained by the conventional dressed atom-photon picture. To accommodate these features, we present a simple interacting Hamiltonian using Chevy ansatz, and have found that the below-gap excitation invokes a substantial reduction of the binding energy of the attractive polarons.

Methods

Sample fabrication

For the fabrication of gate-tunable monolayer WSe₂ devices, we follow the procedures established in previous studies^54–57, which are based on the mechanical exfoliation of the monolayer WSe₂. Thin hexagonal boron nitride (hBN) layer (~15 nm) are transferred onto a 300 nm SiO₂/Si substrate and another hBN layer (~30 nm) is used to encapsulate the whole device (top layer). The monolayer WSe₂ and the thin-film hBN are obtained by exfoliating them from a bulk crystal of WSe₂ (HQ graphene) and the high-quality hBN (National Institute for Materials Science, Japan), respectively. As depicted in Fig. 1b, the WSe₂ layer is grounded by a few-layer graphene electrodes. The bottom gate is patterned using a standard e-beam lithography. Ti/Au with a thickness of 5/45 nm is deposited using a thermal evaporator. The hBN/WSe₂/graphite(electrodes)/hBN layers are picked up in series using a PDMS film covered with a polycarbonate (PC) film, and they are released on a pre-patterned bottom gate. Instead of the conventional dual-gate configuration, our bottom-gate $V_{\mathrm{G}}$ geometry enables to exclude any possible transient pump-probe artifacts from the top gate.

Steady-state and pump-probe spectroscopy

For the reflectance contrast (RC) measurement, we have used a halogen lamp (Thorlabs OSL2) as a source. The laser is focused at the sample with 1 $\mathrm{\mu }\mathrm{m}$ beam size using a $\times$ 50 long working distance objective (Mitutoyo Plan Apo SL, NA = 0.42). A grating monochromator (Dongwoo optron MonoRa 512i) equipped with a CCD (Oxford Newton 970 EMCCD) camera is used to gather and analyze the reflection signal R from the WSe₂ monolayer sample. The reference spectrum $R^{\prime }$ is obtained from the background with hBN right next to the WSe₂ area. The corresponding normalized difference signal $\left(R^{\prime }-R\right)/R^{\prime }$ is plotted in Fig. 1c.

For the ultrafast spectroscopy, the femtosecond pulses at 1.55 eV are generated by a 250 kHz Ti:sapphire regenerative amplifier (Coherent RegA 9040). The femtosecond pulses, with a pulse duration of around 40 fs, are divided into two parts: 75% of the total power of 1.3 W is utilized as pump pulses, while the remaining 25% is focused into a 0.5-mm-thick sapphire disk. The generated white light covers a probe photon energy from 1.65 eV to 1.8 eV. A pair of prisms (Thorlabs SF10) are inserted into both pump and probe paths to compensate the dispersion caused by the presence of dispersive optical elements. The overall temporal resolution of the measurement is around 300 fs. A dual-slotted chopper (Stanford Research Systems SR 540) is used to measure the reflectance without the pump ($R_0$) and the differential reflectance ($\mathrm{\Delta }R$) with the pump. Frequency-synchronized signals are simultaneously collected using a dual lock-in detection technique (Stanford Research Systems SR 830). The spot sizes of the pump and the probe on the sample are 2.5 $\mathrm{\mu }\mathrm{m}$ and 1$\mathrm{\mu }\mathrm{m}$, respectively. The probe light is detected using an avalanche photodiode (Thorlabs APD410A) after the wavelength selection through a monochromator. The pump-probe time delay is controlled using a motorized delay stage. Time zero refers to the time delay where the correlation between the pump pulses and the probe pulses is maximum. The polarization of the pump and probe pulses is controlled by utilizing a set of waveplates (AQWP05M, AHWP05M-580, 10RP52-2) and a linear polarizer (GL10-A, GL10-B, 10GT04). Both RC and the pump-probe experiment are conducted in a closed-cycle Montana cryostat (Cryostation s50), with a constant base temperature of 4 K.

Author contributions

Hyojin Choi, J.Kim, and J.P. fabricated samples. J.L., W.H., J.Kwon, and S.-H.L. performed the device characteristics examination. K.W. and T.T. provided high-quality hBN crystal. Hyojin Choi and J.Kim performed the measurements. Hyojin Choi, J.Kim, A.F., Z.S., M.-H.J., and Hyunyong Choi performed data analysis and discussed the results. Hyunyong Choi and M.-H.J. supervised the project. Hyojin Choi and J.Kim wrote the manuscript with input from all co-authors.

Peer review

Peer review information

Nature Communications thanks Zhensheng Tao and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Data availability

The data that support the finding of this study are available from the corresponding author upon request. The full set of pump-probe data generated in this study are provided in the Supplementary Information file.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-55138-5.