Atomic-scale structure of ZrO₂: Formation of metastable polymorphs

Abstract

Metastable phases can exist within local minima in the potential energy landscape when they are kinetically “trapped” by various processing routes, such as thermal treatment, grain size reduction, chemical doping, interfacial stress, or irradiation. Despite the importance of metastable materials for many technological applications, little is known about the underlying structural mechanisms of the stabilization process and atomic-scale nature of the resulting defective metastable phase. Investigating ion-irradiated and nanocrystalline zirconia with neutron total scattering experiments, we show that metastable tetragonal ZrO₂ consists of an underlying structure of ferroelastic, orthorhombic nanoscale domains stabilized by a network of domain walls. The apparent long-range tetragonal structure that can be recovered to ambient conditions is only the configurational ensemble average of the underlying orthorhombic domains. This structural heterogeneity with a distinct short-range order is more broadly applicable to other nonequilibrium materials and provides insight into the synthesis and recovery of functional metastable phases with unique physical and chemical properties.

Experimentation confirms an orthorhombic metastable ZrO₂ phase, yielding insight into metastable phase synthesis and recovery.

INTRODUCTION

Materials selection for engineering applications generally relies on an equilibrium phase diagram that describes thermodynamic stability with respect to chemical composition, as well as temperature and pressure. Metastable polymorphs can be stabilized by slow kinetic pathways to a stable phase, thus expanding the number of accessible phases beyond their usual phase space (1, 2). Stabilization beyond equilibrium phase space is especially useful because metastable phases often have superior material properties attractive for a myriad of technological applications (3). Exceptional mechanical strength (4), fast ionic and high/low thermal conduction (5, 6), and enhanced electrical/optical properties (7) arise in metastable compounds when synthesis and processing yield their stabilization at expected operating conditions.

From an engineering point of view, induced strain is a common strategy in the stabilization process, as defects and surfaces modify the free energy landscape and affect phase stability (8). Strain for the purpose of metastable phase synthesis can be introduced by various means, such as reduction to nanoscale size (9), growth on a template/substrate (10, 11), thermal/pressure quenching (12), mechanical processing (1, 13), doping (14), and irradiation (15). Structural aspects of metastability, particularly defect-engineered stabilization mechanisms, must be better understood at the atomic scale to develop novel synthesis routes and accelerate the discovery of new metastable phases desirable for next-generation technologies.

Metastability plays a particularly important role in well-studied zirconia (ZrO₂), which exhibits structural transformations among several polymorphs that occur under a wide range of temperature and pressure conditions (16, 17). At standard pressure and temperature, the stable atomic configuration is the monoclinic (P2₁/c) phase, commonly known as baddeleyite, where the number of oxygen neighbors coordinated with each zirconium atom is 7 (fig. S1). Two distinct structures, the high-temperature tetragonal (P4₂/nmc) and cubic ($\mathit{Fm}\overline{3}m$, isostructural with fluorite) polymorphs, both with a Zr coordination number of 8, can be obtained upon heating above ~1400 and 2600 K, respectively (18, 19). Two additional orthorhombic polymorphs with coordination numbers of 7 (Pbca) and 9 (Pnam) are accessible at high pressure (16), and a polar orthorhombic phase (Pca2₁) accounts for ferroelectricity in ZrO₂ thin films (20). The tetragonal and monoclinic structures of ZrO₂ are related by a displacive phase transformation mechanism involving structural distortions and shear deformations (21).

Tetragonal zirconia-based ceramics, like the cubic high-temperature polymorph, are a remarkably useful material for many technologies, owing to impressive mechanical (high strength and toughness), thermal (refractory with low conductivity), and electrical (high dielectric permittivity with fast oxygen conductivity when doped) properties (14). However, tetragonal ZrO₂ is not stable at ambient conditions, and the reversible phase transformation yields the monoclinic phase upon cooling (22). Because tetragonal zirconia cannot be thermally quenched in bulk form, stabilization is typically achieved by aliovalent doping of ZrO₂ (i.e., Y_xZr_1−xO_2−0.5x—partially stabilized zirconia), thereby introducing anion vacancies, substitutional defects, and changes in stoichiometry (18). Although stabilization via doping changes the chemical composition, the tetragonal phase can also be produced in pure stoichiometric ZrO₂ when prepared as a nanocrystalline material, either as a nanometric layer on a substrate (10, 11) or as a nanocrystalline powder (23). The stabilization mechanism at the nanoscale was described by Garvie et al. (23) more than 50 years ago as being driven by strain energy originating from surfaces or interfaces when the characteristic length scale of the system is smaller than ~30 nm (14).

Ion irradiation, which has also been demonstrated to quench metastable high-temperature and high-pressure phases to ambient conditions in numerous cases (15, 24), can similarly be used to transform monoclinic ZrO₂ to the tetragonal polymorph (25). In this case, radiation-induced defects and associated strain fields are believed to be responsible for stabilization, regardless of whether these defects are produced by displacive, knock-on collisions (neutron or low-energy MeV ion irradiation) (8) or by extreme electronic excitations and ionization processes (high-energy GeV ion irradiation) (16). The long-range order (LRO) of each crystalline polymorph, and in particular the monoclinic-to-tetragonal transformation as a function of temperature (19), ion irradiation (26), and crystallite size (14), has been thoroughly characterized using a wide range of analytical techniques, yet the atomic-scale processes involved in the stabilization of metastable phases are not fully understood. Therefore, zirconia serves as an apt model system to unravel the interplay between structural complexity and phase metastability.

RESULTS

Multilength scale characterization

Neutron total scattering, with high sensitivity to the oxygen sublattice, was performed at the world’s most intense spallation source at the Oak Ridge National Laboratory and used to simultaneously probe the short-range order (SRO) and LRO of the metastable tetragonal polymorph. For this study, the metastable phase was prepared by two approaches: as nanocrystalline ZrO₂ (grain size: ~7 nm) and from microcrystalline ZrO₂ processed by intense energetic heavy ion irradiation (1.47-GeV Au ions). Both the SRO and LRO were analyzed using small-box modeling in real space and Rietveld refinement in reciprocal space. A multilength scale simulation of a supercell consisting of several nanoscale domains provided additional insight into how the LRO emerges through averaging of SRO building blocks.

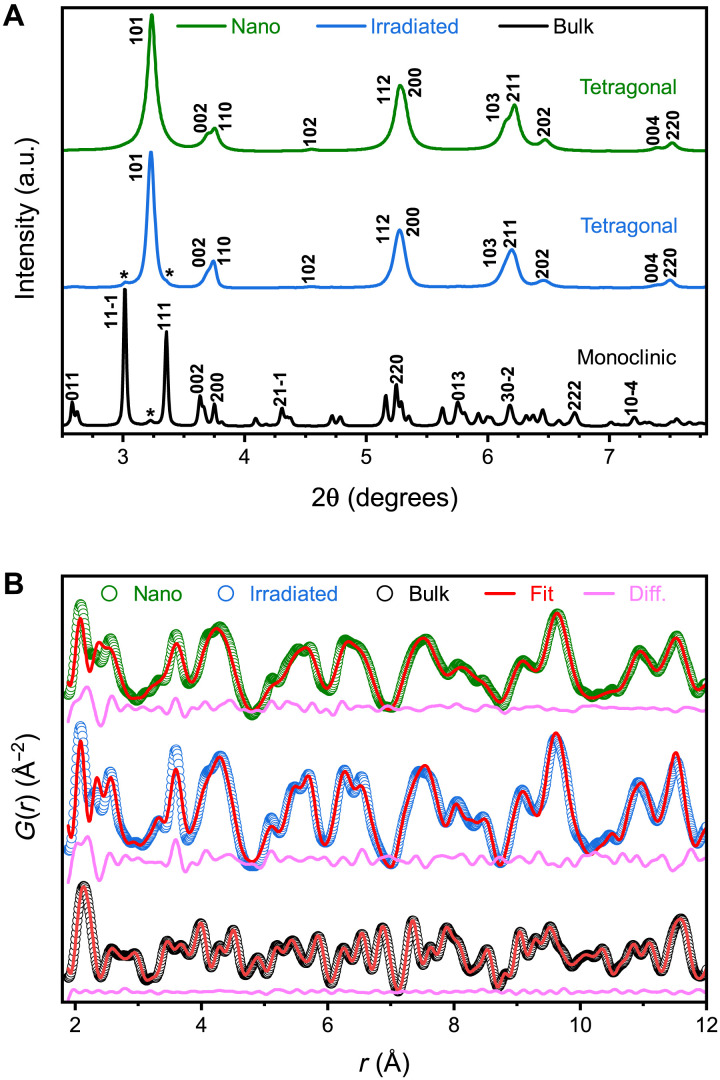
Room temperature neutron (figs. S2 and S3) and synchrotron x-ray diffraction (SXRD) (Fig. 1A) independently confirm that the LRO of the pristine, microcrystalline ZrO₂ sample is the well-known monoclinic polymorph. As expected, the LRO in both nanocrystalline and ion-irradiated microcrystalline ZrO₂ is best described by a structural model derived from the high-temperature tetragonal polymorph (Fig. 1A) (14, 17). The x-ray diffraction (XRD) pattern of the ion-irradiated sample contains minor (<5%) monoclinic contributions remaining from regions of unirradiated material with incomplete ion-track overlap. The nanocrystalline ZrO₂ is completely phase pure, and the pronounced peak broadening is characteristic of the small crystallite size (27) without any detectable splitting of the tetragonal peaks or emergence of additional peaks. No oxygen vacancies were detected by Rietveld analyses or indicated by a change in color of the sample.

Fig. 1. XRD patterns and neutron PDFs for microcrystalline (bulk), irradiated, and nanocrystalline ZrO₂.

(A) XRD patterns for each sample. Miller indices denote prominent diffraction peaks, and asterisks indicate peaks from a secondary phase (<5% phase fraction). a.u., arbitrary units. (B) Neutron PDFs for each sample. Open circles denote the measured PDFs, red curves represent fits of the monoclinic (bulk) or tetragonal (nano and irradiated) model, and magenta curves show the difference between the data and the fit. All datasets are offset vertically for ease of visualization.

The SRO was examined in the three samples by analyzing the high-resolution neutron pair distribution functions (PDFs). This real-space structural representation is a histogram of interatomic distances that quantifies the probability that two atoms are separated by a distance, r (Fig. 1B) (28). The PDF was initially modeled for all three samples using the atomic positions derived from refinement of the XRD patterns (Fig. 1A), i.e., the LRO. As demonstrated by the difference curve, the monoclinic model accurately fits the PDF of the unirradiated, microcrystalline reference sample, indicating a uniform organization across all spatial length scales (i.e., structural homogeneity). In contrast, a substantial deviation from the long-range symmetry is observed in the nonequilibrium phases. The tetragonal structural model (29) fails to describe the PDFs of both metastable zirconia samples at r < 7 Å, representing a volume consisting of about three tetragonal unit cells; the mismatch becomes increasingly pronounced for interatomic distances shorter than ~4 Å. On the other hand, the accuracy of the tetragonal model improves at longer distances (Fig. 1B), indicating a structural discontinuity and spatial heterogeneity with the LRO not accurately describing the underlying atomic-scale configuration. This agrees with prior x-ray PDF analysis of thin-film zirconia, where reduced local symmetry associated with oxygen vacancies explained the short-range deviation from tetragonal symmetry in substoichiometric ZrO_2−x (10). However, regardless of whether the metastable tetragonal phase was obtained as a nanomaterial or by ion irradiation, no deviation from stoichiometry was detected by neutron PDF analysis.

Even more remarkably, none of the conventional ambient (monoclinic P2₁/c, 14), high-temperature (tetragonal P4₂/nmc, 137; cubic $\mathit{Fm}\overline{3}m$, 225) (19), or high-pressure (ortho-I Pbca, 61; ortho-II Pnma, 62) (16) phases reported in the equilibrium phase diagram, or their combinations, describe the SRO (fig. S4). Deviations from the tetragonal model in nanocrystalline ZrO₂ have been hinted at previously in x-ray PDF and extended x-ray absorption fine structure (EXAFS) studies of nanopowders and in thin films, where they were explained as lower symmetry distortions of coordination polyhedra or as “shear-jamming” of their packing sequences (9, 10, 30). However, the analytical methods used in previous investigations lack either the direct real-space resolution or the high oxygen sensitivity characteristic of the neutron PDF analysis.

Landau theory

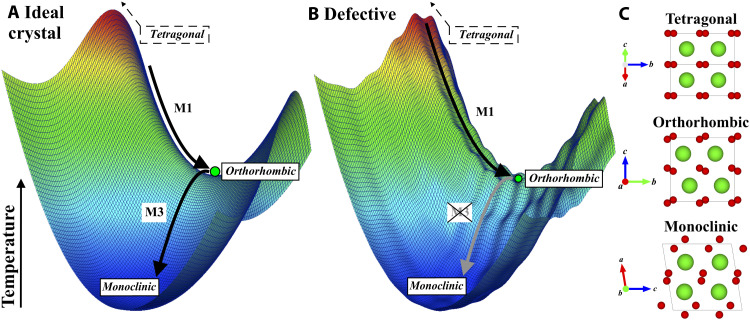
To gain further insight into the local structure of metastable zirconia, representation theory (31) was used to describe the transformation pathway between the high-temperature tetragonal and the ambient monoclinic phases. The Landau energy landscape associated with this transformation, qualitatively shown in Fig. 2A, is characterized by two structural instabilities, which can be described by a sequence of two phonon condensations (32) (see also Supplementary Text). Cooling a tetragonal bulk ZrO₂ crystal triggers the condensation of a first phonon (M1), yielding an unstable orthorhombic Pbcn structure, immediately followed by the condensation of a second phonon (M3), rendering the monoclinic ground state phase.

Fig. 2. Qualitative energy landscape of the two-step phase transformation pathway between the tetragonal (P4₂/nmc) and monoclinic (P2₁/c) phases.

This transformation involves a saddle point of the Landau free energy: an unstable orthorhombic (Pbcn) intermediate polymorph. The transformation pathway is described by the amplitudes of the two phonons M1 and M3 for (A) an ideal crystal and for (B) a defective crystalline structure, alongside (C) the structure of each phase with Zr and O atoms shown in green and red, respectively. Temperature is analogous to free energy in this representation.

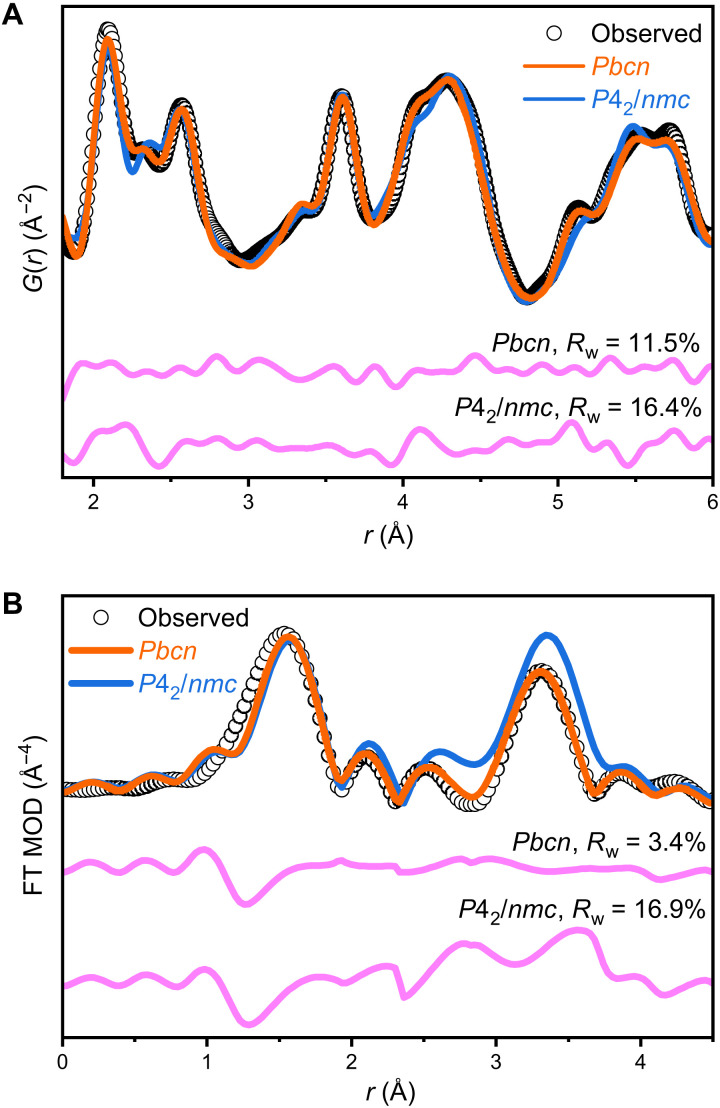
Thus, the tetragonal and monoclinic phases are structurally linked by an intermediate orthorhombic Pbcn phase, occurring at a saddle point of the Landau energy landscape (32). Despite many efforts, this predicted orthorhombic phase has never been observed experimentally as it is unstable in the unirradiated bulk ZrO₂ system (19); however, the Pbcn structural model accurately describes the bonding environment and atomic configuration of the two metastable ZrO₂ samples, as demonstrated by the small-box refinement of neutron PDF data for r values up to 6 Å (Fig. 3A). Refined structural parameters are given in table S1 and can be used to construct the orthorhombic phase observed here. In contrast with the high-pressure orthorhombic and ambient monoclinic phases, the Zr cation maintains a statically distorted eightfold coordination with the O anions in the Pbcn structure, but the distribution of bond lengths is broader than that permitted by the tetragonal model.

Fig. 3. PDF and EXAFS data describe the SRO.

(A) Neutron PDF reveals that the SRO of nanocrystalline ZrO₂ is best fit using an orthorhombic Pbcn phase, which is independently confirmed by (B) the Fourier transform of EXAFS spectra of the same sample. Magenta curves show the difference between the models (colored lines) and the data (black circles), and weighted residuals are reported as R_w.

To further probe the existence of the orthorhombic atomic arrangement within metastable ZrO₂, the nanocrystalline sample was additionally analyzed using synchrotron-based EXAFS (Fig. 3B and table S2) (33). The PDF-derived Pbcn and P4₂/nmc (29) structural models were used with fixed coordination numbers for a better comparison. When applying the Pbcn model to the EXAFS data, a higher level of accuracy was achieved, yielding lower residuals (R_w = 0.034) and more physically meaningful parameters (table S2). In contrast, the P4₂/nmc structure does not accurately fit the data, resulting in a much higher residual (R_w = 0.169), particularly evident in the Zr–Zr scattering paths between 2.8 and 4.0 Å (Fig. 3B). Thus, the EXAFS analysis independently confirms the existence of an orthorhombic SRO in tetragonal ZrO₂ nanopowders, explaining deviations previously reported in EXAFS data of metastable zirconia (9, 30).

Supercell modeling

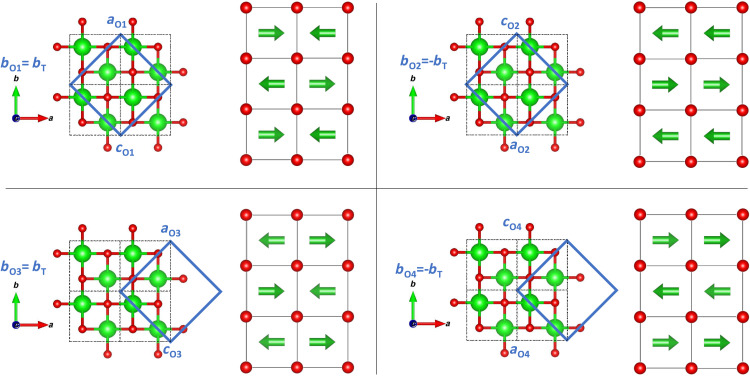
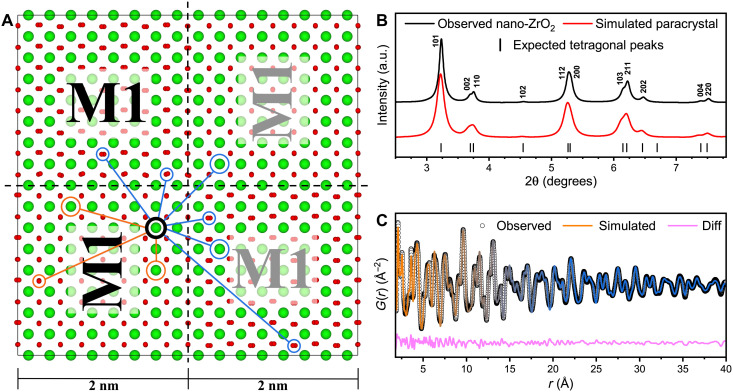
The local atomic configuration of metastable zirconia is fully described by the orthorhombic structural model in the neutron PDF data (Fig. 3A). Because there are no short-range contributions in the PDF from the tetragonal phase, this is clear evidence that there is no coexistence of both phases in the material. The formation of the orthorhombic atomic arrangement is the consequence of the improper ferroelastic phase transition (32) driven by an instability at the tetragonal Brillouin zone boundary M point (for more information, see the Supplementary Materials). Disrupting the transition illustrated in Fig. 2A after the condensation of the first phonon produces degenerate, ferroelastic, orthorhombic domains, differing only by their lattice orientation and origin shift. Correlated atomic displacements related to the Pbcn symmetry are maintained only within a single domain. Box-car refinements of neutron PDFs reveal that the correlation length of each orthorhombic domain is ~2 nm (fig. S5), consistent with the absence of orthorhombic Bragg peaks in the high-resolution XRD data displayed in Fig. 1A and the neutron diffraction data shown in fig. S2. Thus, the apparent tetragonal phase must be the result of an ensemble average of these orthorhombic nanodomains. Group-subgroup symmetry analysis between the Pbcn (SRO) and P4₂/nmc (LRO) space groups indicates that four orientational domain variants are required to establish the tetragonal structure (34). Figure 4 illustrates the unique combination of symmetry operations, superlattice basis, and specific origin choice that produces each variant (see Supplementary Text for detailed derivation). These individual Pbcn variants are spatially distinguished and separated by a nanoscale network of domain walls (35, 36).

Fig. 4. Orientational relation between derivative orthorhombic variants and the tetragonal phase.

Orthorhombic, Pbcn unit cells (blue solid borders) have twice the volume of the tetragonal, P4₂/nmc unit cell (black dashed borders). Zr cations are shown in green; oxygen anions are shown in red. Arrows indicate the direction of the static displacement from the ideal tetragonal site.

This structural complexity and heterogeneous behavior cannot be fully captured by small-box modeling, which assumes homogeneity across all length scales. In addition, PDF refinement does not provide insight into the structural transition from orthorhombic SRO correlations to tetragonal LRO correlations. Therefore, a structural model shown in Fig. 5A was created based on all four orientational variants (Fig. 4) of the 2-nm-sized orthorhombic domains, assembling a 4-nm by 4-nm by 0.5-nm supercell, totaling 768 atoms. Atomic positions were restricted in each domain according to the Pbcn symmetry, and each domain was separated by domain walls and distinguished by its relative orientation (tilted text in Fig. 5A) and phase shift (gray text in Fig. 5A). Each domain within the supercell retained the structural parameters and symmetry constraints of the original Pbcn refinement with respect to its own internal origin but, in each case, rotated or phase shifted with respect to one another. In this supercell, pair correlations describing distances between atoms within each individual orthorhombic domain are identical to each other, even when the domain orientations are different. On the other hand, pair correlations describing distances between atoms across domain walls produce an apparent tetragonal symmetry; circled atoms in Fig. 5A highlight several intra- and interdomain pair correlations.

Fig. 5. Supercell model with simulated XRD and PDF.

(A) A supercell composed of four orthorhombic domains, differentiated by the direction and phase of the displacements corresponding to the M1 phonon, produces an average, long-range structure that is tetragonal, as demonstrated by (B) the simulated XRD pattern of the supercell overlaid with tetragonal peak indices and the measured diffraction pattern of nano-ZrO₂. (C) Simulated PDF describes the transition between the orthorhombic SRO (orange) and tetragonal LRO (blue).

The XRD pattern of the refined supercell (Fig. 5B) was simulated with GSAS-II (37) and reproduces a subset of peaks with narrow widths that can be fully indexed as tetragonal (with a_O ≈ c_O). Comparison to the experimental data (Fig. 5B) shows that the tetragonal LRO can be entirely reproduced by this ensemble average of orthorhombic nanodomains (38).

A neutron PDF was further simulated for the supercell, refined using PDFgui, and compared to the experimental data (Fig. 5C). The simulated PDF accurately captures the structural transition from orthorhombic correlations to long-range tetragonal correlations. Both the orthorhombic model and supercell model capture the short-range correlations equally well when refined over the same length scale (up to ~10 Å). This supercell analysis independently confirms the hypothesis that nonequilibrium zirconia consists of nanoscale orthorhombic domains, separated by domain walls, which yield the tetragonal long-range structure by ensemble averaging. This is in clear contrast with the equilibrium picture of a tetragonal high-temperature phase that is homogeneous across all structural length scales. The supercell quality of the fit to the PDF could be further improved by enlarging the supercell to capture all possible orientational relations between individual orthorhombic domains; because of limitations of building the supercell manually, we considered only one possible configuration.

Stabilization mechanism

This insight into the structural behavior of metastable zirconia with the existence of an otherwise transient orthorhombic atomic arrangement bears important information on its stabilization mechanism. Recovery of orthorhombic domains implies that the condensation of the second phonon (M3) is suppressed, requiring an energy barrier that converts the saddle point into a local minimum in the energetic landscape (Fig. 2B). Details of the underlying structural processes remain speculative based on experimental data alone; however, an interplay of defects and domain walls must play a key role in the stabilization. Orthorhombic domains are an unstable, transient state in the tetragonal-to-monoclinic transformation under equilibrium conditions (19, 32). Under nonequilibrium conditions, characterized by high defect densities, domain walls are elastically pinned and become less mobile (39, 40). This forms a network of persistent domain walls, which are a structural barrier that prevents the condensation of the second phonon (M3).

This intriguing process applies equally to both sample preparation techniques and defect formation mechanisms (nanocrystal synthesis and ion irradiation), suggesting that the interplay of domain walls and defects is a more general stabilization mechanism in zirconia. These defects can be destabilized by thermal annealing, allowing coarsening of the orthorhombic nanodomains and recovery of the monoclinic polymorph observed during heating (41). The expression of a distinct, ordered atomic arrangement within highly defective zirconia also agrees with previous research on disordered ceramics that rationalized the existence of the SRO and structural heterogeneity by a straightforward application of Pauling’s rules (42). The orthorhombic domain structure, and in particular the network of domain walls, may be an efficient way of accommodating high levels of structural defects by minimizing the impact on the overall structure.

DISCUSSION

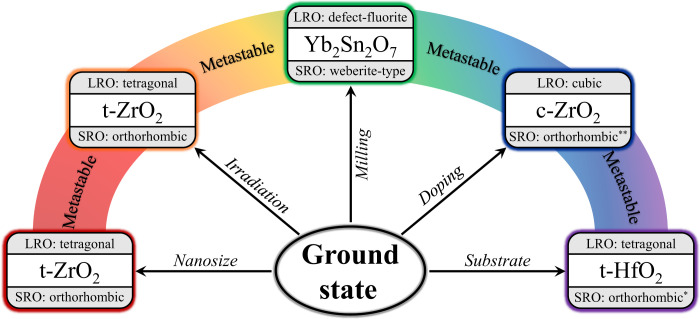
The most important question that remains is whether the structures of other metastable phases are also inherently heterogeneous with the SRO not described by the equilibrium phase diagram. As summarized in Fig. 6, many material systems obtained by far-from-equilibrium processing show a long-range structure that consists of an underlying network of nanodomains with distinct, unexpected symmetry (43, 44). Pyrochlore oxides irradiated by high-energy ions or processed by intense mechanical action illustrate this effect (45, 46). For example, ball-milled Yb₂Sn₂O₇ consists of nanodomains with an orthorhombic weberite-type structure (fig. S6). As for nonequilibrium zirconia, these domains yield a metastable high symmetry structure across the long range through configurational averaging (in this case, a cubic defect-fluorite structure). A weberite-type atomic arrangement is not represented in the phase diagram of A₂B₂O₇ pyrochlore-type oxides and cannot be synthesized as a stable long-range structure (47); however, as with zirconia, it is the preferred atomic arrangement within the metastable phase.

Fig. 6. Metastable phase synthesis routes.

Various synthesis pathways produce metastable phases in which statically distorted structural units, distinct from the equilibrium phase at room temperature, form apparent crystalline structures that are not representative of any physical atomic configuration within the material. The SRO orthorhombic structures of tetragonal HfO₂(*) and cubic ZrO₂(**) are different than the orthorhombic (Pbcn) phase of tetragonal zirconia.

This structural theme can be further expanded to other synthesis and processing methods (e.g., doping and substrate growth), which produce materials that occupy neither the ground state nor the stable high-temperature/pressure phase observed over macroscopic length scales (Fig. 6). Instead, these metastable materials consist of an assembly of nanoscale domains with a distinct local atomic arrangement that is, like orthorhombic zirconia, trapped within a local minimum of the free energy landscape (Fig. 2B). This improved structural description also applies to out-of-equilibrium materials used in many technological applications (6, 48). For example, yttria-stabilized cubic zirconia exhibits high strength and toughness and is used in many everyday technologies such as grinding and cutting tools (14, 18). In this case, doping leads to the recovery of the desired cubic high-temperature phase. Our data along with previous studies (49, 50) reveal that this material phase consists of local nanoscale domains of lower symmetry.

Thin-film (10) and template-grown materials used as multiferroics in numerous devices, including field-effect transistors and high-density ferroelectric random access memory (FeRAM)(51–53) are inherently metastable. These systems have potential uses in exceptionally fast and dense next-generation nonvolatile memory and other microelectronics, enabling further minimization of electronic component size and reduced power consumption (54, 55). Their functional properties and performance critically depend on nanoscale engineering of interfaces and lower symmetry nanodomains that can average to an apparent higher symmetry structure.

Lastly, we suggest that predicting the metastable phases that manifest at the subnanometer scale is possible when displacive transformations involve the condensation of multiple phonons (19, 32). Analyzing the structural distortion modes of parent space-group symmetry with the ISODISTORT software (56) identifies displacive pathways between crystalline structures and accurately suggests the Pbcn structure as an intermediate phase in the tetragonal-to-monoclinic phase transition of ZrO₂.

Using tetragonal ZrO₂ and neutron total scattering, we have provided an important aspect of metastable phases with respect to their atomic-scale structure and stabilization mechanism. We revealed that the recovered metastable phase is structurally highly heterogeneous, and the SRO is best described by an orthorhombic (Pbcn) atomic configuration, presenting the first experimental validation of this previously predicted structural zirconia polymorph. During the two-step displacive tetragonal-to-monoclinic phase transformation, this orthorhombic phase is unstable and exists only as a highly transient structural state in pristine, bulk ZrO₂ (19). However, under nonequilibrium conditions and high defect concentrations, these nanoscale orthorhombic domains are recovered and stabilized by immobilization of domain walls. The interplay of domain walls and defects forms structural barriers, which prevent shear of atomic planes and condensation of the M3 phonon. Orthorhombic nanoscale domains are stabilized to ambient conditions by a modified energetic landscape and yield an apparent tetragonal phase by configurational averaging.

We have shown here that an inherent structural heterogeneity with a distinct SRO is more broadly applicable to other metastable ceramics that are synthesized or processed under nonequilibrium conditions. If a similar stabilization concept characterized by an interplay of nanodomain walls and defects applies also to metastable materials prepared under high pressure, then this may offer a pathway to recover currently unquenchable high-pressure phases (48), which still presents one of the greatest challenges in high-pressure science (3). This is of great interest because many of these material phases exhibit unusual and useful properties, such as near room temperature superconductivity (57), ultrahigh-density hydrogen storage capabilities (58), and superior hardness (48). The concept of structural competition across length scales is already used in the development and optimization of functional metastable thin films. An example is HfO₂, in which nanoscale metastable polar phases exhibit ferroelectric properties that are suppressed when domains interconnect beyond a critical thickness or after repeated cycling (51). By coupling advanced short-range characterization methods with sufficiently high sensitivity and resolution, such as neutron PDF analysis, with representation theory, investigations of other metastable materials can further expand on the proposed phase stabilization concept. Extensive modeling is then required to apply these findings in the discovery of novel metastable phases with useful properties.

MATERIALS AND METHODS

Sample preparation

Pure (99.7%) microcrystalline “bulk” ZrO₂ was purchased from Alfa Aesar, and the concentrations of impurity cations that could stabilize the tetragonal phase (Ca, Y, Ce, Mg, and Ti) were verified to be less than 100 parts per million using a CAMECA SX100 electron microprobe. A nanocrystalline ZrO₂ sample was prepared by the decomposition of anhydrous zirconyl chloride by dissolving a ZrCl₄ precursor in deionized water to form a 0.025 M solution, which was sprayed into liquid nitrogen, forming frozen droplets with diameters on the order of micrometers. The frozen solution was dried at 0.04 mbar using a Christ Alpha 2-4 LSC freeze drier, resulting in anhydrous zirconyl chloride (ZrOCl₂) powder. The dry samples were heated at 450°C for 15 min to eliminate the chloride and produce pure ZrO₂ while limiting grain growth. XRD patterns acquired on a PANalytical X’Pert PRO diffractometer were analyzed using Rietveld refinement (59), confirming that the nanoparticles crystallized in the tetragonal phase and quantifying the nanocrystallite diameter (7.2 ± 0.2 nm—small enough to prevent any texture effects from anisotropic growth of crystallites).

Sample irradiation

To stabilize the metastable tetragonal phase of stoichiometric ZrO₂, pure (99.7%) bulk ZrO₂ from Alfa Aesar was irradiated in vacuum with 1.47-GeV Au ions to a fluence of 10¹³ ions/cm² using the X0 beamline of the UNILAC heavy ion accelerator at the GSI Helmholtz Centre for Heavy Ion Research. Samples were placed in cylindrical aluminum chambers with 1-cm diameter. The sample thickness was chosen using the SRIM-2013 software package (60) to calculate the limited penetration depth (27 μm) over which the ions deposit a constant energy per track length (dE/dx = 40 ± 2 keV/nm), ensuring complete ion penetration and homogeneous energy deposition throughout the sample volume. These irradiation conditions are tailored to produce quantities of fully irradiated material on the order of 100 mg, specifically enabling characterization by neutron total scattering in addition to conventional x-ray characterization techniques. More information about this irradiation scheme can be found elsewhere (43, 45, 61).

Data acquisition and analysis

SXRD experiments were performed at the Brookhaven National Laboratory using the PDF (28-ID-1) beamline of the National Synchrotron Light Source-II (NSLS-II) (62). High-resolution XRD patterns were measured at room temperature with 60-s exposure times for each of the pristine bulk, nanocrystalline, and irradiated powders loaded in 0.0395″ (inner diameter) Kapton tubes with wall thickness of 0.0020″ using an x-ray energy of 74.474 keV (λ = 0.1665 Å) while scanning the beam along the length of the sample to ensure good powder averaging. An identical empty Kapton tube was measured for proper background subtraction, and a LaB6 660b NIST standard was measured to calibrate the detector and produce the instrument parameter file for subsequent Rietveld analysis.

Neutron total scattering was performed using the time-of-flight neutron diffraction NOMAD instrument (63) (BL-1B) of the Spallation Neutron Source at Oak Ridge National Laboratory. Samples were poured into 2-mm quartz capillaries with a wall thickness of 0.01 mm and, to standardize neutron exposure among measurements, placed in the neutron beam until the protons incident on the liquid mercury target reached a total charge of 8 C (around 90 min) at 300 K. Additional measurements were performed using a diamond powder standard to ensure proper detector pixel calibration, and an identical empty quartz capillary was measured for proper background subtraction. Additional low-temperature measurements were performed at 100 K for the bulk and irradiated samples to minimize the effect of thermal vibrations. The scattering from the empty capillary was subtracted from the scattering collected from the sample, and the resulting scattering function, S(Q), was normalized to the scattering from a vanadium rod. The experimental PDFs were produced by the Fourier transform of S(Q) using the following equation

$$G(r)=\frac{2}{\mathrm{\pi }}{\displaystyle \underset{Q_{\text{min}}}{\overset{Q_{\text{max}}}{\int }}}Q[S(Q)-1]\text{sin}(\mathit{Qr})\mathit{dQ}$$ (1)

with a maximum momentum transfer, Q, of 31.4 Å⁻¹ for the irradiated sample and 30.0 Å⁻¹ for the nanocrystalline sample. No Lorch functions or other smoothing functions were applied to any of the total scattering data.

The diffraction data were analyzed using the Rietveld refinement method (59), which was performed for each of the x-ray and neutron diffraction patterns with the GSAS-II software package (37). Refinements were performed for the nanocrystalline sample using 13 parameters: scale, unit cell parameters (a and c), atomic positions, isotropic atomic displacement parameters, microstrain, and six background coefficients. Refinements were performed for the irradiated sample in the same way, with one additional scale factor corresponding to the phase fraction of the remaining monoclinic phase. The monoclinic structure was refined from diffraction patterns of bulk, unirradiated sample using 26 parameters: scale, phase fraction, unit cell parameters (a, b, c, and β), atomic positions, isotropic atomic displacement parameters, microstrain, grain size, and six background coefficients. All neutron diffraction pattern refinements were performed using data collected by detector banks 3, 4, and 5 of NOMAD (refining each dataset separately).

PDF analysis of both the nanocrystalline and irradiated samples was conducted using the PDFgui small-box refinement software (64). The 16 refined parameters included the scale, unit cell parameters (a ≠ b ≠ c for orthorhombic cells and a = b ≠ c for tetragonal cells), atomic positions, anisotropic atomic displacement parameters, nanocrystallite size, and a variable parameter, “delta2,” to account for correlated atomic motion. Attempts were made to fit the high-temperature and high-pressure phases to the experimental PDFs of both samples (fig. S4). Experimental PDFs of irradiated and nanocrystalline ZrO₂ were successfully fit using orthorhombic (Pbcn) symmetry for the short range (r < 1 nm) and tetragonal (P4₂/nmc) symmetry for the long range (r > 1 nm). In the region between, experimental PDFs were additionally fit as a two-phase system with isotropic atomic displacement parameters using the box-car method to determine whether a two-phase mixture was physically present (fig. S5).

X-ray absorption experiments were performed at beamline 16-BM-D of the Advanced Photon Source using the molybdenum sample holder configuration described by Lang et al. (65). A Zr metal foil was used as a calibrant, and the K-edge of Zr was probed by EXAFS analysis. EXAFS spectra of bulk, irradiated, and nanocrystalline ZrO₂ were all measured in transmission mode at room temperature. Using a Si(111) double-crystal monochromator, the x-ray energy was controlled between 17,600 and 19,000 keV with a variable step size ranging from 1 eV at the K-edge to 8 eV in the far postedge region. The collection time at each energy step was 0.5 s, and each absorption scan was repeated three times. Background subtraction, postedge removal, and Fourier transform were done using the Athena software package (66). The P4₂/nmc and Pbcn structures refined from XRD patterns and neutron PDF, respectively, were used to fit the EXAFS spectra. EXAFS fits are presented in Fig. 3B, and fit parameters are given in table S2.

Supplementary Materials

This PDF file includes:

Supplementary Text

Figs. S1 to S6

Tables S1 and S2

References