Helical dislocation-driven plasticity and flexible high-performance thermoelectric generator in α-Mg₃Bi₂ single crystals

Abstract

Inorganic plastic semiconductors play a crucial role in the realm of flexible electronics. In this study, we present a cost-effective plastic thermoelectric semimetal magnesium bismuthide (α-Mg₃Bi₂), exhibiting remarkable thermoelectric performance. Bulk single-crystalline α-Mg₃Bi₂ exhibits considerable plastic deformation at room temperature, allowing for the fabrication of intricate shapes such as the letters “SUSTECH” and a flexible chain. Transmission electron microscopy, time-of-flight neutron diffraction, and chemical bonding theoretic analyses elucidate that the plasticity of α-Mg₃Bi₂ stems from the helical dislocation-driven interlayer slip, small-sized Mg atoms induced weak interlayer Mg-Bi bonds, and low modulus of intralayer Mg₂Bi₂^2- networks. Moreover, we achieve a power factor value of up to 26.2 µW cm^-1 K^-2 along the c-axis at room temperature in an n-type α-Mg₃Bi₂ crystal. Our out-of-plane flexible thermoelectric generator exhibit a normalized power density of 8.1 μW cm^-2 K^-2 with a temperature difference of 7.3 K. This high-performance plastic thermoelectric semimetal promises to advance the field of flexible and deformable electronics.

The authors find that the plasticity of magnesium bismuthide (α-Mg₃Bi₂) arises from helical dislocation-driven interlayer slip, and the dispersion of lightweight Mg atoms also plays a pivotal role in facilitating strain redistribution during plastic deformation.

Introduction

Flexible electronics are extensively utilized in implants, wearable products, and other applications^1–5. These applications emphasize the mechanical properties of materials, including bendability, scalability, plasticity, portability, and lightweight construction. Wearable thermoelectric generators (TEGs) can directly convert body heat into electricity through the Seebeck effect, providing a sustainable self-powered system for electronic devices⁶. Traditional thermoelectric materials (e.g., GeTe, PbTe) exhibit excellent power factor (PF) and figure of merit (zT) values^7,8. However, their rigidity renders them susceptible to cracking under minimal plastic deformation, significantly restricting their use in flexible electronics. Flexible materials endowed with intrinsic plasticity and deformability are essential to ensure that wearable devices can endure repeated deformations. Conducting polymers (e.g., PEDOT, PSS) have emerged as promising next-generation flexible TE materials owing to their low thermal conductivity, adjustable electrical conductivity, and excellent flexibility^9,10. To address the poor electrical transport performance and zT value of conducting polymers, high-performance flexible organic/inorganic hybrids^11–17 have been developed by combining organic and inorganic TE materials. For example, oriented β-Ag₂Se flexible films on polyimide substrates exhibit a high room-temperature PF and zT (PF = 25.9 µW cm⁻¹ K⁻², zT = 1.2), with the maximum output power density of a four-leg thermoelectric generator reaching 124 W m⁻² with a 60 K temperature difference¹⁷. However, devices made with flexible substrates are inherently limited by the mechanical properties of inorganic semiconductors. Enhanced flexibility and plasticity in semiconductors would enable devices to undergo repeated deformation in various scenarios, enhancing device adaptability and stability. Plastic inorganic semiconductors offer a new perspective on flexible materials and devices. These materials possess the ability to be effortlessly processed into self-supporting flexible films of varying thicknesses, thereby granting greater flexibility in the design and manufacture of high-performance flexible TEGs^6,18. Ductile α-Ag₂S provides a new possibility for flexible electronic devices¹⁹. Chemical bonding analysis revealed that the presence of multi-centered, diffuse, and relatively weak Ag-S and Ag-Ag bonds enables α-Ag₂S to exhibit unprecedented metal-like ductility by inhibiting material cleavage and facilitating slip. Subsequently, through alloying with Ag₂Se and Ag₂Te, high-performance binary and ternary plastic alloys have emerged, such as Ag₂(S, Se), Ag₂(S, Te), and Ag₂(S, Se, Te)^20–29. Currently, among n-type plastic inorganic semiconductors, Ag₂Se_0.69S_0.31 has demonstrated the best thermoelectric performance (PF = 22 µW cm⁻¹ K⁻², zT = 0.61)²⁰, while for p-type plastic inorganic semiconductors, the (AgCu)_0.998Se_0.22S_0.08Te_0.7 pseudoternary solid solution exhibits superior properties (PF = 5.1 µW cm⁻¹ K⁻², zT = 0.45)⁶. Moreover, in 2022, flexible π-shaped devices based on liquid-like inorganic plastic materials achieved a record normalized power density (P_max/AΔT² = 30 µW cm^-2 K^-2, where P_max represents maximum power output, A is the cross-sectional area, and ΔT is the temperature difference across the device), surpassing organic based flexible TEGs⁶. Apart from liquid-like plastic inorganic semiconductors, there are van der Waals inorganic semiconductors with exceptional plasticity and deformability, such as InSe³⁰, and SnSe₂³¹. The remarkable plasticity of bulk single crystalline InSe is attributed to interlayer gliding and cross-layer dislocation slip mediated by long-range In-Se coulomb interaction across the van der Waals gap and soft intralayer In-Se bonding³⁰. The deformability factor (Ξ = (E_c/E_s)(1/E_in)) was proposed for prescreening bendable and deformable inorganic semiconductors^30,32–35. The small slipping energy (E_s) indicates an easy interlayer gliding, while the relatively large cleavage energy (E_c) favors a strong interlayer integrity during slip. E_in denotes the in-plane Young’s modulus along the slip direction, and material with a low modulus easily undergoes elastic deformation. Therefore, a larger Ξ value indicates greater material deformability. Herein, the key focus of plastic inorganic materials and devices is identifying materials with greater flexibility, enhanced thermoelectric performance, and low cost.

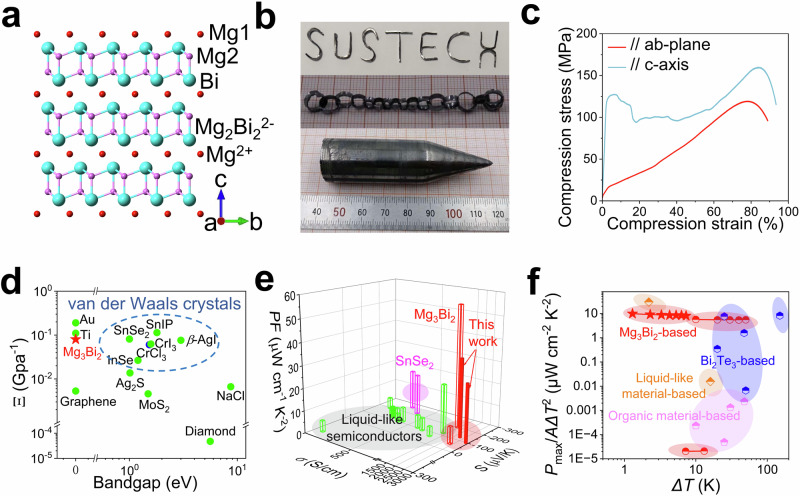
α-Mg₃Bi₂ crystallizes in a trigonal anti-α-La₂O₃ type structure (space group $\mathrm{P}\overline{3}\mathrm{m}1$) below 976 K, transitioning to a cubic Mn₂O₃-type structure (β-Mg₃Bi₂, space group Ia$\overline{3}$) above this temperature^36,37. α-Mg₃Bi₂ is a layered AB₂C₂ Zintl compound, in which Mg atoms occupy two distinct lattice sites (Mg1 and Mg2), as depicted in Fig. 1a. The atom arrangement of α-Mg₃Bi₂ comprises periodic interlayer small-sized Mg²⁺ layers and covalently bounded Mg₂Bi₂²⁻ networks³⁸, as illustrated in Fig. 1a. Recently, the room temperature α-Mg₃Bi₂ has been reported to exhibit significant plastic deformation, which arises from multiple slip systems and the gliding of dislocations^39,40. Zhao et al. have captured the edge dislocation-driven prismatic slip by using the Transmission Electron Microscope (TEM) technique, but the TEM results only showed the heavy Bi atomic arrangement³⁹. In this study, we revealed the atomic arrangements of both heavy Bi and light Mg atoms by using the integrated differential phase contrast (iDPC) technique, and the TEM results indicated the strain-induced helical dislocation-driven interlayer slip of (0001) planes as the microscopic mechanism of plastic deformation. Small-sized Mg atoms lead to weak interlayer bonding, which can allow low modulus Mg₂Bi₂^2- networks to easily slip along the ab-plane, as shown in Fig. 1a. When slipping, weak interlayer Mg-Bi bonds can also guarantee the integrity of the entire system. Furthermore, the fine distortion structures around the helical dislocations, combined with ab initio molecular dynamics (AIMD) simulations and time-of-flight neutron diffraction analysis, revealed that the significant dispersion of lightweight Mg atoms plays a pivotal role in facilitating strain redistribution during plastic deformation. In summary, the intrinsic structure and chemical bonding properties of α-Mg₃Bi₂ contribute to superior plasticity, as shown in Figs. 1b–d and listed in Supplementary Table 1^30,32,34,35. And we have achieved high thermoelectric performance in the n-type α-Mg₃Bi₂ crystal (PF = 35 and 26.2 µW cm⁻¹ K⁻² along the ab-plane and c-axis, respectively), surpassing that of the liquid-like inorganic plastic thermoelectric semiconductors and plastic van der Waals layered semiconductors^6,20–29,31, as shown in Fig. 1e and listed in Supplementary Table 2. Moreover, our α-Mg₃Bi₂-based out-of-plane flexible thermoelectric generator (f-TEG) also demonstrated a high normalized power density of 8.1 μW cm⁻² K⁻² with a temperature difference of 7.3 K. This value is higher than that of other α-Mg₃Bi₂-based f-TEG^40,41, Bi₂Te₃-based^42–46, and organic material-based flexible devices^9,47–49, as shown in Fig. 1f and listed in Supplementary Table 3^6,9,40–50. The high-performance and low-cost plastic inorganic α-Mg₃Bi₂ crystals are expected to drive the development of flexible electronics.

Fig. 1. Structure, plasticity, and thermoelectric properties of α-Mg₃Bi₂ single crystals.

a Crystal structure of α-Mg₃Bi₂, in which Mg atoms occupy two distinct lattice sites (Mg1 and Mg2). The atom arrangement of α-Mg₃Bi₂ comprises periodic small-sized Mg²⁺ interlayers and covalent bonded Mg₂Bi₂²⁻ networks. b An as-grown n-type α-Mg₃Bi₂ crystal, the letters “SUSTECH” and a flexible chain deformed by crystal slabs. c Uniaxial compression experiments. α-Mg₃Bi₂ crystals sustained >90% compression strain. d Deformability factor Ξ of α-Mg₃Bi₂ and several other materials (listed in Supplementary Table 1)^30,32,34,35. e Room-temperature power factors for inorganic plastic inorganic semiconductors (listed in Supplementary Table 2)^{6,20–29,31,39}. The electrical transport performance of α-Mg₃Bi₂ was better than that of liquid-like plastic inorganic semiconductors and van der Waals semiconductors. f Normalized power density (P_max/AΔT²) of out-of-plane flexible thermoelectric devices (listed in Supplementary Table 3)^6,9,40–50, including α-Mg₃Bi₂ based^40,41, liquid-like material-based^6,50, Bi₂Te₃-based^42–46, and organic material-based^9,47–49 devices. Our data are marked by red stars.

Results

The n-type and p-type bulk single crystalline α-Mg₃Bi₂ were grown by the Bridgman method with an Mg-excess and Bi-excess, respectively. The crystal samples are depicted in Fig. 1b and Supplementary Fig. 1. The X-ray diffraction (XRD) pattern of the cleaved α-Mg₃Bi₂ crystal shows (000 L) diffraction peaks in Supplementary Fig. 2a, and the Laue backscatter spectrum also displays (000 L) diffraction spot patterns, as shown in Supplementary Figs. 2b, c, indicating good crystal quality. In addition, the XRD patterns of the powders confirm the absence of second phases in these two crystals (Supplementary Fig. 3), validating the lack of flux residue. As illustrated in Fig. 1b and Supplementary Fig. 4, the cleaved α-Mg₃Bi₂ crystal slabs can be shaped into the letters “SUSTECH” as well as various other shapes without breakage, demonstrating good plasticity and flexibility. The flexibility (f) of materials is most simply demonstrated by bending a material along a radius of curvature without breakage⁵¹. The f is defined as 1/r, where r is the minimum bending radius of curvature; thus, a smaller r indicates greater flexibility⁵¹. The SEM image (Supplementary Fig. 4b) shows a small bending radius (r ≈ 900 µm), and the f was calculated to be 1111.11 m⁻¹. When a material with a thickness h is bent about the minimum radius r, its outer and inner surfaces will experience the greatest tensile and compressive stress, respectively. The maximum tensile strain (ε) can be calculated as h/2r⁵¹, resulting in a tensile strain of approximately 15.2% for the crystal slab, as shown in Supplementary Fig. 4b. To obtain detailed mechanical properties, conventional mechanical tests were performed through compression, tension, three-point bending, and nanoindentation tests, as shown in Fig. 1c, Supplementary Figs. 5, 6. Notably, α-Mg₃Bi₂ crystals sustained > 90% compression strain without cracking along the ab-plane and c-axis, as shown in Fig. 1c and Supplementary Figs. 7a, b. These strain values significantly exceed those of most thermoelectric materials, most of which crack within a 1% compression strain, such as GeTe (0.8%)⁵² and SnTe (7.5%)⁵³. As shown in Supplementary Fig. 5, α-Mg₃Bi₂ crystals exhibited ~ 17% tensile strain and > 30% bending strain. The nanoindentation tests also highlighted the plasticity of the α-Mg₃Bi₂ crystal, in which loading and unloading curves did not align, as shown in Supplementary Fig. 6. The Young’s modulus measured 36.95 GPa in the ab-plane and 42.79 GPa along the c-axis. The obtained mechanical parameters are detailed in Supplementary Table 4. Scanning electron microscopy (SEM) characterization of deformed α-Mg₃Bi₂ crystals provided microscale details of plastic deformation. The fresh cleavage surface in α-Mg₃Bi₂ shows obvious layer structures in Supplementary Fig. 8a. Supplementary Fig. 8b–f shows that the layered structure of α-Mg₃Bi₂ can be forced to slip. Supplementary Fig. 8b clearly shows numerous slip behaviors resulting from compression stress. After the biaxial tensile test, many layers slipped along the ab-plane without visible cleavage, and the layers were also slightly folded, as shown in Supplementary Fig. 8c. Furthermore, numerous interlayer slips were observed in the fractured cross-section, as shown in Supplementary Fig. 8d, e, which contribute to the plastic deformation. Slip plays an important role in plastic deformation in ductile metals, Ag-based liquid-like ductile semiconductors¹⁹, and van der Waals semiconductors^30,35.

Strain-induced interlayer slip and atomic-scale locally distorted structures

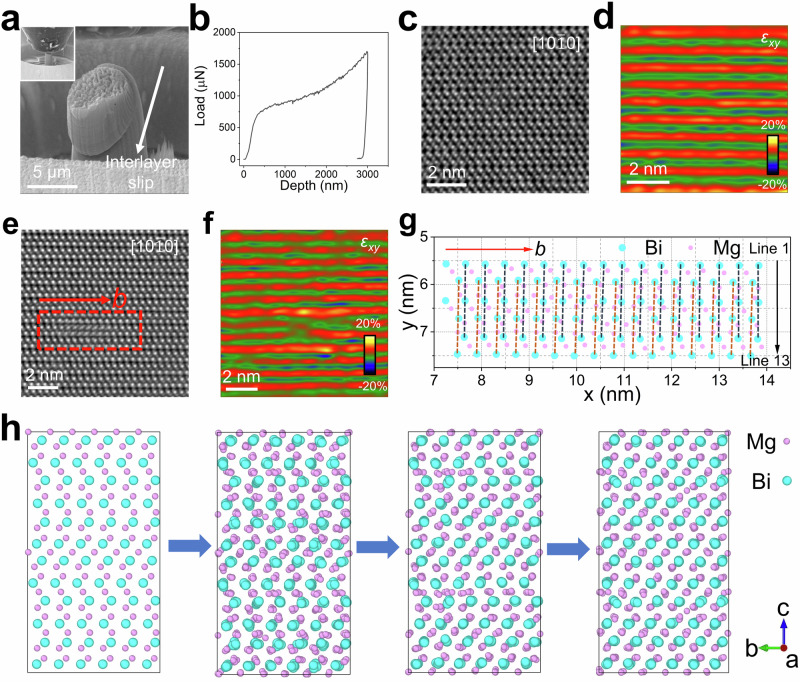
We also captured the dynamic slip process by an in situ SEM uniaxial compression test on a single-crystalline α-Mg₃Bi₂ micropillar along the ab-plane, as shown in Fig. 2a and Supplementary Movie 1. By comparing the changes in the α-Mg₃Bi₂ micropillar before and after the uniaxial compression test, interlayer slip was observed throughout the process. The load-depth curve of the microscopic compression test exhibited only a brief elastic phase, followed by slip-induced strain bursts without breakage, highlighting the superior plasticity of this crystal, as shown in Fig. 2b. Overall, the in situ SEM uniaxial compression test collectively confirmed that interlayer slip resulted in the superior plasticity of bulk single-crystalline α-Mg₃Bi₂.

Fig. 2. The strain-induced locally distorted structures.

a In situ SEM compression test on α-Mg₃Bi₂ micropillar along the ab-plane. In the top left corner of the picture, there is the initial state of the α-Mg₃Bi₂ micropillar. Under compression stress, the plastic deformation was induced by interlayer slip. b Load-depth curve of the in situ SEM compression test along the ab-plane. The atomic-resolution iDPC image along the a-axis and corresponding strain maps of α-Mg₃Bi₂ without any strain (c, d) and after several bends (e, f). There was no redistribution of strain in the unbent crystal slab, but a redistribution of strain was found in the crystal slab after several bends. The solid red arrow represents the Burgers vector (b). g Atom-column displacement map of Mg and Bi in a locally distorted structure (marked in the red box in Fig. 3e), in which Mg atoms were geographically dispersed. There are 13 rows of atoms, and lines 1 through 13 are arranged according to solid black arrows. The solid red arrow represents the Burgers vector (b). h Four representative structural snapshots during the first 3000 steps from nonequilibrium state to equilibrium state in AIMD simulations.

The atomic-scale microstructures of the α-Mg₃Bi₂ single crystal were also investigated using aberration-corrected transmission electron microscopy (TEM) to explore their plasticity. The atomic structures of both unbent and bent crystal slabs along the [10$\overline{1}$0] zone axis were revealed using the integrated differential phase contrast (iDPC) technique, as shown in Fig. 2c–f, in which the image contrast is proportional to the atomic number. Figure 2c illustrates the repetitive layers of Mg1 atoms and Mg₂Bi₂²⁻ networks in an unbent crystal slab. In comparison, multiple helical dislocations were observed in the bent crystal slab, as shown in Fig. 2e and Supplementary Fig. 9. The Burgers vector (b) is oriented parallel to the ab-plane in Fig. 2e, indicating that layered α-Mg₃Bi₂ has undergone interlayer slip driven by helical dislocation in the bent crystal slab. This slip system corresponds to basal slip {0001}〈10$\overline{1}$0〉, characteristic of hexagonal close-packed (HCP) metals⁵⁴. The helical dislocation-induced local distortions are highlighted by the red box in Fig. 2e, and its geometric phase analysis showed a redistribution of the shear strain, as illustrated in Fig. 2f. Compared to the unbent slab, this redistribution of strain can more effectively resist deformation, as depicted in Figs. 2d, f. In addition, similar local distortion structures and the redistribution of strain could be easily observed in other regions of the sample, as shown in Supplementary Fig. 9. The positions of the atoms in the marked region (Fig. 2e) of the iDPC image were used to generate an atom-column displacement map (Fig. 2g) with the software CalAtom. Further details are provided in Supplementary Figs. 10, 11. A total of 13 rows of atoms were selected, with rows 1 through 13 rearranged according to the direction of the black solid arrows in Fig. 2g. As shown in Fig. 2g, the Bi atomic chains, connected by dashed lines, formed a slight angle with the c-axis, whereas the Bi atomic arrangement is perfectly parallel to the c-axis in the initial α-Mg₃Bi₂ crystal (Fig. 2c). This Bi atomic rearrangement provides direct evidence that the layered α-Mg₃Bi₂ has undergone slip along the direction of the Burgers vector. In the locally distorted area surrounding the helical dislocation, Mg atoms have undergone significant dispersion, and interlayer MgBi6 and intralayer MgBi4 polyhedra have experienced severe distortion, as shown in Fig. 2g and Supplementary Fig. 12. Supplementary Fig. 13 presents the helical dislocation model based on the TEM observations. During interlayer slip, the lattice around the helical dislocation becomes distorted, with the lattice above the dislocation undergoing relative slip with respect to the lattice below. TEM observations demonstrated the movable characteristic of Mg1, Mg2, and Bi during dislocation-driven interlayer slip, offering valuable insights into the mechanisms governing the plasticity of α-Mg₃Bi₂.

To further clarify the slip process, the AIMD simulations were performed as illustrated in Fig. 2h, Supplementary Fig. 14, and Supplementary Movies 2, 3. First, the supercell of α-Mg₃Bi₂ was optimized with layer slip distortion and forms a specific helical dislocation, which results in a unique reorientation or flipping of the atomic arrangement around the dislocation planes, highlighted by the red circle (Supplementary Fig. 14b). AIMD simulations were then carried out to track the structural evolution with helical dislocations in a supercell containing 540 atoms over time. The simulation results revealed that atoms around the helical dislocation rearranged within the first 3000 steps, ultimately equilibrating into a defect-free, perfect structure, as shown in four representative snapshots presented in Fig. 2h. Heavier Bi atoms exhibited only small-amplitude vibrations, while the lighter Mg atoms showed large-amplitude vibrations, closely aligning with the experimental observations in Fig. 2g. Furthermore, the interlayer Mg atoms demonstrated a greater degree of dispersion compared to the intralayer Mg atoms, highlighting their more pronounced dynamic behavior within the structure. Both TEM and AIMD results confirm that helical dislocation-driven interlayer slipping processes lead to significant plastic deformation, serving as a microscopic mechanism of plastic deformation for α-Mg₃Bi₂. In addition, the increased dispersed Mg atoms further facilitate strain redistribution throughout the plastic deformation process.

Chemical bonding analysis of the plastic deformation mechanism in α-Mg₃Bi₂

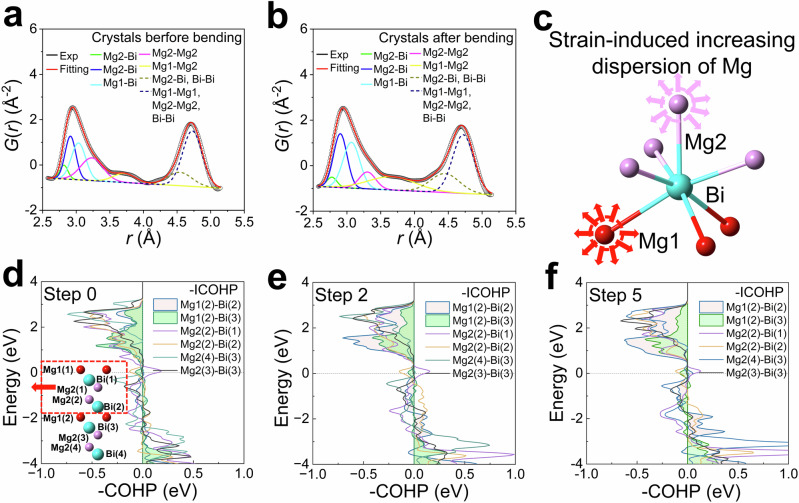
Pair distribution function data were acquired for several small-sized single crystals both before and after repeated bending to observe strain-induced locally distorted structures. Fitting of G(r), defined by formula (1) in the method, revealed the strain-induced increased dispersion of Mg-Bi, Mg1-Mg2, and Mg1-Mg1 bonds, as depicted in Fig. 3a, b. The fitted G(r) data exhibited a broader full width at half maximum (FWHM) of Mg-Bi bonds in bent crystals, as illustrated in Fig. 3a, b, and detailed in Supplementary Table 5. Following bending, the refined nearest neighbor Mg-Bi bond distances, including one Mg1-Bi and two Mg2-Bi bonds, ranged from 2.575 to 3.563 Å, 2.575 to 3.042 Å, and 2.575 to 3.283 Å, respectively, which were greater than those observed before bending (2.635 to 3.436 Å, 2.635 to 3.037 Å, 2.635 to 3.237 Å, respectively), as shown in Fig. 3a–c. The Mg-Bi bond model in Fig. 3c represents how the strain caused Mg atoms to occupy a wider lattice space. The dispersed Mg also led to Mg1-Mg2 bonds spanning a wider range, as indicated in Supplementary Table 5. Consequently, in strain-induced locally distorted structures, Mg-Bi bonds can extend over a broader range to accommodate successive plastic deformation, in alignment with the TEM results.

Fig. 3. Chemical bonding analysis of α-Mg₃Bi₂.

Realspace G(r) fitting results of several small-size single crystals without any strain (a) and after several bends (b) at room temperature. c The strain-induced increasing dispersion of Mg atoms, meaning that the Mg-Bi bond length changed a lot during slip. d–f The crystal orbital Hamilton population (COHP) calculations for steps 0–5 during slip along the [01$\overline{1}$0] direction, aiming to observe the bond characteristics in α-Mg₃Bi₂. The x-axis is the -COHP, and the y-axis is the electron energy around the Fermi level. The values of integrating the crystal orbital Hamilton population (-ICOHP) were also listed in Supplementary Table 6, which represent bond strength.

To explore the structure and bond origin of the plastic deformation mechanism in α-Mg₃Bi₂, the interlayer slip process (Fig. 3d and Supplementary Fig. 15) was simulated by the density functional theory calculations. The active atomic layers in (0001) planes slipped in a period of 11 steps along the [01$\overline{1}$0] direction in our theoretical simulation. The interlayer space of the quasi-two-dimensional configurations varied with interplanar slip distance due to the relative interlayer interactions. And the minimal total energy for each slip step was therefore calculated as a function of interlayer space d, as shown in Supplementary Fig. 16a. The line shape of minimal energy, as a function of slip steps shown in Supplementary Fig. 16b, is a symmetrical normal distribution, which includes a peak of slip energy barrier at step 5. To understand the inherent chemical bonding properties, the crystal orbital Hamilton population (COHP) was calculated to determine how the bonding and antibonding changed among different slip steps^55,56. Because of the symmetric normal slip energy distribution, we present the effective results of steps 0, 2, and 5 in Fig. 3d–f. According to the chemical bonding theory, the bonding states of the occupied states in the valence band contribute to the total energy of a specific system. By integrating the -COHP below the Fermi surface (-ICOHP), as shown in Supplementary Table 6, the Mg-Bi bond strength can be quantified. The calculated -ICOHP values of Mg1(2)-Bi(2), Mg1(2)-Bi(3), Mg2(2)-Bi(1), and Mg2(2)-Bi(2) bonds were 0.194 eV, 0.245 eV, 0.408 eV, and 0.333 eV, respectively, in the configuration without slip displacement. The interlayer Mg-Bi bonds (Mg1(2)-Bi(2) and Mg1(2)-Bi(3)) are weaker than the intralayer Mg-Bi bonds (Mg2(2)-Bi(1) and Mg2(2)-Bi(2)). It was reported that due to the diminutive radius of interlayer Mg²⁺ (0.65 Å), the MgBi6 octahedron deviates from Pauling’s rule^38,57. Thus, the small-sized interlayer Mg1 atoms are the underlying cause of weak interlayer bonding and the intrinsic low κ in α-Mg₃Bi₂³⁸. Under the relative interplanar slip displacement, the interlayer Mg1(2)-Bi(2) bond of the occupied states in the valence band became notably stronger and lowered the system's total energy. The in-phase wavefunction of Mg1(2) and Bi(2) overlapped during interplanar slipping, forming a bonding state resulting in the -ICOHP increasing from 0.194 eV to 0.334 eV at step 2 and further to 0.399 eV at step 5. In contrast, the -ICOHP of interlayer Mg1(2)-Bi(3), intralayer Mg2(2)-Bi(1), and Mg2(3)-Bi(3) bonds became slightly weaker. During the slip process, the antibonding state between atoms coupled with the enhanced bonding state of Mg1(2)-Bi(2), preventing the total energy from significantly decreasing and thus maintaining the structural stability of α-Mg₃Bi₂. Due to the complex coupling of interatomic chemical bonding states, the structure with slip displacement has difficulty undergoing elastic recovery to its initial structure. In addition, Supplementary Fig. 17 shows that the maximum slipping energy E_s was as low as 0.04184 eV/atom, indicating that even a small external force can drive the atomic layers to deviate from their original position. However, the cleavage energy (E_c) of α-Mg₃Bi₂ was ~ 0.130513 eV/atom, which was much higher than the (E_s), as shown in Supplementary Figs. 16, 17. The low E_s points toward easy interlayer slip, while the relatively large E_c value favors strong interlayer integrity during slip. Young’s modulus (E_in) describes the ability of a solid material to resist deformation. For hexagonal quasi-2D α-Mg₃Bi₂, the isotropic in-plane E_in can be expressed as ref. ⁵⁸:

$$E_{in}=2/\left(\frac{c_{33}}{c_{33}\left(c_{11}+c_{12}\right)-2{c_{13}}^2}+\frac{1}{c_{11}-c_{12}}\right)$$ 1

where c_ij is the independent elastic stiffness constant. According to this formula, the in-plane E_in of α-Mg₃Bi₂ was calculated to be only 39 GPa, consistent with nanoindentation test results. Compared to other inorganic plastic van der Waals layered semiconductors and liquid-like semiconductors, as shown in Supplementary Fig. 17b, such a low in-plane elastic modulus E_in is a key feature of macroscopic interlayer plastic deformation. To further quantitatively compare the plastic deformation ability among different materials, the Ξ was calculated to be 0.08, as shown in Fig. 1d. Compared with Ag₂S and van der Waals semiconductors, α-Mg₃Bi₂ has a greater Ξ, indicating better plasticity and deformability.

Thermoelectric performance and f-TEG

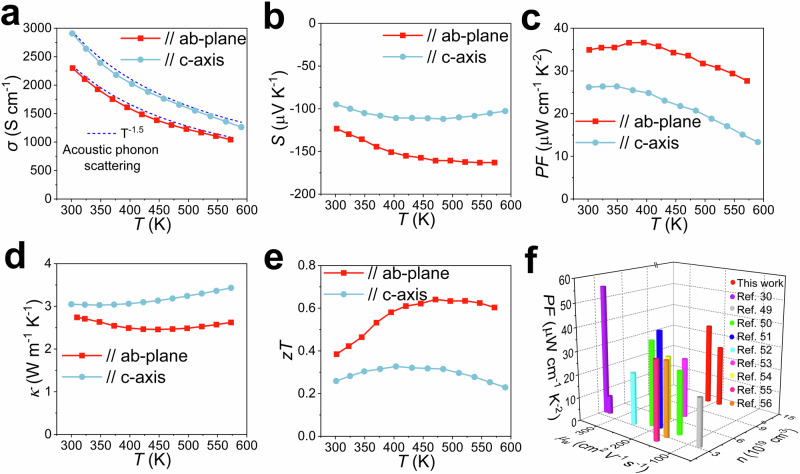
The thermoelectric properties of as-grown n-type single-crystalline α-Mg₃Bi₂ were studied along the ab-plane and c-axis, as shown in Fig. 4. The crystal exhibited good electrical transport performance in both crystallographic directions, with obvious anisotropy. The electrical conductivity (σ) measured ~ 2300 S cm⁻¹ at 300 K and ~ 1042 S cm⁻¹ at 573 K along the ab-plane. In comparison, the σ measured ~ 2907.4 S cm⁻¹ at 300 K and ~ 1263.3 S cm⁻¹ at 590 K along the c-axis, approximately 25% higher than that along the ab-plane between 300–600 K. As shown in Fig. 4a, σ shows a T^-1.5 temperature dependence, conforming to the phonon scattering mechanism with increasing T, demonstrating that the charge carriers are predominantly scattered by phonons. However, the value of the Seebeck coefficient (S) along the c-axis (− 95 µV K⁻¹) was lower than that along the ab-plane (− 123.3 µV K⁻¹) at room temperature. The PF along the ab-plane is 35 µW cm⁻¹ K⁻² at room temperature, reaching a peak of 36.64 µW cm⁻¹ K⁻² at 395 K. While the PF along the c-axis is 26.2 µW cm⁻¹ K⁻² at room temperature. Between 300–600 K, the average PF along the ab-plane was 33.68 µW cm⁻¹ K⁻², while the average PF along the c-axis was about 21.71 µW cm⁻¹ K⁻². The thermal conductivity along the ab-plane was significantly lower than that along the c-axis. A notable bipolar effect with a lower starting temperature was observed in the n-type crystal, as shown in Fig. 4d, characterized by an increasing thermal conductivity with temperature at the high-temperature end. The zT value at 300 K was ~ 0.4 along the ab-plane and ~ 0.26 along the c-axis. The average zT between 300–600 K was ~ 0.57 along the ab-plane and ~ 0.3 along the c-axis. The room-temperature carrier concentration (n) measured 13.3 × 10¹⁹cm⁻³, and the room-temperature Hall mobility (µ) was 108 and 136.4 cm²V⁻¹ s⁻¹ along the ab-plane and c-axis, respectively, as shown in Supplementary Fig. 18a. For this n-type single-crystalline α-Mg₃Bi₂, high mobility and an ultra-high carrier concentration guarantee high conductivity with a high Seebeck coefficient at all temperatures, due to the involvement of highly degenerate transporting bands. The density of state effective mass (m*) was derived from the measured S and n using the single-parabolic-band model. The values of m* of n-type α-Mg₃Bi₂ were 1.59782m_e and 1.2305m_e along the ab-plane and c-axis, respectively, where m_e is electron mass, as shown in Supplementary Fig. 18b. With such a large m*, maximizing thermoelectric performance requires a much higher carrier concentration. The value of PF is proportional to the weighted mobility (µ_w = µ(m*/m_e)^3/2, PF = S²σ ∝ µ_w). The value of µ_w was 218 cm²V⁻¹ s⁻¹ along the ab-plane and higher than that along the c-axis (186.2 cm²V⁻¹ s⁻¹), resulting in a higher PF along the ab-plane. The thermoelectric properties of p-type α-Mg₃Bi₂ were also tested. Although p-type α-Mg₃Bi₂ has a high σ, the very low S leads to poor electrical transport performance due to the involvement of only a single transport band, as shown in Supplementary Figs. 19, 20. Furthermore, the µ_w in p-type α-Mg₃Bi₂ was much lower than that in n-type crystal, as shown in Supplementary Figs. 18, 21. Thus, α-Mg₃Bi₂ is suitable for use as an n-type thermoelectric semimetal. The n-type α-Mg₃Bi₂ crystals also exhibited > 30% bending strain in Supplementary Fig. 22. And several repeated bending deformations were found to have little effect on the electrical resistance, as shown in Supplementary Fig. 23. Figure 4f shows several high-performance n-type α-Mg₃Bi₂-based single crystals and polycrystalline samples. The m* of α-Mg₃Bi₂ was calculated to be ~ 0.53m_e⁵⁹. Alloying Sb increased both the m* and µ_w, resulting in good electrical transport performance, as shown in Fig. 5f and Supplementary Table 7^39,59–66. The PF and µ_w of the reported Mg₃(Bi, Sb)₂ samples were 1.5–3 times higher than those of the α-Mg₃Bi₂ polycrystalline samples⁵⁹. Indeed, the n-type α-Mg₃Bi₂ crystal with an ultra-high carrier concentration in this work has a large m* and high PF, which is among the higher levels of α-Mg₃Bi₂-based thermoelectric materials. The high-profile Ag₂S-based plastic thermoelectric semiconductors exhibited high µ (about 300–1000 cm²V⁻¹ s⁻¹), but light m* (0.14–0.46 m_e)^6,20–29. So, the µ_w and PF of the Ag₂S-based plastic inorganic semiconductors are considerably lower than those of the α-Mg₃Bi₂ single crystals in this work, as illustrated in Fig. 1f.

Fig. 4. Temperature-dependent transport properties of n-type single crystalline α-Mg₃Bi₂ along the ab-plane and c-axis.

Temperature-dependent electrical conductivity (a) (the dashed line shows the temperature dependence expected for acoustic phonon scattering), Seebeck coefficient (b), power factor (c), thermal conductivity (d), and zT value (e). f The power factor (PF), weighted mobility (µ_w), and carrier concentration (n) of some n-type α-Mg₃Bi₂-based single crystals and polycrystalline samples are listed in Supplementary Table 7^39,59–66.

Fig. 5. The α-Mg₃Bi₂-based out-of-plane flexible thermoelectric generator.

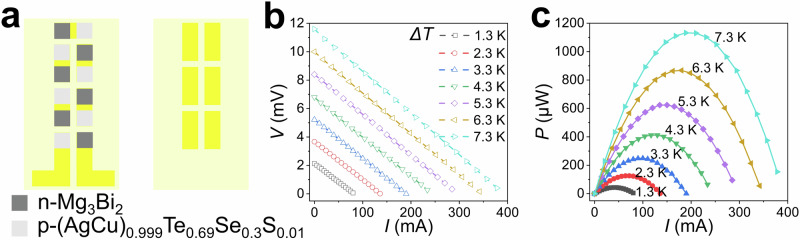
a The design model of the α-Mg₃Bi₂-based flexible device, concluding n-type α-Mg₃Bi₂ and p-type (AgCu)_0.999Te_0.69Se_0.3S_0.01 materials. The thickness of the f-TEG was only 880 µm by micrometer, and the filling factor (f) is 73.5%. (b, c) The output performance of the device. Current (I) dependencies of the output voltage (V) and output power (P).

To further demonstrate the potential applications of single-crystalline α-Mg₃Bi₂ in flexible electronics, a six-couple out-of-plane f-TEG was designed and assembled, followed by a comprehensive evaluation of its output performance. Please note that the out-of-plane f-TEG only utilized the thermoelectric performance of the α-Mg₃Bi₂ single crystals along the c-axis due to the easy cleavage parallel to the ab-plane of the materials, as shown in Supplementary Fig. 27. The α-Mg₃Bi₂-based out-of-plane f-TEG was fabricated using n-type α-Mg₃Bi₂ crystal slabs and p-type (AgCu)_0.999Te_0.69Se_0.3S_0.01 thin plates (Supplementary Figs. 25, 26), as shown in Fig. 5a and Supplementary Fig. 30. The output performance of this f-TEG was characterized by using a home-made test platform (Supplementary Fig. 31). The measured internal resistance (R_in) of the f-TEG was ~ 24.3 mΩ, which was two orders of magnitude lower than that of the flexible Mg₃Bi_1.5Sb_0.5 based TE devices⁴⁰. As shown in Figs. 5b, c, under a temperature gradient (ΔT) of 7.3 K, the measured open circuit voltage (V_oc) and maximum output power (P_max) were 11.6 mV and 1132.11 μW, respectively. The maximum normalized power density (P_max/AΔT²) was calculated to be 8.1 µW cm⁻² K⁻², surpassing many other reported flexible Mg₃Bi₂ based^40,41, Bi₂Te₃-based^42–46, and organic material-based^9,47–49 devices (Fig. 1F). We also tested bending service stability of the f-TEG devices under different bending radius and bending times. The R_in showed small change under varied bending radius (from 15 mm to 50 mm), and the value of ΔR_in/R_in,0 was less than 7% after bending 2000 times under a bending radius of 15 mm, as shown in Supplementary Fig. 32. Moreover, the output performance also exhibited small change even after repeated bending times of 2000 (Supplementary Fig. 33). Therefore, the service stability of our f-TEG is acceptable.

Discussion

In summary, we have conducted a comprehensive investigation of α-Mg₃Bi₂ crystal, examining aspects from plasticity and thermoelectric performance to flexible devices. Atomic-scale strain-induced locally distorted structures and chemical bonding analyses corroborated that the plasticity in α-Mg₃Bi₂ stems from the low modulus of intralayer Mg₂Bi₂^2- networks, small-sized Mg-induced weak interlayer Mg-Bi bonds, and helical dislocation-driven interlayer slip. Furthermore, the dispersed Mg atoms facilitated strain redistribution, promoting plastic deformation. In addition, the high-thermoelectric performance along the c-axis (PF = 26.2 µW cm⁻¹ K⁻²) led to the high output performance of the out-of-plane f-TEG. Our f-TEG featured good service stability and high P_max/AΔT² of 8.1 µW cm⁻² K⁻² with the ΔT of 7.3 K. And numerous comparisons reveal that the thermoelectric and output performance of low-cost α-Mg₃Bi₂-based materials and devices surpass those of most other plastic materials and f-TEGs. Indeed, our work demonstrates that α-Mg₃Bi₂ crystal can be a promising candidate in the field of flexible electronics.

Methods

Raw materials and crystal growth method of α-Mg₃Bi₂ crystals

For n-type α-Mg₃Bi₂, Mg (pieces, 99.95%, Alfa Aesar), Bi (shots, 99.999%, Alfa Aesar), Te (pieces, 99.999%, Alfa Aesar) were weighed with a Mg-excessive ratio of Mg/Bi/Te = 4:2:0.03.

For p-type α-Mg₃Bi₂, Mg (pieces, 99.95%, Alfa Aesar), Bi (shots, 99.999%, Alfa Aesar), were weighed with a Bi-excessive ratio of Mg/Bi = 5:5.

The raw materials were put into Boron Nitride (BN) crucibles with crew plugs, and then the BN crucibles were sealed into quartz tubes. The tubes were placed into a vertical three-temperature-zone Bridgman furnace. For n-type α-Mg₃Bi₂ crystal growth, the furnace temperatures were first set at 1173/1173/1173 K for 12 h to melt the raw materials. Then, the temperatures dropped to 1073/1073/673 K for crystal growth. The growth rate and the crucible rotation speed were set as 0.8–1 mm/h and 15 r.p.m., respectively. When the end of crystal growth, the furnace temperatures dropped to room temperature in 20 h. For p-type α-Mg₃Bi₂ crystal growth, the furnace temperatures were first set at 1073/1073/1073 K for 12 h to melt the raw materials. Then, the temperatures dropped to 973/973/673 K for crystal growth. The growth rate and the crucible rotation speed were set as 1 mm/h and 15 r.p.m., respectively. When the end of crystal growth, the furnace temperatures dropped to room temperature in 20 h.

Preparation of p-type AgCuTe_0.7Se_0.3-based plastic inorganic semiconductors

High-performance p-type AgCu(Se, S, Te) pseudoternary solid solutions⁶ were used to fabricate the out-of-plane flexible thermoelectric generator. We adjusted the ratio of raw materials and optimized the process to obtain the high-performance p-type plastic thermoelectric materials. AgCuTe_0.7Se_0.3-based plastic inorganic semiconductors were prepared by the temperature gradient method. High-purity elements, Ag (pieces, 99.999%, Alfa Aesar), Cu (shots, 99.9%, Alfa Aesar), Te (shots, 99.999%, Alfa Aesar), Se (shots, 99.999%, Alfa Aesar), and S (powders, 99.999%, Alfa Aesar), were weighted out in the assigned atomic ratios (AgCuTe_0.7Se_0.3, AgCuTe_0.69Se_0.3S_0.01, (AgCu)_0.999Te_0.69Se_0.3S_0.01, (AgCu)_0.997Te_0.69Se_0.3S_0.01, (AgCu)_0.995Te_0.69Se_0.3S_0.01, (AgCu)_0.993Te_0.69Se_0.3S_0.01). The raw materials were put into graphite crucibles with crew plugs, and then the graphite crucibles were sealed into quartz tubes. The tubes were placed into a vertical two-temperature-zone Bridgman furnace. The furnace temperatures were first set at 1323/1323 K for 12 h to melt the raw materials. Then the temperature immediately dropped to 1223/1123 K and then dropped to 1023/923 K by 2 K/h. The p-type ingots were annealed at 825 K for 48 h. Finally, the tubes cooled down to room temperature for 10 h.

Property measurements

The electrical conductivity(σ) and Seebeck coefficient (S) of our samples were measured by Ulvac ZEM-3. The thermal conductivity was calculated through the formula of κ = DC_pρ, where D is the thermal diffusivity, which was measured by Netzsch LFA 467 LT, and the heat capacity was 0.254 J g-1 K-1 taken from Xin’ work⁶⁷. The Hall coefficient (R_H) was measured using Lake Shore 8400 Series, a commercial Hall effect measurement system. We used n = 1/eR_H and μ = σR_H to estimate the Hall carrier concentration (n) and mobility (µ), respectively, where e is the elementary charge. The mechanical property tests on bulk α-Mg₃Bi₂ single crystalline samples, including compression, tension, and three-point bending tests and so on were performed using a universal material tensile testing machine (CMT5105) with a constant loading rate of 0.1 mm/min. The crystal sample dimensions for ab-plane and c-axis compression tests were 5.4 × 5.07 × 2.81 mm³ and 4.57 × 4.43 × 5.03 mm³, respectively. The crystal sample dimensions for tension and three-point bending tests were 2.62 × 0.62 × 20.6 mm³ and 3.30 × 2.8 × 24.94 mm³ respectively. The ingot dimensions for the compression test were Φ10.8 × 16 mm³. Nanoindentation tests were performed by using a Nanomechanical indentation instrument (Hysitron TI950).

X-ray diffraction (XRD)

The phase purity and crystal structure of the α-Mg₃Bi₂ crystals were examined by Rigaku MiniFlex 600 XRD equipment with Cu Kα radiation at room temperature. The crystallographic orientation of as-grown α-Mg₃Bi₂ single crystals was analyzed by a Laue X-ray diffractometer (LCS2020W) at room temperature.

In situ scanning electron microscopy (SEM) compression

The α-Mg₃Bi₂ micropillar with a diameter of about 6 mm and length of about 12 mm was fabricated in focused ion beam (FIB) milling (Helios 600i) by Ga⁺ ion beam. The micropillar was fabricated parallel to the ab-plane. Then, the uniaxial compression test on α-Mg₃Bi₂ single crystalline micropillar was performed by a Hysitron PicoIndenter (PI 89) with a flat punch diamond tip with a diameter of 20 µm and the constant loading rate of 10 nm s⁻¹.

Scanning transmission electron microscopy (STEM)

Samples were fabricated by means of FIB milling (Helios 600i), and then subjected to STEM observations. Atomic structures of these samples were investigated by high-angle annular dark field (HAADF) on a double Cs-corrected TEM (FEI Titan Themis G2) operated at 300 kV. The convergence angle and the collection angle for STEM imaging were 25 mrad and 48–200 mrad, respectively. To improve the signal-to-noise ratio, atomic-resolution HAADF-STEM images were obtained by averaging a consecutive series of drift-corrected images. Differential phase contrast (DPC) images were acquired by using segmented dark-field detectors. Before the DPC imaging experiment, the signal from four sectors of the detector was adjusted to ensure linear responses to the beam current. We quantified the Mg shift by directly analyzing the position and intensity of atoms in several iDPC images using CalAtom software^68,69.

Time-of-flight neutron diffraction

Time-of-flight neutron pair distribution function (PDF) analyses were performed using the Multi-Physics Instrument (MPI), a total scattering diffractometer at the China Spallation Neutron Source (CSNS) in Dongguan, China. Two types of samples from p-type α-Mg₃Bi₂ crystal were examined: about fifty small-sized single crystals without any strain and about fifty small-sized single crystals subjected to multiple bends. Each sample was placed into a vanadium can with a diameter of 8.9 mm within a glove box filled with helium gas. The measurements were conducted at 25 °C, with a testing duration of 6 h for each type of sample. The neutron wavelength range spanned from 0.1 to 4.5 Å, providing an optimal Q-resolution of 0.3%. The total scattering S(Q) data within the Q ranges of 0.5 to 31.5 Å^-¹ were transformed into PDF G(r) data through Fourier transformation⁷⁰:

$$G\left(r\right)=\frac{2}{\pi }{\int }_0^{\infty }Q\left[S\left(Q\right)-1\right]\sin \left(Qr\right)dQ$$ 2

where r is the inter-atomic distance, and Q is the scattering vector.

Density functional theory (DFT)

DFT calculations were performed within the Perdew-Burke-Ernzerhof (PBE) generalized gradient approximation using the VASP code^71,72. The 1 × 1 × 2 supercells with 10 atoms were used to simulate the slipping processes of quasi-two-dimensional α-Mg₃Bi₂ with a vacuum layer of 20 Å thick. To account for long-range van der Waals (vdW) interactions, DFT-D3 correction of Grimme with zero-damping function was employed⁷³. In the framework of the projector-augmented-wave (PAW) method⁷⁴, a plane-wave energy cutoff was set to 500 eV, and a 12 × 12 × 6 Monkhorst-Pack k-grid was used to ensure self-consistent convergence of electronic and ionic relaxations at 10⁻⁶eV and 0.01 eV Å^-1, respectively. The chemical bonding was investigated using the crystal orbital Hamilton populations (COHP)^55,56. To analyze the evolution of the structure with helical dislocations over time, ab initio molecular dynamics (AIMD) simulations were also performed using the VASP code^71,75. First, the bulk supercells, containing 135 atoms, were optimized with or without layer slip distortion (Supplementary Fig. 14). In comparison to the perfect lattice, the optimized supercells with distortion form a specific helical dislocation, inducing a unique reorientation of the atomic arrangement around the dislocation planes, as highlighted by the red circle. The optimized supercell with layer slip distortion was then further enlarged to 540 atoms, and after 20,000 time steps of AIMD simulations at room temperature in the canonical ensemble (NVT), with a time step of 2 fs, the system reached equilibrium.

Module fabrication and characterization

Out-of-plane flexible thermoelectric generator (f-TEG): the as-prepared n-type α-Mg₃Bi₂ crystal and p-type (AgCu)_0.999Te_0.69Se_0.3S_0.01 ingots were cut into thin plates with the thickness about 330 μm by using the diamond wire cutting. The metallic barrier layers were both prepared for n-type and p-type materials by using spark plasma sintering (SPS- 211LX) at 773 K under a pressure of 50 MPa for 5 min, as shown in Supplementary Fig. 28. Then the plates were cut into square thermoelectric legs of 4 × 4 mm² by using the diamond wire cutting. The n-type and p-type legs were put into the polyimide-based flexible circuit boards, as shown in Fig. 5a, and the distance between the thermoelectric legs is 1 mm. Finally, commercial low-temperature solder paste and Indium metal were used to weld the thermoelectric legs to the Cu/Au electrodes. The out-of-plane f-TEG was shown in Supplementary Fig. 30. The thickness of the device was tested to be 0.88 mm by micrometer. The total dimension of the six-couple f-TEG with a filling factor of 73.5% was about 0.88 × 9 × 29 mm³.

The output performance of the f-TEG was tested using a homemade apparatus (Supplementary Fig. 24). One end of the f-TEG was put onto a heating element controlled by an automatic temperature-controlling system acting as the hot side, whereas the other end was connected to a circulating water cooling metal plate acting as the cold side in which circulating water with the temperature of 295 K flows. The f-TEG was connected to an electrical circuit with a Keithley 2182 A nanovoltmeter and a Keithley 6514 microammeter. For a particular temperature difference, the output voltage and current were collected using a Keithley 2182 A nanovoltmeter and a Keithley 6514 microammeter, respectively.

For the output performance of an f-TEG, the maximum output power (P_max) is calculated by using the following expression P_max = V_OC²/4 R_in. Where V_OC, R_in represent the open circuit voltage and internal resistance of f-TEG, respectively. When the external load resistance (R_ex) equals the R_in, the maximum output power (P_max) is obtained. The maximum normalized power density (P_max/AΔT²) can be obtained by dividing the P_max by the cross-sectional area (A) and the temperature difference (ΔT) across the device. The actual temperature gradient (ΔT) of thermoelectric legs was estimated by using equation ΔT = V_OC/N(α_p-α_n), where N was the number of p/n pairs in the device, and α_p and α_n were the Seebeck coefficient of p-type and n-type TE leg, respectively⁶. The heating element temperature (T_hot), circulating water temperature (T_cold), and ∆T of the f-TEG device were summarized in Supplementary Table 8.

Author contributions

J.Q.H. designed this work. M.Y.H. synthesized the single crystal samples and carried out the thermoelectric property measurements. J.M.Y. and L.X. performed the TEM characterizations and analysis. Y.W. and L.X. performed the DFT calculations. J.C.X., J.P.X., S.L.L., W.Y., and H.F.L. conducted the Neutron diffraction experiments. M.Y.H. and Q.G. performed the mechanical experiments. M.Y.H. analyzed the data of in situ SEM compression test. M.Y.H. and S.H.Y. fabricated the flexible device. M.Y.H. and B.H.J. analyzed all the data. M.Y.H., Y.W., J.M.Y., and J.Q.H. wrote, and all authors edited this manuscript.

Peer review

Peer review information

Nature Communications thanks Nguyen Tuan Hung, Francisco Palazon and the other anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Data availability

All data are available in the manuscript and supplementary materials.

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-55689-7.