Abstract
Mixed signal analog/digital neuromorphic circuits represent an ideal medium for reproducing bio-physically realistic dynamics of biological neural systems in real-time. However, similar to their biological counterparts, these circuits have limited resolution and are affected by a high degree of variability. By developing a recurrent spiking neural network model of the retinocortical visual pathway, we show how such noisy and heterogeneous computing substrate can produce linear receptive fields tuned to visual stimuli with specific orientations and spatial frequencies. Compared to strictly feed-forward schemes, the model generates highly structured Gabor-like receptive fields of any phase symmetry, making optimal use of the hardware resources available in terms of synaptic connections and neuron numbers. Experimental results validate the approach, demonstrating how principles of neural computation can lead to robust sensory processing electronic systems, even when they are affected by high degree of heterogeneity, e.g., due to the use of analog circuits or memristive devices.
Subject terms: Electrical and electronic engineering, Biomedical engineering, Network models
The authors present characterisations of highly-structured visual receptive fields of any phase symmetry, implemented in an event-based spiking neuromorphic processor. They specifically demonstrate emerging properties of recurrent inhibitory circuits that reduce the drain of hardware resources.
Introduction
The goal of an early visual processing system is to extract as much information as possible about the structural properties of the visual signal, efficiently and quickly. Such a system must provide reliable features of high informative content, with low latency, to best support subsequent processing stages, for example involved in navigation or visual scene interpretation. Recently developed asynchronous event-driven vision sensors combined with brain-inspired spiking neuromorphic processors represent a promising technological solution for implementing such systems. The properties of these sensors and processors include massively parallel operation with a degree of network reconfigurability that can support the definition of different types of real-time visual processing models. However, current prototypes have limited resources for programming arbitrary connectivity patterns among neurons. For this reason, neuromorphic vision front-ends have been restricted so far to implementing relatively simple edge and moving object detectors. For example, recently proposed neuromorphic visual processing for depth perception and stereo-vision operate exclusively on temporal contrast events, disregarding the local spatial structure of the visual signal1,2. Other examples implement simple (e.g., binary) feature matching, by composing local receptors outputs through receptive fields (RFs) with minimal and simple weighting profiles3.
More sophisticated early visual processing systems would require highly structured RFs, e.g., with two-dimensional (2D) wavelet-like profiles to extract local amplitude, phase, and orientation information in a given frequency sub-band (cf. linear visual cortical cell responses, e.g., see ref. 4). Indeed, for many machine vision tasks, images are commonly analyzed by sets of oriented spatial-frequency channels in which some properties of the image are better represented than in image space. The spatio-temporal properties of the resulting harmonic components have been shown to be critically important for extracting primary early vision information. In general, as evidenced in several studies (e.g., see refs. 5–7), by using harmonic patterns for matching instead of image luminance measures, the resulting perception is more reliable, denser, and immune to changing lighting conditions. Since a direct implementation of such wavelet RFs on neuromorphic hardware is hampered by their limited routing resources, designing and validating efficient architectural solutions to obtain compact visual signal analyzers with minimal resource consumption is a challenge of critical importance.
In this paper, we address this challenge, by demonstrating an economic way to implement spike-based early-vision detectors of oriented features in given spatial frequency bandwidths that reproduce the known properties of Gabor-like simple cells RFs in the primary visual cortex (V1)4,8. This work builds on previously proposed preliminary models9,10. The strength of this work lies in the presentation of a coherent framework that combines and integrates previous contributions and extends them with both theoretical contributions that demonstrate the validity of the approach proposed and additional experimental results that highlight the benefits of the neuromorphic setup used. Our experimental results demonstrate how sparse biologically plausible recurrent connectivity schemes lead to the emergence of realistic RFs that exhibit response properties very similar to those measured in cortical neurons. In addition to being a useful result that validates theoretical and modeling studies with a real physical computing substrate that has the same properties and limitations of the biological computing substrate, this work paves the way toward the construction of compact and low-power early vision processing front-end systems for complex vision processing systems.
Results
The overall system setup consists of an event-based vision sensor interfaced directly to a neuromorphic spiking neural network processor that emulates the cortical stage, (see Fig. 1a). The event-based retina-like vision sensor is the Dynamic Vision Sensor (DVS)11, and the spiking neural network processor is a Dynamic Neuromorphic Asynchronous Processor (DYNAP-SE), which comprises mixed-signal analog/digital configurable neurons and synapse circuits12.
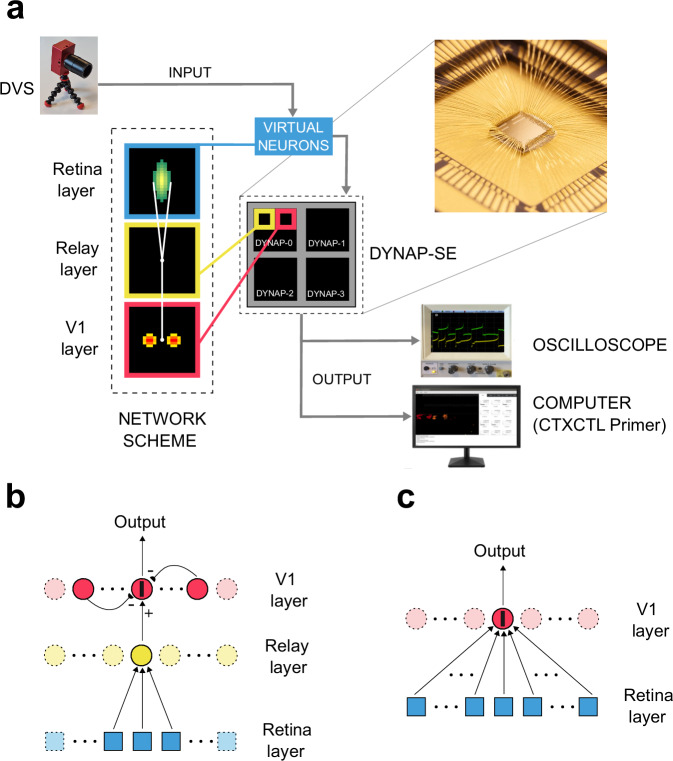
Fig. 1. Connectivity scheme and overall system setup.
a The overall system setup detailing how the model network has been physically mapped on the DYNAP-SE board and a close-up visual of the neuromorphic chip DYNAP-SEL. The DVS sensor output is reproduced by a population of spiking virtual neurons that act as spike generators for the physical silicon neurons on the DYNAP-SE chips. The board can be connected to an oscilloscope, to observe the membrane voltage of selected silicon neurons, and to a computer, through the CTXCTL Primer interface, to monitor the spiking activity of the four chips in real-time. A diagram of the connectivity scheme between the network’s layers is shown in the insets for the retina layer, the relay layer, and V1 layer: green shadings refer to excitatory feed-forward connection, whereas red’s refer to the clustered recurrent inhibitory connections. b One-dimensional representation of the recurrent network interconnection scheme: the target neuron, labeled by a black bar on the V1 layer, receives feed-forward excitation from neurons of the retina layer (cf. the elongated region in the inset of panel a), and recurrent inhibition from V1 neurons located at a fixed distance and displaced symmetrically along an orientation equal to the selectivity bias provided by feed-forward afferent connections (cf. the two red circular clusters in the inset of panel a). The angle of the bar indicates the orientation to which the neuron will be eventually sensitive according to such connectivity scheme. The same pattern of connections is repeated for every neuron of the V1 layer. c One-dimensional pictorial representation of the interconnections of an equivalent strictly feed-forward network, highlighting the larger extent of interconnections (light blue squares on the retina layer) required to obtain the same RF.
The DVS is built on principles that are consistent with the function of a real retina: sparse event-based output, representation of relative luminance changes, and segregation of positive and negative contrast polarities into separate output channels. It is composed of pixels that respond asynchronously to relative changes in light intensity, generating a stream of events that constitutes its output. Each event is transmitted to further processing stages in real-time, as it is produced. The event data encodes the address of the pixel that produced it, and its polarity (ON and OFF for positive and negative intensity changes, respectively). For data logging purposes, the processing pipeline time-stamps each event and stores also the time at which it was produced. Therefore, this data can be either saved for analysis or off-line simulations, or fed in real-time to further processing stages, such as the DYNAP-SE chip. The neuron and synapse dynamics and short-term memory functions are implemented on the DYNAP-SE using parallel analog circuits that run in continuous time, rather than using time-multiplexed digital circuits that discretize time13. The analog circuits operate in the subthreshold domain to minimize the dynamic power consumption and to implement biophysically realistic neural and synaptic behaviors, with biologically plausible temporal dynamics14. In our setup, the DVS activity is recorded for data logging and at the same time transmitted to a DYNAP-SE chips configured to have a specific arrangement of synaptic connections that gives rise to well-structured RFs. The DYNAP-SE chip neurons eventually produce tuning curves with a specific orientation and spatial frequency, mimicking the computation carried out by simple cells in the primary visual cortex15,16. The chip’s signals that represent the membrane voltage of selected silicon neurons can be observed through an oscilloscope, and the spiking activity of the entire chip can be monitored in real time as a stream of address events on a computer by using a custom-designed data-logging software suite17.
Network interconnection scheme
In computational neuroscience, early-level visual feature detectors are usually built from local feed-forward spatial weighting of retinal afferents. Intrinsic feedback is often proposed as an additional mechanism for refining single cells’ basic orientation and the spatial-frequency tuning. In particular, in a previous work18, we showed how the (linear) superposition of a retinocortical (i.e., feed-forward) oriented bias and a recurrent (i.e., feed-back) cross-orientation inhibition gives rise to highly structured Gabor-like RFs when inhibition originates from laterally distributed clusters19. The network is conceptually composed of two layers that represent two homogeneous populations of retinal and cortical (i.e., V1) neurons, respectively (see Fig. 1b). Accordingly, the excitation e of a neuron with orientation preference θ in the spatial position x = (x, y) on the V1 layer can be modeled as the solution of:
| 1 |
where * denotes the spatial convolution operator, s(x) is the visual signal, a is the strength of the feed-forward contribution, and b the strength of inhibition. The feed-forward kernel h0 is modeled as an elongated Gaussian function that weights the afferent contributions from the retinal layer (cf. the green region in the retina layer shown in Fig. 1a):
| 2 |
where σh and p set the size and elongation of the feed-forward kernel, and , are the rotated spatial coordinates. The recurrent inhibitory kernel is modeled by two Gaussian functions displaced along the direction orthogonal to the major axis of the feed-forward kernel (cf. the red regions in the V1 layer shown in Fig. 1a):
| 3 |
where σk and d set the size and distance of the clustered inhibition. We demonstrated18,19 that the linear superposition of feed-forward and recurrent contributions – as defined above – gives rise to a RF h(xθ, yθ) that can be well approximated by a Gabor function, characterized by radial peak frequency k0 and spatial extension σ:
| 4 |
This is the feed-forward resolvent kernel of the recurrent integral equation (see Eq. (1)) that represents how total afferent drive at retina site affects activity at a cortical (V1) site, detecting specific characteristics present in the input pattern of excitation. By properly choosing the parameters of the kernel of recurrent inhibition, the spatial extension on which these characteristics are detected is possibly larger than that of the actual inhibitory connections (see Fig. 1c). This occurs both directly, by physical local interactions, and indirectly, through propagation property of recursion. In this way, one can speak of induced functional couplings not directly related to the presence of corresponding specific wirings.
The preferred orientation selectivity changes when the feed-forward kernel and the recurrent connectivity scheme are jointly rotated by θ, while the peak spatial frequency varies when the displacement of the inhibitory kernels d with respect to their size σk are scaled. Since in this work we deal with spiking neurons, linearity cannot be given for granted and must be verified. To assess network’s performance and characterize the RFs of its output neurons, we used 2D sinusoidal drifting gratings as visual stimuli, widely used to investigate the response of cells in the primary visual cortex16,20,21. By plotting the mean firing rate response of a target neuron with respect to the orientation and the radial spatial frequency, we obtain the tuning curves that characterize neurons’ behavior. The narrower the curves, the better the tuning of a neuron on a preferred combination of orientation and spatial frequency.
Behavioral simulations
Before configuring and testing the hardware implementation of the spiking neural network, we first performed behavioral-level simulations, to ensure that the hardware is compatible with the theory and obtain a ground truth to compare with. The behavioral level software simulations were carried out using Brian2 spiking neural networks (SNNs) simulator22 with a dedicated custom toolbox for taking into account the properties of the silicon neurons and synapses, and many aspects of the neuromorphic processor that are not captured by computational neuroscience simulators23. The simulation process allowed us to verify the assumption of linearity and to tune the key design parameters of the connectivity scheme without having to deal with the restrictions posed by the neuromorphic hardware. The simulated network accounts for the discrete nature of neuron populations (see the Methods section for details). The feed-forward and feed-back kernels used in these simulations are shown in Fig. 2a–b. Two equivalent test networks with known RFs, built by feed-forward connections only, were also used for comparison: synaptic connections for these test networks were defined according to Gabor functions with three and five subregions, as in Fig. 2c.
Fig. 2. Connectivity kernels and test RFs.
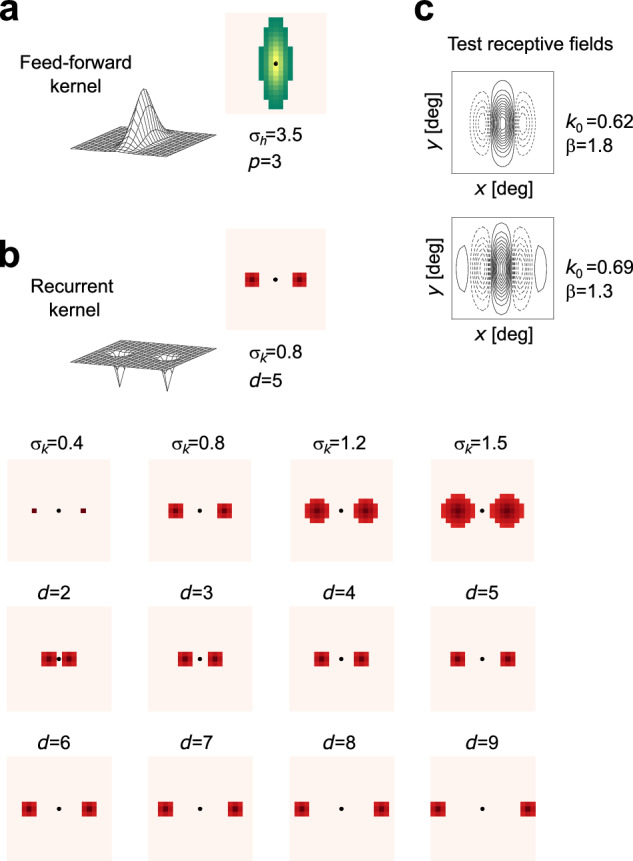
Mesh plots and top-view schemes of the feed-forward kernel (a) and of the feed-back kernels of the recurrent network (b), for the different parameter settings considered. Black dots indicate the position of the target neuron of the V1 layer that receives excitation through the feed-forward kernel on the retina layer, and recurrent inhibition through the feed-back kernel on the V1 layer. This connection scheme is replicated for every neuron of the V1 layer. c Representation of the RFs obtained—for the sake of comparison—direcly through two strictly feed-forward test networks.
Linearity test and feature tuning characterization
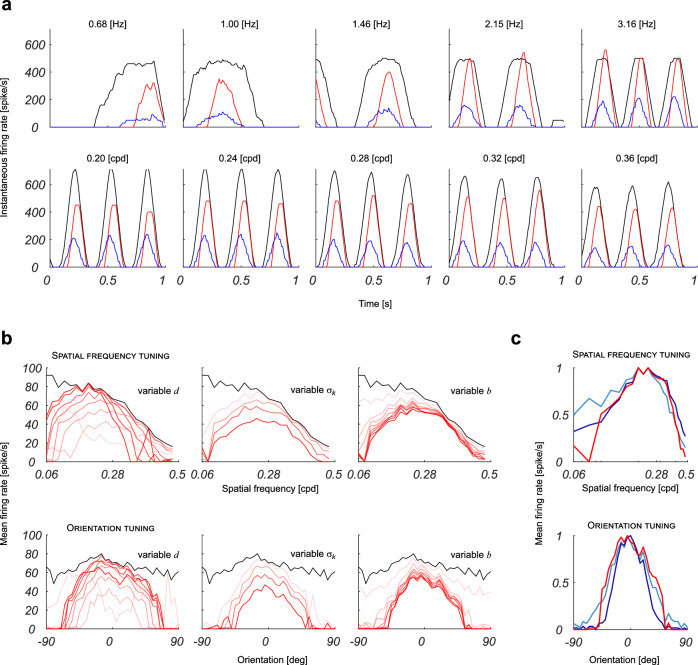
To test the linearity assumption, we stimulated the network with input gratings characterized by a wide range of temporal and spatial frequencies, from 0.68 to 3.16 Hz, and from 0.2 to 0.36 cycles per degree (cpd), respectively. If the linearity assumption holds, the firing rate of the output neuron should be modulated by the same temporal frequency of the grating used as input. We verified that this condition is always satisfied, both when the inhibitory recursion is excluded and when it is applied (see Fig. 3a). Simulations showed that recurrent clustered inhibition does indeed elicit the tuning of the neurons in the V1 layer to specific values of orientation and spatial frequency. The narrowest tuning curves are obtained when recurrent inhibitory connections cluster at a distance d comparable to the width of the feed-forward excitatory kernel σh. Other parameters that play a role in shaping the periodicity of the resulting RF profiles are the spatial extension of the clusters σk and the strength of the recurrent inhibitory connections b. The leftmost panel of Fig. 3b shows how the tuning curves change according to d. Keeping σk fixed at 0.8 and b at 3 ⋅ 103, d = 5 yielded the best tuning curves both for spatial frequency and orientation. For lower values of d the neuron is not properly tuned, and the inhibition reduces the firing rate significantly. For higher values of d the tuning curves broaden and the peak spatial frequency shifts to lower values. By keeping d and b fixed at 5 and 3 ⋅ 103 respectively, the tuning curves are broader for low values of σk while for high values the inhibition lowers the firing rate, as shown in the central panel of Fig. 3b. In the analysis, we have set the weight of the feed-forward excitatory connections a = 1 ⋅ 103. If we compare the normalized curves, σk = 0.8÷1.2 appears to be an optimal choice that yields the sharpest tuning both in orientation and spatial frequency, as well as a minimal relative bandwidth β = 0.8÷1.5 octaves. The value of b has to meet a stability constraint, and, anyhow, changing it beyond a certain value does not significantly affect the tuning of the neuron, as it can be seen in the rightmost column of Fig. 3b. Figure 3c shows the comparison between the tuning curves obtained by recurrent inhibition with optimal parameters and those exclusively obtained through feed-forward excitatory and inhibitory connections from the retina layer, as detailed in Methods. In terms of the spatial frequency tuning curve, the recurrent network yields the best results, whereas the orientation tuning curves are comparable. Anyhow, the recurrent inhibition method requires far less synaptic connections, as shown in Fig. 4, which is a relevant feature if one considers the limitations posed by neuromorphic processors like the DYNAP-SE. A direct comparison with an equivalent 21 × 21 five sub-region RF obtained by a feed-forward scheme shows an advantage for the recurrent network by a factor greater than 3, which progressively increases with the rescaling of the RF’s size. It is worth noting that when the clusterization of the inhibitory kernel with respect to the size of the feed-forward (excitatory) one is chosen above an optimal value (e.g., σk = 0.16 ⋅ d and σh = 0.7 ⋅ d), Gabor-like RFs reach the highest possible number of sub-regions by acting on the strength of inhibition b, which can be increased up to the limit of network instability, with no impact on the number of the required synaptic interconnections. In case we settle for RFs with a larger relative bandwidth (e.g., β ≃ 1.5 octaves, and thus a less number of sub-regions, e.g., three), the higher efficiency of the recurrent network over the feed-forward one drops to a factor of ≃ 1.65, yet paying the price of a reduced selectivity in the spatial frequency domain. If we choose intermediate values, the number of interconnections of a feedforward network that can produce RFs comparable to those obtained with the proposed recurrent connectivity scheme is approximately 2.5 times higher (e.g., a feedforward network for a seven-pixel wide Gabor filter with five subregions requires 481 connections, while its recurrent equivalent requires 191 connections). As a consequence, the number of wires required in an equivalent feedforward architecture is at least 2.5 times longer, assuming a best case scenario in which one interconnection requires just one unity wire element (i.e. a square metal layout block). In this case both area usage and power consumption would increase by at least a factor of 2.5. In practice, area is likely to increase significantly more, because VIAs need to be taken into account in the layout, and additional wire lengths will be needed for routing. The increase in power consumption will depend on the activity (i.e., voltage changes) on those wires. Assuming sparse activations, the factor of 2.5 is a good estimate. Considering that typical vision applications require front-end convolutions with a huge number of RFs, the convenience of recursion-based solutions turns out to be so far substantial.
Fig. 3. Characterization of the RFs emerging from the simulated network.
a The top row shows the response to moving gratings with a fixed spatial frequency of 0.28 cpd and temporal frequencies that vary as indicated; the bottom row shows the response to moving gratings with a fixed temporal frequency of 3.16 Hz and variable spatial frequencies that vary as indicated. Red and black curves refer to the instantaneous firing rates of the central neuron in the simulated V1 layer with and without recursion, respectively; the blue curve refers to the instantaneous firing rate of the afferent neurons in the simulated retina layer. As it can be observed, the firing rate of the neuron of interest in V1 oscillates with the same temporal frequency as the input in the retina layer, attesting to the linear behavior of the network. b Red lines represent the tuning curves for the central neuron of the simulated V1 layer for different values of the parameters d, and b. For each column, two parameters were set to fixed typical values (), whereas the third parameter varies between a minimum and maximum: (first column) 2 d 9 sampled with a step of 1, , = 3 ⋅ 103; (second column) = 5, 0.4 1.5 sampled with a step of 0.4, = 3 ⋅ 103; (third column) = 5, , b {1 ⋅ 102, 5 ⋅ 102, 1 ⋅ 103, 1.5 ⋅ 103, 2 ⋅ 103, 3 ⋅ 103, 4 ⋅ 103, 5 ⋅ 103}. Tuning curves obtained for increasing values of the variable parameters are represented with increasing color saturation. Black lines represent the curves obtained when the recurrent inhibition is removed. c Comparison between the tuning curves for the central neuron of the simulated V1 layer, obtained by the recurrent network for d = 5, = 1.2, and b = 3 ⋅ 103 (red line), and the neurons of the simulated test networks with Gabor-like feed-forward RFs with three subregions (light blue lines) and five subregions (dark blue lines).
Fig. 4. Comparison between recursive and feed-forward scheme in terms of required interconnections.
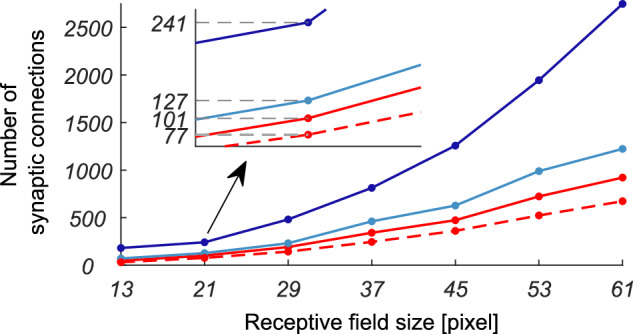
The different curves show the synaptic sparsity advantage of the recurrent implementation of Gabor-like RFs (red curves) over strictly feed-forward ones (blue curves), and how it scales for different sizes and number of sub-regions. Dashed and solid red lines represent the number of total interconnections used for a recurrent implementation of a five sub-region RF when the width of the inhibitory cluster σk was set to 0.8 and 1.2 deg, respectively, corresponding to a relative spatial frequency bandwidth β = 0.8÷0.9 octaves; the size of the feed-forward kernel σh was kept fixed to 3.5. Light and dark blue lines represent the number of interconnections required by equivalent strictly feed-forward RFs of three and five sub-regions, respectively. The inset details the numerical comparison for a five pixel size of the central sub-region. Rescaling was done by maintaining the same proportions among kernels and by flooring to the greatest odd integers for obtaining the resulting sizes in pixels.
The tuning of the neuron to a specific orientation and spatial frequency can be further improved by adding recursive excitatory connections. A way to introduce recurrent excitation is to define a kernel composed of two Gaussian functions equidistant from the target neuron, identical to the inhibitory one but in the orthogonal direction (i.e., aligned with the initial orientation of the feed-forward contribution from the retina layer). Adding recursive excitation, indeed, allows us to obtain narrower tuning curves, but also increases the number of synaptic connections, which can be problematic if the goal is to implement the network on neuromorphic processors where the number of synapses per neuron is limited, such as the DYNAP-SE. Because of this, that network structure was implemented in simulation, only (see Supplementary Information, Fig. S1). The effect is beneficial as long as the strength of the excitation doesn’t exceed a certain threshold, above which the shape of the curve is deformed and the tuning is no longer on the expected value of the feature.
Spatial profiles with arbitrary phase values
Figure 5 a shows three examples of spatial frequency tuning curves and their Fourier transforms for three output neurons. They all present a central positive lobe and two negative side bands resembling Gabor functions with even symmetry, as expected from the network’s architecture. That is equivalent to stating that they all present the same zero phase. Nevertheless, the RFs of nearby cells (e.g., in positions n − k, n, n + k, where k is set as equal to d, in terms of neuron index) can be summed in a convenient way in order to obtain a profile with an arbitrary phase value, using a method similar to the one described in ref. 24. The maximum of the one-dimensional section (on the plane perpendicular to the preferred orientation) of the RF spatial profiles of the lateral neurons will lay in correspondence with the minima of the spatial profile of the RF of the central neuron. The sum can be weighted by coefficients , , so that a spatial profile with the desired phase value ψ can be easily obtained, as shown in Fig. 5b.
Fig. 5. Spatial profiles with arbitrary phase values.
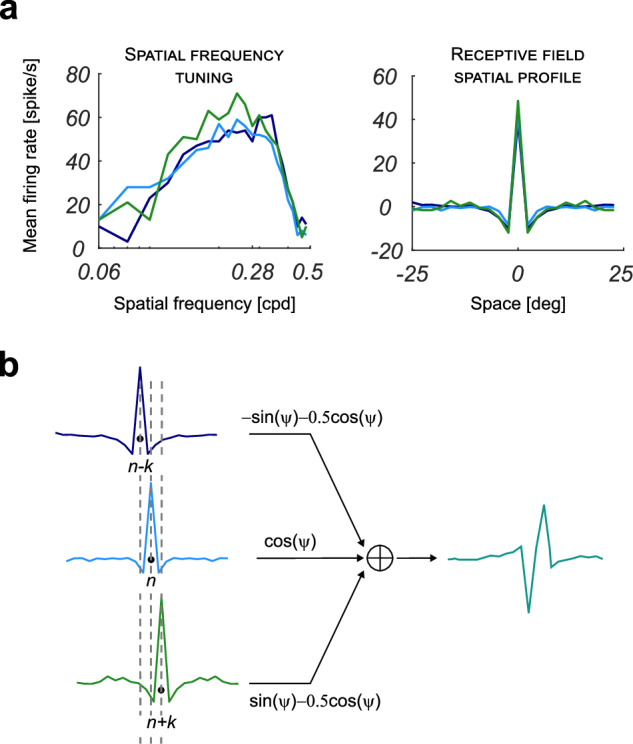
a The spatial frequency tuning curves and their inverse Fourier transforms for three sample neurons of the simulated V1 layer (central neuron and two nearby neurons at distance d from it). The input grating used to obtain the curves had a temporal frequency of 3.16 Hz. b The weighted sum of the spatial profiles to obtain a filter with an arbitrary phase value. The value of k can be chosen as being approximately equal to d.
Two-dimensional spectral response characterization
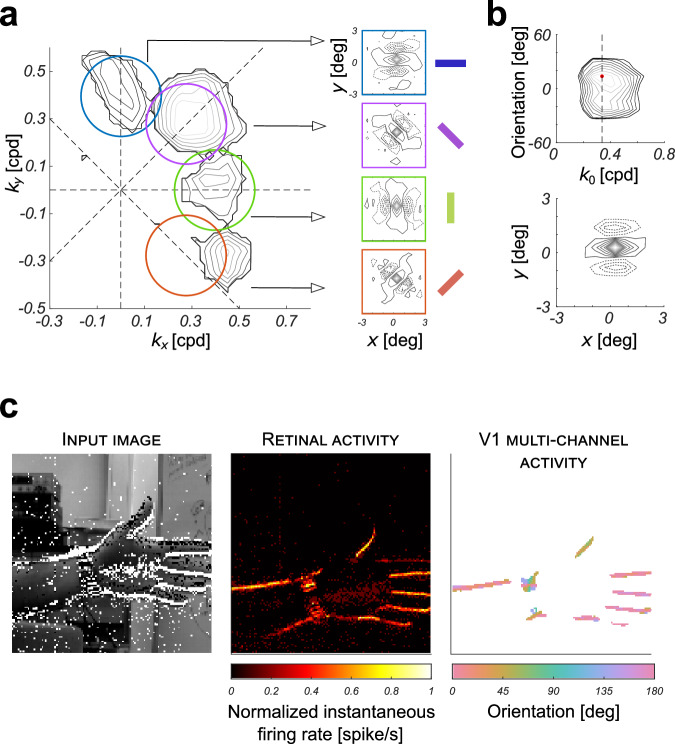
We derived the 2D spectral response profiles H(kx, ky) by varying the stimulus spatial frequency pairs over a square grid of −0.95 × 0.95 cpd with a step of 0.1 cpd in a quasi systematic manner (i.e., covering all combinations in a random order). Spikes occurring during stimulations were accumulated and averaged over 2 grating cycles to approximate the output neurons’ mean firing rate. This process was repeated for all the 20 × 20 spatial frequency pairs. Results are shown as iso-amplitude contour plots. As expected, the amplitude spectral response exhibits two Gaussian-like blobs located almost symmetrically about the origin. The frequency response decays smoothly as one moves away from either peak with a characteristic band-pass filter behavior. Figure 6a show typical examples for the same fixed radial spatial frequency and four different orientations. The RF in Fig. 6b has been obtained by averaging the frequency responses for variable orientations. This is equivalent to a rotation of the spectral coordinates about the origin and has the effect of roughly normalizing the results with respect to orientation. The normalized orientation was set to 0∘, for convenience (horizontal axis). The average major spatial frequency component (i.e., radial peak frequency of the Gabor-like RF) was 0.3387 cpd.
Fig. 6. Two-dimensional spectral response characterization and functional validation.
a Four examples of spectral response profiles of neurons of the simulated V1 layer (for θ = 0°, − 45°, 90°, and 45°) and the corresponding spatial kernels obtained by inverse Fourier transform. The colored contours indicate the -3 dB magnitude of the power spectrum Gabor filter responses of a theoretical orientation hypercolumn. b Average spectral response profile of neurons of the simulated V1 layer normalized with respect to orientation, and the corresponding spatial kernel obtained by inverse Fourier transform. Bandpass cutoff was set at −3 dB. The vertical dashed line identifies the radial peak frequency of the Gabor-like RF. c A snapshot of the measured activity of the DVS for a natural scene, the corresponding firing rate of the simulated retina layer, and the combined response of the simulated V1 layers obtained from four channels with different preferred orientations. The stream of events generated by the DVS is shown in the input image: ON and OFF events are represented as white and black squares overlaid to the corresponding image of the scene acquired with a regular frame-based camera. In the resulting retinal activity, brightest tones indicate higher firing rates. The V1 multichannel activity highlights the local dominant orientation value around each pixel, calculated as , where is the instantaneous firing rate of the corresponding neuron in the V1 layer, and θ ∈ {0°, − 45°, 90°, 45°} is the orientation of the Gabor-like filter. For the sake of simplicity in the visualization, only the neurons of the V1 (ON) layer with a firing rate above a given, fixed threshold (equal to 60% of the average maximum firing rate of the neuron population), were considered in the computation. Cropped DVS240 recording from DVSFLOW16 dataset60.
Extraction of dominant local orientation
The resulting bank of linear filters can be used as a minimal and controllable set of operators for extracting early vision features, from the spiking video stream provided by the DVS, directly. Indeed, the spatial structure of the Gabor-like profiles allows us to aggregate ON and OFF temporal events according to locally oriented band-pass spatial frequency channels, which are frequently used as front-ends of artificial vision systems25,26. Although several tricks should be considered to efficiently implement a full multichannel representation, a flavor of the functionality of the proposed network is presented, for a single scale and four orientation channels. Figure 6c shows the results for a snapshot of a DVS recording featuring a moving hand; the panels show the activity of the DVS, the activity of the retina layer that reproduces ON events as spikes, and the labeled response of the simulated V1 layers obtained from four channels with different preferred orientations. By combining the magnitude responses from the basis channels through a tensor-based method, for each image pixel it is assigned the dominant local orientation, along with its reliability, given by the average firing rate of population of orientation selective neurons. The detected dominant local orientation well matches the actual local orientation in the scene.
Extraction of full harmonic content
In general, input-output characterization of visual RFs is based on the notion of contrast. Accordingly, we can represent the spatial image i as the combination of two components: one part is the average luminance of the stimulus m, the second part is the variation of luminance about the mean, which defines the stimulus contrast c:
| 5 |
where c can be either positive or negative, and m≥0.
In early stages of the visual system, for each contrast polarity channel, local changes of contrast in a cell’s RF yield to changes of that cell rate of response (r) :
| 6 |
where r0 is the neuron’s spontaneous firing rate that we can assume equal for both ON and OFF channels. In order to gain equivalent a linear summation response to a signed contrast pattern within the overall neuron’s RF (composed of ON and OFF subregions), a push-pull mechanism is usually advocated27–29, that collects positive (i.e., excitatory) contribution from relay cells of preferred polarity and negative (i.e., inhibitory) contribution from relay cells of opposite polarity. ON and OFF event detectors in the retina-like DVS camera cannot per se encode negative responses. Yet, assuming a push-pull configuration, events provided by DVS camera can be conceptually combined to obtain positive or negative changes of response on the basis of the sign of contrast. As a result, stimulating an ON neuron by a not appropriate contrast polarity results in a decrease of its response, due to inhibition from the corresponding OFF neuron, which, conversely, has received the appropriate stimulus in its RF:
| 7 |
In other words, we take the excitatory response of the OFF channel as the estimate of the inhibitory response of the ON channel, and the combined response can be written as:
| 8 |
To prove the efficacy of the push-pull mechanism we can test the superposition property. Suppose we have two contrast stimuli c1 > 0 and c2 < 0. The response variations of the ON and OFF channels will be:
| 9 |
| 10 |
respectively, where and and h1, h2 denote the values of the RF profile. By combining the two responses we obtain:
| 11 |
which proves the linearity of the response, provided we model as negative the weights of the OFF subregions. In this way, the RF properly acts as a linear filter by mapping a weighted sum of the signed input contrast of the stimulus to the neural response.
Hence, two identical networks with the previously described structure were implemented, one for the ON events and the other for the OFF events. In this way, retina layers handle ON and OFF events in separate channels. The added information provided by the complementary channel allows the building of a full linear response to luminance contrasts, which opens the possibility of extracting the local phase information from the visual signal by exploiting the response of a quadrature pair of Gabor-like band-pass filters. More precisely, an oriented band-pass channel is capable of measuring the signal’s phase with respect to its orientation. In general, for intrinsically 2D signals (such as corners, junctions, or textures) there does not exist a single symmetry axis, and the phase measure is influenced by the signal’s energy distribution along other symmetry axes that characterize its complex structure. By using a full set of oriented filters (θ ∈ [0∘, 180∘)), each filter gathers information about the signal’s phase with reference to its oriented bandwidth (i.e., across the orientation of the filter) and a vector averaging operation (cf. ref. 30) must be used to decode the local phase. Accordingly, the dominant local image phase for the spatial position index n can be defined as:
| 12 |
with
| 13 |
where Eθ(n) is the energy component, defined as ; ϑ is the dominant orientation, defined ad ; and Cθ(n) and Sθ(n) are the even and odd components obtained by the weighting procedure of nearby impulse responses of the cortical layer, as previously described:
| 14 |
where rθ(n) is the combined firing rate obtained from the push-pull configuration
| 15 |
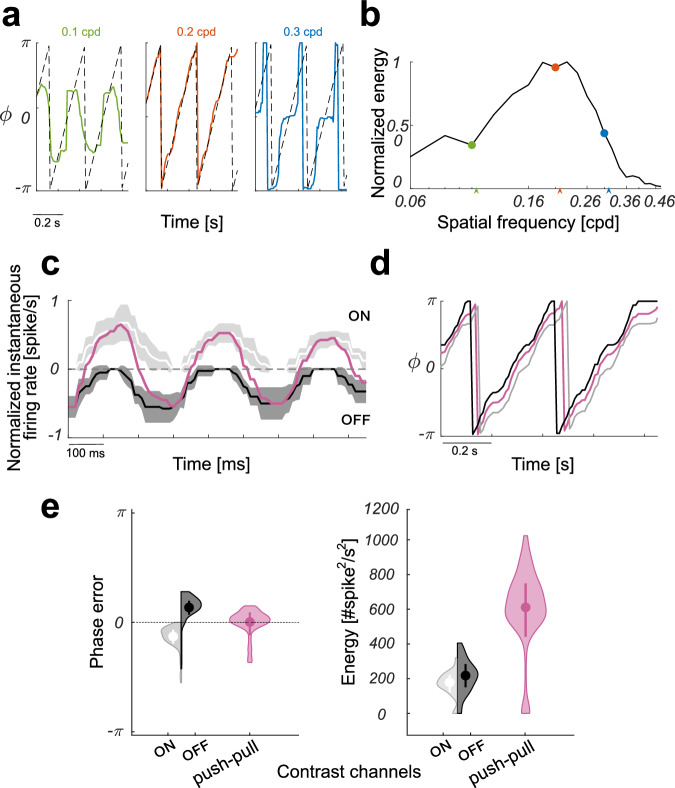
with and the instantaneous firing rates of the neurons in position n of the V1 layer of the ON and OFF channels, respectively. The subscript θ denotes the orientation of the RF. The resulting estimates of the dominant phase component for drifting sinusoidal gratings with orientation coincident with the RF’s orientation are graphed in Fig. 7a. The center plot shows the result obtained when the spatial frequency of the grating (0.2 cpd) corresponds to the preferred filter’s spatial frequency, and demonstrates that the estimate well captures the linear variation of the phase of the sinusoidal grating; the side plots show that the phase estimate degrades for not optimal spatial frequency of the gratings, corresponding to lower values of the local energy of the band-passed visual signal (see also Fig. 7b). In addition, we have conducted a comparative analysis on the accuracy and reliability of the phase estimate obtained with or without the push-pull mechanism. Figure 7c shows the normalized instantaneous firing rates and of a V1 layer neuron in response to a sinusoidal grating with optimal orientation and spatial frequency, and their push-pull combination. The zero mean (i.e., zero dc) feature of the combined response, differently from the others, yields to almost unbiased and reliable phase estimates (see Fig. 7d). The phase error and energy violin plot distributions underline this conclusion, also pointing out the overall higher efficiency of the push-pull response compared to those of the ON and OFF channels, separately (see Fig. 7e). Certainly, these differences would have only negligible effect on the (eventual) classification accuracy achieved from the band-passed images obtained by convolving the original images with the three filters. This because, typically, image classification can well rely upon local image energy peaks, which are sufficient for characterizing the different samples of popular image dataset (e.g., N-MNIST and N-Caltech10131, HOTS32, MNIST_DVS33, the event-based UCF-5034) used for benchmarking. However, the advantage of implementing the proposed filtering stage in the push-pull configuration becomes evident when we compare the efficacy of the associated phase-based feature maps in more complex machine vision problems. Accurate phase detection depends on ideal quadrature pair of bandpass filters to obtain the analytic signal. The dc sensitivity of the real (symmetric) part of the Gabor kernel is therefore an important aspect that cannot be ignored5,35, and can be addressed, for example, by correcting for, or constraining, their shape7. The push-pull configuration automatically cancels the dc sensitivity, which otherwise introduces a positive bias in the real part of the response that would affect the reliability and stability of local phase measurements and thus those of the derived visual features. It is worth noting that, although in principle the value of the phase associated to each orientation channel is correct, its confidence decreases as far as the symmetry axis of the image structure deviates from the orientation axis of the filter. We can thus state that the energy value of the associated wavelet-like transform is not isotropic, since it is not invariant under rotations of the signal. The isotropy of the representation is yet regained when one considers the whole set of oriented channels (i.e., the whole hypercolumn36).
Fig. 7. Estimates of the dominant phase component for the push-pull configuration.
a Estimated dominant phase components ϕ for drifting sinusoidal gratings with different spatial frequencies and orientation coincident with the neuron’s orientation preference. The most reliable phase estimate (red plot) is obtained when the stimulus' spatial frequency matches the peak frequency of the Gabor-like band-pass filter (i.e., ks = 0.2 cpd ≃ k0). The actual (i.e., ground truth) phase signal is displayed for reference as black dashed lines. b Normalized energy E of the band-passed signals for a range of spatial frequencies. Low values of the local energy weaken the reliability of the phase estimates (see green and blue plots in panel a). c Normalized instantaneous firing rates rON and − rOFF of the V1 layer silicon neuron of the ON channel (light gray) and of the OFF channel (dark gray), respectively. The input stimulus was a sinusoidal grating whose orientation and spatial frequency matched the peak frequency of the Gabor-like RF and its orientation preference; the temporal frequency was set to 3.16 Hz. The combined instantaneous firing rate r = rON − rOFF is shown in purple. Firing rates were mediated over ten recording sessions, solid lines represent the mean, whereas shadings represent standard deviation. d The comparison of the stimulus phase estimates for the ON-channel only (gray), the OFF-channel only (black), and their push-pull combination (purple). e The distributions around the means of the population errors of phase estimations, and of their reliability in terms of energy response for the three conditions considered. Solid dots depict the mean and associated error bars represent standard error of the mean. The minor bias in the error and the higher energy make the phase estimate by the push-pull configuration more accurate and reliable than those attainable by single channels. Color codes as in panel (c).
Implementation on the DYNAP-SE board
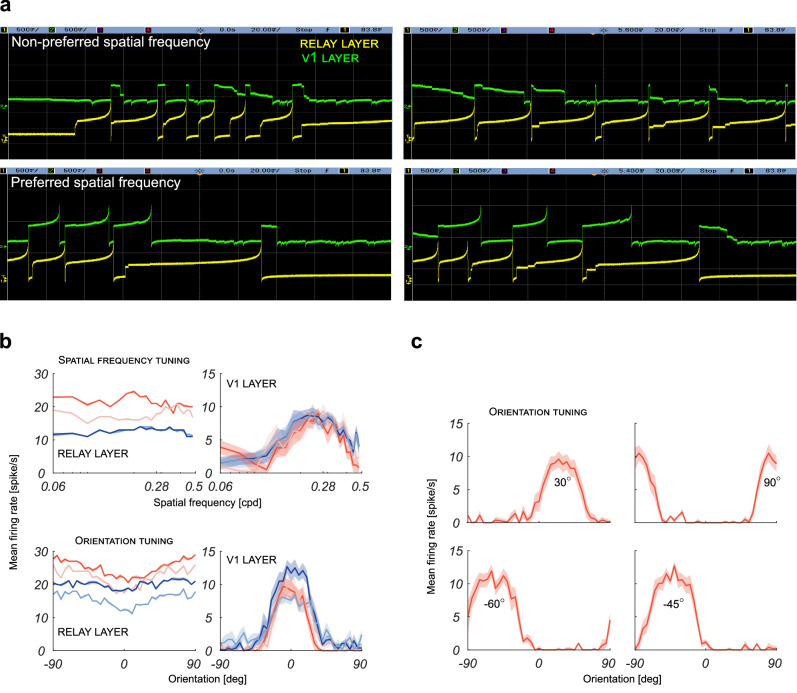
The Brian2 simulations allowed us to study the effect of recurrent inhibition in the SNN and to determine the combination of parameters that yields the best tuning curves, without being restricted by the limitations of the DYNAP-SE for what concerns the maximum number of synapses available per neuron, and the quantization of synaptic weights. On the basis of those simulations, we determined the values of d, σk and b that yielded the best results and with those parameter values we implemented the network on the neuromorphic processor DYNAP-SE. The network structure was slightly modified to overcome the restrictions posed by the DYNAP-SE board: notably, an extra layer of neurons, the relay layer, was added between the retina layer and the V1 layer to increase the number of available synapses, as detailed in Methods. The DVS recordings were reproduced through the activity of the retina layer, and, after implementing the retino-cortical connections, we recorded the spikes of the central neuron of the V1 layer to assess the efficacy of inhibition. The DYNAP-SE board indeed offers the possibility of closely observing the voltage of the membrane capacitor of any neuron on its chips through an oscilloscope. By monitoring the activity of the central neuron of the V1 layer and of one of its afferents in the retina layer, we observe that recurrent inhibition suppresses the spiking in case of non-preferred values of spatial frequency and orientation of the stimulus; the effect of the inhibition is instead much weaker when the preferred stimulus is presented, see Fig. 8a. Since neurons and synapses behavior on the DYNAP-SE is not deterministic due to device mismatches, the resulting tuning curves for spatial frequency and orientation were mediated over ten sessions. Results are shown in Fig. 8b. A neuron that receives only the feed-forward input is not tuned to any specific value of the features and its firing rate changes according to the temporal frequency of the grating (since faster gratings elicit more events on the DVS, and thus higher firing rate of the retina neurons that project to the relay layer and then to the V1 layer). When the recurrent inhibition is switched on, the neuron becomes clearly tuned to a specific spatial frequency and to a specific orientation. The curves obtained for different temporal frequencies overlay: this is evidence of the fact that the emergence of ON and OFF subregions in the RF induced by recurrent inhibition successfully normalizes the firing rate in input. As already done in simulation, configurations of the network aimed to obtain neurons tuned on different orientations were also successfully tested on the DYNAP-SE board, as shown in Fig. 8c.
Fig. 8. Measured response properties of the implemented silicon neurons.
a Voltage traces of the membrane capacitor of the central neurons of the relay layer (yellow line) and V1 layer (green line). Panels exemplify how recurrent inhibition suppresses spike activity in case of stimuli with a non-preferred value for spatial frequency or orientation, and how the inhibitory effect is instead much weaker when stimuli with preferred spatial frequency or preferred orientation are presented. b The corresponding spatial frequency and orientation tuning curves in the relay layer and in the V1 layer. Tuning curves were mediated over ten recording sessions, solid lines represent the mean, whereas shadings represent standard deviation. The relay layer receives feed-forward input only, whereas the V1 layer receives also the contribution of recurrent inhibition. Different colors indicate different temporal frequencies of the gratings used as visual stimuli: 3.16 Hz (red), 2.15 Hz (light red), 1.45 Hz (blue), 1 Hz (lightsteelblue). c Tuning curves obtained by the measured responses of silicon neurons of the V1 layers with different orientation preferences, as indicated. The temporal frequency of the gratings used as visual stimuli was set to 3.16 Hz. As in panel b, solid lines represent the mean, whereas shadings represent standard deviation.
The average estimated power consumption for a neuron of the relay layer and for the corresponding neuron of the V1 layer, when responding to the preferred stimulus at the highest temporal frequency, is 6.54 μJ and 446 nJ, respectively. Details on the estimation are reported in Methods.
The push-pull configuration was also tested, with the ON and OFF branches occupying chips 1 and 3 of the DYNAP-SE board (relay layers on core 0 and 1 of chip 1 and V1 layers on core 0 and 1 of chip 3). As predicted by simulations (see Fig. 7c), when presented a sinusoidal grating with the filter’s preferred orientation and spatial frequency, the combined instantaneous firing rate r = rON − rOFF obtained from the push-pull configuration results in a steeper sinusoidal profile, attesting to the fact that the combined information from the ON and OFF channels refines the filter’s tuning and allows a wider contrast sensitivity. In this way, the push-pull mechanism allows us to gain an equivalent linear response to the (signed) contrast of the image, modeled through a spatial RF with largely distinct ON and OFF subregions.
Discussion
Todays’s neuromorphic systems represent a promising alternative to conventional von Neumann architectures for both understanding and reproducing the properties of biological sensory processing systems, as they are subject to similar constraints in terms of noise, variability, and parameter resolution37. Reproducing the dynamics of biological neural systems using sub-threshold analog circuits and asynchronous digital ones make these systems ideal computational substrate for testing and validating hypotheses about models of sensory processing for a wide range of application domains14,38. In addition, their real-time response properties allow us to test these models in closed-loop sensory-processing hardware setups and to get immediate feedback on the effect of different parameter settings.
As the amount of data in visual processing is intrinsically high, providing sufficient resources for performing complex transformations – from pixels to features – and implementing corresponding computational models is particularly challenging. Indeed, front-end early vision modules have to construct high-dimensional quantitative representations of image properties, referable to local contrast variations across different orientations, and according to different spatial frequencies. Subsequent stages eventually combine these properties in various ways, to provide categorical qualitative descriptors, in which information is used in a non-local way to formulate more global spatial and temporal predictions (e.g., see ref. 39). However, it is only seldom that classical frame-based computational theories can be directly applied to event-based sensory data. Indeed, typically, object detection, pattern recognition, and scene reconstruction rely upon algorithms and computational procedures that well conform to the peculiar properties of the sensory data representation. Considering specifically image classification tasks32,40,41, intrinsically 1D properties, like edges and contours, are often sufficient to obtain a compact and complete feature description that enables a similarity measure to be applied to the different samples of popular image dataset. Other applications, like depth perception, optic flow, or simultaneous localization and mapping (SLAM), more decisively rely upon the timings of events1,42,43. Although fully exploiting the time coding of spikes trains can be extremely efficient, we cannot disregard extracting the information conveyed by the spatial structure (i.e., the texture) of the luminance pattern, which depends on precise relations among the phases of the various harmonics (e.g., see refs. 7,44). We must ensure that such information is not lost. The latter indeed plays a pivotal role in gaining dense feature maps potentially informative for several machine vision applications. Extracting stable spatial image structure requires local operations to regularize the information contained in spike trains. This can be done afterwards, on the result of the interpretation of the event stream (as mostly adopted by event-based machine vision algorithms, e.g., see ref. 45), or concurrently with picking-up sensory signal. Having such an early stage dedicated to the extraction of general-purpose regularized features brings about enormous advantages in terms of adaptability and versatility for compositionally building or learning a variety of higher-order visual descriptors. At a first level of abstraction, it is thus important that the rate coding model of network’s neuronal firing replicates the known encoding properties of the cells in the primary retinocortical pathway, according to a linear filtering model with appropriate kernels (i.e., receptive fields)46 It is well acknowledged that Gabor wavelets are a powerful tool to gain an efficient regularized representation of the information contained in frame-based visual signal, in terms of local amplitude, phase and orientation maps of the transformed signal.
In previous works9,10, we indicatively demonstrated that recurrent clustered inhibition can be successfully used in SNNs, both in simulation and on mixed-signal analog/digital neuromorphic hardware, to economically implement highly structured Gabor-like RFs. The results of this paper corroborate those preliminary findings, specifically extending the analysis of the linearity of the resulting RFs when using the net firing rate of the retina (ON firing rate minus OFF firing rate) instead of both as a whole, or separately. Such a push-pull combination of the complementary ON and OFF channels led to more reliable and unbiased representation of the harmonic content (see phase and energy in Fig. 7e) which would eventually lead to steeper tuning curves of the V1 neurons, resulting in better selectivity to the local orientation, spatial frequency and phase of the visual input. Employing multiple banks of Gabor filters at the front-end of a bio-inspired vision system is not a novel concept per se47–51, and examples of hardware implementations can be found in the literature24,52–56. Yet, here we propose an economic way to implement them in hardware by a spiking neural network, which can be efficiently scaled with the kernel size. The resulting RFs are characterized by spatial profiles and by tuning curves that are typically sharper than the ones obtained using equivalent feed-forward schemes. Furthermore, RFs obtained through a recursive scheme use a lower number of interconnections than that required when using an exclusively feed-forward approach. The advantage of the recurrent network over strictly feed-forward schemes is up to more than 3 × for a five sub-region RF with a size of 21 × 21, and increases with the rescaling of the filter’s size. This is an important feature when dealing with the limitations in terms of available synaptic connections posed by neuromorphic processors.
In summary, the solution proposed in this work demonstrates that an early vision filtering stage can be implemented in mixed-signal neuromorphic hardware in a relatively economic way, with adequate accuracy and stability. Particularly, exploiting both ON and OFF channels – through their push-pull combinations – shows to be an appropriate approach to remove the undesired effect of dc component sensitivity, and thus obtain highly informative phase-based features. The implemented units act as multiple oriented bandpass frequency channels, well supporting a compact and reliable representation of position, orientation and phase of local image patches. As a whole, the resulting harmonic signal description provided by the proposed neuromorphic circuit could be potentially used for a complete characterization of the 2D local structure of the visual signal in terms of phase relationships from all the available oriented channels. The amplitude (i.e., firing rate) information can be used as an indicator for the likelihood of the presence of a certain structure, while the orientation of contrast transitions and their spatial symmetry (i.e., phase,7,57) can be used as an attribute of the visual descriptor.
Methods
Structure of the simulated network
To define the actual connections of each neuron of the V1 layer, the target neuron is considered as being in the central position (0, 0) of the x-y plane. The retina layer and the V1 layer are considered superimposable, and to each neuron of the retina layer is assigned a value sampled from the kernel h0(x, y) centered in (0, 0). The neurons whose values are above a certain threshold are connected to the target neuron with base-weights corresponding to the sampled values of the corresponding kernels. The same process applies for defining the recurrent connections. The base-weights were sampled from the feed-forward and feed-back kernels in Fig. 2a, b. The Gabor functions in Fig. 2c, used to sample the synaptic weights for the test networks, were defined in order to have an excitatory central region width of five pixels (i.e., the same size as that of the feed-forward kernel) by fixing k0 = 0.7 cpd, and σ = 3.5 or σ = 4.7 to obtain a three-subregion or a five-subregion RF, respectively; the threshold was set to 0.1.
Implementation on the DYNAP-SE board
The DYNAP-SE board poses the following restrictions:
each neuron can have at most 64 afferent connections;
each neuron in a core shares the same biases, including the synaptic weight of the afferent connections;
each neuron has two types of excitatory synapses and two types of inhibitory synapses, thus limiting to two the maximum number of different excitatory and inhibitory weights for each core;
only the shunting-type inhibitory synapse could be used since the other type was not effective in lowering the membrane voltage of the target neuron.
To overcome restriction R1, an extra layer of neurons, the relay layer, was added between the retina layer and the V1 layer to increase the number of available synapses. The relay layer receives excitation from the retina layer through the feed-forward kernels, and projects one-to-one connections to the V1 layer, where inhibition takes place. The weights were adjusted so that the network with this new structure behaves in an equivalent way to the simulated one. Due to restrictions R2, R3, and R4, the connection weights that define the kernels cannot be assigned by sampling the Gaussian profiles, as in the simulations, but have to be set to a single value, in the case of the recurrent kernel, or quantized by two levels in the case of the feed-forward kernel. The relay layer and the V1 layer were placed on different cores of the DYNAP-SE chip. The retina layer was assigned to virtual neurons, which are implemented by a module that acts as a spike generator, providing input spikes to the physical neurons on the target chip. The spiking activity of the silicon neurons can be recorded and further processed off chip. The DYNAP-SE board is connected to an oscilloscope to monitor in real time the voltage on the membrane capacitor.
To calculate the power consumption of the neuron of the relay layer and of the central neuron of the V1 layer we considered the following equation, which approximates the power consumption of a silicon neuron on the DYNAP-SE including spike generation and routing as primitive operations2:
| 16 |
where rin and rout are the average input firing rate and average output firing rate, respectively; Espike is the energy required to generate one spike, corresponding to 883 pJ; Epulse is the energy required by the pulse extender circuit, corresponding to 324 pJ; Een is the energy required to encode one spike and append destination, corresponding to 883 pJ; Ebr is the energy required to broadcast one event to the same core, corresponding to 6.84 nJ; Ert is the energy required to route the event to a different core, corresponding to 360 pJ; RT is set to 1 if the spike is sent to a different core, and is set to 0 otherwise.
Visual stimuli recording and conversion
Each grating is described in a polar coordinate system in terms of its orientation θ and (radial) spatial peak frequency ks, with units of degrees (deg) and cycles per deg (cpd), respectively. A Cartesian coordinate system (kx, ky) will be equivalently adopted to characterize the 2D spectral response profiles of the output neurons. The relationships between Cartesian and polar coordinates are:
| 17 |
The stimuli were displayed on a screen at a fixed distance of 40 cm and acquired by the DVS event camera. It is worth noting that a drifting grating is necessary since only moving stimuli are effective in generating DVS response. To generate moving gratings, we used the toolbox PsychoPy58, which automatically allows us to set the spatial frequency in cycles/deg (cpd), given the screen’s distance and its resolution in pixels. The brightness of the screen was set at its maximum and the recordings were carried out in a semi-dark room to reduce the refraction of the screen. Examples of the generated moving sinusoidal gratings, along with additional details on their definition, are given in Supplementary Information, Fig. S2. Since the DVS is sensitive to local contrast changes, bands of ON and OFF events are generated where the sinusoidal profile is steep enough. Conversely, where the profile is almost flat, contrast differences are too small to be detected by the sensor, and no events are generated, resulting in bands without events, which are wider or narrower according to the contrast sensitivity threshold. The spatial frequency information is always preserved since it is encoded in the distance between the bands of events, but the phase is shifted by π/2. A schematic illustration of how a sinusoidal grating is perceived by the DVS sensor is shown in Supplementary Fig. S3. The drift velocity, and accordingly the temporal frequency (i.e., the number of grating cycles that pass a point in the image plane per unit time) are chosen so as to have cells’ linear behavior and cells’ strongest responses (see Supplementary Fig. S4). The jAER59 software was used to record and save the output stream of events of the DVS into AEDAT files. We recall that each event carries information about the position of the pixel that generated it, the timestamp, and the polarity. The AEDAT files were converted by extracting this information and by organizing it into numerical matrices to be used as input to the simulated network or to the spike generator module of the DYNAP-SE.
Linear characterization of the resulting RFs
Predictions about the tuning of the resulting RF can be gained by the transfer function of the linear approximation of the network. Without compromising our conclusions, we can restrict the analysis to the one-dimensional section along the direction orthogonal to the spatial orientation of the RF, which fully defines the bandpass character of the RF profile:
| 18 |
where by capital letters we denote the Fourier transforms of the corresponding quantities in spatial domain. The values of the power spectrum W(k) of the inhibition kernel that tend to nullify the denominator of H(k) dominate the free response of the recurrent network, thus yielding a selective amplification of the input at the corresponding frequency , which shapes the resulting RF. Given the specific choice of the inhibitory kernel, we can straightforwardly demonstrate that, for a sufficient strength of inhibition b, the peak frequency of the resulting Gabor-like RF mainly depends on the distance d of the inhibitory clusters:
| 19 |
In such a condition, the network’s 2D spectral response centered around the peak frequency k0 can be well approximated by a Gaussian function with standard deviation B, whose relative bandwidth (at −3 dB cut-off)
| 20 |
directly impacts on the number of sub-regions of the resulting RF. To analyze network’s behavior independently of its scale, it is convenient to analyze the normalized frequency tuning curve:
| 21 |
where kn = kd, qh = σh/d, and qk = σk/d represent geometric parameters that characterize the relative excitatory and inhibitory interconnection fields of the recurrent network. By analyzing the effect of these parameters18, we observe that the highest number of sub-regions is attainable when qk shrinks towards ~ 0.125, and qh expands towards ~ 0.8, corresponding to a relative bandwidth β that approaches 1 octave.
Comparative assessments
On the basis of the predictions of the linearized network, the highest resolution RF that can be obtained through the recurrent network is given by the Nyquist sampling limit. By using pixels as units, the maximum bandwidth of the filter to avoid aliasing is π pixel−1. Accordingly, the maximum peak frequency achievable is k0 ≤ π − B which, combined with Equation (19) and (20), leads to the minimum integer distance of the inhibitory connections:
| 22 |
The Nyquist condition puts a constraint on the RF localization in space, not in the spatial frequency domain, thus not posing theoretical limits on the maximum number of sub-regions. Yet, we set a relative bandwidth β = 0.9, which corresponds to a RF with five well-defined sub-regions in the minimum mask size of 11 × 11 pixels, and an optimal choice of the spatial extensions of the initial afferent excitatory, and of the recurrent inhibitory connections equal to three and one pixel, respectively. Hence, for such a minimum RF size, we can calculated the minimum number of interconnections required by the recurrent network (3 × 11 + 2) and compared it with the corresponding number required by an equivalent feed-forward implementation (11 × 11). We then quantified the number of interconnections required by the recurrent network when scaling the size of the RF and compared it with the corresponding number of interconnections required by equivalent strictly feed-forward implementations with three and five sub-regions (see Fig. 4). Simulations of the implemented spiking network of 21 × 21 pixels quite well confirmed the predicted advantages of the recurrent network, with d = 5, a feed-forward kernel width of five pixels, and a recursive kernel width ranging between three and five pixels.
In order to analyze the advantages of the push-pull combination of ON and OFF channels, we computed the capacity of the recurrent network to provide and effective estimate (ϕ) of the actual local phase of the input stimulus ϕs, in terms of accuracy and reliability. To this end, in spatial position index n and at time t, the phase error Δϕ(n, t) = ϕ(n, t) − ϕs(n, t) was directly computed in the complex plane by using the following identity:
| 23 |
where C(n, t) and S(n, t) are the responses of a quadrature pair of neurons with Gabor-like RFs centered in fixed spatial positions (for the sake of convenience, to minimize the border effect, we considered a population of eleven neurons symmetrically distributed with respect to the center of the layer, with the same horizontal position index, and on consecutive rows, i.e., n = {(0, − 5), (0, − 4), ⋯ (0, 0), ⋯ (0, 4), (0, 5)}), whereas Cs(n, t) and Ss(n, t) are the actual quadrature components of the stimulus drifting grating s(n, t) characterized by a spatial frequency ks:
| 24 |
In this way, since the four-quadrant inverse tangent atan2 function returns values in the closed interval [π, π], we avoided the attendant problem of phase unwrapping of the angle difference. The reliability of the phase estimate was given by the associated response energy C2(n, t) + S2(n, t), directly.
Supplementary information
Acknowledgements
We would like to thank the international mobility program of the University of Genoa. This work was supported by the Italian Ministry of Research, under the complementary actions to the NRRP “Fit4MedRob - Fit for Medical Robotics” Grant (PNC0000007) to S.P.S, and by the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation program grant agreement No 724295 (NeuroAgents) to G.I.
Author contributions
G.I. and S.P.S. designed and supervised the research; V.B. performed the research; G.I., S.P.S., and V.B. analyzed the data and interpreted the results; S.P.S. and V.B. wrote the manuscript; G.I. revised the manuscript.
Peer review
Peer review information
Nature Communications thanks VISHAL SAXENA and the other anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Data availability
The data that support the findings of this study have been deposited in the Figshare database under accession code 10.6084/m9.figshare.24236932.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-024-55749-y.
References
- 1.Osswald, M., Ieng, S.-H., Benosman, R. & Indiveri, G. A spiking neural network model of 3D perception for event-based neuromorphic stereo vision systems. Sci. Rep.7, 1–11 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Risi, N., Aimar, A., Donati, E., Solinas, S. & Indiveri, G. A spike-based neuromorphic architecture of stereo vision. Front. Neurorobotics14, 93 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Müggler, E., Bartolozzi, C. & Scaramuzza, D. Fast event-based corner detection. In Proceedings of the British Machine Vis. Conf. (BMVC), 1–11 (2017).
- 4.Jones, J. & Palmer, L. An evaluation of the two-dimensional Gabor filter model of simple receptive fields in cat striate cortex. J. Neurophysiol.58, 1233–1258 (1987). [DOI] [PubMed] [Google Scholar]
- 5.Fleet, D. & Jepson, A. Stability of phase information. IEEE Trans. Pattern Anal. Mach. Intell.15, 1253–1268 (1993). [Google Scholar]
- 6.Ogale, A. & Aloimonos, Y. A roadmap to the integration of early visual modules. Int. J. Comput. Vis.72, 9–25 (2007). [Google Scholar]
- 7.Sabatini, S. P. et al. A compact harmonic code for early vision based on anisotropic frequency channels. Comput. Vis. Image Underst.114, 681 – 699 (2010). [Google Scholar]
- 8.Palmer, L. A. & Davis, T. L. Receptive-field structure in cat striate cortex. J. Neurophysiol.46, 260–276 (1981). [DOI] [PubMed] [Google Scholar]
- 9.Baruzzi, V., Indiveri, G. & Sabatini, S. P. Compact early vision signal analyzers in neuromorphic technology. In Proceedings of the 15th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2020), vol. 4, 530–537 (SciTePress, 2020).
- 10.Baruzzi, V., Indiveri, G. & Sabatini, S. P. Emergence of Gabor-like receptive fields in a recurrent network of mixed-signal silicon neurons. In 2020 IEEE International Symposium on Circuits and Systems (ISCAS), 1–5 (IEEE, 2020).
- 11.Lichtsteiner, P., Posch, C. & Delbruck, T. A 128 × 128 120 dB 15 μs latency asynchronous temporal contrast vision sensor. IEEE J. Solid-State Circuits43, 566–576 (2008).
- 12.Moradi, S., Qiao, N., Stefanini, F. & Indiveri, G. A scalable multicore architecture with heterogeneous memory structures for dynamic neuromorphic asynchronous processors (DYNAPs). IEEE Trans. Biomed. Circuits Syst.12, 106–122 (2018). [DOI] [PubMed] [Google Scholar]
- 13.Indiveri, G. & Sandamirskaya, Y. The importance of space and time for signal processing in neuromorphic agents. IEEE Signal Process. Mag.36, 16–28 (2019). [Google Scholar]
- 14.Chicca, E., Stefanini, F., Bartolozzi, C. & Indiveri, G. Neuromorphic electronic circuits for building autonomous cognitive systems. Proc. IEEE102, 1367–1388 (2014). [Google Scholar]
- 15.Hubel, D. & Wiesel, T. Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex. J. Physiol.160, 106–54 (1962). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.De Valois, R. & De Valois, K.Spatial vision (Oxford University Press, 1988).
- 17.Cortexcontrol: A tool for controlling and executing experiments using neuromorphic hardware platforms that communicate through address-event representation. https://gitlab.com/neuroinf/ctxctl_contrib/-/wikis/ctxctl-executables-and-documentation (2020). Unreleased software, Institute of Neuroinformatics, University of Zurich and ETH Zurich.
- 18.Sabatini, S. P. Recurrent inhibition and clustered connectivity as a basis for Gabor-like receptive fields in the visual cortex. Biol. Cybern.74, 189–202 (1996). [DOI] [PubMed] [Google Scholar]
- 19.Sabatini, S. P., Bisio, G. & Raffo, L. Functional periodic intracortical couplings induced by structured lateral inhibition in a linear cortical network. Neural Comput.9, 525–531 (1997). [DOI] [PubMed] [Google Scholar]
- 20.Graham, N. Spatial-frequency channels in human vision: Detecting edges without edge detectors. In Harris, C. (ed.) Visual coding and adaptability, 215–262 (Psychology Press, New York, NY, 1981).
- 21.Jones, J., Stepnoski, A. & Palmer, L. The two-dimensional spectral structure of simple receptive fields in cat striate cortex. J. Neurosci.58, 1212–1232 (1987). [DOI] [PubMed] [Google Scholar]
- 22.Stimberg, M., Brette, R. & Goodman, D. F. Brian 2, an intuitive and efficient neural simulator. eLife8, e47314 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Milde, M. et al. Teili: A toolbox for building and testing neural algorithms and computational primitives using spiking neurons. https://teili.readthedocs.io/en/latest/index.html (2018). Unreleased software, Institute of Neuroinformatics, University of Zurich and ETH Zurich.
- 24.Raffo, L., Sabatini, S. P., Bo, G. M. & Bisio, G. M. Analog VLSI circuits as physical structures for perception in early visual tasks. IEEE Trans. Neural Netw.9, 1483–1494 (1999). [DOI] [PubMed] [Google Scholar]
- 25.Dollár, P., Appel, R., Belongie, S. & Perona, P. Fast feature pyramids for object detection. IEEE Trans. Pattern Anal. Mach. Intell.36, 1532–1545 (2014). [DOI] [PubMed] [Google Scholar]
- 26.Luan, S., Chen, C., Zhang, B., Han, J. & Liu, J. Gabor convolutional networks. IEEE Trans. Image Process.27, 4357–4366 (2018). [DOI] [PubMed] [Google Scholar]
- 27.Tolhurst, D. & Dean, A. The effects of contrast on the linearity of spatial summation of simple cells in the cat’s striate cortex. Exp. Brain Res.79, 582–588 (1990). [DOI] [PubMed] [Google Scholar]
- 28.Hirsch, J. & Marinez, L. Circuits that build visual cortical receptive fields. Trends Neurosci.29, 30–39 (2006). [DOI] [PubMed] [Google Scholar]
- 29.Jo, A. et al. A sign-inverted receptive field of inhibitory interneurons provides a pathway for ON-OFF interactions in the retina. Nat. Commun.14, 5937 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Haglund, L. Adaptive multidimensional filtering. Tech. Rep., Linköping University, Sweden (1992).
- 31.Orchard, G., Jayawant, A., Cohen, G. & Thakor, N. Converting static image datasets to spiking neuromorphic datasets using saccades. Front. Neurosci.9, 437 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Lagorce, X., Orchard, G., Galluppi, F., Shi, B. E. & Benosman, R. B. HOTS: A hierarchy of event-based time-surfaces for pattern recognition. IEEE Trans. Pattern Anal. Mach. Intell.39, 1346–1359 (2016). [DOI] [PubMed] [Google Scholar]
- 33.Serrano-Gotarredona, T. & Linares-Barranco, B. Poker-DVS and MNIST-DVS. Their history, how they were made, and other details. Front. Neurosci.9, 481 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Hu, Y., Liu, H., Pfeiffer, M. & Delbruck, T. DVS benchmark datasets for object tracking, action recognition, and object recognition. Front. Neurosci.10, 405 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Crespi, B., Cozzi, A., Raffo, L. & Sabatini, S. P. Analog computation for phase-based disparity estimation: continuous and discrete models. Mach. Vis. Appl.11, 83–95 (1998). [Google Scholar]
- 36.Hubel, D. H. & Wiesel, T. N. Uniformity of monkey striate cortex: a parallel relationship between field size, scatter, and magnification factor. J. Comp. Neurol.158, 295–305 (1974). [DOI] [PubMed] [Google Scholar]
- 37.Zendrikov, D., Solinas, S. & Indiveri, G. Brain-inspired methods for achieving robust computation in heterogeneous mixed-signal neuromorphic processing systems. Neuromorphic Comput. Eng.3, 034002 (2023). [Google Scholar]
- 38.Mead, C. Neuromorphic electronic systems. Proc. IEEE78, 1629–36 (1990). [Google Scholar]
- 39.Krüger, N., Lappe, M. & Wörgötter, F. Biologically motivated multi-modal processing of visual primitives. Interdiscip. J. Artif. Intell. Simul. Behav.1, 417–428 (2004). [Google Scholar]
- 40.Ramesh, B. et al. DART: Distribution aware retinal transform for event-based cameras. IEEE Trans. Pattern Anal. Mach. Intell.42, 2767–2780 (2020). [DOI] [PubMed] [Google Scholar]
- 41.Messikommer, N., Gehrig, D., Loquercio, A. & Scaramuzza, D. Event-based asynchronous sparse convolutional networks. In Proceedings of the 16th European Conference on Computer Vision (ECCV), Part VIII, 415–431 (2020).
- 42.Shiba, S., Klose, Y., Aoki, Y. & Gallego, G. Secrets of event-based optical flow, depth and ego-motion estimation by contrast maximization. IEEE Transactions on Pattern Analysis and Machine Intelligence (2024). [DOI] [PubMed]
- 43.Jiao, J. et al. Comparing representations in tracking for event camera-based SLAM. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Nashville, TN, USA, 20-25 June 2021, 1369–1376 (2021).
- 44.Morrone, M. & Burr, D. Feature detection in human vision: a phase-dependent energy model. Proc. R. Soc. Lond. Ser. B235, 221–245 (1988). [DOI] [PubMed] [Google Scholar]
- 45.Gallego, G., Rebecq, H. & Scaramuzza, D. A unifying contrast maximization framework for event cameras, with applications to motion, depth, and optical flow estimation. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Salt Lake City, UT, USA, 18-23 June 2018, 3867–3876 (2018).
- 46.Adelson, E. & Bergen, J. The plenoptic function and the elements of early vision. In Landy, M. S. & Movshon, J. A. (eds.) Computational models of visual processing, 3–20 (MIT Press, Cambridge, MA, 1991).
- 47.Daugman, J. Spatial visual channels in the Fourier plane. Vis. Res.24, 891–910 (1984). [DOI] [PubMed] [Google Scholar]
- 48.Watson, A. The cortex transform: rapid computation of simulated neural images. Comput. Vis., Graph., Image Process.39, 311–327 (1987). [Google Scholar]
- 49.Riesenhuber, M. & Poggio, T. Models of object recognition. Nat. Neurosci.3, 1199–1204 (2000). [DOI] [PubMed] [Google Scholar]
- 50.Carandini, M. et al. Do we know what the early visual system does? J. Neurosci.25, 10577–10597 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Dapello, J. et al. Simulating a primary visual cortex at the front of CNNs improves robustness to image perturbations. In Larochelle, H., Ranzato, M., Hadsell, R., Balcan, M. & Lin, H. (eds.) Advances in Neural Information Processing Systems, vol. 33, 13073–13087 (Curran Associates, Inc., 2020). https://proceedings.neurips.cc/paper_files/paper/2020/file/98b17f068d5d9b7668e19fb8ae470841-Paper.pdf.
- 52.Shi, B. E. Focal plane implementation of 2D steerable and scalable Gabor-type filters. J. VLSI Signal Process.23, 319–334 (1999). [Google Scholar]
- 53.O. Y. H. Cheung, O., Leong, P. H. W., Tsang, E. K. C. & Shi, B. E. Implementation of Gabor-type filters on field programmable gate arrays. In Proc. of the 2005 IEEE International Conference on Field-Programmable Technology, 327–328 (2005).
- 54.Choi, T. Y. W., Merolla, P. A., Arthur, J. V., Boahen, K. A. & Shi, B. E. Neuromorphic implementation of orientation hypercolumns. IEEE Trans. Circuits Syst. I: Regul. Pap.52, 1049–1060 (2005). [Google Scholar]
- 55.Shimonomura, K. & Yagi, T. Neuromorphic vlsi vision system for real-time texture segregation. Neural Netw.21, 1197–1204 (2008). [DOI] [PubMed] [Google Scholar]
- 56.Pauwels, K., Tomasi, M., Diaz Alonso, J., Ros, E. & Van Hulle, M. M. A comparison of FPGA and GPU for real-time phase-based optical flow, stereo, and local image features. IEEE Trans. Comput.61, 999–1012 (2012). [Google Scholar]
- 57.Xiao, Z., Hou, Z., Miao, C. & Wang, J. Using phase information for symmetry detection. Pattern Recognit. Lett.26, 1985–1994 (2005). [Google Scholar]
- 58.Peirce, J. et al. PsychoPy2: Experiments in behavior made easy. Behav. Res. Methods51, 195–203 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.The jAER open source project. SourceForge web-site http://sourceforge.net/projects/jaer/ (2006).
- 60.Rueckauer, B. & Delbruck, T. Evaluation of event-based algorithms for optical flow with ground-truth from inertial measurement sensor. Front. Neurosci.10, 176 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
The data that support the findings of this study have been deposited in the Figshare database under accession code 10.6084/m9.figshare.24236932.