Realizing high power factor and thermoelectric performance in band engineered AgSbTe₂

Abstract

AgSbTe₂ is a promising p-type thermoelectric material operating in the mid-temperature regime. To further enhance its thermoelectric performance, previous research has mainly focused on reducing lattice thermal conductivity by forming ordered nanoscale domains for instance. However, the relatively low power factor is the main limitation affecting the power density of AgSbTe₂-based thermoelectric devices. In this work, we demonstrate that hole-doped AgSbTe₂ with Sn induces the formation of a new impurity band just above the valence band maximum. This approach significantly improves the electrical transport properties, contrary to previous strategies that focused on reducing lattice thermal conductivity. As a result, we achieve a record-high power factor of 27 μWcm⁻¹K⁻² and a peak thermoelectric figure of merit zT of 2.5 at 673 K. This exceptional performance is attributed to an increased hole concentration resulting from the formation of the impurity band and a lower formation energy of the defect complexes ($V_{Ag}^{1-}$ + ${Sn}_{Sb}^{1-}$). Besides, the doped materials exhibit a significantly improved Seebeck coefficient by inhibiting bipolar conductivity and preventing the formation of n-type Ag₂Te. Additionally, the optimized AgSbTe₂ is used to fabricate a unicouple thermoelectric device that achieves energy conversion efficiencies of up to 12.1% and a high power density of 1.13 Wcm⁻². This study provides critical insights and guidance for optimizing the performance of p-type AgSbTe₂ in thermoelectric applications.

Sn doping enables a breakthrough in p-type AgSbTe₂ for thermoelectric applications, achieving a zT of 2.5 and 12.1% device efficiency. The authors reveal an impurity band mechanism, offering a strategy for AgSbTe₂ optimization.

Introduction

Thermoelectric (TE) devices provide a simple solution not only for power generation from waste heat but also for precise temperature control and localized cooling^1–4. TE-based products have been widely utilized in consumer electronics, communications, medical, and automotive fields. The performance of a TE material is usually characterized by a dimensionless figure of merit, zT = (S²σ/κ)T, where T is the absolute temperature, S is the Seebeck coefficient, σ is the electrical conductivity, and κ is the thermal conductivity⁵.

The optimization of the performance of TE materials can be approached through two primary strategies; the reduction of the lattice thermal conductivity (κ_L) and the enhancement of the TE power factor (PF). These properties are interconnected, as any modification aimed at optimizing one of these parameters will inevitably influence the other.

AgSbTe₂ is a promising p-type TE material, particularly suitable for applications in the medium temperature range (473–673 K)^6–11. This material exhibits inherently low thermal conductivity, attributable to its spontaneously formed micro/nanostructures and pronounced bond anharmonicity. Additionally, AgSbTe₂ demonstrates a high Seebeck coefficient, which is a consequence of its flat valence band with substantial degeneracy.

Compositional engineering has been widely used as an effective strategy to modulate the AgSbTe₂ band structure and carrier concentration, thereby enhancing TE performance^12–19. For instance, heavy doping of AgSbTe₂ with Se/S effectively increases the hole concentration, leading to a significant improvement in the PF by facilitating the participation of multiple bands in charge transport¹⁹. Numerous studies have reported that the formation of nanoscale superstructures, triggered by enhanced cation ordering through doping with elements such as Cd²⁰, Hg²¹, Yb²², or Ag vacancies²³, results in remarkable increases in zT up to 2.6. This enhancement is primarily due to the notable reduction in κ_L to as low as 0.2 W m⁻¹ K⁻¹²⁰. However, despite such advances, the PF achieved in these studies remains below 20 μWcm⁻¹K⁻², which is significantly lower than that of commercial Bi₂Te₃ materials. While a high zT value is crucial for achieving high TE device conversion efficiency, the relatively low PF continues to limit the overall output power of AgSbTe₂-based TE devices. Thus, further optimization is necessary to simultaneously enhance both zT and PF for practical applications.

Herein, we present a strategy to enhance the electrical transport properties of p-type AgSbTe₂ through the incorporation of Sn as an effective dopant. Sn doping is shown to significantly stabilize the AgSbTe₂ matrix by inhibiting the formation of n-type Ag₂Te and introducing an in-gap band slightly above the valence band maximum (VBM). We demonstrate that this compositional engineering strategy result in exceptionally high PF and zT values. Besides, using this optimized material, a unicouple TE device is fabricated and tested to validate the real application potential of this material.

Results and discussion

Polycrystalline AgSbTe₂ was synthesized via a multi-step process involving the initial melting of a stoichiometric mixture comprising elemental Ag, Sb, and Te. The resulting ingots were subsequently ground and re-consolidated utilizing spark plasma sintering, as detailed in the supplementary information (SI). At ambient temperature, AgSbTe₂ commonly exhibits a rock salt crystal structure, characterized by the random distribution of Ag and Sb ions within the cation sublattice, while Te occupies the anion sites. However, the phase diagram of Sb₂Te₃-Ag₂Te indicates that stoichiometric AgSbTe₂ undergoes thermodynamic instability at temperatures below 633 K, leading to its decomposition into Ag₂Te and Sb₂Te₃ phases^24,25. Detailed investigations into the phase diagram have established that the single stable ternary phase encompasses a broad compositional range (Ag_1-xSbTe₂, x = 0.06–0.28). Consequently, the precise structural configuration of AgSbTe₂ and its stability remain ambiguous. To investigate the crystalline characteristics of the synthesized material, X-ray diffraction (XRD) analysis was conducted. The obtained XRD patterns revealed a predominant face-centered cubic (fcc) crystal structure consistent with AgSbTe₂. Furthermore, the presence of minor weak diffraction peaks was identified, corresponding to the monoclinic phase of Ag₂Te, which confirms the existence of both phases within the synthesized material (Fig. S1). This observation aligns with previous studies, which have consistently reported the presence of precipitated Ag₂Te phase and other impurities coexisting within the AgSbTe₂ matrix, regardless of the synthesis methodologies employed^{13,15,17,19,20,23}.

Given the semiconductor nature of Ag₂Te, characterized by a n-type conductivity, and its structural phase transition occurring around 425 K, even minimal concentrations of Ag₂Te can adversely impact the electrical transport properties of p-type AgSbTe₂. Therefore, suppressing the formation of Ag₂Te impurities becomes critical for optimizing the TE performance of AgSbTe₂.

The inherent instability of pristine AgSbTe₂ is primarily attributed to the presence of antibonding states near the Fermi level, as proved by crystal orbital Hamiltonian population analysis²⁶. The antibonding states arise from the strong hybridization between Sb-5s and Te-5p orbitals, leading to the Te-5p antibonding states shift towards the valence band frontier. From an electronic structure perspective, such antibonding contributions constitute the primary states at the top of the valence band, thereby stimulating intrinsic instability through the formation of charge-compensated defect complexes. Consequently, AgSbTe₂ undergoes spontaneous phase decomposition, forming Ag₂Te and Sb₂Te₃ phases for instance. To suppress this instability, p-type doping emerges as an effective strategy to reduce the electron density associated with these antibonding states, thereby potentially enhancing the stability of the AgSbTe₂ matrix. To this end, our study aims at stabilizing the AgSbTe₂ matrix by incorporating trace amounts of Sn into the cationic sublattice (Fig. 1a). The preference for Sn²⁺ to substitute Sb³⁺ is based on its possession of one fewer valence electron, which facilitates the generation of additional holes, thereby contributing to the stabilization of the AgSbTe₂ structure.

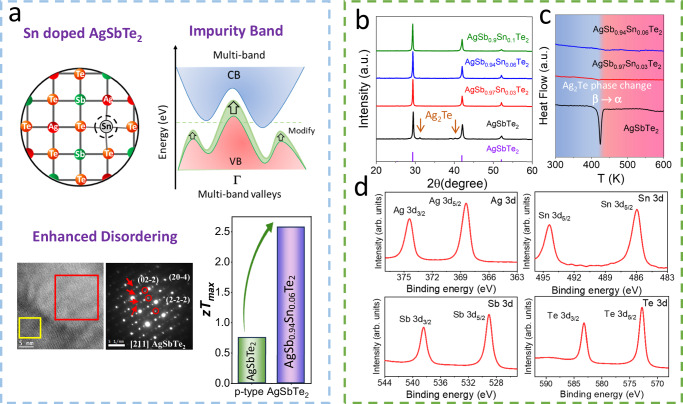
Fig. 1. TE performance and characterizations on Sn doped AgSbTe₂ samples.

a Schematic illustration of improved TE performance in Sn doped AgSbTe₂. b XRD patterns of as-synthesized AgSb_1-xSn_xTe₂ pellets. c DSC curves of AgSbTe₂ and Sn-doped AgSbTe₂. d High-resolution XPS spectra of AgSb_0.94Sn_0.06Te₂ pellet.

XRD analysis confirmed that the Sn-doped material exhibited the cubic AgSbTe₂ phase, with no detectable presence of Ag₂Te (Fig. 1b). Ag₂Te absence was corroborated by differential scanning calorimetry (DSC) analysis, which indicated the suppression of the endothermic peak at 423 K associated with the β-Ag₂Te to α-Ag₂Te phase transition (Fig. 1c). High-resolution X-ray photoelectron spectroscopy (XPS) analysis, as depicted in Fig. 1d, shows only one Sn 3 d doublet at 486.1 eV (3d_5/2). This is associated with a bivalent Sn state^27,28, further confirming the successful integration of Sn²⁺ into the AgSbTe₂ system. Overall, we observed the incorporation of Sn to effectively enhance the thermodynamic stability of AgSbTe₂ by suppressing the formation of Ag₂Te secondary phases.

To comprehensively understand the impact of Sn incorporation on the AgSbTe₂ structure, the electronic band structure (Fig. 2a, b) was analyzed and the formation energies of multiple defects (Fig. 2c, d) were determined using density functional theory (DFT) calculations. The computational analysis of the electronic band structure of pristine AgSbTe₂, as depicted in Fig. 2a, uncovers a semimetallic character with a pseudogap arising from the interplay between dispersive conduction bands and nearly flat valence bands, that aligns with previous research findings^6,9,21. It is worth noting that previous optical reflectance assessments revealed a distinct band gap ranging from 0.30 to 0.35 eV^14,19,29, suggesting a semiconducting behavior. Conversely, DFT calculations and electrical conductivity analyzes portray either a semi-metallic or metallic character^6,9,11,20. This discrepancy may arise from the structural disorder of Ag and Sb atoms. DFT calculations typically assume ordered occupancy to establish the supercell, which can result in deviations from the actual disordered structure. Near the Fermi level, we observe the presence of light electron pockets and heavy hole pockets (predominantly formed by Te-5p orbitals), which suggests that the electrical conductivity in AgSbTe₂ primarily stems from high mobility electrons and low mobility holes. Furthermore, the flat VBM and degenerate valence band structure indicate a larger positive Seebeck coefficient for pristine AgSbTe₂ compared to other TE chalcogenides like PbTe^30,31 and SnTe^32,33.

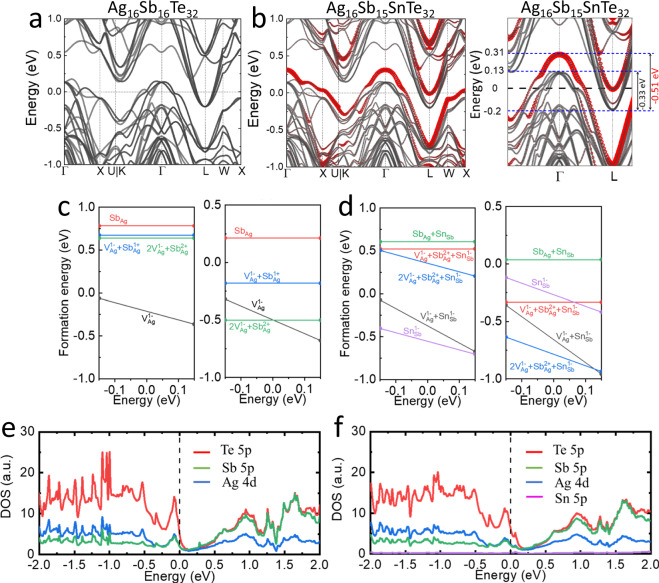
Fig. 2. Theoretical simulations on band structure, defect formation energy, and density of states.

DFT-calculated band structure of (a) Ag₁₆Sb₁₆Te₃₂ and (b) Ag₁₆Sb₁₅SnTe₃₂. Defect formation energies of individual defects and complex defects with respect to the Fermi level: (c) Ag₁₆Sb₁₆Te₃₂ and (d) Ag₁₆Sb₁₅SnTe₃₂. DOS of (e) Ag₁₆Sb₁₆Te₃₂ and (f) Ag₁₆Sb₁₅SnTe₃₂ for the Ag, Sb, and Te atoms. Zero energy corresponds to the Fermi level.

Upon doping with Sn, notable changes occur in the band structure of AgSbTe₂. The VBM undergoes flattening at the Γ point, accompanied by significant band splitting, pointing at an enhancement of the Seebeck coefficient. Specifically, a new impurity band, highlighted in red color, emerges above the VBM due to the substitution of Sn²⁺ for Sb³⁺ (Fig. 2b). This impurity band is partially occupied, with the Fermi energy falling within its energy range. Consequently, thermal carrier generation triggers from the edge of the impurity band rather than the valence band edge. This mechanism results in additional holes in the valence band, as experimentally obtained from Hall measurements (Table S1). Similarly, dopants that introduce in-gap impurity levels, thereby enhancing carrier density and electrical transport properties, have been identified in p‑type Cr₂Ge₂Te₆³⁴ and Cu_1-xAg_xGaTe₂^35,36 compounds for instance.

The negative formation energy of Ag vacancies ($V_{Ag}^{1-}$) suggests their spontaneous generation in undoped AgSbTe₂ (Fig. 2c). $V_{Ag}^{1-}$ acts as an acceptor providing holes. However, the number of carriers is limited due to the self-compensating effect (compensate charge distortion by creating donor defects, such as Sb at Ag site, ${Sb}_{Ag}^{1+}$) that maintains charge neutrality in the system, resulting in a low net hole concentration in AgSbTe₂. In the case of AgSb_1-xSn_xTe₂ (Fig. 2d), Sn doping further decreases the $V_{Ag}^{1-}$ formation energy through the generation of the complex defect ($V_{Ag}^{1-}$ + ${Sn}_{Sb}^{1-}$), which has a much lower formation energy than other defects. The preferential formation of the complex defects, controlled by the amount of Sn introduced, not only introduces a higher concentration of holes but also enhances the stability of AgSbTe₂. This is supported by experimental measurements of charge carrier density over 5–200 K temperature range, obtained using the four-probe method (Figs. S2 and S3). The partial density of states (DOS), as illustrated in Fig. 2e, f, provides additional validation regarding the efficacy of Sn incorporation in decreasing the contribution of the Te-5p states within the AgSbTe₂ system, thereby improving its inherent instability. Overall, Sn doping triggers a synergistic enhancement in hole concentration by modulating the band structure and altering the defect formation energy while at the same time playing a critical role in stabilizing the AgSbTe₂ structure.

Due to the random occupation of Ag and Sb ions within the cation sublattice of AgSbTe₂, we subsequently investigated the effect of Sn doping on the resulting atomic disorder. Atomic disorder represents a great challenge across several TE materials. The exploration of how atomic disorder affects electronic transport traces back to the 1930s^37–41, with initial observations made in Si-Ge and metal alloys. Within solid solutions, defects resulting from atomic disorder serve as scattering centers of charge carriers, consequently limiting their mean free path. Simultaneously, this disorder induces fluctuations in local potential energy, leading to additional scattering of charge carriers and a reduction in their mobility.

Cation doping has been frequently used to enhance Ag/Sb ordering, resulting in the appearance of cation-ordered nanoscale domains (2–4 nm) within polycrystalline AgSbTe₂ matrices^20–23. These nanodomains play a critical role in reducing lattice thermal conductivity. Moreover, the improved cationic ordering serves to disperse disorder-induced localized electronic states, thereby triggering an enhancement in electrical transport properties. Our results show that Sn doping induces a more chaotic lattice structure. High-resolution high-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) micrograph confirm the presence of a face-centered cubic phase (space group: Fm-3m) with a lattice parameter of a = 0.608 nm for the Sn-doped AgSbTe₂ samples (Fig. 3a). Notably, multiple double-diffraction spots observed in the power spectrum of AgSb_0.94Sn_0.06Te₂, circled in red and green, arise from structure disruption within the AgSbTe₂ structure. The composite map obtained from inverse fast Fourier transform (FFT) images in Fig. 3b affirms that the double-diffraction spots are not associated with precipitate-like structures but are generated by the disarrayed lattice. The individual FFT images obtained from the green-circled and red-circled diffraction spots unambiguously reveal the presence of a disrupted structure, particularly in the region circled in red.

Fig. 3. Microstructure characterization on AgSb_0.94Sn_0.06Te₂ sample.

a Atomic resolution HAADF-STEM image obtained from AgSb_0.94Sn_0.06Te₂ sample and its corresponding FFT, the presence of double-diffraction spots are circled in red and green. b Inverse composite and individual FFT images obtained from the red and green circled diffraction spots from panel a. c Schematic illustration of Sn doping induced short-range Ag/Sb ordering in AgSbTe₂. d HRTEM micrograph of a AgSb_0.94Sn_0.06Te₂ grain visualized along its [211] zone axis and (e) corresponding selected area diffraction pattern. HRTEM images and corresponding FFTs of the (f) red and (g) green squared regions in (d).

The disrupted lattice structure arises from multiple short-range Ag/Sb cation-ordering domains within the matrix of Sn-doped AgSbTe₂ (Fig. 3c). In the selected area diffraction pattern derived from the HRTEM micrograph of a AgSb_0.94Sn_0.06Te₂ grain (Fig. 3d), weaker diffraction spots observed in Fig. 3e (corresponding to the AgSbTe₂ phase, indicated by red arrows) are located halfway between the fundamental spots in the selected area electron diffraction pattern (SADP), indicating a doubling of the unit cell caused by cation ordered domains in Sn-doped AgSbTe₂, consistent with previous works^20,21,23. Some reflections exhibit double diffractions (marked with red circles in Fig. 3e), suggesting that the short-range cation ordering domains in the sample may not present uniformly. Micrographs in Fig. 3f, g, which show high-resolution TEM (HRTEM) images of the red and green squared regions from Fig. 3d, along with their corresponding FFTs, further display visible double diffractions. These observations, reinforce the conclusion that the structure of Sn-doped AgSbTe₂ is more disrupted compared to undoped AgSbTe₂ (Fig. S4).

Atomic disorder typically plays a crucial role in inducing additional scattering of charge carriers, thereby reducing their mobility^42–44. The enhance Ag/Sb atomic ordering by Sn doping should decrease scattering and potentially increase mobility. In pristine AgSbTe₂, the carrier concentration is relatively low, around 1.2 × 10¹⁸cm⁻³, while the hole mobility is high, ~288 cm²/Vs at room temperature. However, upon Sn doping, the carrier concentration increases to ~3.5 × 10¹⁹cm⁻³. This substantial increase in carrier concentration is accompanied by a moderate decrease in mobility, with room-temperature carrier mobility dropping to ~31 cm²/Vs (Table S1). While Sn doping improves cation ordering, the concurrent rise in carrier concentration and the introduction of complex defects generate competing scattering mechanisms that more than offset the potential mobility gains from reduced disorder.

For pristine AgSbTe₂, the electrical conductivity (σ) first decreases and then increases with temperature (Fig. 4a). The increase is attributed to the dominance of bipolar contribution, consistent with earlier findings^7,14,18,20. The bipolar effect starts to be noticed at ∼460 K in the undoped AgSbTe₂, slightly surpassing that of the Bi₂Te₃ system (350–400 K), consistently with the small band gap of 0.15 eV in Bi₂Te₃⁴⁵. The bipolar phenomenon also degrades the Seebeck coefficients of pristine AgSbTe₂ in the high-temperature range measured, as minority carriers (electrons) thermally excited across the band gap counteract the positive Seebeck coefficients associated with free hole diffusion. The Seebeck coefficients of pristine AgSbTe₂ increase from 270 µV/K at 300 K to 389 µV/K at 465 K. The high Seebeck coefficient observed in pristine AgSbTe₂ arises from the degenerate valence bands and the existence of a mobility edge proximal to the Fermi level, inducing distortions in the electronic density of states and resulting in an enhanced effective mass (m*). The high Seebeck coefficients measured and the evident bipolar phenomena at high-temperature evidence the semiconductor character of AgSbTe₂.

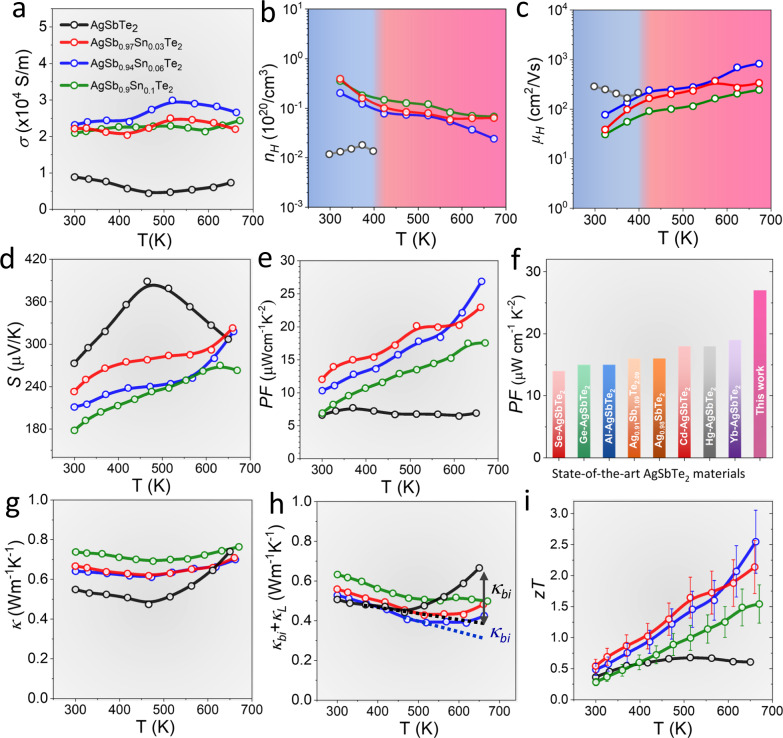
Fig. 4. Transport properties of AgSb_0.94Sn_0.06Te₂ sample.

Temperature-dependent TE properties of AgSb_1-xSn_xTe₂. a Electric conductivity, σ. b Carrier concentration, n_H. c Mobility, µ_H. d Seebeck coefficient, S. e Power factors, PF. f Maximum PF comparison with state-of-art AgSbTe₂ materials^{6,13,14,18,20–23}. g Thermal conductivity, κ. h Combination of bipolar and lattice contribution to the thermal conductivity. i TE figure of merit, zT, the uncertainty of zT measurement is ~20% as indicated by error bar.

Upon the substitution of Sn²⁺ at the Sb³⁺ site, the electrical conductivity shows a significant enhancement over the whole temperature range, with values escalating from 89 S/cm for pristine AgSbTe₂ to 231 S/cm for AgSb_0.94Sn_0.06Te₂ at room temperature. Sn doping in AgSbTe₂ introduces holes, resulting in an increase in carrier concentration, as demonstrated in Fig. 4b, based on measurements using the van der Pauw method over the temperature range of 300–670 K. Consistent trends are observed in both low-temperature (Figs. S2 and S3) and high-temperature (Fig. 4b, c) carrier concentration measurements, confirming that Sn incorporation effectively enhances hole concentration. However, the carrier concentrations obtained in the low-temperature range are higher than those measured at high temperatures. This discrepancy is attributed to differences in the magnetic field strength and data processing methodologies employed in the respective measurement techniques.

Furthermore, the effect of Sn doping on carrier concentration is non-linear across different doping levels. At a 3% Sn doping level, the substitution efficiently introduces hole carriers and predominantly forms simple Sn-related defects, resulting in a substantial increase in carrier concentration. However, at 6% Sn doping, the emergence of compensating defect complexes, such as (${2V}_{Ag}^{1-}$ + ${Sb}_{Ag}^{2+}$), (${Sb}_{Ag}^{2+}$ + ${Sn}_{Sb}^{1-}$), (${2V}_{Ag}^{1-}$ + ${Sb}_{Ag}^{2+}+{Sn}_{Sb}^{1-}$), and enhanced impurity interactions lead to increased carrier scattering and a decrease in net carrier concentration. A higher doping level of 10% Sn could introduce significant local structural distortions in the AgSbTe₂ matrix, potentially altering the band structure, e.g., shifts in the positions of the conduction band minimum or valence band maximum or even induce changes in the DOS near the Fermi level, that could impact both carrier concentration and mobility. Correspondingly, the carrier mobility presents a reverse trend, indicating that mobility is strongly influenced by carrier-carrier scattering and impurity interactions present in the material. The optimal doping concentration, yielding the highest σ from 300 K to 673 K, was 6 mol% Sn doping, as depicted in Fig. 4a. In addition, elevated temperatures can cause thermal excitation of electrons into the conduction band and carrier trapping by localized states, leading to a reduction in the net carrier concentration in Sn-doped AgSbTe₂ with increasing temperature.

The introduction of Sn resulted in a reduction in the Seebeck coefficient due to the increased charge carrier concentration. However, the doped samples still demonstrated decent Seebeck coefficients values, exceeding 170 µV/K across the entire temperature range, as shown in Fig. 4d. Although the upward trend of the Seebeck coefficient in the Sn-doped samples was moderated, a mild increase was still observed beyond 460 K, attributed to a significant reduction in the bipolar effect. While bipolar conduction was not entirely suppressed, it was substantially reduced compared to pristine AgSbTe₂. The sustained Seebeck coefficients stem primarily from the significant decrease in electrons and the alteration in band structure upon Sn doping, characterized by band flattening and splitting, thereby inducing an increased m* conducive to sustaining relatively high Seebeck coefficients.

This combination of substantial enhancement of electrical conductivities and sustained high Seebeck coefficients in AgSb_0.94Sn_0.06Te₂ resulted in greatly increased PF compared to pristine AgSbTe₂ throughout the entire temperature range (Fig. 4e). The peak PF for AgSb_0.94Sn_0.06Te₂ was observed at 673 K, reaching 27 μWcm⁻¹K⁻², surpassing the values reported in Cu_2-xSe^46–48, PbTe^30,49, SnTe^33,50, etc., and to the best of our knowledge, being the highest PF reported for AgSbTe₂, as illustrated in Fig. 4f. The PF attained is comparable to that of commercial Bi₂Te₃-based materials characterized by higher thermal conductivities^51,52, denoting commendable powder density and conversion efficiency in TE generators.

The total thermal conductivity (κ) of pristine AgSbTe₂ initially decreases with increasing temperature, dropping from 0.55 W/m·K at 300 K to 0.48 W/m·K around 450 K (Fig. 4g), and then increased. This rise in thermal conductivity is attributed to the contribution of bipolar thermal conductivity (κ_bi), as illustrated in Figs. 4h and S5. The inherently low thermal conductivity of pure AgSbTe₂ aligns with previous studies that identify it as exhibiting glass-like ultralow intrinsic thermal conductivity, attributed to the strong anharmonicity in the defects, stacking faults, and spontaneously formed nanoscale impurity phase^6,7,15,18,20. In contrast, Sn-doped AgSbTe₂ demonstrates higher κ values compared to the pristine material. This increase is primarily due to enhanced electronic thermal conductivity (κ_e) and a slight elevation in κ_L. The increase in κ_L can be attributed to the elimination of the nanostructed Ag₂Te impurity phase upon Sn doping, which reduces phonon scattering centers and consequently allows for more efficient heat transport through the lattice. While previous studies on Hg²¹, Yb²², and Cd²⁰ doping in AgSbTe₂ have reported decreases in lattice thermal conductivity, our study observes an increase in κ_L suggesting that the specific nature of the doping element and its interactions within the matrix play a critical role in determining the overall thermal behavior.

Besides, upon partial substitution of Sn for Sb in AgSbTe₂, although complete suppression of the bipolar effect was not achieved, a significant reduction in the bipolar thermal conductivity κ_bi was observed. Sn doping in AgSbTe₂ reduces the bipolar effect by increasing the ratio of majority carriers (n_h) to minority carriers (n_e). This occurs through the substitution of Sb³⁺ with Sn²⁺, which introduces additional holes, increases the concentration of $V_{Ag}^{1-}$ that acts as acceptors, and reduces ${Sb}_{Ag}^{2+}$ antisite defects that would otherwise generate electrons, resulting in a higher n_h/n_e ratio and reduced bipolar conduction. The decrease in κ_bi, from 0.25 W/mK in pristine AgSbTe₂ to 0.07 W/mK in Sn-doped AgSbTe₂ at 660 K (Fig. S5), underscores the role of increased n_h/n_e in reducing the detrimental bipolar contribution. With increasing temperature, the minimum κ_L of the AgSb_0.94Sn_0.06Te₂ sample reaches approximately 0.41 W/mK at around 470 K, higher than κ_L reported in enhanced atomic ordering AgSbTe₂ works^20–22. It is worth noting that one previous work⁵³ also explored Sn doping in AgSbTe₂, but key differences in carrier density, bipolar conduction, and impurity phases were observed compared to our work and recent studies^{13,14,17,19,20}, which significantly impact transport properties, leading to distinct TE performance.

The enhanced carrier concentration and sustained high Seebeck coefficients in AgSb_0.94Sn_0.06Te₂ yielded exceptional zT values, reaching a peak of 2.5 and an average zT of 1.32 over the 300–673 K range (Fig. 4i). A zT of ~2.5 is among one of the highest values compared with the existing state-of-the-art TE materials (Figs. S6 and S7), highlighting the potential of AgSbTe₂ for high-efficiency TE applications in mid-temperature range. Furthermore, the reproducibility of these high zT values is confirmed through the analysis of samples from various synthesis batches (Fig. S8) and their performance across multiple heating-cooling cycles (Fig. S9).

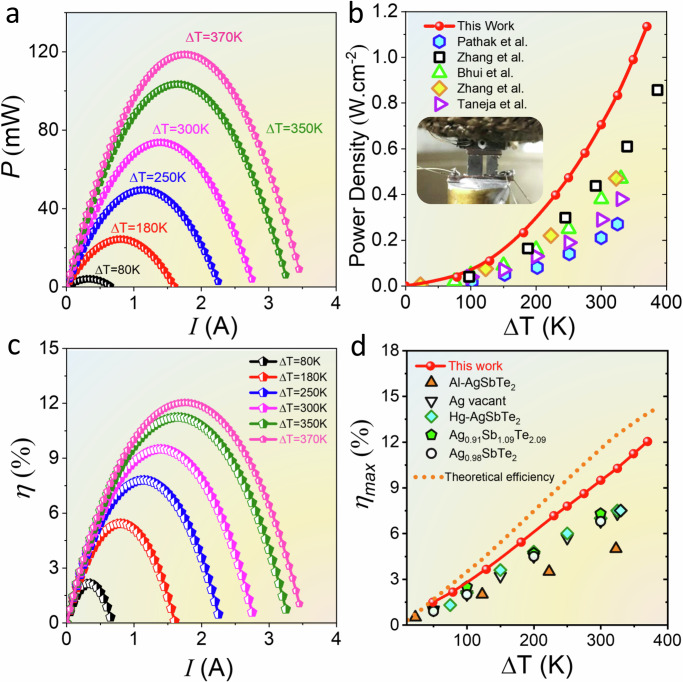
Motivated by the noteworthy zT and PF, we proceeded to fabricate a unicouple TE device comprising a p-type AgSb_0.94Sn_0.06Te₂ leg paired with an n-type skutterudite Yb_0.25Co_3.75Fe_0.25Sb₁₂ leg⁵⁴ (Fig. S11). With a fixed cold-side temperature at 300 K, the open-circuit voltage (V_oc) exhibited a linear increase with ∆T (Fig. S12), indicating low contact resistance in the fabricated device, as confirmed by automated scanning four-probe measurements (Fig. S13). The results demonstrate an ultra-low ohmic contact resistance (<1 μΩ·cm²) between the Cu electrode and the TE legs. Notably, the maximum output power (P_out) escalated from 4.5 mW at ∆T = 80 K to 103 mW at ∆T = 370 K as depicted in Fig. 5a, culminating in a calculated power density of 1.13 W/cm² (Figs. 5b and S14). Besides, an energy conversion efficiency (η) of 12.1% was derived at a temperature differential of ∆T = 370 K (Fig. 5c, d). The device performance was further validated by simulations of internal resistance, V_oc, P_out, Q_in, and η, based on the dimensions of the p/n legs and their transport properties. The simulation results (Fig. S15) demonstrated slightly higher, yet comparable values for V_oc, P_max, η_max, and power density when compared to experimental data. These minor discrepancies are associated with deviations in input parameters or boundary conditions applied in the simulation, supporting the reliability and consistency of the experimental measurements. In addition, thermal treatment and cyclic performance assessments revealed a significant enhancement in the thermal stability of the Sn-doped materials and devices (Fig. S16). Future studies could focus on evaluating the material’s stability over extended periods, which is crucial for the practical application and reliability of TE devices.

Fig. 5. Device performance.

a Current dependent output power of an AgSb_0.94Sn_0.06Te_{2 /} Yb_0.25Co_3.75Fe_0.25Sb₁₂ unicouple module. b Maximum power density as a function of ΔT. c Current-dependent conversion efficiency (η) of the unicouple module. d Comparison of the maximum conversion efficiency (η_max) as a function of ΔT of the AgSb_0.94Sn_0.06Te₂ unicouple device with that of other state-of-art AgSbTe₂ devices^{2,13,14,19,21,23}.

To summarize, the charge carrier density of polycrystalline AgSbTe₂ was optimized by doping with Sn. The substitution of Sb with Sn facilitated the formation of an impurity band above the VBM. Additionally, the incorporation of Sn suppressed bipolar effects and inhibited the formation of n-type Ag₂Te, leading to relatively higher Seebeck coefficients. Consequently, AgSb_0.94Sn_0.06Te₂ alloys exhibited high power factors of up to 27 μWcm⁻¹K^-2. Besides, Sn doping also induced a more chaotic lattice structure characterized by a minimum lattice thermal conductivity of 0.41 W m⁻¹ K⁻¹. Although this enhanced disruption did not effectively reduce the lattice thermal conductivity of AgSbTe₂, the excellent PF compensated for this limitation. Overall, AgSb_0.94Sn_0.06Te₂ achieved a peak zT of 2.5 at 673 K and a zT_ave of 1.32 from 300 to 673 K, outperforming most current state-of-the-art p-type materials in the mid-temperature range. We further engineered a unicouple module with minimized contact resistance, achieving an energy conversion efficiency of up to 12.1% and a power density of up to 1.13 W/cm² at ΔT of 370 K. Overall, this work provided cutting-edge insights into engineering high-performance medium-temperature TE materials and devices for efficient waste heat recovery.

Methods

Materials and synthesis

Silver shots (Ag, 99.9% Thermo Scientific), antimony shots (Sb, Alfa Aesar 99.9999%), tin powder (Sn, Sigma Aldrich 99.99%), and tellurium lumps (Te, Alfa Aesar 99.9 %) were used as received, without further purification. AgSb_1-xSn_xTe₂ samples were produced by mixing high-purity Ag, Sb, Te, and Sn within quartz tubes. The tubes were sealed under vacuum (~10⁻⁴Pa) and slowly heated from room temperature to 1173 K over 6 h, kept at 1173 K for another 6 h, and then slowly cooled down to room temperature for 10 h. The obtained bulk ingots were pulverized to powder and re-consolidated by spark plasma sintering (SPS, Dr. Sinter-625V, Fuji, Japan) at 703 K under a pressure of 40 MPa for 2 min. All consolidated cylinders presented relative densities above 95% of the theoretical value.

Materials characterization

The electrical conductivity and Seebeck coefficient were measured simultaneously (ULVAC-RIKO ZEM-3 system, Japan) using 2 × 2 × 12 mm bars. We estimate an error of ca. 5% in the measurement of both electrical conductivity and the Seebeck coefficient. Temperature-dependent thermal properties were determined by measuring thermal diffusivity with a laser flash system (LFA-467 HT HyperFlash®, Germany). Specific heat was measured on a differential scanning calorimeter (Netzsch DSC 214, Germany, heating/cooling rate of 15 K/min). The thermal conductivity, κ_total, was calculated from κ_total = D × ρ × Cp, where D, ρ, and Cp are thermal diffusivity, density, and specific heat, respectively. The density is measured using the Archimedes method. The estimated error in thermal conductivity measurement is estimated at about ±4%. Electronic thermal conductivity (κ_e) of AgSb_1-xSn_xTe₂ is calculated from Wiedemann-Franz law, κ_e = LσT, where L and σ, are Lorenz number and electrical conductivity. The Lorenz number is calculated based on the measured Seebeck coefficient: L = [1.5 + exp (-|S | /(116 μVK⁻¹))] 10⁻⁸ WΩ K⁻²_, proposed by G. J. Snyder et al⁵⁵. The results presented here are an average of the results obtained after measuring 3 pellets produced under identical conditions. Measurements between different samples have standard deviations below 10%.

X-ray diffraction analysis was carried out on a PANalytical Empyrean with Cu-K_α radiation in 2θ angle range of 10–60°. High temperature (>300 K) charger carrier density and mobility were characterized by a LakeShore Hall Effect System (8400 Series HMS, LakeShore), using four-contact van der Pauw sample configurations with magnetic field of 0.9 T. Low temperature hall resistivity, ρ_xy were performed using a standard four-probe technique in a physical properties measurement system (PPMS, Quantum Design) from 2.2 to 250 K up to 9 T. The field dependences of ρ_xy is obtained using ${\rho }_{xy}=\left[{\rho }_{xy}\left(+{\mu }_{o}H\right)-{\rho }_{xy}\left(-{\mu }_{o}H\right)\right]/2.$ Both samples of pristine and doped-AgSbTe₂ exhibit non-linear field dependence. Since ${\rho }_{xy}\left(H>6\mathrm{T}\right)$ exhibiting linear field dependence, single band model is used and the carrier density n is estimated via $n=\left(\frac{1}{e{R}_{\mathrm{H}}}\right)$, where e is the electric charge and R_H is the Hall coefficient that extracted from the slope of the ${\rho }_{xy}\left(H\right)$. High-resolution transmission electron microscopy (HRTEM) was performed using an FEI Titan G2. TEM samples were prepared by a focused-ion beam (FIB). A field emission scanning electron microscopy (FESEM, FEI Verios G4) operated at 5.0 kV was used to determine the microstructure morphology. Energy-dispersive X-ray spectroscopy (EDX) on an Oxford Aztec spectrometer attached to FEI Verios G4 SEM at 20.0 kV was used to measure the material composition. X-ray photoelectron spectroscopy (XPS) experiments were performed using a Physical Electronics VersaProbe III instrument equipped with a monochromatic Al kα X-ray source (hν = 1,486.6 eV) and a concentric hemispherical analyzer. Charge neutralization was performed using both low-energy electrons (<5 eV) and argon ions. Peaks were charge referenced to CH_x band in the carbon 1 s spectra at 284.8 eV. Measurements were made at a take-off angle of 50° with respect to the sample surface plane. Quantification was done using instrumental relative sensitivity factors that account for the X-ray cross-section and inelastic mean free path of the electrons. The analyzed area was ~200 µm in diameter.

Density functional theory (DFT) calculations

The projector augmented wave (PAW) method⁵⁶ as implemented in Vienna Ab-initio Simulation Package (VASP)⁵⁷ was adopted to perform the first-principles calculations. The exchange-correlation energy was calculated by using the revised generalized gradient approximation (GGA) Perdew-Burke-Ernzerhof (PBEsol)^58,59. The plane-wave cutoff energy was set to 500 eV for all calculations. A Monkhorst-Pack Γ-centered 11 × 11 × 11 k mesh is used for Brillouin zone sampling. The well-studied $Fd\overline{3}m$ AgSbTe₂ conventional cell (64 atoms) was selected as the initial structure. The internal position of atoms was fully relaxed until the residual force between atoms was smaller than 0.01 eV Å⁻¹ and the total energy reached the convergency 10⁻⁸eV. The electronic band structure and density of states were calculated based on the fully relaxed structure.

Defect calculations

The formation energy E(α,q, f) of a defect α with q charge is defined as:

$$E\left(\alpha ,q,f\right)=E_{\mathrm{defect}}-E_{\mathrm{perfect}}+{\sum }_i{\eta }_i{\mu }_i+q\left(f+E_{\mathrm{VBM}}+\mathrm{\Delta }\right)$$ 1

where E_defect and E_perfect are the total energy of AgSbTe₂ and AgSb_1-xSn_xTe₂ with and without charged defects, respectively. n_i refers to the number of α atoms added to or removed from the perfect cell. μ_i is the chemical potential of atom α, which can be obtained by the formation of AgSbTe₂:

$${\mu }_{Ag}+{\mu }_{Sb}+2{\mu }_{Te}=E_f\left(AgSbT{e}_2\right)$$ 2

where E_f(AgSbTe₂) is the formation of AgSbTe₂. The second impurity Ag₂Te and SnTe should be avoided:

$$2{\mu }_{Ag}+{\mu }_{Te}<E_f\left({Ag}_{2}Te\right)$$ 3

$${\mu }_{Sn}+{\mu }_{Te}<E_f\left(S_n{T}_e\right)$$ 4

The equation and inequality above defined a three-dimensional phase space of μ_Ag, μ_Sb and μ_Te.

To simplify the question, we assume there is always excess Tellurium during the synthesis process, which means μ_Te = 0.

COMSOL multiphysics simulation analysis

The TE module performance was simulated using COMSOL Multiphysics 6.2^60,61, employing a p-type AgSb_0.94Sn_0.06Te₂ leg paired with an n-type skutterudite Yb_0.25Co_3.75Fe_0.25Sb₁₂ leg. The simulation accounted for TE effects, electromagnetic-thermal interactions, and temperature-dependent material properties. Material parameters for components such as copper and alumina were sourced from the default database. Appropriate boundary conditions and assumptions were applied, treating the TE module as a steady-state, adiabatic system, with heat radiation and convection on all surfaces neglected. The cold-side temperature was fixed at 300 K, while the hot-side temperature was varied to maintain a consistent temperature gradient. Electrical and thermal contact resistances were set to 5 × 10⁻⁶ Ω·cm² and 5 × 10⁻⁶ KW·m⁻², respectively, in this theoretical design.

Module fabrication and testing

The unicouple module was fabricated based on the techniques reported in our previous work^19,62. The p-type AgSb_0.94Sn_0.06Te₂ leg, with Ni as diffusion-barrier layers and Cu as electrodes, was fabricated by firstly spark plasma sintering the powders of AgSb_0.94Sn_0.06Te₂ at 703 K under a pressure of 40 MPa for 2 min. The obtained bulk pellet was polished and cleaned thoroughly by ultrasonic stirring. The pellet was then diced along the press direction into a certain dimension (P-leg: 2.7 mm (length) × 2.9 mm (width) × 4.8 mm (height)) legs using a wire saw. The reported Yb_0.25Co_3.75Fe_0.25Sb₁₂ skutterudite material by Li et al⁵⁴. was used as the n-type leg. The pellet was then diced along the press direction into a certain dimension leg (N-leg: 1.9 mm (length) × 1.4 mm (width) × 4.8 mm (height)) using a wire saw. The obtained bulk pellet was polished and cleaned in ethanol thoroughly by ultrasonic stirring. Afterward, a layer of Ni was deposited on the top and bottom side of each leg by electroless nickel plating (∼20 μm). The legs were connected by direct bond copper substrates using Gallium-Indium eutectic metal to provide electrical and thermal contact at the junction of thermoelectric leg/header. The output properties of the fabricated unicouple device were measured using a custom-built power generation setup. The measurement method and the testing principle have been explained in our previous works^19,62–65. The schematic diagram of measurement is described in Fig. S9. The output power and conversion efficiency of the unicouple TEGs were simultaneously measured under vacuum condition (∼10⁻⁹Torr) from room temperature to 400°C. The hot side temperature was precisely controlled by a heater that provides constant heat flow (Q_in) to the top side of the module. TEG converts a portion of this heat into output power (P_out) and rejects the rest (Q_out) into the Q-meter which is connected to a water-cooled heat sink (cold side) with constant temperature of ~20 °C. The open circuit voltage (V_oc) and device voltage (V_d) were recorded at a certain current using a voltmeter (KEITHLEY) and a power supply (KEITHLEY 2200-20-5). Using this information, internal resistance (R_i) and P_out were then calculated. The temperatures of hot and cold side were monitored using K-type thermocouples. The system was calibrated thoroughly to minimize the heat loss. The maximum power output from TE modules P_max is calculated using the expression:

$$P_{\max }=\frac{V_{oc}^2}{4R_i}$$

where V_oc is the measured open-circuit voltage and R_i is the module internal resistance. V_oc and device voltage (V_d) were recorded at a certain current using a voltmeter (KEITHLEY) and a power supply (KEITHLEY 2200-20-5). The heat flow ($Q_{out}$) of unicouple decive is calculated by:

$$Q_{out}=Q_{leg\left(p\right)}+Q_{leg\left(n\right)}={\kappa }_p\times \frac{A_p}{l_p}\times \mathrm{\Delta }T+{\kappa }_n\times \frac{A_n}{l_n}\times \mathrm{\Delta }T$$

where κ, A, and ΔT are the thermal conductivity, cross-section area, and temperature difference of TE legs, respectively. Thermal radiation (Q_rad) is defined as Q_rad = $Q_{out}^{\prime }$ – Q_out, where ${\mathrm{Q}}_{\mathrm{out}}^{\prime }$ is measured and calculated from a copper Q-meter which is connected to a water-cooled heatsink. Thermal radiation is determined negligible when ΔT < 420 K in our previous study^19,62, therefore, in this study, Q_out is used to represent the heat flow through the TE module. The conversion efficiency of double-leg modules is quantified by:

$$\eta =\frac{P_{out}}{Q_{in}}=\frac{P_{out}}{Q_{out}+P_{out}}$$

where Q_in represents the heat flow from heat source. The TE module is measured three times and the average values are reported. The maximum standard deviation of conversion efficiency based on three measurement results is used as uncertainties of conversion efficiency and output power. The uncertainty of output power and conversion efficiency is ±1% and ±3%, respectively.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Author contributions

Y.Z. designed this work. Y.Z. and C.X. synthesized the samples and carried out the transport property measurements. L.Z. analyzed the XPS results. A.G. contributed to the TEM analysis. Y.L., L.K.H., H.Z., S.H.L., C.C., and S.C. discussed the content of the paper. Z.L., M.H., R.B.S., and D.W. contributed to the DFT and COMSOL calculations. Y.Z. wrote the manuscript. X.F., T.Z., Z.M., L.D.Z, A.C., and B.P. edited the manuscript.

Peer review

Peer review information

Nature Communications thanks the anonymous reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Data availability

The authors declare that all data supporting the findings of this study are available within the article and its Supplementary Information files or from the corresponding author upon reasonable request.

Competing interests

One Chinese patent application (202410992695X) was filed by Y.Z. and T.Z. The remaining authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-55280-0.