Abstract
Machine learning offers a promising avenue for expediting the discovery of new compounds by accurately predicting their thermodynamic stability. This approach provides significant advantages in terms of time and resource efficiency compared to traditional experimental and modeling methods. However, most existing models are constructed based on specific domain knowledge, potentially introducing biases that impact their performance. Here, we propose a machine learning framework rooted in electron configuration, further enhanced through stack generalization with two additional models grounded in diverse domain knowledge. Experimental results validate the efficacy of our model in accurately predicting the stability of compounds, achieving an Area Under the Curve score of 0.988. Notably, our model demonstrates exceptional efficiency in sample utilization, requiring only one-seventh of the data used by existing models to achieve the same performance. To underscore the versatility of our approach, we present three illustrative examples showcasing its effectiveness in navigating unexplored composition space. We present two case studies to demonstrate that our method can facilitate the exploration of new two-dimensional wide bandgap semiconductors and double perovskite oxides. Validation results from first-principles calculations indicate that our method demonstrates remarkable accuracy in correctly identifying stable compounds.
Subject terms: Computational methods, Solid-state chemistry, Condensed-matter physics
Models relying on domain-specific knowledge suffer from inductive bias. Here, the authors introduce a framework combining electron configuration with stacked generalization, achieving high accuracy and efficiency in predicting compound stability.
Introduction
Designing materials with specific properties has long posed a significant challenge in the field of materials science1–3. A major hurdle stems from the extensive compositional space of materials, wherein the actual number of compounds that can be feasibly synthesized in a laboratory setting only represents a minute fraction of the total space. This predicament, often likened to finding a needle in a haystack, necessitates effective strategies to constrict the exploration space4,5. By meticulously evaluating the thermodynamic stability, it becomes plausible to winnow out a substantial proportion of materials that are arduous to synthesize or endure under certain conditions, thereby notably amplifying the efficiency of materials development. The thermodynamic stability of materials is typically represented by the decomposition energy ()6, which is defined as the total energy difference between a given compound and competing compounds in a specific chemical space. For detailed definitions of , see Supplementary Note 1. This metric is ascertained by constructing a convex hull utilizing the formation energies of compounds and all pertinent materials within the same phase diagram7.
However, the conventional approaches for determining compound stability are characterized by inefficiency. Establishing a convex hull typically requires experimental investigation or density functional theory (DFT) calculations to determine the energy of compounds within a given phase diagram. The computation of energy via these methods consumes substantial computation resources, thereby yielding low efficiency and limited efficacy in exploring new compounds. Despite the high costs associated with DFT for predicting compound stability, its widespread use has paved the way for the development of extensive materials databases, such as Materials Project (MP) and Open Quantum Materials Database (OQMD)8. These databases enable researchers to leverage cutting-edge statistical methodologies under the purview of artificial intelligence and machine learning.
A growing number of researchers have utilized machine learning to predict compound stability9–16. This trend has been primarily driven by the emergence of extensive databases6,17–22, which provide a large pool of samples for training machine learning models23–27, ensuring their predictive ability. By leveraging these databases as training data, machine learning approaches enable rapid and cost-effective predictions of compound stability7,20,28–37. For example, Dipendra et al. developed a deep learning model called ElemNet, which uses the elemental composition of compounds to predict their formation energy29. Despite these advancements, current machine learning methods for predicting compound stability suffer from poor accuracy and limited practical application. One major issue is the significant bias introduced by machine learning models that rely on a single hypothesis. Training a model can be likened to a search for the ground truth within the model’s parameter space, gradually approaching it through optimization algorithms38. However, the lack of well-understood chemical mechanisms in materials39 often leads to models built on idealized scenarios. Consequently, the ground truth may lie outside the parameter space or even far from its boundaries, diminishing the accuracy of predictions. For instance, ElemNet’s assumption that material performance is solely determined by elemental composition may introduce a large inductive bias29, reducing the model’s effectiveness in predicting stability.
In this study, we propose an ensemble framework based on stacked generalization (SG)40,41, which amalgamates models rooted in distinct domains of knowledge. Our approach involves the integration of three models into this ensemble framework to construct a super learner42. The first two models are drawn from existing literature, while the third, named Electron Configuration Convolutional Neural Network (ECCNN), is a newly developed model designed to address the limited understanding of electronic internal structure in current models. The resulting super learner, designated Electron Configuration models with Stacked Generalization (ECSG), effectively mitigates the limitations of the individual models and harnesses a synergy that diminishes inductive biases, ultimately enhancing the performance of the integrated model. In our experiments, the proposed model yields an AUC of 0.988 in predicting compound stability within the Joint Automated Repository for Various Integrated Simulations (JARVIS) database. Furthermore, we observed a considerable enhancement in sample efficiency, as our model attained the equivalent accuracy with only one-seventh of the data required by the existing model. Additionally, we applied our model to explore new two-dimensional wide bandgap semiconductors and double perovskite oxides and unveiled numerous novel perovskite structures. Subsequent validation using DFT further underscored the high reliability of our model.
Results
Model development
The machine learning models discussed in this study are primarily composition-based. Currently, two types of models are available for predicting the properties of inorganic compounds: structure-based models and composition-based models43,44. Structure-based models contain more extensive information, including the proportions of each element and the geometric arrangements of atoms. However, determining the precise structures of compounds can be challenging7,45. In contrast, composition-based models do not encounter this issue, but they are often perceived as inferior due to their lack of structure information. Nonetheless, recent research has demonstrated that composition-based models can accurately predict the properties of materials, such as energy and bandgap45. More importantly, in the discovery of novel materials, composition-based models can significantly advance the efficiency of developing new materials, given that the composition information can be known as a priori. While databases like the Materials Project (MP) contain extensive structural information, this data is often unavailable or difficult to obtain when exploring new, uncharacterized materials. Structural information typically requires complex experimental techniques such as X-ray diffraction or electron microscopy, or computationally expensive methods like Density Functional Theory (DFT). These approaches are time-consuming, costly, and require significant expertise and specialized equipment. In contrast, compositional information can be readily obtained by sampling the compositional space, making it more accessible for high-throughput screening and the exploration of new materials. Therefore, this study mainly considers models that utilize chemical formula-based representations as input.
Composition-based models usually require specialized processing of composition information before it can be used as input for the model. The data directly extracted from the chemical formula only consists of the proportion of each element, providing minimal insight. As a result, it is challenging to develop a high-performance model based solely on this information. In addition, models that solely incorporate element proportions, known as element-fraction models, cannot be extended to account for new elements. If an element is not included in the training database, the model will not be able to predict the effects of that element46. Consequently, before incorporating composition information as input for the model, it is necessary to create hand-crafted features based on specific domain knowledge.
Due to the limited understanding of the relationship between material properties and composition, introducing theories or assumptions about the property-composition relationship into composition-based models can lead to significant biases. At the algorithmic level, it is common to make assumptions that favor one solution over others. For example, convolutional neural networks (CNN) assume that information exhibits spatial locality, enabling weight sharing through sliding filters to reduce the parameter space47. Except for biases in the model itself, prior knowledge is also introduced when transforming the element proportions into model inputs. These assumptions, however, have limited applicability and can result in poor generalization performance.
For instance, Roost assumed that the unit cell within a crystal can be viewed as a dense graph, with atoms represented as nodes connected by edges. However, it is essential to acknowledge that not all nodes in the unit cell have strong interactions with eachother48. Therefore, incorporating such assumptions can lead to limitations in model performance. By recognizing these constraints, we can better understand the trade-offs involved in model design and strive to develop more robust and generalizable models.
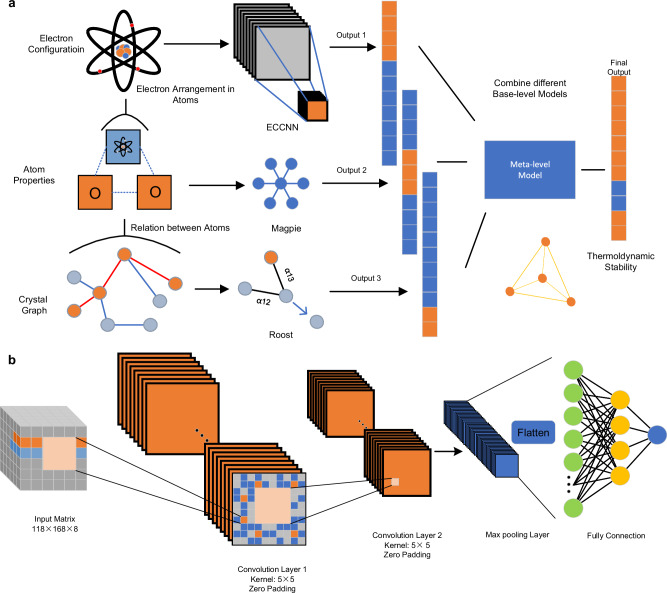
This study proposes a conceptual framework rooted in the SG technique, which amalgamates models grounded in diverse knowledge sources to complement each other and mitigate bias, consequently ameliorating predictive performance. As depicted in Fig. 1a, the framework integrates three foundational models: Magpie30, Roost48, and ECCNN. To ensure complementarity we have selected domain knowledge from different scales: interatomic interactions, atomic properties, and electron configurations (EC). Magpie emphasizes the importance of including statistical features derived from various elemental properties, such as atomic number, atomic mass, and atomic radius. The statistical features encompass mean, mean absolute deviation, range, minimum, maximum, and mode. This broad range of properties captures the diversity among materials, providing sufficient information for accurately predicting their thermodynamic properties. After obtaining the statistics of these atomic features, Magpie was trained by using gradient-boosted regression trees (XGBoost). Roost conceptualizes the chemical formula as a complete graph of elements, employing graph neural networks to learn the relationships and message-passing processes among atoms. By incorporating an attention mechanism, Roost effectively captures the interatomic interactions that play a critical role in determining the thermodynamic stability of materials. Moreover, existing models were found to lack consideration of EC, which may be strongly correlated with stability. The EC delineates the distribution of electrons within an atom, encompassing energy levels and the electron count at each level. This information is crucial for comprehending the chemical properties and reaction dynamics of atoms. A further illustration of the complementarity among the three models is described in Supplementary Note 2. EC is conventionally utilized as an input for first-principles calculations to construct the Schrödinger equation, facilitating the determination of crucial properties such as the ground-state energy and band structure of materials or molecular systems. Compared to manually crafted features, EC stands as an intrinsic characteristic that may introduce less inductive biases. To address this gap, we have developed and integrated our own model, ECCNN, into the framework. The architecture of ECCNN is depicted in Fig. 1b. The input of ECCNN is a matrix with shape of 118 × 168 × 8, which is encoded by the EC of materials. The details of how EC is encoded as input are described in subsection Base-level models. The input then undergoes two convolutional operations, each with 64 filters of size 5 × 5. The second convolution is followed by a batch normalization (BN) operation and 2 × 2 max pooling. The extracted features are flattened into a one-dimensional vector, which is then fed into fully connected layers for prediction. After training these foundational models, their outputs are used to construct a meta-level model, which produces the final prediction. We refer to this framework as ECSG.
Fig. 1. The frameworks of Electron Configuration models with Stacked Generalization (ECSG) and Electron Configuration Convolutional Neural Network (ECCNN).
a ECSG yields predictions of thermodynamic stability by integrating predictions from three complementary base-level models into a meta-level model. The base-level models include: (i) ECCNN uses convolutional neural networks to extract complex features related to the electron configuration; (ii) Magpie emphasizes the importance of including statistical features derived from various atom properties, such as atomic number, atomic mass, and atomic radius30; (iii) Roost conceptualizes the chemical formula as a complete graph of elements, employing graph neural networks to learn the relationships and message-passing processes among atoms48. b The architecture of ECCNN. It begins with input features arranged in a 3D matrix, followed by two convolutional layers. Then, a flatten layer converts features extracted from convolutional layers into a 1D vector. Finally, a multilayer perceptron (MLP) processes the flattened features through fully connected layers to output the final predictions.
Within a given dataset, represents the composition of compounds, while denotes the features of the -th base-level model derived from various domain knowledge, means the label associated with . The objective is to estimate the stability of compounds . The primary procedure of ECSG, as illustrated in Fig. 1 (a), can be delineated as follows:
| 1 |
| 2 |
| 3 |
In Eqs. (1–3), represents the th base-level model, while and denote the parameters and loss function associated with , respectively. signifies the meta-level model, with and corresponding to its parameters and loss function, respectively. The variable indicates the number of base-level models. First, through the dataset , we obtain the optimal parameters for each base-level model , as shown in Eq. (1). Once all the base-level models have been trained, we can obtain , the optimal parameters of the meta-level model , using the data . Here, denotes the output of the trained for . Finally, the super learner’s predictions for compounds , denoted as , can be derived from M. The description above outlines a general process, which becomes more complicated in practical application. To avoid overfitting, K-fold data splitting is performed. More details can be found in the Methods section.
Performance benchmarking against existing models
In this section, we performed a comprehensive comparison between our proposed method and several state-of-the-art baselines, including element-fraction models and models with hand-crafted features, to validate the effectiveness of our proposed ECSG. Among these models, the non-deep learning models Magpie30 and Meredig31 were trained using XGBoost49. The features used by Magpie, Random Forest (RF), and AdaBoost came from the Materials Agnostic Platform for Informatics and Exploration (MAGPIE)30. ElemNet29 is the element-fraction model, while Meredig and Magpie are based on physical attributes. ATCNN treats a compound as a 10 × 10 pixels image, called Atom Table (AT). Each pixel within the AT corresponds to an element, with its intensity representing the proportion of that particular element within the compound. Roost treats compounds as complete graphs and trains them using graph networks. This comparison allows for the evaluation of the ECSG framework’s effectiveness relative to existing models, providing a comprehensive understanding of its performance in predictive tasks.
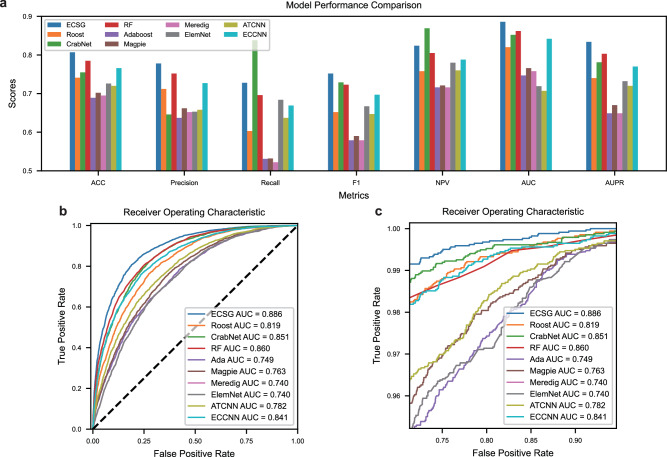
All models were trained using data sourced from the MP dataset, as detailed in the Methods section. We include several metrics, Area Under the receiver operating characteristic Curve (AUC), accuracy (ACC), Precision, Recall, F1-score (F1), negative predictive values (NPV), and Area Under the Precision-Recall curve (AUPR), to provide a more comprehensive evaluation. As shown in Fig. 2a, in all metrics, ECSG outperforms other models in ACC, precision, F1-score, AUC, and AUPR. ECSG performs second best in NPV and Recall, achieving an AUC value of 0.886, while CrabNet performs best in NPV and Recall. The exact values of these metrics are provided in Supplementary Table 1. Although CrabNet improves Recall and NPV by increasing positive predictions, this strategy largely sacrifices precision, resulting in too many false positives. In most cases, the goal is to identify thermodynamically stable materials, and more attention should be paid to samples that are predicted to be positive. Excessive false positive samples can lead to wasted time and resources. Moreover, from the AUC curve in Fig. 2b and the zoomed curve in Fig. 2c, we can see that even when the false positive rate (FPR) approaches 1, ECSG’s performance remains robust, which highlights its consistent reliability across different thresholds. The confusion matrix (Supplementary Fig. 2) also shows the advantage of our model in predicting stable materials. The number of false positive samples of RF (787) is 15.6% more than that of ECSG (681).
Fig. 2. Performance comparison of models across metrics and Area Under the Curve (AUC) curves.
a The hist plot of different models in terms of seven metrics. Source data are provided as a Source Data file. b AUC curves, and (c) zoomed AUC curves of different models. The comparison models include Electron Configuration models with Stacked Generalization (ECSG), Roost48, CrabNet69, Random Forest (RF), AdaBoost (Ada), Magpie30, Meredig31 ElemNet29, Atom Table Convolutional Neural Networks (ATCNN)37 and Electron Configuration Convolutional Neural Network (ECCNN).
Notably, many materials can exist in a thermodynamically metastable state for a prolonged period. Considering this, along with the potential uncertainties/errors associated with DFT6, we slightly relax the threshold restriction when classifying materials stability. Consequently, we utilize thresholds of 25 meV/atom and 40 meV/atom to assign stability labels in the data set. Subsequently, we retrain the ECSG model and other models. The performances of these models are shown in Supplementary Tables 2 and 3. It is worth noting that even with the relaxation of the threshold, ECSG continues to outperform other models. Moreover, as the threshold increases, the performance of almost all models improves, as it becomes more challenging to distinguish material stability near the threshold of 0.
To further demonstrate the robustness of ECSG, we explored its performance on a regression task for predicting . ECSG can also be adapted for regression tasks with minor modifications to output layers. In this case, we trained a regression model using ECSG to predict , by removing the Sigmoid functions from the last layers of the base-level models. The performance of the ECSG regressor can be found in Supplementary Table 4, where the mean absolute error of in the test set is 0.064 eV/atom, surpassing other models in accuracy.
In addition to the MP database, we further trained the ECSG model and other existing models on the OQMD20 and JARVIS50 databases to conduct a more detailed comparison of their performance, as shown in Supplementary Tables 5 and 6. Notably, ECSG exhibits significant advantages in performance, particularly evident in the JARVIS dataset where it surpasses other comparison models in the key indicators such as ACC, F1, AUC, and AUPR, demonstrating its excellent prediction ability. ECSG achieves a remarkable AUC score of 0.988.
However, on the OQMD dataset, while ECSG continues to lead in terms of ACC and AUC, it falls short in the F1 score. This discrepancy may arise from a serious imbalance in the distribution of positive and negative samples in the OQMD dataset. With positive samples accounting for only 11.3% of the dataset, the model may be biased towards predicting samples as negative, leading to a decline in the F1 score. In such a scenario, the F1 score might not accurately reflect the true performance of the model, as it represents the harmonic mean of precision and recall, both of which can be misleading in the presence of sample imbalance. In such cases, focusing on AUPR values is more prudent, as it offers a comprehensive evaluation of the model’s performance across different classification thresholds, particularly valuable in handling imbalanced datasets51. Compared to the AUPR value of 0.775 for Roost, the AUPR value for ECSG increased to 0.840, demonstrating the effectiveness of this method.
The superior performance of our method can be attributed to two factors. Firstly, we utilize SG to integrate models based on different domain knowledge. Individual models, relying solely on single-domain knowledge, may be prone to inductive bias and may exhibit limitations in performance. However, by employing SG to integrate multiple models, we can combine different knowledge sources, allowing them to complement each other and eliminating inductive bias. Secondly, recognizing the absence of models incorporating electronic configuration, we introduce EC information into our framework by ECCNN. Theoretically, if the electronic structure of materials can be obtained, many of their micro properties can be easily known. This can be typically accomplished through first-principles calculations with EC as inputs. However, the advancement in deep learning and artificial intelligence has expanded the potential to leverage original information, like pixels in an image. ECCNN transforms the spatial arrangement of atomic electrons within a material into a three-dimensional matrix. This matrix encapsulates original EC information, which is then processed by a CNN to extract meaningful features about the internal space within each atom. This comprehensive approach, steeped rich domain knowledge, addresses the limitations of existing models and ultimately leads to improved performance.
The significance of our findings lies in their potential to profoundly impact various applications, particularly in the fields of material discovery and design. Accurate predictions of compound stability can provide valuable guidance to researchers, empowering them to prioritize and select promising candidates for further experimental investigation. This streamlined discovery process has the potential to simplify the development process significantly and hasten the creation of new materials with desired properties.
Sample utilization efficiency
The material research community faces the challenge of the scarcity of labeled data, a consequence of the high cost associated with obtaining labels through theoretical computation or experimental procedures. This scarcity hinders the development of effective machine learning models. In this context, sample efficiency becomes a critical metric for evaluating model performance. It refers to the ability of a learning algorithm to effectively utilize small training data while achieving robust generalization performance. Unfortunately, current models often struggle with low sample efficiency when confronted with limited data. This limitation underscores the urgent need for improved approaches to address this issue within the context of material research.
To assess the sample efficiency of our proposed method, we conducted experiments using training sets of varying sizes. Initially, we utilized 90% of the MP database (76,513 samples) as the training set, with the remaining portion (8501 samples) set aside for evaluating the model’s performance. We commenced by training each base-level model individually using only 10% of the training dataset. Subsequently, we gradually increased the size of the training set by adding 10% of the original dataset at each step. Following model training, we evaluated its performance on the test set.
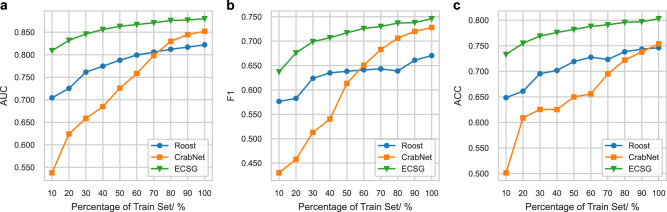
As depicted in Fig. 3, we illustrate the sample efficiency of ECSG and two other models Roost, and CrabNet, each demonstrating good performance as indicated in the benchmarking test. Figure 3a reveals the enhancement in the AUC values for all models as the data size increases, suggesting that larger datasets benefit all models. Particularly notable is the superior performance of ECSG, especially with smaller data sizes. For example, to achieve an AUC of 0.800 on the MP database, ECSG requires only 10% of the training data, whereas the comparison models, Roost and CrabNet, need 70% to reach the same performance level. Similar conclusions can be drawn when comparing performance using other metrics, as evidenced in Fig. 3b, c.
Fig. 3. Model performance under varying training data sizes.
a Area Under the Curve (AUC), (b) f1-score, (c) accuracy (ACC) values of Electron Configuration models with Stacked Generalization (ECSG), Roost48, and CrabNet69 under varying training data sizes from the Materials Project database. The x-axis represents the percentage of the training set used to train the models. Source data are provided as a Source Data file.
The improved sample efficiency of ECSG can be explained from the perspective of minimizing empirical risk. Given a hypothesis , the expected risk is defined as the average loss of across all possible examples drawn from the true conditional probability distributions , as formalized in Eq. (4).
| 4 |
where l is the loss function. However, since is typically unknown, the empirical risk is used as an approximation for by averaging the loss function of all samples, as formalized in Eq. (5).
| 5 |
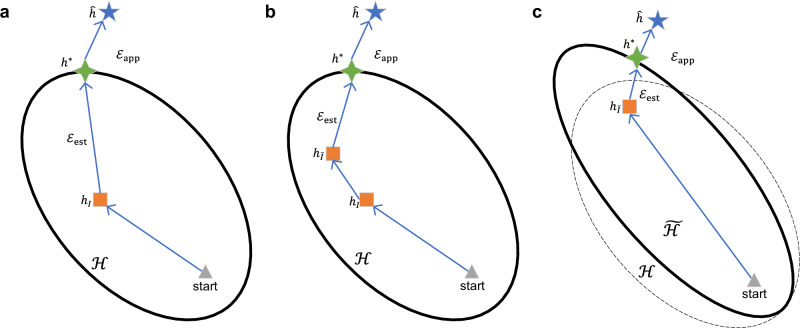
In Fig. 4, three functions are depicted: (1) represents the function that minimizes the expected risk; (2) denotes the function in hypothesis space that minimizes the expected risk; (3) means the function in that minimizes the empirical risk. As shown in Fig. 4a, the total error of can be decomposed into two components, as formalized in Eq. (6):
| 6 |
where quantifies the ability of the functions in to approximate the optimal hypothesis , while measures the extent to which empirical risk can replace expected risk.
Fig. 4. Illustration of error decomposition and the approach of Electron Configuration models with Stacked Generalization (ECSG) to limited data problems.
a Decomposition of error between expected risk and empirical risk. (b, c) show how ECSG solves limited data problems by augmenting data and restricting hypothesis space using domain knowledge. Triangles represent starting points; the blue stars () denote the optimal hypothesis; the green four-pointed stars () and the orange squares () represent the hypotheses that minimize expected risk and empirical risk, respectively, within hypothesis space . The area enclosed by the dotted line () and correspond to the hypothesis space and the resulting hypothesis after incorporating diverse knowledge sources. refers to the error between the optimal hypothesis in and the global hypothesis, while represents the error between or and .
Equation (6) shows that the total error can be reduced by decreasing both and . On the one hand, enhancing the data with domain knowledge can enable the model to be more fully trained, thereby reducing . As shown in Fig. 4a, b, with more informative data, the hypothesis is optimized from to , getting closer to . On the other hand, with the combination of various prior knowledge introduced by base-level models, the hypothesis space can be altered, enabling the learning algorithm to form a more accurate approximation of the true unknown hypothesis, thereby reducing . As depicted in Fig. 4c, The new hypothesis space constrains the possible functions within a more reliable region, which can shorten the optimization path and bring the optimal function in the hypothesis space closer to the truth . In summary, by considering both the data augmentation and the constraint on the hypothesis space, it is possible to minimize the total error and improve the performance of .
These results highlight the remarkable sample efficiency of our method, a vital factor in the domain of material research where labeled data is frequently in short supply. By effectively leveraging a small training dataset, our method notably outperforms existing models. This holds substantial implications for material discovery and design, empowering researchers to attain precise predictions even when faced with limited resources, ultimately reducing the dependence on extensive labeled datasets. Consequently, our approach can streamline research efforts within the field, offering a more efficient and cost-effective approach to exploration and development.
Ablation study
The proposed model integrates a diverse range of ideas from the materials science and machine learning domains. To comprehend the individual contributions of each base model of ECSG to its performance improvement, we tested the performance of each base model after removing it from ECSG.
From Table 1, it is evident that removing Roost has the greatest impact on the results, with significant declines across various metrics—for instance, ACC drops by 0.028 and AUC by 0.025. In comparison, removing ECCNN and Magpie has a smaller effect. For example, after removing Magpie, ACC only decreases by 0.002. Furthermore, when comparing the performance of combining two models to using a single model, removing Roost shows the largest impact. Specifically, when Roost is removed from the combination of Magpie and Roost, ACC drops sharply from 0.799 to 0.702. This suggests that Roost is the most critical contributor to the model’s performance. One possible explanation is that although Roost primarily learns atomic interactions through a graph attention network (GAT), it also incorporates some information about atomic properties when embedding nodes in the graph.
Table 1.
The performance of combining different base models in ECSG on the MP database
| Model | ACC | Precision | Recall | F1 | NPV | AUC | AUPR |
|---|---|---|---|---|---|---|---|
| M1 | 0.766 | 0.727 | 0.669 | 0.697 | 0.788 | 0.842 | 0.770 |
| M2 | 0.741 | 0.712 | 0.603 | 0.652 | 0.758 | 0.820 | 0.740 |
| M3 | 0.702 | 0.662 | 0.532 | 0.590 | 0.721 | 0.766 | 0.670 |
| M1 + M2 | 0.805 | 0.776 | 0.725 | 0.750 | 0.823 | 0.883 | 0.828 |
| M1 + M3 | 0.779 | 0.733 | 0.711 | 0.722 | 0.809 | 0.861 | 0.800 |
| M2 + M3 | 0.799 | 0.761 | 0.729 | 0.745 | 0.822 | 0.873 | 0.813 |
| M1 + M2 + M3 | 0.807 | 0.778 | 0.728 | 0.752 | 0.824 | 0.886 | 0.834 |
M1, M2, and M3 represent the base models ECCNN, Roost, and Magpie respectively.
SG is another essential module in ECSG. To study its contribution, we examined the effects of different model combination methods. Aside from SG, the most common methods are voting and averaging. We compared the results of SG with these methods on the MP database, as shown in Supplementary Table 7. SG performs the best, followed by averaging, while voting lags behind. For example, compared to averaging, SG improves ACC, F1, and AUC from 0.788, 0.719, and 0.865 to 0.807, 0.752, and 0.886, respectively. Voting achieves the lowest scores, with ACC, F1, and AUC at 0.763, 0.693, and 0.747. Other combination methods, such as averaging and weighted averaging, apply preset rules to directly combine the outputs of base models, with fixed weights assigned to each. If the error of a base model on a specific sample is large, it can negatively impact the final prediction, especially when the weight is set improperly. However, SG can dynamically adjust the contribution of each model and assign reasonable weights to different base models, avoiding large errors caused by improper weight assignment.
Integration of structure information
To further enhance the prediction accuracy of the ECSG model, we integrated structure-based models into the framework. Structural information, when available, provides not only the elemental composition but also the spatial arrangement of atoms, offering a more detailed understanding of a material’s properties.
To evaluate the impact of incorporating structural information, we compared the performance of ECSG integrating the Crystal Graph Convolutional Neural Network (CGCNN)36, which relies on structural information, and composition-only ECSG. We added a base-level model CGCNN into ECSG, referred to as ECSG + C, where the final prediction is obtained by SG to combine the outputs of each base model. We downloaded 125,451 structural datasets from the MP, referred to as the MP-structure dataset, covering 89,204 unique compositions, and split them into training and test sets in an 8:2 ratio based on composition. In addition to the seven performance metrics previously discussed, we conducted an additional experiment to evaluate the models’ ability to distinguish polymorphs. The test set contained 1471 samples with polymorphs, from which we paired stable and unstable materials with identical compositions, creating a total of 1038 polymorph pairs. We then assessed the models’ ability to correctly differentiate these pairs, represented by ACC_M in Supplementary Table 8.
As shown in Supplementary Table 8, the structure-based models outperformed the composition-only models across all performance metrics. When structural information was integrated into ECSG, performance improved further. Specifically, ECSG’s accuracy increased from 0.826 to 0.844, and the AUC improved from 0.879 to 0.905. Although incorporating structure information may be less advantageous for exploring new materials, given that structural data is not always readily available in this case, when structures are known, using this information can significantly enhance the model’s predictive accuracy. Consequently, we now offer two distinct input options: one for cases where structural data is unavailable and predictions are based solely on compositional data, and another where both structural and compositional information are utilized for higher accuracy. This flexibility ensures that ECSG remains effective even when only compositional data is accessible, while also offering improved accuracy when structural information is available (Relevant frameworks are available on our GitHub repository).
However, distinguishing polymorphs remains a challenge for all models. CGCNN correctly identified only 19.3% of polymorph pairs. Although the overall performance of ECSG improved after integrating structural data, the ability to distinguish polymorphs decreased to 12.1%. The poor performance in predicting polymorphs likely arises from the limited resolution to effectively distinguish between polymorphs of the same composition. Future research should focus on addressing the challenge of distinguishing the energetics of polymorphs.
Prediction in unknown space
Although we have quantified the accuracy of the ECSG on large-scale databases such as MP, JARVIS, and OQMD, thereby demonstrating the guidance of this method in predicting the thermodynamic stability of compounds, it is worth noting that this approach is not directly equivalent to the problem of materials discovery. This limitation arises because our method primarily evaluates a limited component space that has been previously explored. The data used for training and testing are randomly sampled from the same space. Thus, their data distributions are very similar, which allows us to achieve good results. However, the predictive capabilities of ECSG in space where the data distribution is very different from known space, or even completely unknown, have not been evaluated. To better simulate real-world materials discovery scenarios, which typically involve exploration in unknown spaces, we tested the ability of ECSG to predict the stability of perovskite halides, lithium (Li)-containing oxides, and transition metal oxides in unknown space.
Perovskite halides
First, we use perovskite halides as an example to test the ability of ECSG to predict stability in unknown space. Perovskite, a class of compounds with structural characteristics similar to CaTiO3, typically follows the formula ABX3. Over time, perovskite has garnered increasing attention among researchers52. However, a major challenge in developing new perovskites is the extensive compositional space, which demands a significant investment of time and resources to explore. As depicted in Fig. 5a, b, the presence of diverse atoms occupying the A-site and B-site contributes to the vast compositional space of perovskite.
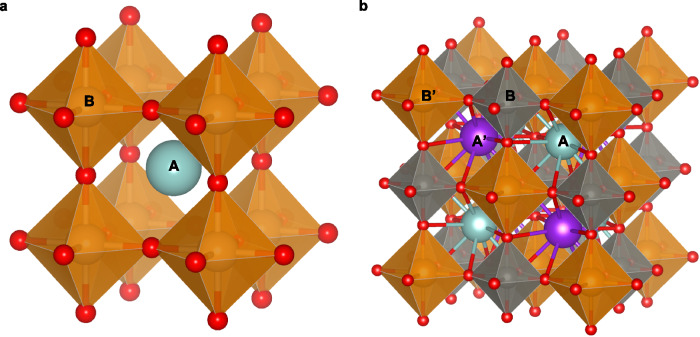
Fig. 5. Illustration of single and double perovskites.
a A single ABX3 perovskite structure. b A double perovskite with two cations in each of the A- and B-sublattices (denoted as AA′BB′X6), respectively. Brown and grey represent A-sites, while purple and green represent B-sites.
In perovskite ABX3, where X represents a halogen element (X = Cl, Br, I), they are referred to as perovskite halides. Perovskite halides are promising candidates for solar cells, which directly convert sunlight into electrical energy, satisfying the demand for renewable energy53. The power conversion efficiency (PCE) of perovskite halides solar cells can achieve 23.3% for a small-area device (9 mm2)54.
We collected thermodynamic stability data for 496 perovskite halides from the literature. Among these materials, there are 408 materials in the MP database. To ensure the perovskite halide data set is independent of the training set, we remove these duplicate samples from MP. All models were retrained using the remaining data in MP and their performance was subsequently tested on the perovskite halide dataset. The performance comparison of ECSG and other models is shown in Supplementary Table 9. ECSG also outperforms other models in predicting the stability of perovskite halides, with ACC and AUC values reaching 0.790 and 0.758, respectively. However, we also observed that the F1 score and the AUPR value of all models in the unknown space are relatively low. This is caused by the unbalanced samples in the test set, with the stable materials being much fewer than the unstable materials. In this context, a lower AUPR value than AUC does not indicate poor performance. For instance, a completely random model would have an AUC value of 0.5, but the AUPR value would equal the proportion of positive samples, P. Therefore, for the baseline model on this dataset, AUC should be 0.500 and AUPR should be 0.122. Our model’s AUPR is 0.474, which is about 4 times that of the random model, indicating a significant improvement. This demonstrates that compared to the previous trial-and-error method, our approach can greatly enhance the efficiency of developing new materials.
Li-containing oxides
In the field of electric vehicles (EVs) and consumer Electronics, Li-ion batteries are the most used power supply units. Li-containing oxides, usually as cathode, are essential components in Li-ion batteries. During the charge and discharge cycles of Li-ion batteries, cathodes facilitate the embedding and release of Li-ions within their structures through redox reactions. To meet the growing demand for enhanced battery performance, materials researchers have been fervently seeking cathode materials with higher energy density and stability. Thus, the discovery of new Li-containing oxides as candidate cathode materials holds paramount importance.
To investigate whether our model is helpful in solving this problem, we verified the predictive ability of ECSG in the space of unexplored Li-containing oxides. Different from testing in perovskite halides, we extract all materials containing Li and O from MP, resulting in 6168 samples, with 750 stable materials. Subsequently, we use the remaining data in MP for training and employ the extracted Li-containing oxides for testing. Notably, as there are no Li-containing oxides in the training set, the model encounters a completely unfamiliar space, thereby enhancing the credibility of its prediction ability.
The test results are presented in Supplementary Table 10. It can be found that ECSG exhibits superior performance across all four evaluation metrics. Consistent with prior findings on perovskite halides, ECSG achieves high scores on ACC and AUC, while exhibiting comparatively lower scores on F1 and AUPR. As previously discussed, this disparity arises from the imbalance of positive and negative samples in the test set. It is important to note that the relatively low AUPR score does not mean poor model performance. AUPR offers valuable insights, particularly when dealing with data imbalance51. Hence, our focus primarily centers on comparing the AUPR values of the models. Notably, among these evaluation metrics, ECSG has the largest lead in AUPR, with an improvement of 13.3% over the second-highest model in AUPR. Conversely, its lead in AUC is more modest, standing at 5.73%. This underscores the superior performance of our method, particularly in the context of testing on imbalanced datasets.
Transition metal oxides
Another material under evaluation in the unknown space is transition metal oxides. These materials exhibit unique properties due to their partially occupied d-shells, even though the s-shell ions of positive metals are fully filled with electrons. This characteristic endows them with a variety of unique properties, including reactive electronic transitions, high dielectric constant, wide bandgap, and good electrical properties. In this study, we use Fe-containing oxides and Mn-containing oxides as examples to test the model’s ability to predict unknown transition metal oxides. Similar to our approach with Li-containing oxides, we extracted 7137 transition metal oxides from the MP database and used the remaining data of MP to train the models. In the extracted datasets, the number of positive samples is 1211, accounting for 17.0% of the total number of samples.
The test results for the trained models on the extracted transition metal oxide dataset are presented in Supplementary Table 11. ECSG continues to exhibit robust predictive capabilities for the stability of transition metal oxides. Except for the F1 score, ECSG achieves the highest score across other metrics. It is important to note the limitations of the F1 score, as it only reflects the model’s ability to predict positive samples and can vary with changes in the classification threshold. Besides, models with high F1 scores do not necessarily perform well in other metrics. For example, despite the superior F1 score of Meredig, it lags behind in other metrics. Overall, ECSG’s performance is the best among all models evaluated.
From these three examples, it can be observed that ECSG maintains high accuracy in predicting material stability, even in unknown spaces, indicating its great potential for discovering new materials. Moving forward, we will conduct a case study combining ECSG and high-throughput technology to explore perovskite oxides in a wider space.
Case studies
Two-dimensional Materials with wide bandgap
To further validate the reliability of the proposed ECSG across multiple application scenarios, we conducted a case study on 2D materials, focusing on identifying wide bandgap semiconductor candidates. Since the discovery of graphene in 2004, 2D materials have rapidly become the forefront of materials science research due to their unique physical and chemical properties. These materials with atomically thin single-layer/few-layer atomic/molecular layer structures have shown broad application prospects in many fields, especially in electronics and optoelectronics55. 2D materials, with their excellent electrical conductivity and photoelectric conversion properties and the two-dimensional characteristics of their structures, make it possible to manufacture lighter, thinner, and stronger electronic products such as smartphones and computers. Although currently developed 2D materials, such as graphene, have excellent performance in many aspects, their small bandgap limits their development in the semiconductor field. Therefore, researchers have begun to turn their attention to finding semiconductor alternatives to graphene. 2D materials with wide bandgap (>2 eV) have attracted widespread attention due to their potential to work under blue and ultraviolet light and are believed to be expected to play a key role in the development of new optoelectronic devices56.
However, designing materials that meet performance requirements but lack thermodynamic stability would hinder their practical use, leading to wasted resources and time. Therefore, in addition to meeting specific property requirements, thermodynamic stability is also required to ensure their practical use. Many of the properties of 2D materials are due to their unique electronic structure. Building on this understanding, we use the ECSG, which incorporates the information of electron configuration, to find potential 2D semiconductor candidate materials with wide bandgap to meet the needs of future technological development.
First, we extracted the composition and stability information of the materials from the entire C2DB database and trained a model to predict the thermodynamic stability of 2D materials57. Then, we tested the trained model on the 2Dmatpedia database, which contains 4743 materials56. Supplementary Table 12 shows the test results of the ECSG model and the comparison model on these materials. The results show that ECSG performs best or second best in all metrics. Although CrabNet outperforms ECSG in recall and NPV, this is mainly due to its tendency to predict more results as positive classes, resulting in a higher false positive rate and thus reduced precision. Although RF also shows suboptimal results in some metrics, its poor performance in recall leads to the omission of many potential candidate materials. According to Supplementary Table 12, ECSG can find 172 more true positive samples than RF, showing its advantage in identifying positive samples. In contrast, the prediction results of ECSG are more balanced and more suitable for practical applications.
After showing that ECSG can achieve good stability prediction performance on the 2Dmatpedia database, we combined the large language model (LLM) DARWIN-7B58, which has been proven to perform well in predicting experimental bandgaps, to screen 2D materials with bandgaps greater than 2 eV. Next, we conducted a statistical analysis of the samples predicted by ECSG to be positive and the samples predicted by Darwin-7B to have a bandgap greater than 0 eV. As shown in Fig. 6, a total of 393 2D materials with bandgap greater than 2.0 eV were found. After verifying the stability using labels from 2dMatpedia, 313 of them were found to meet the stability requirements. The stability prediction accuracy of ECSG for these materials is 79.6%. It was demonstrated that ECSG can be used to screen out materials that meet specific practical applications, avoiding the ineffective screening of experimentally unstable materials and significantly improving the screening efficiency.
Fig. 6. The bandgap histogram of samples that are predicted to be thermodynamically stable.
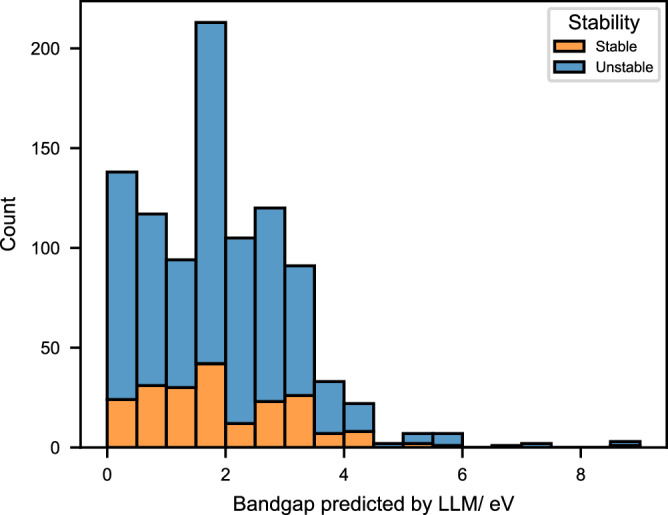
The legends of stable or unstable indicate the true labels in the 2DMatpedia database. The bandgap values were predicted by LLM DARWIN-7B58. Source data are provided as a Source Data file.
Double perovskite oxides
As mentioned above, the chemical formula of perovskite oxides is represented as ABO3. Perovskite oxides are widely used in various fields such as electrode materials for supercapacitors, catalysis, and solid oxide fuel cells59,60.
Initially, we compiled a database of 1333 double perovskite oxides. This database served as the basis for training a super learner through ECSG to predict the stability of perovskite oxides. Given the differing environments of the cations in A-sites and B-sites, base-level models that solely consider element concentration are insufficient to distinguish the sites in perovskite oxides. For example, the elemental compositions of XYO3 and YXO3 are identical, leading to similar stability predictions in composition-only models. However, XYO3 and YXO3 are distinct compounds. To address this issue, we integrated a new base-level model, proposed by Talapatra et al.61, into ECSG. This base-level model utilizes atom-specific features and geometric characteristics of the compound as inputs, effectively overcoming the limitations of the above three models. The resulting ensemble model demonstrated an accuracy, f1-score, and AUC score of 0.971, 0.966, and 0.997, respectively.
We constructed the candidate space of perovskites by enumerating all possible ABO3, A2BB′O6, AA′B2O6, and AA′BB′O6 compounds. In this process, we considered all metal elements up to Bi, resulting in a total of 67 different types of cations that could occupy A-sites or B-sites. This lead to P(67, 2) = 4422 possible ABO3 type perovskites. For A2BB′O6, AA′B2O6, and AA′BB′O6 type perovskites, there were 143,715, 143,715, and 4,598,880 potential combinations, respectively. After filtering for charge neutrality, 4,524,608 unique compounds remained, forming the candidate composition space.
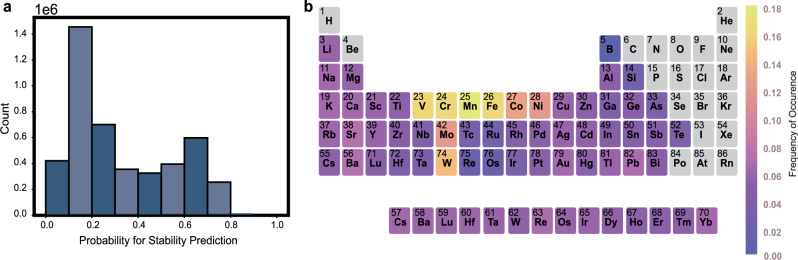
Since the A and B sites can be occupied by different atoms, double perovskite oxides have a huge composition space with more than 4 million possible composition combinations, and the composition space that has been explored so far is only a small part. It is a challenge to screen out candidate materials that meet the conditions in such a huge composition space. In previous studies, we have shown that the learner trained by ECSG can effectively predict samples in unexplored areas. Subsequently, we utilized the trained super learner to predict the stability of all perovskite oxides within this space. The prediction results are depicted in Fig. 7. As illustrated in Fig. 7a, over 40% of compounds have a low probability (less than 0.2) of being stable. By setting the cutoff probability to 0.5, we identified 1,877,443 perovskite oxides predicted to be stable, substantially narrowing down our search range.
Fig. 7. The prediction results of Electron Configuration models with Stacked Generalization (ECSG) in the unknown candidate space.
a Stability probability distribution of perovskite oxides. The x-axis and the y-axis denote the stable probability and the number of perovskite oxides with stable probability x. b Periodic table highlighting the occurrence frequency of elements in the A-site or B-site of predicted stable perovskite oxides. Gray elements represent no occurrences. Source data are provided as a Source Data file.
We randomly selected 35 compounds with stability probabilities greater than 90% (63 in total) for first-principles calculations to validate the accuracy of our machine-learning method. The detailed procedures of the first-principles calculations are expounded upon in the Method section. The findings revealed that, out of the 35 compounds, 25 matched our predictions. Using the convex hull of OQMD and JARVIS as references, 26 and 32 materials are stable among these 35 materials, respectively. The full list of these compounds is shown in Supplementary Table 13. For comparison, we also applied the stability prediction model Talapatra et al.61 After training the model on the same dataset, we randomly selected 35 materials from the top 63 predicted scores in the candidate space for DFT validation. The verification results are shown in Supplementary Table 14. According to the convex hull in MP, OQMD, and JARVIS, only 2, 1, and 6 of the double perovskite oxides selected by the comparison model were stable, respectively. It should be noted that the calculated stability results are based on the currently available databases. As these databases continue to expand and evolve, the calculated stability outcomes may be subject to change.
Through high-throughput experiments, we demonstrated the superiority of our method in predicting the stability of perovskite oxides. The advantages of this method are principally evident in several aspects. Firstly, leveraging machine learning techniques significantly shortens the development cycle of materials, thereby saving time and resources. Compared to traditional trial-and-error methods, our approach allows for the rapid screening of perovskite compounds with potential stability from a vast chemical space, furnishing guidance for subsequent experimental and optimization endeavors. Additionally, our method exhibits strong generalization capabilities, encompassing all inorganic crystalline compounds in the MP database and extending to the specific subset of perovskite compounds.
To further explore the regulation of perovskite oxides stability, we analyzed the element information of these stable compounds in A-sites and B-sites. As shown in Fig. 7(b), stable compounds are most readily formed when perovskite oxides encompass elements such as V, Cr, Mn, Fe, Co, and Ni. Upon observing the position of these elements in the periodic table, it becomes apparent that a majority of these elements belong to the third period’s transition elements.
Discussion
In recent years, machine learning and deep learning techniques have been extensively utilized for predicting compound stability. However, notable challenges remain. One major issue is the unsatisfactory classification accuracy of various models in predicting compound stability. Besides, previous models exhibit inefficiencies in sample efficiency, limiting the practical application of machine learning technologies in the discovery of stable compounds. To tackle these challenges, we propose a machine learning framework called ECSG, which consolidates the strengths of different base-level models. The meta-level model derived from ECSG is superior to each base-level model in all classification metrics and sample efficiency, enabling swift and accurate screening stable compounds. To demonstrate the effectiveness of ECSG, we applied it to predict the stability of perovskite oxides. The prediction model exhibited remarkable performance, achieving an accuracy rate of over 97%. As a result, we identified numerous stable perovskite oxides from a large pool of candidate compounds. By counting the probability of occurrence of each element in these stable compounds, we inferred that the oxides containing elements such as V, Cr, Mn, etc. are highly probable to form stable perovskite oxides.
Our method addresses several critical challenges in applying machine learning in materials science. One challenge is the scarcity of domain knowledge and data, which can result in underperforming machine learning models. Insufficient domain knowledge results in overly simplistic assumptions or theories underpinning the machine learning models, leading to a parameter space that deviates significantly from the ground truth. Furthermore, data scarcity can cause optimization algorithms, such as gradient descent, to converge prematurely on areas far from the ground truth. Our proposed method effectively tackles these issues by combining multiple models to expand the parameter space, even beyond the collective space of individual model spaces, thus increasing the likelihood of approaching the ground truth. By leveraging the mutual complementarity of different base-level models, we significantly reduce the error between predictions and ground truth, even if some individual base-level models are suboptimal.
Our method also offers advantages in integrating heterogeneous data in materials science and engineering. Data in these fields often exhibits heterogeneity, encompassing numerical table data, spectra data, and image data. For example, titanium alloys involve composition data, XRD data, and microscopic images. Different types of data have distinct advantages in machine learning. Different modules can be added to ECSG to process different types of data. We illustrate how to combine heterogeneous data in Supplementary Note 3. Traditional methods often require converting heterogeneous data into a uniform format before inputting it into a model, which can lead to loss of information. However, our model directly leverages these diverse data, obviating the need for additional processing and maximizing data integrity preservation. By employing SG technology, we seamlessly integrate these diverse data types and harness the unique advantages of each, consequently enhancing prediction performance.
We plan to extend the ECSG model to predict several critical material properties, including bandgap, Young’s modulus, and alloy hardness. These properties are essential for a wide range of applications in materials science and engineering. For instance, the bandgap is a key determinant of electrical conductivity, making it a crucial parameter in semiconductor and photovoltaic technologies.
However, we recognize several challenges in expanding ECSG’s scope to these properties. While compositional data provides a robust foundation, it primarily captures the ratios of elements within a material, often neglecting the spatial arrangement of these elements. This limitation becomes significant when predicting properties sensitive to crystal symmetry and doping levels, such as the bandgap. In these cases, compositional data alone may lack the physical and chemical context needed to capture subtle variations, hindering prediction accuracy.
Alloys can form multiple phases, including solid solutions, intermetallic compounds, and amorphous phases. Each phase exhibits distinct chemical compositions and interactions that determine the alloy’s overall properties. A key challenge in applying ECSG to alloys lies in the need to predefine possible phases and their corresponding compositions to ensure accurate predictions.
Moving forward, we plan to address these challenges by developing structure-based models and phase composition prediction models. We will integrate these models into ECSG to capture both compositional and structural aspects, enhancing the framework’s ability to predict complex properties accurately. This ensembling approach will allow ECSG to bridge the gap between compositional and spatial information, making it more effective across diverse material systems.
Methods
Database
In this work, we compared the performance of various models in predicting the stability of inorganic compounds on three large DFT-computed datasets, MP, OQMD, and JARVIS. Before using these databases, data preprocessing was required. After excluding noble gas and radioactive elements, the MP database contained 85,014 compounds with information on thermodynamic properties such as formation energy. Compounds with a below 0 meV/atom were considered stable and are labeled accordingly. The same data processing method was applied to the OQMD and JARVIS databases, and datasets in unknown spaces. The number of positive and negative samples in each database is shown in Supplementary Table 15.
In our experiment, we divided our dataset into a test set , which comprised 10% of the total data, and a training set , which constituted the remaining 90%. To assess sample efficiency, we incrementally increased the training set size in 10% increments of . This meant starting the experiment with only 10% of as the training set, subsequently increasing it to 20%, and finally employing the entire as the training set.
When exploring new perovskite oxides, we utilized a database which includes 3469 single/double perovskite oxides along with their corresponding stability information. The stability of these compounds was calculated using DFT. To ensure compatibility with the data available in the MP database, all parameters and pseudopotential flavors were carefully chosen. Additionally, the partition of the data into training and testing sets within this database was consistent with the MP database.
Base-level models
ECSG contains three base-level models: Magpie, Roost and ECSG. Magpie incorporates chemical information for each element into its material representations using features such as atomic electronegativity, atomic radii, and elemental group. This results in a total of 132 features, generated using the Matminer62, and the model is trained using XGBoost.
Roost utilizes Matscholar embeddings63 and employs a GAT with three message-passing layers. The output network of Roost consists of a deep neural network with 5 hidden layers, each featuring ReLU activations. The hidden units in these layers are 1024, 512, 256, 128, and 64, respectively.
In contrast to conventional computational models for predicting compound stability, ECCNN uniquely incorporates the electronic configuration of elements into its compositional input. Given the complexity of interactions between atoms and electrons within compounds, determining the precise electron arrangements can be challenging. To address this, we simplify the electron arrangements of compounds by representing them as the electron configurations of individual atoms. The input matrix of ECCNN has three dimensions: each row vector represents the electron configuration of an individual element (referred to as EC vectors), the column index corresponds to the type of element, and the third dimension stacks features based on the number of atoms in the chemical formula. This stacked input matrix is then fed into ECCNN for prediction and analysis.
The types of elements in a compound are represented by their electron configurations, which form the core of the model input. According to modern quantum mechanics, the outer-shell electrons of an atom are arranged in orbitals around the atomic nucleus according to their energy levels. The energy levels are arranged in shells, starting with shell 1 for elements in the first period, followed by shells 2, 3, and so on. Within each shell, electrons are further divided into subshells, denoted by letters (s, p, d, and f) each with specific maximum electron capacities: 2 for s, 6 for p, 10 for d, and 14 for f. Therefore, a subshell can be labeled using the notation , where represents the shell number, and corresponds to the subshell index (e.g., 2 s for the s subshell in shell 2). In this study, the elements up to the seventh period are considered. The subshells are organized by increasing electron energy level: 1 s, 2 s, 2p, 3 s, 3p, 4 s, 3 d, 4p, 5 s, 4 d, 5p, 6 s, 4 f, 5 d, 6p, 7 s, 5 f, and 6 d. By using this notation to represent electron configurations, the ECCNN model can effectively capture and utilize the relevant electronic information necessary for predicting compound stability.
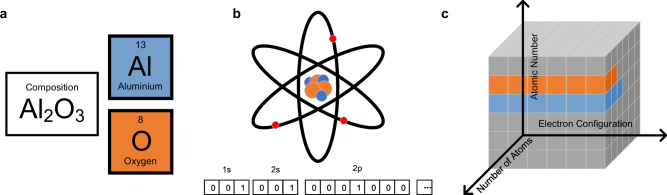
The construction of the features for ECCNN is illustrated in Fig. 8. The first step involves identifying the categories of elements in the compound. As shown in Fig. 8a, elements oxygen and aluminum are identified from the compound Al2O3. To represent the number of electrons in each subshell, one-hot encoding is employed, as displayed in Fig. 8b. Through one-hot encoding, the length of the feature vector for each subshell corresponds to its maximum electron capacity. For example, [0 0 1], [0 1 0], and [1 0 0] represent 0, 1, and 2 electrons in the 2 s subshell, respectively. Subsequently, these subshell feature vectors are concatenated to form atom features with a length of 168. Elements up to the 118th element in the periodic table are considered in this construction process resulting in the type of elements in a compound being represented by a two-dimensional matrix of 118 × 168.
Fig. 8. The feature construction of Al2O3 for Electron Configuration Convolutional Neural Network (ECCNN).
a The elements type, (b) the Electron Configuration (EC) vector for each element, and (c) the inputs matrix of ECCNN. The blue and orange cubes indicate elements Al and O, respectively, while the grey cubes represent regions of the matrix that do not contain information about electron configuration.
Once the type of elements in a compound has been determined, the number of atoms is represented by the third dimension of the input. For inorganic compounds, the molecular weight is generally small. In the training set, the maximum binary length of the atomic count for a single element in the MP dataset is 8, So the length of the third dimension is set to 8, resulting in a final input shape of 118 × 168 × 8. Here, 168 indicates the length of the EC vector, which represents the electron configuration of different elements. 118 represents the number of possible element types in this study, while the 8 channels represent the number of atoms of each element after conversion to binary. For example, if A and B elements in a chemical formula have 2 and 10 atoms respectively, their values in the 8 channels are 01000000 and 01010000. As demonstrated in Fig. 8c, if a compound’s chemical formula contains n atoms of the i-th element, the atom feature for that element is repeated n times in the third dimension, with the remaining positions zero-padded. For example, in the compound Al2O3, there are two Al atoms and three O atoms. In the second dimension, all positions except those occupied by Al and O are set to 0. The electron configuration feature of Al is then repeated twice, and that of O is repeated three times in the third dimension. This representation ensures that the model can effectively capture the composition and structural information of the compound, enabling ECCNN to accurately predict and analyze the stability of the compounds.
Model training
We utilized a highly effective ensemble technique called SG to combine the predictions from these individual models for forecasting the thermodynamic stability of materials. This ensemble method involves two types of models: base-level models and a meta-level model. To create the ensemble model, multiple models (e.g., three models) were trained separately using the available data. The output predictions generated by these models were then collected and used as the training set for a meta-level model. This meta-level model was trained on these predictions to learn how to combine them effectively, ultimately producing the ensemble model’s final predictions.
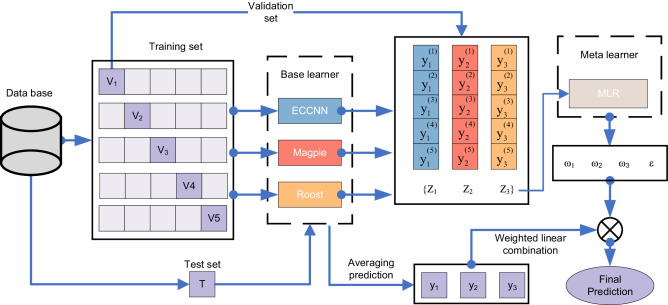
In this study, the base-level models include ECCNN, Roost, and Magpie, denoted as , , and . The meta-level model is a multi-response linear regression (MLR), denoted as . The outputs of the base-level models, , , and , are assigned non-negative weights, , , and , by the meta-level model. The final weighted linear combination forms the ECSG output: , where , , , and are learnable parameters.
The training of the meta-level model requires a five-fold split of the training set. As shown in Fig. 9, for each base model, we iteratively train on four folds and predict on the remaining fold, repeat this five times, and get the prediction of the model on the entire training set. For example, model is trained on the four folds and predicts on the remaining fold , yielding . Repeating this process five times produces the set , forming after concatenation. The same procedure is followed for and to generate and . The meta-model is then trained on {, , } and labels of training set to obtain the parameters , , , and .
Fig. 9. Training and testing process of Electron Configuration models with Stacked Generalization (ECSG).
The outputs of base-level models, including the Electron Configuration Convolutional Neural Network (ECCNN), Magpie35, Roost, are used to train the meta-level model. MLR refers to multi-response linear regression70. Symbols used in the figure are defined as follows: represents the i-th fold of the training set; denotes the prediction of the n-th model on the training set; is the n-th model’s prediction for the i-th fold; indicates the weight assigned to the n-th model by the meta learner; is the intercept in the meta-learner; and is the n-th model’s prediction on the test set. Here, i = 1, 2, 3, 4, 5 and n = 1,2,3.
When predicting new compounds , we average the predictions from , , and trained on each of the four folds in the previous step. This yields outputs , , and , from which we can obtain the prediction of the stability of . This approach has two advantages. Firstly, it increases the diversity of base-level models by utilizing different samples in each cross-validation iteration. Secondly, the training data in the meta-level model remains distinct from the foundational models, reducing the risk of overfitting.
First principles calculation
The total energy calculations in this study were performed using the DFT framework as implemented in the Vienna ab initio simulation package (VASP)64,65. The Generalized Gradient Approximation (GGA) was used in the form of the parameterization proposed by Perdew, Burke, and Ernzerhof (PBE). Brillouin zone integrations were performed using a Monkhorst−Pack mesh with at least 5000 k points per reciprocal atom. Full relaxations were realized by using the Methfessel−Paxton smearing method of order one, followed by a final self-consistent static calculation using the tetrahedron smearing method with Blöchl corrections. A cutoff energy of 533 eV was set for all of the calculations, and spin polarization was accounted for.
Both the cell volumes and ionic positions of the structures were allowed to relax to their cubic ground states. The relaxations were carried out in three stages: the first stage allowed changes in volume (corresponding to the VASP ISIF = 7 tag), the second stage permitted only the ions to relax (corresponding to the VASP ISIF = 2 tag), followed by a final self-consistent static calculation. The relaxation process continued until changes in total energy between relaxation steps were within 1 × 10−6 eV and atomic forces on each atom were less than 0.01 eV/ Å.
As noted earlier, the MP database was employed to extract for all the compounds in the data sets. MP consists of DFT computations of experimentally observed compounds from the ICSD database66, as well as hypothetical compounds that may or may not be experimentally observable. To construct the convex hull for each set of elements comprising A-A′-B-B′-O, the total energy data of all compounds in the MP database was considered and extracted using the database API67.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Supplementary information
Source data
Acknowledgements
This work was supported in part by the Project of Xiangjiang Laboratory (No. 23XJ01011), the Science Foundation for Distinguished Young Scholars of Hunan Province (NO. 2023JJ10080). This work was carried out in part using computing resources at the High Performance Computing Center of Central South University. Z.D. acknowledges the support from his Lee Kuan Yew Postdoctoral Fellowship 22-5930-A0001 and the Ministry of Education, Singapore, under the Academic Research Fund Tier 1 (FY2024).
Author contributions
Hao Z. and Jianxin W. conceived and designed this research project. Hao Z. built and trained the machine learning models and analyzed the results. Haochen Z. assisted with developing the architecture and provided insight and guidance during model optimization and training. Jiong W. and Z.D. performed the DFT calculations. M.L. contributes to the review of writing. All authors participated in preparing and editing the manuscript.
Peer review
Peer review information
Nature Communications thanks the anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Data availability
Source data are provided with this paper in the Source Data file. All described datasets are obtained from various public websites, including MP (https://materialsproject.org), OQMD, and JARVIS. The processed database files are available at https://github.com/Haozou-csu/ECSG68. The results of DFT calculations are available at 10.5281/zenodo.1420767868. Source data are provided with this paper.
Code availability
All the machine learning models are implemented in Python and the source code has been deposited at https://github.com/Haozou-csu/ECSG and 10.5281/zenodo.1420253468.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
The online version contains supplementary material available at 10.1038/s41467-024-55525-y.
References
- 1.Wang, Q. & Zhang, L. Inverse design of glass structure with deep graph neural networks. Nat. Commun.12, 5359 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Bartel, C. J. et al. New tolerance factor to predict the stability of perovskite oxides and halides. Sci. Adv.5, eaav0693 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Yao, Z. et al. Machine learning for a sustainable energy future. Nat. Rev. Mater.8, 202–215 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Yuan, R. et al. Accelerated Search for BaTiO(3)-Based Ceramics with Large Energy Storage at Low Fields Using Machine Learning and Experimental Design. Adv. Sci.6, 1901395 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.George, E. P., Raabe, D. & Ritchie, R. O. High-entropy alloys. Nat. Rev. Mater.4, 515–534 (2019). [Google Scholar]
- 6.Emery, A. A. & Wolverton, C. High-throughput DFT calculations of formation energy, stability and oxygen vacancy formation energy of ABO3 perovskites. Sci. Data4, 170153 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bartel, C. J. et al. A critical examination of compound stability predictions from machine-learned formation energies. npj Comput. Mater.6, 97 (2020). [Google Scholar]
- 8.Saal, J. E., Kirklin, S., Aykol, M., Meredig, B. & Wolverton, C. Materials Design and Discovery with High-Throughput Density Functional Theory: The Open Quantum Materials Database (OQMD). JOM65, 1501–1509 (2013). [Google Scholar]
- 9.Bartel, C. J. Review of computational approaches to predict the thermodynamic stability of inorganic solids. J. Mater. Sci.57, 10475–10498 (2022). [Google Scholar]
- 10.Pandey, S., Qu, J., Stevanović, V., St. John, P. & Gorai, P. Predicting energy and stability of known and hypothetical crystals using graph neural network. Patterns2, 100361 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Liang, Y. et al. A universal model for accurately predicting the formation energy of inorganic compounds. Sci. China Mater.66, 343–351 (2022). [Google Scholar]
- 12.Li, K., DeCost, B., Choudhary, K., Greenwood, M. & Hattrick-Simpers, J. A critical examination of robustness and generalizability of machine learning prediction of materials properties. npj Comput. Mater.9, 55 (2023). [Google Scholar]
- 13.Wang, L., He, Z. & Ouyang, B. Data driven design of compositionally complex energy materials. Comput. Mater. Sci230, 112513 (2023). [Google Scholar]
- 14.Atsumi, T. et al. Chemical Composition Data-Driven Machine-Learning Prediction for Phase Stability and Materials Properties of Inorganic Crystalline Solids. Physica Status Solidi B-Basic Solid State Phys.259, 2100525 (2022). [Google Scholar]
- 15.Gu, G. H., Jang, J., Noh, J., Walsh, A. & Jung, Y. Perovskite synthesizability using graph neural networks. npj Comput. Mater.8, 71 (2022). [Google Scholar]
- 16.Schmidt, J., Pettersson, L., Verdozzi, C., Botti, S. & Marques, M. A. L. Crystal graph attention networks for the prediction of stable materials. Sci. Adv.7, eabi7948 (2021). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Haastrup, S. et al. The Computational 2D Materials Database: high-throughput modeling and discovery of atomically thin crystals. 2D Mater5, 042002 (2018). [Google Scholar]
- 18.Jain, A. et al. Commentary: The Materials Project: A materials genome approach to accelerating materials innovation. APL Mater1, 011002 (2013). [Google Scholar]
- 19.Curtarolo, S. et al. AFLOW: An automatic framework for high-throughput materials discovery. Comput. Mater. Sci.58, 218–226 (2012). [Google Scholar]
- 20.Kirklin, S. et al. The Open Quantum Materials Database (OQMD): assessing the accuracy of DFT formation energies. npj Comput. Mater.1, 1–15 (2015). [Google Scholar]
- 21.Couzinie, J. P., Senkov, O. N., Miracle, D. B. & Dirras, G. Comprehensive data compilation on the mechanical properties of refractory high-entropy alloys. Data Brief21, 1622–1641 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Gorsse, S., Nguyen, M. H., Senkov, O. N. & Miracle, D. B. Database on the mechanical properties of high entropy alloys and complex concentrated alloys. Data Brief21, 2664–2678 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Jha, D. et al. Extracting Grain Orientations from EBSD Patterns of Polycrystalline Materials Using Convolutional Neural Networks. Microsc. Microanal.24, 497–502 (2018). [DOI] [PubMed] [Google Scholar]
- 24.Cecen, A., Dai, H., Yabansu, Y. C., Kalidindi, S. R. & Song, L. Material structure-property linkages using three-dimensional convolutional neural networks. Acta Mater146, 76–84 (2018). [Google Scholar]
- 25.Ye, W., Chen, C., Wang, Z., Chu, I. H. & Ong, S. P. Deep neural networks for accurate predictions of crystal stability. Nat. Commun.9, 3800 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ryan, K., Lengyel, J. & Shatruk, M. Crystal Structure Prediction via Deep Learning. J Am Chem Soc140, 10158–10168 (2018). [DOI] [PubMed] [Google Scholar]
- 27.Yang, Z. et al. Deep learning approaches for mining structure-property linkages in high contrast composites from simulation datasets. Comput. Mater. Sci151, 278–287 (2018). [Google Scholar]
- 28.Jha, D. et al. IRNet: A General Purpose Deep Residual Regression Framework for Materials Discovery. In: Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining - KDD ‘19) (2019).
- 29.Jha, D. et al. ElemNet: Deep Learning the Chemistry of Materials From Only Elemental Composition. Sci. Rep.8, 17593 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Kailkhura, B., Gallagher, B., Kim, S., Hiszpanski, A. & Han, T. Y.-J. Reliable and explainable machine-learning methods for accelerated material discovery. npj Comput. Mater.5, 108 (2019). [Google Scholar]
- 31.Agrawal A., Meredig B., Wolverton C., Choudhary A. A Formation Energy Predictor for Crystalline Materials Using Ensemble Data Mining. In: 2016IEEE 16th International Conference on Data Mining Workshops (ICDMW)) (2016).
- 32.Meredig, B. et al. Combinatorial screening for new materials in unconstrained composition space with machine learning. Phys. Rev. B89, 094104 (2014). [Google Scholar]
- 33.Jha, D. et al. Enhancing materials property prediction by leveraging computational and experimental data using deep transfer learning. Nat. Commun.10, 5316 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Liu, R. et al. Deep learning for chemical compound stability prediction. In: Proceedings of ACM SIGKDD workshop on large-scale deep learning for data mining (DL-KDD)) (2016).
- 35.Ward, L., Agrawal, A., Choudhary, A. & Wolverton, C. A general-purpose machine learning framework for predicting properties of inorganic materials. npj Comput. Mater.2, 16028 (2016). [Google Scholar]
- 36.Xie, T. & Grossman, J. C. Crystal Graph Convolutional Neural Networks for an Accurate and Interpretable Prediction of Material Properties. Phys Rev Lett120, 145301 (2018). [DOI] [PubMed] [Google Scholar]
- 37.Zeng, S. et al. Atom table convolutional neural networks for an accurate prediction of compounds properties. npj Comput. Mater.5, 84 (2019). [Google Scholar]
- 38.Zhou, Z.-H. Ensemble methods: foundations and algorithms. CRC press (2012).
- 39.Agrawal, A. & Choudhary, A. Deep materials informatics: Applications of deep learning in materials science. MRS Commun9, 779–792 (2019). [Google Scholar]
- 40.Sesmero, M. P., Ledezma, A. I. & Sanchis, A. Generating ensembles of heterogeneous classifiers using Stacked Generalization. Wiley Interdiscip. Rev.: Data Min. Knowl. Discovery5, 21–34 (2015). [Google Scholar]
- 41.Wolpert, D. H. Stacked generalization. Neural Networks5, 241–259 (1992). [Google Scholar]
- 42.Van der Laan, M. J., Polley E. C. & Hubbard, A. E. Super learner. Stat. Appl. Genet. Mol. Biol. 6, 25 (2007). [DOI] [PubMed]
- 43.Antunes, L. M., Butler, K. T. & Grau-Crespo, R. Predicting thermoelectric transport properties from composition with attention-based deep learning. Mach. Learn.: Sci. Technol.4, 015037 (2023). [Google Scholar]
- 44.Tian, S. I. P., Walsh, A., Ren Z. & Li Q., Buonassisi T. What Information is Necessary and Sufficient to Predict Materials Properties using Machine Learning? arXiv preprintarXiv:2206.04968, (2022).
- 45.Zhuang, Z. & Barnard, A. S. Structure-Free Mendeleev Encodings of Material Compounds for Machine Learning. Chem. Mater.35, 9325–9338 (2023). [Google Scholar]
- 46.Morgan, D. & Jacobs, R. Opportunities and Challenges for Machine Learning in Materials Science. Annu. Rev. Mater. Res.50, 71–103 (2020). [Google Scholar]
- 47.Gu, J. et al. Recent advances in convolutional neural networks. Pattern recognition77, 354–377 (2018). [Google Scholar]
- 48.Goodall, R. E. A. & Lee, A. A. Predicting materials properties without crystal structure: deep representation learning from stoichiometry. Nat. Commun.11, 6280 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Chen T. & Guestrin C. Xgboost: A scalable tree boosting system. In: Proceedings of the 22nd acm sigkdd international conference on knowledge discovery and data mining) (2016).
- 50.Choudhary, K. et al. The joint automated repository for various integrated simulations (JARVIS) for data-driven materials design. npj Comput. Mater. 6, 173 (2020).
- 51.Hancock, J. T., Khoshgoftaar, T. M. & Johnson, J. M. Evaluating classifier performance with highly imbalanced Big Data. Journal of Big Data10, 42 (2023). [Google Scholar]
- 52.Green, M. A., Ho-Baillie, A. & Snaith, H. J. The emergence of perovskite solar cells. Nat. Photonics8, 506–514 (2014). [Google Scholar]
- 53.Mashrafi, M., Anik, M. H. K., Israt, M. F., Habib, A. & Islam, S. Modeling the path to> 30% power conversion efficiency in perovskite solar cells with plasmonic nanoparticles. RSC Adv13, 19447–19454 (2023). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Rong, Y. et al. Challenges for commercializing perovskite solar cells. Science361, eaat8235 (2018). [DOI] [PubMed] [Google Scholar]
- 55.Ryu, B., Wang, L., Pu, H., Chan, M. K. & Chen, J. Understanding, discovery, and synthesis of 2D materials enabled by machine learning. Chem. Soc. Rev.51, 1899–1925 (2022). [DOI] [PubMed] [Google Scholar]
- 56.Zhou, J. et al. 2DMatPedia, an open computational database of two-dimensional materials from top-down and bottom-up approaches. Sci. Data6, 86 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Gjerding, M. N. et al. Recent progress of the computational 2D materials database (C2DB). 2D Mater8, 044002 (2021). [Google Scholar]
- 58.Xie, T. et al. Large language models as master key: unlocking the secrets of materials science with GPT. arXiv preprint arXiv:2304.02213, (2023).
- 59.Wang, K. et al. Perovskite oxide catalysts for advanced oxidation reactions. Adv. Funct. Mater.31, 2102089 (2021). [Google Scholar]
- 60.Cao, Y. et al. Recent advances in perovskite oxides as electrode materials for supercapacitors. Chemical Communications57, 2343–2355 (2021). [DOI] [PubMed] [Google Scholar]
- 61.Talapatra, A., Uberuaga, B. P., Stanek, C. R. & Pilania, G. A Machine Learning Approach for the Prediction of Formability and Thermodynamic Stability of Single and Double Perovskite Oxides. Chem. Mater.33, 845–858 (2021). [Google Scholar]
- 62.Ward, L. et al. Matminer: An open source toolkit for materials data mining. Comput. Mater. Sci152, 60–69 (2018). [Google Scholar]
- 63.Tshitoyan, V. et al. Unsupervised word embeddings capture latent knowledge from materials science literature. Nature571, 95–98 (2019). [DOI] [PubMed] [Google Scholar]
- 64.Kresse, G. Comput. matter sci. Phys. Rev. B54, 11–169 (1996). [Google Scholar]
- 65.Kresse, G. Software vasp, vienna, 1999; g. kresse, j. furthmüller. Phys. Rev. B54, 169 (1996). [Google Scholar]
- 66.Zagorac, D., Müller, H., Ruehl, S., Zagorac, J. & Rehme, S. Recent developments in the Inorganic Crystal Structure Database: theoretical crystal structure data and related features. J. Appl. Crystallogr.52, 918–925 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Ong, S. P. et al. Python Materials Genomics (pymatgen): A robust, open-source python library for materials analysis. Comput. Mater. Sci68, 314–319 (2013). [Google Scholar]
- 68.Zou, H. et al. Predicting Thermodynamic Stability of Inorganic Compounds Using Ensemble Machine Learning Based on Electron Configuration. ECSG 10.5281/zenodo.14202534 (2024). [DOI] [PMC free article] [PubMed]
- 69.Wang, A. Y.-T., Kauwe, S. K., Murdock, R. J. & Sparks, T. D. Compositionally restricted attention-based network for materials property predictions. npj Comput. Mater.7, 77 (2021). [Google Scholar]
- 70.Ting, K. M. & Witten, I. H. Issues in stacked generalization. J. Artificial Intelligence Res.10, 271–289 (1999). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
Source data are provided with this paper in the Source Data file. All described datasets are obtained from various public websites, including MP (https://materialsproject.org), OQMD, and JARVIS. The processed database files are available at https://github.com/Haozou-csu/ECSG68. The results of DFT calculations are available at 10.5281/zenodo.1420767868. Source data are provided with this paper.
All the machine learning models are implemented in Python and the source code has been deposited at https://github.com/Haozou-csu/ECSG and 10.5281/zenodo.1420253468.