Skillful seasonal predictions of continental East-Asian summer rainfall by integrating its spatio-temporal evolution

Abstract

Skillful seasonal climate prediction is critical for food and water security over the world’s heavily populated regions, such as in continental East Asia. Current models, however, face significant difficulties in predicting the summer mean rainfall anomaly over continental East Asia, and forecasting rainfall spatiotemporal evolution presents an even greater challenge. Here, we benefit from integrating the spatiotemporal evolution of rainfall to identify the most crucial patterns intrinsic to continental East-Asian rainfall anomalies. A physical-statistical prediction model is developed to capture the predictability offered by these patterns through a detection of precursor signals that describe slowly varying lower boundary conditions. The presented model demonstrates a prediction skill of 0.51, at least twice as high as that of the best dynamical models available (0.26), indicating improved prediction for both the spatiotemporal evolution and summer mean of rainfall anomalies. This advance marks a crucial step toward delivering skillful seasonal predictions to populations in need of new tools for managing risks of both near-term climate disasters, such as floods and droughts, and long-term climate change.

This study proposes a physical-statistical model that significantly improves seasonal predictions of the spatiotemporal evolution of East-Asian rainfall anomalies, outperforming current state-of-the-art dynamical models in forecasting climate disasters.

Introduction

The spatiotemporal evolution of continental East-Asian monsoon rainfall during boreal summer (May to September) displays the unique characteristics of stepwise meridional advances and retreats. It advances northward from South China primarily in May, abruptly extends to the Yangtze River Basin and part of Japan in June, and eventually retreats to parts of North China, Korea, and Japan¹. Such a spatiotemporal evolution exhibits significant year-to-year variability, triggering persistent flood and drought disasters across time and regions and generating substantial influences on the economic and societal activities of approximately one-third of the world’s population^2,3. For instance, during the boreal summer of 2020, a significant portion of continental East Asia experienced the heaviest monsoon rainfall since 1961, leading to persistent flooding of the Yangtze River and severe droughts in South China⁴. The disaster displaced millions of residents, triggered a historic public health crisis, and brought devastating socioeconomic impacts. Preventing and mitigating similar disasters rely on more timely, detailed, and accurate seasonal predictions of the spatiotemporal evolution of continental East-Asian summer rainfall anomalies, rather than a prediction of their summer mean patterns^1,5,6. Improvements in seasonal predictions of East-Asian rainfall anomalies can bring substantial socioeconomic benefits for millions of people. Despite great progress in understanding the basic physics of monsoon rainfall variability since 1886, predicting continental East-Asian summer rainfall anomalies remains one of the most challenging tasks in climate prediction, which stems from the complicated interactions among land-ocean-atmospheric modes of variability across seasonal to interdecadal time scales^5–12.

The predictability of East-Asian monsoon rainfall primarily comes from slowly varying boundary conditions, including large-scale circulation patterns^13–16, sea surface temperature^17–22, and land surface conditions such as snow cover and moisture^23,24. However, the seasonal predictions of continental East-Asian rainfall anomalies in coupled global climate models have not demonstrated a satisfactory success so far^10,25,26. For example, the multi-model ensemble (MME) mean of the nine coupled climate models, mainly sourced from the Copernicus Climate Change Service (C3S) as part of the Copernicus Programme²⁷, with some dynamic models having participated in the ENSEMBLES project²⁸, exhibits low prediction skills in predicting the conventional summer mean of East-Asian rainfall anomalies^5,25,29–31. This limitation is largely attributed to the key factors such as initialization, the ability to reproduce coupled ocean-atmosphere processes, and model resolution and performance^32–36. Accurately predicting the spatiotemporal evolution of anomalous summer rainfall over continental East Asia is even more challenging for these dynamical models, as forecast skills decrease rapidly with increasing forecast lead time (Fig. 1 and Supplementary Table 1). Seasonal prediction of East-Asian rainfall anomalies has seen some successes in empirical and statistical models, where stationary relationships between rainfall anomalies and precursors have been employed based on observational large-scale coherent rhythms^26,36,37. However, previous statistical models often focused on specific seasons or months over fixed regions, with less emphasis on capturing the intricate spatiotemporal evolution of rainfall anomalies^1,6,8. Predicting the latter undoubtedly poses an extreme challenge. Only few studies have recognized and developed seasonal predictions for the spatiotemporal evolution of continental East-Asian rainfall anomalies, despite the fact that such predictions are more valuable for formulating prevention and mitigation plans dealing with successive flood and drought disasters^11,26. Meanwhile, skillful seasonal predictions of the spatiotemporal evolution of rainfall anomalies contribute to improve prediction of rainfall spatial distribution at specific times, such as the conventional summer mean. The key question is then how to predict the spatiotemporal evolution of continental East-Asian rainfall anomalies, given the many failed attempts from the current dynamical and statistical models.

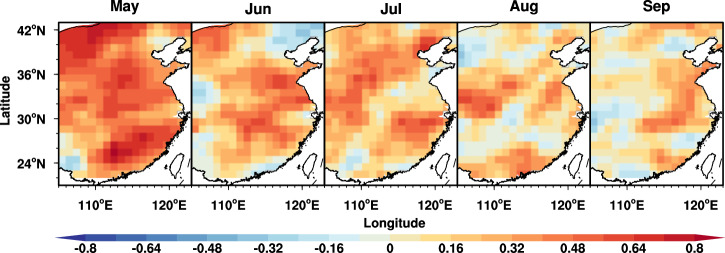
Fig. 1. Seasonal prediction skills of current dynamical models for the spatiotemporal evolution of rainfall anomalies over continental East Asia.

The temporal correlation skills for predicting rainfall anomalies in each month using the multi-model ensemble (MME) mean of the nine dynamical models initiated from May during 1993–2016. The five columns from left to right are for the skills in May, June, July, August, and September, respectively.

The objective of this study is to identify the dominant spatiotemporal evolution patterns of rainfall anomalies over continental East-Asia from a latitude-time domain perspective, capture their representative precursors depicting slowly varying lower boundary conditions, and develop a physically based statistical model utilizing the identified seasonal patterns and precursors to generate skillful seasonal predictions of East-Asian rainfall anomalies. Subsequent section demonstrates that this proposed approach exhibits excellent skills in predicting both the spatiotemporal evolution and conventional summer mean of continental East-Asian rainfall anomalies, showcasing notable improvements compared to the current dynamical MME hindcast.

Results

Spatiotemporal evolution patterns of rainfall anomalies

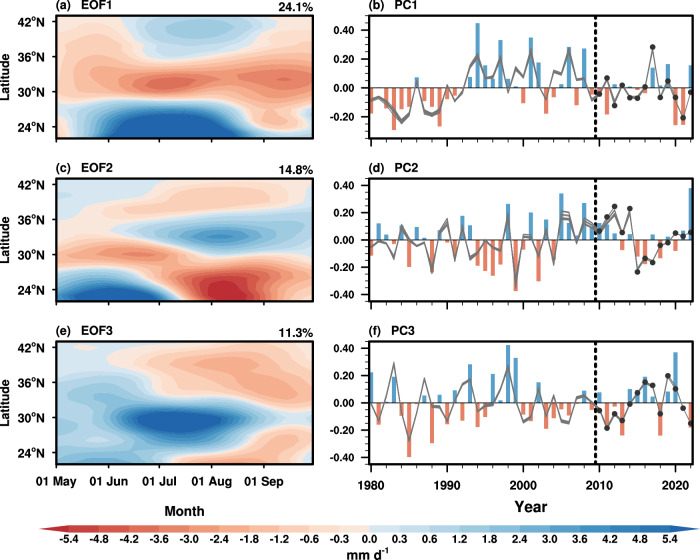
We identify spatiotemporal evolution patterns of the seasonal rainfall anomalies over continental East Asia by applying empirical orthogonal function (EOF) analysis in the latitude-time (day) domain to daily precipitation anomalies zonally averaged from 105° to 123°E (see Methods). Figure 2 shows the three leading EOF patterns and the corresponding year-to-year variations of principal components (PCs). This indicates that the spatiotemporal evolution of East-Asian rainfall anomalies, which vary both seasonally and yearly, can be decomposed into three distinct seasonal spatiotemporal patterns from May to September, each with its own year-to-year PC variation. The variations of these three patterns collectively explain 50.2% of the total variance in summer rainfall variations over continental East Asia. Pattern 1 displays a tripolar pattern characterized by a negative anomaly in central East Asia, sandwiched by strong and weak positive anomalies in southern and northern East Asia, respectively. This tripolar pattern resembles the East Asian portion of the global precipitation mode in summer³⁸. However, it undergoes variations in strength with seasons, with the three anomalous rain belts being strongest in mid-summer, and the central one gradually becomes dominant in later summer. Thus, pattern 1 is referred to as the persistent evolving pattern of East-Asian rainfall anomalies. Pattern 2 presents a seasonal reversal of the dipolar pattern known as South Flood-North Drought. The anomalous rainfall pattern shifts from floods in south and droughts in north during May-June to droughts in south and floods in north during July-September. It also exhibits a seasonal migration of the rainbelt center with a sudden northward jump around July, consistent with findings in previous studies^39,40. Thus, we name pattern 2 as the reversal evolving pattern. Pattern 3 displays the north-south propagation of an anomalous rainbelt dipole, with the southern rainbelt advancing northward and the northern rainbelt retreating southward as season progresses. Hence, pattern 3 is referred to as the propagating evolving pattern. It should be pointed out that the three spatiotemporal patterns aforementioned can also be identified without zonal mean (Supplementary Fig. 1). These three spatiotemporal patterns and their year-to-year variations from station-based data are closely resemble those from other satellite-gauge-based precipitation datasets (Supplementary Figs. 2–5). Therefore, they represent the dominant spatiotemporal patterns of rainfall anomalies over continental East Asia, providing an alternative perspective to describe the spatiotemporal evolution of rainfall anomalies. The sum of the products of the three distinct spatiotemporal patterns and their yearly time series can effectively represent the rainfall anomalies both at a given instant and throughout their slow-varying subseasonal to seasonal evolution.

Fig. 2. Spatiotemporal patterns of continental East-Asian summer rainfall anomalies.

The left panels (a, c, e) display the spatiotemporal evolution patterns corresponding to the leading three modes of empirical orthogonal functions (EOFs) derived from daily precipitation anomalies zonally averaged over East Asia during training period of boreal 1980–2009 summers. The unit of the color bar for the spatiotemporal patterns is mm d^–1. The bars in the right panels (b, d, f) are the year-to-year variability of normalized principal components (PCs) of the three spatiotemporal patterns, and the 13 gray curves correspond to the PC variations obtained from the new physical-statistical prediction model (PSM) covering the periods of 1980–2010, 1980–2011, …, and 1980–2022, respectively. The 13 dots at the end of the 13 gray curves denote independent retrospective forecasts for the period of 2010–2022.

Precursors for year-to-year variations of the spatiotemporal patterns

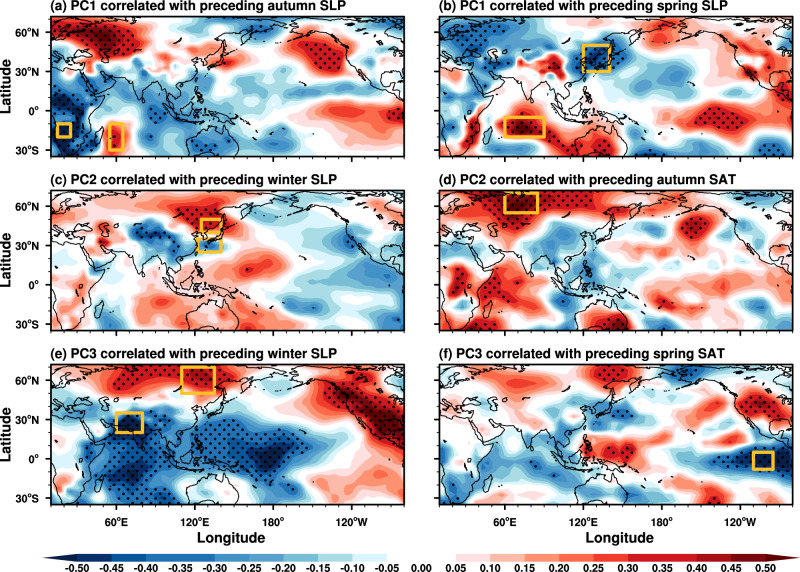
To discern potential precursors (early indicators or predictors) contributing to the year-to-year variability of the three spatiotemporal patterns, we conduct a precursor search guided by insights from prior studies on the Indian monsoon prediction⁴¹. Here we focus on two key variables, sea level pressure (SLP) and surface air temperature (SAT) in preceding seasons (autumn, winter, and spring) during 1980–2009. We search for signals of high significance on the correlation maps between the time series (i.e., PCs) of the three spatiotemporal patterns and the SLP or SAT anomalies in preceding seasons, as shown in Fig. 3. Significant early signals in the SLP anomalies associated with PC1 variation are mainly manifested by high correlations during preceding autumn (Fig. 3a) and preceding spring (Fig. 3b). Upon closer examination, we identify two precursors that meet the criterion of mutual independence: One precursor is the areal mean difference of SLP anomalies over the two yellow boxes in Fig. 3a, denoted as IAP in Table 1, representing a see-saw pattern of SLP between the southwest Indian Ocean and southern Africa in the preceding autumn. The other precursor is the areal mean difference over the two yellow boxes in Fig. 3b, denoted as EIP in Table 1, representing a see-saw pattern of SLP between northern East Asia and Mascarene in the preceding spring. Both the IAP and EIP time series have high correlations with PC1 variation, but only a weak correlation between each other, and thus can be regarded as two relatively independent precursors for the year-to-year variation of the persistent evolving pattern.

Fig. 3. The correlation maps between year-to-year variations of principal components (PCs) and sea level pressure (SLP) or surface air temperature (SAT) anomalies.

The correlation maps of yearly PC1 variation and SLP anomalies in (a) preceding autumn and (b) preceding spring. The correlation coefficients of PC2 variation with (c) SLP anomalies in preceding winter and (d) SAT anomalies in preceding autumn. The correlation maps of PC3 variation with (e) SLP anomalies in preceding winter and (f) SAT anomalies in preceding spring. Significant values marked by black dots exceed the 90% confidence level. The yellow boxes outline the regions used for defining precursors in Table 1.

Table 1.

Definitions of the six precursors associated with year-to-year variations of the three spatiotemporal patterns

Order	Name	Definition
1	IAP	Zonal sea level pressure (SLP) contrast between southwest Indian Ocean (10 to 30°S, 55° to 65°E) and southern Africa (10° to 20°S, 12° to 25°E) in preceding autumn.
2	EIP	Meridional SLP contrast between northern East Asia (30° to 50°N, 120° to 140°E) and Mascarene of Indian Ocean (5° to 20°S, 60° to 90°E) in preceding spring.
3	EWP	Meridional SLP contrast between northern East Asia (40° to 50°N, 125° to 140°E) and western Pacific (20° to 35°N, 120° to 140°E) in preceding winter.
4	ET	Spatial mean surface air temperature (SAT) over mid-latitude Eurasian continent (55° to 70°N, 60° to 85°E) in preceding autumn.
5	ESAP	Meridional SLP difference between high-latitude East Asia (50° to 70°N, 110° to 135°E) and northern South Asia (20° to 35°N, 60° to 80°E) in preceding winter.
6	EPT	El Niño-Southern Oscillation (ENSO)-related SAT averaged over eastern Pacific ($8^{\circ }$S to 5°N, 110° to 95°W) in preceding spring.

Only SLP anomalies in preceding winter and SAT anomalies in preceding autumn are found to have significant correlations with PC2 variation. Again, to maximize these correlation signals for PC2’ seasonal forecast, we identify two precursors that meet the aforementioned criterion. One precursor is the areal mean difference of SLP anomalies over the two yellow boxes in Fig. 3c, denoted as EWP in Table 1, indicating a see-saw pattern of SLP between northern East Asia and the western Pacific in the preceding winter. The other precursor is the area-averaged SAT anomalies over the yellow box in Fig. 3d, denoted by ET in Table 1, representing abnormal pattern of SAT over the mid-latitude Eurasia in the preceding autumn. Both the EWP and ET precursors have good correlations with PC2 variation, and represent two independent precursors of year-to-year variation in the reversal evolving pattern.

Following similar procedures, we identify two precursors for PC3 variation: One precursor is the areal mean difference of SLP anomalies in the preceding winter over the two yellow boxes in Fig. 3e, denoted as ESAP in Table 1, and the other is the area-averaged SAT anomalies in the preceding spring over the yellow box in Fig. 3f, denoted as EPT in Table 1. The former represents a see-saw pattern of SLP between high-latitude East Asia and northern South Asia and latter represent abnormal pattern of SAT over the eastern tropical Pacific. Both the two precursors have good correlations with PC3 variation, and represent independent precursors for the year-to-year variability of the propagating evolving pattern in East-Asian rainfall anomalies.

Collectively, the six precursors account for 50% of the total variance in yearly variations of the three spatiotemporal patterns of summer rainfall anomalies over continental East Asia. As summarized in Supplementary Table 2, these precursors have good correlations with the climate variability modes, such as El Niño-Southern Oscillation (ENSO), which are well recognized as important drivers of East-Asian monsoon rainfall variations through ocean-land-atmospheric feedbacks^1,6,20,42. Specifically, the six precursors correlate with the dominant climate modes over the Pacific Ocean, Indian Ocean, Tibetan Plateau, and East Asia, influencing the interannual variability of continental East-Asian monsoon rainfall. This suggests that the six precursors collectively serve as representative early signals of the associated climate modes, acting as proxies for their combined effects and depicting slowly varying lower boundary conditions that modulate the spatiotemporal evolution of rainfall anomalies over East Asia.

Skillful seasonal predictions of continental East-Asian rainfall anomalies

To demonstrate the utility of the three spatiotemporal patterns and six precursors in improving seasonal predictions of continental East Asia rainfall anomalies, we developed a physical-statistical prediction model (PSM) based on observations in 1980–2009. Such a model directly bridges the year-to-year variations of each spatiotemporal pattern and their two corresponding precursors through multi-regression equations. Then, we used the model to perform a 13-year retrospective prediction as independent validation for each PC variation from 2010 to 2022, utilizing a forward-rolling manner that avoids the use of any future data (see Methods for details). This approach resembles the procedure adopted in the current operational forecasting. Finally, the model generates seasonal forecasts for the spatiotemporal evolution of continental East-Asian rainfall anomalies reconstructed from the three observed evolution patterns and their predicted PC variations.

Note that predicting the spatiotemporal evolution of East-Asian rainfall anomalies, which vary seasonally and yearly, ultimately boils down to predicting the three PC variations. Illustrated by the grey lines in Fig. 2b, d, f, the predicted year-to-year PC variations of the three spatiotemporal patterns by PSM capture the observed counterparts well. The average correlation skills during the independent validation period for predicting variations of the three patterns are 0.75, 0.71, and 0.70, respectively, very close to those in the training period. This suggests that the relationships between the yearly variations of spatiotemporal patterns and precursors in PSM are robust. Thus, these three evolution patterns can be regarded as the predictable modes of anomalous rainfall evolution over continental East Asia.

Through a linear combination of the three spatiotemporal patterns and their predicted PC variations in Fig. 2, the model is used to forecasts the year-to-year variability of the spatiotemporal evolution of East-Asian summer rainfall anomalies during the training and independent prediction periods (Supplementary Fig. 6). PSM forecast against spatiotemporal evolution based on the three patterns in each boreal summer exhibits a high average skill of 0.68 during the entire period (1980–2022), and the average skill remains consistent at 0.68 during both the training and independent prediction periods (Supplementary Fig. 6c). It also illustrates that retrospective prediction skills are higher than 0.5 in 24 out of 30 years from 1980 to 2009, while independent prediction skills exceed 0.5 in 10 out of 13 years from 2010 to 2022.

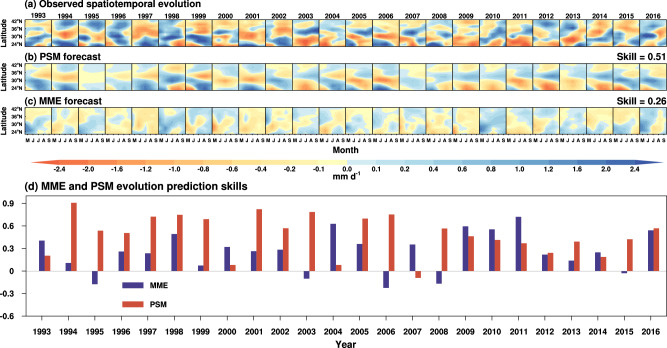
Figure 4 highlights the improved prediction capability of the total spatiotemporal evolution of East-Asian summer rainfall anomalies in each year (Fig. 4a) in PSM (Fig. 4b) compared to that of the MME mean of current dynamical models (Fig. 4c). The year-to-year spatiotemporal evolution of rainfall anomalies predicted by PSM closely resembles to that of observations, including the north-south advances and retreats of the anomalous rainbelt as well as the seasonal flood-drought evolution. However, the MME mean forecast struggles to capture such spatiotemporal evolution features in observations. Figure 4d also illustrates the PSM and MME prediction skills for the total observed spatiotemporal evolution of rainfall anomalies in each year, which is assessed by spatiotemporal pattern correlation between observed (Fig. 4a) and predicted (Fig. 4b, c) evolution for each year, as depicted in Methods section. The results suggest that PSM prediction skills in capturing the spatiotemporal evolution during boreal summer are significantly higher than those of MME mean forecasts in 16 out of the 24 years from 1993 to 2016. The overall prediction skill of PSM during 1993–2016 is 0.51, evaluated by spatiotemporal pattern correlation between Fig. 4a, b, which is nearly twice as high as the corresponding skill (0.26) in the MME mean (Fig. 4a, c).

Fig. 4. Seasonal predictions against the observed spatiotemporal evolution of rainfall anomalies as function of latitude and month over East Asia.

The spatiotemporal evolution is denoted by (a) the observed total rainfall anomalies, (b) the predicted field reconstructed from the three spatiotemporal patterns and their predicted amplitude variations in the physical-statistical prediction model (PSM), and (c) forecasted field from the multi-model ensemble (MME) mean of the current nine dynamical models. The ordinate is latitude and the abscissa is month of boreal summer in each year. d The forecast skills assessed by the spatiotemporal correlation coefficient between forecasted and observed rainfall evolution for each year in the MME mean and PSM. The overall spatiotemporal correlation skill for the period of 1993–2016 is shown in the top right corner of (b) and (c).

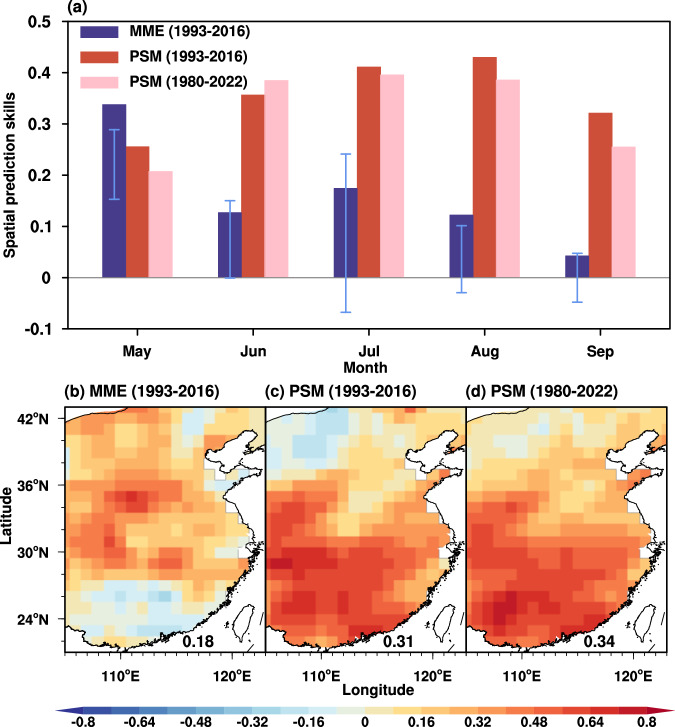
Furthermore, PSM exhibits good performance in predicting rainfall patterns in individual months over East Asia during the period of 1980–2022 and 1993–2016 periods (Fig. 5a). PSM forecasts clearly outperform those of the MME mean in capturing the spatial rainfall patterns as the lead time increases, except in May (Fig. 5a). Meanwhile, the forecasts from all individual dynamical models perform worse than the MME mean forecasts in capturing spatial patterns of rainfall anomalies as the lead time increases (Supplementary Fig. 7). The regions of high forecast skills shift northward as the seasonal rainbelt advances (Supplementary Fig. 8), with only poor skills observed in a small part of northwestern East Asia where seasonal predictability is relatively low^1,21. The improvement of PSM is especially evident in regions where the dynamical MME forecasts show low skills (Fig. 1 and Supplementary Fig. 8). As a byproduct of the model’s skillful predictions for the spatiotemporal evolution of rainfall anomalies, PSM also shows a significant improvement in predicting the conventional summer mean (Fig. 5). Specifically, PSM exhibits a regional mean skill of 0.31 and a multi-year mean skill of spatial correlation at 0.43 during 1993–2016, greatly surpassing that of the MME mean, which are 0.18 and 0.07, respectively, for the same period (Fig. 5b–d and Supplementary Fig. 9). Overall, PSM demonstrates prediction skills at least twice as high as those of the current dynamical models. These results indicate that our model achieves significant improvements in predicting both the spatiotemporal evolution (Figs. 4 and 5) and conventional summer mean (Fig. 5) of continental East-Asian summer rainfall anomalies. It is important to note that the PSM forecasts still clearly outperform the MME forecasts in capturing both the spatiotemporal evolution and spatial patterns (Supplementary Figs. 10-13) of rainfall anomalies, regardless of which observational datasets are used for verification. This advancement has the potential to generate more detailed and skillful seasonal predictions of continental East-Asian climate, thereby facilitating the issuance of reliable early warnings.

Fig. 5. Prediction skills against the observed spatiotemporal evolution and summer mean of continental East-Asian rainfall anomalies.

a The multi-year mean forecast skills assessed by the spatial pattern correlation against the total rainfall anomalies for each month in the multi-model ensemble (MME) mean of the dynamical models and the physical-statistical prediction model (PSM). The blue line segments represent the ranges of prediction skills derived from individual dynamical models. The temporal correlation skills for predicting summer mean rainfall anomalies in June-July-August (JJA) are shown for (b) MME mean and (c, d) PSM. The regional mean of the prediction skill is displayed in the bottom right corner of (b) to (d).

Discussions

Progresses in seasonal predictions of continental East-Asian summer rainfall hold tremendous socioeconomic values but remains a challenging issue given the limited prediction skills of the existing dynamical models^9–12. Different from the conventional focus on seasonal mean of rainfall anomalies over specific regions of East Asia, we here proposed to identify three leading spatiotemporal patterns of continental East-Asian summer rainfall anomalies, from an alternative perspective that considers the seasonal evolution of rainfall anomalies across a space-time domain. These seasonal evolution patterns manifest the persistent, reversal, and propagating features, capturing the most crucial signals of spatiotemporal variability in the East-Asian summer rainfall anomalies. The year-to-year variations in these patterns collectively account for half of the total variance, suggesting the presence of more predictability in the spatiotemporal evolution of East-Asian rainfall anomalies. This is an innovative way to describe the spatiotemporal evolution of rainfall anomalies, as it better captures distinct footprints left by precursory climate signals in the summer rainfall through synthesizing information from both the time and space dimensions.

To maximize the preceding correlation signals for seasonal forecasts of these pattern variations, we successfully identified six effective precursors that collectively explain about 50% of the total variance in interannual variations of spatiotemporal patterns, serving as representative early signals depicting slowly varying lower boundary conditions in the climate system. These precursors play a crucial role in modulating the spatiotemporal evolution of East-Asian summer rainfall anomalies through land-ocean-atmosphere coupling^6,24. In light of this, we develop a physical-statistical prediction model utilizing the three spatiotemporal patterns and six precursors. Our model demonstrates skillful seasonal predictions in both the spatiotemporal evolution and conventional seasonal mean of continental East-Asian summer rainfall anomalies. It achieves a prediction skill more than double that of the MME mean of the current dynamical models. Our findings emphasize the importance of recognizing and introducing non-conventional predictands, (i.e., three spatiotemporal patterns and their yearly time series) when conventional approaches fail, even though the dynamics underlying the lead-lag relationship between the predictands and precursors requires further investigation in the future. This model may have certain limitations when the amplitudes of the precursors are too weak or when applied to more stochastic event occurrences. In these cases, it may struggle to capture slowly predictable signals due to the inherent complexity or rapid variability.

The identified spatiotemporal patterns advance our understanding of the year-to-year variability of the East Asia summer rainfall anomalies. It facilitates the future development of more skillful and detailed prediction models and may serve as a benchmark for evaluating the seasonal forecast capabilities of existing dynamical models. Seamless predictions across seasonal to decadal time scales, as proposed by the Word Climate Research Program⁴³, have attracted widespread attention and found applications in diverse fields including agriculture, energy, finance, health, and water resource management⁴⁴. Our forecast model represents a valuable addition to this class of seamless predictions^45,46. It can be easily extended to seasonal predictions over global domains (e.g., Africa and South America) through identifying non-conventional spatiotemporal predictands and integrating with other methods that are dynamical or empirical in nature^47–51. This advancement marks a crucial step forward delivering skillful seasonal predictions to populations in need of new tools for managing risks of near-term climate disasters and long-term climate change.

Methods

Hindcasts of nine dynamical models

The seasonal forecast precipitation datasets of nine dynamical models from the China Meteorological Administration (CMA)⁵² and the Copernicus Climate Change Service (C3S)^45,53–60 are utilized in this study. These datasets combine seasonal forecast products from multiple global producing centers of the World Meteorological Organization and offer open access to state-of-the-art climate prediction data and tools for all uses²⁷. Supplementary Table 1 provides details on the nine dynamical models, including their full names, references, abbreviations, horizontal resolutions, and hindcast ensemble sizes. The seasonal forecast datasets used in this study are summer season forecasts made on May by nine dynamical models for the period of 1993–2016. Their ensemble mean is done by first interpolating the forecast datasets on common grids at a resolution of 1° longitude and 1° latitude.

Observed datasets

The daily rainfall dataset spanning from 1980 to 2022 is derived from 2420 stations’ surface rain gauge data of the National Meteorological Information Center of CMA. The majority of these stations are located in the East-Asian land region. To obtain a gridded dataset, we interpolate the rainfall station data onto a spatial resolution grid of 1° longitude and 1° latitude grid, using the Cressman-style interpolation algorithm. Then, a 3-month running mean is applied to the gridded dataset to filter out weather noises. We also utilize three additional satellite-gauge-based precipitation datasets (see Supplementary Table 3) to assess the impacts of observational uncertainty on the spatiotemporal patterns and prediction results.

Meanwhile, the monthly sea level pressure (SLP) with a spatial resolution of 2.5° longitude and 2.5° latitude is derived from the National Centers for Environmental Prediction (NCEP) Reanalysis 2⁶¹. The monthly averages of near-surface air temperature (SAT) is obtained from the Met Office Hadley Centre/Climatic Research Unit global surface temperature dataset (version HadCRUT.5.0.2.0) at a resolution of 5° degree grid⁶². The year-to-year time series of six precursors are derived from the areal means of SAT or SLP anomalies in preceding seasons starting at preceding autumn in the previous year and ending at preceding spring of the current year, covering the period from 1979/1980 to 2021/2022. For easy reference, we denote the “previous year” as the year index for precursors, for example, 1979 for the year 1979/1980.

Supplementary Table 2 provides information of six climate indices that represent the circulation patterns and internal modes of climate variability contributing to East-Asian summer rainfall variability^6,13,17,23. This table also includes their correlation coefficients with the six precursors, in which the preceding seasons used in six climate indices are consistent with that of the corresponding precursors. The data sources of these climate indices are listed in Supplementary Table 4.

Spatiotemporal evolution pattern analysis

To identify the spatiotemporal patterns in East-Asian rainfall anomalies during boreal summer (May to September), we employ EOF analysis on the daily precipitation anomalies zonally averaged in 105° to 123°E over East-Asian region. Note that the datasets spanning 1980–2009 and 2010–2022 serve as the training and independent prediction periods, respectively. EOF analysis is applied to the training period, enabling the generation of independent retrospective forecasts during 2010–2022. Specifically, we consider the daily precipitation anomalies after removing its climatology mean, denoted as P(s,day,year), where s represents latitude grid, day signifies the Julian day of a boreal summer, and year denotes the specific year. It reflects both spatial and seasonal variations collectively from year to year. After conducting EOF analysis on P(s,day,year), where (s,day) as the space-day domain and (year) acts as the year-to-year temporal domain, the resulting EOF patterns in a space-day domain and corresponding PC variations can be obtained by

$$P\left(s,day,year\right)={\sum }_j{EOF}_j\left(s,day\right){PC}_j\left(year\right),where\overline{{\left({PC}_j\left(year\right)\right)}^2\equiv 1},$$ 1

where the overbar denotes the 30-year mean of training period and EOF_j has the units of mm/d. The leading three EOF patterns are referred to as the dominant spatiotemporal patterns of East-Asian summer rainfall anomalies. The year-to-year time series of their PCs for the whole study period (1980–2022) can be obtained from

$${PC}_j\left(year\right)=<P\left(s,day,year\right){EOF}_j\left(s,day\right)>,$$ 2

where j = 1, 2, 3. The rainfall anomalies field reconstructed from three spatiotemporal patterns and corresponding PC variations is denoted as P_EP, which is given by

$$P_{EP}\left(s,day,year\right)={\sum }_{j=1}^3{EOF}_j\left(s,day\right){PC}_j\left(year\right),$$ 3

it represents the year-to-year variability in the dominant spatiotemporal evolution of East-Asian rainfall anomalies. The explained variance percentage (EV_j) of the variability associated with each spatiotemporal pattern relative to the total precipitation variability is obtained from

$${EV}_j=<{\left[{EOF}_j\left(s,day\right)\right]}^2>/<{\left[P\left(s,day,year\right)\right]}^2>,$$ 4

where j = 1, 2, 3, and “<>” represents the average over the domain of s and day.

Furthermore, the spatial rainfall patterns of each spatiotemporal pattern are obtained by regressing the total daily precipitation anomalies in spatial resolution grids of latitude and longitude against the corresponding PC variations during the training period. Thus, the daily rainfall patterns associated with P_EP in a specific year can be reconstructed from Eq. (3) by replacing EOF_j(s,day) with the corresponding spatial patterns. The daily rainfall patterns of each EOF and P_EP can generate the monthly rainfall patterns.

The physical-statistical prediction model

Using data in the training period, we built a physical-statistical prediction model to predict the year-to-year variability of each spatiotemporal pattern. This model is based on a multiple regression equation with two predictors, namely

$${\widehat{PC}}_j\left(year\right)={\sum }_i{\alpha }_{i,j}{X}_{i,j}\left(year-1\right),$$ 5

where

$${\alpha }_{i,j}=\frac{\overline{{PC}_j\left(year\right)X_{i,j}\left(year-1\right)}}{\overline{{\left(X_{i,j}\left(year-1\right)\right)}^2}},$$ 6

Where X_i,j represents the two predictors (i = 1, 2) for each spatiotemporal pattern (j = 1, 2, 3). As shown in Fig. 4b, the spatiotemporal evolution of P_EP, regressed by all six precursors, are reconstructed from Eq. (3) by replacing ${PC}_j\left(year\right)$ with${\widehat{PC}}_j\left(year\right)$.

To perform an independent retrospective prediction for the PC variability of three spatiotemporal patterns at the target year $Y_k$ during 2010–2022, where $Y_k$ denotes the target year of (2009 + k), with k ranging from 1 to 13, we apply the above new model in a forward rolling manner (see Supplementary Fig. 14) to predict ${\widehat{PC}}_j\left(Y_k\right)$ at the target year. The overbar in Eq. (6) is applied to the period from 1980 to the year $\left(Y_k-1\right)$ before the target year to update the regression coefficients in the model. This approach enables us to forecast the year-to-year variability of three spatiotemporal patterns from 1980 to the target year, providing an opportunity to validate the robustness of this model. The forecasted P_EP at the target year in the independent prediction period (see Supplementary Fig. 6) is obtained from Eq. (3) by replacing ${PC}_j\left(year\right)$ with ${\widehat{PC}}_j\left(Y_k\right)$. Additionally, the forecasted fields of monthly rainfall patterns on spatial resolution grids can be obtained by the same manner.

Assessment of forecast skills

The spatiotemporal pattern correlation coefficient (STC) between predicted ($\widehat{y}$) and observed (y) evolution fields in both space (s) and time (t) is also utilized to evaluate the prediction skills of spatiotemporal evolution of rainfall anomalies (Fig. 4 and Supplementary Fig. 6), given by

$$STC=\frac{{\sum }_{s=1,t=1}^{M,N}\widehat{y}\left(s,t\right)y\left(s,t\right)}{\sqrt{{\sum }_{s=1,t=1}^{M,N}{\left(\widehat{y}\left(s,t\right)\right)}^2}\sqrt{{\sum }_{s=1,t=1}^{M,N}{\left(y\left(s,t\right)\right)}^2}},$$ 7

where M and N is the number of space and time samples, respectively. Note that the traditional prediction skills²⁵ of spatial pattern or temporal correlations represent a specific form of STC at fixed s or t.

Confidence interval

The statistical significance level is determined through the Student’s t-test. The 90% confidence interval is defined by the 5th and 95th percentile values, while the 99% confidence interval is defined by the 0.5th and 99.5th percentile values. A correlation coefficient value is considered significant at the 90% (99%) when it falls outside the 5th (0.5th) and 95th (99.5th) percentiles.

Author contributions

H.R. designed the original idea and provided supervision. J.M. and M.C. improved the idea for the study and drafted the manuscript. C.Z. downloaded the data and J.M. performed the analysis and made graphic presentations. J.M., H.R., M.C. and Y.D. contributed to the writing and discussed the results. J.L., H.C., C.Z. and L.W. contributed to discussions and the improvement of the manuscript.

Peer review

Peer review information

Nature Communications thanks Shipra Jain and Zhiwei Wu for their contribution to the peer review of this work. A peer review file is available.

Data availability

C3S seasonal forecasts in the Copernicus Climate Data Store are available at https://cds.climate.copernicus.eu/, and the station datasets and seasonal forecasts of precipitation from the CMA are available at https://data.cma.cn/. SAT is publicly available at https://www.metoffice.gov.uk/hadobs/hadcrut5/data/HadCRUT.5.0.2.0/download.html, and SLP from NCEP Reanalysis 2 is available at https://downloads.psl.noaa.gov/Datasets/ncep.reanalysis2/Monthlies/surface/. Dataset of climate indices in Supplementary Table 2 can be downloaded from Uniform Resource Locator listed in Supplementary Table 4. All raw datasets used in this study were obtained from publicly available sources mentioned above. The processed modeling data is accessible on the Zenodo repository under 10.5281/zenodo.14410744.

Code availability

All figures in this article were generated using the open-source programming languages and software of the NCAR Command Language (NCL; http://www.ncl.ucar.edu). The code used in this study is available at the Zenodo repository (10.5281/zenodo.14410744).

Competing interests

The authors declare no competing interests.

Supplementary information

The online version contains supplementary material available at 10.1038/s41467-024-55271-1.