Triply periodic minimal surfaces for thermo-mechanical protection

Abstract

Triply periodic minimal surface (TPMS) metamaterials show promise for thermal management systems but are challenging to integrate into existing packaging with strict mechanical requirements. Composite TPMS lattices may offer more control over thermal and mechanical properties through material and geometric tuning. Here, we fabricate copper-plated, 3D-printed triply periodic minimal surface primitive lattices and evaluate their suitability for battery thermal management systems. We measure the effects of lattice geometry and copper thickness on pressure drop, mechanical properties, and thermal conductivity. The lattices as internal filling structures in a multichannel cold plate exhibited pressure drops under 6.5 kPa at a 1 LPM flow rate. Pressure drop decreased when the number of channels (width of the cold plate) was increased. With a 0.43% copper volume loading, the lattice more than tripled in thermal conductivity but still retained a polymer-like compliance. A higher lattice relative density did not affect the thermal conductivity but caused a higher elastic modulus and compressive strength, and a stiffer cyclic loading response. The lattice design demonstrates that the structural parameters that control pressure drop, mechanical, and thermal conductivity can be decoupled, which can be used to achieve a wide range of disparate properties in complex multiphysics systems.

Introduction

Periodic cellular architectures have received considerable attention in efforts to achieve multifunctional performance that combines thermal, fluidic, and mechanical requirements. Cellular solids such as foams, honeycombs, and 3D lattices have been the subject of extensive research as lightweight structures^1–3. The 3D structure and relative density (porosity) of cellular materials determine properties such as strength, stiffness and thermal conductivity. Advances in additive manufacturing (AM) enable the fabrication of cellular solids with increased geometrical complexity for strong, lightweight structures with high energy absorption^4,5. For instance, nanocomposites with tunable three-dimensional hierarchical architectures demonstrate excellent specific strength, energy absorption, and recoverability⁶.

Recently, 3D lattices based on triply periodic minimal surfaces (TPMS) have gained attention in the fields of both thermal and structural engineering^7,8. TPMS lattices are characterized by smooth, interconnected, and non-intersecting surfaces with a three-dimensional periodicity that partitions space into two separate yet continuously connected subdomains⁹. These continuous internal channels with a high areal density are attractive for use in heat exchangers¹⁰. The continuous curvature leads to high surface area and increased fluid-wall interactions while reducing flow separation^11,12. Certain TPMS structures (Schwartz primitive) are particularly promising for thermofluidic applications, as they exhibit low pressure drop due to their large pore size and high thermal conductivities compared to other lattice types^13–15. TPMS lattices also have higher mechanical energy absorption than traditional lattice structures at similar relative densities^16,17.

While TPMS lattices are promising for thermal management applications, they often must be integrated into existing architectures that present strict thermomechanical requirements. The lattices must be flexible and conformal to the cooling surface, compliant enough to allow for material or thermal expansion, and conductive enough to enable high heat transfer¹⁸. This combination of properties is challenging to achieve in a single material or structure, as both thermal conductivity and elastic modulus tend to increase with stronger interatomic forces¹⁹. Polymer-metal composites can improve the thermal conductivity while maintaining the mechanical performance and flexibility of polymer^20,21. Previous studies on polymer-metal composites have found that thermal conductivity increases linearly with metal loading at ultralow metal loading, below 1% by volume^22–24. Composite metal-polymer TPMS lattices are a promising strategy to achieve thermally conductive polymers that contain fluid channels, to enable compliant thermal management systems.

One of the emerging applications of thermomechanically sturdy lattice channels is in battery thermal management systems for electric vehicles, which require the prolonged operation and safety of lithium ion battery packs. Conventional battery thermal management systems employ liquid cold plates, which direct fluid through internal channels to collect waste heat from adjacent battery surfaces. These cold plates are often located on the underside of battery modules in a bottom cooling configuration^25,26. While bottom cooling offers advantages in terms of structural simplicity and ease of manufacturing, it faces limitations in cooling performance due to the limited contact area between the bottom surface of the batteries and the upper side of the cold plates. This results in significant temperature variations along the height direction of the batteries^27,28. As the energy density of EV battery packs continues to rise, there is increasing demand for enhanced heat dissipation. Inter-cell liquid cooling, where cold plates are placed between adjacent battery cells, is a promising solution²⁹.

In contrast to conventional bottom liquid cooling, inter-cell cold plates face more stringent thermomechanical requirements. From a thermal perspective, they must efficiently dissipate heat over a larger distance while maintaining minimal pressure drop. Simultaneously, from a mechanical standpoint, these plates must accommodate the significant compressive strain resulting from battery swelling during repetitive charging cycles^18,30. The internal structure of the cold plate must have a high surface area for effective heat conduction but also enable efficient, non-tortuous liquid flow³¹. Previous work has found that cooling channels embedded with primitive TPMS lattices can significantly improve the heat dissipation compared to typical straight channel tubes³². Thus, porous, thermally conductive polymer channels based on TPMS lattices can combine these thermomechanical properties for multifunctional cold plates.

In this study, we fabricate TPMS lattices with high fluidic transport and thermal conductivity, and sufficient mechanical compliance to accommodate the expansion of battery cells. Polymer TPMS lattices are additively manufactured and then plated with copper. Pressure drop, monotonic and cyclic compression, and thermal conductivity are measured to understand the influence of lattice geometry and copper thickness on thermomechanical properties. Our study contributes to the design of high-performance battery thermal management systems for use in electric vehicles.

Results

Pressure drop

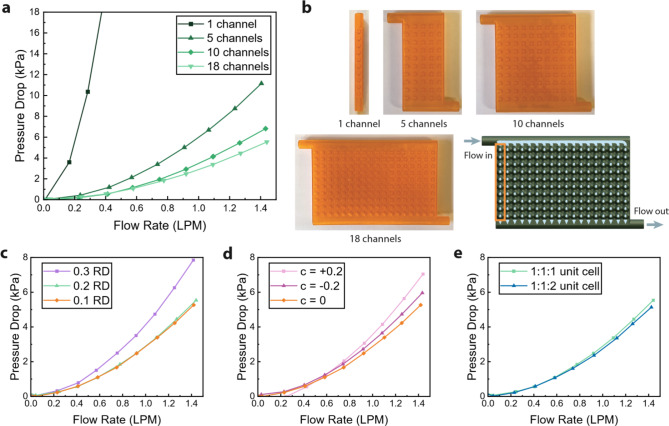
Figure 1 summarizes the measured pressure drop values for the cold plates. As expected, the pressure drop increased with flow rate for all samples. Figure 1a shows the pressure drop for varying channel numbers. The sample with one channel was constructed as a straight rectangular channel with a single line of lattices within, rather than a manifold. All other multi-channel samples were designed as a Z-type manifold. Each sample, regardless of the number of channels, featured the same channel length of 10 unit cells along the flow direction. The primitive lattice divides the flow volume into two sections, inside and outside of the unit cell. For the cold plate with one channel, the channel walls enclosed the flow on all four sides parallel to the flow direction. For all other cold plates, the channel wall enclosed the flow only on two sides, allowing the fluid to mix between each channel. In all cases, the fluid flowed through both the inner and outer domains.

Fig. 1.

Pressure drop measurements. (a) Measured pressure drop in cold plates with different number of channels (0.2 RD, c = 0, and 1:1:1 unit cells). (b) Images of cold plates with 1, 5, 10, and 18 channels. (c) Pressure drop in cold plates with different relative densities (18 channels, c = 0, and 1:1:1 unit cells). (d) Pressure drop in cold plates with different level-set parameters (18 channels and 1:1:1 unit cell). (e) Pressure drop in cold plates with different unit cell aspect ratios (18 channels and c = 0).

The pressure drop decreased for increasing channel numbers due to the larger flow volume. Because the fluid was split into a greater number of channels, the effective velocity through each channel decreased, reducing the overall pressure drop. The pressure drop did not decrease proportionally to the flow volume: the pressure drop decreased by lower amounts for higher channel numbers, implying that the pressure drop will plateau at a large channel number. The diminishing effect of channel number on pressure drop can be attributed to the uneven flow distribution for more channels within the cold plate.

Cold plates with 0.1 and 0.2 relative density (RD) lattices showed no apparent difference in pressure drop behavior, but the cold plate with 0.3 RD lattices exhibited a higher pressure drop (Fig. 1c). As the relative density increased, the lattice wall thickness increased and the connections between unit cells became more narrow. These served as bottlenecks that force the fluid to contract and then expand, increasing the hydraulic losses due to the restricted flow path.

Figure 1d shows the pressure drop for varying values of the level-set parameter c. Though the effect is minor, the cold plate with c = 0 exhibited a slightly lower pressure drop than the samples with c = 0.2 and c = -0.2. The lattice with c = 0 divided the flow domain into two equal halves, with the same volume in the interior and exterior of the lattice. Meanwhile, the lattices with c = 0.2 and c = -0.2 exhibited a higher flow volume in the interior or exterior of the lattice, respectively. The even division of the flow domain for c = 0 avoided excessively narrow connections between unit cells or the space along the channel walls, minimizing the pressure losses.

Figure 1e shows that the stretched unit cell exhibited no difference in pressure drop from the unstretched unit cell. The stretched unit cell (aspect ratio of 1:1:2), which was doubled in length along the flow direction, has the same wall thickness as the unstretched unit cell and 0.22 RD. Thus, the main difference in the stretched unit cell was the decreased number of connecting necks along the channel due to the halved number of unit cells per channel. This measurement suggests that the number of connecting necks was not the main factor that impacted pressure drop, at least for lattices around 0.2 RD.

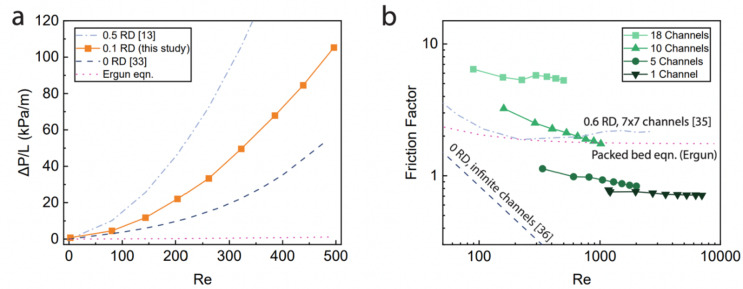
Experimental pressure drop and friction factor data is compared to simulation results (Fig. 2). As evident from Fig. 2a, the pressure drop for the cold plates is fairly consistent with previous modeling of primitive lattice fluid channels. The pressure drop is higher than simulation results from Rathore et al., which studied flow in the primitive type lattice with an infinitesimal wall thickness (effectively 0 RD)³³. The lower wall thickness and larger pore size in this simulation resulted in lower pressure drop than this experiment. Another simulation of flow in a primitive lattice assumed that fluid is only in the interior half of the total volume (effectively 0.5 RD)¹³. The simulated pressure drop was higher than in the current study due to the lack of flow in the exterior of the lattice. Meanwhile, the Ergun equation for flow in packed beds underestimated the pressure drop results. This is because the TPMS lattices may have areas of stagnant flow near channel walls, the lattice structure may separate flow into discontinuous paths and the lattice exhibited high tortuosity compared to spherical particles³⁴. At low relative densities, as in the cold plates studied here, flow within the lattice has significantly limited paths compared to a packed bed with equivalent relative density.

Fig. 2.

Comparison of this work with other works measuring Schwarz primitive lattices. (a) Pressure drop normalized by channel length for the cold plate with 0.1 RD (18 channels, c = 0, and 1:1:1 unit cells) plotted against the Ergun equation (packed bed), and simulations of Schwartz primitive lattice. (b) Friction factor for cold plates with varying channel numbers (0.2 RD, c = 0, 1:1:1 unit cells) plotted against the Ergun equation and correlations for Schwartz primitive lattices.

The friction factor is plotted against the Reynold’s number for varying channel numbers in Fig. 2b. As the channel number increased, the friction factor increased due to the higher overall flow resistance per channel in wider cold plates. Compared to the other samples, the single channel sample has two extra surfaces on the sides of the channel to direct flow. Additional channels allowed the fluid to spread out laterally, reducing the velocity per channel and creating an uneven flow distribution. The friction factor predicted by the Ergun equation for packed beds overlapped with the results from the cold plate with 10 channels. The predicted friction factor for 0.6 RD primitive lattices was also similar to that of the cold plate with 10 channels³⁵. This simulation used a square cross section of 7 × 7 repeating unit cells perpendicular to the flow direction, which is more channels than the present work. All of the experimentally measured friction factors are higher than simulations of zero-thickness (0 RD) primitive lattices³⁶. This simulation assumes an infinite plane of unit cells perpendicular to the flow direction. This demonstrates the trade-off between different design parameters: more channels can increase the flow resistance, while lower relative density and wall thickness decrease the flow resistance.

Mechanical properties

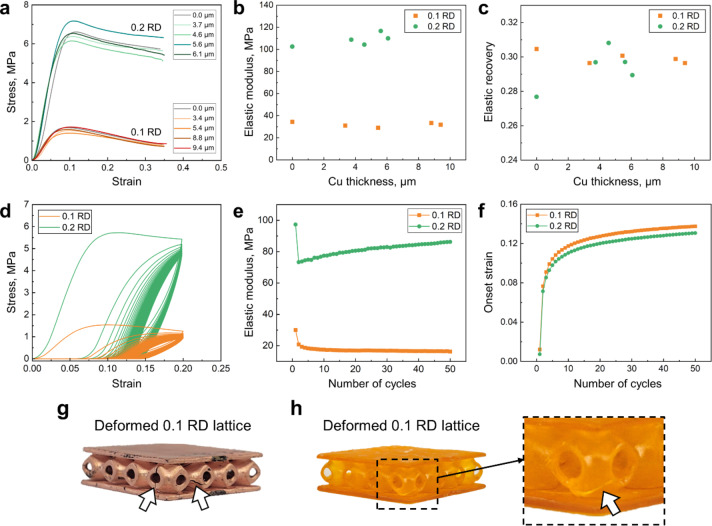
Figure 3 shows the measured mechanical properties during compression up to a strain of 0.35 (Fig. 3a–c) and during cyclic compression up to 50 cycles (Fig. 3d–f). The compressive strength (defined as the maximum strength in each stress-strain curve) was approximately 1.6 MPa for 0.1 RD lattices and 6.6 MPa for 0.2 RD lattices. The elastic modulus was 34 MPa for 0.1 RD lattices and 103 MPa for 0.2 RD lattices. The dependence of these properties on relative density is expected for cellular foams and lattices^3,37. The elastic recovery, determined as the ratio of the recovered height to the total height, i.e. the amount of elastic strain recovered after compression, was independent of relative density. The elastic recovery was approximately 0.3 (upon compression up to 0.35) for all tested samples, as shown in Fig. 3c. While 0.2 RD samples exhibited cracks in some of the unit cells, as shown in Fig. 3g (highlighted by arrows), the cracked cells were predominantly located at the outer periphery of the lattice structures. The majority of the unit cells remained free of cracks, and no cracks were detected within the internal cells, contributing to the high compliance of the designed lattice structures.

Fig. 3.

Results of mechanical tests. (a) Stress-strain curves for as-printed and Cu-plated TPMS lattice structures (c = 0, 4 × 4 unit cells) under compression up to 0.35 strain. (b) Elastic moduli and (c) elastic recovery of the lattices as a function of Cu thickness. (d) Stress-strain curves for 50 cyclic compression cycles up to 0.2 strain. (e) Elastic moduli and (f) onset strain (strain at 0.1 MPa stress during loading) as a function of the number of cycles. (g) Deformed 0.2 RD lattice after uniaxial compression testing, displaying the formation of vertical and horizontal cracks, as highlighted by arrows. (h) Deformed 0.1 RD lattice after cyclic compression testing with a crack, as indicated by an arrow.

Compressive strength, elastic moduli, and elastic recovery were found to have negligible dependence on the thickness of the plated Cu (Fig. 3a-c). This is likely due to the fact that the Cu layer (up to 10 μm in thickness) is less than 5% of the thickness of the polymer layer (210–420 μm for 0.1 or 0.2 RD, respectively). Therefore, the properties of the polymer dominate despite the significantly higher strength and modulus of Cu. Overall, the limited correlation between Cu thickness and mechanical properties of the lattice suggests that thermal properties (which do depend on Cu thickness) can be controlled independently of mechanical properties. Furthermore, the mechanical properties of the 0.1 RD lattices closely matched the requirements for potential applications as cold plates in BTMS for EVs. While the specific target modulus and peak stress can vary depending on battery cell dimensions and stack forces, it is generally observed that the peak stress imposed on the cold plates during a charging cycle remains around a few MPa, typically less than 1 MPa^38–40.

When subjected to cyclic compression ranging from 0 to 0.2 strain, the elastic modulus of the as-printed lattice structures depended on the number of cycles (Fig. 3d-f). An initial drop in elastic modulus was observed after the first cycle in both the 0.1 RD and 0.2 RD samples. In subsequent cycles, the elastic modulus of the 0.2 RD sample increased, whereas that of the 0.1 RD sample decreased, as shown in Fig. 3e. In the 0.1 RD sample, the modulus stabilized at approximately 17 MPa after around 10 cycles. However, for the 0.2 RD sample, the modulus continued to rise, reaching up to 86 MPa, albeit at a reduced rate as the number of cycles increased. The observed increase in the elastic modulus after the initial drop in the 0.2 RD sample (Fig. 3e) implied the possibility of strain-induced realignment of polymer chains, potentially contributing to the strain hardening phenomenon⁴¹. Further investigation is required for a comprehensive explanation.

Figure 3f shows the onset strain, defined as the strain corresponding to a 0.1 MPa stress on a loading curve, against the number of cycles. The plot shows a significant increase in the onset strain during the first cycle. The trend of increasing onset strain with an increasing number of cycles, up to approximately 0.14 strain, was consistently observed in both the 0.1 and 0.2 RD samples, suggesting the gradual accumulation of plastic strain over the cyclic loading. Although cracks were observed in the corner unit cells of the samples, as shown in Fig. 3h, their contribution to the onset strain appears negligible, given the high recovery observed in the lattice structures. Given the actual permanent deformation was approximately 0.05 (measured in uniaxial compression tests up to 0.35 strain), the increasing onset strain may suggest that the rate of elastic recovery in the designed lattices was slower than the applied strain rate of 0.001 s^− 1.

Thermal conductivity

The thermal conductivity was measured for both 0.1 and 0.2 RD lattice samples, first for as-printed polymer lattices, and then for Cu-plated lattices (lattices shown in Fig. 8). Figure 4 summarizes the effect of copper plating thickness on thermal conductivity values. The as-printed 0.2 RD lattice exhibited a higher thermal conductivity than the 0.1 RD lattice due to the larger wall thickness, enabling a wider heat transfer pathway. After copper plating, the lattices at different relative densities exhibited no marked difference in thermal conductivity values, as the copper dominated the heat transfer of the material. The thermal conductivity values increased approximately linearly with the copper layer thickness for both relative densities.

Fig. 8.

TPMS lattice samples used for compression and conductivity tests. (a) CAD model lattice samples. Images of (b) as-printed and (c) Cu-plated samples.

Fig. 4.

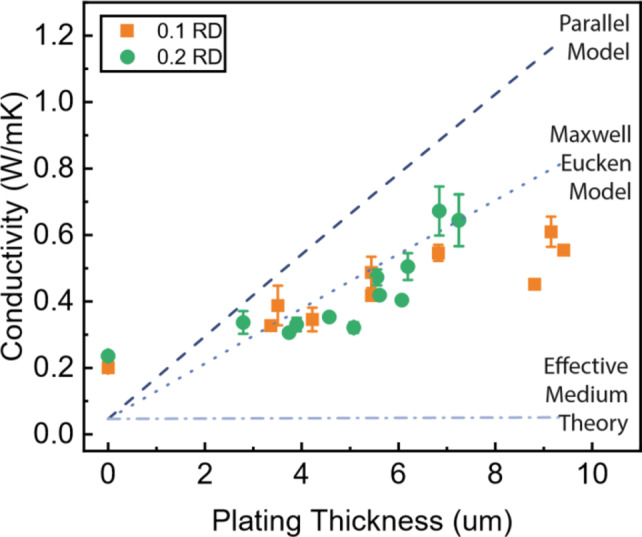
Thermal conductivity of Cu-plated TPMS lattice structures as a function of Cu thickness. Data is compared to simulations from⁴² based on three composite material models. Models were plotted for 0.15 RD.

The thermal conductivity enhancement, given as a percentage improvement in conductivity compared to a neat polymer sample, is often used to evaluate thermal composites²⁰. The lattices reached as much as a 216% conductivity improvement at a copper volume loading of 0.43%, suggesting that the lattices can reach superior conductivity enhancements at ultralow loading compared to filler composite materials that consist of a polymer matrix filled with thermally conductive particles, wires or plates^22–24. This high conductivity improvement can be attributed to the efficient thermal conduction pathways formed by the external copper layer. In contrast to filler composite materials, which contain a disjoint network of conductive fillers at ultralow loading, these Cu-plated lattices contained a highly connected copper layer around the polymer scaffold to minimize thermal contact interfaces and provide a more efficient heat transfer path. As expected, the 0.1 RD lattices exhibited a higher conductivity enhancement than the 0.2 RD lattices due to the lower initial conductivity of the as-printed lattices. At Cu layer thicknesses higher than 10 μm, cracking and delamination of the Cu layers were observed, suggesting that mechanically induced cracking would cause delamination and lower the thermal conductivity of the plated lattices.

The expected thermal conductivity of primitive lattices was simulated by Abueidda et al.⁴². The effective conductivity of the lattice depends on both the lattice relative density and the bulk material conductivity, which was calculated from three theoretical material models: the parallel model, the Maxwell-Eucken model, and the Effective Medium Theory model.

The parallel model assumes a layered composition of two materials, with both materials parallel to the direction of the heat flux. The overall thermal conductivity can be calculated as:

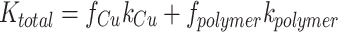1

with f denoting the volume fraction of each material. The Maxwell-Eucken model assumes a composite material with one continuous phase and one dispersed phase⁴³. In our study, the copper can be assumed as the continuous material and the polymer as the dispersed material, as the majority of heat conduction occurs in the copper. The overall thermal conductivity can be calculated as:

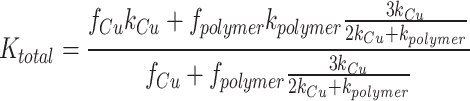2

Lastly, the Effective Medium Theory model assumes a composite material with two randomly interspersed phases⁴⁴. The overall thermal conductivity can be calculated as:

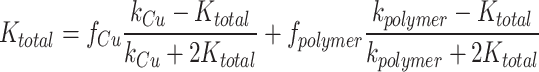3

Clearly, the parallel model overestimated the conductivity, as the copper and polymer layers did not align perfectly with the heat flux direction due to the lattice curvature. The experimental thermal conductivity values followed the Maxwell-Eucken model more closely. Deviations from the model may be due to inconsistent Cu plating thicknesses across the structure. For structures with complex curvature, the Maxwell-Eucken model represents the upper bound of possible conductivity values. The close agreement of the measured thermal conductivity values with the Maxwell-Eucken model suggests that the majority of the heat transfer occurs within a continuous copper layer.

Thermomechanical property evaluations

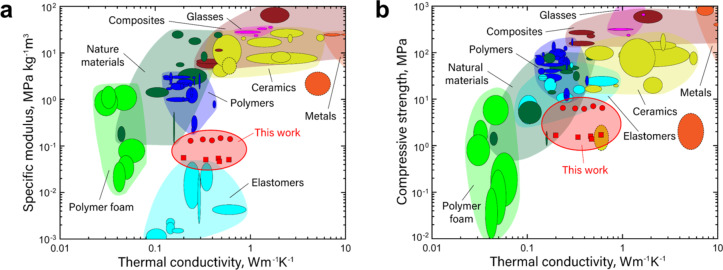
Figure 5 shows specific elastic modulus plotted against thermal conductivity, and compressive strength plotted against thermal conductivity. The lattice structures demonstrated specific moduli of 0.05 kg^− 1m³ for 0.1 RD lattices and 0.14 kg^− 1m³ for 0.2 RD lattices. The specific compressive strength values corresponded to 1.6 MPa for 0.1 RD lattices and 6.6 MPa for 0.2 RD lattices. The lattices have similar specific stiffness as polymer foams, but an order of magnitude greater thermal conductivity (Fig. 5a). The specific modulus of the lattices is between that of polymers and elastomers, with similar thermal conductivity. The lattices have similar compressive strength as polymer structures, polymer foams, and natural materials (see Fig. 5b), and higher thermal conductivity than these polymer foams and natural materials. The lattices expand the design space for thermo-mechanical materials. In certain applications, such as battery thermal management systems, having the highest modulus and strength per thermal conductivity is not desired. Rather, having a balance of properties that can support device performance over many cycles is key. The required thermomechanical metrics vary widely depending on the amount of pressure applied by the battery cells, the battery energy density, and the thermal management system design, including cooling channel dimensions. Generally, these target values fall within the tens of MPa for elastic modulus, in the hundreds of kPA for compressive strength, below 30 kPa for pressure drop, and in the tens or even hundreds of W/mK for thermal conductivity. Our composite lattice structures have demonstrated a promising move towards these target values, achieving all but the thermal conductivity.

Fig. 5.

Material property plot for thermomechanical properties. (a) Specific modulus vs. thermal conductivity. (b) Compressive strength vs. thermal conductivity. The solid red circle represents 0.2 RD samples, while the solid square represents 0.1 RD samples.

Discussion

In this study, we used 3D printing to fabricate Cu-polymer triply periodic minimal surface (TPMS) primitive lattices. Fluid flow through enclosed channels formed by the lattices, mechanical strength, modulus and elastic recovery, and thermal conductivity were evaluated. Our findings suggest that multi-material TPMS-based cellular materials may be suitable for use as cold plates in battery thermal management systems. The key conclusions from our study can be summarized as follows:

• Pressure drop increased when the number of channels was reduced and relative density was increased. The level-set parameter c and unit cell aspect ratios had a negligible effect on the pressure drop. Cold plates with larger flow spreads and higher relative densities exhibited a higher friction factor, in line with existing literature findings.

• Relative density had a large impact on elastic moduli and compressive strength, but no impact on elastic recovery. Variations in copper plating thickness had minimal impact on the mechanical properties, resulting in the lattices retaining a polymer-like compliance.

• The cyclic compression behavior was different for 0.1 and 0.2 RD. Following an initial drop in modulus after the first compression cycle, 0.2 RD lattices exhibited stiffening, while 0.1 RD lattices experienced a decrease and then a plateau in elastic modulus. Both relative densities displayed an increase in the onset strain during 50 cycles of deformation.

• The thermal conductivities of the lattices remained consistent across various relative densities but increased with copper plating thickness, reaching 0.7 W/mK. 0.44% copper loading led to a 216% increase in conductivity. This large enhancement is due to the highly interconnected copper heat pathways.

Our study highlights that mechanical and thermal performance can be independently adjusted by modifying relative density and copper loading, respectively. This ability to decouple pressure drop, mechanical, and thermal behaviors is useful for the design of efficient battery thermal management systems. For cold plate applications, further optimization of the manifold geometry could reduce the pressure drop. While the thermal conductivity was likely not improved enough for efficient battery cooling, the thermal conductivity can be further increased by increasing the Cu layer thickness and decreasing the polymer thickness. Future work is needed to investigate additional ductile materials with high thermal conductivities. The evaluation of cold plate performance in a realistic battery system would further contribute to the design utility.

Methods

Design and 3D printing

TPMS lattices are 3D periodic surfaces that exhibit zero-mean curvature at every point. The surfaces are typically modeled with a first order approximation of their respective Fourier series, resulting in an implicit function with a finite number of trigonometric functions⁴⁵. The Schwarz primitive surface can be modeled with the following equation:

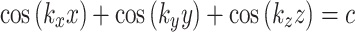4

in which c is the level-set parameter to adjust the “offset” of the surface, where c = 0 represents a surface that subdivides the unit cell into two phases of equal volume. In (4), k_i describes the function periodicity and can be further modeled by.

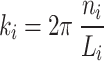where L_i represents the total lattice size and n_i represents the number of unit cell tessellations in the x, y, and z directions.

In this study, Schwartz primitive lattices were modeled by thickening the periodic surface described in Eq. 4. Samples either had a unit cell size of 5 × 5 × 5 mm (1:1:1 aspect ratio), or 5 × 5 × 10 mm (1:1:2 aspect ratio). CAD models of these unit cells are shown in Fig. 6a, b. Relative density, channel number, and level-set parameter c(offset) (Fig. 6c) were other geometric parameters that were explored. All geometric parameters are listed in Table 1. The flow domain refers to the internal dimensions of the cold plate, or the overall space in which fluid flows.

Fig. 6.

CAD models of TPMS unit cells. (a) Unit cell with 0.1 relative density and level-set parameter c = 0. (b) Unit cell with 1:1:2 aspect ratio. (c) Zero-thickness surface representations of unit cells with varying level-set parameters (c). The arrow marks the direction of increasing c values, with the c = + 0.2 surface on the outside and c =-0.2 on the inside.

Table 1.

Geometric parameters of all lattices. Parameters that are varied are shown in bold.

Parameter studied	Wall thickness [mm]	Relative density ρ	Number of channels	Level-set parameter c	Unit cell size [mm]	Overall flow domain [mm]
Relative density	0.212	0.1	18	0	5 × 5 × 5	90 × 60 × 5
	0.423	0.2	18	0	5 × 5 × 5	90 × 60 × 5
	0.635	0.3	18	0	5 × 5 × 5	90 × 60 × 5
Number of Channels	0.423	0.2	1	0	5 × 5 × 5	5 × 60 × 5
	0.423	0.2	5	0	5 × 5 × 5	25 × 60 × 5
	0.423	0.2	10	0	5 × 5 × 5	50 × 60 × 5
	0.423	0.2	18	0	5 × 5 × 5	90 × 60 × 5
Unit cell offset	0.212	0.13	18	-0.2	5 × 5 × 5	90 × 60 × 5
	0.212	0.1	18	0	5 × 5 × 5	90 × 60 × 5
	0.212	0.13	18	+ 0.2	5 × 5 × 5	90 × 60 × 5
Unit cell stretch	0.423	0.2	18	0	5 × 5 × 5	90 × 60 × 5
	0.423	0.22	18	0	10 × 5 × 5	90 × 60 × 5

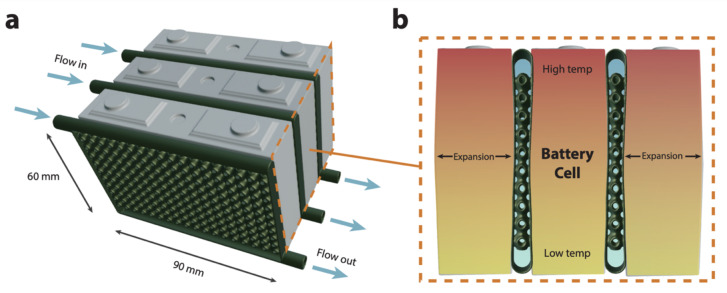
Lattices have a height of one unit cell. This is the best geometry for use as a cold plate in prismatic battery packs. For battery applications, the TPMS-based cold plate design offers a number of benefits compared to conventional bottom cooling, as illustrated in Fig. 7²⁵. First, placing the cold plate between battery cells increases the contact area available for cooling.

Fig. 7.

Illustration of TPMS lattice structures as cold plates for battery cooling. (a) Illustration of TPMS cold plates as inter-cell cooling channels in a lithium-ion battery pack. (b) Cross-sectional view showing thermal gradient and a bulging effect due to expansion at the center of the battery cell.

The top-to-bottom flow direction means that the coldest fluid is at the top of the battery cell, which is commonly the hottest area due to the electric terminals²⁸. The cold plate separates each battery cell, so it can act as a thermal barrier under thermal runaway. The cold plates also serve as structural supports. During charging cycles and across the battery cell lifetime, the middle of the battery may bulge due to material or thermal expansion, or the formation of gases from electrolyte decomposition⁴⁶. This bulging effect follows a parabolic shape, with a plateau at the center of the battery, due to constraints at the ends of the cell and the parabolic temperature profile (caused by Joule and entropy heating) which gives rise to a parabolic thermal expansion³⁰. While commercial lithium-ion prismatic cells swell by less than 0.5 mm at the center, corresponding to a 0.13 strain in our system, advanced cells with higher energy densities may expand even more^18,30. The mechanical compliance of the cold plate can be designed to compensate for this expansion, such that intimate contact with the battery cell is maintained. This offers an advantage over traditional metal cold plates, whose stiffness does not readily accommodate battery expansion.

All samples were fabricated via vat photopolymerization (masked stereolithography, MSLA) with an SL1S printer (Prusa Research). The software package nTopology was used to generate output .stl files for 3D printing. A commercial acrylic polymer (Prusa 3DM ABS Orange Tough Resin) was used with a 0.025 mm layer height and a 5 s layer exposure time. As provided by the manufacturer (Prusa), the acrylic polymer material has a tensile modulus of 1900–2200 MPa, a tensile strength of 40–50 MPa, and a 4–6% elongation at break. All samples were washed in isopropyl alcohol and post-cured in ultraviolet light with a 405 nm wavelength for 10 min (Prusa CW1S).

Electroless plating of Cu

Printed samples used for thermal and mechanical testing underwent Cu plating using an electroless plating process. A summary of the overall fabrication method, along with photos of as-printed and Cu-plated samples, are shown in Fig. 8. Initially, the surfaces of the printed primitive lattices were activated with a Pd-Sn colloid catalyst, following the procedure outlined in Recipe 3 as specified in the reference⁴⁷. The Pd-Sn colloid solution was prepared using the following steps. First, 0.25 g of Palladium chloride was dissolved in a solution consisting of 150 mL of water and 75 mL of 37% hydrochloric acid. To this solution, 1 gram of stannous chloride was added while vigorously stirring the mixture with a magnetic stirrer. The resulting solution was continuously agitated for two hours, after which it was allowed to rest overnight. Finally, the remaining 11.5 g of stannous chloride were introduced to the solution while maintaining constant agitation. The chemicals used for the process are listed in Table 2. The samples were immersed in the colloid solution for five minutes and subsequently rinsed with deionized (DI) water for 10–20 s, repeating the rinsing process a couple of times. The sample is then airbrushed with a gentle stream of air to remove any excess water.

Table 2.

Chemical composition of the Pd-Sn colloid catalyst.

Chemicals	Quantity
Palladium (II) chloride, PdCl2	0.25 g
Stannous chloride, SnCl2 2H2O	12.5 g
37% Hydrochloric acid, HCl	75 mL
Water, H2O	150 mL

The activated samples were then subjected to electroless plating using the bath compositions and conditions listed in Table 3⁴⁸. The pH of the solution, at approximately 28 degrees Celsius, fell within the range of 12.3 to 12.4. Following surface catalyzation, the samples were promptly immersed in a heated plating bath with a temperature around 80 °C. The plating duration ranged from 10 to 45 min in order to achieve varying thicknesses of Cu layers.

Table 3.

Chemical composition of the electroless Cu plating bath and plating conditions.

Chemicals	Concentration
Copper (II) sulfate pentahydrate, CuSO4 5H2O	0.036 M
Glyoxylic acid, C2H2O3	0.2 M
Ethylenediaminetetraacetic acid (EDTA), C10H16N2O8 2,2®-Bipyridyl, C10H8N2	0.06 M 10 ppm
Sodium hydroxide, NaOH	Proper amount (to adjust pH)
Bath pH	12.2–12.4 @ 28 °C
Bath temperature	80–85 °C

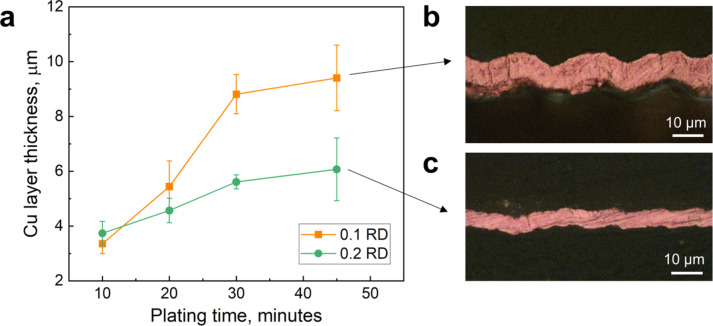
For a precise evaluation of the deposited Cu layer thickness, the plated samples underwent a series of processes involving cutting into sections, mounting, grinding, and polishing, all in preparation for cross-sectional imaging. The thickness of the Cu layer was determined through seven individual measurements, which were then averaged for precision. Figure 9 illustrates how the thickness of the Cu layers varied with plating time, accompanied by optical microscope images depicting cross-sectional views of the Cu layers plated for 45 min. The initial plating rate, specifically during the first 30 min, was notably higher for 0.1 RD samples, measuring 0.27 μm per minute compared to 0.1 μm per minute for 0.2 RD samples. As a result, even though both the 0.1 RD and 0.2 RD samples were plated for the same duration of 45 min, the average Cu thickness differed significantly, measuring 9.4 μm for the former and 6.0 μm for the latter as also shown in the images in Fig. 9b-c. This discrepancy may be due the lower porosity of the 0.2 RD lattices, which may restrict the mass transport of electroless plating chemicals to the interior of the lattice.

Fig. 9.

Thickness of plated copper layers. (a) Thickness of the Cu layer as a function of plating time. Cross-sectional images of Cu layers after 45 min of plating for (b) 0.1 and c) 0.2 RD samples.

Pressure drop testing

For pressure drop testing, a cold plate using a Z-type cooling manifold was designed. Internal channels were made of Schwartz primitive unit cells, with a width of one unit cell each and length of 10 unit cells along the direction of flow. The cold plates were tested in a flow loop as described by⁴⁹. Water was used as the working fluid, driven by a rotary motor (Micropumps, GC-M35) and measured by a mass flow meter (Tactical, TFM-C-015 LMAN). The pressure difference at the inlet and outlet of the cold plate was measured with differential pressure transducers (Omega, PX429-015GI). A 500 W preheater (ThermoFisher A25) and 3500 W chiller (Thermo Flex 3500) were located ahead of and behind the test section, respectively. Both the mass flow meter and the pressure transducers were connected to a data acquisition module (National Instrument, DAQ-9174) and controlled with LabVIEW software.

To calibrate the experiment, the inlet and outlet were directly connected to measure the baseline pressure drop across the flow loop tubing. The pressure drop across the cold plate can be described by

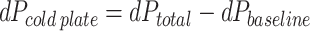6

where dP_total is the pressure drop measured directly across the inlet and outlet transducers, and dP_baseline is the baseline pressure drop of the flow loop tubing.

To reduce uncertainty due to fluctuations in the measured flow rate and pressure drop, data was collected for 10 s at a rate of five measurements per second at each flow rate. The resulting 50 data points were then averaged across both x (flow rate) and y (pressure drop) values, and the means were taken as the measured flow rate and pressure drop. The mean pressure drop values closely follow a quadratic fit, which was used to find the baseline pressure drop to subtract from the measured data.

Pressure drop is commonly reported as a function of the Reynold’s number, given by:

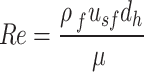7

Where 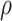_f is the fluid density, u_sf is the superficial velocity of the fluid through the lattice structure, d_h is the hydraulic diameter, and is the fluid viscosity. In our experiments, Re was varied by changing the inlet velocity. Due to the primitive lattice’s complex geometry, the hydraulic diameter is calculated as a function of the pore volume and surface area¹³:

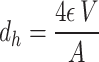8

Where V is the volume, A is the wetted surface area, and 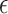is the porosity, or the fraction of fluid in the bounding volume:

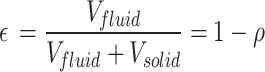9

Here, 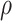is the relative density. The Fanning friction factor offers a dimensionless form of pressure drop to describe the resistance to flow in a structure. For the primitive lattice geometry, it is written as:

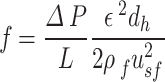10

Where 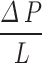is the pressure drop per axial length L of the channel(s).

Compression testing

Lattice structures of one unit cell in height, and 4 × 4 unit cells in lateral dimensions were used in compression tests (see Fig. 8). The lattice core is sandwiched by flat plates of 0.6 mm thickness. The same samples were used for thermal conductivity measurements.

Compression tests were conducted using the MTS 1234 machine, with a strain rate of 0.001 s^− 1 and a data acquisition rate of 10 Hz. Displacement measurements were acquired through head displacement, and the measured load was divided by the cross-sectional area of the samples (20 mm × 20 mm) to calculate the applied stress. The samples were compressed to a strain of 0.35, to evaluate the maximum possible elastic recovery, and a strain of 0.2 for cyclic testing to model a realistic use case throughout the lifetime of the cell. The height of the internal cell, excluding the top and bottom plates, was used to calculate applied strain. For example, in a sample with a total thickness of approximately 6.4 mm, the average cell height measured around 4.7 mm. The thicknesses of the internal cells were measured three times before and after the compression tests using a caliper to obtain the average cell height. Elastic recovery was calculated as the difference between the average cell height before and after deformation.

Cyclic compression tests were performed on as-printed 0.1 and 0.2 RD samples. An exemplary 0.2 RD sample is shown in Fig. 3b. These samples were strained to 0.2 over 50 cycles at a strain rate of 0.005 s^− 1. Load and displacement data were collected at a sampling rate of 5 Hz. The elastic modulus and onset strain (the strain at 0.1 MPa) were extracted for each cycle to assess the evolving mechanical properties of the lattice structures under cyclic loading.

Thermal conductivity measurement

Comparative infrared (IR) microscopy was used to directly measure the effective thermal conductivity of the lattice structures without the need for thermocouples (Fig. 10)^50–52. The lattice structures shown in Fig. 3 were used in these experiments. The lattice structure was placed between two reference layers and adhered with a thermal interface material (TIM) to reduce the thermal contact resistance. Silicone thermal paste (k_TIM = 12.8 W/mK) was used as the TIM to ensure a negligible thermal resistance contribution from the TIM. To generate a constant one-dimensional heat flux, a heater was attached to the top side of the test stack and a heat sink copper block was placed below the test stack. A silicone thermal pad (k_silicone = 1.5 W/mK) was used as a reference material to ensure comparable thermal conductivities across the sample and reference layers. The surface of the test stack was painted black to ensure a uniform emissivity across all layers.

Fig. 10.

Thermal conductivity measurement setup. (a) Image of the test stack. (b) Representative image taken via IR microscopy. (c) Representative temperature gradient obtained from the region inside the red box shown in (b). The areas marked in gray represent the interfaces between the silicone reference layers and the TPMS lattice.

A two-dimensional temperature profile of the test stack surface was generated using an IR camera (FLIR, A655) with a temperature measurement uncertainty of ± 2 °C. A measurement area in the center of the test stack was used to eliminate convective edge effects (Fig. 10b). The steady-state temperature profile was averaged perpendicular to the heat flux to obtain a one-dimensional temperature gradient (Fig. 10c). A least-squares fit was used to estimate the temperature gradients in each layer. The temperature gradient in each layer was then compared to estimate the lattice effective thermal conductivity:

11

where 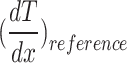is the average of the temperature gradients in the two reference layers. The polymer plates on the top and bottom of the lattice sample, as well as the boundary thermal contact resistances, were omitted from the measurement. The measured thermal conductivity is that of the lattice core.

Author contributions

SC and JK fabricated samples, conducted the experiments, and wrote the main manuscript. YL developed thermal measurement methodology. KG provided equipment and resources. MA and WG supervised the project. All authors reviewed the manuscript.

Data availability

All data is summarized within the manuscript. The raw datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.

Declarations

Competing interests

The authors declare no competing interests.