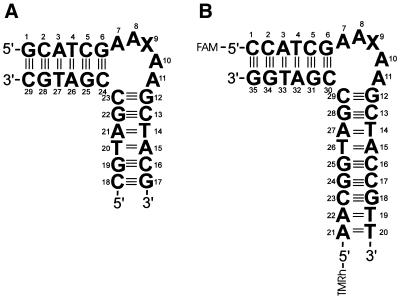Solution structure of dAATAA and dAAUAA DNA bulges

Abstract

The NMR structure analysis is described for two DNA molecules of identical stem sequences with a five base loop containing a pyrimidine, thymin or uracil, in between purines. These five unpaired nucleotides are bulged out and are known to induce a kink in the duplex structure. The dAATAA bulge DNA is kinked between the third and the fourth nucleotide. This contrasts with the previously studied dAAAAA bulge DNA where we found a kink between the fourth and fifth nucleotide. The total kinking angle is ∼104° for the dAATAA bulge. The findings were supported by electrophoretic data and fluorescence resonance energy transfer measurements of a similar DNA molecule end-labeled by suitable fluorescent dyes. For the dAAUAA bulge the NMR data result in a similar structure as reported for the dAATAA bulge with a kinking angle of ∼87°. The results are discussed in comparison with a rAAUAA RNA bulge found in a group I intron. Generally, the sequence-dependent structure of bulges is important to understand the role of DNA bulges in protein recognition.

INTRODUCTION

Systematic studies of unusual DNA structures deviating from the double-helical DNA set the ground for understanding the principles of nucleic acid architecture. Bulges in nucleic acids are formed when bases in one strand have no pairing partner in the opposite strand. The bulge induces a sharp kink. In RNA such structures are of biological relevance and contribute to the three-dimensional structure of the molecule. RNA bulges constitute versatile structural motifs in the assembly of RNA architectures (1). Three-dimensional structures of bulges elucidate mechanisms by which they execute intermolecular recognition. Bulges may be created in DNA during recombination between imperfectly homologous sequences. The mutual relation between kinked DNA structures and DNA binding specificity was demonstrated previously (2,3). Recently, the role of a DNA bulge in protein recognition was reported (4). HMG-D, a high mobility group protein, was shown to bind preferentially to bulge sites in DNA. This previous electrophoretic study (4) was very recently confirmed by an NMR model (5). The binding of the tumor supression protein p53 to DNA also prefers bulges over other mismatches (6). Bulges in DNA were also shown to act as potential binding sites for therapeutic drugs, e.g. neocarcinostatin (7). Bulged nucleic acids have been studied by various biophysical methods. Five-nucleotide bulges have been described as important structure elements in RNA. In the crystal structure of a self-splicing group I intron, Cech and coworkers (8) found a 5-nt bulge rAAUAA that is necessary for the tertiary folding of the structural domain including helices P4, P5 and P6. The solution conformation of the rAAUAA bulge was studied by Tinoco and coworkers (9) using NMR. In contrast to these RNA bulges, the structure of DNA bulges with >3 nt was unknown hitherto. As reported previously, we determined the first solution structure of a pentanucleotide bulge, dAAAAA, in DNA by NMR (10). In this dAAAAA bulge, four adenines form a continuous stack on the preceding guanine of the 5′ flanking double-helical stem, followed by a sharp kink. The fifth adenine at the 3′-end of the bulge is stacked upon the subsequent guanine of the 3′ flanking double-helical stem. We were interested in the sequence-dependent bulge structure of a modified bulge sequence, i.e. dAATAA and dAAUAA. We find that the thymidine in the center of the loop of the dAATAA bulge changes the stacking behavior: the 5′ dAAT stacks 5′ on the helix followed by a kink. The two 3′ adenines of the bulge stack 3′ on the helix. The solution structure of the dAAUAA bulge is similar to the dAATAA bulge. Likewise, the kink is located between the 5′ dAAU and the last two 3′ adenines of the bulge. We compare the solution structure of the dAAUAA bulge DNA with the crystal and solution structure of the rAAUAA RNA bulge found in the group I intron.

MATERIALS AND METHODS

Sample preparation

Synthesis, purification and desalting of the three oligonucleotides, 5′-d-GCATCGAATAAGCTACG-3′ (I), 5′-d-GCATCGAAUAAGCTACG-3′ (II) and 5′-d-CGTAGCCGATGC-3′ (III), followed the procedure described in our preceding paper (10).

The two NMR samples were prepared by combining equimolar amounts of the oligonucleotides I + III and II + III, respectively, in a phosphate buffer containing 100 mM NaCl and 0.05 mM EDTA at pH 7.0. For brevity, the resulting DNA bulge molecules will be designated dT-bulge (I + III) and dU-bulge (II + III), respectively. The samples were lyophilized three times from D₂O and finally dissolved in 550 µl of 99.996% D₂O. The sample concentrations were 1.6 (dT-bulge) and 3.8 mM (dU-bulge) in duplex. For assignments of exchangeable protons, DNA samples in 10% D₂O and 90% H₂O were prepared. The pH values were measured in the NMR tubes. The correct formation of the duplexes with double-helical stems was verified by UV spectroscopy in diluted solution at 200 mM NaCl. The observed melting temperatures are 33.6°C for the dT-bulge (2.6 µM DNA) and 39.0°C (3.8 µM DNA) for the dU-bulge.

Preparation of the fluorescence-labeled DNA sequences

Labeled single-stranded DNA fragments were obtained from NAPS (Göttingen, Germany); the DNA sequences are: 5′-d-(FAM-) CCATCGAAAAAGCTACCGTT-3′ (IV); 5′-d-(FAM-)CCATCGAATAAGCTACCGTT-3′ (V); and 5′-d-(TMRh-)AACGGTAGCCGATGG-3′ (VI).

The resulting DNA molecules (IV + VI) and (V + VI) will be designated as dAF- and dTF-bulge, respectively. They were synthesized and labeled as described previously (11). The fluorescent dye 6-carboxyfluorescein (FAM) is used as a 5′-label on the sequences (IV) and (V), and 5-carboxytetramethylrhodamine (TMRh) labels the 5′ on the sequence (VI).

In short, the DNA sequences (IV) and (V) were synthesized using β-cyanoethyl phosphoramidite chemistry and 5′-labeled with FAM in a final coupling step on the DNA synthesizer using fluorescein phosphoramidite (Applied Biosystems, Foster City, CA, USA). The succinimidyl ester of 5-carboxytetramethylrhodamine (TMRh) from Molecular Probes (Eugene, OR, USA) was attached to the 5′-amino group at the end of a six-carbon linker in 0.2 M carbonate buffer (pH 9.0) on the sequence (VI). The labeled fragments were purified by reversed-phase HPLC and by PAGE (11,12).

Spectroscopic studies

Absorption and fluorescence measurements were taken on a Specord M500 (Zeiss, Germany) and a SLM 48000S instrument (SLM Aminco, Urbana, IL, USA), respectively. Polarization artifacts were avoided by using ‘magic angle’ conditions. The fluorescence samples were excited at 490 nm for the fluorescence resonance energy transfer (FRET) spectra and at 560 nm for the acceptor spectra. The fluorescence spectra were collected over a broad range of emission wavelength from 500 to 650 nm and from 570 to 650 nm and corrected for buffer signals. All measurements were carried out at 15°C.

Fluorescence anisotropies r were calculated from fluorescence intensity measurements by a vertical excitation polarizer with vertical and horizontal emission polarizers according to:

with the experimental correction factor (13).

Fluorescence resonance energy transfer

The efficiency of FRET E from a fluorescence donor to an acceptor is related to the donor–acceptor distance R according to:

E = R₀⁶/(R₀⁶ + R⁶)

R₀ is the Förster distance at which the energy transfer efficiency is 50%, calculated from:

R₀ = 9790·(Jκ²φ_Dn^–4)^1/6 Å

where J is the spectral overlap integral of the dyes, φ_D the quantum yield of the donor in absence of the acceptor, n the refraction index of the medium and κ² the orientation of the transition dipole moments (14–16). For a rapid randomization of the relative donor–acceptor orientation κ² is 2/3 (17). The low anisotropies of the donor fluorescein implies that this is a good approximation for this study (18), so that the efficiency of energy transfer E is sensitive only to the donor–acceptor distance R.

The FRET efficiency E was determined by measuring the intensity of the sensitized emission of the acceptor normalized to the fluorescence of the acceptor alone (19):

(ratio)_A = E·(ɛ^D,490/ɛ^A,560) + (ɛ^A,490/ɛ^A,560)

(ratio)_A is linearly dependent on the efficiency of energy transfer, E. It normalizes the measured sensitized FRET signal for the concentration, for the quantum yield of the acceptor and for any errors in percentage of acceptor labeling. ɛ^D and ɛ^A are the molar absorption coefficients of the donor and acceptor at the given wavelength (490 or 560 nm).

Observing the DNA curvature with electrophoretic mobility shift assay

Each 5 µl of the dAF- or dTF-bulge (200 nM) were loaded on a native 20% polyacrylamide gel. The electrophoresis was done at 100 V in a 1× TBE buffer (100 mM Tris, 83 mM borate, 1 mM EDTA at pH 8.0). The gels were directly scanned using a FluorImager 595 (Molecular Dynamics, Amersham Biosciences, Freiburg, Germany) and analyzed with the ImageQuaNT software.

NMR experiments

¹H- and ³¹P-NMR experiments were run on Varian Unity INOVA spectrometers at 500, 600 and 750 MHz. All 2D measurements were carried out at 27°C unless indicated otherwise.

Imino proton spectra were obtained by using the solvent suppression 1331 pulse sequence (20) with the carrier set at the H₂O resonance. Data were collected for a spectral width of 12 kHz. The temperature was varied between 0 and 50°C.

2D NOE spectra with mixing times of 80, 140, 200 and 400 ms were recorded in D₂O at 600 MHz (dU-bulge: 750 MHz). A spectral width of 6000 Hz was used and the carrier frequency set to the HDO resonance frequency. A total of 1024 FIDs of 2K (800–950 FIDs of 6K) complex data points were collected in t₁ with 64 scans. NOESY data sets were multiplied with a Gaussian window function in both dimensions and zero-filled to give a final 8K × 8K (4K × 4K) matrix.

2D NOE in H₂O at 5°C were done using the WATERGATE sequence (21).

An E.COSY (22) was recorded at 600 MHz using 2K complex points, 1024 (800) experiments in the t₁ dimension with 120 (96) scans and a spectral width of 5000 (6000) Hz. After linear prediction of 512 points in the t₁ dimension and apodization in both dimensions with a 70° shifted squared sine bell, zero filling was used to obtain a final 8K × 8K data set. This corresponds to a digital resolution of 0.63 (0.75) Hz/point in both dimensions.

A proton-detected ³¹P–¹H heteronuclear correlation spectrum was collected with a spectral width of 5000 Hz in the ¹H dimension and 500 Hz in the ³¹P dimension: 2048 complex points in the t₂ (¹H) dimension and 80 complex points in the t₁ (³¹P) dimension with 1600 scans at each t₁ value were collected (23).

To selectively detect the H2 protons of the adenines in the bulge, partially recovered one-dimensional NMR spectra were recorded using the inversion recovery pulse sequence (24).

The spectra processing was performed with NMRPipe/NMRDraw software (25).

Distance and torsion angle restraints

In general, the restraints were obtained from the NMR data as described previously (10). As initial model structure for the MARDIGRAS calculations (26), the reported structure of the dA-bulge (10) was used for the dT-bulge.

The determination of the sugar, backbone and glycosidic torsion angles were carried out following standard procedures (27,28) as described elaborately in our preceding paper (10). In particular, the ³J_H1′H2′1 were used to determine the range of the pseudorotation angle (the pucker always fixed at 36°). This allows the calculation of the range of the pertinent torsion angle F_H1′H2′1 (29).

Structure calculation

The distance geometry calculations were performed by torsion angle dynamics (TAD) applying the program DYANA (30). The 15 ‘best’ conformers with the smallest target function values were selected for energy minimization using the AMBER91 force field (31) in AMBER5.0 (32).

Structural analysis

The conformational and helical parameters were obtained from the averaged ‘best’ structure applying the programs MOLMOL (v.2.6) (33) and CURVES (v.4.1) (34). The kink angle is defined as the angle between the axes of the two double-helical stems flanking the bulge and was obtained by the use of the programs CURVES and ARC-FIT (Peter Slickers, personal communication) as described in our preceding paper (10).

RESULTS

Duplexes with unpaired bases (bulges) are structural motifs in nucleic acids and kink the helix axis. We are interested in the sequence dependence of these structures and a comparison of DNA with RNA bulges. Bulge structures containing three (35) and five unpaired bases in RNA (9) and DNA (10), respectively, have already been published.

Subsequent to dAAAAA (10), here we report on two DNA molecules containing five unpaired bases with a modified sequence (AATAA in the dT-bulge, AAUAA in the dU-bulge) between two double-helical stems. The residues of the dT-bulge and dU-bulge are numbered as given in Figure 1A. In position 9, X = T for the dT-bulge and X = U for the dU-bulge. For the FRET experiments, the sequences apart from the bulge are slightly modified and labeled with fluorescent dyes at the 5′-ends of the two strands as shown in Figure 1B. In position 9, X = A for the dAF-bulge and X = T for the dTF-bulge.

Figure 1.

Structure of the DNA bulges. (A) NMR samples, X = A (dA-bulge), X = T (dT-bulge) X = U (dU-bulge). (B) Fluorescence samples, X = A (dAF-bulge), X = T (dTF-bulge). Fluorescence labels: FAM (6-carboxyfluorescein) and TMRh (5-carboxytetramethylrhodamine).

¹H-NMR measurements

Exchangeable protons. Similar to the previous findings in the NMR spectra of the dAAAAA-bulge in H₂O (10), we observed the imino protons of G and T in the low-field region between 12 and 14 p.p.m. inclusively of the base pairs flanking the bulge (G6 and G12). This is a direct evidence for the formation of Watson–Crick base pairs in the two stems of the bulge molecules. Admittedly, the imino resonance of G12 at the junction to the bulge is broad at 25° and disappears at 30° in the spectra both of the dT- and the dU-bulge. The corresponding imino resonance of G6 is heavily overlapped by five (dT-bulge) and six (dU-bulge) other imino protons and cannot be observed individually as a function of temperature.

Non-exchangeable protons. Both duplex parts of the two bulges are found to be consistent with right-handed duplexes, S-type sugar puckering and anti glycosidic torsion angle based upon the NOESY cross-peak pattern and intensities (36). For the assignment of the proton resonances, the NOESY, DQF-COSY and ³¹P–¹H heteronuclear correlation spectra have been used. It was difficult to assign all eight adenine H2 protons. The adenines in the bulges lack most (or all) of the cross-peaks usually observable in A·T Watson–Crick base pairs. In the 1D-NMR spectra of the dT-bulge, at optimized T1 values we found only seven peaks with long T1. However, the intensity of the peak at 7.79 p.p.m., easily assigned to the H2 proton of A3, is nearly 2-fold of all others and is assumed to be composed of both H2 protons of A3 and A10.

For both bulges, the sequential walks are interrupted for several of the connectivities between C24 and C23 as previously reported also for the dA-bulge (10). Only the connectivities of the C23H3′ proton to the H5 and H6 of C24 can be observed.

The obtained coupling constants ³J_{H1^′–H2′} and the sum Σ1′ (³J_{H1′–H2′} + ³J_{H1′–H2″}) of both bulges have values consistent with S-type puckering of all deoxyribose residues: 7.8–10.7 Hz for ³J_{H1′–H2′} and 11.7–17.7 Hz for Σ1′ (29,37).

Upfield shifts have been found for the H4′ protons of T9 and U9 in the two bulges. This can be explained by stacking of the H4′ proton over the neighbored 3′ base. The ring-current of the base can produce the observed shift as has been reported previously for loops (28) and bulges (10). Also, the H2′ resonances of T9 and U9 in the two bulges are shifted to extremely low values: 1.60 and 1.56 p.p.m., respectively. Likewise, among the H2″ shifts, T9 and U9 have the lowest values (1.96 and 1.95 p.p.m., respectively).

Distance and torsion angle restraints

Interproton distance restraints were established using three MARDIGRAS distance sets (see NMR experiments) which were calculated from NOE intensities of the three mixing times, 80, 140 and 200 ms (400 ms mixing time was used merely for assignment), using a rotation correlation time of 2.5 ns (see 10). The 645 NMR-derived interproton distances of the dT-bulge are comprised of 386 intra-residue and 251 sequential distances (Table 1). For the dU-bulge, we used 671 distance restraints, 397 intra-residue and 274 sequential distances. Additionally, 235 torsion angle restraints are used in the structure calculation of the T-bulge as well as the U-bulge. Hydrogen bonding restraints have been introduced in the stem regions as described previously (10).

Table 1. Structural statistics of the 15 NMR conformers derived from TAD calculations representing the solution structure of the DNA dT-bulge and dU-bulge molecules.

	A2TA2	A2UA2
NOE distance restraints	645	671
Sequential distances	251	274
Intra-residue distances	386	397
Non-NOE distance restraints	6	0
Hydrogen bonding restraints	26	26
Torsion angle restraints	235	235
Average restraints per residue	31	32
DYANA target function (Å2)	2.77 ± 0.01	2.55 ± 0.01
Distance limit deviations >0.2 Å	0	0
Dihedral angle deviations >5°	0	0
Mean pairwise RMSD, all heavy atoms (Å)	1.23 ± 0.46	0.86 ± 0.41
RMSD relative to mean structure, all heavy atoms (Å)	1.18 ± 0.46	0.74 ± 0.34

Structure calculation

The distance geometry calculations were performed with the program DYANA (30). After initial structure calculations, we observed in the dT-bulge several short proton–proton distances in the bulge loop region that were not defined by experimental distance restraints. If no NOESY cross-peaks were observed in the 200 and 400 ms NOE spectra, these distances were introduced as ‘non-NOE’ distance restraints with a lower limit of 0.45 nm (9,10). Most of them have been removed in the course of the calculations, but six were left in order to obtain a set of structures that does not violate the experimental findings. After energy minimization, the resulting 15 ‘best’ structures of the two bulges were selected (Fig. 2) and a mean structure created.

Figure 2.

Stereoview of the 15 ‘best’ NMR conformers of the dA-bulge (top), dT-bulge (center) and the dU-bulge (bottom). All hydrogen atoms are omitted for clarity. The 15 NMR conformers are deposited at the Brookhaven Protein Data Bank (ID codes: 1QSK, 1JRV and 1JS7, respectively). The stereoview of the dA-bulge is reprinted with permission from Dornberger et al. (10). Copyright (1999) American Chemical Society.

The structure of the dU-bulge was obtained by the same procedure. However, in this case we could avoid the introduction of non-NOE distance restraints in the course of the structure refinement. The statistics of the 15 ‘best’ structures of the dT- and the dU-bulge are shown in Table 1. The number of sequential NOE distance restraints (251 and 274, respectively) is high compared with this number for the dA-bulge of 149.

Fluorescence resonance energy transfer and gel shift assay

We studied the two DNA bulges dAF (dAAAAA in the bulge) and dTF (dAATAA in the bulge) by electrophoretic mobility shift assay and by fluorescence spectroscopy. The dAF and dTF molecules are both 5′-labeled by fluorophores, FAM and TMRh, and have some variations in the stem sequence at the duplex ends compared with the NMR samples but coincide with the five base pairs flanking the bulge (Fig. 1).

The electrophoretic data, comparing the dAF-bulge and the dTF-bulge, are very similar. The migration of the dT-bulge is only slightly slower than that of the dA-bulge (Fig. 3).

Figure 3.

Electrophoretic mobility shifts of the dAF-bulge (dA₅) and dTF-bulge (dA₂TA₂) molecules.

The anisotropy of the donor fluorescein of labeled bulged molecules was determined. It increases just slightly for both dAF-bulge and dTF-bulge from 0.075 in single-labeled DNA to 0.10 in double-labeled DNA indicating a free mobility of the donor dye.

The distance between two fluorophores attached covalently to the 5′-DNA helix ends was deduced from FRET efficiency measurements (Table 2). We have to regard the end-fraying of the terminal base pairs of double-helical DNA that may include also movement of the terminal parts of the flexible backbone. This effect will deteriorate the precision of the FRET measurement. By this, the dye-to-dye distances are subject to an estimated error of ±0.2 nm. Thus, within the limits of error, we find similar end-to-end distances of the dAF-bulge and the dTF-bulge (Table 2). We modeled classical B-DNA double helices (Fig. 1B) with the labeling dyes attached at the 5′ ends of the NMR bulge structures (Fig. 1A). In the obtained modeled structures we calculated the dye-to-dye distances for the dAF-, dTF- and dUF-bulge, respectively (Table 2). The dye-to-dye distances are not only dependent on the kinking angle of the two helix stems but also on other structural parameters like, for example, the twist angles within the stems. These values are consistent with the measured FRET distances.

Table 2. Results of the FRET analysis for the DNA dAF-bulge and dTF-bulge molecules.

	dAF-bulge	dTF-bulge	dUF-bulge
Measured FRET efficiency	0.47 ± 0.02	0.42 ± 0.02	–
Dye distance (experimental) (nm)	5.1 ± 0.2	5.3 ± 0.2	–
Dye distance, calculated from model (nm)	5.6	5.2	5.4

DISCUSSION

The dAATAA is kinked at the TpA step

The overall structure of the dT-bulge shows similar features as the previously reported structure of the dA-bulge dAAAAA (10) with a sharp kink within the bulge and all bulge bases in an intra-helical position. However, the position of the kink is different. In the dA-bulge, the kink was observed between the penultimate (position 10) and the final (3′) adenine (position 11). In the dT-bulge, the kink is observed between the central thymine in position 9 and the subsequent penultimate 3′ adenine in position 10. Moreover, the kink of the dT-bulge is more pronounced with an angle of 104° (±12°) than in the dA-bulge (73° ± 11°). The structure is well defined (Table 1 and Fig. 2) with an average of 31 restraints per residue and a mean pairwise root mean squared deviation (RMSD) of 0.123 nm of all heavy atoms of the 15 best structures. The kink position is supported by the complete absence of base–base proton NOEs between T9 and A10. Also the T9H1′–A10H8 NOESY cross-peak is absent and the corresponding T9H2′–A10H8 peak is extremely weak. On the other hand, the sequential NOESY connectivities between H1′, H2′1, H2′2 and the 3′-neighbored H8/H6 have been observed for the steps A7–A8, A8–T9, A10–A11 and A11–G12. Again, this is in agreement with the obtained NMR structure that shows stacking between these base pairs interrupted by the kink at the step T9–A10.

At the kink position, the backbone is characterized by large positive values of the angles α (121°) and γ (114°) of A10. This is completely different to the dA-bulge where there was a strong deviation of the angle x at A10 (10).

The dAAUAA bulge kinks at the same position as the dAATAA bulge

By inspection of the NMR data of the dU-bulge, we observe a resemblance to the corresponding data of the dT-bulge indicating a close similarity between the solution structure of the dT-bulge and the dU-bulge. This is based mainly upon the qualitative agreement of the NOESY cross-peak pattern in the kink region, i.e. the TpA and the UpA step, respectively. The distances T9H2′–A10H8 and U9H2′–A10H8 are much longer than the corresponding H2′–H8 distances in other parts of the bulge or in the base-paired stem regions, reflected in significantly decreased volumes of the T9H2′–A10H8 and U9H2′–A10H8 cross-peaks (data not shown).

The solution structure of the dU-bulge was obtained by the same procedure as for the dT-bulge. The 15 ‘best’ structures of the dU-bulge are of the same quality as those of the dT-bulge (Table 1 and Fig. 2). The mean pairwise RMSD is even better and the number of restraints per residue is slightly higher than for the dT-bulge. A similar structure of the dU-bulge as for the dT-bulge was expected since only a methyl group is removed from T9. All bulge bases are intra-helical and involved in stacking interactions. The overall bend of the dU-bulge gives an angle of 87° ± 9° between the values obtained for the dA-bulge (73°) and the dT-bulge (104°). The mean structures of the dT-bulge and the dU-bulge are shown in Figure 4.

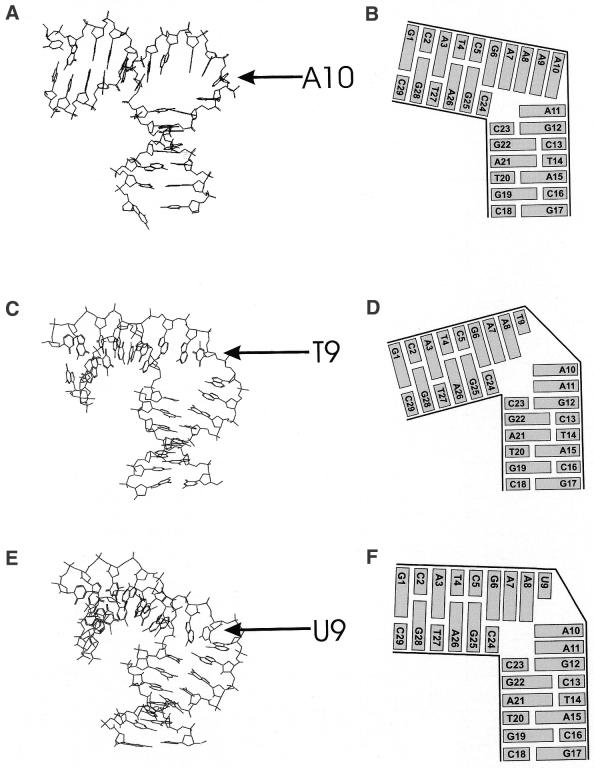
Figure 4.

NMR solution structure (mean structure) of the dA-bulge (A and B), dT-bulge (C and D) and the dU-bulge (E and F). A10, T9 and U9 are marked by arrows. Structures are deposited at the Brookhaven Protein Data Bank (ID codes: 1JRW for the dT-bulge and 1JS5 for the dU-bulge). (B), (D) and (F) are schematical sketches to illustrate solely the stacking behavior of the bulge bases with respect to the two flanking duplex areas. (A) and (B) are reprinted with permission from Dornberger et al. (10). Copyright (1999) American Chemical Society.

Why is the kink between T9 (U9) and A10?

Obviously, stacking is the driving force for the formation of a more or less rigid structure within the bulge loop. A local sharp kink is associated with loss of stacking energy. In the dA-bulge, the first four adenines A7–A8–A9–A10 are part of a continuous stack from G1 up to A10. However, the fifth adenine A11 of the bulge is stacked upon the subsequent G12.

In the dT-bulge, the central A9 is substituted by a thymine T9. It is well known that pyrimidine bases are worse candidates for stacking than purine bases. Thus, we expect the interruption of the stacking by the sharp kink either at the ApT step between A8 and T9 or at the TpA step between T9 and A10.

In double-stranded DNA, experimental data agree in a qualitative trend of decreasing stability AA/TT > AT/TA > TA/AT (38). Assuming that a transfer to single-stranded DNA is justified, we would expect decreasing stability ApA > ApT > TpA. If we have to sacrifice one of the stacking steps in the AATAA bulge, the TpA step between T9 and A10 is energetically the least profitable. From this point of view, a break of stacking in the bulge is energetically favorable between T9 and A10. The alternative of a kink between A8 and T9 should be less profitable. The break of a ApT stack would sacrifice more free energy than a break of a TpA step. This consideration is in full agreement with our findings in the dT-bulge and also holds for the dU-bulge with a kink between U9 and A10.

Comparison of the solution structures of the three bulges

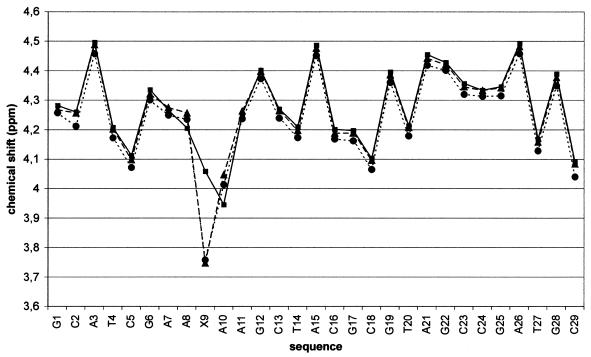
Chemical shift and kinking site. The NMR data support the position of the kink in the bulge even without any structure calculation. A critical parameter is the chemical shift which is strongly dependent on the position of the viewed proton in the ring current field of the neighbored adenine. The different position of the kink in the three investigated DNA bulges is clearly reflected in the chemical shifts. The strongly shifted H2′, H2″ and H4′ signals of T9 as well as of U9 support a very similar structure of the two bulges at this critical kink position. The chemical shift data of the three bulges with dA, dT and dU in the central position of the pentanucleotide bulge clearly indicate the kink position at A10 for the dA-bulge and at X9 (X = T, U) for the dT- and dU-bulge. A typical example is the chemical shift of the H4′ protons (Fig. 5).

Figure 5.

Chemical shift of the H4′ protons of the three bulges. dA-bulge (squares, solid line); dT-bulge (triangles, broken line); dU-bulge (circles, dotted line).

The ³¹P chemical shifts are correlated with the backbone conformation. While the ³¹P chemical shifts at the kinking position A10 of the dT- and dU-bulge are highly negative (–1.04 and –0.70 p.p.m., respectively), the ³¹P chemical shift at the kinking position A11 of the dA-bulge is extremely low (–0.17 p.p.m.). This points towards different backbone conformations at the kinking site of the dA-bulge on the one hand and the dT- and dU-bulge on the other hand.

Inter-base parameters in the bulge region. A close inspection of the inter-base parameters in the bulge region using the program CURVES shows exceptionally extreme values at the kinking site. By this, we have a clear distinction between the dA-bulge on the one hand and both the dT-bulge and the dU-bulge on the other hand. The parameters are always extreme at base step 10/11 of the dA-bulge, but at base step 9/10 of the dT-bulge and dU-bulge. At these positions—which are the respective sites of the kink—we have negative shift, low rise, high tilt and low twist (see Supplementary Material). The roll angle is very different for both groups, highly negative for the dA-bulge and highly positive for the dT-bulge and dU-bulge (see Supplementary Material). Remarkably, the different bulge structures are reflected also in the flanking base pair C5/C6 outside of the bulge: the dT-bulge as well as the dU-bulge have large positive roll at C5/G6, compensated by negative roll at A7/A8 in the bulge. The dA-bulge lacks this large fluctuation of the roll.

Inter-base parameters in the second strand. The second strand opposing the bulge is expected to be irregular at the site of the kink. The neighbored base step G25/C24 is characterized by some extreme values of tilt, roll and twist. Particularly, a negative roll of the dA-bulge at this base step is contrasted by positive roll angles of the dT- and dU-bulge. Furthermore, the twist of the dA-bulge is extremely high (47.5°) compared with ordinary values of the dT-bulge (34.4°) and dU-bulge (32.3°) for the base step G25/C24.

The equivalent base step neighbored to the bulge, C23/G22, shows again ordinary twist angles for the dT- and dU-bulge (33–34°) and only slightly higher twist (37°) for the dA-bulge.

Inter-base pair parameter. The base pair parameters of the two duplex parts of the bulge have extreme values at the junction sites to the bulge, i.e. C5G25/G6C24 and G12C29/C13G28. In particular, the roll at C5G25/G6C24 is negative (–4°) for the dA-bulge and highly positive (13–14°) for the dT- and dU-bulge. Again, the base-pair twist of the dA-bulge is extremely high (43.2°) compared with ordinary values of the dT- and dU-bulge (31–34°), similarly to the inter-base values of the second strand.

The inter-base pair parameters at the other junction site, G12C23/C13G22, show neither unusual values nor significant differences between the three bulges.

Backbone parameters at the kinking site C23–C24. In the second strand 5′-C18–C29-3′ (Fig. 1) all bases are base paired with partners of the first strand 5′-G1–G16-3′. A special situation occurs at C23–C24 where the 5-nt bulge is inserted in the first strand. The kink in the second strand is situated between C23 and C24, consequently we expect unusual backbone parameters.

A detailed inspection of the mean solution structures of the dT- and the dU-bulge reveals some differences. In both bulges, the glycosidic angle χ and the torsion angle γ exhibit no unusual values at C23 and C24, but the torsion angle x has unusually small negative values in the two bulges at C23 (–39°, –64°) with respect to the usual range of –80° to –100°.

However, differences between the dT-bulge and the dU-bulge are evident for the torsion angles α, β and ɛ of C23. While α and β are in the normal range for the dU-bulge, these two torsion angles have unusually large values in the dT-bulge. On the other hand, ɛ is unusually small at C23 in the dU-bulge but not in the dT-bulge.

In the dA-bulge we find only one unusual torsion angle x at C23. As in the dT- and dU-bulge, this torsion angle x is unusually small (–49.5°).

Concluding remarks. Chemical shift data as well as inter-base parameters in the bulge region suggest different kink positions of the dA-bulge (10/11) on the one hand and dT- and dU-bulge (9/10) on the other hand. The inter-base parameters in the second strand (C18–C29) reveal at C24/G25 negative roll but positive twist for the dA-bulge and positive roll for the dT- and dU-bulge. While the inter-base pair parameter of the C5G25/G6C24 step are different for the dA-bulge (negative roll, high twist) and for the dT- and dU-bulge (positive roll), those parameters of the other flanking base pairs G12C23/C13G22 have no conspicuous values. Finally, all three bulges have an unusually small torsion angle x at C23.

Comparison of the electrophoretic mobility and FRET experiments with the NMR solution structures

Polyacrylamide gel electrophoresis of DNA molecules is sensitive to the curvature, bending or kinking within the DNA helix (39). The electrophoretic data, comparing the dAF-bulge and the dTF-bulge, predicted a slightly more strongly kinked dT-bulge compared with the dA-bulge (Fig. 3). This prediction has been confirmed by the NMR structural data.

The FRET data are a suitable complement to the NMR structural data (10). The NMR data suffer from the absence of distance restraints >0.6 nm; only connections between neighboring base pairs are deduced. FRET is able to yield data on distances up to 10 nm (40). The FRET data and the modeled data (Table 2) are consistent and are in agreement with a strongly kinked structure as delivered by the NMR results.

The AAUAA bulge in DNA and RNA

A pentanucleotide bulge rAAUAA has been found in the P4–P6 160-nt domain group of the Tetrahymena thermophila intron, a group I self-splicing intron (8). In the crystal structure, the ‘A-rich bulge’ is described as flanked by a U·A base pair at the 5′-end and by a G at the 3′-end. The 3′-terminal A forms a hydrogen bond to a U. A model of this RNA bulge was studied in solution by NMR (9). In their study, a 25-nt hairpin with two stems and a rAAUAA bulge was investigated. The bulge is flanked by a U·A base pair at the 5′-end and by a G·U base pair at the 3′-end. In general, the number of NMR constraints—218 distance constraints and 160 torsion angle constraints—was much smaller compared with our experiments (more than 600 distance constraints and 235 torsion angle constraints). The position of the central U was not well defined by the NOE constraints. In the resulting model structures, two families of structures emerged. In both families, the adenines are stacked upon the flanking helical stems. The central U, however, has probably an extra-helical position. In the bulge, the sugar puckering was found to be in a conformational equilibrium between C2′-endo (S-type) and C3′-endo (N-type) expected for a non-rigid conformation of the bulge. The bulge creates a kink of ∼90° between the flanking helical stems. This is in contrast to the crystal structure of the intron where the flanking helices are nearly co-axial (8). In addition, in the crystal structure the adenines corresponding to the first two adenines of the bulge are looped out forming tertiary contacts.

Comparing the AAUAA RNA and DNA solution structures, we have to consider the different flanking sequences in the stems. In the DNA bulge, we have dG at the 5′-end as well as at the 3′-end. At the junctions framing the bulge we have purine–purine steps within one strand that may behave differently than the U–A pyrimidine–purine step at the 5′ starting point of the bulge in the RNA sample. The rigid structure of the DNA bulge is in contrast to the obviously flexible structure of the central part in the RNA bulge. This may be explained at least partially by the favorable purine–purine stacking of the adenines of the DNA bulge on the flanking guanines of the stems. The observed structural flexibility of the RNA bulge rAAUAA can be of advantage for the function of the AAUAA bulge as an important element for tertiary contacts in the group I intron.

Generally, this study contributes to the insights in nucleic acid architecture. Bulges can form L-shaped molecules, the bulge structure is depending on the sequence not only of the bulge but also of the flanking base pairs. The sequence-dependent structure of the DNA bulges is of biological importance because of their role in protein recognition.

SUPPLEMENTARY MATERIAL

Supplementary material is available at NAR Online. This information includes: Tables S1 and S2, chemical shifts of all assigned nuclei of the dT- and the dU-bulge, respectively; Figure S1, the helical parameters tilt, roll and twist of the dA-, dT- and dU-bulge; Table S3, inter-base and inter-base pair helical parameters as well as torsion angles of the backbone of the dA-, dT- and dU-bulge.

PDB nos 1JRV, 1JS7