Abstract
Increasing evidence supports the hypothesis that amyloid β-protein (Aβ) assembly is a key pathogenic feature of Alzheimer's disease. Thus, understanding the assembly process offers opportunities for the development of strategies for treating this devastating disease. In prior studies, Aβ was found to form micelle-like aggregates under acidic conditions. These structures exhibited an average observed hydrodynamic radius of 7 nm. They were found to be in rapid equilibrium with Aβ monomers or low molecular weight oligomers, and were centers of fibril nucleation. Here the technique of small angle neutron scattering has been used to determine the structure of these Aβ micelles. The data reveal that the micellar assemblies comprise 30–50 Aβ monomers and have elongated geometries. The best fit of the data to a uniform spherocylinder yields a radius ≈2.4 nm and cylinder length ≈11 nm. These structure parameters remain constant over more than a decade in concentration range. The concentration independence of the length of the cylindrical aggregate indicates the presence of an internal nonrepetitive structure that spans the entire length of the Aβ assembly.
Alzheimer's disease (AD) is a progressive neurodegenerative disorder characterized in part by extensive amyloid deposition in the brain parenchyma and vasculature (1). These amyloid deposits are formed by the amyloid β-protein (Aβ), a proteolytic fragment of the larger amyloid β-protein precursor (AβPP) (2). Compelling data support the hypothesis that Aβ production and fibril assembly are linked to AD (3). For example, mutations in gene encoding AβPP, or in genes encoding proteins involved in the Aβ metabolism, are associated with familial forms of AD or of cerebral amyloid angiopathy. In all cases thus far studied, these mutations increase Aβ production, increase the relative amount of the particularly amyloidogenic 42-residue form of Aβ, or alter the biophysical properties of the mutant Aβ peptide facilitating its self-association or retarding its catabolism. Recent studies in humans, in transgenic mice, and in vitro, suggest that important effectors of Aβ-mediated neuronal injury and death may be small oligomeric assemblies of Aβ (4). Understanding the earliest phases of Aβ fibril formation, in particular oligomerization and other prenucleation interactions, is thus of great importance for identifying potential therapeutic targets.
Previously (5), quasielastic light scattering (QLS) spectroscopy was used to monitor the kinetic evolution of the size distribution of Aβ(1–40) assemblies formed under acidic conditions. These experiments showed that above a critical concentration c* ≈ 0.1 mM, Aβ formed micelle-like structures with an average observed hydrodynamic radius Rh ≈ 7 nm. These micelles‖ formed immediately on dissolution of the protein and were in equilibrium with low molecular weight, possibly monomeric, components of the Aβ solution. Analysis of the temporal evolution of the fibril length distribution at different total Aβ concentrations revealed that micelles are centers of fibril nucleation (6). This conclusion explained the observed concentration independence of the final fibril size and the fibril growth rate at total Aβ concentrations exceeding c*, the critical concentration.
The ability of the Aβ micelles formed at low pH to control Aβ fibril nucleation makes their structure of particular interest. One method to elucidate the details of this structure is small angle neutron scattering (SANS). SANS experiments can provide useful information regarding the aggregation number, shape, and dimensions of the structure in question. Previous studies (7, 8) have demonstrated the feasibility of SANS measurements on fibrillar Aβ(10–35) in D2O. Using quasielastic light scattering spectroscopy, we found that in 0.1 N DCl in D2O the kinetics of Aβ(1–40) fibrillization is very similar to that observed in HCl/H2O solution. Importantly, in the deuterated environment, as in water, particles with hydrodynamic radius Rh ≈ 7 nm were found above the critical concentration. We report here the results of SANS studies of the structure of Aβ micelles formed in 0.1 N DCl/D2O and the effects of Aβ concentration on this structure.
Materials and Methods
Sample Preparation.
Aβ(1–40) was synthesized on an automated peptide synthesizer (Applied Biosystems, Model 430A) by using fluorenylmethoxycarbonyl (Fmoc) chemistry, as described (9). All samples were prepared by diluting the lyophilized peptide into 0.1 N DCl in D2O. Two sets of experiments were performed. In the first set, samples of Aβ at concentrations of 2.2 mg/ml and 5.0 mg/ml were centrifuged at 104 × g for 10 min to remove preexisting aggregates. For the second set of experiments, samples were filtered through a 20-nm inorganic membrane filter (Anatop 10 plus, Whatman) to final concentrations of 0.60, 0.40, 0.31, 0.27, 0.22, and 0.05 mg/ml as determined by quantitative amino acid analysis (AAA) following the SANS experiments. Aliquots of each sample also were taken for QLS. The aliquot for SANS was frozen immediately at −80°C and transported to the reactor at −20°C.
Quasielastic Light Scattering.
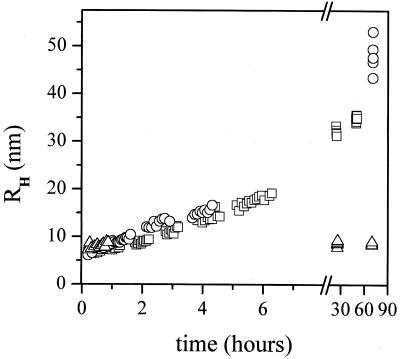
QLS experiments were performed with a 144-channel Langley-Ford model 1097 correlator (Langley-Ford, Amherst, MA) and a Coherent Innova 90 argon laser (514 nm; Coherent Radiation, Santa Clara, CA). The scattering angle was 90°. The sample holder temperature was controlled using an Endocal water bath (Neslab Instruments, Portsmouth, NH). The measured correlation functions were analyzed as described by Thomas et al. (10). QLS experiments confirm that the course of fibrillogenesis in DCl/D2O (used for SANS measurements) at 25°C was very similar to that observed in HCl/H2O, though slightly slower. Furthermore, it was shown that freezing and thawing of Aβ dissolved in 0.1 N DCl/D2O, as in 0.1 N HCl/H2O (11), did not alter the course of fibrillogenesis. SANS experiments require several hours, more than the duration of the initial lag phase of the fibrillogenesis process at room temperature. Fortunately, the rate of fibril growth slows dramatically at lower temperatures (11). To evaluate the feasibility of SANS studies of micelle structure, QLS experiments were carried out at 4°C in 0.1 N DCl/D2O at an Aβ concentration c0 = 0.4 mg/ml. These experiments showed that the light scattering is dominated for at least 70 h by particles of Rh ≈ 7 nm (Fig. 1). Additional QLS experiments were conducted on aliquots taken from samples prepared for SANS measurements to verify the particle size distribution of these samples.
Figure 1.
Time evolution of the apparent hydrodynamic radius of Aβ aggregates, obtained by QLS, at concentration 0.40 mg/ml. The solvents are 0.1 N HCl in H2O at 25°C (□); 0.1 N DCl in D2O at 25°C (○); 0.1 N DCl in D2O at 4°C (▵).
SANS.
SANS experiments were conducted at National Institute of Standards and Technology, Center for Neutron Research, Gaithersburg, MD. The 40-m SANS station was used with an incident wavelength λ = 5 Å with a spread Δλ/λ = 11%. The neutron source to sample distance was 13.12 m. All measurements were 1 h long. Samples from the first set, with nominal concentrations of 2.2 mg/ml and 5.0 mg/ml, were measured twice, at 4°C and then at 10.9°C. A Helma cuvette of 2 mm thickness and circular side 25 mm in diameter was used. At each temperature, the measurements were done at two different sample-to-detector distances. One provides magnitudes of the Q-vector in the range 0.0054–0.04 Å−1 (sample-to-detector distance of 10 m) and the other from 0.011–0.28 Å−1 (sample-to-detector distance of 2 m). Low Q range measurements were made first. In the second set of experiments, six samples with concentrations from 0.05–0.60 mg/ml were measured at 4°C, in high Q range only. A Helma cuvette of 5 mm thickness and 19 mm diameter was used. The actual concentrations of these samples were determined a posteriori by AAA and were found to be 0.60, 0.40, 0.31, 0.27, 0.22, and 0.05 mg/ml.
SANS data analysis.
Data of SANS are presented in terms of I(Q), the differential scattering cross section per unit volume, which is the probability for a neutron to be scattered into a unit solid angle per unit path length. I(Q) is measured in cm−1 and depends on Q, the scattering (Bragg) wave vector,
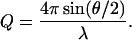 |
1 |
Here λ is the wavelength of the neutrons and θ is the scattering angle. For a monodisperse solution, I(Q) is given by (12)
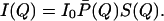 |
2 |
Here P̄(Q), the normalized structure factor, accounts for the shape of the scattering particle, and S(Q), the interparticle structure factor, accounts for the correlation between the position of micelles due to interaction. The forward cross section I0 is given by
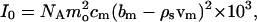 |
3 |
where cm is the molar concentration of micelles (mol/l), mo is the number of Aβ monomers in a single micelle, and NA is Avogadro's number. The contrast, bm − ρsvm, measured in centimeters, accounts for the difference of neutron scattering power between Aβ and that of the solvent (D2O in this case). The contrast depends on the scattering length density of D2O, ρs = 6.34 × 1010 cm−2, on the sum of the scattering lengths of all the amino acids in the peptide, bm, and on the sum of the dry volumes of each amino acid, vm. We calculated parameters bm and vm by using values provided by Jacrot and Zaccai (13). Assuming that all labile hydrogens undergo hydrogen/deuterium (H/D) exchange, bm − ρsvm = −1.81 × 10−10 cm; assuming no H/D exchange, bm − ρsvm = −2.43 × 10−10 cm.
In a dilute solution, when correlations between particles can be neglected, S(Q) = 1. The angular dependence of the neutron scattering is then determined by the particle structure factor P̄(Q), which depends on the size and shape of the scattering particle (12). The experimentally observed intensity of neutron scattering decreases with angle much slower than expected for spherical scatterers, clearly showing that our samples contained elongated objects. Many reasonable models, such as the ellipsoid, the cylinder, or the spherocylinder, could fit our data equally well. The overall features of the object (length, aspect ratio, and mass) do not depend on the model used to fit the data in any significant way. We chose here the spherocylindrical model (cylinder of length L with hemispherical end caps of radius R) and used matlab (Mathworks, Natick, MA) software to numerically calculate values of spherocylinders' structure factor within the data fitting procedure.
Determination of aggregation number mo and critical concentration c*.
In previous work (5, 11), a monomer–micelle equilibrium was postulated to exist at the initial stage of Aβ(1–40) fibrillogenesis. Let the solution of Aβ have a molar concentration cm of micelles and a molar concentration c1 of monomers. The total molar concentration (c0) of Aβ is then
 |
4 |
For simplicity we assume that all micelles have the same
aggregation number mo and the same structure. In
this simple two-state model, the concentration of micelles is
proportional to c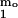 and can be
written as (11)
and can be
written as (11)
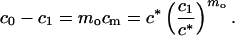 |
5 |
Eq. 5 introduces the critical micellar concentration c*. According to Eq. 4, c1 in Eq. 5 can be replaced by co − mocm producing an equation
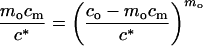 |
6 |
that implicitly expresses cm as a function of c0 and two parameters: the aggregation number m0 and the critical concentration c*. By calculating cm from Eq. 6 and substituting the result into Eq. 3, we can obtain the dependence of I0 on c0 for any parameters c* and mo. We then can determine the values of the parameters that best fit the experimentally observed concentration dependence of neutron scattering intensity.
Results and Discussion
In Fig. 1 we compare the fibrillogenesis in solutions of 0.40 mg/ml of Aβ(1–40) in 0.1 N DCl/D2O at 25°C and 4°C and in 0.1 N HCL/H2O at 25°C. This figure shows that the initial size of the aggregates present in solution is approximately 7 nm in all three cases. The initial rate of fibril growth observed at 25°C is similar in both solutions, although fibers seem to grow slightly faster in D2O. After approximately 2 days, fibrils reach their final size, which is bigger in the case of D2O. This greater size may result from a slightly faster elongation rate, a slower nucleation rate, and fewer preexisting seeds in the D2O sample (6). The data in Fig. 1, obtained by QLS, suggests that the micelle-like aggregates formed at low pH immediately on dissolving Aβ in heavy water are the same as those formed in H2O. At 4°C, the rate of fibril growth slows dramatically (11). Indeed, in 0.1 N DCl/D2O at 4°C no aggregation occurs for at least 70 hours. This provides a window of time sufficient for SANS experiments.
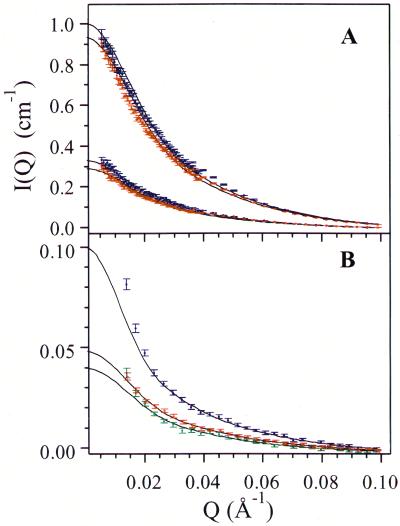
The results of SANS experiments are summarized in Fig. 2. This figure shows the differential cross section of neutron scattering I(Q) of Aβ samples in a Q range from 0.0054–0.1 Å−1. The data obtained in the first set of experiments for the samples with concentrations c0 of 5.0 mg/ml and 2.2 mg/ml are shown in Fig. 2A. We see that in both samples the shape of I(Q) at 4°C (red) is the same as that at 10.9°C (blue). Thus, the particle structure factor of the micelles is independent of temperature. However, at 10.9°C, I(Q) values are slightly higher than that at 4°C. This increase of scattering intensity is probably a consequence of aggregation or fibril formation in the samples. Indeed, measurements at 10.9°C were conducted after measurements at 4°C and samples were subjected to an additional freeze–thaw cycle. Fig. 2B presents results for the second set of samples. These measurements were taken at 4°C at high Q range only. The data for samples with concentrations of 0.60 mg/ml, 0.40 mg/ml, and 0.31 mg/ml are shown. At lower concentrations, the SANS scattering intensity was too weak to produce meaningful structural information.
Figure 2.
Differential cross section per unit volume of neutron scattering I(Q) versus magnitude of the scattering vector Q. (A) c0 = 5.0 mg/ml (top data points) and 2.2 mg/ml (bottom data points). The solid lines correspond to the theoretical fit for a spherocylinder. Data at 10.9°C (blue) and at 4°C (red) are fitted separately. (B) I(Q) for the second set of samples with lower concentrations: blue, c0 = 0.60 mg/ml; red, c0 = 0.40 mg/ml; green, c0 = 0.31 mg/ml. The solid lines are the theoretical fits with the parameters listed in Table 1.
Solid lines in Fig. 2 are the best theoretical fits to a spherocylindrical model determined individually for each concentration and temperature. In the fitting procedure we have assumed that all scatterers have the same size and shape. As is shown in Fig. 2 our data are consistent with this assumption in the region Q > 0.025 Å−1 for all concentrations studied. We believe that the deviations shown in Fig. 2 for Q < 0.025 Å−1 are produced by large aggregates or fibrils. Indeed, the existence of such aggregates was confirmed in control QLS measurements. Alternatively, one could invoke polydispersity in the micelle distribution to better fit the low Q scattering data. However, thermodynamic consideration shows that, in the case of a significantly polydisperse distribution, an increase in concentration should shift the equilibrium in favor of larger micelles, resulting in an increase in the mean size. This increase is not borne out by the data.
The parameters of the spherocylinders, R and L,
as well as the intensity of forward scattering,
I , used in fits of the 4°C data, are
listed in Table 1. It is clear from Table
1 that the radii of the putative spherocylindrical micelles are the
same at all concentrations, within the experimental error of
measurements. The parameter L also shows no systematic
concentration dependence. We believe that the variation of the
parameters R and L observed in Table 1 is due to
the presence of aggregates or fibrils and not to the actual changes in
micelle dimensions—i.e., in all of our samples particles of the same
size are responsible for neutron scattering. This being the case, the
normalized background-corrected neutron scattering intensity
P̄(Q) is the same and only the magnitudes
I0 vary in proportion to the micelle
concentration (cm). Indeed, on a logarithmic
scale, data curves representing scattering at different concentrations
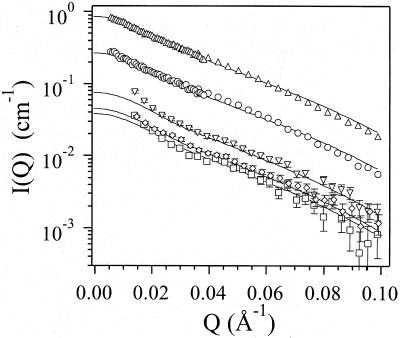
are parallel to each other (Fig. 3). Note
that the slow, nearly linear decrease of log I(Q) in a
significant range of Q values above 0.03 Å−1
indicates scattering from elongated structures. Solid lines in Fig. 3
represent the best fit of the entire set of SANS data assuming
scattering from the same uniform spherocylindrical particles with
R = 2.4 nm and L = 11 nm. Keeping these
parameters fixed, we determined the cross section of forward scattering
for every individual measurement, I
, used in fits of the 4°C data, are
listed in Table 1. It is clear from Table
1 that the radii of the putative spherocylindrical micelles are the
same at all concentrations, within the experimental error of
measurements. The parameter L also shows no systematic
concentration dependence. We believe that the variation of the
parameters R and L observed in Table 1 is due to
the presence of aggregates or fibrils and not to the actual changes in
micelle dimensions—i.e., in all of our samples particles of the same
size are responsible for neutron scattering. This being the case, the
normalized background-corrected neutron scattering intensity
P̄(Q) is the same and only the magnitudes
I0 vary in proportion to the micelle
concentration (cm). Indeed, on a logarithmic
scale, data curves representing scattering at different concentrations
are parallel to each other (Fig. 3). Note
that the slow, nearly linear decrease of log I(Q) in a
significant range of Q values above 0.03 Å−1
indicates scattering from elongated structures. Solid lines in Fig. 3
represent the best fit of the entire set of SANS data assuming
scattering from the same uniform spherocylindrical particles with
R = 2.4 nm and L = 11 nm. Keeping these
parameters fixed, we determined the cross section of forward scattering
for every individual measurement, I . As
seen in Table 1, the difference between I
. As
seen in Table 1, the difference between I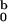 ,
deduced with the assumption that the size and shape of micelles remains
fixed at all concentrations, and I
,
deduced with the assumption that the size and shape of micelles remains
fixed at all concentrations, and I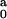 ,
obtained without this assumption, is within the experimental
uncertainty. Thus, above the critical micelle concentration, our
experiments show no concentration dependency in the size and shape of
Aβ micelles.
,
obtained without this assumption, is within the experimental
uncertainty. Thus, above the critical micelle concentration, our
experiments show no concentration dependency in the size and shape of
Aβ micelles.
Table 1.
Summary of the micelle dimensions at each C0 value
| c0, mg/ml | R, nm | L, nm |
I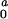
|
I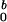
|
|---|---|---|---|---|
| 5.0 | 2.3 ± 0.1 | 11.1 ± 0.3 | 0.926 | 0.927 |
| 2.2 | 2.3 ± 0.1 | 10.5 ± 0.4 | 0.279 | 0.289 |
| 0.6 | 2.5 ± 1.2 | 13.9 ± 7.0 | 0.102 | 0.084 |
| 0.40 | 2.4 ± 0.1 | 11.5 ± 1.2 | 0.050 | 0.049 |
| 0.31 | 2.5 ± 0.2 | 11.4 ± 3.9 | 0.044 | 0.042 |
Parameters R and L are the dimension of the
spherocylinder obtained from the fit of individual data,
I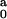 being the corresponding intensity of
forward scattering. Parameter I
being the corresponding intensity of
forward scattering. Parameter I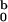 is the
intensity of forward scattering that provides the best fit for fixed
R = 2.4 nm and L = 11.0 nm.
is the
intensity of forward scattering that provides the best fit for fixed
R = 2.4 nm and L = 11.0 nm.
Figure 3.
The same experimental data as in Fig. 2, shown in logarithmic scale.
The solid lines are calculated for a spherocylinder with dimensions
R = 2.4 nm and L = 11.0 nm and
I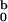 listed in Table 1. All data shown were
taken at 4°C. Two topmost curves correspond to samples of 5.0 mg/ml
(▵) and 2.2 mg/ml (○) both at high and low
Q range. The rest of the measurements, low Q
range only, are: c0 = 0.60 mg/ml
(▿); c0 = 0.40 mg/ml (◊,
offset slightly to the right for clarity); and
c0 = 0.31 mg/ml (□).
listed in Table 1. All data shown were
taken at 4°C. Two topmost curves correspond to samples of 5.0 mg/ml
(▵) and 2.2 mg/ml (○) both at high and low
Q range. The rest of the measurements, low Q
range only, are: c0 = 0.60 mg/ml
(▿); c0 = 0.40 mg/ml (◊,
offset slightly to the right for clarity); and
c0 = 0.31 mg/ml (□).
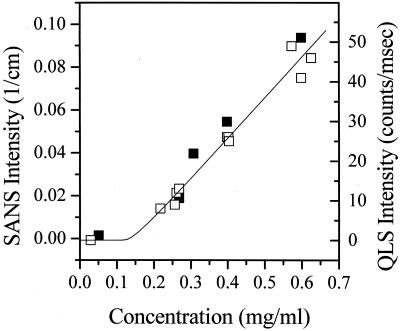
Having determined the structural parameters of micelles, we now turn to
an analysis of the concentration dependence of the intensity of neutron
scattering. From this we can find parameters m0
and c* that best fit the experimental
I0(c0). In Fig.
4 we show with filled squares (█) the
forward cross sections of neutron scattering
I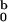 at various Aβ concentrations. In
addition to data from Table 1 (only the three lowest concentrations are
shown), we present forward cross sections for concentrations of 0.05
mg/ml and 0.27 mg/ml. Although at these concentrations the
intensity of scattering is too low to give reliable structural
information, the overall scattering cross section can be determined. At
the lowest concentration of 0.05 mg/ml, no scattering from micelles
is observed. In effect, this sample provides the background neutron
scattering intensity. The solid line in Fig. 4 shows the dependence of
I0 on the total concentration
c0 predicted by Eqs. 3 and
6. Open squares (□) represent the relative QLS intensity
of light scattered at 90°, scaled to overlay the SANS data. Both SANS
and QLS data agree with each other and are well described by the
theoretical curve.
at various Aβ concentrations. In
addition to data from Table 1 (only the three lowest concentrations are
shown), we present forward cross sections for concentrations of 0.05
mg/ml and 0.27 mg/ml. Although at these concentrations the
intensity of scattering is too low to give reliable structural
information, the overall scattering cross section can be determined. At
the lowest concentration of 0.05 mg/ml, no scattering from micelles
is observed. In effect, this sample provides the background neutron
scattering intensity. The solid line in Fig. 4 shows the dependence of
I0 on the total concentration
c0 predicted by Eqs. 3 and
6. Open squares (□) represent the relative QLS intensity
of light scattered at 90°, scaled to overlay the SANS data. Both SANS
and QLS data agree with each other and are well described by the
theoretical curve.
Figure 4.
SANS and QLS scattering intensities as functions of concentration at
4°C. (█, SANS forward cross section
I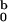 ; □, QLS intensity normalized
so as to overlay with SANS data. The solid line represents the
theoretical prediction for c* = 0.15 mg/ml and
m0 = 29.
; □, QLS intensity normalized
so as to overlay with SANS data. The solid line represents the
theoretical prediction for c* = 0.15 mg/ml and
m0 = 29.
The physical interpretation of the data presented in Fig. 4 is as
follows. For c0 < c*, Eq. 5
shows that c1 < c* and
m0cm ≅ 0—i.e., very few micelles
are present, and c0 ≅ c1. On the
other hand, for c0 > c*, c1
≡ c* will satisfy Eq. 5 for all
c0. Hence
m0cm ≅ c0
− c*. Thus for c0 > c* the
dependence of I0 versus
c0 is represented by a line with x
intercept of c* and with a slope of
NAm (bm
− ρsvm)2 ×
103 = 5.74 × 1010 cm2.
It should be noted that the critical micellar concentration observed in
the present work, c* = 0.15 mg/ml, is about one-third of
that reported previously by Lomakin et al. (5). This
discrepancy arises because the nominal peptide concentrations in the
earlier study were determined by dissolving lyophilized peptide to a
desired concentration without controlling the effects of insoluble
aggregated material or adventitiously bound nonpeptide material. In
contrast, in the present work the concentration of the protein was
determined by amino acid analysis (AAA) after filtration through 20-nm
filters in order to remove preexisting fibrils and aggregates.
(bm
− ρsvm)2 ×
103 = 5.74 × 1010 cm2.
It should be noted that the critical micellar concentration observed in
the present work, c* = 0.15 mg/ml, is about one-third of
that reported previously by Lomakin et al. (5). This
discrepancy arises because the nominal peptide concentrations in the
earlier study were determined by dissolving lyophilized peptide to a
desired concentration without controlling the effects of insoluble
aggregated material or adventitiously bound nonpeptide material. In
contrast, in the present work the concentration of the protein was
determined by amino acid analysis (AAA) after filtration through 20-nm
filters in order to remove preexisting fibrils and aggregates.
From the observed slope we can calculate the value m0 if the contrast value bm − ρsvm is known. Using the contrast −1.81 × 10−10 cm obtained by assuming that all labile hydrogen atoms in Aβ are exchanged by deuterium, we obtain m0 = 54. Kheterpal et al. (14) have shown that in monomeric Aβ(1–40) such an exchange indeed takes place, whereas in fibrillar Aβ(1–40) only about 50% of the labile hydrogen undergo H/D exchange. Furthermore, evidence provided by Rene et al. (15) indicates that under acidic conditions certain amino groups undergo slow H/D exchange relative to the duration of our experiments. We therefore do not know accurately the level of H/D exchange. However, both the fact that Aβ forms micelle-like aggregates in which hydrophobic regions are less accessible to solvent, and that acidic (0.1 N DCl) conditions were used, should reduce the number of labile hydrogen atoms that were actually replaced by deuterium during the experiments. Thus, the actual contrast is higher than the value used above and m0 = 54 is therefore an overestimation of the actual aggregation number. A lower limit on m0 can be obtained if we incorporate a maximum contrast value of −2.43 × 10−10 cm corresponding to no H/D exchange. The slope of the data in Fig. 4 then yields a value m0 = 29. Note that previously (5) an estimate 15 < m0 < 70 had been reported and that m0 = 25 had been chosen for analysis.
The volume of a spherocylinder with R = 2.4 nm and L = 11 nm is 257 nm3. For m0 = 29 (in the absence of H/D exchange), this corresponds to 8.8 nm3/monomer. For Aβ monomer with a molecular weight 4,330 this value implies a dry density of 0.8 g/cm3, which is more than we would expect for hydrated protein. If all labile H atoms undergo H/D exchange (m0 = 54), the apparent density becomes even higher, 1.5 g/cm3. This value suggests that our model of a uniform spherocylinder underestimates the actual particle size. In reality, H/D exchange occurs mostly on the surface of micelle-like aggregates where hydrophilic groups are concentrated. Consequently, the contrast of the outer layer of these micelles is reduced and the value of R = 2.4 nm probably reflects the radius of the hydrophobic core of the micelle rather than its geometrical radius. Also, the hydrodynamic radius of a spherocylinder [calculated using expressions provided by de la Torre and Bloomfield (16)] with dimensions of R = 2.4 nm and L = 11 nm is Rh = 4.7 nm. This value is less than the Rh observed in QLS experiments, which is typically ≈7 nm (Fig. 1). However, it should be noted that a few large fibers formed in solution can significantly increase the average Rh observed in QLS experiments (Q = 0.00325 Å−1) in which particles up to ≈30 nm in radius contribute to the scattering proportional to their mass squared. These fibers are practically unobserved in SANS measurements because, in the Q range above 0.025 Å−1, particles larger than ≈10 nm scatter only proportional to their mass. It is clear that the SANS and the QLS methods probe different features of the particles. The value of Rh = 4.7 nm likely provides the lower limit for the actual Rh.
The fact that the Aβ micelle-like intermediates in our experiments are elongated objects that do not change size with Aβ concentration has important consequences. Elongated, worm-like micelles are well known (10, 17). However, the length of those micelles increases with concentration. Indeed, if the object is built from repetitive units arrayed in one dimension, it therefore can be of any length and if this object is in equilibrium with monomers, then an increase in concentration should lead to an increase in the average aggregation number, according to Le Chatelier's principle. No increase in the size of the Aβ micelles was observed in the SANS experiment over greater than a decade of concentration variation nor was any concentration dependence of the hydrodynamic radius seen in previous QLS measurements (5, 11). At the same time, compelling evidence indicates that Aβ micelles are in equilibrium with monomers and/or oligomers. Furthermore, our SANS data clearly indicate an assembly with an elongated structure. We therefore conclude that these micellar structures differ significantly from classical cylindrical micelles in that they are not built from repetitive units. One potential model of the structure of the spherocylindrical Aβ micelle is shown schematically in Fig. 5. In this model the micelle is an elongated cylindrical object in which Aβ monomers are stretched along the cylinder axis.
Figure 5.
Schematic model of Aβ assembly consistent with SANS data.
Our SANS experiments confirmed that upon dissolution under acidic condition in concentration above c* = 0.15 mg/ml, Aβ monomers form micelle-like aggregates consisting of about 30 monomers. These aggregates are of elongated shape with a particle structure factor that is well described by a uniform spherocylinder with a radius of R = 2.4 nm and a length of the cylindrical part of L = 11 nm. The size and the shape of the aggregate remains the same over a decade of concentrations.
Acknowledgments
We are grateful to Ms. Margaret Condron for expert technical assistance. We are grateful to the National Institute of Standards and Technology, Center for Neutron Research for providing SANS beam time for this research. This work was supported by National Institutes of Health Grant 1PO1AG14366 (to G.B.B. and D.B.T.) and by the Foundation for Neurologic Diseases (D.B.T.). The work of S.H.C. was supported by a grant from Materials Chemistry Program of the U.S. Department of Energy.
Abbreviations
- Aβ
amyloid β-protein
- SANS
small angle neutron scattering
- QLS
quasielastic light scattering
Footnotes
The term “micelle(s)” is used herein for convenience in order to describe an oligomeric Aβ assembly with physicochemical and structural properties consistent with those of well characterized micelle-forming substances.
References
- 1.Selkoe D J. Neuron. 1991;6:487–498. doi: 10.1016/0896-6273(91)90052-2. [DOI] [PubMed] [Google Scholar]
- 2.Selkoe D J. Nature (London) 1999;399:A23–A31. doi: 10.1038/399a023. [DOI] [PubMed] [Google Scholar]
- 3.Hardy J. Proc Natl Acad Sci USA. 1997;94:2095–2097. doi: 10.1073/pnas.94.6.2095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Klein W L, Krafft G A, Finch C E. Trends Neurosci. 2001;24:219–224. doi: 10.1016/s0166-2236(00)01749-5. [DOI] [PubMed] [Google Scholar]
- 5.Lomakin A, Chung D S, Benedek G B, Kirschner D A, Teplow D B. Proc Natl Acad Sci USA. 1996;93:1125–1129. doi: 10.1073/pnas.93.3.1125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Lomakin A, Teplow D B, Kirschner D A, Benedek G B. Proc Natl Acad Sci USA. 1997;94:7942–7947. doi: 10.1073/pnas.94.15.7942. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Thiyagarajan P, Burkoth T S, Urban V, Seifert S, Benzinger T L S, Morgan D M, Gordon D, Meredith S C, Lynn D G. J Appl Crystallogr. 2000;33:535–539. [Google Scholar]
- 8.Burkoth T S, Benzinger T L S, Urban V, Morgan D M, Gregory D M, Thiyagarajan P, Botto R E, Meredith S C, Lynn D G. J Am Chem Soc. 2000;122:7883–7889. [Google Scholar]
- 9.Walsh D M, Lomakin A, Benedek G B, Condron M, Teplow D B. J Biol Chem. 1997;272:22364–22372. doi: 10.1074/jbc.272.35.22364. [DOI] [PubMed] [Google Scholar]
- 10.Thomas H G, Lomakin A, Blankschtein D, Benedek G B. Langmuir. 1997;13:209–218. [Google Scholar]
- 11.Kusumoto Y, Lomakin A, Teplow D B, Benedek G B. Proc Natl Acad Sci USA. 1998;95:12277–12282. doi: 10.1073/pnas.95.21.12277. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Chen S-H. Annu Rev Phys Chem. 1986;37:351–399. [Google Scholar]
- 13.Jacrot B, Zaccai G. Biopolymers. 1981;20:2413–2426. [Google Scholar]
- 14.Kheterpal I, Zhou S, Cook K D, Wetzel R. Proc Natl Acad Sci USA. 2000;97:13597–13601. doi: 10.1073/pnas.250288897. . (First Published November 21, 2000; 10.1073/pnas.250288897) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Rene R, Sehr P, Wagner G, Wurthrich K. J Mol Biol. 1979;130:19–30. doi: 10.1016/0022-2836(79)90549-7. [DOI] [PubMed] [Google Scholar]
- 16.de la Torre J G, Bloomfield V A. Q Rev Biophys. 1981;14:81–139. doi: 10.1017/s0033583500002080. [DOI] [PubMed] [Google Scholar]
- 17.Blankstein D, Thurston G, Benedek G B. J Phys Chem. 1986;85:7268–7288. [Google Scholar]