Complex-periodic spiral waves in confluent cardiac cell cultures induced by localized inhomogeneities

Abstract

Spatiotemporal wave activities in excitable heart tissues have long been the subject of numerous studies because they underlie different forms of cardiac arrhythmias. In particular, understanding the dynamics and the instabilities of spiral waves have become very important because they can cause reentrant tachycardia and their subsequent transitions to fibrillation. Although many aspects of cardiac spiral waves have been investigated through experiments and model simulations, their complex properties are far from well understood. Here, we show that intriguing complex-periodic (such as period-2, period-3, period-4, or aperiodic) spiral wave states can arise in monolayer tissues of cardiac cell culture in vitro, and demonstrate that these different dynamic states can coexist with abrupt and spontaneous transitions among them without any change in system parameters; in other words, the medium supports multistability. Based on extensive image data analysis, we have confirmed that these spiral waves are driven by their tips tracing complex orbits whose unusual, meandering shapes are formed by delicate interplay between localized conduction blocks and nonlinear properties of the culture medium.

As a general feature of the diffusively coupled network of nonlinear oscillators with excitable kinetics, spiral waves have been observed and studied in a variety of different physical (1), chemical (2), mathematical (3), and biological (4–7) systems. In many cases, these studies are motivated by potential application in understanding and preventing various cardiac arrhythmias (8–14). Wave activities in a real heart can take a few qualitatively different forms: (i) circular (or pacemaker) waves initiated by pacemakers as in a normal heart, (ii) monomorphic or polymorphic self-sustained spiral waves (an abnormal state that is responsible for some reentrant tachycardia), and (iii) a turbulent jumble of small wavelets that continuously form and break up (a deadly condition known as fibrillation) (15–21).

The existence of cardiac spiral waves is now well confirmed through several different in vitro (22–26) as well as in situ (7, 15, 18) preparations. Stable two-armed cardiac spirals, each arm being evenly separated from the other, were also recently reported (27). In all cases, however, these spiral waves may be considered regular because they produce a simply periodic dynamics locally. In similar preparations, but under some different conditions, one can also observe quite irregular and turbulent wavelets that resemble fibrillations of real hearts (22, 28). In many cases, these turbulent states have no vestige of spiral waves and are very difficult to characterize. Subsequently, revealing and understanding any intermediate states relating the two extremes have become important. Some examples along this line of investigation are bursting rhythms (23, 28) and alternans (29–32).

Here, we report a class of intermediate states that arise in two-dimensional monolayer tissues of dissociated cell culture from rat ventricles: In addition to regular [period (P)-1 oscillatory] spiral waves and turbulent wavelets, intriguing spiral waves with P-2, P-3, and P-4 oscillatory dynamics are found. They form spontaneously without any extrinsic manipulation. Besides, abrupt and spontaneous transitions among different periodic states are found to be common in this system. Analysis on their tip trajectory orbits suggest that there are many localized inhomogeneities interacting with spiral tips. We find that these inhomogeneities are either nonconducting small thin segments like infarcts or partially conducting small domains, often acting as two-way valves. These two different types of inhomogeneities and nonlinear dispersive nature of the cultured cardiac tissues as excitable media may explain the existence of the observed complex-periodic spiral waves.

Materials and Methods

Cell Culture. Confluent isotropic monolayers of rat ventricle cells were prepared and maintained by using protocols described in refs. 26 and 33. Briefly, ventricles of neonatal (1–2 days old) rats were dissociated with trypsin, counted, and plated on 35-mm polystyrene Petri dishes (Nunclon Δ, Nalge Nunc) that were coated with extracellular matrix protein, collagen type IV. The plating cell density was kept at 2.0 × 10³ cells per mm² for all experiments. Individual myocytes were randomly oriented at the time of initial plating; thus, there was no direction-dependent anisotropy in the wave conduction, unlike in a real heart tissue. At the early stage of the culture, cells tend to form small mounds of aggregates but they smear out to form a macroscopically homogeneous tissue as the culture becomes mature.

Optical Mapping and Image Analysis. A custom-built propagation-induced phase-contrast macroscope and an observation/incubation chamber (26) were used to optically map the mechanical contraction patterns of the cultured cardiac tissues noninvasively. No fluorescent dye was required. For details regarding the optics and the experimental setup, see Figs. 5 and 6 and Supporting Methods, which are published as supporting information on the PNAS web site. The view-field was set to be 15 mm × 15 mm. Images were captured by a charge-coupled device (CCD) camera (CA-D6–0256W, DALSA). Although the CCD camera was capable of capturing 8-bit monochrome images with spatial resolutions of 256 × 256 pixels at a maximum frame rate of 423 frames per second, the spatial and temporal resolutions were reduced to 85 × 85 pixels (3 × 3 binning applied in real-time) and 50 frames per second, respectively, to achieve stable long-term and uninterrupted image acquisition without any temporal gap.

The acquired images were later filtered spatiotemporally with a temporal Wiener filter with a passband of 0.2 to 10 Hz and a spatial low-pass filter with 3 × 3 homogeneous convolution mask for enhancement. Time series plotted in the figures were extracted from the image sequences after the temporal filtering had been applied but before the spatial filtering. The interbeat intervals (IBIs) were calculated as the temporal distances between two nearby local maxima in the time series. Each local maximum was identified as the peak of a local quadratic fit. Thus, the uncertainty in picking out the locations of local maxima was not more than a few milliseconds; although our images were sampled at 20-ms intervals, the sampling error of our CCD camera itself was around 1 ms. Activation time maps were produced from the sequence of the spatiotemporally filtered images as defined in ref. 26. The locations of moving spiral tip were traced by visual inspections: They were identified as the end point of one of the spiral contours in the activation time map whose tangent line is perpendicular to the direction of the wave propagation.

Results and Discussion

Under our culture condition, some coherent activity starts to emerge naturally as early as 1 day in vitro, i.e., 1 day after plating. Initially, many small irregular wave segments constantly emerge and decay as they spread slowly. As the culture becomes more mature, these wave segments become more organized in shape and compete with each other to yield a few spiral waves dominating the whole view field. These spirals are mainly regular ones rotating rigidly about small, more or less circular cores, resulting in P-1 oscillations throughout the whole tissue as discussed in ref. 26. The conduction speed and frequency of these spiral waves increase steadily over several days and more or less stabilize after about a week as the samples become mature. These mature tissues often produce quite complex activities, as depicted in Fig. 1.

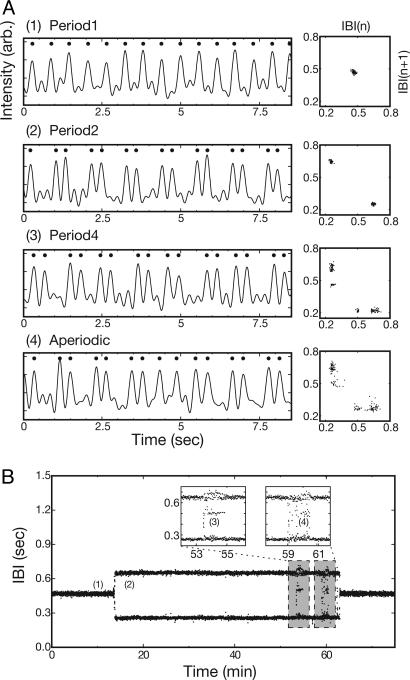
Fig. 1.

Complex-periodic local oscillations in in vitro cardiac tissue. (A) Time series of intensity variation caused by the local mechanical contractile motion of the cardiac cell tissue and the corresponding return maps of IBIs exhibiting P-1 (1), P-2 (2), P-4 (3), and aperiodic (4) oscillations. (B) Time series of IBIs exhibiting various oscillatory states and their spontaneous transitions. The time series is acquired at the point marked by a white cross in Fig. 3A. In A, dots mark the peaks in the time series, i.e., activations. The return maps of IBIs are constructed based on time series data taken over 1-min durations each. B Insets show the P-4 and aperiodic states in more detail. This observation is made with a 12-days in vitro sample.

Fig. 1 A shows four different time series of the mechanical contractile activity of a localized area in the tissue. As the accompanying return maps of IBIs well illustrate, the four different cases have quite distinct dynamics of their own; namely, P-1 for 1, P-2 for 2, P-4 for 3, and aperiodic for 4. Although this set of examples is superficially similar to a cascade of period-doubling bifurcations in some aspects (29, 34), the transitions here are not really due to a period-doubling bifurcation at all: All of these time series are obtained under the exactly same experimental condition except for being acquired at a different time as indicated in Fig. 1B. In other words, the transitions among different states are not driven by a systematic parameter change. Even accounting for the possibility of “overdrive suppression” (29) due to the wave activities themselves, these transitions do not show the key characteristics of a proper period-doubling bifurcation. In fact, the observed transitions are quite abrupt and irregular. Most important of all, they originate from complex spiral tip dynamics.

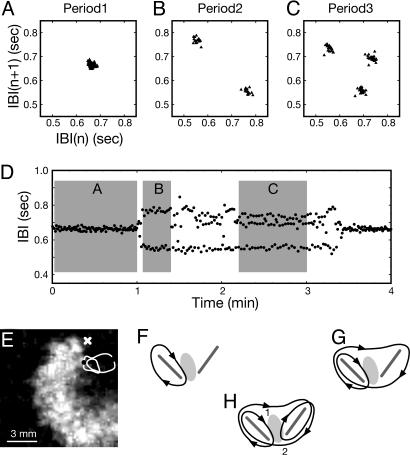
Before we explain and discuss the origin of the complex local oscillations shown in Fig. 1, we show another similar, yet simpler example (see Fig. 2) for a pedagogical reason. The culture sample used here is prepared with the exactly same protocol used for the previous case. As in the previous case, this preparation also exhibits some complex-periodic local oscillations as shown clearly in the return maps of Fig. 2: In addition to the regular P-1 (Fig. 2 A) and P-2 (Fig. 2B) oscillations, P-3 (Fig. 2C) oscillation is found. Moreover, there exists a multistability as in the previous example: The different periodic states abruptly switch back and forth without any discernible patterns (Fig. 2D). The direct origin of these different periodic oscillations is found to be a single rotating spiral wave (Fig. 2E) whose tip meanders along three different closed orbits (black lines in Fig. 2 F–H); the spiral tip trajectory shown in Fig. 2H, for example, produces the local P-3 oscillation of Fig. 2C, whereas the one shown in Fig. 2 F and G corresponds to the P-1 (Fig. 2 A) and P-2 (Fig. 2B) oscillation, respectively. In other words, whenever the spiral tip travels along a different trajectory, a new pattern emerges in the local temporal activity. In a sense, each complex-periodic tip motion acts as an extrinsic complex-periodic forcing from the view point of the bulk medium outside the spiral core region.

Fig. 2.

Complex-periodic meandering spiral wave around a pair of conduction blocks (see Movie 1). (A–C) Return maps of IBIs indicating P-1, P-2, and P-3 oscillation, respectively. (D) Time series of IBIs exhibiting P-1, P-2, and P-3 oscillatory states and spontaneous transitions among them. (E) Spatiotemporally enhanced grayscale image of a cardiac spiral wave. Black dot, current spiral tip location; white line, tip trajectory for two revolutions; white “x,” location at which the IBI data of A–D are taken. (F–H) Qualitative representation of the orbits (black lines with embedded arrowheads indicate the direction of tip motion) traced by the spiral tip corresponding to the P-1 (A), P-2 (B), and P-3 (C) oscillations. Pairs of gray line segments and oval-shaped gray areas in F–H schematically illustrate the linear (absolute) conduction blocks and the partial conduction block, respectively. Each return map of A–C is plotted based on parts of time series as marked with gray rectangles in D. The whole observation is made with a 5-days-in vitro sample.

With this unusual phenomenon, a question emerges naturally; namely, what can possibly cause these irregular, multiloop tip trajectories? Based on extensive amount of image analysis, we give a plausible explanation for them here. For all three different oscillations shown in Fig. 2 A–C, the tip of the spiral wave is pinned to a pair of small (absolute) conduction blocks as schematically depicted by two gray line segments in Fig. 2 F–H. The tip simply cannot pass through these nonconducting zones and can only encircle them. Interesting situations arise with a “partial (or functional) conduction block” in between the pair of absolute conduction blocks (as marked by a gray oval in Fig. 2 F and G). This partial conduction block can conduct waves on different modes: It conducts every time (Fig. 2F), every three times (Fig. 2G), or every other time (Fig. 2H) when the tip tries to pass the zone. Therefore, it has a nontrivial function of directing the spiral tip to different passages.

In the case of Fig. 2H, for example, the spiral tip passes through the oval zone from top to bottom (1 → 2) at its first attempt and encircles the left-hand side loop but fails to pass the same zone at the second turn to make a longer excursion to the right-hand side loop, and the same tip subsequently makes a complete turn around the right-hand side loop passing the oval zone from bottom to top (2 → 1). When the tip reaches the bottom side for the second time, however, it fails to pass the zone and moves on to the left-hand side loop. Then, the whole cycle repeats itself. In other words, the three-loop closed orbit shown in Fig. 2H can be attributed to the existence of a pair of absolute conduction blocks and a 2:1 partial conduction block in between. As a result, the localized partial conduction block is excited only twice as the spiral completes three successive turns. The identification of these conduction blocks is detailed in Fig. 7, which is published as supporting information on the PNAS web site.

Along the same line of argument, the two-loop closed orbit shown in Fig. 2G can be explained by the presence of a 3:1 partial conduction block or an asymmetric partial conduction block (2:1 partial conduction from 1 to 2, and absolute block from 2 to 1) between the pair of absolute conduction blocks. The origins of these functional conduction blocks is largely unknown, but their possible nature will be discussed later in this article. Movie 1, which is published as supporting information on the PNAS web site, shows the spiral waves in P-1, P-2, and P-3 states.

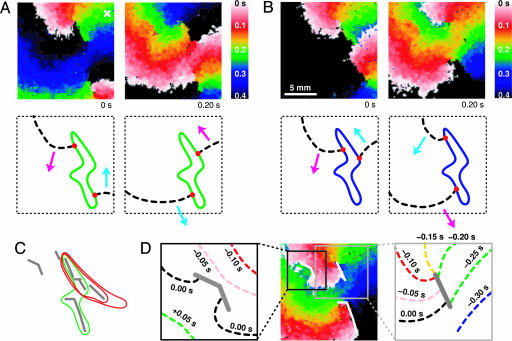
The behavior of spiral tip dynamics imposed by the conduction blocks becomes more intriguing for a case of double-arm spirals. In fact, the four different oscillations of Fig. 1 result from a co-rotating two-arm spiral wave (i.e., two spiral arms sharing a common orbit) interacting with an aggregate of several localized conduction blocks. We first describe the dynamics of the simplest example; namely, the P-1 oscillation shown in Fig. 1 A1. This seemingly simple local periodic oscillation originates from a co-rotating pair of spiral arms, shown in Fig. 3A, rotating around a simply connected, yet unusually shaped loop (green loop in Fig. 3A). The most significant feature of this pair of spirals is that they are evenly separated from each other by a phase angle of π about the center of the loop or, equivalently, by an equal distance along the loop. Consequently, a P-1 oscillation results as both spiral waves sweep through the marked position in a periodic manner (period τ = 467 ± 10 ms).

Fig. 3.

Activation time map images of a pair of co-rotating spiral waves and their tip orbits generating P-1 oscillation of Fig. 1 A1 in A and P-2 oscillation of Fig. 1 A2 in B (see Movie 2, which is published as supporting information on the PNAS web site). The activation time maps on the right of A and B are taken 0.20 s after those on the left. The diagrams below the activation time map images illustrate the pair of co-rotating wave fronts (dashed black lines) and the orbits traced by the tips [green in A and blue in B, with the tips themselves as red dots]. The tip orbit corresponding to the P-4 oscillation of Fig. 1 A4 is indicated with a red, double-looped orbit in C. C also includes the P-1 (and P-2) orbit in a green, single-looped orbit and the neighboring conduction blocks in gray line segments. The single activation time map of D indicates three different conduction blocks in white solid line segments. All image frames have the same dimension except for D Insets. D Insets show wave fronts at different times compared to the time of the activation time map of D. Activation times in the activation time map images are indicated with a continuous spectrum of colors where white, red, green, blue, and black indicate 0.0, 0.1, 0.2, 0.3, and 0.4 s or more, respectively.

Interestingly, the P-2 oscillation depicted in Fig. 1 A2 also originates from the same pair of spirals. This pair, however, is asymmetric (see Fig. 3B) in contrast to the previous one (see Fig. 3A) responsible for the P-1 oscillation: Now, there exists a significant detuning in the two phase angles separating the spirals or in the two distances connecting two tips along the orbit. This difference subsequently gives rise to two alternating periods (τ₁ = 646 ± 8 ms and τ₂ = 254 ± 7 ms; average 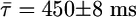) in the local time series. The spontaneous transition to this asymmetric state occurs at around t = 14 min in Fig. 1B.

The P-4 oscillation depicted in Fig. 1 A3 has its origin at the same asymmetric pair of rotating spirals. There is an important change, however, in that the new orbit traced by the pair of spiral tips has two loops (red orbit) instead of the single loop of P-1 and P-2 (blue orbit) as illustrated in Fig. 3C. The asymmetric pair rotates around one loop and the other in an alternating manner, thus generating a P-4 oscillation locally; the four periods are (degenerate) τ_1,2 = 265 ± 11 ms, which corresponds to the shorter temporal distance of the asymmetric pair that does not change significantly between P-2 and P-4 states, τ₃ = 504 ± 9 ms, and τ₄ = 661 ± 23 ms, with their average being 424 ± 13 ms. So, one may state that the transition from P-1 to P-2 occurs from a symmetry breaking in the angular separation of the rotating pair of spirals, whereas the transition from P-2 to P-4 is induced by the tip orbit splitting into two loops. Finally, the aperiodic oscillation of Fig. 1 A4 is also made possible by the same pair of spirals whose tip follows a more complex orbit (data not shown).

As in the single spiral case of Fig. 2, aggregates of localized inhomogeneities are responsible for the existence of these complex periodic spiral wave states. Fig. 3C schematically depicts all of the relevant line-shaped conduction blocks (gray line segments) along with the tip orbits of P-1 and P-2 (blue) and P-4 (red) states. As the diagram well illustrates, the collection of line-shaped conduction blocks form a set of small mazes that guides the spiral tips by its intricate structure. The spiral tips appear to find an optimal path, often returning to themselves, to form a closed loop as shown in Fig. 3 A–C. The conduction blocks shown in Fig. 3C are identified and accumulated by visual inspections on a long (≈1 h) temporal sequence of activation time map images such as the one given in Fig. 3D. Basically, we have found thin line-shaped structures across which waves cannot propagate. Activation time map images are suitable for visualizing such structures because they reflect the time course of wave fronts in a single frame as illustrated in Fig. 3D Insets.

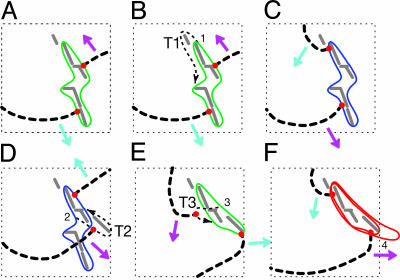
With the intricate collection of conduction blocks having been identified, the nature of each transition becomes more apparent. The transition from P-1 to P-2 shown in Fig. 1 B1 and B2, for example, is due to a phase slip: One of the evenly separated spiral arms traveling along the P-1 orbit (see Fig. 4A) fails to follow the previous path at point 1 (see Fig. 4B) and makes a longer excursion along a transient passage marked as “T1” before returning back to the original orbit. As a result, the balance between the two spiral arms is disrupted. This disturbance creates several transient rotations that quickly stabilize to an asymmetric state (see Fig. 4C) resulting in P-2 dynamics; note that the spirals are no longer evenly separated, whereas the shape of the orbit remains very much the same as before. In other words, the same spiral tip in the same cardiac tissue can exhibit two qualitatively different dynamic states. One may attribute this bistability to a nonlinearly dispersive nature of the cardiac tissue as an excitable medium.

Fig. 4.

Transitions from P-1 to P-2 and P-2 to P-4 rendered from the changes in orbits of spiral wave tips. (A) P-1 orbit (green line). (B) P-1 orbit (green line) and a transient passage T1. (C) P-2 orbit (blue line). (D) P-2 orbit (blue line) with a transitory passage T2. (E) another P-1 orbit (green line) with a transient passage T3. (F) P-4 orbit (red line). All transient and transitory tip passages (T1, T2, and T3) are marked by black dotted lines, wave fronts are marked by black dashed lines, tip locations are marked by red dots, and the conduction blocks are shown in gray solid lines. The indices 1–3 in B, D, and E mark specific locations where phase slips take place, and the index 4 marks the location of possible 2:1 partial conduction block that splits the orbit into a double-loop.

As discussed previously, the transition from P-2 to P-4 dynamics is driven by a change in the orbit traced by the spiral tips. This change involves a few intermediate steps. First, the leading wave (marked by a magenta arrow) takes a short cut at 2 after the transitory passage T2 as shown in Fig. 4D. The two spiral tips then trace a different single-loop (green) of Fig. 4E with an even separation for several turns. This transient P-1 state ends as one of the waves takes a tight turn at 3 (in Fig. 4E) after the transient passage T3. After this event, both spiral tips travel along the double-loop orbit shown in Fig. 4F. Here, the alternation between the two loops appears to be caused by a localized functional 2:1 conduction block located near the point 4. Coupled with the uneven phase separation between the two spiral arms in which the trailing wave (indicated with a cyan arrow in Fig. 4F) follows the same path taken by the leading wave (magenta arrow), a P-4 rhythm with a pair of degenerate period (τ₁ = τ₂) ensues. The transition from P-4 back to P-2 is more or less an opposite process of the transition from P-2 to P-4, and this also holds true for the P-2 to P-1 orbit transition. In all cases, some transient passages become active to allow a wave conduction every now and then, and these intermittent slips lead to a different nearby orbit. In other words, the transitions seem to be driven by some stochastic process, and, as such, the transient states that we have described here should not be interpreted as a universal bifurcation sequence but as independently stable states coexisting in the system. Movie 3, which is published as supporting information on the PNAS web site, shows transitions from the P-1 to P-2 state and from the P-2 to P-4 state.

The underlying mechanisms of the complex periodic spiral waves that we have discussed so far have assumed an appropriately located partial conduction block in addition to linearly shaped lesion-like absolute conduction blocks. Here, we have termed partial conduction block to be a localized defect that blocks or allows wave conduction in a regular fashion—once in every two, or more generally, n times in m incident waves. It is a quite well established fact that excitable media in general, including cardiac tissues, need a substantial duration of refractory period to sustain excitability for the propagation of subsequent waves. In the case of cardiac tissues, there is evidence (29) that the refractory period has long-term components that span minutes and even hours in addition to the conventional subsecond components. Such time-dependent change in cardiac tissue excitability is known as the cardiac memory effect (35–37). One may speculate that the refractory period is longer for the area of partial conduction block as compared with the bulk medium so that whereas the bulk medium allows wave conduction in a 1:1 manner, the partial conduction block allows it only in a conditional basis, for example. From a functional point of view, an appropriately located localized 2:1 partial conduction block in an otherwise homogeneous excitable medium can serve as a valve redirecting the spiral tip along different passages. Of course, their existence becomes important only when they interact with spiral wave tips: Blocks located away from spiral cores do not change the tip trajectory, and subsequently they cannot influence the overall dynamics of the bulk medium.

The microscopic or cellular origins of both lesion-like linear conduction blocks and partial conduction blocks remain elusive at the moment. Visual inspections on phase-contrast microscope images focused on the areas that should contain the blocks do not reveal any noticeable inhomogeneities that match the shapes of the blocks identified through dynamic activation time image sequence analysis. We have also visualized the spatial distribution of gap junctions, through which passive ionic conduction takes place, by means of a connexin-43 immunostaining method to find no discernible spatial abnormalities that can be related to the identified blocks. Based on these results, we can speculate that the thickness of the linear conduction blocks may be very thin, on the order of a single cardiac cell or maybe even less, and very minute changes in the densities of the cell or gap junction might be all that are necessary for the conduction blocks to exist. If this is the case, the spatial resolution of our phase-contrast images and that of connexin-43 images may be far too low to identify them.

In summary, we have presented experimental observations of complex-periodic cardiac spiral waves in an in vitro cardiac system and discussed their origins. They are found to be present in many of the mature cardiac sample tissues (>20% of n ∼ 100) that we have investigated so far. These observations are significant for a few different reasons.

First of all, such diverse complex-periodic and multistable wave structures are revealed in an experimental cardiac system. Complex-periodic spiral waves in general comprise a very important research topic of current interest in broad discipline of studying nonequilibrium wave dynamics in general, because they stand between simply periodic spiral waves and spatiotemporally irregular states. There are several different experimental (38–41) and model chemical reaction-diffusion systems (42–44) that are known to exhibit such wave structures; therefore, they may be a generic feature of any complex-oscillatory media, just as the regular spiral is regarded as a hallmark of excitable or simply oscillating media. Cardiac tissues are by all means a highly nonlinear medium that can support various complex rhythmic activities (8, 45, 46). Therefore, it may be natural to expect that such complex-periodic wave structures would also exist in cardiac systems and possibly be involved in the transition from reentrant tachycardia to fibrillation. This article indeed demonstrates that various types of complex-oscillatory spiral waves can exist in a cardiac system; but we should indicate that the complex rhythms of the observed cardiac spiral waves originate not from a complex homogeneous kinetics of the medium but from a delicate interplay between local inhomogeneities and the tip of spiral wave.

Second, we have shown that localized conduction blocks can influence the overall dynamics of the waves in cardiac tissues in a quite nontrivial way. It is well known that infarcts in damaged cardiac tissues from post-myocardial infarction hearts can often pin spiral waves down and keep them for awhile until they lead to a state of fibrillation (12, 17, 34, 47–49). Our experimental results explicitly demonstrate that infarcts can be more than just a pinning site: Complex spiral tip dynamics can emerge from such a small set of conduction blocks in an otherwise homogeneous cardiac tissue. Moreover, the transition from P-2 to P-4 that occurs with orbit change can be a model example for pleomorphic (or multiple reentrant) ventricular tachycardia from post-myocardial infarction ventricles in which more than one reentrant path exists and reentries often share part of the reentrant orbit (50, 51).

Third, our observations demonstrate that complex-periodic cardiac rhythms may be related with unusual spiral tip dynamics: The different trajectories of the spiral tip drive different complex rhythms of the whole medium. This result, in turn, suggests a potentially important medical implication; namely, some pathological heart tissues in vivo that carry spatial inhomogeneities (52, 53) are quite likely to develop complex-periodic reentry waves with higher affinity to fatal fibrillatory states.

In conclusion, we have demonstrated two fascinating examples of complex-periodic cardiac spiral waves and provided a pedagogical explanation for their origin and nature in connection with localized conduction blocks. One of the main issues that remain to be studied is the long-term stability of the observed complex-periodic states and the origin of their multistability. For instance, it would be important to understand what specific property of the system supports the asymmetric pair of waves for the case of P-2 and P-4 states with double-armed spirals. In this regard, we note that some excitable media with non-monotonic dispersion curves are reported to be able to support such a wave structure (54). Whether this is a relevant explanation, however, remains to be studied further. Our experimental work is also not complete in that we have failed to identify the physiological nature of the conduction blocks. Further experimental studies would include the explicit determination of these conduction blocks, as well as the discovery of similar wave states in different preparations with a different cell density and a different degree of inhomogeneity. In addition, the artificial creation of linear lesions and/or plantation of artificial partial conduction blocks with reduced excitability can be conducted to recreate the meandering tip trajectories in a more controlled way, both in laboratory experiments and numerical model studies.