Abstract
Recent studies reveal that the core sequences of many proteins were nearly optimized for stability by natural evolution. Surface residues, by contrast, are not so optimized, presumably because protein function is mediated through surface interactions with other molecules. Here, we sought to determine the extent to which the sequences of protein ligand-binding and enzyme active sites could be predicted by optimization of scoring functions based on protein ligand-binding affinity rather than structural stability. Optimization of binding affinity under constraints on the folding free energy correctly predicted 83% of amino acid residues (94% similar) in the binding sites of two model receptor-ligand complexes, streptavidin-biotin and glucose-binding protein. To explore the applicability of this methodology to enzymes, we applied an identical algorithm to the active sites of diverse enzymes from the peptidase, β-gal, and nucleotide synthase families. Although simple optimization of binding affinity reproduced the sequences of some enzyme active sites with high precision, imposition of additional, geometric constraints on side-chain conformations based on the catalytic mechanism was required in other cases. With these modifications, our sequence optimization algorithm correctly predicted 78% of residues from all of the enzymes, with 83% similar to native (90% correct, with 95% similar, excluding residues with high variability in multiple sequence alignments). Furthermore, the conformations of the selected side chains were often correctly predicted within crystallographic error. These findings suggest that simple selection pressures may have played a predominant role in determining the sequences of ligand-binding and active sites in proteins.
Keywords: computational protein design, enzyme design, protein evolution
A central goal of theoretical protein design is to understand the properties that define the space of amino acid sequences compatible with a given protein structure (1). Substantial progress has stemmed from the hypothesis that protein stability plays a major role in shaping these properties (2-4). Recent work has focused on the question of whether natural protein sequences have reached equilibrium within sequence space. Remarkably, this question has been answered largely in the affirmative for protein core sequences. Kuhlman and Baker (3) demonstrated, by using an extensive test set of protein backbones drawn from seven fold families, that more than half of core residues were predicted correctly simply by minimizing a folding free energy function in sequence space; moreover, the resulting sequence distributions closely reproduced those observed naturally. However, protein surface residues were not predicted correctly using this approach: <15% of all predicted surface residues matched the native residues. Jaramillo et al. (4) subsequently carried out a more extensive analysis of the degree of core vs. surface sequence optimization to examine whether the observed discrepancy might be caused by inadequacies in the potential function, rendering the methodology incapable of handling the balance between electrostatics and solvent interactions in surface regions. They concluded, after testing various solvation models, that (i) the magnitude of the discrepancy was large enough to be real, not an artifact of the accuracy of the potentials used, and (ii) natural sequences at surface positions might have been selected, at least in part, for mediating intermolecular interactions, probably at the expense of protein stability.
In the present work, we explore the concept of equilibrium in sequence space for the pivotal functional surface residues of proteins, namely ligand-binding and enzyme active sites. The immediate question that arises is: What is the appropriate function that takes the place of the folding free energy minimized in protein core design? As a step toward answering this question, we have carried out sequence optimization by using a scoring function based on ligand-binding affinity. Enzyme active sites, however, would appear to be subject to more complex evolutionary selective pressures to be capable of not just reactant binding but also catalytic turnover. Therefore, we have incorporated these effects into our algorithm through geometric constraints on catalytic residues.
We test the adequacy of this simple approach to binding-site sequence optimization by using a set of model receptor-ligand and enzyme-substrate complexes drawn from diverse functional families. In these calculations, the ligand is held fixed in its native conformation, in a manner analogous to the fixed backbone assumption in protein core engineering tasks (1). Because binding and active sites are solvated and/or contain many polar and charged residues that form directed contacts to their ligands, energy functions, solvation models, and sampling algorithms capable of high-resolution structure prediction are used to appropriately address this problem.
Methods
In the case of each protein-ligand complex, a set of some 10 amino acid residues that form essential contacts to the ligand were chosen for sequence optimization. Essential contacts were determined by identifying residues involved in H-bonds, salt bridges, van der Waals or hydrophobic contacts, by examination of mutagenesis data, and by multiple sequence alignments (MSAs). Selected positions where the amino acid variability was high in MSAs were omitted from optimization. See below for details; see also Supporting Text and Figs. 6-12, which are published as supporting information on the PNAS web site.
Various optimization algorithms (including Monte Carlo, genetic algorithms, and simulated annealing) have been used for the prediction of multiple side-chain conformations in the context of core sequence selection (5). The binding-site sequence optimization considered here is a constrained optimization problem wherein the binding affinity scoring function is optimized under the restriction that the total protein energy is a minimum for any given sequence, in addition to any catalytic constraints. The approach we adopted to this problem consisted of the following three steps: (i) side chain conformational optimization, (ii) calculation of substrate binding affinity, and (iii) selection of the residue type/conformation with the highest binding affinity that satisfied the auxiliary constraints. These steps were iterated until convergence in the ligand binding affinity was achieved. The side-chain optimization was based on a self-consistent approach where each residue was optimized (in both conformation and identity) in turn, whereas the identities of all others were held fixed. The first step involved determining the lowest-energy protein structure for each residue type at a given sequence position (in the presence of the ligand), with the exception of Cys and Pro (omitted because they are not generally involved in molecular recognition). The all-atom OPLS force field was used to describe protein energetics (6), and the solvation free energy was estimated by using an implicit solvent model consisting of the surface-generalized Born model of polar solvation (7) and Levy's nonpolar estimator (8). The sampling of single side-chain conformations was accomplished by using a highly detailed (10° resolution) rotamer library (9). Because conformational states of most side chains were coupled to residues not subject to mutation, the conformations of all side chains within 5 Å of the mutated side chain were optimized at each step as well. For combinatorial optimization, all side chains were initially built onto the fixed backbone in a random rotamer state, and then each was optimized in turn, holding the others fixed. The procedure was iterated to convergence, followed by complete energy minimization (10) to remove any clashes.
Calculation of the ligand-binding affinity for each such mutant structure was accomplished by using the Glidescore semiempirical scoring function (11), which consists of (i) a lipophilic-lipophilic contact term, (ii) a H-bonding term separated into weighted components based on donor and acceptor charge, (iii) contributions from Coulomb and van der Waals interaction energies between the ligand and the receptor, and (iv) a solvation model based on the computational introduction of explicit waters plus the employment of empirical scoring terms measuring the exposure of various groups to the explicit waters. The shape and properties of the receptor were represented on an OPLS-AA vdW and electrostatic grid.
The sequence and structure that displayed the highest binding affinity, while satisfying an additional constraint that the total protein energy was no more than 15% higher than that of the native, was retained, and the next residue was chosen randomly from the remaining list. (The cutoff of 15%, generous enough to avoid undue bias toward the native sequence, was chosen such that the energy of the initial all-Ala active site sequence fell within the acceptable interval for each protein studied.) These three steps were repeated at each residue position until the binding affinity changed by <0.1 kcal/mol per cycle. Five to 10 iterations (≈5 cycles per iteration) of this algorithm were carried out for each enzyme to ensure adequate sampling. The starting point for these iterations was either an all-Ala active site or a random sequence seed satisfying the dual requirements of a stable protein and a finite affinity. To generate random seeds, starting from the native sequence, the affinities resulting from the replacement of a given amino acid with the remaining 17 while holding the others fixed were tabulated, and the amino acid was replaced by another chosen randomly from the top 5. This procedure was repeated in turn for all mutated residues.
In selected cases, we assessed the effect of small perturbations in the ligand pose geometry on predicted sequences, by redocking the ligand using the Glide docking algorithm. This algorithm approximates a complete systematic search of the conformational, orientational, and positional space of the docked ligand (12) through an initial rough positioning and scoring phase followed by torsionally flexible energy optimization on an OPLS-AA nonbonded potential grid and Monte Carlo sampling. Details of the energy functions and sampling methods used are provided in Supporting Text.
Results and Discussion
Representative Protein-Ligand Complexes Subjected to Sequence Optimization. Unlike work on core design, where test proteins are generally grouped according to protein fold (3, 4), our protein-ligand complexes were chosen based on the chemical structure of the ligand, and enzymes were selected based on the mode of catalysis, because similar ligands/substrates are often recognized by proteins of different folds. For each test complex, the amino acid residues subjected to sequence optimization, along with the contact modes of the ligand-side-chain interactions, are listed in Figs. 1 and 7. Schematic diagrams of the binding/active sites of these proteins can be found in Fig. 6.
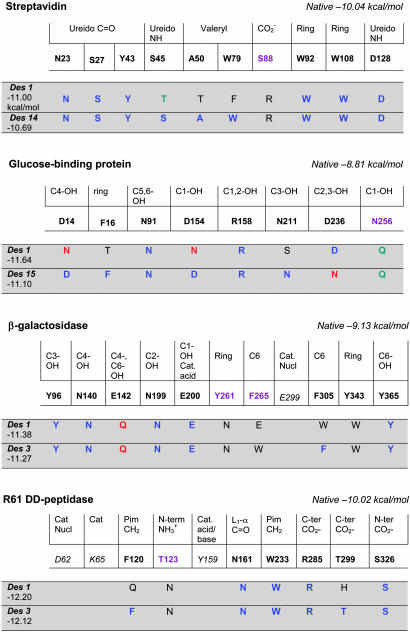
Fig. 1.
Comparison of native and computationally optimized active-site sequences. For each receptor-ligand or enzyme-substrate complex, residues forming essential contacts with the ligand/substrate or in the catalytic mechanism are listed (bold denotes computationally repredicted; italic denotes catalytic, conformationally optimized under constraints with fixed identity; purple denotes functionally promiscuous or displaying high variability in MSAs). Complementary moieties on substrates are listed above the native residues. Computationally predicted active site sequences are listed in the gray bars. The first sequence is that displaying the highest binding affinity while satisfying all geometric constraints. The second sequence is that displaying highest sequence identity to the native active site within the top 0.6 kcal/mol of ranked sequences. Designed number corresponds to rank in calculated sequence list. Blue amino acids, identical to native; red, isosteric to the native and engages in same mode of interaction with substrate (e.g., Tyr vs. Phe, Gln vs. Glu); green amino acids, same type as native and engaging in same mode of interaction (e.g., Asp vs. Glu, Lys vs. Arg); black, none of the above. Native energy corresponds to binding affinity of native sequence/structure after side-chain conformational optimization. Catalytic constraints: β-gal, residue 200 capable of acid/base catalysis and within 3.0 Å of C1-OH, Glu-299 within 3.5 Å of scissile C; R61 DD-peptidase, Lys-65 ε-N within 3.0 Å of Tyr-159's O, Tyr-159's O within 3.0 Å of Ser-62's O. Des, designed; Cat, catalytic; nucl, nucleophile; pim, pimelyl; ter, terminus. Results for thymidylate synthase are in Fig. 7. Ligands/substrates are listed in Table 1.
The receptor protein streptavidin binds biotin with an affinity among the highest known for natural protein-ligand interactions (Kd ∼ 10-15 M) (13). The most important interactions contributing to this high affinity are three H-bonds between the ligand's ureido carbonyl group and the side chains of Asn-23, Ser-27, and Tyr-43; in addition, two ureido NH groups are H-bonded to Ser-45 and Glu-128. Also, the Ser-88 hydroxyl forms a H-bond with biotin's valeryl carboxylate, although this interaction is not as critical because the carboxylate is the primary covalent attachment site for biotin. We subjected 10 residues in streptavidin's binding site, all those established by mutagenesis data to be essential for binding as well as Ser-88, to computational sequence optimization.
The lower-affinity complex of periplasmic glucose-binding protein and glucose also was examined to assess the effect of binding affinity on sequence optimization. Active site residues in this complex are particularly challenging to predict because 8 of 10 are polar and engaged in H-bonds with the ligand. Moreover, the polar side chains are positioned optimally for H-bonding to glucose through networks of H-bonds with side chains outside the contact shell of the ligand (14); the conformations of these latter side chains also must be predicted correctly to reproduce the native sequence. Eight residues in the glucose contact shell were sequence-optimized. His-152 was excluded because of the high amino acid degeneracy at this position found in position-specific profiles calculated from MSAs (see Supporting Text).
Enzymes catalyzing the transformations of three primary types of biological substrates, peptides (R61 DD-peptidase), sugars (β-gal), and nucleotides (thymidylate synthase), were chosen as initial models for active site sequence optimization. The efficiency of peptide hydrolysis by Ser protease enzymes like the R61 DD-peptidase is sensitive to the relative geometric orientation of conserved catalytic triad residues; thus, constraints on these residues were imposed. The mechanism of β-gals is similar to that of proteases in that it involves an addition-elimination and general acid/base processes, but reactivity is not highly sensitive to other proximal residues (15).
Bacterial DD-peptidases, the target enzymes of β-lactam anti-biotics, catalyze the peptidoglycan cross-linking step of bacterial cell-wall biosynthesis. For our calculations, we used the most specific substrate known for any DD-peptidase, glycyl-l-α-amino-ε-pimelyl-d-Ala-d-Ala, complexed to the enzyme from Streptomyces R61 (16). There are seven noncatalytic amino acid residues in the contact shell of the R61 peptide substrate involved in critical contacts to the latter through their side chains; all seven were subjected to sequence optimization, with geometric constraints imposed on the catalytic triad. Tyr-159 is believed to function as the general base for proton abstraction from the Ser-62's hydroxyl group, with Lys-67 conferring electrostatic stabilization of the phenolate; therefore, the Lys-65 ε-N was constrained within H-bonding distance of Tyr-159's O, and that atom, in turn, was constrained to within 3.0 Å of the Ser O.
In β-gals, which catalyze the scission of β(1-3) and β(1-4) galactosyl bonds in oligosaccharides, hydrolysis takes place through general acid catalysis wherein Glu-200 is the proton donor and Glu-299 the nucleophile (15). All of the amino acid residues that form contacts to the galactose ligand, with the exception of Glu-299, were subjected to optimization, with position 200 limited to residues capable of acid-base catalysis and the distance of Glu-299's O- to the scissile carbon constrained to 3.5 Å. A tighter geometric constraint was imposed on the distance between Glu-200's O- and the galactose C1-OH (3.0 Å) to account for proton abstraction.
Thymidylate synthase (Fig. 7), which transforms dUMP into dTMP, is one of the most phylogenetically conserved enzymes in nature (17). Selected noncatalytic residues from its active site were sequence-optimized along with residue 177, which plays an auxiliary role in methyl transfer by stabilizing an incipient negative charge that develops on the dUMP C═O in the transition state. A H-bond donor constraint was placed on this residue.
Computationally Optimized Binding/Active Site Sequences. Statistics of the success of the sequence optimization protocol in repredicting native active site sequences are summarized in Table 1. The data pertain to the predicted active site sequences within the top 0.6 kcal/mol of the rank-ordered sequence lists (filtered for geometric constraints on catalysis) that are most similar to the native sequences. Generally, a sequence with at least 60% sequence identity to the native active site is found within the top 0.6 kcal/mol (and usually within the top 10-15 sequences). Fig. 1 displays the top-ranked sequences, as well as those most similar to the native, for selected proteins. Importantly, for every position in every complex studied, the native amino acid is one of the three most frequently found in the optimized sequence distributions (Figs. 2 and 8).
Table 1. Active-site sequence design results for receptor-ligand and enzyme-substrate complexes.
| Number of residues
|
|||||
|---|---|---|---|---|---|
| Protein/enzyme | Ligand/substrate | Predicted* | Correct/similar† | Mean correct‡ | rmsd correct,§ Å |
| Streptavidin | Biotin | 10 (9) | 9/9 | 7.89 | 0.18 |
| Glucose-binding protein | α-Glucose | 8 (7) | 6/8 | 3.70 | 0.51 |
| Streptomyces R61 | Glycyl-l-α-amino-ε-pimelyl-d-Ala-d-Ala | 7 (6) | 6/6 | 3.96 | 0.55 |
| DD-peptidase | |||||
| Penicillium β-gal | α-Galactose | 10 (8) | 6/7 | 5.73 | 0.62 |
| E. coli thymidylate synthase | dUMP | 6 | 6/6 | 3.81 | 1.02¶ |
| Total | 41 | 33 [80%]/36 [88%] | |||
Number excluding residues with auxiliary functions or showing high variability in MSAs is listed in parentheses. With this correction, 92% of residue predictions are correct (97% similar).
“Correct” refers to number of residues predicted correctly in the sequence from the top 0.6 kcal/mol of ranked sequences (binding affinity plus constraints) that displays highest sequence identity to native. “Similar” includes residues isosteric or functionally identical to native amino acid.
“Mean correct” refers to the average number of residues within the top 1 kcal/mol of ranked sequences that match the native sequence.
“rmsd correct” compares the conformations of the correctly predicted residues in the sequence from the “Correct/similar” column to their crystallographic conformations.
Excluding Arg-21, which was predicted correctly despite omission of nearby crystallographic water.
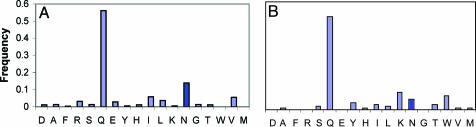
Fig. 2.
Computed (A) and MSA (B) amino acid frequencies for residue 256 of glucose-binding protein, representative of positions where the highest-affinity predicted sequence did not match the native active site sequence. Dark blue bars designate the native amino acid at that residue position. Computed frequencies are derived from the sequences displaying binding affinities within 2 kcal/mol of the tightest binding sequence (subject to catalytic constraints).
The accuracy of computational sequence prediction was particularly high for the streptavidin-biotin complex, where 9 of the 10 residues subject to optimization were predicted correctly. The only error occurred at residue 88, where the native Ser was replaced by Arg. As noted, however, this residue position is most likely not optimized for biotin binding, because it is in contact with the carboxyl group that is used for linking the ligand to biopolymers (13). Therefore, sequence optimization for maximal binding affinity correctly predicts the identities of all amino acid residues essential for the high affinity of streptavidin for biotin.
Of the eight amino acid residues in glucose-binding protein involved in direct contacts to glucose that were subjected to selection, six are predicted correctly in a top-ranked sequence, with native-like amino acids predicted at the remaining two (236 and 256). The prediction that Asn confers higher binding affinity than Asp at positions 14 and 154 (in the top-ranked sequence) is consistent with the epimeric promiscuity of the glucose-binding pocket (14). Different Asp oxygens at this position are used by the protein to recognize glucose vs. galactose (see Fig. 6 for schematics). Asp Oγ1 at position 14 forms H-bonds to the equatorial C4-OH of glucose; the predicted Asn-14 Oγ is located at roughly the same coordinates as the crystallographic Oγ1. However, Asp Oγ2 is needed to H-bond to the axial C4-OH of galactose. Thus, evolution apparently chose a more versatile and less discriminate residue (Asp) at position 14 instead of the tighter binding one (Asn). An Asp rather than Asn residue at position 154 also is used to bind both anomeric hydroxyls of glucose and galactose (residue selection was carried out here for the α-anomer). For the β-gal enzyme, discussed further below, the application of catalytic constraints results in a similarly high level of sequence identity to native, with discrepancies occurring primarily at positions engaging in promiscuous hydrophobic rather than directed contacts (residues 261, 265, and 303). A bulky and inflexible Trp residue, which confers high binding affinity but may be incompatible with alternate substrates (or substrate motion during catalysis), is selected at two of three of these positions.
In the R61 DD-peptidase active site, six of the seven residues involved in ligand contacts, Phe-120, Asn-161, Trp-233, Arg-285, Thr-299, and Ser-326, are predicted correctly by the sequence optimization algorithm. At residue 123, the native Thr ranks second after Asn in terms of amino acid frequency in the computed sequence distributions (see Fig. 7). In general, the most frequently occurring amino acid types are primary candidates for refinement in an extended conformational sampling algorithm incorporating ligand docking (simple ligand redocking did not substantially alter binding affinity for any of the complexes studied). As an example, we carried out such refinement for position 123 in R61 DD-peptidase. To determine whether the error at position 123 could be attributed to the use of the native ligand pose, which might be unphysical for nonnative residues, ligand redocking and side-chain conformation prediction were iterated for the Asn-123 mutant and the converged binding affinity compared with that of native complex refined according to the same protocol. Indeed, the affinity of the Asn-123 mutant fell to -9.23 kcal/mol, less stable than the native complex by ≈1 kcal/mol. Thus, remarkably, all polar and nonpolar residue contacts to the peptide substrate were predicted correctly.
The impeccable sequence prediction of the thymidylate synthase active site (six of six residues selected correctly, Fig. 7), consistent with its phylogenetic conservation, was accomplished without the inclusion of active site waters present in the crystal structure. The ability to reproduce the effects of crystal waters through the use of theoretical solvation models is essential in the computational design of solvent-exposed active sites.
Examination of position-specific residue frequencies calculated from MSAs in many cases resolves discrepancies between native and predicted amino acids. For example, residue 256 in glucose-binding protein is predicted as Gln, which is the most frequently occurring amino acid at this position in the MSA profile (Fig. 2). Residue 123 in R61 DD-peptidase is highly degenerate in sequence alignments, with Gln (homologous to the originally predicted Asn) occurring most frequently (see Fig. 11). The hydrophobic residues 261 and 265 in β-gal are among the most variable in the active site MSA (see below). Ignoring discrepancies that are correlated with MSA variability or that can be attributed to independent functional pressures (e.g., Ser-88 in streptavidin), 92% of binding site residues are predicted correctly in a sequence within the top 0.6 kcal/mol, with 97% similar to native.
Effects of Geometric and Protein Stability Constraints on Predicted Sequence Distributions. As noted above, sequence optimization in enzyme active sites is more complicated than that in ligand-binding sites, because of the dual requirements for both binding and catalysis. In principle, this optimization could be carried out either by designing a new scoring function or by imposing additional constraints on the binding-affinity scoring function. Because our goal in this initial study of active-site sequence optimization was to identify the simplest natural algorithms that might have produced native active-site sequences, we implemented the latter strategy. The highest-affinity sequence was retained at each step of the self-consistent algorithm, irrespective of whether it satisfied the geometric constraints; the final rank-ordered sequence list was later filtered for those sequences that satisfied the constraints (unlike the constraint on total protein energy, which had to be enforced after each step of self-consistent optimization to produce native-like active-site sequences).
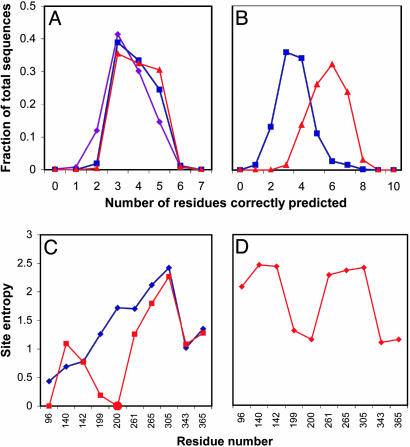
What are the comparative roles played by ligand-binding affinity and geometric constraints in determining enzymes' natural active-site sequences? To shed light on this issue, we examined the number of amino acids predicted correctly within sequence distributions comprised of (i) the sequences with substrate-binding affinities within 1 and 2 kcal/mol, respectively, of the highest-affinity predicted sequence, and (ii) sequences within these windows both with and without catalytic constraints (Fig. 3). We found that catalytic constraints had an effect on sequence similarity that often varied widely, even within a single enzyme family, in a way that could not be easily predicted on the basis of simple structural inspection. For example, the requirement that residue 200 in β-gal adopt a catalytic identity (Glu or Asp) and remain within 3.0 Å of the galactose O1 had a dramatic impact on the number of amino acids predicted correctly, shifting the mean of the distribution from approximately three to approximately six residues correct. For the R61 DD-peptidase, narrowing the window of binding affinities for acceptable sequences had a greater effect than catalytic constraints; the catalytic residues in the most tightly binding sequences generally adopted suitable geometries spontaneously, without as much of a need for additional filters. Nonetheless, the predicted sequence distributions for this protein demonstrate a measurable sensitivity to catalytic filters, particularly to the distance between the general base Tyr-159 and the nucleophile Ser-62; restricting this distance <3.0 Å, which promotes proton abstraction, increases the fraction of native-like sequences.
Fig. 3.
Similarity of predicted sequence distributions to native (A and B), sequence (site) entropies for predicted and MSA residue distributions (C and D), and the effect of catalytic constraints. Purple traces correspond to sequence distributions drawn from binding affinity windows of +2 kcal/mol (relative to the highest affinity predicted sequence), blue traces to +1 kcal/mol, and red traces to +1 kcal/mol with catalytic constraints. Constrained residues are depicted as heavy dots. (A) R61 DD-peptidase. (B and C) Calculated sequence distribution and site entropies for Penicillium sp. β-gal. (D) Site entropies of β-gal residues derived from MSA using an E-value cutoff of 10.
The Shannon entropy at a residue position i (subsequently referred to as the site entropy), defined as Si = -∑a= 1... 20[f(ia) ln f(ia)], where the sum is over all amino acid types and f(ia) is the frequency of amino acid a, is a standard measure of the variability of the amino acid identity at that site (3). Unlike sequence similarity distributions, site entropies represent a quantitative measure, in an information-theoretic sense, of the effects of catalytic constraints on the number of amino acid identities consistent within a given window of binding energies. Fig. 3 depicts representative data on site entropies as functions of both binding energy and catalytic constraints. Although geometric constraints on catalytic residues can increase the site entropies of certain residues, the general trend is to decrease entropies. Clearly, the effects are not localized to only geometrically constrained residues, as is particularly apparent in the case of β-gal. Remarkably, calculated site entropies for active-site residues of this enzyme closely mirror those derived from MSA amino acid frequencies, not only for hydrophobic residues 261 and 265 (where high MSA entropies correlate with discrepancies between native and predicted sequences) but also for the remainder of the active site (Fig. 3). A similar correspondence between predicted and natural sequence entropies was reported for core residues (2), albeit without the added complexities of ligand conformational freedom, catalytic constraints, and hydration.
The finding that the imposition of simple fixed constraints (rather than optimization of a more complex scoring function incorporating, e.g., contributions from both binding affinity and protein stability) can reproduce natural ligand-binding site sequences is important because it reveals features of the binding site fitness landscape that may have simplified the natural evolutionary search for optimal sequences. With respect to the restriction on folding free energy, the simplest explanation for the success of this constraint is that the total system energy and ligand-binding affinity are correlated, in the sense that steric clashes in the binding site rendering the protein unstable are also prone to compromise the ligand-binding affinity. This conjecture is supported by our observation that sequence seeds generated by “excitations” from an all-Ala active site (self-consistently, as described in Methods) generally demonstrated better convergence to the native sequence than did the completely random seeds used in core design studies. Completely random seeds, even those satisfying the dual constraints on total protein energy and binding affinity, are more likely to be trapped in local extrema in the rugged constrained affinity landscape than are seeds generated iteratively with each move from the untrapped all-Ala starting sequence generated in adherence to these constraints.
Structural Accuracy of Designed Binding/Active Sites. Unlike some prior studies that have addressed the convergence of protein core sequence evolution, which used large databases of proteins but neither examined the sources of discrepancy between predicted and native sequences nor assessed the structural accuracy of correct sequences (3, 4), theoretical analysis of the design of ligand-binding and active sites requires high-resolution predictions. The demands placed on the accuracy of the potential energy function used in design are considerably greater for surface than for core residues (18). Importantly, most approaches to sequence optimization have used so-called dead-end elimination algorithms, incapable of sampling energy functions incorporating accurate models of solvation, for side-chain conformation prediction (19-21). By contrast, our algorithm is capable of sampling a potential incorporating a realistic treatment of solvation effects (the surface-generalized Born continuum model), which is critical for accurate predictions of the side-chain conformations of charged and polar residues in highly solvated binding sites. Although scoring of affinity in our algorithm uses a semiempirical potential without continuum solvation (incorporating explicit waters instead), generation of mutant protein structures before scoring is carried out in continuum solvent. This feature appears to be essential to the accurate reprediction of native active-site sequences, in contrast to generating relatively high-affinity sequences (22), of which there are undoubtedly many. In particular, the subtle effects of catalytic constraints in enzymes are especially sensitive to sub-angstrom shifts in side-chain conformations.
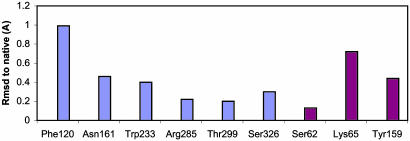
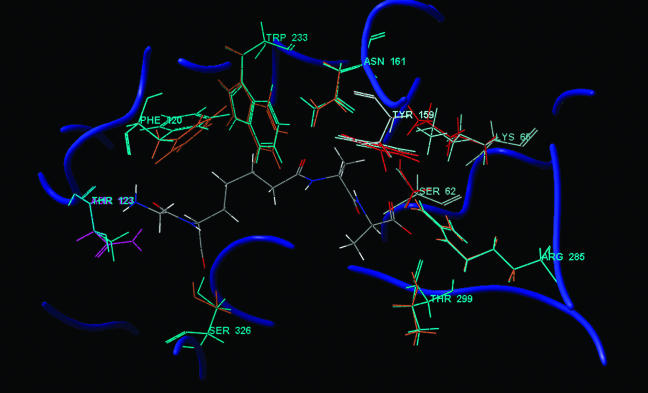
Representative data regarding the geometric accuracy of sequences/structures produced by our algorithm are presented in Fig. 4. The rms deviations (rmsds) of side chains whose identities matched those of the native residues, as well as selected catalytic side chains that were not subject to sequence selection, are displayed. With few exceptions, the rmsds are <1 Å, even when the identities of some of the neighboring side chains are selected incorrectly. Given the resolution of the crystal structures used (typically ≈2.5 Å; see details in Supporting Text), the majority of rmsds are approaching the limits of crystallographic accuracy. In Fig. 5, the structure of the computationally optimized active site of the R61 DD-peptidase is neatly superimposed on that of the native active site, illustrating the accuracy of simultaneous sequence and structure prediction.
Fig. 4.
Structural accuracy of side-chain conformation prediction for correctly selected active site residues in Streptomyces R61 DD-peptidase. The rmsds were calculated over all side-chain heavy atoms. Purple bars denote conformationally optimized (but not sequence-optimized) catalytic residues.
Fig. 5.
Comparison of crystallographic and predicted active-site side-chain identities/geometries for R61 DD-peptidase (DD-peptidase) bound to the d-Ala-d-Ala peptide substrate. Crystallographic conformations of side chains directly involved in binding the ligand are shown in orange; predicted side chain conformations at these positions from the most similar high-affinity optimized sequence (Fig. 1) are shown in blue where residue identities match the native sequence and in purple where they do not. Side chains involved in catalysis but not directly in binding (and subjected to the geometric constraints listed in Fig. 1) are shown in red (crystallographic conformation) or white (predicted conformation). The substrate was fixed in its crystallographic conformation for this calculation. The prediction of Asn-123 in place of Thr-123 was corrected upon iteratively redocking the substrate to the active site and repredicting the conformations of the respective side chains.
Conclusions
We have found that most binding-site amino acid residues of receptor proteins and enzymes from several diverse families are optimized or nearly optimized for simple scoring functions based on ligand-binding affinity, under the constraint that residues involved in catalysis are restricted to catalytically favorable conformations. In the case of enzyme active sites, correct sequences are sometimes predicted on the basis of binding affinity alone, but geometric constraints are often essential. Given the scope of possible scoring functions that could in principle be relevant for active-site optimization, it is striking that nature has apparently used a simple scoring function for the selection of many residues. Moreover, this finding suggests that efficient enzymes can be computationally designed in a similar fashion. From an evolutionary standpoint, there are far more active-site backbone structures in the natural protein universe than there are protein folds; hence, any given backbone structure may have been less extensively sampled. In light of this fact, it is remarkable that the active sites examined here display a level of correlation between predicted and natural sequences at least comparable with that found in protein cores. Although we have not rigorously assessed the extent of sequence equilibrium, close correlation in the positions of variability between predicted and natural sequence distributions, as assessed by site entropies, has been observed. Future work should examine the generality of these observations for additional enzymes and determine whether the residues at which discrepancies occur can be correctly predicted using more sophisticated scoring functions or whether these positions have been incompletely optimized for catalysis by natural evolution.
Supplementary Material
Acknowledgments
We thank Dr. Ramy Farid for helpful suggestions regarding the use of multiple sequence alignments. This work was supported by a National Institutes of Health Postdoctoral Research Fellowship (to R.C.) and National Institutes of Health Grant GM52018 (to R.A.F). A.M.K. was supported by National Institutes of Health Grant GM66712.
Author contributions: R.C. and R.A.F. designed research; R.C. performed research; R.C., A.M.K., and R.A.F. analyzed data; and R.C. wrote the paper.
Abbreviations: MSA, multiple sequence alignment; rmsd, rms deviation.
References
- 1.Raha, K., Wollacott, A. M., Italia, M. J. & Desjarlais, J. R. (2000) Protein Sci. 9, 1106-1119. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Koehl, P. & Levitt, M. (2002) Proc. Natl. Acad. Sci. USA 99, 1280-1285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Kuhlman, B. & Baker, D. (2000) Proc. Natl. Acad. Sci. USA 97, 10383-10388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Jaramillo, A., Wernisch, L., Hery, S. & Wodak, S. J. (2002) Proc. Natl. Acad. Sci. USA 99, 13554-13559. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Voigt, C. A., Gordon, D. B. & Mayo, S. L. (2000) J. Mol. Biol. 299, 789-803. [DOI] [PubMed] [Google Scholar]
- 6.Kaminski, G. A., Friesner, R. A., Tirado-Rives, J. & Jorgensen, W. J. (1998) J. Phys. Chem. B 105, 6474-6487. [Google Scholar]
- 7.Ghosh, A., Rapp, C. S. & Friesner, R. A. (1998) J. Phys. Chem. B 102, 10983-10990. [Google Scholar]
- 8.Gallicchio, E., Zhang, L. Y. & Levy, R. M. (2002) J. Comput. Chem. 5, 517-529. [DOI] [PubMed] [Google Scholar]
- 9.Jacobson, M. P., Kaminski, G. A., Rapp, C. S. & Friesner, R. A. (2002) J. Phys. Chem. B 106, 11673-11680. [Google Scholar]
- 10.Xiang, Z. & Honig, B. (2001) J. Mol. Biol. 311, 421-430. [DOI] [PubMed] [Google Scholar]
- 11.Jacobson, M. P., Pincus, D. L., Rapp, C. S., Day, T. J., Honig, B., Shaw, D. E. & Friesner, R. A. (2004) Proteins 55, 351-367. [DOI] [PubMed] [Google Scholar]
- 12.Friesner, R. A, Banks, J. L., Murphy, R. B., Halgren, T. A., Klicic, J. J., Mainz, D. T., Repasky, M. P., Knoll, E. H., Shelley, M., Perry, J. K., et al. (2004) J. Med. Chem. 47, 1739-1749. [DOI] [PubMed] [Google Scholar]
- 13.Weber, P. C., Ohlendorf, D. H., Wendoloski, J. J. & Salemme, F. R. (1989) Science 243, 85-88. [DOI] [PubMed] [Google Scholar]
- 14.Vyas, N. K., Vyas, M. N. & Quiocho, F. A. (1988) Science 242, 1290-1295. [DOI] [PubMed] [Google Scholar]
- 15.Rojas, A. L., Nagem, R. A. P., Neustroev, K. N., Arand, M., Adamska, M., Eneyskaya, E. V., Kulminskaya, A. A., Garratt, R. C., Golubev, A. M. & Polikarpov, I. (2004) J. Mol. Biol. 343, 1281-1292. [DOI] [PubMed] [Google Scholar]
- 16.McDonough, M. A., Anderson, J. W., Silvaggi, N. R., Pratt, R. F., Knox, J. R. & Kelly, J. A. (2002) J. Mol. Biol. 322, 111-122. [DOI] [PubMed] [Google Scholar]
- 17.Hardy, L. W. & Nalivaika, E. (1992) Proc. Natl. Acad. Sci. USA 89, 9725-9729. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Gordon, D. B., Marshall, S. A. & Mayo, S. L. (1999) Curr. Opin. Struct. Biol. 9, 509-513. [DOI] [PubMed] [Google Scholar]
- 19.Mooers, B. H. M., Datta, D., Baase, W. A., Zollars, E. S., Mayo, S. L. & Matthews, B. W. (2003) J. Mol. Biol. 332, 741-756. [DOI] [PubMed] [Google Scholar]
- 20.Desjarlais, J. R. & Clarke, N. D. (1998) Curr. Opin. Struct. Biol. 8, 471-476. [DOI] [PubMed] [Google Scholar]
- 21.Desmet, J., De Maeyer, M., Hazes, B. & Lasters, I. (1992) Nature 356, 539-542. [DOI] [PubMed] [Google Scholar]
- 22.Looger, L. L., Dwyer, M. A. Smith, J. J. & Hellinga, H. W. (2003) Nature 423, 185-189. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.