Skip to main content
PMC home page
Biochemical Journal logoLink to Biochemical Journal
. 1973 May;134(1):11–26. doi: 10.1042/bj1340011

Amino acid absorption by mouse ascites-tumour cells depleted of both endogenous amino acids and adenosine triphosphate

M Morville 1,*, M Reid 1, A A Eddy 1
PMCID: PMC1177783  PMID: 4723218

Abstract

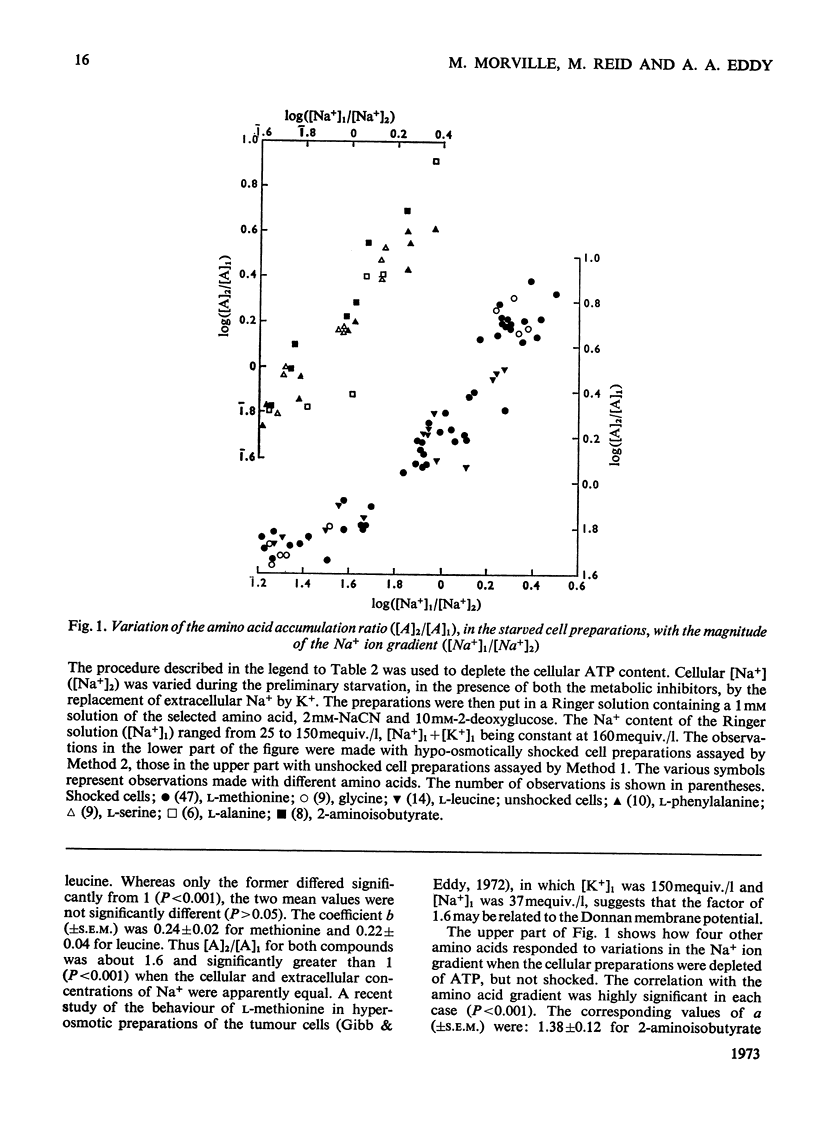
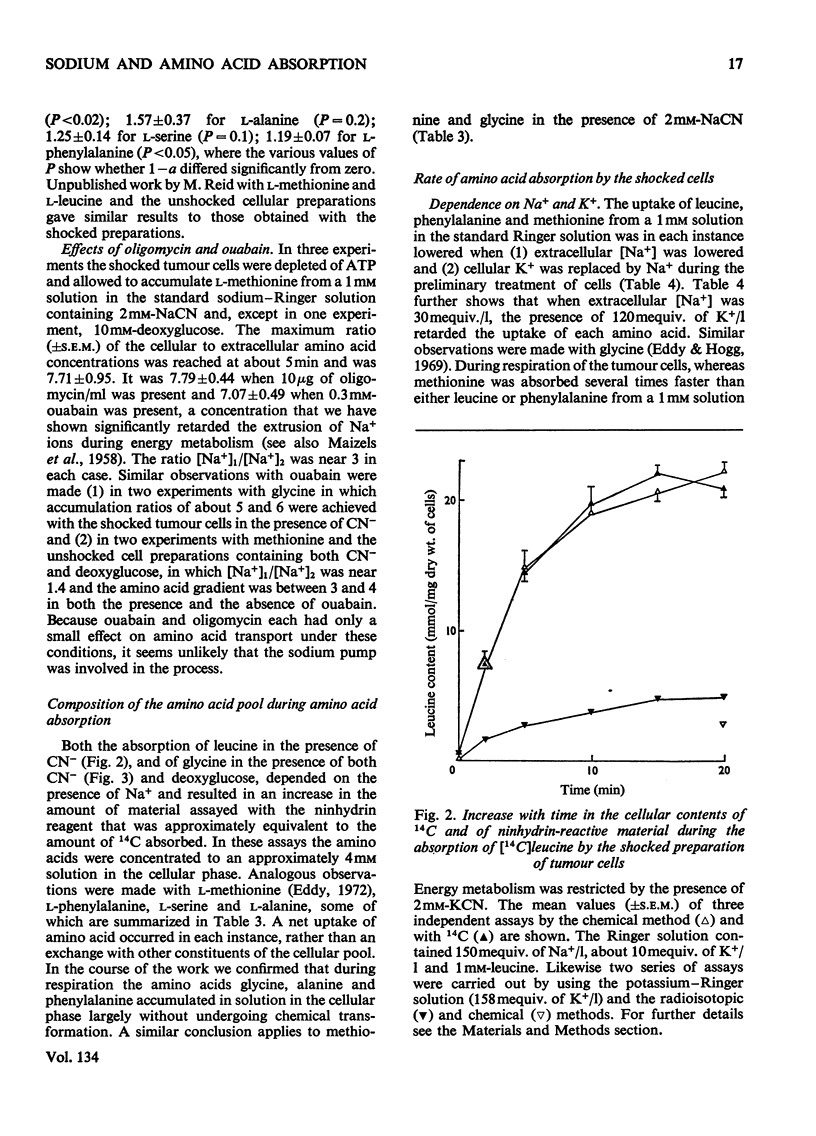
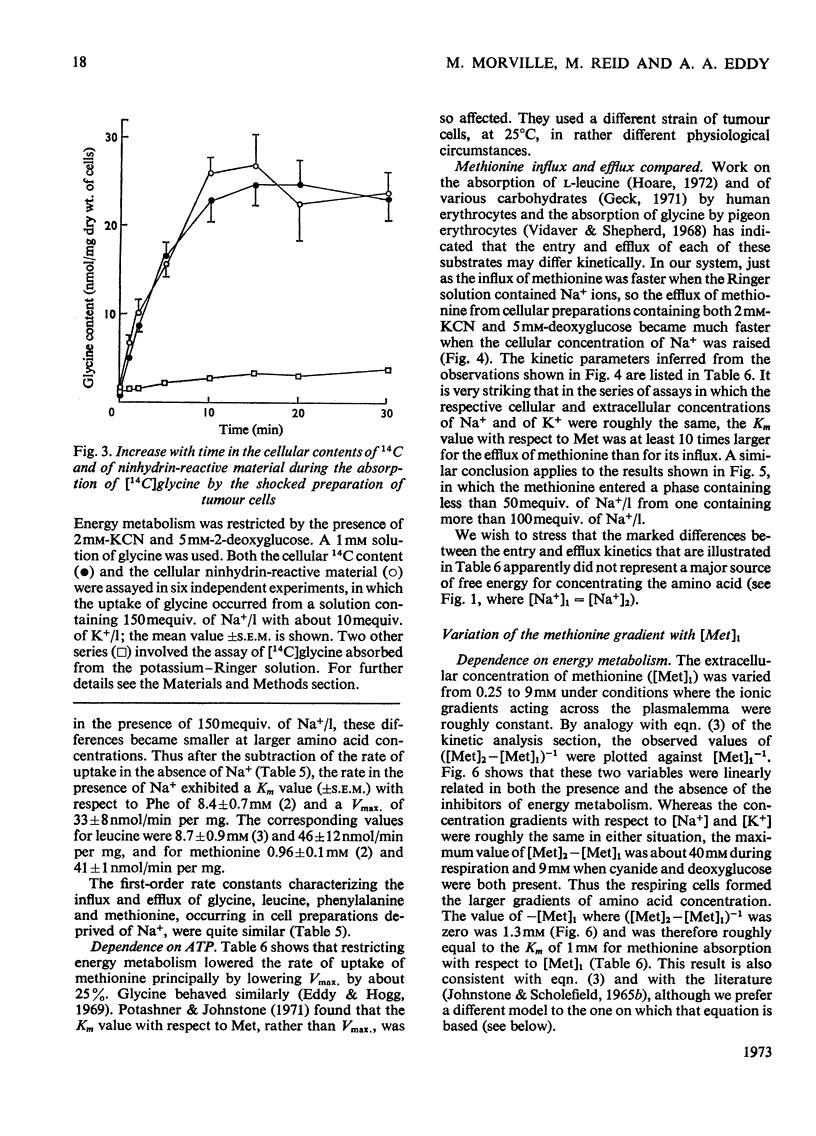
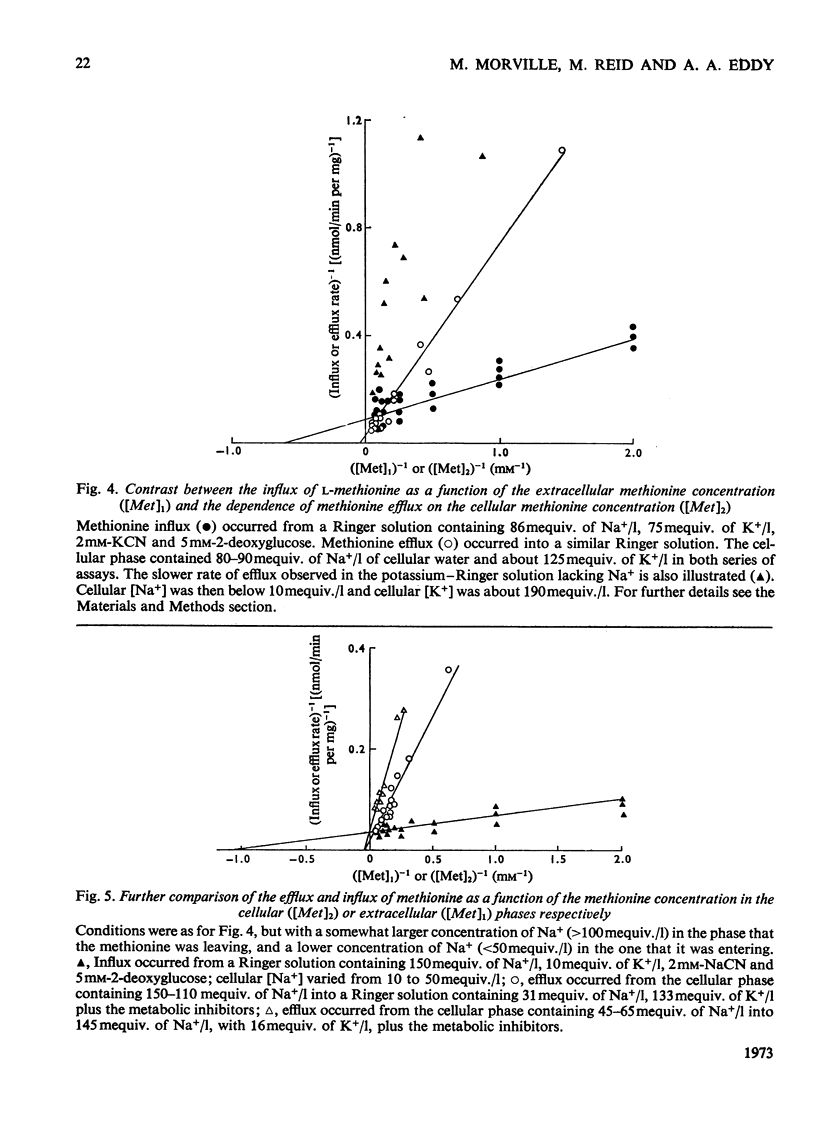
1. Despite the depletion of both their content of exchangeable endogenous amino acids and reserves of ATP, starved hypo-osmotically shocked preparations of the tumour cells accumulated relatively large amounts of 14C-labelled 2-aminoisobutyrate, l-alanine, glycine, l-leucine, l-methionine, l-phenylalanine and l-serine, against their respective concentration gradients, by a process apparently driven by the spontaneous flow of Na+ ions into the cellular phase. Dependent on (a) which compound was used, (b) its concentration and (c) the direction of the Na+ ion gradient, the peak value of the ratio of the cellular to extracellular amino acid concentration varied from about 0.4 to 7. 2. The extent to which ATP increased the ratio was defined for l-methionine. 3. Chemical analysis of the cellular amino acid content showed that this increased in parallel with the absorption of 14C. 4. The accumulation of l-methionine and of glycine, against their own concentration gradients, continued in the presence of either 0.3mm-ouabain or 10μg of oligomycin/ml. Thus the sodium pump was probably not involved in the process when ATP was lacking. 5. l-Leucine caused 0.72±0.12 (s.e.m.; 6) extra equivalents of Na+ to enter the shocked starved tumour cells in parallel with the uptake of leucine itself. Only a small loss of K+ was induced. 6. The influx and efflux of l-methionine in preparations depleted of ATP were both markedly accelerated by the presence of Na+ ions. 7. The observations provide further examples of the application of the ion-gradient hypothesis, according to which Na+ ions act as co-substrates of the amino acid pump. The quantitative importance of parallel Na+-independent systems was studied with a new mathematical model.

Full text

PDF
20

Selected References

These references are in PubMed. This may not be the complete list of references from this article.

  1. Britton H. G. Fluxes in passive, monovalent and polyvalent carrier systems. J Theor Biol. 1966 Jan;10(1):28–52. doi: 10.1016/0022-5193(66)90177-9. [DOI] [PubMed] [Google Scholar]
  2. CHRISTENSEN H. N., RIGGS T. R., FISCHER H., PALATINE I. M. Amino acid concentration by a free cell neoplasm; relations among amino acids. J Biol Chem. 1952 Sep;198(1):1–15. [PubMed] [Google Scholar]
  3. Eddy A. A. A net gain of sodium ions and a net loss of potassium ions accompanying the uptake of glycine by mouse ascites-tumour cells in the presence of sodium cyanide. Biochem J. 1968 Jun;108(2):195–206. doi: 10.1042/bj1080195. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Eddy A. A. A sodium ion concentration gradient formed during the absorption of glycine by mouse ascites-tumour cells. Biochem J. 1969 Nov;115(3):505–509. doi: 10.1042/bj1150505. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Eddy A. A., Hogg M. C. Further observations on the inhibitory effect of extracellular potassium ions on glycine uptake by mouse ascites-tumour cells. Biochem J. 1969 Oct;114(4):807–814. doi: 10.1042/bj1140807. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Eddy A. A., Mulcahy M. F., Thomson P. J. The effects of sodium ions and potassium ions on glycine uptake by mouse ascites-tumour cells in the presence and absence of selected metabolic inhibitors. Biochem J. 1967 Jun;103(3):863–876. doi: 10.1042/bj1030863. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Eddy A. A., Nowacki J. A. Stoicheiometrical proton and potassium ion movements accompanying the absorption of amino acids by the yeast Saccharomyces carlsbergensis. Biochem J. 1971 May;122(5):701–711. doi: 10.1042/bj1220701. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Eddy A. A. The effects of varying the cellular and extracellular concentrations of sodium and potassium ions on the uptake of glycine by mouse ascites-tumour cells in the presence and absence of sodium cyanide. Biochem J. 1968 Jul;108(3):489–498. doi: 10.1042/bj1080489. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Geck P. Eigenschaften eines asymmetrischen Carrier-Modells für den Zuckertrnasport am menschlichen Erythrozyten. Biochim Biophys Acta. 1971 Aug 13;241(2):462–472. doi: 10.1016/0005-2736(71)90045-9. [DOI] [PubMed] [Google Scholar]
  10. Gibb L. E., Eddy A. A. An electrogenic sodium pump as a possible factor leading to the concentration of amino acids by mouse ascites-tumour cells with reversed sodium ion concentration gradients. Biochem J. 1972 Oct;129(4):979–981. doi: 10.1042/bj1290979. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Hoare D. G. The temperature dependence of the transport of L-leucine in human erythrocytes. J Physiol. 1972 Mar;221(2):331–348. doi: 10.1113/jphysiol.1972.sp009754. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. JOHNSTONE R. M., SCHOLEFIELD P. G. THE NEED FOR IONS DURING TRANSPORT AND EXCHANGE DIFFUSION OF AMINO ACIDS INTO EHRLICH ASCITES CARCINOMA CELLS. Biochim Biophys Acta. 1965 Jan 25;94:130–135. doi: 10.1016/0926-6585(65)90016-6. [DOI] [PubMed] [Google Scholar]
  13. Jacquez J. A., Schafer J. A. Na+ and K+ electrochemical potential gradients and the transport of alpha-aminoisobutyric acid in Ehrlich ascites tumor cells. Biochim Biophys Acta. 1969;193(2):368–383. doi: 10.1016/0005-2736(69)90197-7. [DOI] [PubMed] [Google Scholar]
  14. Johnstone R. M. Glycine accumulation in absence of Na+ and K+ gradients in Ehrlich ascites cells: shortfall of the potential energy from the ion gradients for glycine accumulation. Biochim Biophys Acta. 1972 Sep 1;282(1):366–373. doi: 10.1016/0005-2736(72)90341-0. [DOI] [PubMed] [Google Scholar]
  15. Johnstone R. M., Scholefield P. G. Amino acid transport in tumor cells. Adv Cancer Res. 1965;9:143–226. doi: 10.1016/s0065-230x(08)60447-9. [DOI] [PubMed] [Google Scholar]
  16. Kimmich G. A. Active sugar accumulation by isolated intestinal epithelial cells. A new model for sodium-dependent metabolite transport. Biochemistry. 1970 Sep 15;9(19):3669–3677. doi: 10.1021/bi00821a004. [DOI] [PubMed] [Google Scholar]
  17. MAIZELS M., REMINGTON M., TRUSCOE R. The effects of certain physical factors and of the cardiac glycosides on sodium transfer by mouse ascites tumour cells. J Physiol. 1958 Jan 23;140(1):61–79. doi: 10.1113/jphysiol.1958.sp005916. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. OXENDER D. L. STEREOSPECIFICITY OF AMINO ACID TRANSPORT FOR EHRLICH TUMOR CELLS. J Biol Chem. 1965 Jul;240:2976–2982. [PubMed] [Google Scholar]
  19. Potashner S. J., Johnstone R. M. Cation gradients, ATP and amino acid accumulation in Ehrlich ascites cells. Biochim Biophys Acta. 1971 Mar 9;233(1):91–103. doi: 10.1016/0005-2736(71)90361-0. [DOI] [PubMed] [Google Scholar]
  20. Potashner S., Johnston R. M. Cations, transport and exchange diffusion of methionine in Ehrlich ascites cells. Biochim Biophys Acta. 1970 Jun 2;203(3):445–456. doi: 10.1016/0005-2736(70)90184-7. [DOI] [PubMed] [Google Scholar]
  21. Reid M., Eddy A. A. Apparent metabolic regulation of the coupling between the potassium ion gradient and methionine transport in mouse ascites-tumour cells. Biochem J. 1971 Oct;124(5):951–952. doi: 10.1042/bj1240951. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Schafer J. A., Heinz E. The effect of reversal on Na + and K + electrochemical potential gradients on the active transport of amino acids in Ehrlich ascites tumor cells. Biochim Biophys Acta. 1971 Oct 12;249(1):15–33. doi: 10.1016/0005-2736(71)90079-4. [DOI] [PubMed] [Google Scholar]
  23. Schultz S. G., Curran P. F. Coupled transport of sodium and organic solutes. Physiol Rev. 1970 Oct;50(4):637–718. doi: 10.1152/physrev.1970.50.4.637. [DOI] [PubMed] [Google Scholar]
  24. Vidaver G. A., Shepherd S. L. Transport of glycine by hemolyzed and restored pigeon red blood cells. Symmetry properties, trans effects of sodium ion and glycine, and their description by a single rate equation. J Biol Chem. 1968 Dec 10;243(23):6140–6150. [PubMed] [Google Scholar]
  25. Whittam R., Wheeler K. P. Transport across cell membranes. Annu Rev Physiol. 1970;32:21–60. doi: 10.1146/annurev.ph.32.030170.000321. [DOI] [PubMed] [Google Scholar]

Articles from Biochemical Journal are provided here courtesy of The Biochemical Society

RESOURCES