A Populationwide Coalescent Analysis of Icelandic Matrilineal and Patrilineal Genealogies: Evidence for a Faster Evolutionary Rate of mtDNA Lineages than Y Chromosomes

Abstract

Historical inferences from genetic data increasingly depend on assumptions about the genealogical process that shapes the frequencies of alleles over time. Yet little is known about the structure of human genealogies over long periods of time and how they depart from expectations of standard demographic models, such as that attributed to Wright and Fisher. To obtain such information and to examine the recent evolutionary history of mtDNA and Y-chromosome haplotypes in the Icelandic gene pool, we traced the matrilineal and patrilineal ancestry of all 131,060 Icelanders born after 1972 back to two cohorts of ancestors, one born between 1848 and 1892 and the other between 1798 and 1742. This populationwide coalescent analysis of Icelandic genealogies revealed highly positively skewed distributions of descendants to ancestors, with the vast majority of potential ancestors contributing one or no descendants and a minority of ancestors contributing large numbers of descendants. The expansion and loss of matrilines and patrilines has caused considerable fluctuation in the frequencies of mtDNA and Y-chromosome haplotypes, despite a rapid population expansion in Iceland during the past 300 years. Contrary to a widespread assumption, the rate of evolution caused by this lineage-sorting process was markedly faster in matrilines (mtDNA) than in patrilines (Y chromosomes). The primary cause is a 10% shorter matrilineal generation interval. Variance in the number of offspring produced within each generation was not an important differentiating factor. We observed an intergenerational correlation in offspring number and in the length of generation intervals in the matrilineal and patrilineal genealogies, which was stronger in matrilines and thus contributes to their faster evolutionary rate. These findings may have implications for coalescent date estimates based on mtDNA and Y chromosomes.

Introduction

Whether estimating the age of the most recent common ancestor or interpreting geographic patterns of genetic variation, inference depends on assumptions about the evolutionary process that gave rise to patterns of genetic variation observed in contemporary populations. Genetic drift is a key component of microevolution in a population’s gene pool. Disregarding the effects of selection, migration, and mutation, allele frequencies drift randomly as a result of differential reproduction (and gametic sampling in the case of diploid loci). The rate of genetic drift over time (measured in years) is a function of the effective population size, which is primarily dependent on three demographic factors: (i) the shape and variance of the distribution of offspring to parents in the population (Crow and Kimura 1970; Cavalli-Sforza and Bodmer 1971), (ii) the length of generation intervals between parents and their offspring, and (iii) the existence of an intergenerational correlation in one or both of these aspects of reproductive behavior (Nei and Murata 1966; Donnelly and Marjoram 1989). The impact of these factors over time can be assessed by studying the genealogies linking contemporary members of a population back to successive generations of ancestors. The structures of such genealogies provide empirical data about the magnitude of random allele frequency changes expected to have occurred in a gene pool. Since sufficiently extensive and deep genealogies are rare, only a few such detailed empirical studies of human microevolution have been undertaken, in a limited number of populations—such as the Saguenay from Quebec (Heyer 1995; Austerlitz and Heyer 1998), Islanders of Tristan da Cuhna (Roberts and Bear 1980), Utah Mormons (O’Brien et al. 1994), and the Åland Islanders (O’Brien et al. 1994). Previous studies have demonstrated that rates of drift vary both among populations and at different periods within the same populations (Skolnick et al. 1976; Roberts and Bear 1980; O’Brien et al. 1994). The impact of different genealogical structures on gene pools has also been partially explored through simulation (O’Brien et al. 1994; Austerlitz and Heyer 1998).

Populationwide analyses of real genealogies provide important information for the application of coalescent theory to human genetic data. Modeled genealogies lie at the heart of the coalescent approach, where they are typically assumed to be produced by a Wright-Fisher demographic model (Hudson 1990). It is recognized that the assumptions of this demographic model are violated in most naturally reproducing populations, for reasons such as population-size fluctuation, intergenerational correlation in fertility, variance in the number of offspring that exceeds the mean and differences in the length of generation intervals. As a consequence, all parameters estimated from genetic data using the coalescent are scaled by factors that cause genealogies to depart from the Wright-Fisher expectation (Nordborg 2001). The key to obtaining the true values of scaled parameters lies in knowledge about how such factors affect genealogies. Although departures from Wright-Fisher demography are usually inferred directly from genetic data, the most important source of information are real genealogies. Such empirical information should allow for more robust and accurate inferences based on the coalescent approach to human molecular data.

The primary focus of this study was to explore the rate of evolutionary change in matrilineal and patrilineal genealogies from the entire Icelandic population over a 300-year period and examine the relative impact of the underlying demographic factors discussed above. We concentrated on these genealogical pathways for three main reasons. First, unlike diploid autosomal loci, there is no uncertainty about transmission patterns due to gametic sampling. Second, matrilineal and patrilineal genealogies define the transmission of mtDNA and Y chromosomes, respectively, which are among the most widely used genetic markers in studies of human population history. Third, as matrilineal and patrilineal genealogical structures do not overlap, their comparison can shed light on the genetic consequences of differences in the reproductive behavior of males and females (Charlesworth 2001). Thus, for example, it has been assumed that the widespread practice of polygyny and high variance in male reproductive success causes Y chromosomes to drift at a faster rate than mtDNA lineages (Cavalli-Sforza and Bodmer 1971, Seielstad et al. 1998, Avise 2000). Accurate empirical knowledge about the deep structure of genealogies along which alleles are transmitted through time in populations, and the underlying demographic factors that give rise to these genealogies, is crucial for the growing field of studies that use approaches such as that of the coalescent to make inferences about the genealogical relationships between alleles or haplotypes.

Material and Methods

Genealogical Database and Selection of Cohorts

Matrilineal and patrilineal genealogies were extracted from the deCODE Genetics genealogical database (not part of the Icelandic Healthcare Sector Database), which includes all 280,000 living Icelanders and, when analyses commenced (June 2002), recorded genealogical links for just over 650,000 individuals (Gulcher and Stefánsson 1998; Guðmundsson et al. 2000). Starting with a cohort of all Icelanders born after 1972 (N=131,060), we used a genealogical coalescent approach to trace matrilines and patrilines back in time to two different cohorts of ancestors born between 1698 and 1742 and between 1848 and 1892, respectively. Inevitably, the further back in time lineages are traced, the greater the decay of genealogical information. Thus, the former ancestor cohort was selected to take advantage of genealogical depth, whereas the latter cohort was selected to maximize population coverage. All analyses were performed on an encrypted version of the genealogical database in which birth dates are rounded to the nearest multiple of 5 (for example, the birth year 1700 stands for the range 1698–1702, and 1705 stands for the range 1703–1707).

Obviously, the lineages traced back to matrilineal and patrilineal ancestors in the 1698–1742 or 1848–1892 cohorts represent only a part of the total number of Icelanders that were actually born during these two periods. As not all of these Icelanders have yet been entered into the genealogical database, historical census data was used to provide estimates of the total numbers of individuals who were born between 1698–1742 and 1848–1892, respectively, and who survived childhood. The size of the 1698–1742 cohort taken as the 0–44 year age group from the 1703 Icelandic national census (Jónsson and Magnússon 1997), which is by far the most detailed source of demographic data on the Icelandic population for this period. Historical census data (Jónsson and Magnússon 1997) was used to estimate the 1848–1892 birth cohort size by summing the 15–19 year age groups for the years 1867, 1872, 1877, 1882, 1887, 1892, 1897, 1902, and 1907.

Coalescent Lineage Tracing Approach

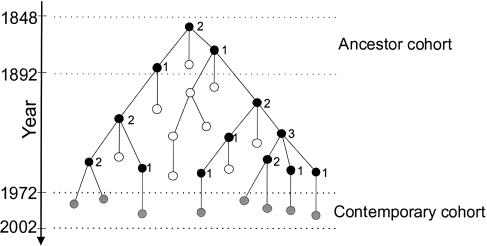
Members of the ancestor cohorts were linked to one or more descendant born after 1972 through a genealogical coalescent structure as follows (see fig. 1). Matrilines were only traced back from contemporary females and patrilines only from contemporary males. Moving back in time, the number of matrilines or patrilines decreases as a function of the number of coalescent events, which occur when two or more sisters are traced to a single mother (a matrilineal coalescent event) or two or more brothers are traced to a single father (a patrilineal coalescent event). By the time we reach the first year of each ancestral cohort (1698 or 1848), this process defines groups of one or more contemporary individuals, each of which is descended, through a coalescent genealogy, from a single matrilineal or patrilineal ancestor. Such matrilineal and patrilineal coalescent genealogies were reconstructed for all Icelanders born after 1972, to explore the genealogical and demographic processes that shaped the mtDNA and Y-chromosome pools of the Icelandic population.

Figure 1.

Coalescent structures of matrilineal and patrilineal genealogies. These were determined by tracing back in time from females and males born after 1972 (grey circles). The black circles represent matrilineal or patrilineal ancestors who have descendants in the contemporary cohort. The number of offspring who leave descendants in the contemporary cohort is shown next to the black circles. As we move back in time, each coalescent event reduces the total number of matrilines or patrilines, until we are left with the single earliest ancestor in the ancestor cohort. After the coalescent tracing procedure has ended, it emerges that this ancestor has eight descendants in the contemporary cohort. White circles represent individuals with no descendants in the contemporary cohort. Such individuals are invisible to the coalescent approach. Coalescent events are not recorded for these individuals, and they are not counted among the offspring attributed to their mother or father. Hence, information is only stored about direct matrilineal and patrilineal ancestors of individuals in the contemporary cohort. Note that generation intervals vary in length, with the result that three descendants from the contemporary cohort are linked to the ancestor through four generations, whereas five such descendants are linked through five generations.

By definition, the coalescent approach adopted in this study includes only individuals in the matrilineal and patrilineal genealogies who either are members of or have descendants in the contemporary cohort. Past individuals with no matrilineal or patrilineal descendants in the contemporary cohort are excluded from our analysis. A coalescent approach was chosen for two primary reasons. First, there is an inherent selective bias against recording of genealogical data for individuals in the past with no contemporary descendants, particularly for individuals that did not reproduce at all. As the degree of selection bias against such individuals is impossible to assess with any certainty, our knowledge about the nature and quality of the data is arguably increased by their exclusion. Second, in accordance with the general philosophy of the coalescent, we argue that, to gain an understanding of the evolutionary history of a contemporary population, it is sufficient to consider only the ancestors of the population’s present members.

Evaluating Correlation in Reproductive Behavior within Matrilineal and Patrilineal Coalescent Genealogies

A product-moment correlation coefficient was used to estimate parent-offspring correlation in reproductive behavior in matrilines and patrilines. In the context of matrilines this correlation can be divided into two separate factors: a correlation in offspring numbers (i.e., between the numbers of daughters linked to mothers and their daughters) and a correlation in generation intervals (i.e., between the two generation intervals separating each female-mother-grandmother trio). Both forms of correlation were estimated nonparametrically for Icelandic matrilineal and patrilineal genealogies.

A Stochastic Model to Evaluate the Impact of Intergenerational Correlation in Reproductive Behavior

To establish the impact of an intergenerational correlation in reproductive behavior on the structure of Icelandic matrilineal and patrilineal genealogies we developed a forward-in-time stochastic model that describes the unfolding of matrilineal and patrilineal coalescent genealogies traced backward in time. The stochastic model describes the number of matrilineal or patrilineal contemporary descendants that derive from a single ancestor born at a specific time in the past. The model assumes that genealogies linking descendants to their ancestor are generated by randomly selecting offspring numbers and generation intervals from global distributions. In other words, it is assumed that no kind of correlation in reproductive behavior influences the formation of the genealogies. In our application of the stochastic model, the global distributions of offspring numbers and generation intervals were extracted from the real genealogies. On the basis of this stochastic model, it is then possible to simulate genealogies and compare the resultant distributions of descendants per ancestor to distributions from the actual genealogies, by means of a simple χ² test. This approach enables us to verify the existence and relative impact of a correlation in reproductive behavior in the real genealogies. The stochastic model is described in appendix A.

Results

Distribution of Descendants among Ancestors

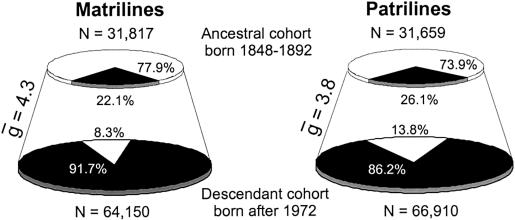
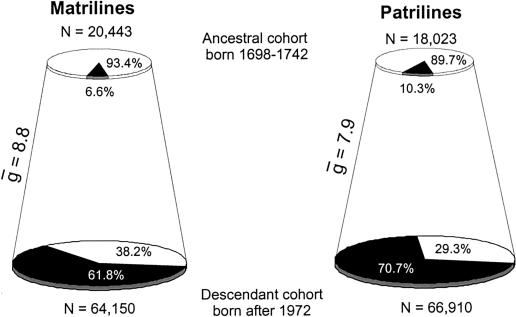
Figure 2 shows the number of contemporary descendants successfully traced to matrilineal and patrilineal ancestors born between 1848 and 1892 (black slices) as proportions of their respective cohorts in the Icelandic population (see also table 1). These results demonstrate even over a short timeframe of a few hundred years, during which the size of the Icelandic population increased almost fivefold, only a minority of potential ancestors actually contributed mtDNA or Y chromosomes to the contemporary population. The vast majority of contemporary females (58,832 or 91.7%) are descended from only 22% (7,041) of the potential matrilineal ancestors born between 1848 and 1892, and most contemporary males (57,686 or 86.2%) are descended from only 26% (8,275) of the potential patrilineal ancestors. The results are even more striking for matrilines and patrilines traced back to the 1698–1742 ancestor cohort. Because of the decay of genealogical information as we go further back in time, a greater proportion of the contemporary cohort could not be successfully traced back to ancestors. However, 62% (39,615) of contemporary females are descended from only 6.6% (1,356) of the potential matrilineal ancestors born between 1698–1742 and 71% (47,335) of contemporary males are descended from only 10.3% (1,859) of the potential patrilineal ancestors (see fig. 3 and table 1). The higher percentage of patrilineal links to the 1698–1742 ancestor cohort results from a more comprehensive recording of paternity in early Icelandic historical sources (a consequence of male bias in most historical documents).

Figure 2.

Contributions of the 1848–1892 ancestors to the contemporary cohort. The areas of the circles on the left represent all Icelandic females born between 1848 and 1892 (top) and after 1972 (bottom) who survived early childhood. The black slice in the bottom-left circle represents the proportion of females born after 1972 who could be traced successfully to a matrilineal ancestor born between 1848 and 1892. The black slice in the top-left circle represents these matrilineal ancestors as a proportion of the entire 1848–1892 cohort. The white slice in the bottom-left circle represents the 5,318 contemporary females who could not be traced to matrilineal ancestors born between 1848 and 1892. The white slice in the top-left circle represents the 24,776 females born between 1848 and 1892 who either do not have matrilineal descendants born after 1972 or could not be linked to matrilineal descendants in the genealogical database. The circles on the right present equivalent information for males and patrilines. The parameter stands for the average number of generations between members of the ancestor cohort and their descendants in the contemporary cohort.

Table 1.

Distribution of Descendants among Matrilineal and Patrilineal Ancestors

	Ancestor Cohort
	1848–1892		1698–1742
Statistic	Matrilines (N=7,041)	Patrilines (N=8,275)	Matrilines (N=1,356)	Patrilines (N=1,859)
No. of descendants	58,832	57,686	39,615	47,335
Mean (SE)	8.36 (.101)	6.97 (.071)	29.21 (.969)	25.46 (.597)
Variance	71.7	41.75	1,274.31	661.79
Coefficient of variation	101.29	92.70	122.21	101.04
Skewness (SE)	2.54 (.029)	2.21 (.026)	3.84 (.066)	2.27 (.057)
Maximum	109	72	392	224

Figure 3.

Contributions of the 1698–1742 ancestors to the contemporary cohort (see legend for fig. 2)

Note that of those lineages that reach dead ends before 1892, a sizeable proportion is likely to be matrilineally or patrilineally descended from foreign nationals who immigrated to Iceland during the past century and whose ancestors are therefore typically not found in Icelandic historical records. These individuals cannot be identified in the encrypted version of the genealogical database used for these analyses. However, estimates based on census data (Jónsson and Magnússon 1997) and the unencrypted genealogical database indicate that as many as 6,000 females and 5,500 males with ancestral ties outside Iceland who were born after 1900 are included in the genealogical database, many of whom are likely to contribute to the matrilineal and patrilineal dead-ends shown in figures 2 and 3.

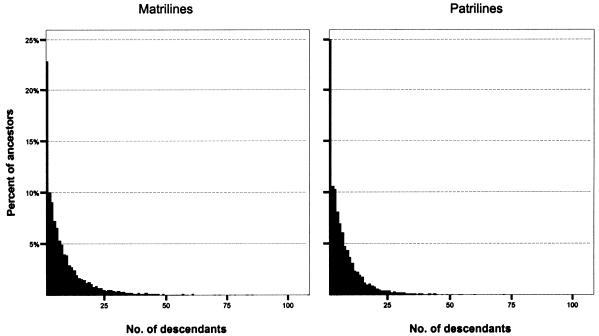
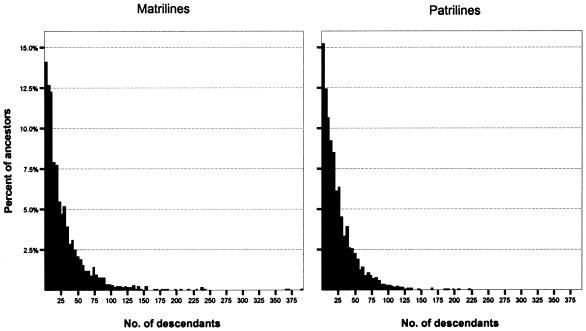
More can be learned about the microevolutionary histories of Icelandic matrilines and patrilines by examining the distribution of descendants among ancestors. Descriptive statistics for these distributions, presented in table 1, reveal notable differences between the genealogical pathways of mtDNA and Y chromosomes. Thus, in the case of the 1848–1892 ancestor cohort, we start with more contemporary females than contemporary males but end with considerably fewer matrilineal ancestors than patrilineal ancestors. Accordingly, the matrilineal ancestors have a greater average number of descendants (8.36) than do the patrilineal ancestors (6.97). As shown by the histograms in figure 4, the distribution of descendants among ancestors is strongly positively skewed for both matrilines and patrilines, but the matrilineal distribution is more heavily skewed and exhibits a greater variance.

Figure 4.

Histograms of descendants per ancestor for matrilines and patrilines (1848–1892 ancestor cohort)

The same pattern emerges from lineages traced back to the 1698–1742 ancestor cohort, but with even more striking differences (table 1; figs. 3 and 5). In this case, matrilineal ancestors have, on average, 29.2 descendants, whereas patrilineal ancestors have an average of 25.5 descendants. The variance for matrilines is almost double that for patrilines, and the coefficient of variation reveals the more uneven distribution of descendants among matrilineal ancestors. An informative indicator of the disparity observed between matrilines and patrilines is the 75% difference between the most prolific matrilineal ancestor in the 1698–1742 cohort (392 descendants) and that of the most prolific patrilineal ancestor (224 descendants). In fact, seven matrilineal ancestors contribute more descendants than the most prolific patrilineal ancestor.

Figure 5.

Histograms of descendants per ancestor for matrilines and patrilines (1698–1742 ancestor cohort)

Because of the heavily skewed distribution of descendants among ancestors a nonparametric test (χ²) was used to evaluate the statistical significance of the differences observed for matrilines and patrilines. For this purpose the number of descendants per ancestor was grouped into 10 categories for the 1848–1892 cohort (1–2, 3–4, 5–6, 7–8, 9–10, 11–12, 13–16, 17–20, 21–30, and 31–max) and 10 categories for the 1698–1742 cohort (1–5, 6–10, 11–15, 16–25, 26–35, 36–45, 46–60, 61–80, 81–125, and 126–max). For both cohorts, the differences between the matrilineal and patrilineal distributions were found to be statistically significant (p<.001 for the 1848–1892 cohort and p=.014 for the 1698–1742 cohort).

On the basis of these results, it is possible to draw two key conclusions. First, when lineages are traced back the same number of years, it emerges that contemporary Icelandic females are descended from fewer matrilineal ancestors than is the case for contemporary Icelandic males and patrilineal ancestors. Thus, the effective population size is smaller for matrilines (mtDNA) than for patrilines (Y chromosomes). Second, not only are fewer matrilineal ancestors contributing more descendants on average, the relative dispersion of descendants per ancestor is also greater for matrilineal ancestors than for patrilineal ancestors. In short, matrilines are evolving at a faster rate than patrilines.

Faster Generational Turnover in Matrilines

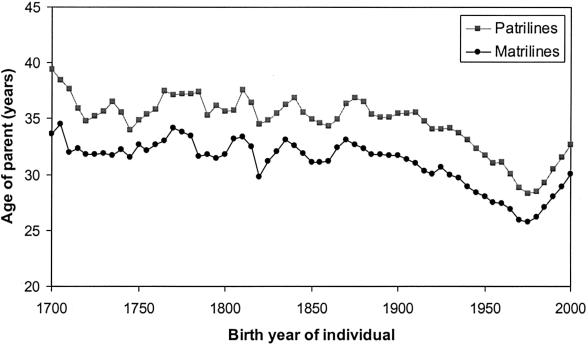
Table 2 presents information about the length of time separating ancestors from their descendants both in generations and years. These results reveal an important cause of the faster rate of matrilineal drift: over the same period of time, a greater number of generations tend to separate contemporary females from their matrilineal ancestors than is the case for contemporary males and their patrilineal ancestors. Thus, while an average of 4.3 generations have passed between female ancestors in the 1848–1892 cohort and their matrilineal descendants, an average of only 3.8 generations have passed in patrilines. For the 1698–1742 ancestor cohort matrilines have, on average, evolved almost a whole generation longer than patrilines. The underlying cause is a difference in the average length of generation intervals (see table 2). Figure 6 shows the difference between average matrilineal and patrilineal generation intervals, by birth year of child, for the period 1698–2000.

Table 2.

Generation Intervals between the Contemporary and Ancestor Cohorts

	Ancestor Cohort
	1848–1892		1698–1742
Parameter andStatistic	Matrilines	Patrilines	Matrilines	Patrilines
Total years:a
Mean	122.6	121.0	268.4	268.0
SD	13.0	13.8	14.8	14.1
N	58,832	57,686	39,615	47,335
No. of generations:a
Mean	4.27	3.80	8.8	7.9
SD	.62	.60	.79	.80
N	58,832	57,686	39,615	47,335
Generation interval:b
Mean	28.12	31.13	28.72	31.93
SD	6.57	7.57	6.76	8.06
N	128,296	122,822	99,169	117,486

^aCases represent each contemporary descendant and his or her ancestor.

^bCases represent each unique mother-daughter or father-son pair in the matrilineal and patrilineal coalescent genealogies, respectively.

Figure 6.

Changes in the average length of matrilineal and patrilineal generation intervals by birth year of offspring from 1698 to 2000. Generation intervals are defined as the birth year of an offspring subtracted from the birth year of the parent.

The matrilineal and patrilineal generation intervals reported in this study are similar to those published by Tremblay and Vézina (2000), whose findings were based on 100 French Canadian genealogies. The shorter matrilineal generation interval observed in both studies can be assumed to stem from the tendency of females to reproduce earlier in life than males and from the ability of males to continue reproducing to a later age than females.

Reproductive Variance within Generations

As reflected in the concept of the variance effective population size (Crow and Kimura 1970), reproductive variance within generations is a prime determinant of the rate of evolution due to random genetic drift. In the context of our coalescent genealogies, reproductive variance is measured as the variance in the number of daughters attributed to mothers and sons attributed to fathers. Note that, because of the nature of coalescent tracing backward in time, these offspring distributions differ from conventional offspring distributions in demographic surveys based on completed fertility. Specifically, only offspring belonging to the contemporary cohort or offspring with descendants in the contemporary cohort are counted in the coalescent genealogies. The difference becomes increasingly important the further back in time we trace lineages of descent.

Descriptive statistics for the number of daughters per mother and sons per father in the coalescent genealogies are shown in table 3. For both ancestor cohorts, patrilines exhibit slightly higher averages and variances than matrilines. However, the relative spread of the distributions is almost identical when coefficients of variation are examined. The same degree of similarity between matrilines and patrilines is observed when the distribution of offspring numbers is examined by year (data not shown). On the basis of this evidence, we conclude that reproductive variance within generations is unlikely to be a key factor underlying the faster rate of evolution in matrilines.

Table 3.

Distribution of Number of Offspring to Parents

	Ancestor Cohort
	1848–1892		1698–1742
Statistic	Matrilines	Patrilines	Matrilines	Patrilines
Mean	1.63	1.65	1.59	1.61
Variance	.763	.785	.727	.752
Coefficient of variation	53.73	53.71	53.63	53.84
Na	76,505	73,411	60,910	72,010

^aN = number of parents born prior to 1972.

Intergenerational Correlation in Reproductive Behavior

As reflected by the previous two sections, an intergenerational correlation in reproductive behavior can have two separate elements. First, a correlation in the number of offspring produced by individuals and the number of offspring produced by their parents. Second, a correlation in the generation intervals between each individual-parent-grandparent trio. As far as we are aware, this latter type of correlation has not been discussed previously in the literature. A positive correlation in either case will have the effect of increasing the rate of evolution in genealogies, speeding up the lineage-sorting process and increasing the variance in the number of descendants left by a given cohort of ancestors (see Donnelly and Marjoram [1989] for a theoretical treatment of intergenerational offspring correlation).

Table 4 reports the product-moment correlation for the number of offspring and generation intervals in the matrilineal and patrilineal genealogies. In all cases, a relatively weak—but highly significant—positive correlation is observed. Two other noteworthy findings are revealed. First, the correlation in reproductive behavior is always stronger for lineages traced to the older 1698–1742 ancestor cohort. Second, matrilines exhibit a slightly higher correlation than patrilines when results for equivalent ancestor cohorts are compared.

Table 4.

Matrilineal and Patrilineal Parent-Offspring Product-Moment Correlation in Reproductive Behavior

	Ancestor Cohort
	1848–1892		1698–1742
DemographicFactor andStatistic	Matrilines	Patrilines	Matrilines	Patrilines
No. of offspring:a
rc	.058	.041	.079	.051
N	69,464	65,136	59,554	70,151
pd	0	0	0	0
Generation interval:b
rc	.046	.024	.071	.041
N	58,354	51,180	57,941	67,827
pd	0	0	0	0

^aDefined as the number of offspring identified by the coalescent tracing of matrilineal and patrilineal genealogies for each unique mother-daughter or father-son pair. Only parent-offspring pairs born prior to 1972 were included.

^bEach female-mother-grandmother or male-father-grandfather triplet yields two generation intervals and the correlation between these intervals for all such triplets are presented in these columns. Only individual-parent-grandparent triplets where the individual was born prior to 1972 were included.

^cThe product-moment correlation coefficient.

^dStatistical significance based on a test of whether r>0.

Evaluating the Relative Impact of Intergenerational Correlation in Reproductive Behavior on Evolutionary Rates of Matrilines and Patrilines

Here, we compare expected distributions of descendants per ancestor derived from simulations (see the “Materials and Methods” section and appendix A) to those obtained from the real genealogies. The simulations make use of distributions of offspring numbers and generation intervals from the real matrilineal and patrilineal genealogies, but assume independence of these distributions between generations—that is, an individual’s reproductive behavior is independent to that of his or her father or mother. The relative impact of reproductive correlation on the real genealogies should be reflected in the degree of difference between the distributions of descendants per ancestor in the real and simulated genealogies. Simulations were performed 5,000 times for each cohort of matrilineal and patrilineal ancestors.

Tables 5 and 6 present the expected distributions of descendants from the simulations and the observed distributions from the real genealogies for the 1848–1892 and 1698–1742 ancestor cohorts, respectively. A statistical evaluation by means of a χ² test reveals highly significant differences between the distributions of descendants per ancestor from the real and simulated genealogies for all ancestor cohorts. In each case, an excess of ancestors with few or many descendants, and a deficit of ancestors with intermediate numbers of descendants, is observed in the real genealogies. Accordingly, the variance in the number of descendants per ancestor is greater in the real genealogies than in the simulated genealogies. For 5,000 simulations of three out of four ancestor cohorts, we never observe a variance greater than or equal to that obtained from the corresponding real genealogies. Only in the case of the patrilineal 1698–1742 cohort do we obtain a minority of cases (139/5,000) where simulations yield greater variances than the real genealogies.

Table 5.

Observed Distributions of Descendants per Ancestor Compared with Simulation-Based Expectations: 1848–1892^a

	Matrilines		Patrilines
	ExpectedValue	ObservedValue	ExpectedValue	ObservedValue
Frequency by no. of descendants:
1–2	.1984	.2284	.2377	.2492
3–4	.1808	.1907	.2054	.2098
5–6	.1439	.1379	.1539	.1505
7–8	.1118	.1024	.1126	.1078
9–10	.0862	.0780	.0817	.0795
11–12	.0662	.0557	.0589	.0541
13–16	.0893	.0751	.0729	.0694
17–20	.0522	.0493	.0377	.0350
21–30	.0534	.0540	.0320	.0334
31–max	.0178	.0285	.0072	.0114
Total no. of ancestors	35,205,000	7,041	41,375,000	8,275
χ2 p		0		0
Variance	54.77	71.70	36.91	41.75
Variance pb		0		0

^aCoalescent genealogies were simulated 5,000 times from each set of ancestors.

^bThe proportion of times, in 5,000 simulations, in which the variance of descendants per ancestor in the simulated genealogies was at least as great as that in the observed genealogical data.

Table 6.

Observed Distributions of Descendants per Ancestor Compared with Simulation-Based Expectations: 1698–1742^a

	Matrilines		Patrilines
	ExpectedValue	ObservedValue	ExpectedValue	ObservedValue
Frequency by no. of descendants:
1–5	.1466	.1777	.1672	.1840
6–10	.1359	.1549	.1503	.1495
11–15	.1164	.1165	.1252	.1221
16–25	.1810	.1630	.1882	.1840
26–35	.1271	.1202	.1257	.1151
36–45	.0892	.0715	.0834	.0807
46–60	.0848	.0752	.0743	.0726
61–80	.0603	.0560	.0481	.0495
81–125	.0462	.0420	.0316	.0360
126–max	.0123	.0229	.0059	.0065
Total no. of ancestors	6,780,000	1,356	9,295,000	1,859
χ2 p		0		0
Variance	795.86	1,274.31	586.42	661.79
Variance pb		0		.0278

^aCoalescent genealogies were simulated 5,000 times from each set of ancestors.

^bThe proportion of times out of 5,000 simulations in which the variance of descendants per ancestor in the simulated genealogies was at least as great as that in the observed genealogical data.

These differences between the simulated and real genealogies demonstrate the cumulative effect of intergenerational correlation in fertility on the real genealogies. In accordance with the stronger matrilineal correlation reported in table 4, this cumulative effect is greater in matrilines. Furthermore, even though the reported correlation between two consecutive generations is relatively weak, the cumulative effects over many generations can be substantial—as demonstrated by the marked differences between the real and simulated genealogies across only 268 years that separate the 1698–1742 matrilineal ancestor cohort from its contemporary descendants (table 6).

It should be noted that a temporal autocorrelation of offspring numbers and generation intervals was detected in the simulated genealogies (see table 7). This temporal autocorrelation is caused by sociohistorical changes in reproductive behavior, namely the decline in generation intervals (see fig. 6) and average offspring numbers (data not shown) in Iceland during the past 300 years. As the simulated genealogies are produced from the same series of offspring and generation interval distributions as the real genealogies, it follows that the correlation coefficients reported for the real genealogies (table 4) must also be partially due to temporal autocorrelation (obviously, no temporal autocorrelation was observed when genealogies were simulated by use of fixed distributions of offspring numbers and generation intervals for each consecutive year).

Table 7.

Intergenerational Correlation (r) of Reproductive Behavior in the Simulated Genealogies^a

	Ancestor Cohort
	1848–1892		1698–1742
DemographicFactor andStatistic	Matrilines	Patrilines	Matrilines	Patrilines
No. of offspring:
Mean r	.006	.009	.025	.021
SD	.0044	.0047	.0043	.0040
pb	0	0	0	0
Generation interval:
Mean r	.053	.014	.084	.048
SD	.0049	.0057	.0047	.0043
pb	.927	.047	.998	.954

^aCorrelation coefficients were estimated using the same set of 5,000 simulations presented in tables 5 and 6.

^bThe proportion of times correlation coefficients, r, from 5,000 simulations are at least as great as those estimated from the real genealogies (see table 4).

In the case of temporal autocorrelation, an individual’s reproductive behavior is dependent not on that of his or her parent per se but on the sociohistorical norms governing reproduction at that particular point in time. A temporal autocorrelation is therefore distinct from an intergenerational correlation, where contemporaneous individual differences in reproductive behavior are dependent on parental differences in reproductive behavior (this cannot occur in the simulated genealogies). Table 7 shows that the real genealogies exhibit a significantly greater intergenerational correlation in offspring numbers than the simulated genealogies, demonstrating the existence of a true parent-offspring correlation (in addition to temporal autocorrelation) in the real genealogies. In contrast, the correlation observed for generation intervals in the real genealogies appears to be solely caused by temporal autocorrelation. In fact, the simulated genealogies tend to yield overestimated temporal autocorrelation for generation intervals, a finding that is likely to reflect the fact that the underlying stochastic model does not take into account that parents with large numbers of offspring tend to also exhibit a greater than average variance in generation intervals (because reproduction takes place over a longer period of time).

Discussion

Rate and Pattern of Evolution in Matrilines and Patrilines

The analysis of matrilineal and patrilineal genealogies has revealed fine details of the demographic processes that have shaped patterns of genetic diversity in the Icelandic mtDNA and Y-chromosome pools during the past 300 years. Tracing lineages back from all Icelanders born after 1972 over the same period of time, we find relatively fewer matrilineal ancestors than patrilineal ancestors. Accordingly, matrilineal ancestors contribute, on average, a larger number of descendants than patrilineal ancestors. Moreover, the variance in the number of descendants is higher among matrilineal ancestors. In short, matrilines appear to be evolving at a faster rate than patrilines. These genealogical differences have a decisive impact on the fate of mtDNA or Y-chromosome haplotypes that were present in the ancestral cohorts, as the faster rate of matrilineal drift will translate into a faster evolutionary rate of mtDNA haplotypes. Hence, mtDNA haplotypes have had both a greater probability for rapid expansion in the Icelandic gene pool and a greater probability to be lost. The key demographic factor underlying the faster rate of matrilineal drift in Iceland is the 10% shorter matrilineal generation interval. A slightly higher matrilineal intergenerational correlation in offspring numbers and generation intervals is also a significant contributing factor. However, reproductive variance within generations is almost identical for matrilines and patrilines and therefore does not account for the faster evolutionary rate of matrilines. These results challenge the widespread assumption that Y chromosomes should exhibit a faster evolutionary rate because of greater reproductive variance among males (Cavalli-Sforza and Bodmer 1971; Seielstad et al. 1998; Avise 2000).

It is informative to compare the results from the Icelandic genealogies to expectations from a simple and well-known model like the Wright-Fisher demographic model. Simulating matrilineal or patrilineal genealogies 10,000 times under this model, with an effective population size of 1,000 individuals, we compare the expected number of generations of evolution needed to obtain a variance and coefficient of variation of descendants per ancestor greater than or equal to those observed in the real genealogies (see table 1). In the case of patrilines from the 1848–1892 and 1698–1742 ancestor cohorts, no less than 13 and 52 generations, respectively, are needed to generate greater variances by use of the Wright-Fisher model (the actual number of patrilineal generations were 3.8 and 7.9, respectively). For matrilines, 17 and 74 generations are needed, respectively (the actual number of matrilineal generations were 4.3 and 8.8, respectively). A comparison of coefficients of variation reveals that the Wright-Fisher model exceeded the 1848–1892 patrilineal ancestor cohort after 25 generations, but did not do so within the time of 100 generations in the case of the other ancestor cohorts.

Overall, then, our findings indicate a considerable effect of genetic drift on the matrilineal and patrilineal genealogical pathways of mtDNA and Y-chromosome haplotypes in Iceland during the past 300 years. This is in spite of a rapid population expansion during this period, which would be expected to yield less drift than the constant population size Wright-Fisher demographic model. We note that alleles at autosomal loci would also be affected by such an accelerated rate of genetic drift, and this may partially account for the unusual allele frequencies observed in Iceland at loci such as PAH (Guldberg et al. 1997) and BRCA2 (Barkardóttir et al. 2001). In general, our results suggest that Icelanders will tend to carry a reduced number of alleles or haplotypes at autosomal loci, relative to larger and less isolated European populations, and that alleles and haplotypes rare elsewhere may have expanded to polymorphic frequencies in Icelanders.

We have identified two different forms of intergenerational correlation in reproductive behavior that have influenced the structure of Icelandic matrilineal and patrilineal genealogies. The first is a temporal autocorrelation, wherein the reproductive behavior of an individual is dependent on his or her year of birth. This can be caused by historical demographic trends—for example, a populationwide decline or increase in fertility over time. The second is a parent-offspring correlation, wherein an individual’s reproductive behavior is to some extent dependent on that of his or her parent and consistent with a parental environmental influence on the reproductive behavior of offspring. A third type of intergenerational correlation could be described as lineage dependency, wherein there is a genetic influence of the transmitted lineage on the reproductive behavior of its bearer and where natural selection is in part responsible for the rate of expansion or loss of these lineages. As discussed below, we do not find evidence for lineage dependency in Icelandic matrilines or patrilines, although a weak effect cannot be ruled out. The dissection of an overall intergenerational correlation of reproductive behavior into its underlying components can be stated explicitly for coalescent genealogical data and we present the formulaic details for an intergenerational correlation of offspring numbers in appendix B.

Potential Biases and Estimates of the Total Number of Icelandic Matrilineal and Patrilineal Ancestors

We note that biases in the recording of genealogical data are unlikely to underlie the differences observed in this study between the evolutionary rates of matrilines and patrilines. First, the same kind of differences are observed for lineages traced back to the 1698–1742 ancestor cohort (with more complete information about patrilines) as in the case of lineages traced back to the 1848–1892 ancestor cohort (with slightly more complete information about matrilines). Second, even with 29% and 38% of contemporary individuals unlinked to patrilineal and matrilineal ancestors, respectively, in the 1698–1742 cohort, the number of linked individuals is sufficiently large to make sizeable biases in the underlying demographic factors (i.e., offspring numbers, generation intervals, and reproductive correlation) very unlikely. As false paternity is typically more common in genealogical records than false maternity, this could represent another potential biasing factor in our analyses. However, the direction of such a bias is not clear. If there is a small set of true fathers that are responsible for a large portion of false paternities, then the genealogical data would tend to underestimate reproductive variance within patrilines. A systematic bias in the opposite direction could also be envisaged, leading to an overestimate of patrilineal reproductive variance. Significantly, if false paternities are attributable to a random set of true fathers (arguably the most likely situation), then patrilineal reproductive variance is overestimated in the genealogical database, thereby increasing the true difference in evolutionary rates between matrilines and patrilines. The current rate of false paternities in Iceland is relatively small, estimated at 1.49% per generation on the basis of genotype data analyzed by deCODE Genetics (this estimate includes laboratory handling error).

An issue related to the discussion of potential biases in genealogical data is the question of whether it is possible to provide reasonable estimates for the total number of ancestors in the 1848–1892 and 1698–1742 cohorts, effectively by approximating the number of additional ancestors that would be required to account for all those individuals in the contemporary cohort that could not be traced to ancestors in these cohorts. This problem is not at all straightforward, in that it touches on possible biases in the way genealogical data has been recorded in the genealogical database. Thus, it could be that many presently unlinked contemporary individuals will eventually be traced to existing ancestors—in which case, the total number of ancestors will not increase, leading to an increase in the average number of descendants per ancestor. Alternatively, presently unlinked contemporary individuals may be primarily descended from ancestors not yet identified—in which case, the total number of ancestors will increase, leading to a decrease in the average number of descendants per ancestor.

A comparison of the results presented here with those of equivalent analyses (Helgason 2001), performed on two years older version of the deCODE Genetics genealogical database is informative for this issue. In this study an average of 24.3 contemporary females were traced to matrilineal ancestors (23,936/985) and 22.3 males to patrilineal ancestors (35,233/1,579) in the 1698–1742 cohort. Equivalent figures for the 1848–1892 ancestor cohort were 7.6 for matrilines (52,066/6,873) and 6.4 for patrilines (51,472/8,068). A comparison of these figures with those from table 1 reveals not only that there has been a substantial increase in the overall number of contemporary individuals traced to ancestors, but also that in each case the average number of descendants per ancestor has increased. Accordingly, it seems reasonable, perhaps even conservative, to extrapolate the average number of descendants per ancestor reported in table 1 to the entire contemporary cohort, with the result that all 64,150 contemporary females could be descended from 7,677 (24.1%) matrilineal ancestors from the 1848–1892 cohort and only 2,196 (10.7%) ancestors from the 1698–1742 cohort. In comparison, all 66,910 contemporary males could be descended from 9,598 (30.3%) and 2,628 (14.6%) patrilineal ancestors from the same ancestor cohorts, respectively. This necessarily implies a smaller number of matrilineal and patrilineal ancestors at the time Iceland was settled 1,100 years ago—perhaps only a few hundred.

Genetic Evidence of Evolutionary Rates in Icelandic mtDNA and Y-Chromosome Pools

Previous studies have noted that the frequency spectra of mtDNA and Y-chromosome haplotypes in Icelanders indicate genetic divergence from source populations of Scandinavia and the British Isles caused by random genetic drift (Helgason et al. 2000a, 2000b, 2001). The following discussion is based on mtDNA haplotypes defined by sequence variation between sites 16055–16390 in the first hypervariable segment of the control region and Y-chromosome haplotypes defined by variation at biallelic loci 92R7, M9, SRY-1532, YAP, TAT, and microsatellite loci DYS19, DYS390, DYS391, DYS392, and DYS393 (Helgason et al. 2000a, 2000b, 2001). No fewer than 29 of 117 Icelandic mtDNA haplotypes (N=467) have a frequency >1%, and 11 of these were not found in samples from Scandinavia (N=539) and the British Isles (N=749). In the case of Y-chromosome haplotypes, there were 21 of 50 Icelandic haplotypes with a frequency >1%, but only 3 were not found in the same source populations (Iceland, N=181; Scandinavia, N=233; and the British Isles, N=283). There were a total of 442 mtDNA haplotypes in samples from Scandinavia or the British Isles, of which 18 have a frequency >1% in one or both populations. Five of these mtDNA haplotypes were not observed in the Icelandic sample. In the case of Y chromosomes, there were a total of 127 haplotypes observed in the source populations, of which 29 had a frequency of >1% in one or both populations; 10 of these were not found in Icelanders.

Thus, on the one hand, the genetic data indicate that a greater number of initially rare mtDNA haplotypes have drifted to high frequencies than is the case for Y chromosomes. On the other hand, a similar proportion of common mtDNA and Y-chromosome haplotypes appear to have either been lost from the Icelandic gene pool or were not among the founding lineages. Using mtDNA and Y-chromosome haplotypes from contemporary individuals (Helgason et al. 2000a, 2000b; Sigurðardóttir et al. 2000) along with the encrypted genealogies, we were able to determine many of the haplotypes carried by matrilineal and patrilineal ancestors from the 1698–1742 cohort. Tables 8 and 9 show the numbers of ancestors identified as carriers of the most common Icelandic haplotypes.

Table 8.

mtDNA Haplotypes at >1% Frequency in Icelanders^[Note]

		Frequency of Haplotype
HVS1 Sequence Motif	Haplogroup	Iceland	ScotlandandIreland	Norway	No. of Ancestors with Haplotype	TotalNo. ofDescendantswithHaplotype	AverageNo. ofDescendantswithHaplotype	MaximumNo. ofDescendantswithHaplotype
Anderson	H	9.90	16.42	20.22	34	2,105	61.9	372
16129A	H	5.58	.80	.74	13	784	60.3	179
16126C 16188T 16257T 16294T 16296T	T	4.57	0	0	11	803	73	392
16069T 16126C	J	4.57	6.81	4.64	11	595	54.1	145
16224C 16311C	K	4.31	2.14	1.86	10	828	82.8	238
16249C 16311C	H	3.81	0	.19	14	659	47.1	113
16129A 16239T	H	2.28	0	0	6	529	88.2	231
16129A 16223T 16391A	I	2.28	2.67	.93	3	78	26	44
16304C 16305G	H	2.28	0	0	4	225	56.3	78
16224C 16311C 16320T	K	2.03	.53	.37	7	646	92.3	244
16311C	H	2.03	1.20	1.11	6	272	45.3	89
16192T 16256T 16270T 16291T 16294T	U5	2.03	0	0	6	269	44.8	108
16167T 16274A 16304C	H	2.03	0	0	5	208	41.6	84
16093C	H	1.78	.40	.19	2	149	74.5	139
16356C	U4	1.78	.80	1.67	10	266	26.6	95
16069T 16126C 16145A 16172C 16192T 16222T 16261T 16362C	J	1.78	0	0	4	212	53	103
16093C 16126C 16153A 16294T	T	1.52	0	0	5	315	63	156
16126C 16153A 16294T	T	1.52	0	.93	3	185	61.7	87
16189C 16343G 16390A	U5	1.52	0	0	7	543	77.6	142
16189C 16223T 16278T	X	1.52	.40	0	3	123	41	85
16069T 16126C 16145A 16172C 16222T 16261T	J	1.52	.67	.74	3	247	82.3	132
16129A 16172C 16223T 16311C	I	1.27	.53	0	2	167	83.5	118
16239G	H	1.27	.27	0	1	18	18	18
16069T 16126C 16145A 16172C 16192T 16222T 16261T	J	1.27	2.00	.93	5	186	37.2	76
16069T 16126C 16193T	J	1.27	.27	.00	7	371	53	102
16124C 16298C 16362C	V	1.02	.00	.00	3	246	82	136
16126C 16294T	T	1.02	.80	.56	3	64	21.3	32
16129A 16223T 16311C	I	1.02	.00	.00	4	70	17.5	37
16183C 16189C	H	1.02	.00	.00	4	107	26.8	42

Note.— HVS1 sequence motifs were identified for a total of 277 ancestors in the 1698–1742 cohort, who together account for 15,437 females in the contemporary cohort. Thus, matrilineal ancestors whose haplotypes could be identified had, on average, 55.73 descendants. Haplotypes of each ancestor were determined on the basis of haplotypes from 1 to 11 descendants. It was then assumed that all descendants carried the same haplotype as their ancestor.

Table 9.

Y-Chromosome Haplotypes at >1% Frequency in Icelanders^[Note]

		Frequency of Haplotype
Y-Chromosome Haplotype	Haplogroup	Iceland	ScotlandandIreland	Scandinavia	No. ofAncestorswithHaplotype	TotalNo. ofDescendantswithHaplotype	AverageNo. ofDescendantswithHaplotype	MaximumNo. ofDescendantswithHaplotype
0 0 1 0 0 13 11 10 14 23	2	20.99	3.53	12.45	26	1278	49.15	191
1 1 1 0 0 13 13 11 14 24	1	12.71	16.25	6.01	12	518	43.17	76
1 1 0 0 0 13 11 11 15 25	3	11.60	.71	4.72	11	511	46.45	110
1 1 1 0 0 13 12 10 13 23	1	4.42	0	0	5	299	59.80	101
1 1 1 0 0 13 13 11 14 25	1	3.87	5.65	1.29	3	250	83.33	224
1 1 0 0 0 13 11 10 15 25	3	3.31	.35	.86	3	110	36.67	53
1 1 0 0 0 13 11 11 16 25	3	3.31	.35	1.72	2	138	69.00	80
1 1 1 0 0 13 13 10 14 24	1	3.31	13.78	3.00	3	144	48.00	69
1 1 1 0 0 13 13 11 14 23	1	3.31	6.01	2.15	3	92	30.67	35
0 0 1 0 0 13 11 10 14 22	2	2.21	1.41	11.16	3	193	64.33	125
1 1 1 0 0 13 12 11 13 23	1	2.21	0	.86	1	68	68.00	68
0 0 1 0 0 13 11 10 16 23	2	1.66	0	.43	1	185	185.00	185
0 0 1 0 0 15 12 10 15 23	2	1.66	1.41	.43	2	47	23.50	39
1 1 1 0 0 13 14 11 14 25	1	1.66	8.13	.43	2	12	6.00	7
0 0 1 0 0 13 11 10 14 24	2	1.10	.00	1.72	2	73	36.50	42
1 1 0 0 0 13 11 10 16 25	3	1.10	.00	1.72	2	66	33.00	40
1 1 0 0 0 13 11 11 15 24	3	1.10	.00	.86	1	36	36.00	36
1 1 1 0 0 13 13 10 13 24	1	1.10	0	0	1	40	40.00	40
1 1 1 0 0 13 13 10 14 23	1	1.10	3.89	1.72	1	12	12.00	12
1 1 1 0 0 13 13 11 14 26	1	1.10	.35	.43	1	121	121.00	121
1 1 1 0 0 13 13 9 14 23	1	1.10	0	0	1	30	30.00	30

Note.— Y-chromosome haplotypes were defined by combining alleles at the loci 92R7, M9, SRY1532, TAT, YAP, DYS393, DYS392, DYS391, DYS19, and DYS390 and were identified for a total, in the 1698–1742 cohort, of 106 patrilineal ancestors, who together account for 5,412 males in the contemporary cohort. Thus, patrilineal ancestors whose haplotypes could be identified had, on average, 51.06 descendants. The haplotypes of each ancestor were determined on the basis of haplotypes from 1 to 11 descendants. It was then assumed that all descendants carried the same haplotype as their ancestor.

In general, mtDNA or Y-chromosome haplotypes that are more frequent in Iceland than in either source population are likely to have been inherited from ancestors that have, through the effects of random genetic drift, contributed more than an average number of matrilineal or patrilineal descendants to the contemporary Icelandic gene pool. If we arbitrarily define potential expansion haplotypes as those whose frequency in Iceland is at least 1% greater than in either source population, then it emerges that matrilineal ancestors carrying such mtDNA haplotypes contribute, on average, 61.3 descendants, compared with an average of 55.7 descendants for all ancestors assigned an mtDNA haplotype. Equivalent numbers for patrilineal ancestors and Y-chromosome haplotypes are 52.1 and 51.1 descendants, respectively. A prime example of rapid lineage expansion in the Icelandic gene pool is presented by the third most common mtDNA haplotype (sequence motif 16126C, 16188T, 16257T, 16294T, 16296T). This haplotype has not yet been observed in the source populations from Scandinavia and the British Isles and, to date, has been encountered only once in a database of >8,000 European mtDNA sequences (in a German sample; see Pfeiffer et al. 1999). According to our data, this lineage has undergone considerable expansion in the Icelandic gene pool during the past 300 years, with 11 matrilineal ancestors born between 1698 and 1742 contributing 803 female contemporary descendants (including 1 ancestor who contributed the maximum 392 matrilineal descendants).

Two lines of evidence support the conclusion that the observed fluctuation of haplotype frequencies is primarily due to random genetic drift, rather than positive selection. First, the ancestors who contribute the greatest number of descendants have different haplotypes that belong to a variety of different haplogroups (see tables 8 and 9). Second, the haplotypes carried by these ancestors are also carried by ancestors who contribute relatively few descendants. Thus, we suggest that the intergenerational correlation in fertility observed for both matrilines and patrilines derives from the social transmission of reproductive behavior (Skolnick et al. 1976; Austerlitz and Heyer 1998), rather than from selection based on the fitness of the haplotypes themselves.

General Implications

A higher generational turnover in matrilines has implications for our understanding of the differential impact of the sexes on the recombinant reshuffling of chromosomes as they are transmitted through genealogies. Previous studies have reported higher rates of recombination in chromosomes transmitted from females (Yu et al. 2001; Kong et al. 2002). Consequently, a mutation transmitted from an ancestor through a series of daughters passes through a greater number of meioses, and its chromosomal background is subject to more numerous recombination events per meiosis than is the case for the same mutation passed on the same number of years through a chain of sons. In other words, the power to detect a particular mutation, either by linkage or by association, will be greatest when the mutation has been transmitted exclusively through a patrilineal genealogical path and will be smallest when the mutation has been transmitted exclusively through a matrilineal genealogical path. Although the genealogical pathways of particular chromosomal segments will typically be unknown to researchers, we note that our findings lead to a greater expected variance in the size of shared segments surrounding mutations than would be predicted if there were no differences between matrilineal and patrilineal genealogies.

The generation interval is a crucial parameter used to scale mutation-time age estimates of genetic variants into years. One recent study estimated the age of the most recent common ancestor (MRCA) of human mitochondria (Mitochondrial Eve) as 171,500 years, on the basis of a 20-year generation interval (Ingman et al. 2000). Another study estimated the age of the MRCA of human Y chromosomes as 59,000 years, on the basis of a 25-year generation interval (Thomson et al. 2000). Most empirical studies support the use of a longer generation interval for Y chromosomes (Murdock and White 1969). However, it is questionable whether 20 and 25 years are appropriate intervals for matrilines and patrilines, respectively. Genealogical estimates in this study and that of Tremblay and Vézina (2000) indicate that 30 and 35 years may be more suitable. These estimates from genealogical data are broadly consistent with demographic data from hunter-gatherer populations such as the !Kung, whose females have an average age at first birth of 20 years and average age at last birth of 31 years—implying a matrilineal generation interval of about 25 years (Howell 2000). Husbands are typically 6–13 years older than wives—implying a patrilineal generation interval of 31–38 years. It is not known whether !Kung hunter-gatherers are representative of Paleolithic demography that takes up most of the period from the present and back to the MRCAs for mtDNA and Y chromosomes. However, the fact that generation intervals in such culturally different groups as the !Kung, Icelanders, and French Canadians are greater than those typically used to estimate the ages of MRCAs indicates that the aforementioned ages of the MRCAs for mtDNA and Y chromosomes could be underestimated by 25%–50%. Given that the !Kung demographic data suggests that patrilineal generation intervals are generally underestimated more than those of matrilines, it follows that estimates for the age of MRCA for Y chromosomes will be underestimated to a greater extent than for mtDNA.

Also significant for appropriate scaling of mutation-time age estimates is the issue of parent-offspring correlated reproductive behavior, which was identified in Icelandic matrilineal and patrilineal genealogies and may be universal features of human demography (see also Nei and Murata 1966; Austerlitz and Heyer 1998). Obviously, if such correlations derive from differential fitness attributable to mtDNA or Y-chromosome haplotypes, then the correlated genealogical process is one of natural selection. However, an equally plausible explanation may be the cultural transmission of reproductive behavior (Austerlitz and Heyer 1998) or the social inheritance of particular living conditions. In this case, the correlated genealogical process is best described as enhanced genetic drift. A failure to take an intergenerational correlation in fertility into account when scaling mutation time into years will yield overestimates of the time to the MRCA. Thus, for example, under the neutral model it is generally assumed that the ages of mutations are reflected by their frequencies. One consequence of an intergenerational correlation in reproductive behavior is that alleles can reach high frequencies at a much faster rate than under the neutral model.

Thus, in the presence of intergenerational correlation, application of the neutral model is likely to yield overestimates of the ages of mutations. As in the Icelandic genealogies, both Nei and Murata (1966) and Austerlitz and Heyer (1998) reported a higher matrilineal than patrilineal correlation of fertility. Consequently, the ages of mtDNA mutations may be subject to relatively more overestimation than in the case of Y chromosomes. We note that consideration of these demographic differences between matrilines and patrilines would reduce the discrepancy observed between the 171,500 years age of “mitochondrial Eve” (Ingman et al. 2000) and the mere 59,000 years age of “Y-chromosome Adam” (Thomson et al. 2000).

Of course, cross-cultural variability in demographic factors—such as polygyny (which increases male reproductive variance but also increases the age difference between husbands and wives) or high male mortality due to warfare—could counteract the effects of shorter matrilineal generation intervals and stronger intergenerational correlation. Accordingly, rates of matrilineal and patrilineal evolution may vary between populations and different periods in the history of the same population. Further genealogical studies in other populations are needed to determine the generality of our findings. The potential evolutionary consequences of the differences observed between matrilines and patrilines in Iceland, along with reported cytogenetic sex differences in mutation and recombination rates (Brinkmann et al. 1998; Yu et al. 2001; Kong et al. 2002), underscore the importance of paying more attention to the disparate genetic legacy of the sexes.

Appendix A: A Stochastic Model Describing the Number of Matrilineal or Patrilineal Descendants That Derive from a Single Ancestor

Let τ be the time between the birth of an ancestor and the starting time of the contemporary cohort, and let Δτ be the time length of the contemporary cohort. For each ancestor, let N_k be the number of descendants born in the kth generation. Let H_k be the number of descendants in the kth generation that are born before the end of the contemporary cohort, that is, before time τ + Δτ. Let Q_k be the number of descendants in the kth generation that are born in the contemporary cohort, that is, born between time τ and Δτ. Further, let N_k,i be the number of offspring of the ith individual of the H_k−1 individuals from the (k−1)th generation. The N_k,i variables are assumed to be independent and have the same distribution for a given generation k, but the distribution can vary between generations.

Let T_k be the generation time interval between the birth of a parent in the (k−1)th generation and that of a daughter or son in the kth generation. Let p_k be the probability that an individual in the kth generation is born before time τ + Δτ, given that his or her parent is born before time τ + Δτ, that is,

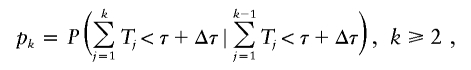and p₁=P(T₁<τ+Δτ). Let r_k be the probability that an individual in the kth generation is born in the contemporary cohort given that he or she is born before time τ + Δτ, and that his or her parent is born before time τ + Δτ, that is,

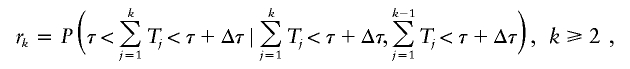and r₁=P(τ<T₁<τ+Δτ∣T₁<τ+Δτ). The T_k variables are assumed to be independent, but can have varying distributions in different generations. The distribution of a sum of T_k variables can be easily computed using convolution when the distributions for the T_k variables are independent, discrete, and finite.

The model can be stated as follows.

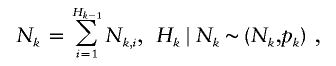The number of descendants in the contemporary cohort, denoted by M, is then the sum

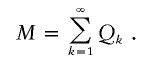Note that because the model generates coalescent genealogies N_k,i⩾1. However, depending on Δτ (the time length of the contemporary cohort) it is possible for M=0. This can occur when an individual born before the start of the contemporary cohort only has children born after the end of the contemporary cohort. With the overall timespan and Δτ used in this study the probability of M=0 is very small.

For the sake of simplicity and intelligibility the model makes use of distributions for N_k,i and T_k (estimated from the real genealogies) for each successive generation, k, from a cohort of ancestors. Because of variation in the length of generation intervals (T_k), individuals separated from their ancestors by the same number of generations can have very different birth years. Such temporal discordance is not problematic, providing that the distributions for N_k,i and T_k are relatively stable over time. However, in cases where distributions for N_k,i and T_k change markedly over time, the generation-time approach adopted in the stochastic model will result in a smoothing out of such temporal demographic differences. While this does not affect the simulation of M and other random variables of the model, it can artificially amplify or reduce the level of temporal autocorrelation in reproductive behavior caused by such demographic trends.

The present study and previous work (Jónsson and Magnússon 1997) demonstrate that the reproductive behavior of Icelanders has changed during the past 150 years. Hence, to obtain accurate assessments of temporal autocorrelation in reproductive behavior, we chose to simulate coalescent genealogies on the basis of the stochastic model using N_k,i and T_k distributions based on birth years of parents and their offspring, respectively (as opposed to the number of generations from ancestors). For each iteration of the simulation, the model variables N_k, H_k, Q_k, and M were generated, and the intergenerational sample correlation for offspring numbers and generation intervals was calculated for comparison with parameter estimates obtained from the real coalescent genealogies.

Appendix B: Calculation of Intergenerational Correlation of Offspring Numbers from the Parameters of the Stochastic Model

Let N_p and N_o denote the number of offspring of a parent and his or her offspring, respectively. The intergenerational correlation, denoted by ρ_po, is defined as the correlation between N_p and N_o—that is,

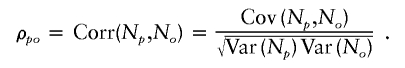The means and the variances of N_p and N_o are assumed to be equal. Let I be a random variable denoting a coalescent genealogy from a randomly selected ancestor. The index i denotes the ith such coalescent genealogy. Let μ_i and σ²_i denote the overall mean and variance of N_p and N_o within the ith coalescent genealogy—that is, μ_i=E(N_p∣I=i)=E(N_o∣I=i) and σ²_i=Var(N_p∣I=i)=Var(N_o∣I=i). The variance of N_p (and N_o) is

where σ²_μ=Var(μ_I) is the variance of the means of N_p within coalescent genealogies and σ²₀=E(σ²_I) is the expected value of the variances of the N_p within coalescent genealogies. The covariance between N_p and N_o is

where Cov{E(N_p∣I),E(N_o∣I)}=Cov(μ_I,μ_I)=σ²_μ and E{Cov(N_p,N_o∣I)} is the expected value of the intralineage covariance within coalescent genealogies. Let K denote a randomly selected generation. Let N_K denote the number of offspring of a parent in the Kth generation. By splitting Cov(N_p,N_o∣I) into an expectation over generations within the Ith genealogy, we have

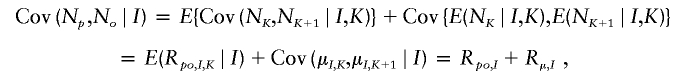where R_po,I,K=Cov(N_K,N_K+1∣I,K), R_po,I=E(R_po,I,K∣I) and R_μ,I=Cov(μ_I,K,μ_I,K+1∣I). Further, let R_po=E(R_po,I), and let R_μ=E(R_μ,I). The term R_po represents the direct parent-offspring covariance, and R_μ is an auto-covariance in the means of N_p and N_o across generations. The expectation of Cov(N_p,N_o∣I) becomes E(R_po,I+R_μ,I)=R_po+R_μ and, finally,

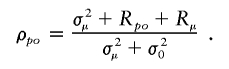The term σ²_μ is expected to be zero if offspring numbers are independent of the lineage carried by parents (i.e., no lineage dependence). Simulations based on the stochastic model (appendix A) necessarily yield σ²_μ=0 and R_po=0, because the number of offspring attributed to each individual is independent of its parent and lineage. The correlation that was observed in the simulations must therefore be due to temporal autocorrelation, that is R_μ. Hence, the intergenerational correlation of offspring numbers in the stochastic model becomes ρ_po=R_μ/σ²₀. The statistically significant excess of ρ_po in the real matrilineal and patrilineal genealogies demonstrates that, in reality, σ²_μ>0 and/or R_po>0.