Abstract
Recombination rates vary both across the genome and between different species, but little information is available about the temporal and physical scales over which such rates change. To shed light on these questions, we performed a high-resolution analysis of a genomic region within the β-globin gene cluster that is known to experience elevated recombination rates in humans. For this purpose, we developed new linkage disequilibrium–based methods that thoroughly search for subsets of the data with unusually high or unusually low estimated values of the population-recombination parameter (4Nr, where N is the effective population size and r is the crossover rate between adjacent base pairs). By resequencing a 15-kb segment in a human population sample, we were able to narrow the recombinational hotspot to a segment <2 kb in length that coincides with the β-globin replication origin. In addition, we analyzed the orthologous region in samples of rhesus macaques and common chimpanzees. Whereas the analysis of the chimpanzee data is complicated by the sample structure, the macaque data imply that this region may not be a hotspot in that species. These results suggest a time scale for the evolution of hotspots in primates. Furthermore, they allow us to propose diverged sequence elements that may contribute to the differences in the recombinational landscape in the two species.
Introduction
Recombination rates are known to change both across the genome (Ashburner 1989; True et al. 1996; Broman et al. 1998; Yu et al. 2001; Kong et al. 2002) and between different species (True et al. 1996; Rogers et al. 2000), but little specific information is available about the temporal and physical scales over which recombination rates change. Most of our knowledge about recombination-rate variation comes from comparisons between physical and genetic maps. The resolution of these studies is limited by the marker density used and the number of meioses analyzed; in humans, the average distance between markers in genetic maps is several hundred kilobases (Broman et al. 1998; Kong et al. 2002). Information about recombination-rate variation at smaller scales can be acquired either from further typing of markers in pedigrees (Smith et al. 1998; Yip et al. 1999; Badge et al. 2000) or from sperm typing (Li et al. 1988; Hubert et al. 1994; Jeffreys et al. 2000; May et al. 2002; Schneider et al. 2002). The latter has the advantage that an essentially unlimited number of meioses can be considered. The disadvantage is that it requires great cost and effort and is informative about the recombination process in male meioses only.
One alternative to the direct measurement of fine-scale recombination rates is to infer local recombination rates from patterns of linkage disequilibrium (LD). In a seminal paper, Chakravarti and colleagues (1984) used patterns of LD in the human β-globin region to infer the presence of a recombinational hotspot (i.e., a small region with recombination rates much higher than the genomewide average). Because of the sparseness of the available marker map, the putative hotspot could not be narrowed to <11 kb. This proposal was subsequently supported by experimental studies. One study mapped crossovers in three families to a 1.5-kb region that stretches from ∼900 bp 5′ of the β-globin gene to intron 2 (Smith et al. 1998), whereas a sperm-typing study estimated a recombination rate of 80 cM/Mb for an 11-kb region 5′ of the β-globin gene (Schneider et al. 2002).
Sperm-typing studies in other areas of the human genome have identified hotspots in the class II region of the major histocompatibility complex (Jeffreys et al. 2000, 2001) and the Xp/Yp pseudoautosomal region (Lien et al. 2000; May et al. 2002). In both regions, crossovers clustered into hotspots that were 1–2 kb wide (Jeffreys et al. 2000, 2001; May et al. 2002), and patterns of LD were generally consistent with the experimentally estimated recombination rates (Jeffreys et al. 2001; May et al. 2002; Li and Stephens, in press). Whereas hotspots are abundant in the yeast genome (Petes 2001), it is not known whether this extreme variation in local recombination rates is a widespread feature of the human genome or is confined to specific genomic regions. Likewise, it is not known whether hotspots are present in all eukaryotic genomes or what factors influence their rise and fall. For example, allele-specific hotspots (with the hotspot allele more likely to initiate the double-strand break [DSB]), such as those identified in yeast and humans (Nicolas et al. 1989; Jeffreys and Neumann 2002), are expected to disappear over time (Boulton et al. 1997). The fate of these hotspots is likely to be affected by a number of factors, including recombination rate, effective population size, and mating structure.
Here, we develop new LD-based techniques for estimating local recombination rates and apply them to the analysis of the full resequencing data we generated for the β-globin hotspot in humans, rhesus macaques, and common chimpanzees. The main goal is to infer the size and recombination rate of the hotspot. In particular, we use estimates of the population recombination parameter ρ (which is equal to 4Nr, where N is the effective population size and r is the recombination rate per generation) to quantify levels of LD. In population genetics, estimates of ρ are natural multilocus measures of LD (Pritchard and Przeworski 2001); if N is known, estimates of ρ can lead indirectly to estimates of the underlying recombination rates (Andolfatto and Przeworski 2000; Przeworski and Wall 2001; Wall 2001; Li and Stephens, in press). We ask the following questions: (1) How do patterns of LD and estimates of ρ in the human data compare with previous estimates (Schneider et al. 2002) of recombination rates? (2) Is there evidence for heterogeneity in recombination rates across the 11-kb region identified as a hotspot by Schneider et al. (2002)? (3) Is there evidence for an orthologous hotspot in chimpanzees and macaques?
Material and Methods
DNA Samples
Sequence variation was surveyed in DNA samples from both parents of eight Hausa nuclear families (16 unrelated individuals) from Yaounde (Cameroon); one child from each family was also surveyed to determine the phase of heterozygous sites in the parents. In addition, sequence variation was surveyed in DNA samples from 16 unrelated rhesus macaque fibroblast cell lines from the Primate Resource at the Coriell Cell Repository and from 16 unrelated common chimpanzees from the Yerkes Primate Center (kindly provided by J. C. Garza). This study was approved by the institutional review board of the University of Chicago.
PCR Amplification and Sequencing
Primers for amplifications and sequencing were designed on the basis of the GenBank sequence entry NG_000007.2. All nucleotide positions in the present article, for both human and nonhuman primate data, refer to this entry. With few exceptions, PCR primers were designed to amplify a 700–900-bp fragment with ⩾200-bp overlap between amplicons. Amplification primers were used for sequencing; additional sequencing primers were designed, adjacent to insertion/deletion polymorphisms, for nearly complete coverage in both orientations.
Primers for amplification and sequencing of the macaque samples were designed using available GenBank sequences (M18797, J00334, X05665, J00327, and AF205410). A gap of ∼800 bp and a gap of ∼5 kb were present in the reference sequence. To span these gaps, an amplification primer pair for each gap was anchored in the available sequence. Sequence was then determined for the gap by use of a chromosome walking strategy. Primers for amplification and sequencing of the chimpanzee samples were designed using available GenBank sequences (X02345, AF339363, and AF339362).
PCR products were prepared for sequence analysis by treatment with a combination of shrimp alkaline phosphatase and exonuclease I (USB). Dye-terminator sequencing was performed with the ABI Big Dye, version 3, terminator cycle sequencing kit and then analyzed on an ABI 3100 or ABI 3700 automated sequencer. All sequences were assembled and analyzed using the Phred-Phrap-Consed package (Nickerson et al. 1997). All putative polymorphisms and software-derived genotype calls were visually inspected and individually confirmed using Consed.
Haplotype Phase Determination in Humans
The haplotype phase for 84% of the 287 heterozygous genotypes in the parents of each human nuclear family could be determined by sequencing DNA from one child. For the uninformative cases, phase was assigned by allele-specific PCR (ASP) of each allele at a site in each parent. Thirty-six of the 47 heterozygous genotypes phased by ASP occurred in a single family in which the child’s data could not be used for pedigree analysis. Primer sequences and annealing temperatures are available on the Di Rienzo lab Web site.
Estimating the Population Recombination Rate (ρ)
We use both a composite likelihood method (Hudson 2001) and a summary likelihood method (Wall 2000) for estimating ρ. These methods have been shown to be more accurate than other summary methods (Wall 2000; Hudson 2001), whereas full-likelihood methods are computationally unfeasible for data sets as large as those considered in the present study (Fearnhead and Donnelly 2001). The first method calculates the likelihood of the haplotype configuration for a pair of sites and then multiplies the likelihoods over all pairs to form a composite likelihood. This method can be applied both when the phase of double heterozygotes is (assumed to be) unknown (denoted by 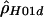 ) and when individual haplotypes have been experimentally determined (denoted by
) and when individual haplotypes have been experimentally determined (denoted by 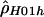 ). A program, MAXDIP, is available for calculating
). A program, MAXDIP, is available for calculating 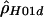 . The second method summarizes data by use of the number of distinct haplotypes (H) and the minimum number of inferred recombination events (RM) (cf. Hudson and Kaplan [1985]) and then determines, by simulation, the value of ρ that maximizes the probability of obtaining the observed summaries of the data (denoted by
. The second method summarizes data by use of the number of distinct haplotypes (H) and the minimum number of inferred recombination events (RM) (cf. Hudson and Kaplan [1985]) and then determines, by simulation, the value of ρ that maximizes the probability of obtaining the observed summaries of the data (denoted by 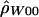 ). This method was applied only to experimentally phased data.
). This method was applied only to experimentally phased data.
We used only biallelic polymorphic sites, including both SNPs and indels, in all analyses. First, we estimated ρ using all of the data (for each species, separately); then, we estimated ρ locally using a sliding window that considered all subsets with exactly 20 contiguous polymorphic sites. A program, RECSLIDER, is available for calculating sliding-window estimates of 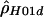 . Note that the two methods that require phase information can be used only with the human data, since phase was undetermined in the other species.
. Note that the two methods that require phase information can be used only with the human data, since phase was undetermined in the other species.
Identifying Hotspots and Coldspots
To identify potential hotspots and coldspots, we considered all possible contiguous subsets of the data and took the one with the largest number of polymorphic sites where 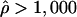 (hotspots) or
(hotspots) or 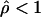 (coldspots); in this case,
(coldspots); in this case, 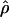 is the estimate for each whole subset. To assess the significance of putative hotspots (coldspots), we ran coalescent simulations (cf. Hudson [1983]), and tabulated the proportion of simulated data sets containing a contiguous subset that is as large or larger than the identified hotspot (coldspot) with a ρ estimate >1,000 (<1). These simulations take n=32, θ (which is equal to 4Nμ, where μ is the locuswide mutation rate per generation) equal to θW (i.e., the estimate of θ from the data using the methods of Watterson [1975]), and
is the estimate for each whole subset. To assess the significance of putative hotspots (coldspots), we ran coalescent simulations (cf. Hudson [1983]), and tabulated the proportion of simulated data sets containing a contiguous subset that is as large or larger than the identified hotspot (coldspot) with a ρ estimate >1,000 (<1). These simulations take n=32, θ (which is equal to 4Nμ, where μ is the locuswide mutation rate per generation) equal to θW (i.e., the estimate of θ from the data using the methods of Watterson [1975]), and 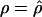 (for the whole region, as described above). We ran 2,000 replicates for each of the different estimators of ρ.
(for the whole region, as described above). We ran 2,000 replicates for each of the different estimators of ρ.
Simultaneously Estimating Multiple Recombination Rates
We generalize 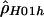 by relaxing the assumption that all base pairs have the same recombination rate. We define a hotspot to be between base pairs 68700 and 70400 (see the “Results” section) and assume that ρ/bp is constant for all sites inside the hotspot and constant for all sites outside the hotspot. We then find the values of ρ (for the hotspot and nonhotspot regions) that maximize the composite likelihood described by Hudson (2001). We call the vector of these estimates
by relaxing the assumption that all base pairs have the same recombination rate. We define a hotspot to be between base pairs 68700 and 70400 (see the “Results” section) and assume that ρ/bp is constant for all sites inside the hotspot and constant for all sites outside the hotspot. We then find the values of ρ (for the hotspot and nonhotspot regions) that maximize the composite likelihood described by Hudson (2001). We call the vector of these estimates 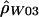 . Composite likelihood calculations were first performed over a coarse two-dimensional grid of ρ values followed by a finer grid in the region of parameter space of interest.
. Composite likelihood calculations were first performed over a coarse two-dimensional grid of ρ values followed by a finer grid in the region of parameter space of interest.
A Likelihood Approach to Assess Differences across ρ Estimates
For each of the three ρ estimation methods, we calculated the likelihood of (a summary of) the data as a function of ρ. For 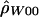 , this was straightforward: we took Pr(H,RM|ρ). For the other two, it was not completely clear how to proceed, since both are composite likelihoods. We tabulated how likely it is that simulated data have a ρ estimate near the actual estimate. For example, if
, this was straightforward: we took Pr(H,RM|ρ). For the other two, it was not completely clear how to proceed, since both are composite likelihoods. We tabulated how likely it is that simulated data have a ρ estimate near the actual estimate. For example, if 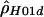 was the estimate of ρ from the actual data, and if
was the estimate of ρ from the actual data, and if 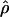 was the comparable estimate from simulations with ρ=ρ0, then we estimated
was the comparable estimate from simulations with ρ=ρ0, then we estimated 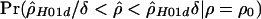 from coalescent simulations. We took a δ value of 1.15 and ran at least 2×105 replicates over a range of different ρ values. We did this for base pairs 68700–70400. Owing to computational constraints, we were unable to calculate the likelihood curve for
from coalescent simulations. We took a δ value of 1.15 and ran at least 2×105 replicates over a range of different ρ values. We did this for base pairs 68700–70400. Owing to computational constraints, we were unable to calculate the likelihood curve for 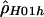 (in humans). To obtain approximate CIs, we made the standard asymptotic assumptions regarding the distribution of the likelihood ratio statistic. We caution that there is no evidence that these assumptions are valid for our analyses; nonetheless, we proceeded because the approximate CIs serve as a valuable heuristic.
(in humans). To obtain approximate CIs, we made the standard asymptotic assumptions regarding the distribution of the likelihood ratio statistic. We caution that there is no evidence that these assumptions are valid for our analyses; nonetheless, we proceeded because the approximate CIs serve as a valuable heuristic.
Results
Overview
Three overlapping segments (fig. 1) that span the putative β-globin hotspot were sequenced in each individual from samples of humans (Hausa from Cameroon), common chimpanzees, and rhesus macaques. Basic summaries of the polymorphism data are presented in table 1. We found a total of 110 biallelic mutations (103 SNPs and 7 indels) in humans, 44 (42 SNPs and 2 indels) in chimpanzees, and 38 (35 SNPs and 3 indels) in macaques. In humans, the levels of variation are almost twice as high as levels of noncoding variation in the same population sample (Frisse et al. 2001). The levels of variation in chimpanzees are higher than have been reported at other loci (Deinard and Kidd 1999; Kaessmann et al. 1999; Dufour et al. 2000; Satta 2001). However, the distribution of variation across individuals suggests that this may be due to the unintended sampling of multiple subspecies: ∼39% of the polymorphic sites are private to two chimpanzees. This is consistent with the high level of sequence divergence observed at nuclear loci among chimpanzee subspecies (A. Fischer, M. Przeworski, and S. Pääbo, personal communication). This is also consistent with the finding of mtDNA sequences typical of Pan troglodytes verus and P. t. troglodytes in samples from the Yerkes Primate Center (J. C. Garza, personal communication) and raises the possibility that some of the chimpanzees from this colony are subspecies hybrids. The level of genetic diversity in macaques is substantially smaller than in the other two species. This is consistent with what little is known about general levels of variation in macaques (Deinard et al. 2002). Full tables of all of the segregating polymorphisms are available on the Di Rienzo lab Web site.
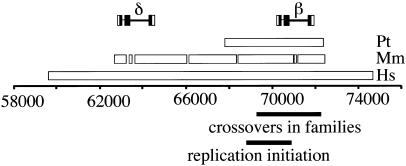
Figure 1.
Map of the region containing the β-globin hotspot with nucleotide positions numbered relative to GenBank sequence entry NG_000007.2. The segments surveyed are indicated, by species, above the line. The location of crossover breakpoints observed in family studies (Smith et al. 1998) and the location of the replication initiation origin (Kitsberg et al. 1993; Aladjem et al. 1995) are indicated below the line. Gaps in the macaque segment indicate portions that were not surveyed. “Pt” refers to chimpanzees, “Mm” to rhesus macaques, and “Hs” to humans.
Table 1.
Summary of Polymorphism Data
To quantify general levels of LD in the β-globin region, we estimated ρ for the data using three different methods. The estimates are displayed in table 2. The ρ estimate in chimpanzees is roughly comparable to the human estimates, but the estimate in macaques is more than an order of magnitude lower. This observation may be due to differences in both the species’ effective population sizes and/or their underlying recombination rates (see the “Discussion” section). Analogous results, by use of a simple model of gene conversion, can be found on the Di Rienzo lab Web site.
Table 2.
Estimates of ρ
| Species and Estimator | ρ/bp(×1,000) | ln(lik)a |
| Humans: | ||
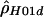
|
3.08 | −76,534.88 |
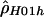
|
12.54 | −33,937.75 |
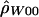
|
21.27 | −3.77 |
| Chimpanzees: | ||
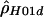
|
5.92 | −8,409.78 |
| Rhesus macaques: | ||
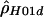
|
.17 | −12,344.81 |
“lik” refers to either the likelihood (for 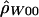 ) or the composite likelihood (for
) or the composite likelihood (for 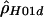 or
or 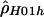 ) of the data.
) of the data.
The large differences between 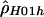 and
and 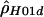 for the human data (table 2) are somewhat surprising. Both use the same composite likelihood method (Hudson 2001); they differ only in whether they utilize the phase information in double heterozygotes. We stringently rechecked our data to make sure this discrepancy was not the result of poor data quality or sampling of closely related individuals. Furthermore, no significant departures from Hardy-Weinberg equilibrium were detected. It is interesting that estimates of
for the human data (table 2) are somewhat surprising. Both use the same composite likelihood method (Hudson 2001); they differ only in whether they utilize the phase information in double heterozygotes. We stringently rechecked our data to make sure this discrepancy was not the result of poor data quality or sampling of closely related individuals. Furthermore, no significant departures from Hardy-Weinberg equilibrium were detected. It is interesting that estimates of 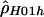 based on inferred (Stephens et al. 2001)—rather than observed—haplotypes yielded intermediate values (results not shown). We also examined various explanations for this discrepancy, including alternative models of demography or recombination (i.e., crossing over and gene conversion), but none of them could fully explain our observations (results not shown). Note that we explored a limited range of models and parameter values; thus, it cannot be excluded that more complex models and/or more extreme parameter values may explain our observation.
based on inferred (Stephens et al. 2001)—rather than observed—haplotypes yielded intermediate values (results not shown). We also examined various explanations for this discrepancy, including alternative models of demography or recombination (i.e., crossing over and gene conversion), but none of them could fully explain our observations (results not shown). Note that we explored a limited range of models and parameter values; thus, it cannot be excluded that more complex models and/or more extreme parameter values may explain our observation.
Describing the Variation in Recombination Rate along the Sequence
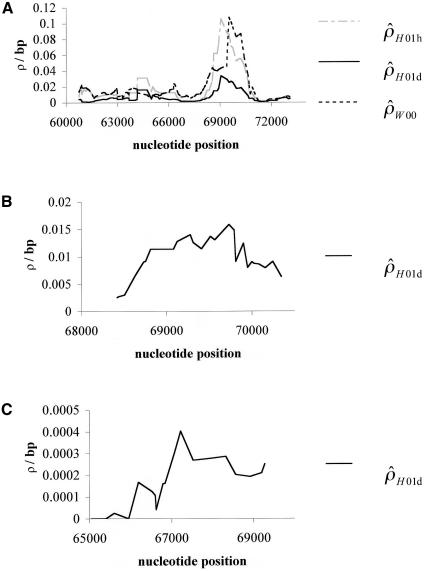
To see whether there may be variation in recombination rates across the 15-kb segment surveyed in humans, we estimated ρ using a sliding window (see the “Methods” section and fig. 2). The human data (fig. 2A) are quite dramatic, with a large peak centered around position 69500 and valleys on each side. The estimate of ρ without phase data (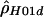 ) is substantially lower than the other two estimates for most of the sequence, but it still shows a peak in roughly the same location. Recurrent mutations at hypervariable sites, such as CpG sites, could inflate the recombination rate estimates and, if such sites were spatially clustered, could generate spurious evidence for a hotspot. However, no polymorphic CpG sites are present in the region identified as a hotspot (positions 68700–70400). Nevertheless, we repeated the analysis by omitting the polymorphic sites occurring at CpG sites; the conclusions about recombination rate variation were unaffected. The putative hotspot defined by the peak in figure 2A is just 5′ of the β-globin gene and overlaps with the region of crossover clustering that was documented by Smith et al. (1998).
) is substantially lower than the other two estimates for most of the sequence, but it still shows a peak in roughly the same location. Recurrent mutations at hypervariable sites, such as CpG sites, could inflate the recombination rate estimates and, if such sites were spatially clustered, could generate spurious evidence for a hotspot. However, no polymorphic CpG sites are present in the region identified as a hotspot (positions 68700–70400). Nevertheless, we repeated the analysis by omitting the polymorphic sites occurring at CpG sites; the conclusions about recombination rate variation were unaffected. The putative hotspot defined by the peak in figure 2A is just 5′ of the β-globin gene and overlaps with the region of crossover clustering that was documented by Smith et al. (1998).
Figure 2.
Sliding-window analyses for the human (A), chimpanzee (B), and macaque (C) β-globin data. Subsets of 20 segregating sites were plotted at their middle base position. Here, 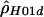 and
and 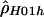 denote the diploid and haploid composite likelihood estimates, respectively, from Hudson (2001), whereas
denote the diploid and haploid composite likelihood estimates, respectively, from Hudson (2001), whereas 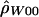 denotes the summary likelihood estimate from Wall (2000).
denotes the summary likelihood estimate from Wall (2000).
In contrast, the sliding-window plots for the other two species (fig. 2B and 2C) do not seem to have elevated ρ estimates near position 69500 and are inconclusive about recombination rate heterogeneity in the β-globin region.
Testing the Significance of Hotspots and Coldspots
It is not clear from visual inspection whether the peaks and valleys shown in figure 2A result from recombination hotspots and coldspots or whether they merely represent the chance fluctuations of the evolutionary process. To test this explicitly, we identified potential hotspots and coldspots (subsets with extremely high or extremely low ρ estimates) and then ran simulations to determine how unlikely they are under a null model with uniform recombination rates (see the “Methods” section). The results are presented in table 3. All three methods identified a human hotspot just 5′ of the β-globin gene that is significant at the .05 level. Polymorphic sites occur at approximately the same density within and outside the hotspot, which suggests that the peak in estimated recombination rate is not an artifact of heterogeneous polymorphism levels. The evidence for a coldspot is more mixed: two different regions were identified, but significance was achieved for only one of the three tests. Analogous analyses of the chimpanzee and macaque data did not identify any significant hotspots or coldspots (results not shown).
Table 3.
Identified Hotspots and Coldspots in Humans
| Method and Start bpa | End bpb | Sc |
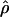 d d
|
Pe |
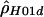 : : |
||||
| 68657 | 70226 | 12 | 1340. | .043 |
| 60372 | 61853 | 18 | .09 | .486 |
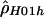 : : |
||||
| 68443 | 70558 | 15 | >1,200. | .009 |
| 70876 | 72406 | 13 | .9 | .104 |
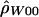 : : |
||||
| 68782 | 70558 | 13 | 1500. | .050 |
| 70226 | 72609 | 20 | 0. | .002 |
Position of the first polymorphism in the hotspot/coldspot.
Position of the last polymorphism in the hotspot/coldspot.
Total number of segregating sites.
Estimate is for the whole region (not per base pair).
Significance determined from 2,000 replicates. See the “Methods” section for details.
Estimates of ρ Based on a Model with Two Recombination Rates
From the endpoints identified in table 3, we chose a 1.7-kb hotspot region from positions 68700–70400 for further study. To obtain a more accurate estimate, we generalized 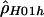 to consider multiple rates. Here, we used the data from the entire surveyed segment to jointly estimate ρ for the hotspot region and ρ for the rest of the sequence. The advantage of this method is that more pairs of sites can be used (i.e., pairs where none or one of the markers is in the hotspot) to estimate the hotspot recombination rate. We estimated
to consider multiple rates. Here, we used the data from the entire surveyed segment to jointly estimate ρ for the hotspot region and ρ for the rest of the sequence. The advantage of this method is that more pairs of sites can be used (i.e., pairs where none or one of the markers is in the hotspot) to estimate the hotspot recombination rate. We estimated 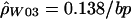 for the hotspot and
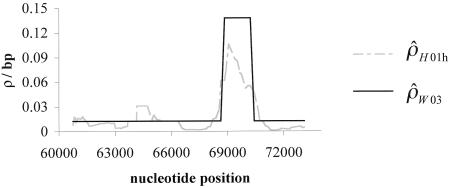
for the hotspot and 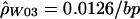 for the remaining region. The estimated recombination rate for the hotspot is substantially smaller than the estimate shown in table 3 and slightly larger than the peak sliding-window estimate shown in figure 2. Simulations suggest that estimates of ρ by use of
for the remaining region. The estimated recombination rate for the hotspot is substantially smaller than the estimate shown in table 3 and slightly larger than the peak sliding-window estimate shown in figure 2. Simulations suggest that estimates of ρ by use of 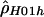 show a strong upward bias when there are few segregating sites (Andolfatto and Wall, in press). Figure 3 shows a comparison of the rates estimated using the sliding-window approach (fig. 2A) and the rates estimated using the two-rate model. There is a reasonable degree of concordance between these two methods. Note that the estimate of ρ for the nonhotspot region is roughly an order of magnitude larger than was estimated in 50 noncoding regions from the same population (Frisse et al. 2001; L. Frisse and A. Di Rienzo, unpublished data).
show a strong upward bias when there are few segregating sites (Andolfatto and Wall, in press). Figure 3 shows a comparison of the rates estimated using the sliding-window approach (fig. 2A) and the rates estimated using the two-rate model. There is a reasonable degree of concordance between these two methods. Note that the estimate of ρ for the nonhotspot region is roughly an order of magnitude larger than was estimated in 50 noncoding regions from the same population (Frisse et al. 2001; L. Frisse and A. Di Rienzo, unpublished data).
Figure 3.
Sliding-window estimate of ρ (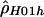 ) for the human data (as in fig. 2A), compared with the two-rate estimate (
) for the human data (as in fig. 2A), compared with the two-rate estimate (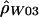 ) described in this article.
) described in this article.
Likelihood Analyses
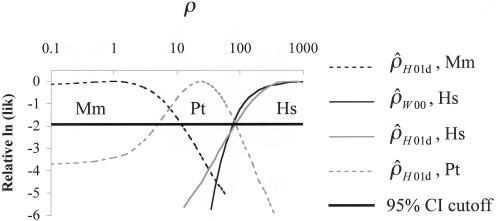
The point estimates of recombination rates show large differences across species, but part of this may be just the inherent error in the estimates. To get a sense of the uncertainty in the estimated values, we calculated the likelihood of the data as a function of ρ (see the “Methods” section). Figure 4 plots likelihood curves for base pairs 68700–70400. The maximum likelihood estimates for humans and macaques differ by three orders of magnitude, with the chimpanzee estimate almost exactly intermediate between the other two species. The ∼95% CIs for ρ (for the whole region) have a range from 0–12 in macaques to 5–86 in chimpanzees and 82–∞ in humans (through use of 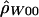 ). On the basis of this analysis, we conclude that the difference in ρ estimates between humans and macaques reflects, in part, substantial differences in the true ρ values for the two species.
). On the basis of this analysis, we conclude that the difference in ρ estimates between humans and macaques reflects, in part, substantial differences in the true ρ values for the two species.
Figure 4.
The likelihood of ρ estimates as a function of ρ, for different estimators and species, and the putative hotspot region (nucleotide positions 68700–70400). “Mm” refers to rhesus macaques, “Hs” to humans, and “Pt” to chimpanzees. Likelihoods were estimated over a grid of 36 ρ values, with a range of 0.1–1,000.
Discussion
A previous sperm-typing study of the β-globin region identified an 11-kb area with elevated recombination rates (Schneider et al. 2002). On the basis of patterns of LD, we conclude that recombination rate is heterogeneous within this 11-kb region in humans and that a small subregion of 1–2 kb experiences much higher recombination rates. We localized this subregion to just 5′ of the β-globin gene. The size of this recombinational hotspot is similar to the size of hotspots identified elsewhere (Jeffreys et al. 2000, 2001; May et al. 2002). Moreover, crossover breakpoints observed elsewhere in family studies fall into this subregion (Smith et al. 1998). The present study adds to the growing evidence supporting a direct connection between patterns of LD and local rates of recombination (Chakravarti et al. 1984; Badge et al. 2000; Jeffreys et al. 2000, 2001; May et al. 2002; Schneider et al. 2002; Li and Stephens, in press). This connection immediately implies that local rates of recombination change slowly relative to Ng, where N is the effective population size and g is the generation time. However, our analysis of the orthologous region in macaques suggests that, if this hotspot is present, its recombination rate must have changed. The change would have occurred over a time scale substantially larger than Ng.
Because of the method used to search for a hotspot, it could be argued that the true hotspot is smaller. However, a closer inspection shows that this is not the case. Obligate recombination events (cf. Hudson and Kaplan [1985]) are spread out uniformly from bases 68700 to 70400. In addition, estimates of ρ for the first half of this hotspot are as large as estimates of ρ for the latter half (results not shown). We conclude that the patterns of LD are suggestive of a hotspot that is ⩾1.5 kb in length.
Given the ρ values estimated in humans (fig. 3), we can see how these compare with the recombination rates estimated by Schneider et al. (2002). Our hotspot intersects with ∼1 kb of the 11-kb hotspot region that they identified. Therefore, our ρ estimate for the entire 11-kb region can be found by adding 1 kb at 0.138/bp with 10 kb at 0.0126/bp, for a total of 264. If we assume N=11,600 (Frisse et al. 2001), this corresponds to an r of 0.57%, which is roughly two-thirds of what was estimated on the basis of sperm data. Although previous studies of human polymorphism data have generally found estimates of ρ to be higher than expected from estimates of r and N (Wiuf 2000; Ardlie et al. 2001; Frisse et al. 2001; Przeworski and Wall 2001), our results are still consistent with these previous studies when the uncertainty in estimating N, r, and ρ is taken into account. In addition, it should be noted that differences between the male and female recombination rates may contribute to the difference between population-based estimates and those based on sperm analysis. Our work, along with a recent study of the TAP2 region (Li and Stephens, in press), suggests that population genetic analyses can provide reasonably accurate estimates (e.g., within a factor of 2) of local recombination rates.
In yeast, hotspots could be classified into three major categories: α hotspots require the binding of transcription factors, β hotspots are associated with nuclease-sensitive chromatin, and γ hotspots are associated with high-percentage G + C content (Petes 2001). Given the erythroid-specific expression of the β-globin gene, it seems unlikely that the hotspot we identified is the result of transcription factor binding. A minor nuclease-sensitive site is observed immediately 5′ to the β-globin gene in adult erythroblasts (Groudine et al. 1983) but not in all other tested cell types. Although the pattern of nuclease sensitivity of the hotspot region in the germ line has not been characterized, the tissue-specific and developmentally regulated expression of the β-globin gene suggests that this is not a β-hotspot. Likewise, the moderate-percentage (41%) G + C content also acts to rule out a γ hotspot. It is interesting that the hotspot we identified in humans (table 3) overlaps, with remarkable precision, the well-characterized replication origin for the β-globin cluster lying between positions 68848 and 70784 (Kitsberg et al. 1993). A general connection between meiotic replication and recombination initiation has been established in yeast (Borde et al. 2000). Moreover, a study of the distribution of DSBs on yeast chromosome III identified a few cases of replication origins in the proximity of DSB-rich domains (Baudat and Nicolas 1997). For one of these replication origins, ARS307, it was shown that its deletion reduces the rate of both crossover and gene conversion in the hotspot 2 kb away; conversely, the insertion of the replication origin into a coldspot region stimulates crossover and gene conversion (Rattray and Symington 1993). This stimulation appears to be independent of active DNA replication. Because replication origins are characterized by domains that are easily unwound (DNA unwinding elements [DUEs]), they may create an accessible chromatin structure prone to DSBs and recombination.
We gathered orthologous sequence data from chimpanzees and macaques to infer (indirectly, through patterns of LD) whether local recombination-rate variation is conserved over millions of years. In particular, we wanted to know whether the region orthologous to the human hotspot was a hotspot in other species as well. We found high levels of LD in macaques, and figure 4 suggests that ρ for the hotspot region is several times smaller (and may be as much as 1,000-fold smaller) in macaques relative to humans. Two possible explanations for this are: (1) macaques do not have a hotspot between bases 68700 and 70400 and (2) there is a hotspot in macaques in the orthologous location, but Nr is many times smaller (in macaques relative to humans). Little is known about N and r in macaques, but it seems unlikely that the results shown in figures 2 and 4 can be explained solely by a smaller population size and smaller overall genetic-map length in macaques. A recently constructed genetic map for the baboon is ∼22% shorter than the human map. It is not clear whether this might generalize to the macaque map, since closely related species (e.g., Drosophila melanogaster and D. mauritiana) can show large differences in total genetic-map length (True et al. 1996). Figure 2C shows no sign of a peak in bases 68700–70400, which we might expect under the second explanation. Though we see no evidence for an orthologous hotspot in macaques, additional population genetic data are necessary to fully rule out the alternative explanation.
Under the assumption that macaques do not have a hotspot in the orthologous location to the human hotspot, we next asked whether more closely related species (e.g., chimpanzees) do. The situation here is less clear. Our samples were identified as P. t. verus, but our polymorphism data contain several low-frequency variants in strong LD with each other. Coupled with the high levels of variation that we observe (table 1), this led us to suspect that some of the samples may contain P. t. troglodytes ancestry. If so, the patterns of LD in this mixed sample could be quite different, and the observed intermediate ρ estimate in the hotspot region (fig. 4) may be inaccurate. Population structure generally tends to increase levels of LD (Pritchard and Przeworski 2001; results not shown), so it is possible that there is a hotspot in chimpanzees, similar in intensity to the human hotspot, that we cannot identify in our sample.
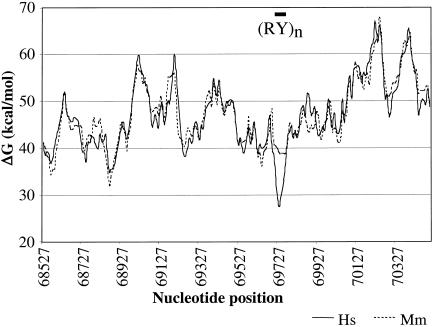
Our comparative analysis of the β-globin hotspot may yield some clues about the specific sequence features that underlie the increase in recombination rate. A 16-bp consensus sequence for the Pur protein (at position 70246) (Kitsberg et al. 1993; Aladjem et al. 1995) and a purine-pyrimidine ([RY]n) repeat (at position 69733) had been implicated in the β-globin hotspot (Smith et al. 1998). More specifically, it was proposed that Pur binding promotes duplex opening over a region containing a reiterated AT motif at some distance from the recognition site. In our data, the Pur element shows 100% sequence identity in humans, chimpanzees, and macaques. Given that an orthologous hotspot is not likely in macaques, this suggests that the Pur-binding site is not sufficient for increasing recombination rates. Conversely, the helical stability of the (RY)n repeat region in macaques is markedly higher compared with humans (fig. 5) and chimpanzees. DUEs are associated with replication origins in yeast and can be detected as domains of low helical stability. Furthermore, it was shown that the level of helical stability is inversely related to replication efficiency (Natale et al. 1992). Thus, given the overlap between the human hotspot and the β-globin replication initiation region, one can speculate that the different structure of the (RY)n repeat might contribute to the different recombinational landscapes in humans and macaques.
Figure 5.
Sliding-window plot of DNA helical stability within the hotspot region for the human and macaque sequences. The position of the (RY)n repeat coincides with a domain of low helical stability in the human but not the macaque sequence. Helical stability was calculated using the program WEB-THERMODYN (Huang and Kowalski 2003), under the assumption of a temperature of 37°C and an ionic strength of 10 mM. “Hs” refers to humans,” and “Mm” refers to rhesus macaques.
Overall, our results highlight the potential and the challenges of LD-based studies in nonhuman primates. LD-based analyses of closely related species can provide information on the tempo and mode of hotspot evolution as well as the factors affecting the presence and distribution of hotspots across a genome. Furthermore, sequence comparisons across orthologous regions that contain conserved (or not conserved) hotspots may identify sequence elements that play a role in recombination initiation. It should be noted that LD approaches require the analysis of population samples that fit the assumptions of the evolutionary model used to make inferences about recombination rates. Alternatively, more realistic models should be developed for the analysis of specific populations. The availability of “true” population samples of nonhuman primates would greatly enhance the power of these approaches.
Acknowledgments
We are especially grateful to D. Bishop for helpful discussions throughout the course of this project. We thank P. Andolfatto, C. Langley, M. Przeworski, and an anonymous reviewer, for comments on the manuscript; R. Fitzpatrick, for technical assistance; and J. Beck and K. Smith at the Coriell Institute, for providing useful information on the macaque samples. L.F. was supported by National Research Service Award postdoctoral fellowship HG00219. J.D.W. was supported by National Institutes of Health (NIH) grant HG2772 to J. Pritchard. This work was supported by NIH grant HG02098 (to A.D.).
Electronic-Database Information
Accession numbers and URLs for data presented herein are as follows:
- Di Rienzo Laboratory, http://genes.uchicago.edu/fri/drnzores.html (for primers, sequence variation data, and supplemental results)
- GenBank, http://www.ncbi.nlm.nih.gov/ (for human [accession number NG_000007.2], macaque [accession numbers M18797, J00334, X05665, J00327, and AF205410], and chimpanzee [accession numbers X02345, AF339363, and AF339362] reference sequence information)
- MAXDIP, http://genapps.uchicago.edu/axis/index.html (a Web service for estimating
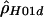 )
) - RECSLIDER, http://genapps.uchicago.edu/recslider/index.html (a Web service for estimating
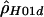 on a sliding window and for performing coalescent simulations)
on a sliding window and for performing coalescent simulations) - WEB-THERMODYN, http://wings.buffalo.edu/gsa/dna/dk/WEBTHERMODYN/ (a Web service for calculating the helical stability of a DNA sequence)
References
- Aladjem MI, Groudine M, Brody LL, Dieken ES, Fournier RE, Wahl GM, Epner EM (1995) Participation of the human β-globin locus control region in initiation of DNA replication. Science 270:815–819 [DOI] [PubMed] [Google Scholar]
- Andolfatto P, Przeworski M (2000) A genome-wide departure from the standard neutral model in natural populations of Drosophila. Genetics 156:257–268 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andolfatto P, Wall JD. Linkage disequilibrium patterns across a recombination gradient in African Drosophila melanogaster. Genetics (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ardlie K, Liu-Cordero SN, Eberle MA, Daly M, Barrett J, Winchester E, Lander ES, Kruglyak L (2001) Lower-than-expected linkage disequilibrium between tightly linked markers in humans suggests a role for gene conversion. Am J Hum Genet 69:582–589 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashburner M (1989) Drosophila: a laboratory handbook. Cold Spring Harbor Laboratory Press, Cold Spring Harbor, NY [Google Scholar]
- Badge RM, Yardley J, Jeffreys AJ, Armour JA (2000) Crossover breakpoint mapping identifies a subtelomeric hotspot for male meiotic recombination. Hum Mol Genet 9:1239–1244 10.1093/hmg/9.8.1239 [DOI] [PubMed] [Google Scholar]
- Baudat F, Nicolas A (1997) Clustering of meiotic double-strand breaks on yeast chromosome III. Proc Natl Acad Sci USA 94:5213–5218 10.1073/pnas.94.10.5213 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Borde V, Goldman ASH, Lichten M (2000) Direct coupling between meiotic DNA replication and recombination initiation. Science 290:806–809 10.1126/science.290.5492.806 [DOI] [PubMed] [Google Scholar]
- Boulton A, Myers RS, Redfield RJ (1997) The hotspot conversion paradox and the evolution of meiotic recombination. Proc Natl Acad Sci USA 94:8058–8063 10.1073/pnas.94.15.8058 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Broman KW, Murray JC, Sheffield VC, White RL, Weber JL (1998) Comprehensive human genetic maps: individual and sex-specific variation in recombination. Am J Hum Genet 63:861–869 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chakravarti A, Buetow KH, Antonarakis SE, Waber PG, Boehm CD, Kazazian HH (1984) Nonuniform recombination within the human β-globin gene cluster. Am J Hum Genet 36:1239–1258 [PMC free article] [PubMed] [Google Scholar]
- Deinard A, Kidd K (1999) Evolution of a HOXB6 intergenic region within the great apes and humans. J Hum Evol 36:687–703 10.1006/jhev.1999.0298 [DOI] [PubMed] [Google Scholar]
- Deinard AS, Lerche NW, Smith DG (2002) Polymorphism in the rhesus macaque (Macaca mulatta) NRAMP1 gene: lack of an allelic association to tuberculosis susceptibility. J Med Primatol 31:8–16 10.1034/j.1600-0684.2002.1o022.x [DOI] [PubMed] [Google Scholar]
- Dufour C, Casane D, Denton D, Wickings J, Corvol P, Jeunemaitre X (2000) Human-chimpanzee DNA sequence variation in the four major genes of the renin angiotensin system. Genomics 69:14–26 10.1006/geno.2000.6313 [DOI] [PubMed] [Google Scholar]
- Fearnhead P, Donnelly P (2001) Estimating recombination rates from population genetic data. Genetics 159:1299–1318 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frisse L, Hudson RR, Bartoszewicz A, Wall JD, Donfack J, Di Rienzo A (2001) Gene conversion and different population histories may explain the contrast between polymorphism and linkage disequilibrium levels. Am J Hum Genet 69:831–843 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Groudine M, Kohwi-Shigematsu T, Gelinas R, Stamatoyannopoulos G, Papayannopoulou T (1983) Human fetal to adult hemoglobin switching: changes in chromatin structure of the beta-globin gene locus. Proc Natl Acad Sci USA 80:7551–7555 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang Y, Kowalski D (2003) WEB-THERMODYN: sequence analysis software for profiling DNA helical stability. Nucleic Acids Res 31(13):3819–3821 10.1093/nar/gkg562 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hubert R, MacDonald M, Gusella J, Arnheim N (1994) High resolution localization of recombination hot spots using sperm typing. Nat Genet 7:420–424 [DOI] [PubMed] [Google Scholar]
- Hudson RR (1983) Properties of a neutral allele model with intragenic recombination. Theor Popul Biol 23:183–201 [DOI] [PubMed] [Google Scholar]
- ——— (2001) Two-locus sampling distributions and their application. Genetics 159:1805–1817 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hudson RR, Kaplan NL (1985) Statistical properties of the number of recombination events in the history of a sample of DNA sequences. Genetics 111:147–164 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jeffreys AJ, Kauppi L, Neumann R (2001) Intensely punctate meiotic recombination in the class II region of the major histocompatibility complex. Nat Genet 29:217–222 10.1038/ng1001-217 [DOI] [PubMed] [Google Scholar]
- Jeffreys AJ, Neumann R (2002) Reciprocal crossover asymmetry and meiotic drive in a human recombination hot spot. Nat Genet 31:267–271 10.1038/ng910 [DOI] [PubMed] [Google Scholar]
- Jeffreys AJ, Ritchie A, Neumann R (2000) High resolution analysis of haplotype diversity and meiotic crossover in the human TAP2 recombination hotspot. Hum Mol Genet 9:725–33 10.1093/hmg/9.5.725 [DOI] [PubMed] [Google Scholar]
- Kaessmann H, Heissig F, von Haeseler A, Pääbo S (1999) DNA sequence variation in a non-coding region of low recombination on the human X chromosome. Nat Genet 22:78–81 10.1038/8785 [DOI] [PubMed] [Google Scholar]
- Kitsberg D, Selig S, Keshet I, Cedar H (1993) Replication structure of the human beta-globin gene domain. Nature 366:588–590 10.1038/366588a0 [DOI] [PubMed] [Google Scholar]
- Kong A, Gudbjartsson DF, Sainz J, Jonsdottir GM, Gudjonsson SA, Richardsson B, Sigurdardottir S, Barnard J, Hallbeck B, Masson G, Shlien A, Palsson ST, Frigge ML, Thorgeirsson TE, Gulcher JR, Stefansson K (2002) A high-resolution recombination map of the human genome. Nat Genet 31:241–247 [DOI] [PubMed] [Google Scholar]
- Li HH, Gyllensten UB, Cui XF, Saiki RK, Erlich HA, Arnheim N (1988) Amplification and analysis of DNA sequences in single human sperm and diploid cells. Nature 335:414–417 10.1038/335414a0 [DOI] [PubMed] [Google Scholar]
- Li N, Stephens M. Modelling linkage disequilibrium, and identifying recombination hotspots using SNP data. Genetics (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lien S, Szyda J, Schechinger B, Rappold G, Arnheim N (2000) Evidence for heterogeneity in recombination in the human pseudoautosomal region: high resolution analysis by sperm typing and radiation-hybrid mapping. Am J Hum Genet 66:557–566 [DOI] [PMC free article] [PubMed] [Google Scholar]
- May CA, Shone AC, Kalaydjieva L, Sajantila A, Jeffreys AJ (2002) Crossover clustering and rapid decay of linkage disequilibrium in the Xp/Yp pseudoautosomal gene SHOX. Nat Genet 31:272–275 10.1038/ng918 [DOI] [PubMed] [Google Scholar]
- Natale DA, Schubert AE, Kowalski D (1992) DNA helical stability accounts for mutational defects in a yeast replication origin. Proc Natl Acad Sci USA 89:2654–2658 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nickerson DA, Tobe VO, Taylor SL (1997) PolyPhred: automating the detection and genotyping of single nucleotide substitutions using fluorescence-based resequencing. Nucleic Acids Res 25:2745–2751 10.1093/nar/25.14.2745 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nicolas A, Treco D, Schultes NP, Szostak JW (1989) An initiation site for meiotic gene conversion in the yeast Saccharomyces cerevisiae. Nature 338:35–39 10.1038/338035a0 [DOI] [PubMed] [Google Scholar]
- Petes TD (2001) Meiotic recombination hot spots and cold spots. Nat Rev Genet 2:360–369 10.1038/35072078 [DOI] [PubMed] [Google Scholar]
- Pritchard JK, Przeworski M (2001) Linkage disequilibrium in humans: models and data. Am J Hum Genet 69:1–14 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Przeworski M, Wall JD (2001) Why is there so little intragenic linkage disequilibrium in humans? Genet Res 77:143–151 10.1017/S0016672301004967 [DOI] [PubMed] [Google Scholar]
- Rattray AJ, Symington LS (1993) Stimulation of meiotic recombination in yeast by an ARS element. Genetics 134:175–188 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rogers J, Mahaney MC, Witte SM, Nair S, Newman D, Wedel S, Rodriguez LA, Rice KS, Slifer SH, Perelygin A, Slifer M, Palladino-Negro P, Newman T, Chambers K, Joslyn G, Parry P, Morin PA (2000) A genetic linkage map of the baboon (Papio hamadryas) genome based on human microsatellite polymorphisms. Genomics 67:237–247 10.1006/geno.2000.6245 [DOI] [PubMed] [Google Scholar]
- Satta Y (2001) Comparison of DNA and protein polymorphisms between humans and chimpanzees. Genes Genet Syst 76:159–168 10.1266/ggs.76.159 [DOI] [PubMed] [Google Scholar]
- Schneider JA, Peto TE, Boone RA, Boyce AJ, Clegg JB (2002) Direct measurement of the male recombination fraction in the human β-globin hot spot. Hum Mol Genet 11:207–215 10.1093/hmg/11.3.207 [DOI] [PubMed] [Google Scholar]
- Smith RA, Ho PJ, Clegg JB, Kidd JR, Thein SL (1998) Recombination breakpoints in the human β-globin gene cluster. Blood 92:4415–4421 [PubMed] [Google Scholar]
- Stephens M, Smith NJ, Donnelly P (2001) A new statistical method for haplotype reconstruction from population data. Am J Hum Genet 68:978–989 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tajima F (1983) Evolutionary relationship of DNA sequences in finite populations. Genetics 105:437–460 [DOI] [PMC free article] [PubMed] [Google Scholar]
- ——— Statistical method for testing the neutral mutation hypothesis by DNA polymorphism. Genetics 123:585–595 [DOI] [PMC free article] [PubMed] [Google Scholar]
- True JR, Mercer JM, Laurie CC (1996) Differences in crossover frequency and distribution among three sibling species of Drosophila. Genetics 142:507–523 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wall JD (2000) A comparison of estimators of the population recombination rate. Mol Biol Evol 17:156–163 [DOI] [PubMed] [Google Scholar]
- ——— (2001) Insights from linked single nucleotide polymorphisms: what we can learn from linkage disequilibrium. Curr Opin Genet Dev 11:647–651 10.1016/S0959-437X(00)00248-3 [DOI] [PubMed] [Google Scholar]
- Watterson GA (1975) On the number of segregating sites in genetical models without recombination. Theor Popul Biol 7:256–276 [DOI] [PubMed] [Google Scholar]
- Wiuf C (2000) A coalescence approach to gene conversion. Theor Popul Biol 57:357–367 10.1006/tpbi.2000.1462 [DOI] [PubMed] [Google Scholar]
- Yip SP, Lovegrove JU, Rana NA, Hopkinson DA, Whitehouse DB (1999) Mapping recombination hotspots in human phosphoglucomutase (PGM1). Hum Mol Genet 8:1699–1706 10.1093/hmg/8.9.1699 [DOI] [PubMed] [Google Scholar]
- Yu A, Zhao C, Fan Y, Jang W, Mungall AJ, Deloukas P, Olsen A, Doggett NA, Ghebranious N, Broman KW, Weber JL (2001) Comparison of human genetic and sequence-based physical maps. Nature 409:951–953 10.1038/35057185 [DOI] [PubMed] [Google Scholar]