Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 1997 Sep;73(3):1382–1394. doi: 10.1016/S0006-3495(97)78170-0

Inversion of Markov processes to determine rate constants from single-channel data.

M B Jackson 1
PMCID: PMC1181037  PMID: 9284305

Abstract

The determination of rate constants from single-channel data can be very difficult, in part because the single-channel lifetime distributions commonly analyzed by experimenters often have a complicated mathematical relation to the channel gating mechanism. The standard treatment of channel gating as a Markov process leads to the prediction that lifetime distributions are exponential functions. As the number of states of a channel gating scheme increases, the number of exponential terms in the lifetime distribution increases, and the weights and decay constants of the lifetime distributions become progressively more complicated functions of the underlying rate constants. In the present study a mathematical strategy for inverting these functions is introduced in order to determine rate constants from single-channel lifetime distributions. This inversion is easy for channel gating schemes with two or fewer states of a given conductance, so the present study focuses on schemes with more states. The procedure is to derive explicit equations relating the parameters of the lifetime distribution to the rate constants of the scheme. Such equations can be derived using the equality between symmetric functions of eigenvalues of a matrix and sums over principle minors, as well as expressions for the moments, derivatives, and weights of a lifetime distribution. The rate constants are then obtained as roots to this system of equations. For a gating scheme with three sequential closed states and a single gateway state, exact analytical expressions were found for each rate constant in terms of the parameters of the three-exponential closed-time distribution. For several other gating schemes, systems of equations were found that could be solved numerically to obtain the rate constants. Lifetime distributions were shown to specify a unique set of real rate constants in sequential gating schemes with up to five closed or five open states. For kinetic schemes with multiple gating pathways, the analysis of simulated data revealed multiple solutions. These multiple solutions could be distinguished by examining two-dimensional probability density functions. The utility of the methods introduced here are demonstrated by analyzing published data on nicotinic acetylcholine receptors, GABA(A) receptors, and NMDA receptors.

Full text

PDF
1382

Selected References

These references are in PubMed. This may not be the complete list of references from this article.

  1. Bauer R. J., Bowman B. F., Kenyon J. L. Theory of the kinetic analysis of patch-clamp data. Biophys J. 1987 Dec;52(6):961–978. doi: 10.1016/S0006-3495(87)83289-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Benveniste M., Mayer M. L. Kinetic analysis of antagonist action at N-methyl-D-aspartic acid receptors. Two binding sites each for glutamate and glycine. Biophys J. 1991 Mar;59(3):560–573. doi: 10.1016/S0006-3495(91)82272-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Blatz A. L., Magleby K. L. Adjacent interval analysis distinguishes among gating mechanisms for the fast chloride channel from rat skeletal muscle. J Physiol. 1989 Mar;410:561–585. doi: 10.1113/jphysiol.1989.sp017549. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Blatz A. L., Magleby K. L. Correcting single channel data for missed events. Biophys J. 1986 May;49(5):967–980. doi: 10.1016/S0006-3495(86)83725-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Clements J. D., Westbrook G. L. Activation kinetics reveal the number of glutamate and glycine binding sites on the N-methyl-D-aspartate receptor. Neuron. 1991 Oct;7(4):605–613. doi: 10.1016/0896-6273(91)90373-8. [DOI] [PubMed] [Google Scholar]
  6. Colquhoun D., Hawkes A. G. A note on correlations in single ion channel records. Proc R Soc Lond B Biol Sci. 1987 Feb 23;230(1258):15–52. doi: 10.1098/rspb.1987.0008. [DOI] [PubMed] [Google Scholar]
  7. Colquhoun D., Hawkes A. G. On the stochastic properties of single ion channels. Proc R Soc Lond B Biol Sci. 1981 Mar 6;211(1183):205–235. doi: 10.1098/rspb.1981.0003. [DOI] [PubMed] [Google Scholar]
  8. Crouzy S. C., Sigworth F. J. Yet another approach to the dwell-time omission problem of single-channel analysis. Biophys J. 1990 Sep;58(3):731–743. doi: 10.1016/S0006-3495(90)82416-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. French R. J., Wonderlin W. F. Software for acquisition and analysis of ion channel data: choices, tasks, and strategies. Methods Enzymol. 1992;207:711–728. doi: 10.1016/0076-6879(92)07052-p. [DOI] [PubMed] [Google Scholar]
  10. Horn R., Lange K. Estimating kinetic constants from single channel data. Biophys J. 1983 Aug;43(2):207–223. doi: 10.1016/S0006-3495(83)84341-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Horn R., Vandenberg C. A. Statistical properties of single sodium channels. J Gen Physiol. 1984 Oct;84(4):505–534. doi: 10.1085/jgp.84.4.505. [DOI] [PMC free article] [PubMed] [Google Scholar]
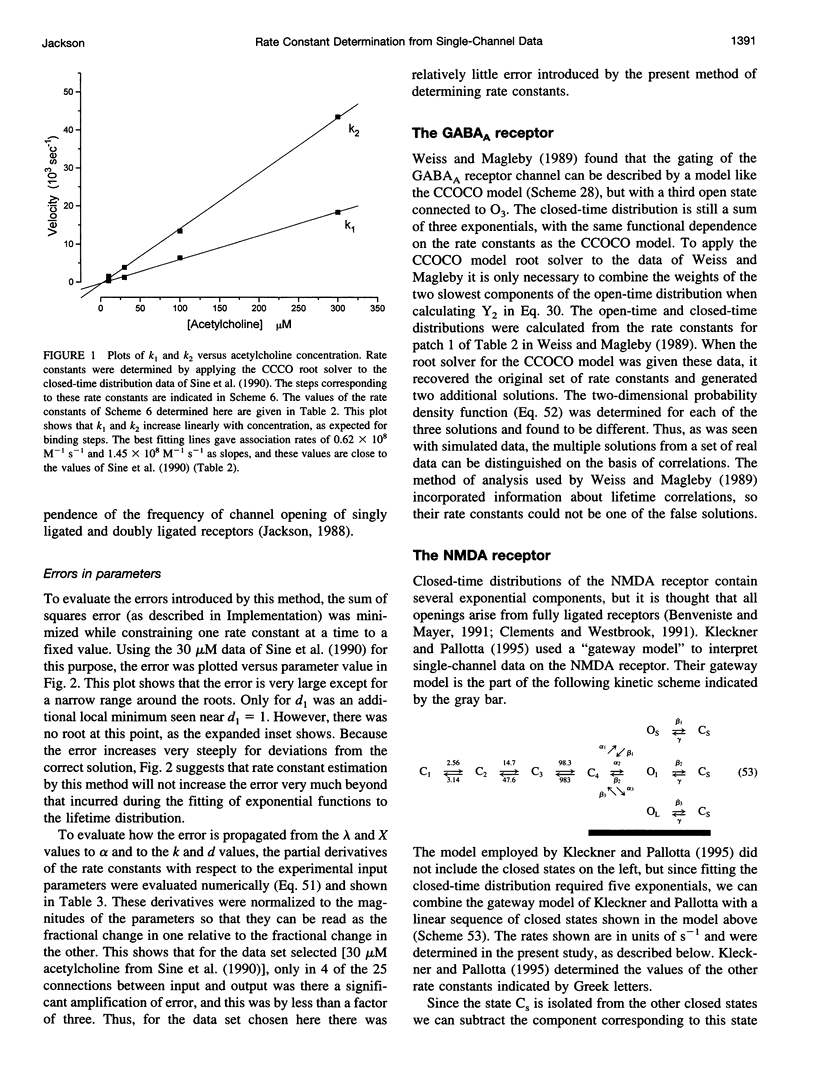
  12. Jackson M. B. Dependence of acetylcholine receptor channel kinetics on agonist concentration in cultured mouse muscle fibres. J Physiol. 1988 Mar;397:555–583. doi: 10.1113/jphysiol.1988.sp017019. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Jackson M. B. Ion channels. Single-channel analysis. Methods Enzymol. 1992;207:729–746. doi: 10.1016/0076-6879(92)07053-q. [DOI] [PubMed] [Google Scholar]
  14. Kienker P. Equivalence of aggregated Markov models of ion-channel gating. Proc R Soc Lond B Biol Sci. 1989 Apr 22;236(1284):269–309. doi: 10.1098/rspb.1989.0024. [DOI] [PubMed] [Google Scholar]
  15. Kleckner N. W., Pallotta B. S. Burst kinetics of single NMDA receptor currents in cell-attached patches from rat brain cortical neurons in culture. J Physiol. 1995 Jul 15;486(Pt 2):411–426. doi: 10.1113/jphysiol.1995.sp020822. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Magleby K. L., Weiss D. S. Identifying kinetic gating mechanisms for ion channels by using two-dimensional distributions of simulated dwell times. Proc Biol Sci. 1990 Sep 22;241(1302):220–228. doi: 10.1098/rspb.1990.0089. [DOI] [PubMed] [Google Scholar]
  17. Qin F., Auerbach A., Sachs F. Estimating single-channel kinetic parameters from idealized patch-clamp data containing missed events. Biophys J. 1996 Jan;70(1):264–280. doi: 10.1016/S0006-3495(96)79568-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Roux B., Sauvé R. A general solution to the time interval omission problem applied to single channel analysis. Biophys J. 1985 Jul;48(1):149–158. doi: 10.1016/S0006-3495(85)83768-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Sine S. M., Claudio T., Sigworth F. J. Activation of Torpedo acetylcholine receptors expressed in mouse fibroblasts. Single channel current kinetics reveal distinct agonist binding affinities. J Gen Physiol. 1990 Aug;96(2):395–437. doi: 10.1085/jgp.96.2.395. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Weiss D. S., Magleby K. L. Gating scheme for single GABA-activated Cl- channels determined from stability plots, dwell-time distributions, and adjacent-interval durations. J Neurosci. 1989 Apr;9(4):1314–1324. doi: 10.1523/JNEUROSCI.09-04-01314.1989. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES