Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 1997 Nov;73(5):2359–2375. doi: 10.1016/S0006-3495(97)78266-3

Does conformational free energy distinguish loop conformations in proteins?

J L Pellequer 1, S W Chen 1
PMCID: PMC1181139  PMID: 9370431

Abstract

Limitations in protein homology modeling often arise from the inability to adequately model loops. In this paper we focus on the selection of loop conformations. We present a complete computational treatment that allows the screening of loop conformations to identify those that best fit a molecular model. The stability of a loop in a protein is evaluated via computations of conformational free energies in solution, i.e., the free energy difference between the reference structure and the modeled one. A thermodynamic cycle is used for calculation of the conformational free energy, in which the total free energy of the reference state (i.e., gas phase) is the CHARMm potential energy. The electrostatic contribution of the solvation free energy is obtained from solving the finite-difference Poisson-Boltzmann equation. The nonpolar contribution is based on a surface area-based expression. We applied this computational scheme to a simple but well-characterized system, the antibody hypervariable loop (complementarity-determining region, CDR). Instead of creating loop conformations, we generated a database of loops extracted from high-resolution crystal structures of proteins, which display geometrical similarities with antibody CDRs. We inserted loops from our database into a framework of an antibody; then we calculated the conformational free energies of each loop. Results show that we successfully identified loops with a "reference-like" CDR geometry, with the lowest conformational free energy in gas phase only. Surprisingly, the solvation energy term plays a confusing role, sometimes discriminating "reference-like" CDR geometry and many times allowing "non-reference-like" conformations to have the lowest conformational free energies (for short loops). Most "reference-like" loop conformations are separated from others by a gap in the gas phase conformational free energy scale. Naturally, loops from antibody molecules are found to be the best models for long CDRs (> or = 6 residues), mainly because of a better packing of backbone atoms into the framework of the antibody model.

Full text

PDF
2366

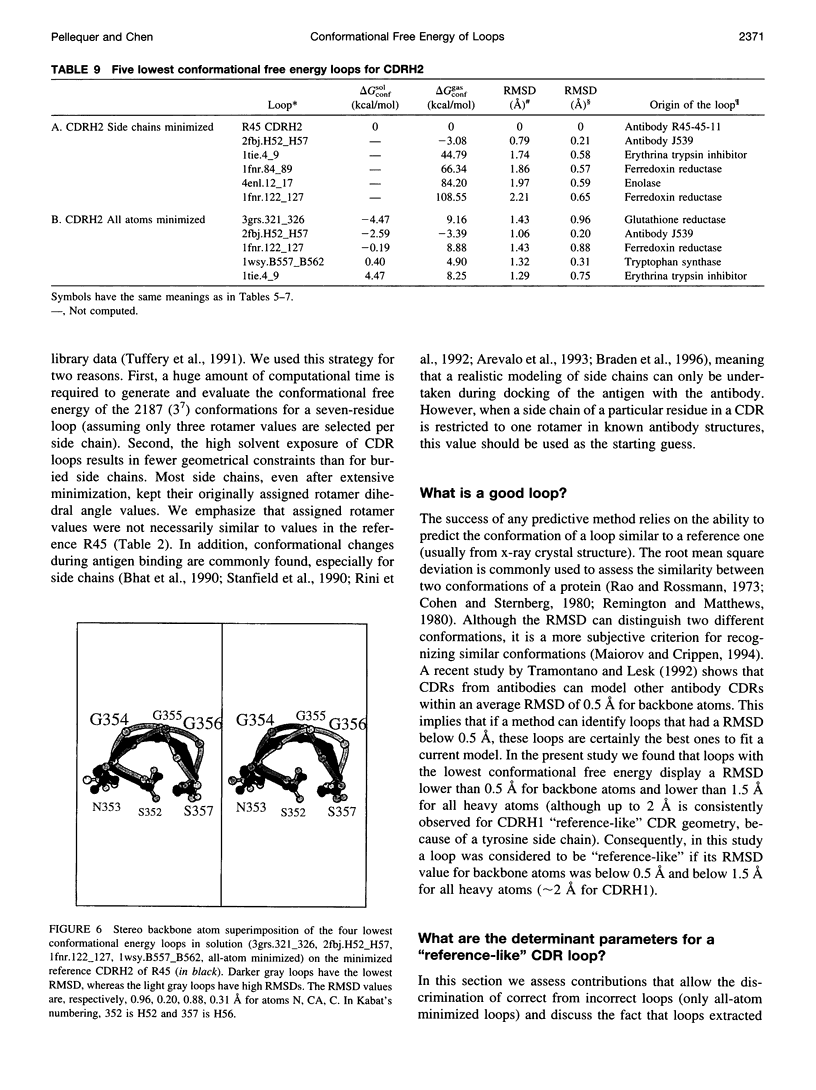
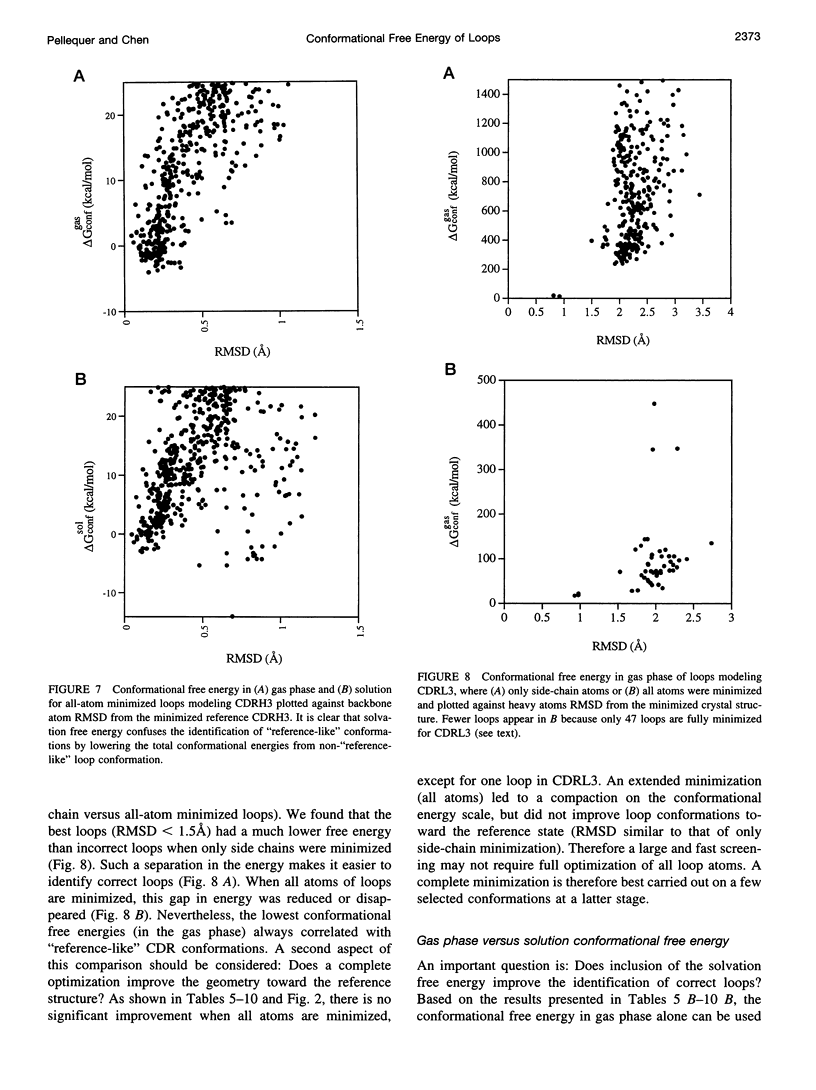
Images in this article

2366FIGURE 1
on p.2366
2368FIGURE 3
on p.2368
2369FIGURE 4
on p.2369
2370FIGURE 5
on p.2370
2371FIGURE 6
on p.2371

Selected References

These references are in PubMed. This may not be the complete list of references from this article.

  1. Altschuh D., Vix O., Rees B., Thierry J. C. A conformation of cyclosporin A in aqueous environment revealed by the X-ray structure of a cyclosporin-Fab complex. Science. 1992 Apr 3;256(5053):92–94. doi: 10.1126/science.1566062. [DOI] [PubMed] [Google Scholar]
  2. Arevalo J. H., Stura E. A., Taussig M. J., Wilson I. A. Three-dimensional structure of an anti-steroid Fab' and progesterone-Fab' complex. J Mol Biol. 1993 May 5;231(1):103–118. doi: 10.1006/jmbi.1993.1260. [DOI] [PubMed] [Google Scholar]
  3. Bernstein F. C., Koetzle T. F., Williams G. J., Meyer E. F., Jr, Brice M. D., Rodgers J. R., Kennard O., Shimanouchi T., Tasumi M. The Protein Data Bank: a computer-based archival file for macromolecular structures. J Mol Biol. 1977 May 25;112(3):535–542. doi: 10.1016/s0022-2836(77)80200-3. [DOI] [PubMed] [Google Scholar]
  4. Bhat T. N., Bentley G. A., Fischmann T. O., Boulot G., Poljak R. J. Small rearrangements in structures of Fv and Fab fragments of antibody D1.3 on antigen binding. Nature. 1990 Oct 4;347(6292):483–485. doi: 10.1038/347483a0. [DOI] [PubMed] [Google Scholar]
  5. Braden B. C., Fields B. A., Ysern X., Goldbaum F. A., Dall'Acqua W., Schwarz F. P., Poljak R. J., Mariuzza R. A. Crystal structure of the complex of the variable domain of antibody D1.3 and turkey egg white lysozyme: a novel conformational change in antibody CDR-L3 selects for antigen. J Mol Biol. 1996 Apr 19;257(5):889–894. doi: 10.1006/jmbi.1996.0209. [DOI] [PubMed] [Google Scholar]
  6. Bruccoleri R. E., Haber E., Novotný J. Structure of antibody hypervariable loops reproduced by a conformational search algorithm. Nature. 1988 Oct 6;335(6190):564–568. doi: 10.1038/335564a0. [DOI] [PubMed] [Google Scholar]
  7. Bruccoleri R. E., Karplus M. Prediction of the folding of short polypeptide segments by uniform conformational sampling. Biopolymers. 1987 Jan;26(1):137–168. doi: 10.1002/bip.360260114. [DOI] [PubMed] [Google Scholar]
  8. Brünger A. T., Karplus M. Polar hydrogen positions in proteins: empirical energy placement and neutron diffraction comparison. Proteins. 1988;4(2):148–156. doi: 10.1002/prot.340040208. [DOI] [PubMed] [Google Scholar]
  9. Carlacci L., Englander S. W. The loop problem in proteins: a Monte Carlo simulated annealing approach. Biopolymers. 1993 Aug;33(8):1271–1286. doi: 10.1002/bip.360330812. [DOI] [PubMed] [Google Scholar]
  10. Chothia C., Lesk A. M. Canonical structures for the hypervariable regions of immunoglobulins. J Mol Biol. 1987 Aug 20;196(4):901–917. doi: 10.1016/0022-2836(87)90412-8. [DOI] [PubMed] [Google Scholar]
  11. Chothia C., Lesk A. M. The relation between the divergence of sequence and structure in proteins. EMBO J. 1986 Apr;5(4):823–826. doi: 10.1002/j.1460-2075.1986.tb04288.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Cohen F. E., Sternberg M. J. On the prediction of protein structure: The significance of the root-mean-square deviation. J Mol Biol. 1980 Apr;138(2):321–333. doi: 10.1016/0022-2836(80)90289-2. [DOI] [PubMed] [Google Scholar]
  13. Devereux J., Haeberli P., Smithies O. A comprehensive set of sequence analysis programs for the VAX. Nucleic Acids Res. 1984 Jan 11;12(1 Pt 1):387–395. doi: 10.1093/nar/12.1part1.387. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Dunbrack R. L., Jr, Karplus M. Backbone-dependent rotamer library for proteins. Application to side-chain prediction. J Mol Biol. 1993 Mar 20;230(2):543–574. doi: 10.1006/jmbi.1993.1170. [DOI] [PubMed] [Google Scholar]
  15. Eisenmenger F., Argos P., Abagyan R. A method to configure protein side-chains from the main-chain trace in homology modelling. J Mol Biol. 1993 Jun 5;231(3):849–860. doi: 10.1006/jmbi.1993.1331. [DOI] [PubMed] [Google Scholar]
  16. Epp O., Lattman E. E., Schiffer M., Huber R., Palm W. The molecular structure of a dimer composed of the variable portions of the Bence-Jones protein REI refined at 2.0-A resolution. Biochemistry. 1975 Nov 4;14(22):4943–4952. doi: 10.1021/bi00693a025. [DOI] [PubMed] [Google Scholar]
  17. Feldmann R. J., Potter M., Glaudemans C. P. A hypothetical space-filling model of the V-regions of the galactan-binding myeloma immunoglobulin J539. Mol Immunol. 1981 Aug;18(8):683–698. doi: 10.1016/0161-5890(81)90060-2. [DOI] [PubMed] [Google Scholar]
  18. Fine R. M., Wang H., Shenkin P. S., Yarmush D. L., Levinthal C. Predicting antibody hypervariable loop conformations. II: Minimization and molecular dynamics studies of MCPC603 from many randomly generated loop conformations. Proteins. 1986 Dec;1(4):342–362. doi: 10.1002/prot.340010408. [DOI] [PubMed] [Google Scholar]
  19. Fischmann T. O., Bentley G. A., Bhat T. N., Boulot G., Mariuzza R. A., Phillips S. E., Tello D., Poljak R. J. Crystallographic refinement of the three-dimensional structure of the FabD1.3-lysozyme complex at 2.5-A resolution. J Biol Chem. 1991 Jul 15;266(20):12915–12920. [PubMed] [Google Scholar]
  20. Furey W., Jr, Wang B. C., Yoo C. S., Sax M. Structure of a novel Bence-Jones protein (Rhe) fragment at 1.6 A resolution. J Mol Biol. 1983 Jul 5;167(3):661–692. doi: 10.1016/s0022-2836(83)80104-1. [DOI] [PubMed] [Google Scholar]
  21. Gilson M. K., Honig B. Calculation of the total electrostatic energy of a macromolecular system: solvation energies, binding energies, and conformational analysis. Proteins. 1988;4(1):7–18. doi: 10.1002/prot.340040104. [DOI] [PubMed] [Google Scholar]
  22. Herron J. N., He X. M., Mason M. L., Voss E. W., Jr, Edmundson A. B. Three-dimensional structure of a fluorescein-Fab complex crystallized in 2-methyl-2,4-pentanediol. Proteins. 1989;5(4):271–280. doi: 10.1002/prot.340050404. [DOI] [PubMed] [Google Scholar]
  23. Hubbard T. J., Blundell T. L. Comparison of solvent-inaccessible cores of homologous proteins: definitions useful for protein modelling. Protein Eng. 1987 Jun;1(3):159–171. doi: 10.1093/protein/1.3.159. [DOI] [PubMed] [Google Scholar]
  24. Jones T. A., Thirup S. Using known substructures in protein model building and crystallography. EMBO J. 1986 Apr;5(4):819–822. doi: 10.1002/j.1460-2075.1986.tb04287.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Kabat E. A., Wu T. T., Bilofsky H. Unusual distributions of amino acids in complementarity-determining (hypervariable) segments of heavy and light chains of immunoglobulins and their possible roles in specificity of antibody-combining sites. J Biol Chem. 1977 Oct 10;252(19):6609–6616. [PubMed] [Google Scholar]
  26. Kabsch W., Sander C. Dictionary of protein secondary structure: pattern recognition of hydrogen-bonded and geometrical features. Biopolymers. 1983 Dec;22(12):2577–2637. doi: 10.1002/bip.360221211. [DOI] [PubMed] [Google Scholar]
  27. Koehl P., Delarue M. A self consistent mean field approach to simultaneous gap closure and side-chain positioning in homology modelling. Nat Struct Biol. 1995 Feb;2(2):163–170. doi: 10.1038/nsb0295-163. [DOI] [PubMed] [Google Scholar]
  28. Koehl P., Delarue M. Application of a self-consistent mean field theory to predict protein side-chains conformation and estimate their conformational entropy. J Mol Biol. 1994 Jun 3;239(2):249–275. doi: 10.1006/jmbi.1994.1366. [DOI] [PubMed] [Google Scholar]
  29. Lascombe M. B., Alzari P. M., Poljak R. J., Nisonoff A. Three-dimensional structure of two crystal forms of FabR19.9 from a monoclonal anti-arsonate antibody. Proc Natl Acad Sci U S A. 1992 Oct 15;89(20):9429–9433. doi: 10.1073/pnas.89.20.9429. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Lasters I., Desmet J. The fuzzy-end elimination theorem: correctly implementing the side chain placement algorithm based on the dead-end elimination theorem. Protein Eng. 1993 Sep;6(7):717–722. doi: 10.1093/protein/6.7.717. [DOI] [PubMed] [Google Scholar]
  31. Lee C., Subbiah S. Prediction of protein side-chain conformation by packing optimization. J Mol Biol. 1991 Jan 20;217(2):373–388. doi: 10.1016/0022-2836(91)90550-p. [DOI] [PubMed] [Google Scholar]
  32. Mainhart C. R., Potter M., Feldmann R. J. A refined model for the variable domains (Fv) of the J539 beta(1,6)-D-galactan-binding immunoglobulin. Mol Immunol. 1984 Jun;21(6):469–478. doi: 10.1016/0161-5890(84)90062-2. [DOI] [PubMed] [Google Scholar]
  33. Maiorov V. N., Crippen G. M. Significance of root-mean-square deviation in comparing three-dimensional structures of globular proteins. J Mol Biol. 1994 Jan 14;235(2):625–634. doi: 10.1006/jmbi.1994.1017. [DOI] [PubMed] [Google Scholar]
  34. Marquart M., Deisenhofer J., Huber R., Palm W. Crystallographic refinement and atomic models of the intact immunoglobulin molecule Kol and its antigen-binding fragment at 3.0 A and 1.0 A resolution. J Mol Biol. 1980 Aug 25;141(4):369–391. doi: 10.1016/0022-2836(80)90252-1. [DOI] [PubMed] [Google Scholar]
  35. Martin A. C., Cheetham J. C., Rees A. R. Modeling antibody hypervariable loops: a combined algorithm. Proc Natl Acad Sci U S A. 1989 Dec;86(23):9268–9272. doi: 10.1073/pnas.86.23.9268. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Moult J., James M. N. An algorithm for determining the conformation of polypeptide segments in proteins by systematic search. Proteins. 1986 Oct;1(2):146–163. doi: 10.1002/prot.340010207. [DOI] [PubMed] [Google Scholar]
  37. Padlan E. A., Cohen G. H., Davies D. R. On the specificity of antibody/antigen interactions: phosphocholine binding to McPC603 and the correlation of three-dimensional structure and sequence data. Ann Inst Pasteur Immunol. 1985 Mar-Apr;136C(2):271–276. doi: 10.1016/s0769-2625(85)80058-1. [DOI] [PubMed] [Google Scholar]
  38. Padlan E. A., Silverton E. W., Sheriff S., Cohen G. H., Smith-Gill S. J., Davies D. R. Structure of an antibody-antigen complex: crystal structure of the HyHEL-10 Fab-lysozyme complex. Proc Natl Acad Sci U S A. 1989 Aug;86(15):5938–5942. doi: 10.1073/pnas.86.15.5938. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Ponder J. W., Richards F. M. Tertiary templates for proteins. Use of packing criteria in the enumeration of allowed sequences for different structural classes. J Mol Biol. 1987 Feb 20;193(4):775–791. doi: 10.1016/0022-2836(87)90358-5. [DOI] [PubMed] [Google Scholar]
  40. Presta L. G., Rose G. D. Helix signals in proteins. Science. 1988 Jun 17;240(4859):1632–1641. doi: 10.1126/science.2837824. [DOI] [PubMed] [Google Scholar]
  41. Rao S. T., Rossmann M. G. Comparison of super-secondary structures in proteins. J Mol Biol. 1973 May 15;76(2):241–256. doi: 10.1016/0022-2836(73)90388-4. [DOI] [PubMed] [Google Scholar]
  42. Remington S. J., Matthews B. W. A systematic approach to the comparison of protein structures. J Mol Biol. 1980 Jun 15;140(1):77–99. doi: 10.1016/0022-2836(80)90357-5. [DOI] [PubMed] [Google Scholar]
  43. Ring C. S., Kneller D. G., Langridge R., Cohen F. E. Taxonomy and conformational analysis of loops in proteins. J Mol Biol. 1992 Apr 5;224(3):685–699. doi: 10.1016/0022-2836(92)90553-v. [DOI] [PubMed] [Google Scholar]
  44. Rini J. M., Schulze-Gahmen U., Wilson I. A. Structural evidence for induced fit as a mechanism for antibody-antigen recognition. Science. 1992 Feb 21;255(5047):959–965. doi: 10.1126/science.1546293. [DOI] [PubMed] [Google Scholar]
  45. Saul F. A., Amzel L. M., Poljak R. J. Preliminary refinement and structural analysis of the Fab fragment from human immunoglobulin new at 2.0 A resolution. J Biol Chem. 1978 Jan 25;253(2):585–597. [PubMed] [Google Scholar]
  46. Shenkin P. S., Yarmush D. L., Fine R. M., Wang H. J., Levinthal C. Predicting antibody hypervariable loop conformation. I. Ensembles of random conformations for ringlike structures. Biopolymers. 1987 Dec;26(12):2053–2085. doi: 10.1002/bip.360261207. [DOI] [PubMed] [Google Scholar]
  47. Sheriff S., Silverton E. W., Padlan E. A., Cohen G. H., Smith-Gill S. J., Finzel B. C., Davies D. R. Three-dimensional structure of an antibody-antigen complex. Proc Natl Acad Sci U S A. 1987 Nov;84(22):8075–8079. doi: 10.1073/pnas.84.22.8075. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Smith K. C., Honig B. Evaluation of the conformational free energies of loops in proteins. Proteins. 1994 Feb;18(2):119–132. doi: 10.1002/prot.340180205. [DOI] [PubMed] [Google Scholar]
  49. Stanfield R. L., Fieser T. M., Lerner R. A., Wilson I. A. Crystal structures of an antibody to a peptide and its complex with peptide antigen at 2.8 A. Science. 1990 May 11;248(4956):712–719. doi: 10.1126/science.2333521. [DOI] [PubMed] [Google Scholar]
  50. Strong R. K., Campbell R., Rose D. R., Petsko G. A., Sharon J., Margolies M. N. Three-dimensional structure of murine anti-p-azophenylarsonate Fab 36-71. 1. X-ray crystallography, site-directed mutagenesis, and modeling of the complex with hapten. Biochemistry. 1991 Apr 16;30(15):3739–3748. doi: 10.1021/bi00229a022. [DOI] [PubMed] [Google Scholar]
  51. Summers N. L., Karplus M. Modeling of globular proteins. A distance-based data search procedure for the construction of insertion/deletion regions and Pro----non-Pro mutations. J Mol Biol. 1990 Dec 20;216(4):991–1016. doi: 10.1016/S0022-2836(99)80016-3. [DOI] [PubMed] [Google Scholar]
  52. Tramontano A., Lesk A. M. Common features of the conformations of antigen-binding loops in immunoglobulins and application to modeling loop conformations. Proteins. 1992 Jul;13(3):231–245. doi: 10.1002/prot.340130306. [DOI] [PubMed] [Google Scholar]
  53. Tuffery P., Etchebest C., Hazout S., Lavery R. A new approach to the rapid determination of protein side chain conformations. J Biomol Struct Dyn. 1991 Jun;8(6):1267–1289. doi: 10.1080/07391102.1991.10507882. [DOI] [PubMed] [Google Scholar]
  54. Vix O., Rees B., Thierry J. C., Altschuh D. Crystallographic analysis of the interaction between cyclosporin A and the Fab fragment of a monoclonal antibody. Proteins. 1993 Apr;15(4):339–348. doi: 10.1002/prot.340150402. [DOI] [PubMed] [Google Scholar]
  55. Wilson C., Gregoret L. M., Agard D. A. Modeling side-chain conformation for homologous proteins using an energy-based rotamer search. J Mol Biol. 1993 Feb 20;229(4):996–1006. doi: 10.1006/jmbi.1993.1100. [DOI] [PubMed] [Google Scholar]
  56. de la Paz P., Sutton B. J., Darsley M. J., Rees A. R. Modelling of the combining sites of three anti-lysozyme monoclonal antibodies and of the complex between one of the antibodies and its epitope. EMBO J. 1986 Feb;5(2):415–425. doi: 10.1002/j.1460-2075.1986.tb04227.x. [DOI] [PMC free article] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES