Tension-dependent Regulation of Microtubule Dynamics at Kinetochores Can Explain Metaphase Congression in Yeast

Abstract

During metaphase in budding yeast mitosis, sister kinetochores are tethered to opposite poles and separated, stretching their intervening chromatin, by singly attached kinetochore microtubules (kMTs). Kinetochore movements are coupled to single microtubule plus-end polymerization/depolymerization at kinetochore attachment sites. Here, we use computer modeling to test possible mechanisms controlling chromosome alignment during yeast metaphase by simulating experiments that determine the 1) mean positions of kinetochore Cse4-GFP, 2) extent of oscillation of kinetochores during metaphase as measured by fluorescence recovery after photobleaching (FRAP) of kinetochore Cse4-GFP, 3) dynamics of kMTs as measured by FRAP of GFP-tubulin, and 4) mean positions of unreplicated chromosome kinetochores that lack pulling forces from a sister kinetochore. We rule out a number of possible models and find the best fit between theory and experiment when it is assumed that kinetochores sense both a spatial gradient that suppresses kMT catastrophe near the poles and attachment site tension that promotes kMT rescue at higher amounts of chromatin stretch.

INTRODUCTION

During mitosis, a dynamic array of kinetochore microtubules (kMTs) serve to accurately segregate a duplicated genome into two complete sets of chromosomes (Inoue and Salmon, 1995; Rieder and Salmon, 1998; Nasmyth, 2002; Howard and Hyman, 2003; Scholey et al., 2003). Budding yeast offers an attractive system for answering fundamental questions about the regulation of kMT dynamics, because each kinetochore is thought to be attached to only one kMT plus-end (Peterson and Ris, 1976; Winey et al., 1995; O'Toole et al., 1999). The relative simplicity of the yeast spindle, with ∼16 kMT minus-ends anchored at each pole, makes this an excellent system for computational modeling. Although the dynamics of individual kMTs have not been directly observed in vivo, kMT-plus ends seem to exhibit dynamic instability, switching stochastically between extended periods of polymerization and depolymerization (Maddox et al., 2000; Pearson et al., 2001). In general, regulation of microtubule (MT) dynamic instability involves control of four parameters: the rates of polymerization and depolymerization, and the frequencies of catastrophe (transition from growing to shortening) and rescue (transition from shortening to growing) events. In budding yeast, kinetochore movement during metaphase is coupled to individual kMT growth and shortening, which likely occurs solely by polymerization and depolymerization at the kinetochore-attached kMT plus-ends (Maddox et al., 2000; Pearson et al., 2003).

Labeling of single centromere proximal markers in yeast indicates that sister centromeres separate toward opposite sides of the spindle during metaphase and exhibit abrupt transitions in their direction of movement, as would be expected for dynamic instability of kMTs (He et al., 2000; Tanaka et al., 2000; Goshima and Yanagida, 2001; Pearson et al., 2001). Fluorescently labeled kinetochores persist in clusters midway between each spindle pole body and the spindle equator during yeast metaphase, and therefore the oscillations of fluorescent probes on chromosome arms suggest that dynamic kMT plus-ends coordinate congression of kinetochores to a steady-state, bilobed metaphase configuration in yeast (Pearson et al., 2001; Krishnan et al., 2004).

Green fluorescent protein (GFP) kinetochore fusions, such as Cse4-GFP, allow for live cell imaging of kinetochores in yeast spindles (Meluh et al., 1998; Chen et al., 2000; Pearson et al., 2001). In our previous work, a stochastic model of kMT plus-end dynamics in the budding yeast metaphase spindle was developed and then evaluated by simulating images of kinetochore-associated fluorescent probes (Sprague et al., 2003). Although individual kMT dynamics cannot be resolved, computer simulations of kMT dynamics combined with statistical measures of how well the simulation data predict experimental fluorescence kinetochore distributions recorded by live cell imaging can be used to build an understanding of budding yeast mitotic spindle kMT dynamics (Sprague et al., 2003). Through this analysis, it was demonstrated that a model based on any set of constant dynamic instability parameters was insufficient to explain how kinetochores tend to cluster midway between the poles and the equator in yeast metaphase spindles (Sprague et al., 2003). However, reasonable agreement between simulated and experimental data for the distribution of kinetochores was found using a model with a temporally stable spatial gradient between the spindle poles in either catastrophe or rescue frequency combined with constant values for the other frequency (Sprague et al., 2003). For example, in the spatial gradient models, higher frequencies of catastrophe in the middle of the spindle relative to the poles promoted kinetochore movement poleward, or higher frequencies of rescue near the poles relative to the middle of the spindle promoted kinetochore movement away from the poles.

It has been proposed for higher eukaryotes that mechanical tension on the kinetochore could modulate MT stability, acting as a key regulator of kMT dynamics (Nicklas, 1988; Skibbens et al., 1993, 1995; Rieder and Salmon, 1994, 1998; Inoue and Salmon, 1995; Skibbens and Salmon, 1997). Recent evidence in Xenopus extract spindles indicated that mechanical stress regulates MT dynamics locally at the kinetochore–MT attachment site, such that tension between sister kinetochores may promote MT polymerization (Maddox et al., 2003; Cimini et al., 2004). In addition, tension between sister kinetochores is important for the stability of kMT attachments and for turning off the spindle checkpoint that regulates anaphase onset in yeast (Dewar et al., 2004). Due to the significant spacing between sister kinetochores in yeast metaphase (∼700 nm), communication between sister kinetochores is likely facilitated via mechanical tension through the intervening chromatin, because chemical signaling over such a distance would be improbable.

Here, we have used computer simulation to explore how mechanical tension at the kinetochore might contribute to metaphase chromosome alignment in budding yeast. First, we established that spatial gradient models similar to those described by Sprague et al. (2003) do not predict the low incidence of kinetochores crossing the equator, as observed experimentally by measurements of fluorescence recovery after photobleaching (FRAP) of the kinetochore-associated protein Cse4-GFP (Pearson et al., 2004). We then tested four various ways that kinetochore tension alone or in combination with catastrophe or rescue gradients between the poles would predict the extent of kinetochore movements as measured by the Cse4-green fluorescent protein (GFP) FRAP data. The best fit to the experimental data was achieved by kinetochores sensing a stable gradient between the poles to spatially control kMT plus-end catastrophe frequency and by sensing tension generated via chromatin stretching between sister kinetochores to control kMT plus-end rescue frequency. This model also quantitatively reproduces metaphase kinetochore distributions and kMT dynamics as measured by GFP-Tubulin FRAP experiments without parameter value adjustment between different experimental data sets. In addition, by eliminating simulated tension between sister kinetochores, the model quantitatively reproduces the kinetochore distribution in yeast mutants (cdc6) that enter mitosis with unreplicated chromosomes. In these cells, chromosomes in mitosis have single kinetochores and thus lack the tension generated via chromatin stretching from a sister kinetochore. Kinetochores in cdc6 mutant spindles achieve average positions up close to the poles, positions not predicted by the rescue gradient model.

All of the simulations were based on the explicit assumptions that 1) kMT dynamics are at steady state during metaphase (Figure S1 and Supplemental Material), 2) there is one kinetochore attached per MT, 3) MT assembly dynamics occur only at the kinetochore, 4) kinetochores do not detach from MTs during steady-state metaphase, and 5) the kinetochore marker Cse4-GFP closely tracks the plus-end dynamics of kMTs (see Figure S2). In addition, spindle length was held constant during each simulation, although the exact distribution of experimentally observed spindle lengths was reproduced in both wild-type and cdc6 simulations such that spindle length was allowed to vary between each simulation. A number of alternate models were considered and failed to reproduce one or more of the four different experimental results (Table S1 and Supplemental Material). In this way, we show that a model in which the kinetochore regulates kMT dynamics by sensing both distance from its sister kinetochore (via tension) and spindle position relative to the middle of the spindle (via a catastrophe gradient) is able to reproduce experimentally observed kinetochore dynamics and congression in yeast metaphase.

MATERIALS AND METHODS

Yeast Strains and Media

The yeast strains used for this study were KBY2125 (MATa cdc6GAL-CDC6: URA cdc15-2 PDS1 myc:LEU2 pKK1 cse4::HB SPC29CFPKAN), KBY2010 (MATa trp1-63, leu2-1, ura3-52, his3-200, lys2-801 cse4::HYG pKK1) and KBY2012 (MATa trp1-63, leu2-1, ura3-52, his3-200, lys2-801 cse4::HYG SPC29-CFP-KAN pKK1). Fluorescent constructs to generate GFP-labeled kinetochores (Cse4-GFP) and cyan fluorescent protein (CFP)-labeled centromeres (Spc29-CFP) were described previously (Pearson et al., 2001).

Cell growth techniques and conditions were described previously (Sprague et al., 2003). However, KBY2125 was grown in galactose media for expression of Cdc6p. Unreplicated chromosomes were generated by arresting an asynchronous culture in S phase with 200 mM hydroxyurea (HU) for 2 h. Cells were then washed into glucose media to repress Cdc6p expression with HU for 1 h, released from HU into glucose media, and allowed to complete replication and progress through mitosis. Cells were then allowed to progress into a second mitosis with unreplicated chromosomes. Control cells were created by repeating the S-phase arrest protocol in galactose only to maintain Cdc6p expression.

Fluorescence Microscopy

All cell imaging was performed as reported previously (Pearson et al., 2001; Sprague et al., 2003).

Simulation of MT Dynamics

A Monte Carlo technique was used to simulate individual kMTs undergoing dynamic instability using MATLAB (version 6.0; Mathworks, Natick, MA) as described previously (Sprague et al., 2003). Additional details provided in Supplemental Material.

Simulation of Image Formation by Fluorescence Microscopy

Simulated kinetochore positions were compared with experimentally obtained images of kinetochore-bound fluorescence by simulation of the image formation process in fluorescence microscopy (Sprague et al., 2003). Briefly, it was assumed that each kinetochore remained attached to the tip of its kMT for the duration of the simulated experiments. At specified time points in each simulated experiment, a simulated fluorescence image of the spindle was generated by convolving the three-dimensional point spread function of the microscope with the kinetochore and spindle pole body position matrices (Sprague et al., 2003).

Simulation of Cse4-GFP and GFP-Tubulin FRAP Experiments

FRAP experiments were simulated by modeling experimental fluorescence bleaching events and quantifying recovery over time. Detailed simulation methods are described in Supplemental Materials.

Simulation of Kinetochore Distribution in cdc6 (Replication-deficient) Spindles

As in the simulation of wild-type spindles, the spindle length and relative background noise for each cdc6 replication-deficient experimental image were matched to create a simulated fluorescence image of each mutant spindle. All remaining aspects of the MT dynamics simulations were identical to wild-type cells, with the exception that eight kMTs were modeled per spindle pole rather than 16 for replicated chromosomes. It was assumed that, on average, the 16 single kinetochores were distributed in equal numbers to each pole.

RESULTS

Model Assumptions

As in previous work (Sprague et al., 2003), we have used a simplified model of the yeast metaphase spindle to test mechanisms for the congression of kinetochores to a metaphase configuration. All models considered assumed that kMTs exhibit dynamic instability, as observed in yeast cytoplasmic MTs (Carminati and Stearns, 1997; Shaw et al., 1997; Tirnauer et al., 1999; Kosco et al., 2001; Gupta et al., 2002) (see Supplemental Material for further review).

In terms of spindle structure, the model was constructed to be consistent with electron micrographs of the yeast spindle (Winey et al., 1995), where kMT tips were only allowed to grow straight from the spindle pole (i.e., no microtubule curving or splaying was allowed). In addition, any kMT that grew the entire length of the spindle to the opposite pole immediately switched to a shortening state, whereas any kMT that completely shortened to its spindle pole immediately switched to a growth state.

In the simulation, all growth and shortening was assumed to take place at the kMT plus-ends. Minus-end depolymerization (i.e., poleward flux) was not required to reproduce results in any of the simulations. Rates of kMT polymerization and depolymerization were assumed to be constant over the length of the spindle, and unaffected by force, as suggested by recent measurements in Xenopus extract spindles (Tirnauer et al., 2004).

In all cases, kinetochores were assumed to remain attached to the plus-end tip of the kMT throughout the simulation, an assumption supported by lack of recovery in Cse4-GFP FRAP experiments (Pearson et al., 2004). In addition, possible lateral interactions between chromosomes and kMTs are ignored in the simple Hookean spring model for tension between sister kinetochores. For example, chromosomes could become transiently associated with interpolar MTs so that the forces on the two kinetochores would not be equal and opposite, as we assumed. In the interest of parsimony, we opted for the simplest possible model that explains all of the data analyzed.

Models without Tension-dependent Dynamic Instability Parameters Allow Equator Crossing

To determine the extent of kinetochore equator crossing in yeast metaphase spindles, kinetochore-associated Cse4-GFP fluorescence in one-half-spindle was photobleached and spindles observed for 10 min. A mean Cse4-GFP recovery percentage of 4.5 ± 7.3% (n = 9; Figure 1D) was observed in 10-min recovery time experiments (Pearson et al., 2004). This low level of fluorescence recovery indicates that kinetochores are highly constrained to their respective half-spindle (Pearson et al., 2004). Because cells proceed normally into anaphase after photobleaching of Cse4-GFP, it is not likely that photodamage has affected normal kinetochore dynamics. In addition, FRAP experiments performed using centromere-proximal GFP-lacI/lacO markers indicated that these markers were stably oriented to their respective bud or mother cell, supporting a low incidence of kinetochores switching attachment to their respective poles in yeast metaphase spindles (Pearson et al., 2004). Sister centromeres rarely reassociate after separation during metaphase, such that switching from one spindle-half to another would be unlikely (Goshima and Yanagida, 2001; Pearson et al., 2001).

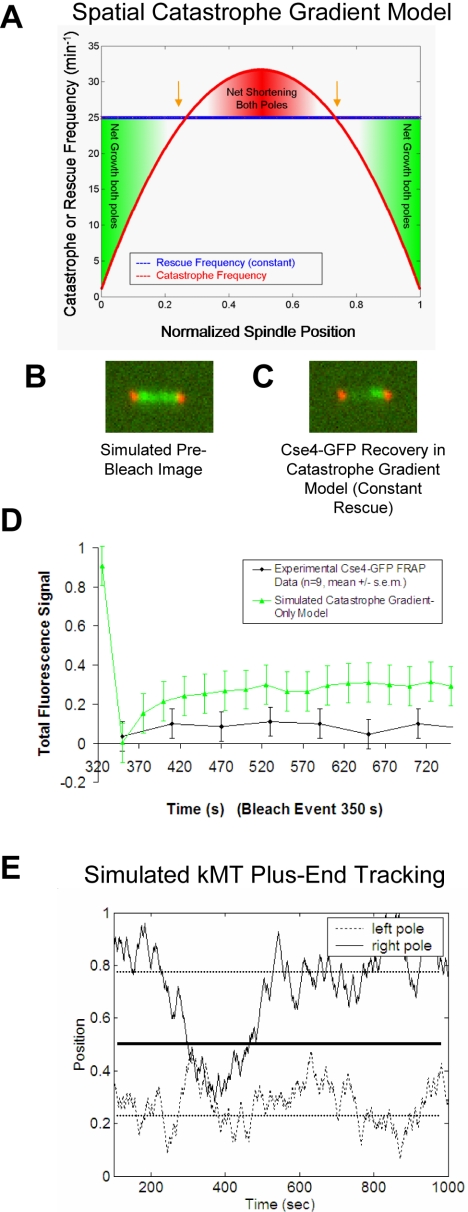
Figure 1.

Position-dependent gradient models for the regulation of kMT dynamics fail to reproduce Cse4-GFP FRAP experimental results. (A) The catastrophe gradient model: kMT plus-end catastrophe frequency peaks at the spindle equator, whereas plus-end rescue frequency remains constant. (B) Representative simulated image before the bleach event using the catastrophe gradient model (kinetochore-associated Cse4-GFP, green; spindle pole body-associated Spc29-CFP, red). (C) Significant fluorescence recovery of kinetochore-associated Cse4-GFP fluorescence using the spatial catastrophe gradient model does not reproduce experimental results. (D) Representative Cse4-GFP FRAP experimental and simulated time series of fluorescence recovery. Kinetochore-associated markers in one-half-spindle were bleached and then observed over time to quantify fluorescence recovery. Because Cse4-GFP is stably bound at the kinetochore, fluorescence recovery results exclusively from redistribution of kinetochores between spindle halves. The lack of recovery observed experimentally indicates that kinetochores remain constrained to their own half-spindle throughout the experiment. Models with position-dependent catastrophe frequencies only (i.e., no tension dependence) do not limit spindle-equator crossing sufficiently to reproduce experimental results. (E) Typical simulated plus-end kMT positions at steady state using the spatial catastrophe gradient model for regulation of MT dynamics. The representative trace shows a pair of sister kMT plus ends and their movements relative to the spindle poles and the equator. Although individual kinetochores separate and oscillate on either side of the spindle equator, kinetochores frequently move into the opposite half-spindle for extended periods of time.

A limitation of this experiment and of yeast spindles in general is that individual kinetochores cannot be directly tracked. For this reason, simulation is extremely helpful in understanding how the dynamics of individual kinetochores could be regulated to reproduce the low level of fluorescence recovery, as observed in the Cse4-GFP FRAP experiments.

kMT dynamics were simulated using models with spatial gradients in catastrophe and rescue frequency for plus-ends as a function of position along the spindle axis (Sprague et al., 2003) (Figure 1A). Cse4-GFP FRAP simulations were run for each model using parameter values that were optimized to best reproduce the experimentally observed kinetochore distributions for wild-type metaphase spindles (a constraint not imposed in previous work; Pearson et al., 2004). Position-dependent models for regulation of kMT plus-end catastrophe frequency (Figure 1A) or rescue frequency performed poorly in the Cse4-GFP FRAP simulations (Table 1 and Figure 1, B–D), meaning that these models do not effectively constrain kinetochores to the correct half-spindle (Figure 1E). Here, we calculate a “probability of fit” (p value) to evaluate statistically how well the mean experimental Cse4-GFP fluorescence recovery percentage would fit into a set of 50 mean simulated recovery percentages (n = 13, each simulation; see Supplemental Material for details). Models with calculated p values < 0.05 on any single test were considered to be unacceptable, whereas models with p > 0.05 could not be statistically ruled out. In general, both the catastrophe gradient model and the rescue gradient model predict clustering of kinetochores into a bilobed metaphase configuration (peak kinetochore clustering at gold arrows, Figure 1A). However, the symmetry of each of these two models does not provide sufficient a directional cue at the kMT plus-end to ensure that kinetochores remain confined to the half-spindle to which they are directly attached. This results in equator-crossing events, because kinetochores tend to cluster on either side of the equator, without regard to their spindle pole body attachment side and without regard to the behavior of their sister kinetochore (Figure 1E).

Table 1.

Cse4-GFP FRAP simulation results

Model description	Simulated mean Cse4-GFP recovery %a	Probability of fit to experimental results (p value)b
Experimental results	4.5 ± 7.3c
Position-dependent regulation of kMT catastrophe frequencya	13.8 ± 2.5	<0.02
Position-dependent regulation of kMT rescue frequencya	19.2 ± 10.1	<0.02
Position-dependent catastrophe + tension-dependent rescuea	6.5 ± 1.7	0.24
Position-dependent rescue + tension-dependent catastrophea	8.3 ± 2.0	0.05

^aAll mean recovery percentages are reported for model parameter sets that are optimized to qualitatively reproduce steady-state Cse4-GFP kinetochore clustering in yeast metaphase spindles

^bThe probability of fit (p value) was calculated through comparison of experimental mean recovery values to the range of simulated recovery values over 50 experiments (see Supplemental Material for calculation details). The 10-min time point data was used for comparison with simulation, because the simulation was allowed to run for a simulated recovery time of 10 min before evaluation of simulated recovery

^cExperimental results reported for 10-min recovery times (n = 9) (Pearson et al., 2004)

Models Including Tension-dependent Dynamic Instability Parameters Limit Equator Crossing and Reproduce Kinetochore Cse4-GFP FRAP Experiments

Because both the catastrophe and rescue gradient models failed, we then considered models in which the parameters of kMT plus-end dynamic instability depended not only on position but also on tension generated by the stretch of chromatin between sister kinetochores. In this model, sister kinetochores are assigned such that the position of each kinetochore in the spindle has a direct impact on the dynamics of its sister kinetochore in the opposite half-spindle based on the amount of centromere stretch. High tension is proposed to promote rescue and thus kinetochore movement away from the kMT-attached pole, or alternatively low tension is proposed to promote catastrophe and therefore kinetochore movement toward the pole.

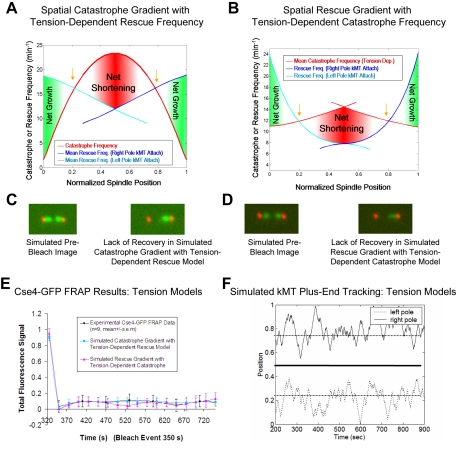
Two models that included position-dependent gradients and tension to control catastrophe or rescue frequencies at kMT plus-ends successfully reproduced the lack of Cse4-GFP FRAP observed experimentally (Table 1 and Figure 2, A–E). Therefore, both of these models effectively control kinetochore dynamics by keeping centromeres in their respective half-spindle (Figure 2F) and thus act to minimize fluorescence recovery in the simulated Cse4-FRAP experiment. The reason these models succeed is because as a simulated kinetochore enters the opposite half-spindle during plus-end assembly, it tends to approach its sister kinetochore. This reduces tension, destabilizing the kMT plus-end, so that the kinetochore rapidly returns to its own half-spindle (Figure 2F).

Figure 2.

Models where kinetochores sense both spindle position to regulate kMT plus-end catastrophe frequency and tension due to chromatin stretch to regulate kMT plus-end rescue frequency successfully reproduce Cse4-GFP FRAP experimental results. Excursions of kMT plus-ends into the opposite spindle half are limited, and therefore these models quantitatively reproduce Cse4-GFP FRAP experimental results. (A) The spatial model for regulation of kMT plus-end catastrophe frequency with kMT rescue frequency regulated by tension generated via chromatin stretch between separated sister kinetochores: rescue frequencies shown are mean values calculated for a given spindle position during the simulation, because rescue frequency is directly dependent on the sister kinetochore separation distance. Dependence of kMT plus-end rescue frequency on tension between sister kinetochores is directional, such that mean rescue frequencies tend to decrease as kMTs lengthen, due to decreased separation between sister kinetochores. For this distribution, Vg = Vs = 2.0 μm/min and the spring constant is ρ^* = 0.9 μm^-1. Gold arrows correspond to the spindle locations of predicted peaks in kinetochore-associated Cse4-GFP fluorescence. (B) The spatial model for regulation of kMT plus-end rescue frequency with kMT catastrophe frequency regulated by tension between sister kinetochores. (C) Representative simulated images for the Cse4-GFP FRAP experiment using a model where the kinetochore senses spindle position to regulate kMT plus-end catastrophe frequency and senses tension generated via chromatin stretch to regulate kMT plus-end rescue frequency. For the model shown in A, there is negligible visible recovery in Cse4-FRAP experiment simulations, reproducing experimental results. (D) Simulated Cse4-GFP FRAP images for the model shown in B. (E) Representative Cse4-GFP FRAP experimental and simulated time series of fluorescence recovery. Models that include regulation of kMT plus-end switching frequencies based on tension between sister kinetochores reproduce experimental results. (F) Typical simulated plus-end kMT positions at steady state for the models shown in A and B. Here, equator crossing is limited, because kMT plus-ends are less likely to experience rescue events as kinetochores move closer to their sisters. Kinetochores rarely cross the equator, but remain dynamic, moving toward the spindle equator and back to the poles.

Ranges of acceptable parameter values across all wild-type kMT models and experiments are listed in Table 2. The ranges of values for growth and shrinking velocities are similar to those measured for cytoplasmic MTs during metaphase, and catastrophe and rescue frequency model values are somewhat higher than values reported for cytoplasmic MTs (Table 2). The “spring constant” determines the magnitude of the tension effect. Although a lower tension effect can be somewhat offset by increasing the gradient in catastrophe frequency, a minimum value for the spring constant (0.8 μm^-1) is required to impart directionality to the model, thus maintaining kinetochores in the correct half-spindle throughout the simulation. To reject a given model, parameter sets were tested and optimized over a wide range of parameters, similar to previous work (Sprague et al., 2003).

Table 2.

Wild-type model parameter value ranges and constraints

Parameter description	Symbol	Range of acceptable values (all wild-type models)
Growth velocity	Vg	1.0-2.0 μm/mina
Shortening velocity	Vs	1.0-2.0 μm/minb
Spring constantc	ρ*	0.8-1.5 μm-1
Catastrophe frequency	kc	0.25-35 min-1d
Rescue frequency	kr	2.0-25 min-1e

^aCytoplasmic MT measurements, V_g = 0.5 μm/min (Carminati and Stearns, 1997)

^bCytoplasmic MT measurements, V_s =1.35 μm/min (Carminati and Stearns, 1997)

^cApplies to models with tension-dependent switching frequencies only

^dLonger cdc6 mutant spindles result in a higher calculated catastrophe frequency at the spindle equator, as shown in Figure 4A. Cytoplasmic MT measurements, k_c = 0.12 min^-1 (Carminati and Stearns, 1997)

^eCytoplasmic MT measurements, k_r = 0.36 min^-1 (Carminati and Stearns, 1997)

Experimental Metaphase Kinetochore Distributions Are Correctly Predicted by Models Including Tension-dependent Dynamic Instability Parameters

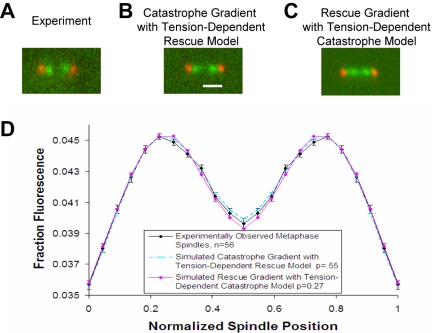
To further assess models combining stable spatial gradients in catastrophe or rescue frequency with tension-dependent parameters, simulations of kMT dynamics were run and the plus-end positions were recorded at the conclusion of each simulation. These positions were used to generate simulated fluorescence images of kinetochore-bound Cse4-GFP (Figure 3, B and C). Statistical comparison of simulated Cse4-GFP images to the experimentally observed steady-state metaphase kinetochore fluorescence distribution was then used as a computational screen for selection of valid models (see Figure S1 and Supplemental Material for analysis of steadystate metaphase). The two models where catastrophe and rescue frequency depend on both a spatial gradient and kinetochore tension were successful in predicting the average distribution of kinetochores between the poles at metaphase (Figure 3, A–D, and Table S1). Spatial gradient models with no tension-dependent parameters qualitatively reproduced experimentally observed metaphase kinetochore clustering but resulted in low calculated p values (Table S1). By quantitatively analyzing experimental spindle images to include steady-state metaphase spindles only (see Supplemental Material), models for regulation of kMT dynamics are more tightly constrained compared with our previous work (Sprague et al., 2003).

Figure 3.

The models shown in Figure 2, A and B, reproduce experimental metaphase kinetochore clustering. (A) Experimental metaphase spindle image of Cse4-GFP–labeled kinetochores (green) relative to Spc29-CFP–labeled spindle poles (red). (B) Representative simulated image using the model as shown in Figure 2A. Tight kinetochore-associated fluorescence clusters are comparable with the experimental image. Bar, 1000 nm. (C) Representative simulated image using the model as shown in Figure 2B. (D) Quantitative analysis of average simulated kinetochore clustering observed via Cse4-GFP compared with mean experimental results. Simulation results reproduce experimental results for both the model shown in Figure 2A and the model in Figure 2B.

Kinetochore Distributions in Metaphase Spindles Lacking Tension Are Correctly Predicted by the Catastrophe Gradient with Tension-dependent Rescue Model

To test the hypothesis that tension between sister kinetochores regulates kMT dynamics in yeast, we performed experiments using a replication deficient cdc6 mutant that is incapable of developing tension between sister kinetochores (Stern and Murray, 2001). Here, chromosomes in mitosis have single kinetochores and lack the tension generated via chromatin stretching from a sister kinetochore.

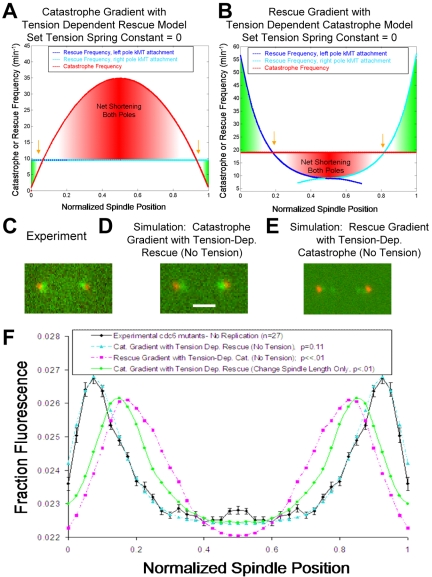
Kinetochore positions at metaphase in cdc6 mutants were quantified using the Cse4-GFP fluorescence distribution (n = 27 cells, 54 spindle halves). The cdc6 mutant cells generally had spindles with kinetochore clusters very near to each spindle pole body, as shown in Figure 4C. The peak in mean kinetochore-associated fluorescence relative to the pole was ∼0.21 μm in cdc6 mutants, compared with ∼0.39 μm in control metaphase cells, a ∼46% reduction in mean kMT length. These experimental results indicate that kMT dynamics are altered in spindles lacking tension between sister kinetochores, resulting in net shortening of average kMT lengths.

Figure 4.

Experimental measurement and simulation of the kinetochore-associated fluorescence distribution in cdc6 mutant cells. (A) In a model where kinetochores regulate kMT plus-end rescue frequency by sensing tension generated through the stretch of chromatin between sister kinetochores, cdc6 mutant cells with single-kinetochore chromatin can be modeled by reducing the tension spring constant to zero and increasing simulated spindle lengths to match experimentally observed values. Gold arrows indicate the locations of predicted peaks in kinetochore-associated fluorescence. For this distribution, Vg = Vs = 1.7 μm/min and the spring constant is ρ^* = 0 μm^-1. (B) The tension spring constant is reduced to zero in a model where the kinetochores regulate kMT plus-end catastrophe frequency by sensing tension generated via the stretch of chromatin between sister kinetochores. (C) The experimental effect of loss of tension in Cdc6p depleted cells. Kinetochores (Cse4-GFP, green) are clustered near the poles (Spc29-CFP, red), indicating that the net kMT length is shorter in the mutant spindles compared with wild-type cells. (D) Simulated effect of loss of tension between sister kinetochores using a model where rescue frequency is regulated by tension. Kinetochores are clustered very near to the poles, qualitatively and quantitatively reproducing experimental observations of cdc6 mutant cells. Bar, 1000 nm. (E) Simulated effect of loss of tension using a model where catastrophe frequency is regulated by tension at the kinetochore. (F) Quantitative analysis of simulated kinetochore clustering compared with experimental fluorescence distribution in tension-deficient spindles. Models with increased spindle length but without tension loss do not reproduce experimental results (p < 0.01). In addition, the rescue gradient model with tension dependent catastrophe frequency fails to reproduce experimental results (p < 0.01).

Before simulation of the cdc6 mutant data, parameter value sets for each model to be tested were adjusted to reproduce the Cse4-GFP fluorescence distribution for GALCDC6 control cells grown in galactose media (with replication) and arrested in HU (p > 0.10). Specifically, V_g and V_s were reduced by ∼15% in all models compared with previous yeast strain simulations, although values remained well within the range of values given in Table 1. Tension-dependent catastrophe and tension-dependent rescue models were then used to simulate kinetochore movements in the cdc6 mutants by reducing the spring constant in each model to zero (Figure 4, A and B). This reduction effectively eliminated any tension effect on kMT dynamics. A catastrophe frequency gradient together with a tension-dependent rescue frequency model modified such that the chromatin spring constant was reduced to zero was successful in quantitatively reproducing the kinetochore distribution in tension deficient spindles (p = 0.11; Figure 4, A, D, and F). In contrast, a model based on a position-dependent rescue gradient with the spring constant for a tension-based catastrophe frequency model reduced to zero performed very poorly in predicting kinetochore positions in cdc6 mutants (p << 0.01; Figure 4, B, E, and F). The position-dependent rescue gradient model relies on a high rescue frequency at the poles, which decreases toward the spindle equator. This tends to push kinetochore clusters toward the equator, such that rescue gradient models are ineffective in reproducing kinetochore clusters very near to the poles, as was experimentally observed in the cdc6 mutant phenotype. These results argue against a spatial rescue gradient model for regulation of budding yeast kMT dynamics during metaphase.

Thus, a model where the kinetochore senses spindle position to regulate kMT plus-end catastrophe frequency and senses tension generated from the stretch of chromatin between sister kinetochores to regulate kMT plus-end rescue frequency was the single model that was able to reproduce all experimental results (see Table S1 and Supplemental Material for further details).

GFP-Tub1 FRAP Experiments Are Correctly Predicted by Simulated kMT Dynamics

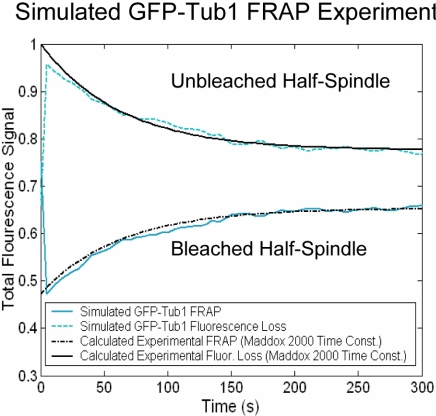
The final step in our analysis was to ask how well simulated kinetochore dynamics predict metaphase kMT dynamics. GFP-Tub1 FRAP experiments were simulated using the parameter value sets as defined above (Table 1) and then compared with published results (Maddox et al., 2000). Interpolar MTs were assumed to be stable and nondynamic in the simulation, such that all recovery was the result of kMT plus-end dynamics, as in Figure 2F. GFP-Tub1 recovery profiles for simulated kMT dynamics qualitatively and quantitatively reproduced experimental results (Figure 5) for the parameter values of dynamic instability listed in Table 1. The average experimental time to half-maximal recovery was 52 ± 24 s (n = 6; Maddox et al., 2000), compared with a simulated half-maximal recovery time of 53 ± 15 s (n = 6). Growth and shortening velocities were highly constrained in simulations of the GFP-Tub1 FRAP data. Rapid velocities (>2 μm/min) generally resulted in faster MT turnover than is experimentally observed.

Figure 5.

Simulation of GFP-Tub1 FRAP experiments. Experimentally, GFP-Tub1 labeled spindles are imaged, and half-spindles are photobleached at time t = 0 (Maddox et al., 2000). FRAP of the bleached half-spindle and loss-of-fluorescence in the unbleached half-spindle are quantified experimentally and in simulations. Simulated results are compared with live cell experimental data from Maddox et al. (2000). For the simulation results shown, Vg = Vs = 2.0 μm/min and the spring constant is ρ^* = 0.9 μm^-1. Catastrophe and rescue frequency are modeled as shown in Figure 2A. GFP-Tub1 recovery profiles for simulated kMT dynamics qualitatively and quantitatively reproduce experimental results (p = 0.96). The average experimental time to half-maximal recovery was 52 ± 24 s (n = 6; Maddox et al., 2000), compared with a simulated half-maximal recovery time of 53 ± 15 s (n = 6).

DISCUSSION

The Extent of Kinetochore Oscillation Is Limited in Models with kMT Plus-End Dynamic Instability Regulated by Tension, Thus Reproducing Cse4-GFP FRAP Results

Regulation of kMT dynamics in a local tension-dependent manner results in a “self-correcting” system, in which the range of chromatin stretching, and therefore the mean sister kinetochore separation distances, are tightly controlled. In a model where catastrophe is regulated by a spatial gradient and rescue is regulated by tension between sister kinetochores, kMT lengths will tend to be most stable at moderate tension values (Figures 2A and 6A, gold arrows), away from the high catastrophe zone at the spindle equator. In this way, congression of kinetochores to a metaphase configuration can be accurately reproduced regardless of the initial positions of the MT-attached kinetochores, as shown in Figure 6B.

Figure 6.

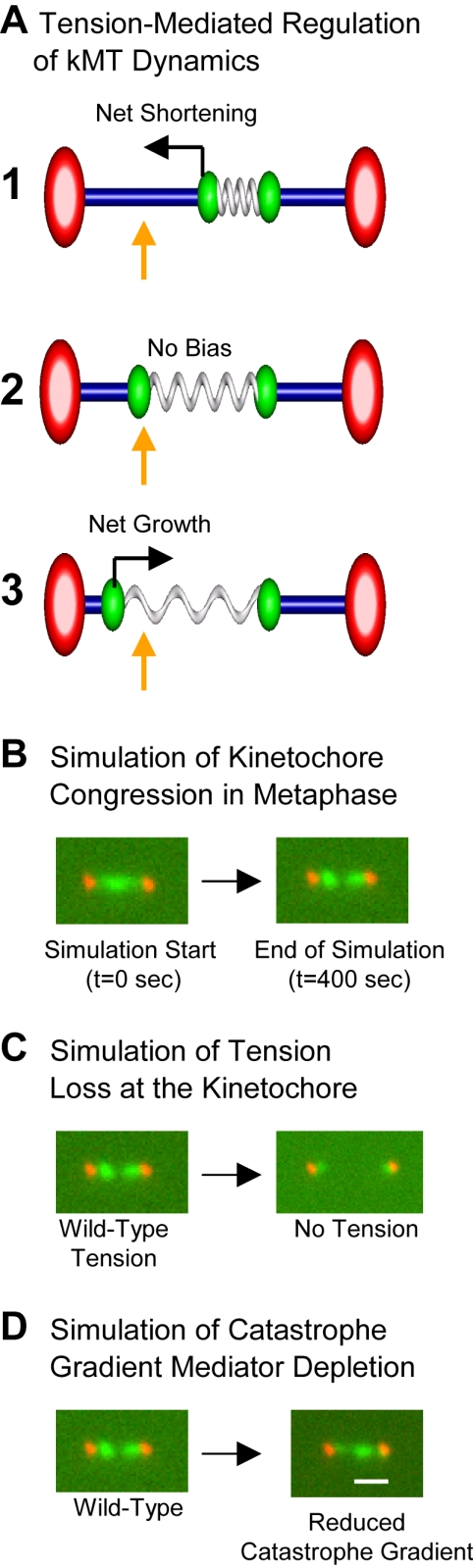
Model for metaphase congression in budding yeast. For clarity, the right kinetochore is fixed at its mean position, whereas the left kinetochore moves, although both kinetochores are dynamic in simulation, each affecting the relative tension experienced by its assigned sister. Kinetochores are green, spindle pole bodies red, kMTs blue, and the cohesin/chromatin “spring” is gray. Gold arrows indicate spindle locations of predicted peaks in kinetochore-associated fluorescence. (A, 1) The left kinetochore is near to the spindle equator, under low tension, resulting in a high catastrophe and low rescue frequency for the kMT plus-end originating from the left pole. This biases the left kMT plus-end toward net depolymerization. (A, 2) The left kinetochore in the quarter spindle area with “proper” sister separation and moderate tension has equal probabilities of catastrophe and rescue at the left kMT plus-end. Therefore, the left kMT is not biased toward either growing or shrinking. (A, 3) The left kinetochore is near the left kMT spindle pole body and under high tension, resulting in a low catastrophe and high rescue frequency at the kMT plus-end. This biases the left kMT plus-end toward net polymerization. (B) Simulation of congression: from an initially random distribution of kinetochore localization at the initiation of the simulation (t = 0), the simulation results in alignment of kinetochores into a metaphase configuration within a few minutes. (C) Simulation of anaphase via loss of tension: after normal metaphase alignment, a sudden loss of tension results in simulated kinetochore movement to average positions close to the spindle poles. This is observed experimentally for Cdc6p-depleted cells and during anaphase A (Guacci et al., 1997; Straight, 1997; Pearson et al., 2001). Simulated spindle lengths were increased to match experimentally observed Cdc6p depleted spindles. (D) A representative simulated image in which a theoretical catastrophe gradient mediator molecule is depleted. Bar, 1000 nm. A threefold decrease in peak catastrophe frequency at the equator results in one focused cluster of kinetochore-associated fluorescence that stochastically moves from one spindle-half to another and transiently separates into two closely spaced clusters. Thus, a gradient in catastrophe frequency drives the separation of sister kinetochores to generate chromatin stretch.

Tension-based control of kMT dynamics is particularly efficient in limiting excursions of kMTs across the spindle equator. Because Cse4-GFP protein is stably bound to the kinetochore during metaphase (Pearson et al., 2004), recovery of bleached Cse4-GFP in FRAP experiments results exclusively from unbleached kinetochores shifting from the unbleached half-spindle to the bleached half-spindle after the bleach event. Lack of any significant recovery in Cse4-GFP FRAP experiments implies that kinetochores in metaphase spindles remain constrained to the half-spindle in which their kMT is anchored. This half-spindle fidelity is reproduced effectively in models where the kinetochore senses tension developed from chromatin stretch to regulate kMT plus-end dynamics (Figure 2). As a kMT grows across the spindle equator, its attached kinetochore moves closer to its sister, reducing tension (Figure 6A, 1). After a catastrophe event near the spindle equator, low tension ensures that the kMT will undergo steady depolymerization to return the kinetochore to its correct half-spindle. This tension-dependent rescue effect is consistent with studies on animal cell kinetochores (Skibbens et al., 1995; Skibbens and Salmon, 1997) and with experimental fluorescence speckle microscopy experiments by Maddox et al. (2003), in which Xenopus extract MTs switched from polymerization to depolymerization when there was loss of tension at the kinetochore. Modeling of the Cse4-GFP FRAP experiment indicates that recovery is highly sensitive to even a small percentage of MT plus-ends growing across the spindle equator, because significant recoveries (∼14%) were predicted in simulations using a position-dependent catastrophe gradient model (no tension-based regulation), in which approximately three kMTs (of 32 total) were present in the wrong half-spindle at any given time during the simulation. Accurate replication of GFP-Tub1 FRAP experiments indicates that simulated kMT dynamics approximate the kMT turnover in yeast metaphase spindles, such that although kinetochores rarely cross the equator, they remain dynamic, oscillating back and forth between the spindle equator and their attached pole (Figure 2E).

Lack of Tension at the Kinetochore in cdc6 Mutants Results in Net kMT Depolymerization, Both Experimentally and in Simulation

The model with a spatial gradient in kMT plus-end catastrophe frequency and with kMT plus-end rescue frequency dependent on tension at the kinetochore provided an excellent fit to the cdc6 mutant experimental data, where lack of tension results in clustering of kinetochore-associated fluorescence very near to each spindle pole body (Figure 6C). In this model, loss of tension at the kinetochore significantly reduces overall kMT rescue frequency, allowing kinetochores to move on average closer to the spindle pole bodies (Figure 4). Peak catastrophe frequencies increase at the equator as a natural consequence of increasing spindle length in the spatial catastrophe gradient model.

A model based on a spatial rescue gradient with catastrophe frequency at the kMT plus-end dependent on the stretch on chromatin between sister kinetochores performed very poorly in reproducing tension-deficient cdc6 mutants (Figure 4, E and F). In this model, rescue frequencies are high at the poles, and decrease with distance from each pole, similar to polar ejection forces in vertebrate spindles. A high rescue frequency at the spindle pole moves simulated kinetochore clusters in tension-deficient spindles toward the equator, thus failing to reproduce the experimentally observed average kinetochore positions for cdc6 mutants. In the above-mentioned assays, we have identified a model where kinetochores sense both a stable gradient between the poles to control kMT plus-end catastrophe frequency, and tension developed from chromatin stretch to control kMT plus-end rescue frequency. This is the best model, because it successfully reproduces all four simulated experiments with an overall probability of p > 0.10.

Implications of Tension-dependent kMT Plus-End Dynamic Instability for Budding Yeast Mitosis

Tension-based regulation of kMT dynamics provides a mechanism for kinetochores under high tension to relieve this tension by switching from poleward movement, which builds tension, to an away from pole movement, which relieves tension (Figure 6A, 3) (Maddox et al., 2003). Without a means to relieve tension, kinetochores could possibly detach from kMTs due to high mechanical stress on the MT–kinetochore attachment (Skibbens et al., 1995; Skibbens and Salmon, 1997; Maddox et al., 2003). If not resolved before anaphase, such detachments would lead to aneuploidy.

Low tension at the kinetochore may have critical consequences for the fidelity of chromosome segregation as well. Spindle assembly checkpoint signaling requires tension between sister kinetochores (Nicklas and Ward, 1994; Biggins and Murray, 2001; Stern and Murray, 2001; Zhou et al., 2002; Biggins and Walczak, 2003; Cleveland et al., 2003), and low tension could act to destabilize attachment of MTs to kinetochores (Nicklas et al., 2001; Biggins and Walczak, 2003; Dewar et al., 2004).

Thus, a model where the kinetochore senses both spindle position to regulate kMT plus-end catastrophe frequency and tension generated via chromatin stretch to regulate kMT plus-end rescue frequency has the overall effect of limiting the range of tensions experienced at the kinetochore compared with a model with position-dependent switching frequencies only. Limiting the range of tensions to intermediate levels (Figure 6A, 2) may help the spindle avoid MT detachment by reducing high forces on the kinetochore and allow the checkpoint to be turned off by limiting low tension. The net result is that both high and low tension on kinetochores are unfavorable, resulting in a congressed state of approximately uniform separation distance between sister kinetochores.

In contrast to Cdc6p-depleted spindles, in which kinetochore localization near the poles suggests that lack of tension results in net depolymerization of kMTs, loss of tension and kMT attachment in ndc10 kinetochore mutants does not result in significant MT depolymerization (Pearson et al., 2003). Therefore, it may be that the kinetochore itself acts to depolymerize kMTs via a catastrophe gradient, an effect that could be antagonized by tension. Loss of attachment could thus allow for net polymerization of MTs, as is observed for interpolar MTs.

A Mechanism for Tension-dependent Regulation of kMT Dynamics

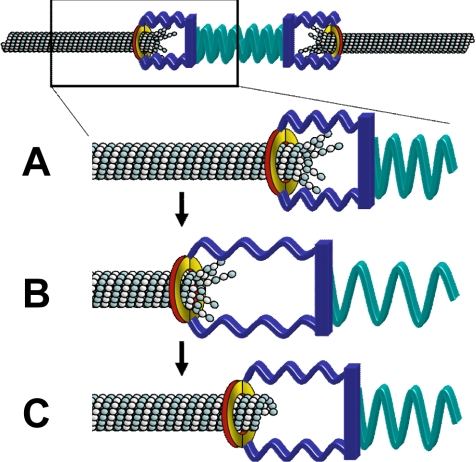
Our analysis shows that tension promotes kMT assembly by increasing rescue. What could be a mechanism by which tension promotes rescue? One possibility for tension-dependent regulation of kMT dynamics is a purely physical effect that could be mediated by the kinetochore. For example, recent work with the purified components of the Dam1p/DASH complex shows that the complex forms rings around microtubules in vitro (Miranda et al., 2005; Westermann et al., 2005). This type of structure could form a sleeve that surrounds the kMT tip and links to other kinetochore components (reviewed by Cheeseman et al., 2002), although the existence of rings in vivo remains an open question (McIntosh, 2005). As shown schematically in Figure 7A, the kinetochore-associated sleeve could move toward the kMT minus-end during depolymerization via protofilament splaying and peeling. As a kinetochore moves away from its sister, tension will build in the intervening chromatin (green spring), and in the kinetochore itself (blue spring), advancing the sleeve toward the kMT plus end. This would in turn force kMT protofilaments to straighten (Figure 7B). The straightening of protofilaments could suppress tubulin departures from the kMT tip and thereby promote rescue (Figure 7C).

Figure 7.

A speculative mechanism for tension-dependent rescue. (A) In this hypothetical mechanism, the kinetochore sleeve (possibly formed via the Dam1/DASH complex) is pushed toward the kMT minus end via protofilament splaying during depolymerization. Simultaneous depolymerization at the sister kMT plus end tends to build tension, stretching the kinetochore (blue spring) and the chromatin (green spring). (B) As tension builds, the sleeve is pulled toward the kMT plus-end to limit protofilament splay. (C) Protofilament straightening stabilizes the tip against further depolymerization and so promotes rescue. The stabilized tip rescues and starts to polymerize.

What would be the force required to promote rescue? The answer hinges on how much energy is required to straighten a curled GDP-tubulin dimer. Previous analyses estimate the mechanical energy stored in the lattice upon GTP hydrolysis to be ∼2.1–2.5 k_BT (Caplow and Shanks, 1996; VanBuren et al., 2002). This amount of energy is equal to ∼10 pN-nm, so that the force required to straighten one GDP dimer of length 8 nm would be F = 10 pN-nm/8 nm = 1.25 pN. Because there are 13 protofilaments, there would a requirement of F_total = 13 × 1.25 pN = 16 pN. Is this characteristic force plausible? Previous analysis of chromatin stretching in budding yeast metaphase showed that the centromere proximal chromatin is highly stretched, to the point where individual nucleosomes are almost certainly forced off the chromatin (Pearson et al., 2001). Studies with laser tweezers in vitro show that ∼15–20 pN is required to force nucleosomes off of double-stranded DNA (Brower-Toland et al., 2002). Thus, the typical tension generated via chromatin stretch during yeast metaphase is approximately equal to that estimated as necessary for kMT protofilament straightening.

Models Lacking a Spatial Gradient in Catastrophe Frequency Result in Loss of Sister Kinetochore Separation at Metaphase

The catastrophe frequency gradient shown in Figure 2A is an essential model element. In a model that includes a spatial gradient in catastrophe frequency, kMT plus-ends experience a peak in catastrophe frequency at the spindle equator. This has the effect of destabilizing kMT plus-ends located at the spindle equator, such that kinetochores tend to cluster on either side of the equator in a bilobed metaphase configuration.

A model in which kinetochores sense both a spatial gradient in catastrophe frequency and attachment site tension to promote rescue results in specific predictions for spindles with a reduced catastrophe gradient, as might be observed in mutants depleted of a theoretical catastrophe gradient mediator molecule (Figure 6D). In simulations with the catastrophe gradient modified such that the peak catastrophe frequency at the equator is threefold less than in wild-type simulations, whereas catastrophe frequency at the poles remains unchanged, metaphase kinetochore clusters collapse into a single, focused cluster that stochastically moves between spindle halves and transiently separates into closely spaced separated clusters (representative simulated image, Figure 6D).

What could be the origin of a position-dependent catastrophe gradient? A spatially segregated antagonistic kinase/phosphatase pair could establish a stable gradient in phospho-state of a regulatory substrate (Brown and Kholodenko, 1999; Sprague et al., 2003). If the substrate is capable of promoting kMT catastrophe in a manner dependent on its phosphorylation state, then there will be a position-dependent catastrophe gradient over the length of the spindle. In yeast, Stu2p acts at kMT plus-ends to promote dynamics (Kosco et al., 2001; Pearson et al., 2003; Van Breugel et al., 2003) and may be required to promote transient sister chromatid separation (He et al., 2001). Given that Stu2p is known to affect kMT dynamics, it seems to be a likely candidate for the gradient, although it is not clear how phosphorylation might be involved. Another possibility is Gsp1 (Ran), which could modulate kMT dynamics via a gradient of Ran-GTP, an MT stabilizer (Kalab et al., 2002). Other microtubule-associated proteins implicated in regulating MT dynamics, such as Kip3p (an MT depolymerase), Kar3p, Cin8p, or Dam1p could mediate a gradient in kMT plus-end catastrophe as well.

In conclusion, by using computer simulations that account for both presumed kMT dynamics and the imaging of those dynamics, a method we call “model-convolution,” we have identified a model for kMT dynamics in the yeast metaphase spindle. Certainly, the mitotic spindle is complex, but our analysis shows that a number of simple models, and even some relatively sophisticated models, ultimately fail to describe the observed behavior. Through a process of continual model scrutiny via integrated modeling and experiment, we expect that alternative plausible scenarios of similar complexity can be tested and key experimental predictions made (e.g., as with Cse4-GFP distribution in the cdc6 mutant). Because individual kMT dynamics have not been resolved in live cells, the ability to simulate kinetochore dynamics in wild-type and genetically manipulated spindles will provide a useful tool for future studies aimed at understanding the complex mechanisms underlying mitosis.