Functional conformational motions in the turnover cycle of cholesterol oxidase

Abstract

Reexamining experimental data of single-molecule fluorescence correlation spectroscopy for cholesterol oxidase, we find that the existing Michaelis–Menten models with dynamical disorder cannot explain strong correlations between subsequent turnover cycles revealed in the diagonal feature in the joint statistical distribution of adjacent “on” times of this enzyme. We suggest that functional conformational motions representing ordered sequences of transitions between a set of conformational substates are involved, along with equilibrium conformational fluctuations in the turnover cycle of cholesterol oxidase. A two-channel model of single-enzyme dynamics, including a slow functional conformational motion in one of the channels, is proposed that allows us to reproduce such strong correlations.

Functionally important conformational motions are nonequilibrium processes that lead from one state of a protein to another and follow binding or dissociation of a ligand (1, 2). In enzymes, such ordered slow conformational motions can constitute an inherent part of a turnover cycle. Their functions may consist of transporting a substrate to the active center inside a macromolecule or bringing it into an appropriate arrangement with respect to this center. Generally, these are physical intramolecular motions that are needed for the occurrence of catalytic conversion and must precede it. Using time-resolved x-ray methods, functional conformational motions in Ha-ras p21 protein on GTP hydrolysis (3) and in a cytochrome P-450 enzyme (4) were recorded. In these experiments, enzyme molecules formed a crystal but could nonetheless perform their characteristic catalytic cycles. Today, many examples of ordered conformational motions in proteins, resolved by x-ray crystallography methods, are known (5–7) (see also the database at http://molmovdb.mbb.yale.edu/molmovdb). Thermal conformational fluctuations for single macromolecules in solution were observed by using fluorescence correlation spectroscopy (FCS) (9, 10) and FRET methods (11). Conformational movements of enzymes in aqueous solvents could also be detected by NMR (12). Using FRET measurements, nonequilibrium conformational changes in single molecules of T4 lysozyme under reaction conditions were observed (13). Single-molecule FCS provides a powerful tool for monitoring chemical transitions during catalytic turnover cycles of individual molecules, and such experiments have been already performed for a number of enzymes, including cholesterol oxidase (14) and horseradish peroxidase (15, 16). Simultaneous monitoring of chemical turnover cycles and physical processes of conformational changes was not, however, possible in the single-molecule experiments. Therefore, functional conformational motions during a turnover cycle for enzymic reactions in solution could not be identified. Nonetheless, the presence of such functional motions can be deduced by special statistical analysis of experimental data. In a previous publication, such statistical analysis, based on the memory functions (16), was performed for the enzyme horseradish peroxidase (17). Here, we examine the data for cholesterol oxidase and show that an essential statistical property of joint probability distributions of adjacent cycle times in this enzyme is not explained by the Michaelis-Menten (MM) mechanism with thermal conformational fluctuations, but can be reproduced by evoking functional conformational motions inside the turnover cycle.

Models of Single-Enzyme Dynamics

In FCS experiments, only two discrete states where an enzyme is fluorescent (“on”) or nonfluorescent (“off”) can be distinguished. Typically, an enzyme molecule is fluorescent while a (fluorescent) product is already formed but has not yet left the enzyme and stays within it so that an enzyme–product complex exists (in cholesterol oxidase, the cofactor toggles between the oxidized fluorescent and the reduced nonfluorescent state). The experimental data represent long stochastic sequences of on and off times for single-enzyme molecules. Thus, any conclusions about the mechanisms of operation of enzymes and properties of individual turnover cycles of an enzyme molecule can be drawn only by complicated statistical analysis of this stochastic data. Theoretical modeling of single-enzyme dynamics plays therefore a principal role in the statistical analysis of the FCS data. By constructing various stochastic models of enzyme dynamics, one can generate stochastic sequences of on and off times for such models and compare their statistical properties with the experimental data. In this manner, appropriate theoretical models can be identified and their parameters can be fitted.

The simplest model of enzymic activity corresponds to the MM mechanism where an enzyme can be found in two states and its activity consists of independent stochastic transitions between them. In this classical view, the polypeptide chain is only providing a kind of solid support for the catalytic center. The MM model is known to lead to exponentially decaying autocorrelation functions of the fluorescence signal. Such exponential dependence is not seen in the FCS experiments, and therefore this simple model is rejected.

In an extension of the MM model proposed by Xie and coworkers (14, 18), equilibrium conformational fluctuations in the enzyme molecule are taken into account. Such thermal fluctuations, which are present even in the absence of the reaction, correspond to random wandering among a set of different conformational substates. Depending on a conformational substate, transition rates between two discrete functional states in a MM model can differ. Thus, these rates become randomly modulated with time, and experimentally observed nonexponential behavior of autocorrelation functions is thus reproduced. Statistical properties of enzymes in different MM models with dynamic disorder caused by thermal conformational fluctuations have been investigated (19, 20). Further extensions of the MM model, using N conformational substates and assuming thermal conformational fluctuations, have been considered by Agmon (21) and Flomenbom et al. (22). In all of these models, functional conformational motions are not involved in the theoretical description.

A different view on single-enzyme dynamics is that functional conformational motions may play a principal role in a turnover cycle. Binding of substrates can trigger a slow nonequilibrium conformational motion inside an enzyme molecule, representing an ordered sequence of conformational changes. This slow mechanical motion is essential and the catalytic conversion of the substrates followed by release of products cannot be completed until the whole sequence of conformational transitions has taken place. Thus, not only the different chemical states but also different physical functional conformational substates should be distinguished inside a turnover cycle and included into a model. This approach, advocated by Blumenfeld in ref. 23, has previously been used in general theoretical studies on synchronization of turnover cycles of individual enzymes in allosterically regulated reactions (24–28). A theory with a sequence of functional nonequilibrium states could well describe experimental data on optical synchronization of turnover cycles in the photosensitive cytochrome P-450-dependent monooxygenase system (29) and similar models were evoked to describe statistics of nonequilibrium conformational changes in T4 lysozyme molecules (13). An analytical study of a model with nonequilibrium cyclic transitions between many intermediate states has been performed (8).

Is it possible to detect the presence of functional conformational motions by statistical analysis of FCS data? The difficulty is that, in addition to functional motions, equilibrium thermal fluctuations are always present. Such thermal fluctuations involve a large number of conformational degrees of freedom in a protein molecule, in contrast to a single pathway coordinate characteristic of the functional motion. Therefore, even when functional conformational motions are present, such statistical properties as, for example, second-order autocorrelation functions may still be dominated by thermal conformational fluctuations and the effects of dynamical disorder. To identify functional conformational motions, one needs statistical methods sensitive to the presence of ordered characteristic motions, which are repeated, with low variations, in many subsequent turnover cycles.

Analyzing the data of FCS experiments with horseradish peroxidase, Edman and Rigler (16) proposed to use a memory function constructed through the third-order autocorrelation function of the fluorescence signal. This memory function, computed for the experimental data, contained new information: slow damped oscillations absent in the standard plots of the second-order autocorrelation functions. Subsequently, a dynamical model of horseradish peroxidase including two functional cyclic motions has been constructed, which successfully reproduced this behavior seen in the memory functions (17).

In the experimental study (14), not only the autocorrelation functions of on times, but also joint probability distributions of durations of two adjacent on times have been constructed. The characteristic feature of such distributions was a narrow diagonal feature, implying that a long turnover cycle was often followed by another long cycle with a close duration. The original interpretation (14, 18) of this behavior was that cholesterol oxidase follows a MM mechanism with equilibrium conformational fluctuations that modulate the transition rates. Indeed, by fitting the model parameters, the nonexponential behavior of the second-order autocorrelation function of the fluorescence signal and of on times could be reproduced. However, joint distributions of adjacent on times have not been constructed there. In the next section, we construct such distributions for the 2 × 2 and diffusive models of ref. 18 and show that they do not contain the principal diagonal feature. Thus, these theoretical models, which are based on the MM mechanism with thermal conformational fluctuations and do not include functional conformational motions, do not reproduce some essential aspects of the experimental data. In the following section, we first determine the joint distributions of adjacent on times for a simple model with a cyclic functional motion. Although they already contain a characteristic diagonal feature, short turnover cycles are very rare in this model, in contrast to the experimental data. Based on this observation, we propose an improved model where an enzyme toggles between two operation modes, one characterized by the MM mechanism and the other one involving slow conformational relaxation along a functional path. Equilibrium conformational fluctuations are taken into account here by assuming that they modulate the velocity of motion along the functional path. This model is able to reproduce both the behavior of autocorrelation functions and the joint probability distributions seen in the experiments.

MM Mechanism with Thermal Conformational Fluctuations

Cholesterol oxidase first oxidizes cholesterol (substrate S) to cholesterone (product P), while the cofactor FAD is being reduced to FADH₂ (see Fig. 1 A). In the second part of this reaction, oxygen is reduced to H₂O₂, while the cofactor FADH₂ is being oxidized to FAD. In the experiments (14), the fluorescence radiation from the cofactor FAD is recorded, which is fluorescent only in its oxidized form FAD (on state), whereas the fluorescence is absent in the reduced form FADH₂ (off state). If the substrate concentration is so high that binding of a substrate molecule to the enzyme occurs almost instantaneously, this MM scheme can be simplified (Fig. 1C). Here, the half-reaction of FADH₂ oxidation is denoted by the green dashed line in Fig. 1C. Because the enzyme remains nonfluorescent during this part of reaction, its details are irrelevant for the statistics of on times (i.e., subsequent durations of stay in the fluorescent FAD·S state).

Fig. 1.

Different theoretical models of enzyme operation. The complete MM model for cholesterol oxidase (A), the FAD reduction half reaction of the simplified MM model (B), the 2 × 2 model (C), the diffusive model (D), the stochastic oscillator model (E), and the superposition model (F). Circular lines with arrows in the last two models schematically represent motions along a functional path.

As pointed out by Xie and coworkers (14), this classical description is not consistent with the experimental data. According to it, all reaction cycles are statistically independent and, therefore, correlations between subsequent on times must be absent. To explain observed correlations, equilibrium conformational fluctuations in cholesterol oxidase have been taken into account (14, 18). The characteristic correlation times of such fluctuations were longer than the turnover time of the enzyme so that its properties could remain modified within several subsequent cycles. To account for such equilibrium fluctuations, two models were proposed (18). In the 2 × 2 model, the enzyme toggles between two equilibrium conformations E and E′ with different rate constants k₂₁ and k₂₂; the transition rates between these conformations are k_E and k_E′, (Fig. 1B). In the diffusive model (Fig. 1D), the rate constant k₂ depends as

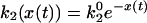[1]

on the effective conformational coordinate x obeying the stochastic Langevin equation

[2]

where f(t) is the Gaussian white noise with 〈f(t)f(t′)〉 = 2λθδ(t - t′) and the zero mean value (〈f〉 = 0). Introducing the stochastic binary signal ξ(t), where ξ = 1 for the fluorescent on state and ξ = 0 otherwise, the autocorrelation function can be defined as

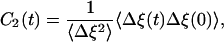[3]

where Δξ(t) = ξ(t) - 〈ξ〉. By fitting such autocorrelation functions to the experimental data, the parameters of both models were determined (18). For molecule A, they were k₂₁ = 9.0 s^-1, k₂₂ = 1.36 s^-1, k_-2 = 1.03 s^-1, k_E′ = 0.13 s^-1, k_E = 0.0417 s^-1 in the 2 × 2 model, and k⁰₂ = 3.8 s^-1, k_-2 = 1.2 s^-1, λ = 0.1 s^-1, θ = 0.8 in the diffusive model. With the fitted parameter values, the autocorrelation function r(m) of on times separated by m cycles was constructed and was found to be similar to the experimental dependence. This function is defined (14, 18) as

[4]

where τ_j is the duration of the fluorescent on state in the cycle j and Δτ_j = τ_j - 〈τ〉.

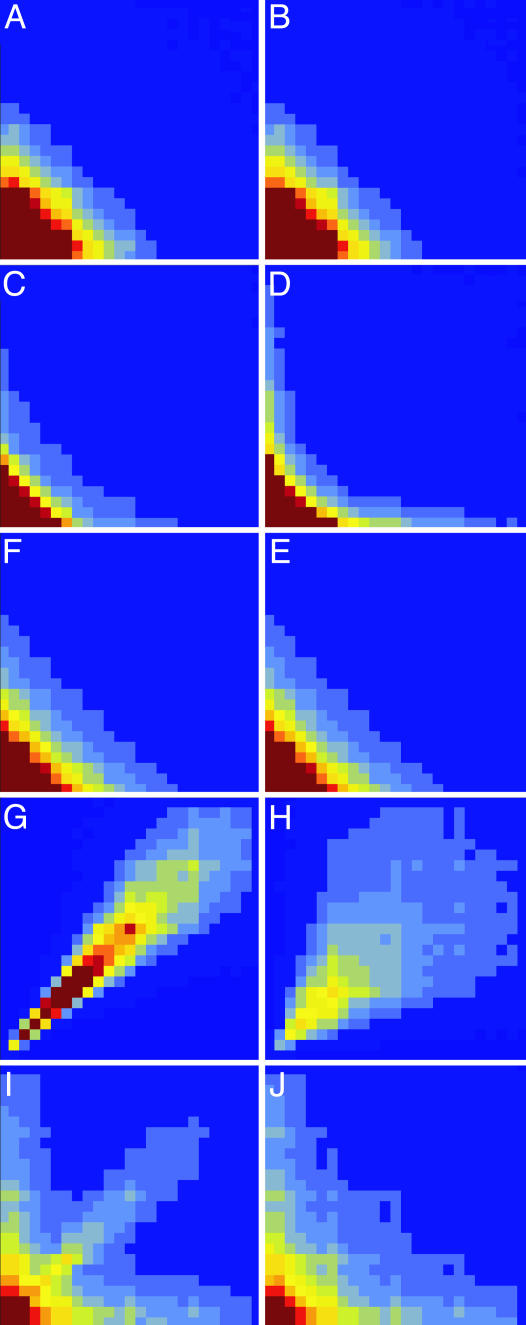
In the experiments (14), 2D probability distributions (histograms) p(τ_j, τ_j+1) and p(τ_j, τ_j+10) for durations of adjacent on times and the on times separated by 10 turnovers were constructed. The distribution p(τ_j, τ_j+1) contained the characteristic diagonal feature, indicating that adjacent long on times were strongly correlated. This feature was not seen in the respective distribution of on times separated by 10 cycles, where only the “wings” extending along the horizontal and vertical axes remained. In theoretical studies (14, 18), such probability distributions were not determined and analyzed. We have constructed the distributions p(τ_j, τ_j+1) and p(τ_j, τ_j+10) for the 2 × 2 model (Fig. 2 C and D) and the diffusive model (Fig. 2 E and F) using the fitted parameter values given above. We see that the characteristic narrow diagonal feature is actually absent from both theoretical models. For comparison, Fig. 2 A and B shows such distributions for the two-state MM model (Fig. 1C) where we have p(τ_j, τ_j+m) = p(τ_j)p(τ_j+m).

Fig. 2.

2D normalized histograms for the reduced MM model (A and B), the 2 × 2 model (C and D), the diffusive model (E and F), the stochastic oscillator model (G and H), and the superposition model (I and J). (Left) Histograms p(τ_j, τ_{j + 1}) for adjacent on times. (Right) Histograms p(τ_j, τ_{j + 10}) for on times separated by 10 cycles are displayed. The model parameters are k₂ = 3.9 s^-1 (A and B), k₂₁ = 9.0 s^-1, k₂₂ = 1.36 s^-1 k_-2 = 1.03 s^-1, k_E′ = 0.13 s^-1, k_E = 0.0417 s^-1 (C and D), 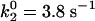, k_-2 = 1.2 s^-1, λ = 0.1 s^-1, θ = 0.8 (E and F), φ_m = 4, φ_p = 3.2, v₀ = 2 s^-1, λ = 0.0466 s^-1, θ = 0.08, σ = 0.01 s^-1, k_-2 = 100 s^-1 (G and H), and φ_m = 4, φ_p = 3.2, v₀ = 2 s^-1, λ = 0.0466, s^-1, θ = 0.08, σ = 0.01 s^-1, k₂ = 7.8 s^-1, k_-2 = 100 s^-1, k_E′ = 200 s^-1, and k_E = 200 s^-1 (I and J). The scales along vertical and horizontal axes are from 0 to 2 s (A–D), 0 to 5 s (E and F), and 0 to 1 s (G–J).

The absence of the diagonal feature is due to the fact that, in both models, only one on state is included and the on time essentially represents a waiting time for the spontaneous decay of such a state. However, waiting times for decay processes are always subject to strong fluctuations. Even if the decay rate constant remains much reduced within several cycles because of a conformational fluctuation, this property does not yet ensure that long subsequent waiting times are strongly correlated, i.e. their durations are close to one another as needed for the presence of a narrow diagonal feature.

These conclusions do not contradict the results of the studies (19, 20) where exact distributions of adjacent on times have been analytically constructed for the two-channel model. The attention in these studies has been focused on the difference distribution of on times, given by

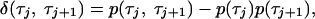[5]

where p(τ) is the single-time probability distribution of on times. This difference distribution can be viewed as an analogue of the memory function (16), which is, however, defined not for the fluorescence signal, but for a stochastic sequence of subsequent on times. If the memory and, thus, correlations between subsequent on times are absent, the difference function should vanish. Thus, the difference distribution can also be viewed as the non-Markovian part of the joint probability distribution of adjacent on times.

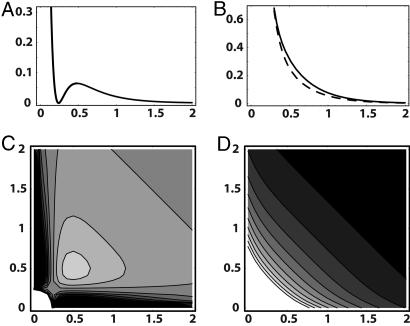
It has been shown (19, 20) that difference distributions for the MM models with dynamic disorder show some diagonal features. Using the analytical results (19, 20), we have determined the profile δ(τ, τ) of the difference distribution along the diagonal cross section (τ_j = τ_j+1) (Fig. 3A) and the full 2D contour plot of the difference distribution (Fig. 3C) for the 2 × 2 model by using the best-fit parameter values from ref. (18). It can be seen that the difference distribution indeed displays a weak and broad diagonal feature in this model.

Fig. 3.

Statistical properties of the two-channel model. Difference distribution function δ(τ₁, τ₂) of adjacent on times (C) and the corresponding total joint distribution of adjacent on times (D), plotted by using the analytical solution (19, 20) for the two-channel model. The same parameters as in Fig. 2C. Additionally, profiles δ(τ, τ)(A) and p(τ, τ)(B, solid line) of these distributions are displayed. The dashed curve (B) shows the Markovian part p²(τ) of the joint probability distribution.

However, in the experiments (14), the difference distributions were not constructed and the diagonal features were already seen for the total distributions of adjacent on times, i.e. for p(τ_j, τ_j+1) = δ(τ_j, τ_j+1) + p(τ_j)p(τ_j+1). Therefore, we have also determined such total distributions for the 2 × 2 model, using analytical results (19, 20) and the best-fit parameter values from ref. 18. Fig. 3B (solid curve) displays the profile p(τ, τ) of the total distribution along the diagonal cross section (τ_j = τ_j+1). Additionally, in Fig. 3B we show by the dashed line the plot of p(τ_j)p(τ_j+1) along the same cross section (the local distance between the solid and the dashed curves corresponds to the local difference shown in Fig. 3A). Because the difference is small, the behavior of the total distribution is dominated by the Markovian part p(τ_j)p(τ_j+1). Fig. 3D displays the full 2D contour plot of the total distribution p(τ_j, τ_j+1), corresponding to Fig. 3B. The diagonal feature is absent here. Note that the distribution in Fig. 3D, computed by using the exact analytical results (19, 20), coincides with the distribution in Fig. 2C, which is constructed by direct stochastic simulations of the 2 × 2 model. Using analytical results (19, 20), we have systematically constructed total joint probability distributions p(τ_j, τ_j+1) for the 2 × 2 model in a broad range of parameters and could never see the characteristic diagonal feature in such plots, in contrast to the plots of the difference distributions.

Thus, our analysis reveals that the MM models with dynamical disorder are not sufficient to explain the data of single-molecule experiments. In the next section, such models are extended by including functional conformational motions inside a turnover cycle.

Cyclic Functional Conformational Motions

In the first scheme shown in Fig. 1E, after completion of the backward FADH₂ oxidation half reaction (denoted by a green dashed line), the enzyme immediately starts its new reaction cycle by binding substrate S and forming the enzyme–substrate complex E–FAD·S. In contrast to the MM scheme (Fig. 1C), the enzyme–substrate complex should pass here through a definite sequence of functional conformational substates until the enzyme–product complex E–FADH₂·P is formed and the product P is released. The series of conformational transitions between subsequent substates represents a functional conformational motion inside the molecule; it is denoted by a thick circular line with an arrow in Fig. 1E. Generally, the functional motion is not terminated with the release of the product, and E–FADH₂ should pass through some other conformational substates before it reaches a conformation where the FADH₂ oxidation half reaction may start. The enzyme is fluorescent only inside the part of its cycle (red) until the substrate is converted into the product and the fluorescent cofactor switches to its nonfluorescent form (blue).

In a rough approximation, this functional intramolecular motion can be described as diffusive downhill drift along an effective conformational phase coordinate φ obeying the stochastic Langevin equation

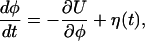[6]

where U is an effective phase-dependent potential. The functional motion represents a process of slow conformational relaxation which begins from the initial phase state φ = 0 and ends when the final state φ = φ_m is reached; the product is released in the state φ = φ_p. The Gaussian white noise η(t) with 〈η(t)η(t′)〉 = 2σδ(t - t′) takes into account short-time thermal fluctuations inside the molecule. In addition to such rapid fluctuations, the molecule possesses dynamical disorder that is caused by equilibrium conformational fluctuations. These slow fluctuations are also present while the enzyme undergoes relaxation; they involve conformational degrees of freedom that are different from the coordinate φ of the functional motion. Similar to ref. 18, we can take them into account by assuming that the potential U = U(φ, x) depends on an additional conformational coordinate x that obeys Eq. 2. For simplicity, we assume that the potential U has a constant slope, i.e. the drift velocity v = -∂U/∂φ is independent from the phase. This drift velocity, which is related to transitions between different conformational substates along the directed functional path, depends on the conformational coordinate x as (cf. Eq. 1)

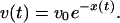[7]

If x is large, the drift velocity is reduced and the cycle time increases. If the correlation time of x(t) is larger than the cycle duration, this increase is maintained for several cycles.

2D probability distributions of on times for this stochastic oscillator model are shown in Fig. 2 G and H. The narrow diagonal feature is already present in such distributions, but they do not show the wings extending along both axes, which are seen in the experimental plots (14). Such wings indicate that a long on time is often followed by a much shorter on time and vice versa.

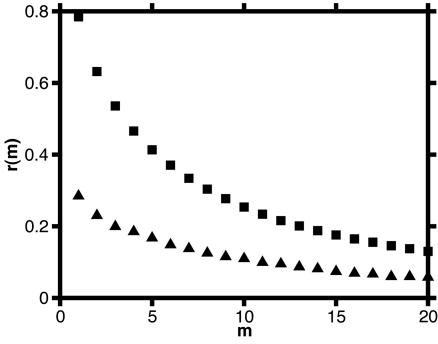
The agreement with the experimental data is further improved in the second model shown in Fig. 1F. Here, the enzyme toggles in the E–FADH₂ stage between two conformations E and E′ opening different reaction pathways. In the state E, the turnover cycle includes a functional conformational motion (as in Fig. 1E). In the state E′, the enzyme follows a MM scheme with a single rate-limiting transition (as in Fig. 1C). The probability distributions of on times for this superposition model are displayed in Fig. 2 I and J. In the distribution of on times in adjacent cycles, they contain both the diagonal feature and the wings. In the distribution of on times separated by 10 cycles, the diagonal feature is missing. Fig. 4 shows the autocorrelation functions r(m) of on times separated by m turnover cycles in the single-cycle and the superposition models. Both the histograms (Fig. 2 I and J) and the autocorrelation function (Fig. 4) for the superposition model qualitatively agree with the experimental data (cf. figures 3 and 4a in ref. 14).

Fig. 4.

The autocorrelation function r(m) of on times calculated for the oscillator model (squares) and the superposition model (triangles). The parameter values are the same as in Fig. 2 G and H and I and J, respectively.

For the on times, separated by 10 turnover cycles, correlations should already be absent. Therefore, the histogram in Fig. 2 J shows, effectively, the product p(τ₁)p(τ₂) of two single-time distributions. This means that the difference between the histograms in Fig. 2 I and J should correspond to the non-Markovian part δ(τ_j, τ_j+1) defined by Eq. 5. Hence, the diagonal feature is contained to the non-Markovian part of the joint probability distribution of adjacent on times. In contrast to the MM models, it is strong and located in a region where the Markov part p(τ₁)p(τ₂) is already small. This diagonal feature is associated with the channel where the functional motion, characterized by the drift along a conformational coordinate, is present. For this channel, the turnover time is long. The second channel with the MM dynamics is fast. The turnover cycles proceeding through this channel give rise to the part of the probability distribution located near τ₁ = τ₂ = 0. The enzyme randomly toggles between the two channels, and the wings in the histogram correspond to the events when a short MM cycle is followed by a long cycle with a functional motion or vice versa.

Conclusions and Discussion

This study indicates that functional conformational motions inside a turnover cycle, along with thermal conformational fluctuations, were probably present in the single-molecule experiments (14). Their fingerprint is the presence of a diagonal feature in the joint distribution of durations of adjacent on times, found in the experiments. Whereas the MM models with dynamics disorder caused by thermal fluctuations successfully reproduce the behavior of autocorrelation functions in such experiments, they do not yield such characteristic diagonal features. The disagreement is not accidental and should be expected for any kind of a MM model. In such models, on times represent waiting times for a single stochastic transition. When slow conformational fluctuations are included, the transition rate becomes temporally modulated and may stay decreased over several subsequent turnover cycles, leading to significantly longer waiting times. This is enough to explain the presence of correlations between subsequent on times and the nonexponential decay of temporal correlations. However, the presence of a narrow diagonal feature in experimental histograms further requires that two adjacent long waiting times should have close durations, which is not true for any MM model, even if the transition rates are temporally modulated. Pronounced narrow diagonal features in the experimental data indicate that slow functional conformational motions should be involved in the turnover cycle of cholesterol oxidase. Instead of having a single rate-limiting transition, in this case a protein molecule has to pass through a definite sequence of conformational substates before catalytic substrate conversion is completed. The total on time then represents a sum of many independent waiting times for subsequent stochastic transitions between substates, and its statistical dispersion gets reduced.

Our analysis does not reject the original theoretical models of cholesterol oxidase by Xie and coworkers (18) but shows how they can be extended to incorporate functional conformational motions. Indeed, by comparing the enzyme mechanisms depicted in Fig. 1 B and F, significant similarities are obvious. In both schemes, the enzyme has two channels characterized by characteristic times that differ by an order of magnitude. In both schemes, the enzyme is toggling between the fast and the slow channels. However, in the original scheme, both channels follow the MM mechanism and correspond to a single transition, whereas the enzyme goes through a definite sequence of conformational transitions in the slow channel in our model. It is this property of the superposition model that allows us to reproduce the diagonal feature in the joint probability distributions. Note that some details of the model may still be changed without altering the principal results. In this study, we only wanted to demonstrate that the inclusion of functional motions can qualitatively improve the theoretical predictions.

On the other hand, our proposed model for cholesterol oxidase bears similarities with the previous model for horseradish peroxidase (17). In both models, an enzyme can follow two different pathways. When a product molecule is released, a short continuous cycle (in horseradish peroxidase) or a rapid MM cycle can follow. However, if this short cycle has not taken place within a relatively short time after the product release, a much longer path with a functional conformational motion is entered. It is this slow path that was responsible for the appearance of slow oscillations in the memory function for horseradish peroxidase and gives rise to a narrow diagonal feature in the joint probability distribution of adjacent on times in cholesterol oxidase.

The possible presence of functional conformational motions inside enzymic turnover cycles, known from direct x-ray timeresolved observations of enzymic activity in crystals, has so far been largely ignored in theoretical interpretations of single-enzyme dynamics based on the data of fluorescence correlation spectroscopy. In our previous publications (16, 28) and in this article, we have demonstrated that the presence of such motions can be deduced from these data by using special methods of statistical analysis. We have shown that, for both horseradish peroxidase (28) and cholesterol oxidase, functional conformational motions should be taken into account to explain essential qualitative features contained in the data. It would be interesting to apply such approaches for the statistical analysis and interpretation of single-molecule experimental data for other enzymes.