Circuit topology and the evolution of robustness in two-gene circadian oscillators

Abstract

Many parameters driving the behavior of biochemical circuits vary extensively and are thus not fine-tuned. Therefore, the topology of such circuits (the who-interacts-with-whom) is key to understanding their central properties. I here explore several hundred different topologies of a simple biochemical model of circadian oscillations to ask two questions: Do different circuits differ dramatically in their robustness to parameter change? If so, can a process of gradual molecular evolution find highly robust topologies when starting from less robust topologies? I find that the distribution of robustness among different circuit topologies is highly skewed: Most show low robustness, whereas very few topologies are highly robust. To address the second evolutionary question, I define a topology graph, each of whose nodes corresponds to one circuit topology that shows circadian oscillations. Two nodes in this graph are connected if they differ by only one regulatory interaction within the circuit. For the circadian oscillator I study, most topologies are connected in this graph, making evolutionary transitions from low to high robustness easy. A similar approach has been used to study the evolution of robustness in biological macromolecules, with similar results. This suggests that the same principles govern the evolution of robustness on different levels of biological organization. The regulatory interlocking of several oscillating gene products in biological circadian oscillators may exist because it provides robustness.

Quantitative models of cellular circuits have recently experienced a renaissance. Such models help understand processes as different as bacterial chemotaxis (1), circadian rhythms (2–10), organismal development (11–15), and the behavior of synthetic circuitry (16–19). Most such models represent biological circuits through differential equations. The state variables in these equations correspond to the concentrations or activities of gene products. The interactions of these gene products are represented through biochemical parameters such as binding affinities of transcriptional regulators to DNA, dissociation constants of ligand–receptor complexes, or kinetic rate constants of enzymes. A nearly universal problem is that quantitative information about these biochemical parameters is absent, even for experimentally well studied systems. In other words, some knowledge on the topology of a circuit, who interacts with whom, may exist, but the strengths of the interactions are usually unknown. Even where measurements of biochemical parameters are available, they are often order-of-magnitude estimates rather than quantitative measurements with known precision. Sets of parameters that reproduce experimentally known phenomena may or may not reflect biological realities.

In a living organism, all biochemical parameters that determine the behavior of a cellular circuit change continually. Such change has three sources: mutations, noise internal to the organism, and environmental change. Mutations are relatively rare. In contrast, internal noise is ubiquitous and substantial. Much of it consists of stochastic variation in gene expression and expression regulation (20–25). Such noise makes all biochemical parameters affecting a circuit's behavior appear to fluctuate randomly. Environmental change, such as a change in temperature, salinity, or nutrient availability, can similarly affect many parameters at once. These observations suggest that biological circuits are not fine-tuned to exercise their functions only for precise values of their biochemical parameters. Instead, they must be able to function under a range of different parameters. In other words, they must be robust to parameter change. These insights have led to explorations of the robustness of circuits in processes as different as bacterial chemotaxis and embryonic development (1, 11, 12, 15, 26–31).

Incessant parameter change and the resulting requirement for robust circuit functioning have one important implication: They render robust circuit architectures or topologies (instead of different parameters within one topology) an important subject of study (12, 14, 15). The focus of this contribution is such an analysis for several hundred variants of a cellular circuit model that has been successfully used to describe circadian rhythms in different organisms (6, 32, 33).

Circadian rhythms are activity cycles with a period of ≈24 h. Their phase can typically be changed by light stimuli, but they often also continue to operate when such stimuli are absent, such as in constant light or darkness. In recent years, the molecular mechanisms behind these clocks have begun to be characterized in multiple organisms (34, 35). Despite limited conservation of clock genes (35), circadian clocks exhibit two important similarities. First, the principal clock mechanism is simple. It minimally involves one gene that is expressed to produce a mRNA and a protein product that may undergo further modification and exerts direct or indirect negative feedback on the expression of its own gene. Examples include the frequency (frq) gene in the fungus Neurospora crassa, the timeless (tim) gene in the fruit fly Drosophila melanogaster, and the kaiC gene in the cyanobacterium Synechococcus spp (36–38). This simple mechanism will generate sustained oscillations in protein concentrations only if the negative feedback is slow. That is, there must be a delay between the time at which the gene product's concentration rises because of its expression and the time at which the gene product represses its own expression. At least two mechanisms can cause such a delay, multistep processing of gene products and strong cooperativity in gene regulation. If, for example, the repression step is cooperative, then repression may become effective only after the protein's concentration has reached a critical threshold. The two mechanisms are equivalent in that they can cause the feedback delay necessary for oscillation. Unfortunately, it is not clear which of these mechanisms is prevalent in living cells. Pertinent information is available only in some cases. For example, the promoter of the Drosophila tim gene contains the closely spaced transcription factor-binding sites that are indicative of cooperative transcriptional regulation (39). The second common feature of many circadian oscillators is that they consist of not one but two or more oscillating gene products whose regulation is linked. This holds in organisms as different as the fungus Neurospora, the fruit fly Drosophila, and mammals (34, 35, 40–44).

My point of departure is whether interlocked circadian oscillators may be an accident of life's history (there are infinitely many ways to obtain limit cycle oscillations in regulatory systems), or whether such interlocking may exist because it provides especially robust oscillations (3, 4, 10, 26, 27). I explore this question by extending a well established model for an elementary circadian oscillator (45) involving one gene and three of its products to a two-gene sixproduct oscillator, which allows several hundred different circuit topologies that differ in how gene products regulate each other's activity. Are differences in robustness among these topologies slight, or are some topologies much more robust than others? If so, what are the robust topologies? Are similar topologies also similarly robust? After having asked these questions, I ask an even more important one: Can evolutionary searches in a space of possible circuit topologies discover highly robust topologies when starting from circuits with low or intermediate robustness?

Methods and Results

Many Topological Variants of a Simple Oscillator Model. The basic oscillator module I use is a Goodwin oscillator (45), which has been successfully used to model circadian oscillations in the fungus N. crassa. Not only can it exhibit stable circadian oscillations of an appropriate frequency, but it also correctly predicts the response of circadian rhythms to stimuli such as temperature pulses, light pulses, and an inhibitor of protein synthesis (6, 32, 33). In this elementary oscillator, a gene expresses a mRNA molecule R that is translated into protein P. This protein is modified, such as through dimerization or phosphorylation, to generate an inhibitor P′ of its own expression. Why use this simple oscillator and not one of several other oscillator models that have been developed in recent years (2–5, 8, 10, 46)? First, all available models contain unconfirmed biochemical assumptions and are thus no less phenomenological than the model I use. In addition, these others have one disadvantage: They involve many more parameters, which makes them intractable for the purpose of exploring many different circuit topologies.

I here first explore how the ubiquitous regulatory linking (34, 35) of oscillatory molecules may affect the robustness of circadian oscillations. I do so in the simplest possible scenario, that of two gene products that can regulate each other's expression or activity either transcriptionally or posttranscriptionally (Fig. 1a and Supporting Text, which is published as supporting information on the PNAS web site). The behavior of each circuit is determined by between 10 and 16 different parameters, depending on circuit topology. Even for this simple system, there are >700 possible circuit topologies or ways of regulatory linkage between the molecules involved. Notice that the system of Fig. 1a (equation 2 in Supporting Text) is not simply a coupled oscillator. The reason is that in some topologies, the feedback of 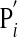on 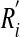is absent, such that the systems (R₁, P₁, P_1′) and (R₂, P₂, P_2′) would not oscillate when considered separately, yet the interaction between them leads to oscillations.

Fig. 1.

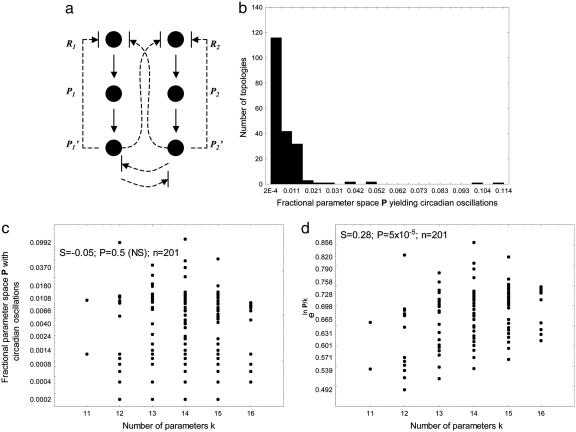
Different oscillator topologies vary greatly in their robustness. (a) Circadian oscillator topologies. Shown are six molecular species (circles) that are the mRNA (R) and protein (P) products of two genes, 1 and 2. The upper and lower solid vertical arrows represent translation and posttranslational modification, respectively, of these species. Arrows terminated by a crossbar indicate that a regulatory interaction can be either activatory or inhibitory. Solid lines indicate interactions that are present in all of the circuit topologies examined here. Dashed lines indicate regulatory interactions that may be present or absent, depending on topology. There are six such regulatory interactions, each of which can be activating, repressing, or absent. This amounts to a total of 378 possible circuit topologies that I explore here (3⁶ = 729 total topologies minus symmetric topologies, as defined in Supporting Text). (b) Histogram of the fractional parameter space volume P leading to oscillatory solutions for 201 topologies for which at least one in 5 × 10³ randomly chosen parameter combinations leads to oscillatory solutions. (c) Statistical association between the number of parameters and P. (d) Statistical association between the number of parameters and e^{ln P/k}.

Different Topologies Have a Highly Skewed Distribution of the Likelihood P to Produce Circadian Oscillations. Biological circadian oscillators have two germane features: a stable oscillatory period of ≈24 h and entrainability, the sensitivity of the oscillation's phase to periodic lighting. The second feature is realized in very different ways in different organisms and would require an organism-specific model. For reasons of tractability, I thus focused on the first of these features, which is a necessary prerequisite for all circadian oscillators. For each possible circuit topology (Fig. 1a), I chose 5 × 10³ parameter combinations at random from a parameter space within which circadian oscillations are known to occur (6, 32, 33) for the elementary oscillator (R_i, P_i, 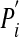). For each of these parameter combinations, I examined whether the circuit adopts limit cycle oscillations with a period of ≈24 h. Limit cycle oscillations have two features typical of circadian oscillators: they are stable to minor perturbations of regulator concentrations, and they persist over time even when the organism is not subject to periodic driving forces (e.g., light exposure) (34, 47). The fraction of randomly chosen parameters that yield circadian oscillations is an estimate of the fractional volume (P) of parameter space that admits such oscillations. I show in Fig. 4, which is published as supporting information on the PNAS web site, that P can serve as a proxy for a circuit's robustness to perturbations: Changing parameters at random in a topology with high P is more likely to yield a parameter combination leading to circadian oscillations than in a topology with low P.

Fig. 1b shows the distribution of P for those 201 circuit topologies where at least one in 5 × 10³ randomly chosen parameter combinations yields circadian oscillations. At least two features of this distribution are worth pointing out. First, P varies not slightly but dramatically among different topologies. Specifically, P varies by nearly 2 orders of magnitude among circuit topologies. For some topologies, only one or a few of the thousands of randomly chosen parameter combinations yield circadian oscillations. For others, >5% of parameter combinations yield such oscillations. Another striking feature of this distribution is its skewness. For the vast majority of topologies, only a small fraction P of parameters yield circadian oscillations. In contrast, a small number of topologies have a large P. For example, only 4.5% (9) topologies have P > 0.02. Fig. 5, which is published as supporting information on the PNAS web site, shows and briefly discusses nine among the topologies with the highest associated P. The topology (not shown) for which species one and two oscillate separately and do not affect each other's concentration is ≈1 order of magnitude less robust than the most robust topologies. The increased complexity of interlocking oscillators may thus not be an accident of natural history: It may indeed provide greater robustness to mutation than single oscillators (3, 10, 48).

The skewness evident from Fig. 1b is not an artifact of the specific conditions for which I evaluated the behavior of the oscillator. It is observed for different tolerances in the oscillator period, for different allowed minimum and maximum amplitudes in the oscillations, for different initial conditions, and for different degrees of cooperativity in the regulatory interactions modeled.

The Skewed Distribution of P Is Not Just the Result of Varying Numbers of Parameters. An obvious candidate explanation for the dramatic differences in P among circuit topologies is their differences in the number of parameters. For a circuit topology with many regulatory interactions, and thus more parameters, a randomly chosen parameter combination might be much less likely to yield stable oscillatory behavior of the right period. However, Fig. 1c shows this is not the case. Fig. 1c plots P against the number of parameters k in a topology and shows a nonsignificant statistical association between the two (Spearman s = -0.05; P = 0.5). Fig. 1d shows a complementary analysis based on the following considerations. If along each axis of parameter space the same proportion or fraction p of randomly chosen parameters were to admit oscillatory solutions, then P = p^k, and p = e^{ln P/k}. Although p is almost certain to vary among different parameters (48), e^{ln P/k} can still be thought of as a per-parameter likelihood of finding circadian oscillations in a random search of parameter space, or as a per-parameter robustness of a circuit topology. Fig. 1d plots e^{ln P/k} against the number of parameters k. Strikingly, p does not decrease but increases with the number of parameters: The more complex a topology is, the more likely it will yield oscillatory solutions. At the same time, both Fig. 1 c and d show that for any given number of parameters k, there is wide variation of P and e^{ln P/k}. Variation in the number of parameters alone can thus not explain variation in robustness.

Robust Topologies Are Connected in a Topology Network. Much like in any kind of cellular circuit, genetic change in a circadian oscillator can take place in two different ways: First, it can affect biochemical parameters within a given oscillator topology. Second, it can generate new oscillator topologies through mutations that eliminate or add regulatory interactions. This second kind of change is frequent enough to be of evolutionary relevance (49).

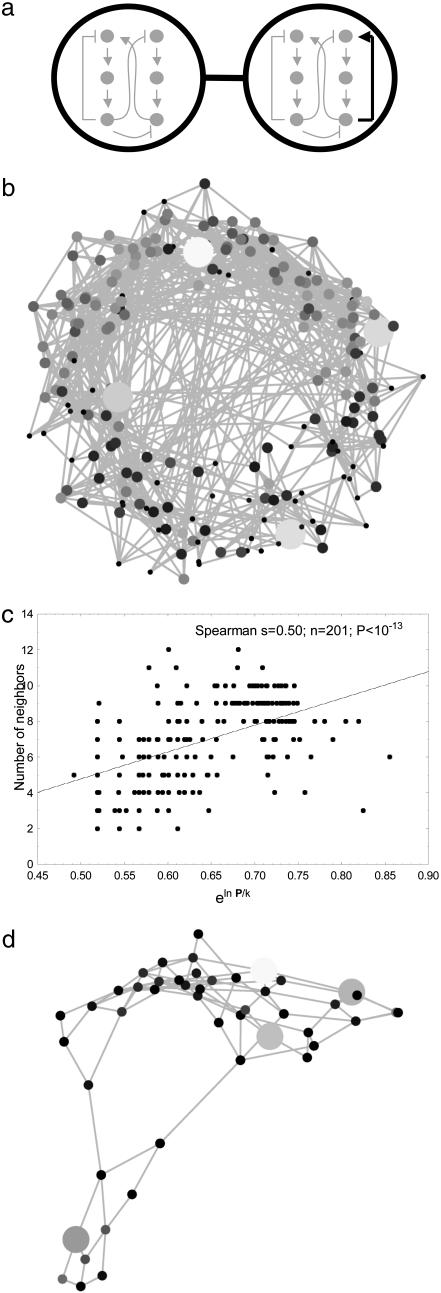
The key evolutionary question with respect to robust oscillator topologies is whether a blindly groping evolutionary search could ever find such robust circuit topologies. This question is best posed by considering the following graph or network representation of oscillator topologies. Consider a graph where each node corresponds to an oscillator topology that is capable of displaying circadian oscillations. Connect two nodes (topologies) by an edge if the two topologies differ by only one regulatory interaction (Fig. 2a). Such neighboring topologies can arise from each other by genetic change that affects only one regulatory interaction. The question whether robust oscillator topologies can be found through a series of such changes, i.e., through gradual evolution, is a question about the structure of this graph. There is a spectrum of possibilities with two extremes. First, the nodes (oscillator topologies) of this graph may be disconnected. That is, a topology capable of circadian oscillations has no neighboring topologies also capable of producing such oscillations. This would mean that robust topologies cannot be reached from less robust topologies, because functional oscillators are isolated islands in this graph. At the opposite extreme, this graph might consist of one densely connected component, where any two topologies are connected by a path of edges. In this case, stepwise evolutionary alteration of a circuit topology could start from any one topology and reach any other topology via intermediate topologies that admit circadian oscillations.

Fig. 2.

A graph connecting circuits of different topology. (a) Illustration of the concept behind this graph. Shown are two nodes of this graph (large circles). Each node corresponds to a circuit of a given topology that allows circadian oscillations (drawings inside the circles). The circuits shown correspond to topologies 198₁₀ and 207₁₀, both of which have P > 0. The two nodes are connected, because they are topological neighbors, i.e., they differ by only one regulatory interaction (bold arrow in right-hand circle). (b) The structure of this graph for all oscillator topologies where at least one in 5 × 10³ random parameter combinations yielded circadian oscillations. Topologies (circuits) with large P are indicated by larger circles and lighter shading than topologies with small P. (c) Nodes (circuit topologies) with many neighbors in the graph in Fig. 2a show greater e^{ln P/k}. (d) The same graph for those 47 oscillator topologies where at least one in 100 parameter combinations yielded circadian oscillations.

Fig. 2b shows an image of this graph for 201 topologies in which at least a fraction P = 2 × 10^-4 of randomly chosen parameter combinations yielded circadian oscillations. This graph consists of one connected component. (Any two pairs of topologies in such a component are connected by a path of edges.) And not only is the graph connected, its connectivity is high. On average, a node (topology) in this graph has 7.03 (S.D., 2.29) neighboring topologies that also yield circadian oscillations. The graph does not contain any bridges, i.e., edges whose removal causes the graph to become fragmented into more than one component. Finally, both the edge and vertex connectivity of this graph are equal to two. This means that at least two edges or at least two nodes need to be removed to fragment the graph into two components. Similar topologies, that is, circuits close together in this graph, also tend to have similar P (Fig. 6, which is published as supporting information on the PNAS web site). Perhaps surprisingly, one also finds that the number of neighbors any one node (topology) has in this graph increases with P (Fig. 2c; Spearman s = 0.5, P < 10^-13). In other words, more robust oscillator topologies also have more neighboring topologies that yield circadian oscillations.

The topology graph's connectedness is preserved if one eliminates from this graph topologies with the lowest robustness, as indicated by a low P.Fig.2d shows an example, the graph including only nodes (topologies) with P > 0.01. It contains 47 topologies, has no bridges, and has edge and vertex connectivity of two, exactly like the graph of Fig. 2b containing all circuits. More generally, if one varies the threshold P at which a node becomes part of the graph, one finds threshold values of P for which this topology graph is not connected. However, the number of disconnected components into which the graph becomes partitioned is always small (less than five), regardless of P. In addition, for thresholds of P where the number of nodes (topologies) exceeds 40, the largest component contains >94% of all nodes. All this is also consistent with the positive association between P and a topology's number of neighbors, and with the similar P of similar topologies. It also holds for varying model assumptions, such as for lower tolerance in the oscillator period, different allowed minimum and maximum amplitudes in the oscillations, different initial conditions, and different degrees of cooperativity in the regulatory interactions modeled. It also holds if the circuit topologies (nodes) to be included in the graph are identified not by a minimal value of P but through a minimal robustness to vector and/or scalar perturbation (results not shown). In sum, circuits of different robustness are connected in graphs of oscillator topologies that can readily be traversed by changes of individual regulatory interactions.

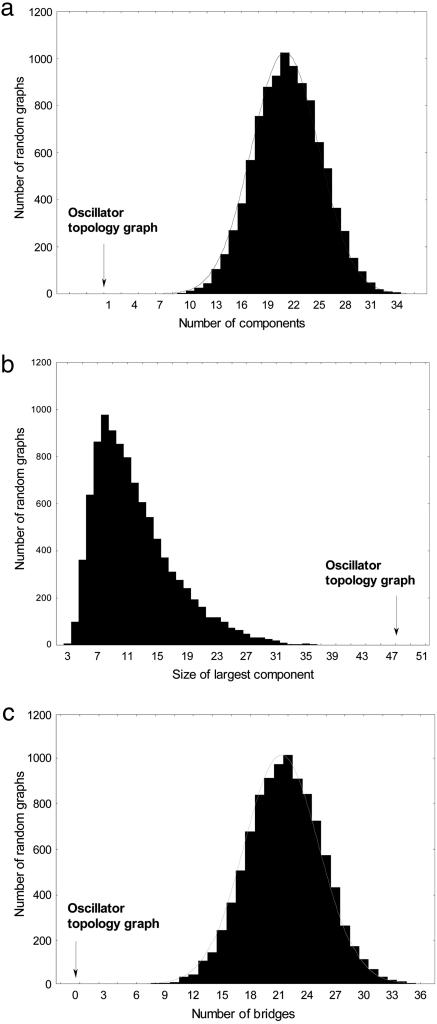
Is the structure of this topology graph significantly different from that of a random graph? For my purpose, a random graph is a graph with the same number of nodes as the topology graph, but where the nodes are drawn at random from all possible topologies, regardless of whether a topology allows circadian oscillations or not. I first addressed this question by generating 10,000 random graphs with the same number of nodes as the graph shown in Fig. 2d and determined the distribution of several different graph statistics for these 10,000 random graphs. First, both the vertex and the edge connectivity (as defined above) is two for the graph of Fig. 2d, but zero for all of the 10,000 random graphs. The reason is that none of these graphs is connected in the first place. The random graphs consist of many more and smaller components than the oscillator topology graph (Fig. 3 a and b; random means ± standard error, x̄ ± s = 21.4 ± 0.038, x̄ ± s = 12.02 ± 0.053, for number and size of components, respectively). In addition, they also contain many more bridges, edges whose removal renders a component disconnected (Fig. 3c; x̄ ± s = 21.7 ± 0.039). Each of these statistics in the oscillator topology graph is multiple standard deviations removed from the mean of the random graphs (Fig. 3). This means that the graph is much more cohesive than a random graph. To analyze similarly large samples of much larger graphs is computationally infeasible. However, a more limited analysis based on a sample of 100 random graphs shows that for all oscillator topology graphs containing between 100 (P > 1.8 × 10^-3) and 15 topologies (P > 1.8 × 10^-2), the mean number of components and the size of the largest component differ by at least 10 standard errors from the randomized graph. For larger oscillator topology graphs, these two statistics begin to approach that of a random graph. However, even for the largest graph examined here (P > 2 × 10^-4, Fig. 2a), structural differences remain. For example, the vertex and edge connectivity of random graphs is smaller (x̄ ± s = 0.85 ± 0.058; n = 65 for both), and the number of bridges is greater (x̄ ± s = 2.9 ± 0.23) than in the oscillator topology graph (respective values are 2, 2, and 0 for each of these indicators).

Fig. 3.

Oscillator topology graphs vs. random topology graphs. Shown are the distributions of three graph characteristics for 10,000 random graphs whose nodes correspond to circuit topologies (Fig. 2a) compared (vertical arrows) with the structure of the graph of Fig. 2d, which has 47 nodes, each of which yields oscillations with P > 0.01. Each random graph was established by choosing a random sample of 47 of a total of 378 possible topologies and defining topologies as neighboring that differ by only one regulatory interaction. As opposed to the topologies of the oscillator topology graph, many of these randomly chosen topologies may not yield oscillations. (a) Number of components (groups of nodes connected to each other but to no other node). (b) Size of the largest component. (c) Number of bridges.

Discussion

In the most elementary biochemical circuits yielding circadian oscillations, one gene product represses its own synthesis with a time delay caused by either cooperative repression or multistep expression regulation (45). I here examine the arguably simplest possible extension of this circuit. It involves two genes, their products, and auto- as well as cross-regulation on both the transcriptional and posttranscriptional level. Even for the small number of variable transcriptional and posttranscriptional regulatory interactions, the circuit has several hundred different topological variants. The fraction P of randomly chosen parameter combinations that yield circadian oscillation in any one of these topologies is a proxy for its robustness to perturbations of either multiple or single parameters.

P has a skewed distribution: Most topologies have very low robustness, whereas very few have high robustness. Importantly, in the most robust topologies, the two genes influence each other's expression, and these topologies are ≈1 order of magnitude more robust than a topology for which the two gene products do not influence each other's expression. This observation, even though made in the context of a simple model, presents a possible explanation for the abundant regulatory interlocking and coupling of gene expression in circadian oscillators of living cells. It may be an example of biological complexity that exists for a reason (50): to ensure robust behavior, in this case of circadian oscillations. Such complexity, however, is not a sufficient precondition for robustness: Many circuit topologies are less robust than the most basic singlegene oscillators, and others do not permit any circadian oscillations at all.

These observations suggest that an evolutionary perspective is necessary to understand whether interlocking of biochemical oscillators can lead to increased robustness. If only few two-gene oscillators have increased robustness or any other desirable feature, compared with the most elementary oscillator, can natural selection find these oscillators through gradual genetic change of the regulatory structure of a circuit? To address this question, I analyzed the structure of a graph of circuit topologies. In this graph, a node corresponds to a circuit topology. Two topologies are immediate neighbors in the graph if they differ by only one regulatory interaction. For the circuits examined here, most or all circuit topologies that yield oscillations exist in one connected component. This means that gradual evolutionary changes in circuit topology can generate any circuit topology from any other topology within such a component, without transitions through circuits that do not allow circadian oscillations. In addition, more robust topologies also have more topological neighbors that yield circadian oscillations, which further facilitates such gradual change. Are circuit topologies with a desirable property connected in circuit graphs also for many other types of biological circuits? We do not know. A general answer to this question would be a major step in our understanding of how biological circuits can evolve.

The above results show parallels to studies of structural robustness in RNA and proteins (51–58), where graph-based models have proven very useful in understanding the evolution of robustness. Briefly, all macromolecules of different amino acids or nucleotide sequences that adopt the same secondary or tertiary structure can be represented as a graph. Each node of the graph corresponds to one individual sequence adopting the structure. Two nodes (sequences) are immediate neighbors if they differ by a single amino acid or nucleotide. Many or all such sequences may be connected in graph components that can be traversed by single point mutations without ever generating a sequence that does not adopt a given structure. However, some of the molecules in this graph are more robust than others to single point mutations. That is, random changes of individual amino acids or nucleotides in such robust molecules are less likely to lead to altered structures than such changes in other sequences. Because structure is a prerequisite for function, the evolutionary implication is clear: Robust structures can evolve neutrally, through gradual evolutionary change that leaves a molecule's structure unchanged. Analogously, robust circuit topologies may evolve neutrally. If so, similar principles govern the evolution of robustness on different levels of biological organization.

The work presented here has considerable limitations. Some of these limitations are biological. First, which is the correct mathematical form of the regulatory interactions among circuit components? The time delay afforded by multistep processing and cooperative regulation occurs in many regulatory phenomena, but its mechanistic basis is still unknown. Second, can all of the circuit types examined here be biochemically realized? Both transcriptional regulation and some forms of posttranscriptional regulation such as protein phosphorylation rely on short signal sequences in a (DNA or protein) target molecule. This suggests that evolution has considerable flexibility in exploring alternative circuit topologies, but there may be some circuit architectures that it cannot “access.” Third, I do not explicitly address temperature compensation, an important aspect of the robustness of circadian oscillators, whose mechanistic basis is also unknown. However, the kind of robustness I examine here may contribute to temperature compensation, because a network more robust to random fluctuations in all parameters will also show better temperature compensation. Fourth, many biological circuits and their parts are multifunctional. By necessity, their analysis often focuses on one or a few functions, and robustness of this function does not necessarily mean robustness of other functions. However, the robustness of one function may allow the network to acquire other functions (14, 58). Finally, and most importantly, which quantitative oscillator model is the correct one? We do not know, because the biochemical interactions among oscillator components are not fully understood for any organism.

A second class of limitations is computational. Because of these limitations, one can explore only a limited number of alternative circuit topologies; one can sample only a limited region of parameter space; one has to restrict oneself to some criteria of circuit functioning (stable oscillations of an appropriate period) at the expense of others (oscillator entrainment by light); and one can explore only a very limited number of model variations. These limitations also preclude precise estimates of the examined topologies' robustness to mutations.

If the results reported here have not identified one model of circadian oscillations as the correct or most robust one, what, then, is their value? First, they point to the importance of an evolutionary perspective: Although circuits with a desirable feature may exist, it may be impossible to reach them through gradual evolution from other circuits. Only if many different circuit types are connected in a graph like that of Fig. 2 a and d does such evolution become possible. Another glance at simple models of protein and RNA folding serves to make a second point (51–58). Such models may not have explained the folding properties of any one macromolecule. Instead, they point to general principles important for the folding and robustness of all macromolecules. Future work may show whether the simple principles identified here, great differences in robustness among different circuits and evolutionary accessibility of robust circuits, hold for many genetic circuits.