Abstract
Intermolecular interactions between charged membranes and biological polyelectrolytes, tuned by physical parameters, which include the membrane charge density and bending rigidity, the membrane spontaneous curvature, the biopolymer curvature, and the overall charge of the complex, lead to distinct structures and morphologies. The self-assembly of cationic liposome–microtubule (MT) complexes was studied, using synchrotron x-ray scattering and electron microscopy. Vesicles were found to either adsorb onto MTs, forming a “beads on a rod” structure, or undergo a wetting transition and coating the MT. Tubulin oligomers then coat the external lipid layer, forming a tunable lipid–protein nanotube. The beads on a rod structure is a kinetically trapped state. The energy barrier between the states depends on the membrane bending rigidity and charge density. By controlling the cationic lipid/tubulin stoichiometry it is possible to switch between two states of nanotubes with either open ends or closed ends with lipid caps, a process that forms the basis for controlled chemical and drug encapsulation and release.
Keywords: polyelectrolyte lipid complexes, small angle x-ray scattering, nanotube-based drug delivery, membrane, tubulin
The interactions between charged lipids and oppositely charged biopolymers are relevant to a variety of biomedical and biological processes, including endocytosis, protein transport (1), drug-based and protein-based gene delivery (2–5), and lipid-based gene delivery (6, 7). The highly ordered structures formed by polyelectrolyte–lipid complexes (PLCs) are of great interest in materials science as templates (8) and building blocks for hierarchical supramolecular assembly. The structure of PLCs may be tailored, which, in turn, profoundly affects their function (6). At issue here is the following question: What are the structures that form when charged membranes are complexed with oppositely charged polyelectrolytes?
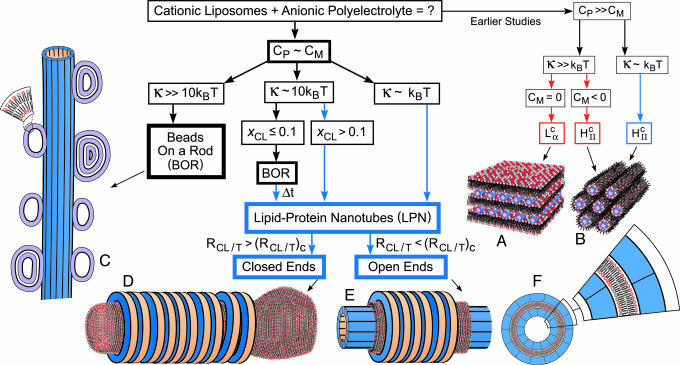
Earlier studies (Fig. 1) focused on complexes with high mismatch between the membrane spontaneous curvature, CM, and the polyelectrolyte curvature, Cp ≡ 2/Dp, where Dp is the polyelectrolyte diameter. When the membrane bending rigidity, κ, is significantly greater than kBT, where kB is Boltzmann constant and T is the temperature, the elastic free energy dominates the electrostatic energy, and the symmetry of the complex is set by the lipid-phase symmetry. Examples include the multilamellar phase (2–4, 7, 9–11),  , for CM = 0 (Fig. 1 A), where the polyelectrolyte chains (DNA, for example) are intercalated between lipid bilayers and the inverted hexagonal phase (6, 11),
, for CM = 0 (Fig. 1 A), where the polyelectrolyte chains (DNA, for example) are intercalated between lipid bilayers and the inverted hexagonal phase (6, 11), 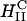 , for CM < 0 (Fig. 1B), consisting of DNA inserted within inverted micelles arranged on a hexagonal lattice. Thus in the PLCs studied to date the lipids formed the template for the complex structure, with the polyelectrolytes incorporated into that template. The only exception is when the membrane is very soft, κC ≈ kBT, in which case the electrostatic energy dominates and HII is formed with DNA (6), even if CM = 0 (Fig. 1B).
, for CM < 0 (Fig. 1B), consisting of DNA inserted within inverted micelles arranged on a hexagonal lattice. Thus in the PLCs studied to date the lipids formed the template for the complex structure, with the polyelectrolytes incorporated into that template. The only exception is when the membrane is very soft, κC ≈ kBT, in which case the electrostatic energy dominates and HII is formed with DNA (6), even if CM = 0 (Fig. 1B).
Fig. 1.
Assembly pathways of cationic liposomes and anionic polyelectrolytes. Red arrows and boxes indicate structures that are dominated by the elastic energy of the membranes, and blue ones indicate structures that are dominated by electrostatic energy. Earlier studies examined biological polyelectrolytes with curvature, Cp, that is very different from the membrane spontaneous curvature, CM, and found the lamellar phase, 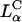 (A) and the inverted hexagonal phase
(A) and the inverted hexagonal phase 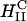 (B), under different conditions as indicated. We studied the structures that are formed when Cp is comparable to CM. For high membrane bending rigidities, κ, BOR structure is formed (C). Lowering κ and increasing the mole fraction of cationic lipids in the membrane, xCL ≡ NCL/(NCL + NNL), where NCL and NNL are the numbers of cationic and neutral lipids, respectively, favors the LPN structure. At intermediate κ and low xCL, the BOR structure is observed and over time, Δt ≈ 60 h, transforms into the LPN. When the cationic lipids/tubulin stoichiometry of the complex, RCL/T ≡ NCL/NT, where NT is the number of tubulin dimers, overcomes some critical value, (RCL/T)C, the LPNs have closed ends with lipid caps (D); otherwise the LPNs have open ends (E). (F) A cross section of the LPN and a magnified slice.
(B), under different conditions as indicated. We studied the structures that are formed when Cp is comparable to CM. For high membrane bending rigidities, κ, BOR structure is formed (C). Lowering κ and increasing the mole fraction of cationic lipids in the membrane, xCL ≡ NCL/(NCL + NNL), where NCL and NNL are the numbers of cationic and neutral lipids, respectively, favors the LPN structure. At intermediate κ and low xCL, the BOR structure is observed and over time, Δt ≈ 60 h, transforms into the LPN. When the cationic lipids/tubulin stoichiometry of the complex, RCL/T ≡ NCL/NT, where NT is the number of tubulin dimers, overcomes some critical value, (RCL/T)C, the LPNs have closed ends with lipid caps (D); otherwise the LPNs have open ends (E). (F) A cross section of the LPN and a magnified slice.
In this article we explore the structure and symmetry of PLCs when CM and CP are comparable in complexes of cationic liposomes and microtubules (MTs), for which CP ≈ 0. Using synchrotron small angle x-ray diffraction (SAXRD) and transmission electron microscopy (TEM), we find two unique structures that do not maintain the lipid symmetry. For soft and intermediate rigid membranes we find that the cationic liposomes spread and coat the MTs, and the external lipid layer is decorated by tubulin oligomers, forming a unique lipid–protein nanotube (LPN). In this regime the complex adapts a wrapped geometry, which is favored by the electrostatic energy at a low elastic cost when CP ≈ CM. The tubule geometry has not yet been accounted for in current statistical mechanical continuum elastic models of fluid membranes comprised of symmetric bilayers with zero spontaneous curvature (12). By controlling the cationic lipid/tubulin stoichiometry, RCL/T, of the complex the LPN can switch between a state with open ends (Fig. 1E) to a state with closed ends with lipid caps (Fig. 1D). These smart LPNs are smaller in diameter than cylindrical tubules (13) and multilamellar cylindrical vesicles (14) that may form in appropriate conditions of lipid self-assembly.
For high κ, or intermediate κ and low membrane charge density, σ, we find that vesicles adsorb onto the MT and appear as “beads on a rod” (BOR), as shown schematically in Fig. 1C. This is the most trivial structure that can form when vesicles interact with polyelectrolytes and was previously hypothesized for lipid–DNA complexes (15), where Cp » CM, but later was theoretically (16, 17) and experimentally (6, 7) proven unstable. Here, we discovered how to obtain BOR. This state, however, based on our observations described below, seems to be, at least at intermediate κ, a kinetically trapped state. The ground state of the system follows the MT template and forms the LPN (Fig. 1 D and E). We study in detail how the key parameters κ, σ, and RCL/T control the assembled structures. Apart from demonstrating different self-assembly modes these results enable us to describe the self-assembly pathways of lipids and polyelectrolytes under a consistent framework (Fig. 1 and see Fig. 4D).
Fig. 4.
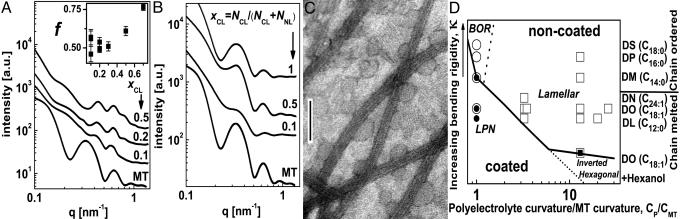
Variation of the membrane bending rigidity, κ, and polyelectrolyte curvature, Cp.(A) Radially averaged raw SAXRD data of MTs and MT–lipid complexes, using DLTAP/DLPC solutions with xCL ≡ NCL/(NCL + NNL), as indicated. (Inset) f as a function of xCL, based on analysis as in Fig. 3. (B) Radially averaged raw SAXRD data of MT and MT–lipid complexes, using DPTAP/DPPC solutions with xCL, as indicated. For all of the samples in A–C, RCL/T ≡ NCL/NT = 160 × xCL.(C) TEM image of the MT–lipid complexes, using DPTAP/DPPC solutions with xCL = 0.5. (Scale bar: 100 nm.) (D) A diagram of the observed stable states of PLCs in the κ and Cp/CMT, space parameters, where CMT = 0.076 nm–1 is the curvature of MT. Cp/CMT = 1, 3.25, 3.46, 13, 20, and 26 correspond to MT, filamentous actin (3), M13 virus (9), DNA (6, 7, 10, 37), poly(glutamic acid) (4), and the polypeptides (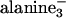 glutamic acid)36/48 (2), respectively. The lipid tails used (with mixtures of trimethyl ammonium propane and PC head groups) are indicated on the right. DL, dilauryl; DO, dioleoyl; DN, dinervonyl; DM, dimyristoyl; DP, dipalmitoyl; DS, distearoyl. Based on literature data (6, 30–32) and theory (28) (see Materials and Methods) the membranes are shown in ascending κ order as indicated by the arrow on the left. κ ≈ o(kBT) when the cosurfactant hexanol is added to DO, κ ≈ o(10 kBT) for DL, DO, and DN and κ » 10 kBT for DM, DP, and DS. Open squares represent the lamellar phase (Fig. 1 A), solid square shows the inverted hexagonal phase (Fig. 1B), open circles indicate the BOR structure (Fig. 1C), and solid circles indicate the LPN (Fig. 1 D and E). The solid line is a guide for the eye to indicate the transition from the noncoated states (BOR or lamellar phase) to the coated states (LPN and inverted hexagonal). The broken lines are guides for the eye to indicate secondary separations within the coated and noncoated states.
glutamic acid)36/48 (2), respectively. The lipid tails used (with mixtures of trimethyl ammonium propane and PC head groups) are indicated on the right. DL, dilauryl; DO, dioleoyl; DN, dinervonyl; DM, dimyristoyl; DP, dipalmitoyl; DS, distearoyl. Based on literature data (6, 30–32) and theory (28) (see Materials and Methods) the membranes are shown in ascending κ order as indicated by the arrow on the left. κ ≈ o(kBT) when the cosurfactant hexanol is added to DO, κ ≈ o(10 kBT) for DL, DO, and DN and κ » 10 kBT for DM, DP, and DS. Open squares represent the lamellar phase (Fig. 1 A), solid square shows the inverted hexagonal phase (Fig. 1B), open circles indicate the BOR structure (Fig. 1C), and solid circles indicate the LPN (Fig. 1 D and E). The solid line is a guide for the eye to indicate the transition from the noncoated states (BOR or lamellar phase) to the coated states (LPN and inverted hexagonal). The broken lines are guides for the eye to indicate secondary separations within the coated and noncoated states.
MTs are net negatively charged polymers (see details in Materials and Methods), which self-assemble from αβ-tubulin heterodimer protein subunits into hollow cylinders, which are ≈26 nm in diameter. The tubulin dimers are arranged head to tail in protofilaments and form the MT wall. The protofilaments are in a straight conformation during MT polymerization and adopt a curved conformation during MT depolymerization. Previous studies showed that tubulin may form several alternative structures, including rings, double rings, and MT coated by rings (18–23). MTs are therefore ideal biopolymers for investigating different self-assembly modes. Determining how such structures are formed provides information about the assembly potential of tubulin dimers and the various kinds of binding interactions between dimers and between tubulin and other proteins (21, 24).
Materials and Methods
Tubulin was purified from bovine brains as described (25, 26). Tubulin concentrated to 45 ± 5 μM in PEM buffer [50 mM Pipes/1 mM MgCl2/1 mM EGTA/0.02% (wt/vol) NaN3, adjusted to pH 6.8 with ≈70 mM NaOH], 1 mM GTP, and 5% glycerol was incubated at 36 ± 1°C for 20 min. The MT wall charge density (per unit volume), σMT, in those conditions was estimated (27) as –0.2 e/nm3, based on the primary structure of tubulin. MT depolymerization was prevented by adding Taxol at 1:1 Taxol-to-tubulin mole ratio. MTs remained stable for several days at room ambient temperature, as indicated by SAXRD and TEM measurements, performed as described (26).
Five cationic lipids of increasing bending rigidity, κ, were used: dilauryl(C12:0)-trimethyl ammonium propane (DLTAP), dioleoyl(C18:1)-trimethyl ammonium propane (DOTAP), dimyristoyl(C14:0)-trimethyl ammonium propane (DMTAP), dipalmitoyl(C16:0)-trimethyl ammonium propane (DPTAP), and distearoyl(C18:0)-trimethyl ammonium propane (DSTAP) (Avanti Polar Lipids). Except oleoyl, which has one unsaturated bond, the remaining tails all are saturated. A chain packing statistical model of membranes (28) and experiments (29) show that k ∝ δP, where δ is the membrane thickness. P ≈ 3 in the case of fluid membrane, the C12:0 and C18:1 tails, for which δ ≈ 1.2 and 1.4 nm, respectively (30). Membranes with ordered chains, the C14:0, C16:0, and C18:0 tails, for which δ ≈ 1.5, 1.8, and 2 nm, respectively, are significantly more rigid, and the scaling of κ with δ is expected to be with a larger P (31, 32). The membrane charge density, σ, was adjusted by adding homologous neutral lipid of the same hydrophobic tail to the charged lipid, but with the respective phosphatidylcholine (PC) head group instead: dilauryl(C12:0)-PC (DLPC), dioleoyl(C18:1)-PC (DOPC), dimyristoyl(C14:0)-PC (DMPC), dipalmitoyl(C16:0)-PC (DPPC) and distearoyl(C18:0)-PC (DSPC). Liposome solutions were prepared at 10–30 mg/ml in Millipore water (18.2 MΩ cm), as described (7). Equal volumes of MTs and liposome solutions were mixed, and the resulting complexes were characterized by SAXRD and TEM. σ is set by the area per lipid head group (7) A0 ≈ 0.7 nm2, for all lipids used, and the mole fraction of cationic lipids,
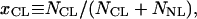 |
where NCL and NNL are the numbers of cationic and neutral lipids, respectively. The relative cationic lipid/tubulin stoichiometry, RCL/T, is defined as
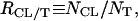 |
where NT is the number of tubulin dimers. RCL/T ≈ 40 is the mixing isoelectric point.
Samples were not oriented; thus SAXRD scans collected on a 2D detector exhibited a powder pattern and were radially averaged. Intensity as a function of momentum transfer, q, was plotted. To model the data, as in other MT-related scattering studies (20, 26, 33), a series of power laws that pass through the minima of the scattering intensities was subtracted. The assumption here is that the size distribution is very narrow. The following results are based on several different experiments (at least three for each data point, using different tubulin purification preparations and different liposome solutions). Within each sample several different regions were examined.
Results and Discussion
A set of TEM images covering the structures in the phase diagram of MT–membrane (κ ≈ 10 kBT) complexes are shown in Fig. 2. For cationic lipid mole fraction, xCL = 0.1, we initially find the weakly positive charged vesicles (beads) adsorbed onto the negatively charged MT wall (rod), forming the BOR structure (Fig. 2 lower right). Bridges are occasionally formed between adjacent MTs, forming small-sized bundles of MTs crosslinked via vesicles (Fig. 2 lower center). This state is, however, kinetically trapped: over longer times, ≈60 h, the adsorbed vesicles “wet” the MT surface, forming the LPN (Fig. 2 lower left). For xCL > 0.1 the LPN forms immediately upon mixing. The images (Fig. 2, above the broken line) reveal that the LPN is made of three layers. Intact MTs are coated by a lipid bilayer (appears brighter in the images, as the ionic stain avoids the hydrophobic lipid tails), which in turn are coated by tubulin oligomers (forming rings or spirals). The oligomer orientation is perpendicular to the internal MT protofilament direction and their density increases with xCL. Oligomer formation is enabled because the cationic membranes lead to MT depolymerization, resulting in curved protofilaments. By using the slowly hydrolyzable GTP analogue, GMPCPP, oligomer formation is prevented. The three-layered LPN structure arises because of the mismatch between the charge densities of MTs and cationic membranes. The oligomers coat the external lipid monolayer to optimize the electrostatic interactions and counterion release. When Taxol is not added to stabilize the MTs, the LPN is much shorter.
Fig. 2.
TEM images of the various states. Whole-mount images of pure MTs (top right), as a control, and liposomes–MT complexes, using DOTAP/DOPC solutions with xCL ≡ NCL/(NCL + NNL) and RCL/T ≡ NCL/NT values as indicated. For xCL = 0.1 (below the broken line) the kinetically trapped BOR and bridging states are shown on the right, and the LPN state after time Δt ≈ 60 h, (indicated by arrow) is shown on the left. Cross sections of pure MT (top left) and the LPN structure (little square) are also shown. The mixing isoelectric point RCL/T = 40 is indicated.
At a given mole fraction of cationic lipids, xCL, when the total MT surface area exceeds the total membrane area, the MTs are only partially coated (Fig. 2, xCL = 0.5 and cationic lipid/tubulin stoichiometry, RCL/T = 40), forming LPNs with open ends. When the reverse is true, some of the excess vesicles are attached primarily to the ends of the LPNs (Fig. 2, xCL = 0.5, RCL/T = 120), forming LPNs with closed ends with lipid caps. The oligomer density at a given xCL is similar for both open and closed LPNs. The ability to switch from open to closed LPNs forms the basis of controlled drug encapsulation and release.
TEM images and SAXRD measurements were performed on pure MT solutions (Figs. 2 and 3) and are in agreement with earlier studies (20, 26, 27, 33, 34). The SAXRD profile of MTs (Fig. 3A) is consistent with the form factor of isotropic hollow cylinders (Fig. 3B). Based on MT structural data (34, 35), we modeled the MT as three concentric cylindrical shells, of a high electron density region surrounded by two low ones, as shown in Fig. 3C, keeping the same total wall thickness and mean electron density as those of MTs.∥ The thickness and location of the high electron density region, within the MT wall, and the inner MT radius are fitting parameters in this model.
Fig. 3.
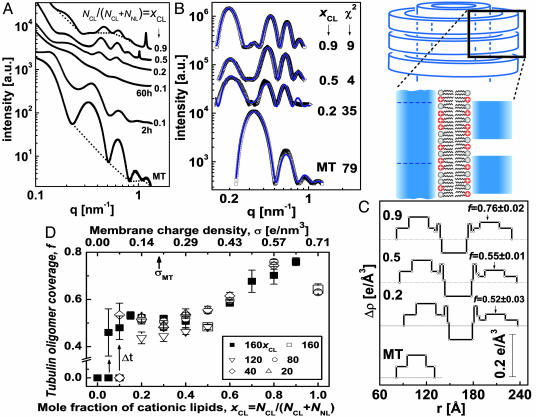
Synchrotron small angle x-ray scattering data, analysis, and a state diagram. (A) Radially averaged scattering intensities of MTs and MT–lipid complexes (solid symbols), using DOTAP/DOPC solutions with xCL ≡ NCL/(NCL + NNL) as indicated. RCL/T ≡ NCL/NT is given by RCL/T = 160 × xCL, corresponding to the point at which the total amount of lipid is exactly enough to coat each MT with a bilayer (calculated as in ref. 16). For xCL = 0.1 two scans are shown, 2 and 60 h after preparing the sample. The broken curves are examples of the assumed background (20, 26, 33). (B) Scattering data from A, after background subtraction (open symbols). The solid curves are the fitted scattering models. Their x2 values are as shown. (C) The variation of the radial electron density, Δρ(r), relative to water (broken lines), of the MTs and complex walls, obtained from fitting the scattering data in B to models of concentric cylinders. r is the distance from the center of the cylinders. The tubulin oligomer coverage, f, values obtained from the nonlinear fit are indicated on the right. The schematic represents a vertical cut through the MT–membrane–tubulin complex wall, corresponding to Δρ(r). (D) State diagram: f as a function of xCL (or σ), when lipids can fully cover the MTs. Each data point is based on scattering data and models as in A–C. Solid squares corresponds to RCL/T = 160 × xCL. Open symbols represent different RCL/T values, as indicated. For 0 < xCL ≤ 0.1 we initially get f = 0 (corresponding to the BOR structure). Over time, Δt ≈60 h, shown by the arrows, we obtain LPNs with higher f values.
A set of SAXRD data for MT–lipid (DOTAP/DOPC) complexes is shown in Fig. 3A. For xCL > 0.1 the SAXRD scans show broad oscillations that are different from that of MTs and correspond to the form factor of the LPNs. For xCL = 0.1, 2 h after MTs and membranes were mixed, the SAXRD scan is consistent (for q > 0.2 nm–1) with the form factor of isotropic MT solutions. At smaller angles there is an additional broad Gaussian correlation peak, centered at q = 0.139 nm–1, corresponding to 45 nm. The SAXRD scan is therefore consistent with the BOR and bridging states (Fig. 2). The existence of a correlation peak suggests that the size distribution of the bridging vesicles is relatively narrow. SAXRD scans taken 60 h after mixing (Fig. 3A) show that this structure slowly evolves into the form factor of the LPNs.
To gain quantitative insight into the organization of the complexes, we analyzed the background-subtracted SAXRD data, shown in Fig. 3B, by fitting to a model. We extended the isotropic concentric cylindrical shells model of MTs to include the second lipid bilayer and the third tubulin layer (Fig. 3C). The radial electron density profile of the inner MT wall and outer tubulin monolayer are based on the fit to the MT scattering data.** The parameters for the electron density profile of the lipid bilayer are based on literature data (3, 30). Finally, the third tubulin layer is multiplied by the fraction, f, of tubulin coverage relative to the inner MT wall. f is the unknown** parameter in this model and is allowed to float freely. The scattering models (Fig. 3B) fit very well to the data.
The SAXRD scans may also have a resolution-limited strong peak (Fig. 3A, xCL = 0.5, 0.9), corresponding to the (001) peak of a 1D lamellar structure with a period of, for example, 5.3 nm (q001 = 1.18 nm–1) for xCL = 0.9 and 6.2 nm (q001 = 1.02 nm–1) for xCL = 0.5. Independent control measurements on liposome solutions of the same compositions and buffer concentration showed exactly the same peaks. The peaks were therefore attributed to excess lipid vesicles in the lamellar phase that are associated with the complexes (closing the ends of the LPNs, see Fig. 2). The intensity of the peaks is increasing monotonically with the cationic lipid/tubulin stoichiometry, RCL/T, as expected.
Fig. 3D summarizes a series of SAXRD scans as in Fig. 3A analyzed as in Fig. 3 B and C. A states diagram is obtained, in which f is plotted as a function of xCL (or σ) at various RCL/T values. For xCL = 0, corresponding to pure DOPC membrane, SAXRD scans show only the isotropic MT form factor. This state (indicated as f = 0) is stable for days, indicating that the LPN is induced by the cationic lipids. At 0 < xCL ≤ 0.1, we have kinetically trapped states of BOR and bridging (also indicated by f = 0) that evolve slowly into the LPN. For xCL > 0.1, we only see the LPN with f values that increase monotonically with xCL. RCL/T has little effect on f, in agreement with the TEM images (Fig. 2).
The lipids in the fluid membrane can rearrange to optimize their interactions with tubulin. At low membrane charge density, σ, one could expect much lower f values, assuming most of the charged lipids simply go to the internal monolayer, to neutralize the MT charge. But mixing entropy favors having charged lipids equally distributed in both monolayers (11, 16). This entropy gain induces coating of tubulin oligomers, resulting in f > 0.4 even at low σ. As σ increases more charged lipids can go to the external monolayer, enable the adsorption of more tubulin oligomers, and increase f. This tubulin coverage increase is favorable also because of better screening of the repulsive electrostatic interactions between the negatively charged tubulin oligomers at higher σ. This repulsion may be the reason for obtaining only partial coverage at all σ (and perhaps contribute to the weak increase of f at low σ). To confirm this hypothesis, the effect of added monovalent salt was studied. We found that the oligomer density increases with monovalent salt concentration and full coverage is achievable. For example, at xCL = 0.5 full tubulin oligomer coverage is obtained with 100 mM KCl. We also found that above some critical concentration, which is a function of σ (for example, 150 mM for xCL = 0.5), the complexes do not form, and the SAXRD scans show only the isotropic MT form factor, indicating that electrostatic interactions drive the formation of the complexes.
By changing the hydrophobic tail of the lipids, the membrane bending rigidity, κ was varied (see Materials and Methods). When DLTAP/DLPC lipid solutions were used, κ was lower than DOTAP/DOPC, whereas for DPTAP/DPPC solutions the lipids were in their ordered phase at room temperature and κ was much higher. As shown in Fig. 4A, we find that with DLTAP/DLPC the kinetically trapped states were not observed, and only the LPN was observed, even at low σ. The f values are within the range of those obtained with DOTAP/DOPC solutions. In contrast, the SAXRD scans with DPTAP/DPPC solutions show (Fig. 4B) only the isotropic MT form factor for all σ. TEM images (Fig. 4C) are consistent with this finding and indicate that the dominate structure is that of BOR and only occasionally bridging is observed. This structure is stable for days and the transition to the LPN was not observed. It shows that κ along with σ are setting the energy barrier between the BOR structure and the LPN.
Our results enable us to make an interesting integration with earlier studies on PLCs. In Fig. 4D we plot the observed state diagram of PLCs as a function of the polyelectrolyte curvature/MT curvature, Cp/CMT, and the relative κ of the lipids used. The pathways between the different phases are shown in Fig. 1. To simplify the presentation in Fig. 4D, we do not include the σ dependence, as it alters specific details within the observed phases. To understand the observations we need to consider the interplay between the electrostatic and membrane elastic interactions in the complexes (1). Pure electrostatic interactions favor tubular or inverted hexagonal structures, as the distance between the cationic lipids and the anionic moieties on the polyelectrolyte is minimized and counterion release is optimized. But this energy gain has to be balanced by the bending energy cost. A membrane of curvature C has elastic energy per unit area, Fel, that is given by Fel = 0.5 κ(C – CM)2.
For low Cp and high κ we observe only the BOR structure (Fig. 1C), as Fel is too high to form the tubular structure, at least within several days. Decreasing κ lowers Fel and increasing σ increases the electrostatic interactions and counterion release, so both can stabilize and favor the formation of the equilibrium tubular complexes (Fig. 1 D and E). Increasing Cp increases Fel by two orders of magnitude when going from MTs to DNA. This increase resists the tubular structure and favors the noncoated lamellar phase (Fig. 1 A). At high Cp, the electrostatic cost of the lamellar structure is much lower, as the membrane can access most of the charges on the polyelectrolytes. At high Cp, a massive reduction in κ (by an order of magnitude, compared with DOTAP) reduces Fel and yields the inverted hexagonal phase (Fig. 1B), which optimizes the electrostatic interactions between the membrane and the polyelectrolytes. The tubular structure in this case is considerably less stable, because of the additional bending energy of the external monolayer (16). However, this structure involves a small frustration free energy penalty resulting from excess chain stretching of some lipid tails into the corners of the hexagonal array (16). This frustration energy increases massively with decreasing Cp and becomes intolerably high when the lipid tails need to be exposed to water in the increasingly empty voids in the corners of the hexagonal array. At this point the inverted hexagonal phase cannot exist and the stable alternative is the LPN observed here.
Conclusions
We have described and characterized two types of polyelectrolyte–lipid complexes (PLCs), the beads on a rod (BOR) and the lipid–protein nanotube (LPN) structures, the conditions for their formation, and the transition between them. By controlling the cationic lipid/tubulin stoichiometry the LPN can be tailored to have open or closed ends with lipid caps. Because the main governing concepts for this self-assembly are general (1, 11, 16, 36) we expect synthetic analogs to follow similar assembly pathways, so that synthetic versions mimicking the LPNs (e.g., replacing MTs with rigid polyelectrolytes) may have applications in chemical and gene (38–42) encapsulation and delivery. Finally, positively charged membranes are commonly used for nonviral drug and gene delivery and introduced into cells (6). Our results suggest that their association with MTs, leading to possible changes in their structure and dynamics in cells, is an important consideration in delivery applications with cationic lipids.
Acknowledgments
We thank K. Ewert, K. Linberg, and S. Richardson for experimental help, D. McLaren for help with cartoons, and O. Farago, N. Gov, A. Zilman, D. Harries, A. Ben-Shaul, D. Sackett, P. Pincus, and T. Deming for discussions. This work was supported by National Institutes of Health Grant GM-59288 (to U.R., D.J.N., Y.L., and C.R.S.), National Science Foundation Grants DMR-0503347 and CTS-0404444 (to U.R., D.J.N., Y.L., and C.R.S.), and National Institutes of Health Grant NS13560 (to H.P.M. and L.W.). The University of California, Santa Barbara Materials Research Laboratory received support from National Science Foundation Grant DMR-0080034. The Stanford Synchrotron Radiation Laboratory, where some of this work was done, is supported by the U.S. Department of Energy. U.R. received fellowship support from the International Human Frontier Science Program and the European Molecular Biology Organizations.
Author contributions: U.R. and C.R.S. designed research; U.R. and D.J.N. performed research; U.R., Y.L., H.P.M., and L.W. contributed new reagents/analytic tools; U.R. and C.R.S. analyzed data; and U.R. and C.R.S. wrote the paper.
This paper was submitted directly (Track II) to the PNAS office.
Abbreviations: PLC, polyelectrolyte–lipid complex; MT, microtubule; SAXRD, small angle x-ray diffraction; TEM, transmission electron microscopy; LPN, lipid–protein nanotube; BOR, beads on a rod; DLTAP, dilauryl(C12:0)-trimethyl ammonium propane; DOTAP, dioleoyl(C18:1)-trimethyl ammonium propane; DPTAP, dipalmitoyl(C16:0)-trimethyl ammonium propane; PC, phosphatidylcholine; DLPC, dilauryl(C12:0)-PC; DOPC, dioleoyl(C18:1)-PC; DPPC, dipalmitoyl(C16:0)-PC.
Footnotes
The mean electron density of tubulin is obtained from the partial specific volume of tubulin (0.725 ml/g) (35), the ratio between the electron and mass densities (0.5445 e/g, calculated based on the primary tubulin structure) and the mean volume of the tubulin unit cell within the MT wall (≈5 × 5 × 8 nm3) (34). Assuming the rest of the tubulin unit cell volume is occupied by water molecules (of density 333 e/nm3) we find that the mean electron density of the MT wall is 411 e/nm3.
Fluctuations are effectively included by allowing the lipid tail length and inner MT radius (≈8.1 nm) to change within physically reasonable limits. The third tubulin layer is assumed to have the mirror image of the inner MT wall electron density profile (taken from the MT fitted model), to reflect what we believe is the correct orientation of the tubulin dimers in the outer layer. It is perpendicular to the internal MT protofilament direction and the side of the dimer facing the MT lumen is flipped inside out (Fig. 1 D and E). Using three different lipid solutions with different tail lengths, we obtained the expected shifts in the form factor, indicating that we identify correctly the location of the lipid bilayer.
References
- 1.Harries, D., Ben-Shaul, A. & Szleifer, I. (2004) J. Phys. Chem. B 108, 1491–1496. [Google Scholar]
- 2.Koltover, I., Sahu, S. & Davis, N. (2004) Angew. Chem. Int. Ed. 43, 4034–4037. [DOI] [PubMed] [Google Scholar]
- 3.Wong, G. C. L., Tang, J. X., Lin, A., Li, Y., Janmey, P. A. & Safinya, C. R. (2000) Science 288, 2035–2039. [DOI] [PubMed] [Google Scholar]
- 4.Subramanian, G., Hjelm, R. P., Deming, T. J., Smith, G. S., Li, Y. & Safinya, C. R. (2000) J. Am. Chem. Soc. 122, 26–34. [Google Scholar]
- 5.Dalkara, D., Zuber, G. & Behr, J. P. (2004) Mol. Ther. 9, 964–969. [DOI] [PubMed] [Google Scholar]
- 6.Koltover, I., Salditt, T., Radler, J. O. & Safinya, C. R. (1998) Science 281, 78–81. [DOI] [PubMed] [Google Scholar]
- 7.Radler, J. O., Koltover, I., Salditt, T. & Safinya, C. R. (1997) Science 275, 810–814. [DOI] [PubMed] [Google Scholar]
- 8.Liang, H., Angelini, T. E., Ho, J., Braun, P. V. & Wong, G. C. L. (2003) J. Am. Chem. Soc. 125, 11786–11787. [DOI] [PubMed] [Google Scholar]
- 9.Yang, L., Liang, H., Angelini, T. E., Butler, J., Coridan, R., Tang, J. X. & Wong, G. C. L. (2004) Nat. Matt. 3, 615–619. [DOI] [PubMed] [Google Scholar]
- 10.Artzner, F., Zantl, R., Rapp, G. & Radler, J. O. (1998) Phys. Rev. Lett. 91, 5015–5018. [Google Scholar]
- 11.May, S., Harries, D. & Ben-Shaul, A. (2000) Biophys. J. 78, 1681–1697. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Safran, S. A. (1994) Statistical Thermodynamics of Surfaces, Interfaces, and Membranes (Addison–Wesley, Reading, MA).
- 13.Spector, M. S., Easwaran, K. R. K., Jyothi, G., Selinger, J. V., Singh, A. & Schnur, J. M. (1996) Proc. Natl. Acad. Sci. USA 93, 12943–12946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Chiruvolu, S., Warriner, H. E., Naranjo, E., Idziak, S. H. J., Radler, J. O., Plano, R. J., Zasadzinski, J. A. & Safinya, C. R. (1994) Science 266, 1222–1225. [DOI] [PubMed] [Google Scholar]
- 15.Felgner, P. L., Gadek, T. R., Holm, M., Roman, R., Chan, H. W., Wenz, M., Northrop, J. P., Ringold, G. M. & Danielsen, M. (1987) Proc. Natl. Acad. Sci. USA 84, 7413–7417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.May, S. & Ben-Shaul, A. (1997) Biophys. J. 73, 2427–2440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Dan, N. (1998) Biochim. Biophys. Acta 1369, 34–38. [DOI] [PubMed] [Google Scholar]
- 18.Unger, E., Bohm, K. J., Muller, H., Grossmann, H., Fenske, H. & Vater, W. (1988) Eur. J. Cell. Biol. 46, 98–104. [PubMed] [Google Scholar]
- 19.Jacobs, M., Bennett, P. M. & Dickens, M. J. (1975) Nature 257, 707–709. [DOI] [PubMed] [Google Scholar]
- 20.Fernando-Diaz, J., Andreu, J. M., Diakun, G., Towns-Andrews, E. & Bordas, J. (1996) Biophys. J. 70, 2408–2420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Erickson, H. P. & Voter, W. A. (1976) Proc. Natl. Acad. Sci. USA 73, 2813–2817. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Karagiannidou, T., Eleftheriou, E. P., Tsekos, I., Galatis, B. & Apostolakos, P. (1995) Ann. Bot. 76, 23–30. [Google Scholar]
- 23.Nogales, E., Wolf, S. G. & Downing, K. H. (1998) Nature 393, 199–203. [DOI] [PubMed] [Google Scholar]
- 24.Westermann, S., Avila-Sakar, A., Wang, H., Niederstrasser, H., Wong, J., Drubin, D. G., Nogales, E. & Barnes, G. (2005) Mol. Cell 17, 277–290. [DOI] [PubMed] [Google Scholar]
- 25.Farrell, K. W. & Wilson, L. (1984) Biochemistry 23, 3741–3748. [DOI] [PubMed] [Google Scholar]
- 26.Needleman, D. J., Ojeda-Lopez, M. A., Raviv, U., Miller, H. P., Wilson, L. & Safinya, C. R. (2004) Proc. Natl. Acad. Sci. USA 101, 16099–16103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Needleman, D. J., Ojeda-Lopez, M. A., Raviv, U., Ewert, K., Jones, J. B., Miller, H. P., Wilson, L. & Safinya, C. R. (2004) Phys. Rev. Lett. 93, 198104-1. [DOI] [PubMed] [Google Scholar]
- 28.Szleifer, I., Kramer, D. & Ben-Shaul, A. (1988) Phys. Rev. Lett. 60, 1966–1969. [DOI] [PubMed] [Google Scholar]
- 29.Safinya, C. R., Sirota, E. B. S., Roux, D. & Smith, G. S. (1989) Phys. Rev. Lett. 62, 1134–1138. [DOI] [PubMed] [Google Scholar]
- 30.Liu, Y. F. & Nagle, J. F. (2004) Phys. Rev. E 69, 040901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Sackmann, E. (1994) FEBS Lett. 346, 3–16. [DOI] [PubMed] [Google Scholar]
- 32.Rawicz, W., Olbrich, K. C., McIntosh, T., Needham, D. & Evans, E. (2000) Biophys. J. 79, 328–339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Andreu, J. M., Bordas, J., Diaz, J. F., Garcia de Ancos, J., Gil, R., Medrano, F. J., Nogales, E., Pantos, E. & Towns-Andrews, E. (1992) J. Mol. Biol. 226, 169–184. [DOI] [PubMed] [Google Scholar]
- 34.Li, H., DeRosier, D. J., Nickolson, W. V., Nogales, E. & Downing, K. H. (2002) Structure (London) 10, 1317–1328. [DOI] [PubMed] [Google Scholar]
- 35.Lee, J. C., Frigon, R. P. & Timasheff, S. N. (1973) J. Biol. Chem. 248, 7253–7262. [PubMed] [Google Scholar]
- 36.Wu, Y., Cheng, G., Katsov, K., Sides, S. W., Wang, J., Tang, J., Fredrickson, G. H., Moskovits, M. & Stucky, G. D. (2004) Nat. Matt. 3, 816–822. [DOI] [PubMed] [Google Scholar]
- 37.McManus, J. J., Radler, J. O. & Dawson, K. A. (2003) Langmuir 19, 9630–9637. [Google Scholar]
- 38.Huang, L., Hung, M. C. & Wagner, E. (1999) Nonviral Vectors for Gene Therapy (Academic, San Diego).
- 39.Mahato, R. I. & Kim, S. W., eds. (2002) Pharmaceutical Perspective of Nucleic Acid-Based Therapeutics (Taylor and Francis, London).
- 40.Chaudhuri, A., ed. (2003) Curr. Med. Chem. 10, 1185–1315.12678793 [Google Scholar]
- 41.Safinya, C. R., ed. (2004) Curr. Med. Chem. 11, 133–266. [DOI] [PubMed] [Google Scholar]
- 42.Huang, L., Hung, M. C. & Wagner, E. (2005) Non-Viral Vectors for Gene Therapy (Elsevier, San Diego), 2nd Ed., Part 1.