Unusual compactness of a polyproline type II structure

Abstract

Polyproline type II (PPII) helix has emerged recently as the dominant paradigm for describing the conformation of unfolded polypeptides. However, most experimental observables used to characterize unfolded proteins typically provide only short-range, sequence-local structural information that is both time- and ensemble-averaged, giving limited detail about the long-range structure of the chain. Here, we report a study of a long-range property: the radius of gyration of an alanine-based peptide, Ace-(diaminobutyric acid)₂-(Ala)₇-(ornithine)₂-NH2. This molecule has previously been studied as a model for the unfolded state of proteins under folding conditions and is believed to adopt a PPII fold based on short-range techniques such as NMR and CD. By using synchrotron radiation and small-angle x-ray scattering, we have determined the radius of gyration of this peptide to be 7.4 ± 0.5 Å, which is significantly less than the value expected from an ideal PPII helix in solution (13.1 Å). To further study this contradiction, we have used molecular dynamics simulations using six variants of the AMBER force field and the GROMOS 53A6 force field. However, in all cases, the simulated ensembles underestimate the PPII content while overestimating the experimental radius of gyration. The conformational model that we propose, based on our small angle x-ray scattering results and what is known about this molecule from before, is that of a very flexible, fluctuating structure that on the level of individual residues explores a wide basin around the ideal PPII geometry but is never, or only rarely, in the ideal extended PPII helical conformation.

The unfolded and denatured states of proteins have recently received significant attention from experimentalists (1–13) and theoreticians alike (14–21). Because the unfolded state represents one half of the protein-folding free energy diagram, the presence of any residual structure in the unfolded state carries significant implications for both thermodynamics and kinetics of protein folding. With regards to thermodynamics, permanent structure in the unfolded state significantly lowers the entropy of the unfolded state, thereby affecting the free energy change of folding. With regards to kinetics, the presence of preformed native-like contacts potentially speeds up the folding process. When it comes to structure, a consensus has recently begun to emerge about a significant presence of the polyproline type II (PPII) backbone geometry in the unfolded/denatured state (12, 18, 20–25). The evidence for this view comes predominantly from spectroscopic studies on model peptides (12, 22–28, 61, 62) and computer simulations (18, 20, 21, 29–32, 62).

The unfolded state of proteins, in addition to being intrinsically important in the context of protein folding, presents a fruitful “laboratory” for studying the question of the relative importance of local and global structural information in protein structure determination. The observables used in protein structure determination can be divided into those that probe the local structure of the polypeptide chain [e.g., circular dichroism (CD) spectra, sequencelocal nuclear Overhauser effects (NOEs), vicinal couplings, chemical shifts, vibrational and Raman spectra, and high-angle x-ray reflections) and those that report on its global, long-range structure (e.g., long-range NOEs, low-angle x-ray reflections, FRET, and EPR spectra). Usually, in folded, native protein structures, these two types of information complement each other and are mutually consistent on the level of single structure representation. However, the unfolded state of proteins, given its dynamic and heterogeneous nature, defies representation as a single 3D structure. What is more, it may provide seemingly contradictory structural information when comparing the short-range with the long-range structure. The so-called “reconciliation problem” of protein folding (11, 19, 33), namely how local native-like structure of denatured proteins can be consistent with their overall random-walk-like behavior, is one example.

In this study, we have used small-angle x-ray scattering (SAXS) technique (34) to measure the radius of gyration (R_gyr) of the alanine-based XAO peptide, Ace-(Daba)₂-(Ala)₇-(Orn)₂-NH2 (where Daba stands for diaminobutyric acid and Orn stands for ornithine). This peptide was previously determined to adopt a PPII fold based on NMR spectroscopic evidence (³J_NHα coupling values and NOEs) and CD (12, 22), as well as computer simulations (20). This molecule, not observed to form α-helical structure, is believed to be an ideal system for studying the unfolded state of proteins under folding conditions (i.e., in the absence of chemical or physical denaturants). R_gyr, in contrast to the predominately sequence-local geometric features analyzed previously, is a global structural property of a molecule (34) and as such provides structural information, which may not be deducible from short-range information. Indeed, the R_gyr that we measure (7.4 ± 0.5 Å) is >40% less than what would be predicted for a fully extended PPII helix (13.1 Å). The structural picture that we postulate, based on these results and what is know from previous research, is that of a very flexible, fluctuating molecule that on the level of individual residues samples a broad basin around the ideal PPII geometry but is never, or only rarely, in the ideal extended PPII helical conformation.

Materials and Methods

Peptide Synthesis. The peptide [sequence: Ace-(Daba)₂-(Ala)₇-(Orn)₂-NH2] was synthesized at the Stanford University Protein and Nucleic Acid Facility by using solid-phase synthesis and standard fluorenylmethoxycarbonyl synthetic chemistry on the Applied Biosystems MALDI-TOF mass spectrometry and reverse-phase HPLC.

SAXS. SAXS measurements were carried out at the BESSRC-CAT beamline 12-ID at the Advanced Photon Source (Argonne, IL). Immediately before data taking, the samples were centrifuged for 10 min at 11,000 × g. The measurements were performed at 25 ± 1°C in a custom-made, thermostated flow cell at a photon energy of 12 keV (1 eV = 1.602 × 10^–19 J). For each condition, a total of 40 measurements of 1.0-s integration time each were taken. All data were image-corrected and circularly averaged after data taking. The 40 profiles for each condition were averaged, and buffer-scattering profiles were subtracted for background correction. There were no signs of aggregation or radiation damage. The measurements were taken for different peptide concentrations (15, 10, 5, 2.5, and 1.25 mg/ml) in both 30 (all except 1.25 mg/ml) and 100 mM acetate buffer (pH 4.6) in the presence of 5 mM radical scavenger N-tert-butyl-α-(4-pyridyl)nitrone N′-oxide. The radii of gyration were determined by Guinier analysis (34).

CD Spectroscopy. CD spectra were recorded at 25 ± 1°C in 10 mM acetate buffer (pH 4.6) and 10 mM phosphate buffer (pH 7) on a 62A DS spectrometer (Aviv Associates, Lakewood, NJ) equipped with a Hewlett–Packard 89100A temperature control unit by using quartz cuvettes with 1.0-mm pathlengths. Data were collected in 1-nm increments from 260 to 180 nm with triple averaging at each point. Under all conditions, the peptide gives rise to virtually indistinguishable spectra.

Molecular Dynamics Simulations. Equilibrium distributed computing simulations. The simulations were carried out on the Folding@Home distributed computing cluster (35) by using the gromacs (36, 37) simulation package, the TIP3P water model (38), and six variants of the AMBER force field. These variants are AMBER-94 (39), AMBER-96 (40), AMBER-99 (41), and three variants in which the torsional potentials of these standard force fields were modified, AMBER-GS (AMBER-94 with φ/ψ potentials removed) (42), AMBER-99φ (AMBER-99 with AMBER-94 φ potential) (32), and AMBER-GS-S (AMBER-94 with φ/ψ potentials and 1–4 van der Waals scaling removed) (43). The basic side chains were protonated by assuming low pH, and the N and C termini were capped with acetyl and amide groups, respectively. Four chloride ions were added to neutralize the net charge. Simulations were carried out at constant temperature and pressure (298 K, 1 atm; 1 atm = 101.3 kPa) in a periodic cubic box of the side length of ≈35 Å (1,338 water molecules if started extended; 1,351 if started helical or PPII). The temperature and pressure were controlled by coupling the system to external baths with relaxation times of 0.1 and 1.0 ps, respectively (44). Electrostatics was handled by using the reaction-field method with dielectric permittivity of 80, and 9.0-Å cutoffs were applied to nonbonded interactions. Nonbonded pair lists were updated every 10 steps of molecular dynamics, and the integration step size was 2.0 fs in all simulations. Covalent bonds involving hydrogen atoms were constrained by using the LINCS algorithm (45).

The parameters for Daba were obtained from those for Orn by modifying the charges by hand to distribute the extra remaining charge throughout the C_βH2 group in Daba. Charges that were the same in Lys and Orn (i.e., the terminal group, CH2 next to the terminal group and backbone) were kept unchanged.

For each of the six force fields, the simulations were started from three different configurations as follows: the ideal PPII conformation (all φ = –75°, ψ = 145°), the ideal Pauling α-helical conformation (all φ = –57°, ψ = –47°), and the fully extended configuration (all φ = –180°, ψ = 180°). For each of the starting structures, 1,000 independent simulations were run for tens of nanoseconds each (average length of individual trajectories was anywhere between 40 and 42 ns, depending on the force field and starting configuration used). After ≈20 ns, all three starting structures converged to highly similar ensembles under each force field used (see Fig. 2). The analysis detailed in Table 1 and Fig. 2 was performed on the composite ensembles consisting of all of the structures, sampled every 100 ps, that came after the 20 ns time-point in all of the trajectories whose length was >20 ns. The simulations were run for an aggregate time of 700 μs (1,800 CPU years) over 4 wall-clock weeks.

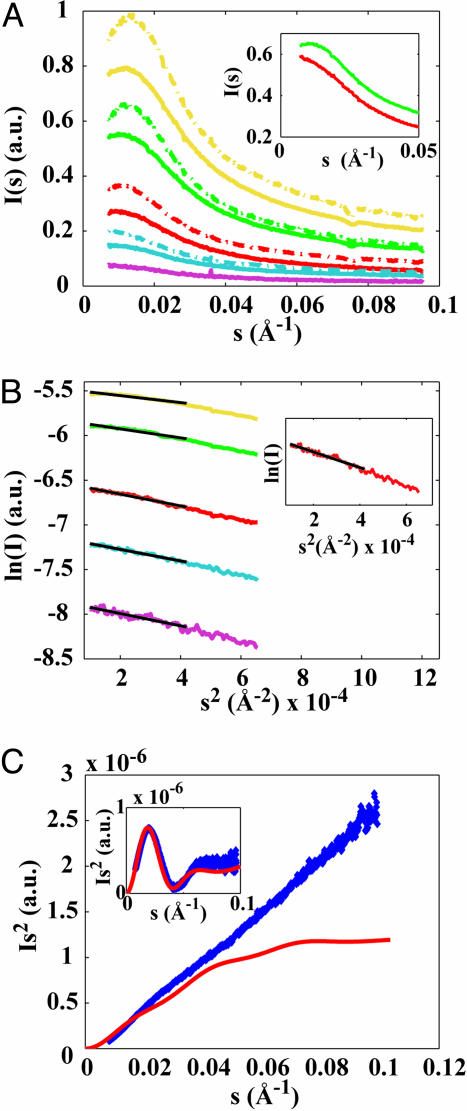
Fig. 2.

SAXS analysis of the XAO peptide. (A) SAXS profiles of XAO at different peptide concentrations in 30 mM (dashed lines) and 100 mM acetate buffer (solid lines). Peptide concentrations are 15 mg/ml (yellow), 10 mg/ml (green), 5 mg/ml (red), 2.5 mg/ml (blue), and 1.25 mg/ml (purple). (Inset) Low s scattering for 10 mg/ml XAO in 100 mM acetate buffer without (green) and with 200 mM NaCl added (red). Profiles in Inset are vertically offset for clarity. (B) Guinier analysis and fits of the R_gyr for XAO in 100 mM acetate buffer. The fitting range is indicated by the black solid lines. Fitted R_gyr values are 5.5 Å (15 mg/ml, yellow), 6.2 Å (10 mg/ml, green), 7.1 Å (5 mg/ml, red), 7.0 Å (2.5 mg/ml, blue), and 7.2 Å (1.25 mg/ml, purple). (Inset) The scattering profile extrapolated to zero protein concentration yields an R_gyr of 7.4 Å. (C) The Kratky plot of XAO at 5 mg/ml in 100 mM acetate (blue diamonds) and the theoretical prediction for the ideal PPII helix (red solid line). Inset shows horse heart cytochrome c (1.25 mg/ml in 100 mM acetate, pH 4.6) measured on the same setup and used as a molecular weight standard (blue diamonds), and a theoretical profile using the known crystal structure with Protein Data Bank ID code 1CRC and crysol as described (blue solid line).

Table 1. Comparison between the experimental and the simulation values for XAO for the theoretical SAXS estimate of the R_gyr, the average ideal geometric R_gyr, 〈R_gyr²〉^1/2, and the ³J_NHα-coupling constants.

Force field	Rgyr (saxs), Å	〈Rgyr2〉1/2, Å	〈3JHNα〉Ala, Hz
A-94	7.9 ± 0.1	6.5 ± 0.4	4.9 ± 0.1
A-GS-S	7.7 ± 0.1	6.3 ± 0.3	3.8 ± 0.2
A-96	10.9 ± 0.2	9.6 ± 1.4	6.7 ± 0.1
A-99	8.0 ± 0.1	6.7 ± 0.4	6.8 ± 0.4
A-99φ	8.1 ± 0.1	6.7 ± 0.5	5.4 ± 0.1
A-GS	7.6 ± 0.1	6.3 ± 0.2	4.0 ± 0.1
GR-53A6	10.9 ± 0.2	9.2 ± 1.5	7.5 ± 2.2
Exp.	7.4 ± 0.5	n/a	≈5.6

The theoretical SAXS estimates of the R_gyr were calculated based on average crysol-based Guinier plots of 100 randomly chosen simulated structures. The errors were calculated from the standard errors of the linear Guinier fits. Exp., experimental; A, AMBER force field; GR, GROMOS force field. The experimental ³J_NHα values were adopted from ref. 22. The coupling constants were calculated by using the Karplus equation and the Vuister-Bax parameterization (60) and were averaged over all seven alanine residues in the molecule. The errors for ³J_NHα-constants correspond to standard deviation over the seven alanines.

GROMOS simulations. We also have simulated the XAO peptide by using the GROMOS 53A6 force field (46) and the gromos md package (47, 48) on a Pentium cluster. We have carried out 10 independent simulations starting from the extended PPII configuration for 31.5 ns each, in explicit single point charge water (49) (5,471 molecules) in the presence of four chloride ions to neutralize the net charge. The simulations were run in a cubic box (size ≈ 55 Å) under periodic boundary conditions. The temperature (298 K) and pressure (1 atm) were kept constant by coupling the system to external temperature and pressure baths with relaxation times of 0.1 and 0.5 ps, respectively (44). Nonbonded interactions were treated by using a triple range scheme with 8- and 14-Å cutoffs (for details, see ref. 46). The electrostatic interactions were treated by using the reaction-field method with a cutoff of 14 Å and dielectric permittivity of 61. Nonbonded pair lists were updated every 5 steps, and the integration step size was 2 fs in all simulations. The bonds including hydrogen atoms were constrained by using the SHAKE algorithm (50) with a relative geometric accuracy of 10^–4. The parameters for Orn and Daba were derived from those of lysine. The analysis was carried out on the composite ensemble consisting of all of the structures between 29.5 and 31.5 ns in the simulations sampled every 20 ps from the 10 trajectories (a total of 1,000 structures). The gromos simulations were performed with a smaller degree of sampling compared with the distributed computing simulations with AMBER. However, as all geometrical descriptors of the gromos ensemble that we looked at reach plateau in 10 ns or so, we believe that the final ensemble analyzed in the case of gromos captures well the equilibrium ensemble and that it would not significantly collapse further.

Structural Definitions. In Fig. 3, a residue is defined to be α-helical or PPII if both of its dihedral angles fall within ±15° from the canonical α-helical (φ =–62°, ψ =–41°) or PPII geometry (φ = –75°, ψ = 145°). The structures in Fig. 4B were generated by using the following definitions. For the extended structure, all alanine residues adopt the ideal PPII geometry (φ =–75°, ψ = 145°); for the structure bent in the middle, all alanine residues adopt the ideal PPII geometry (φ = –75°, ψ = 145°) except Ala-6, which adopts α-helical geometry (φ = –62°, ψ = –41°). In both cases, the capping Daba and Orn residues adopt antiparallel β-helical geometry (φ = –139°, ψ = 135°). Shi and Kallenbach (personal communication, N. Kallenbach) observed that the coupling constants of the Daba and Orn residues in the XAO peptide were larger than those of alanines, suggesting they may have higher β-sheet content. However, not all of them could be measured because of overlap. If the caps are put in the PPII conformation, it results in only minor differences in the predicted R_gyr (a decrease of <2%). If they are put in the α-helical conformation (making them as compact as they can probably be), the predicted R_gyr drops by only 5%.

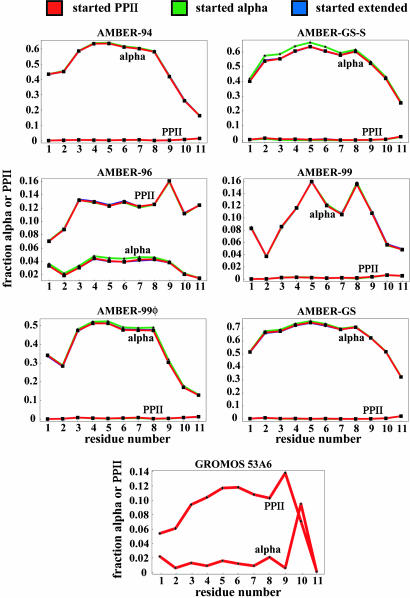
Fig. 3.

α-Helical vs. PPII secondary structure content from the simulations using six different variants of the AMBER force field and the GROMOS 53A6 force field. In the case of the AMBER force field, the simulations were started from the PPII, extended, and α-helical conformations, yet they all converge to identical values: the lines corresponding to different starting configurations superimpose almost perfectly for all six variants of AMBER. The GROMOS 53A6 simulations all were started from the ideal PPII configuration.

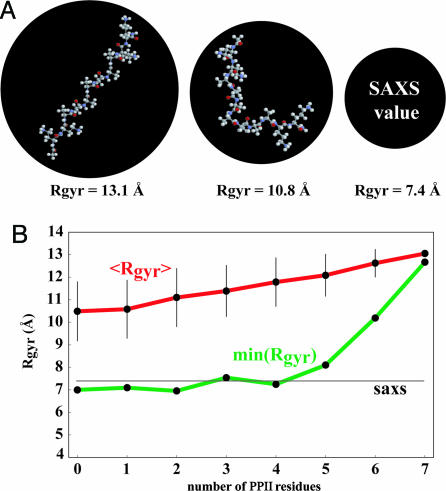
Fig. 4.

Unusual compactness of XAO. (A) Comparison of the measured R_gyr of the XAO peptide (7.4 Å) with the theoretical R_gyr estimates for a fully extended PPII configuration (13.1 Å) and a hypothetical structure in which two PPII segments are positioned perpendicularly to each other (10.8 Å). The radii of the black circles are proportional to the corresponding molecular radii of gyration. See Materials and Methods for the exact definition of structures shown. (B) The average theoretical solution SAXS estimates for the R_gyr, 〈R_gyr〉, and the theoretical SAXS estimate for the R_gyr of the most compact member, min(R_gyr), of an ensemble consisting of 500 randomly generated structures having the indicated number of PPII residues. The horizontal line (saxs) denotes the measured value of R_gyr. See Materials and Methods for how the structures were generated.

Generation of Ensembles with a Given PPII Content. The ensembles described in Fig. 4B were generated by the following method. A given number of randomly chosen alanine residues were assigned PPII dihedral angles (randomly chosen from the window φ = –75 ± 15°, ψ = 145 ± 15°), whereas the remaining alanine residues were assigned randomly chosen dihedral angles from the remainder of the accessible area of the Ramachandran map. The Daba and Orn caps were all placed in the antiparallel β-sheet configuration. The structures generated in such a way were screened for steric clash and, in the absence thereof, were added to the ensemble. The procedure was repeated until all ensembles contained 500 structures.

Calculating Theoretical Scattering Profiles and Effective R_gyr Values. The effective R_gyr values measured by SAXS differ from the ideal, geometry-based values due to the surface layer of ordered water surrounding the molecule. The theoretical expected R_gyr values in solution of the simulated structures (see Fig. 4 and Table 1) were calculated by using Guinier analysis on the predicted scattering profiles generated by using crysol software (51) with all the input parameters set at their default crysol values.

Results

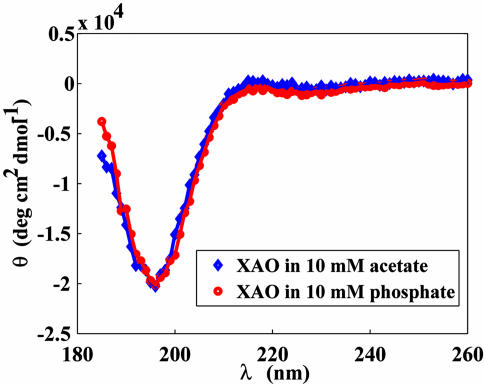
The XAO peptide in aqueous solution exhibits a CD spectrum characteristic of the PPII conformation (Fig. 1) (12, 22). The spectrum shows a strong negative band at 196 nm and a weak positive band at ≈215 nm. These features have been observed with unfolded polypeptides (52–54) and fully agree with what was seen by Kallenbach and coworkers with the XAO peptide (12, 22). In light of the simulations discussed below, it is of particular importance to mention the complete absence of α-helical features in the CD spectra of XAO.

Fig. 1.

CD spectra of the XAO peptide in 10 mM acetate buffer (pH 4.6) (blue diamonds) and 10 mM phosphate buffer (pH 7.0) (red circles).

The SAXS profiles (Fig. 2A) reveal a downturn in scattering intensity for very small momentum transfer s at high protein concentration (15 and 10 mg/ml), which can be attributed to interparticle interference due to repulsive, electrostatic interactions between peptide molecules. The interparticle interference vanishes with decreasing peptide concentration and is more pronounced at lower buffer concentration, because lower buffer corresponds to fewer counterions and reduced Debye-screening. To further test this hypothesis, we collected scattering data for fixed peptide and buffer concentration and found that the addition of 200 mM NaCl indeed reduces the interference effect significantly (Fig. 2A Inset), consistent with the picture of Debye-screening of electrostatic repulsion. We performed Guinier fits [fits of a straight line in ln(I) vs. s² plots] to obtain the R_gyr of the peptide. The presence of interparticle interference leads to different fitted R_gyr values for profiles recorded at different concentration (Fig. 2B), reaching a plateau at ≈5 mg/ml. Given that the interparticle interference vanishes with decreasing concentration, we take the values at low protein concentrations (5 mg/ml and lower) to be most representative of the true R_gyr of the peptide. To further validate the thus-obtained value, we extrapolate the scattering profile to zero concentration by using linear regression on the data set with the concentration as the independent variable and performing a Guinier fit on the extrapolated profile (Fig. 2B Inset). Fits using both different fitting ranges and the data set for XAO in 30 mM acetate buffer gave similar values for the fitted R_gyr values, to within ±0.5 Å. We therefore estimate the R_gyr to be 7.4 ± 0.5 Å in the infinite dilution limit. The Guinier fit in the infinite dilution limit also gives the correct molecular weight for the peptide, within errors, from the forward-scattering intensity and comparison with cytochrome c standard. Finally, the Kratky plots of I(s)s² as a function of s show a linear rise (Fig. 2C), which according to the Porod theory (34) [whereby a random coil scatters as I(s) ∼ 1/sfor large s] indicates that the peptide is not fully folded/does not have a single well defined structure.

The measured R_gyr of the XAO peptide is significantly lower than the value predicted for an ideal PPII helix (≈13 Å). To study this discrepancy further, we have carried out explicit solvent simulations of the peptide by using six different variants of the AMBER force field and the GROMOS 53A6 force field. The ability of some of these force fields to predict α-helical properties has been demonstrated before (30, 43). For AMBER-99φ, it was recently found that it quantitatively reproduces most kinetic and thermodynamic observables for the F_s peptide (32, 55). However, for the XAO peptide all seven force fields fail at reproducing the experimental data with respect to both the secondary structure content and the R_gyr of the peptide. In Fig. 3, we show what fraction of the time a given residue adopts α-helical and PPII geometry, and it is clear that, except for AMBER-96 and GROMOS 53A6, all other force field variants clearly prefer this molecule to be α-helical. However, even in the case of AMBER-96 and GROMOS 53A6, the PPII fraction is still quite low, and both predict high R_gyr values. Interestingly, the force fields with the greatest helicity make the most accurate predictions of R_gyr. Understanding this apparent paradox will be an important future step in modeling small alanine-based peptides. It is no surprise then that this α-helical preference of most of the force fields combined with low PPII content also would reflect itself in the average predicted R_gyr or ³J-coupling values (Table 1).

Discussion

On the basis of NMR experimental evidence, Kallenbach and coworkers (22) recently described the XAO peptide as adopting the PPII fold. Based on CD spectra, vicinal ³J_NHα coupling values, and the absence of sequential α-helical NOEs, they have proposed that each of the seven central alanine residues adopts PPII conformation. In this study, we have measured the R_gyr of this molecule to be 7.4 ± 0.5 Å, which is much less than what would be expected from an extended PPII helix (Fig. 4A). How can this discrepancy be explained?

The ³J_NHα coupling values and CD report on the local, short-range structure of the peptide and contain little information on the long-range structure or the correlations between different segments of local structure. The following simple model illustrates this point. Let us assume that each residue is 70% of the time in PPII conformation: this assumption would lead to a strong local PPII signal, such as for instance ³J_NHα coupling values characteristic of PPII. However, in this case, the residues, say, four amino acids apart would be only 25% of the time (70% raised to the 4th power ≈ 25%) simultaneously in the same PPII configuration, assuming that they behave independently from each other. As a consequence, the extended rod-like PPII helix would immediately be excluded as a potentially dominant long-range configuration. For longer sequence separations, this decorrelation is of course even greater. Because of intrinsic dynamics and structural heterogeneity of the peptide, the sum of local structural information need not equal global information. Indeed, in the original study of the XAO peptide, Kallenbach and coworkers (22) suggested that the structure of the molecule exhibits significant fluctuations around the ideal PPII helix. Here we should emphasize that we do not at all question the accuracy of the NMR results reported by Kallenbach and coworkers (22). What our SAXS results do make us question is the interpretation of the long-range structure of XAO based on such local measurements. The structure of this molecule is not an extended PPII helix but is an ensemble of interconverting conformations that locally prefer the broad basin around the PPII geometry but globally have to be represented by something akin to a random walk. This explanation is consistent with the R_gyr and the linear Kratky plots measured (Fig. 2C). One analogy that exemplifies well the seeming contradiction between our results and the results by Kallenbach is that of wave-particle duality of light. Neither wave nor particle pictures are completely correct or completely wrong, but they complement each other: for complete description one needs to consider both aspects. In the same vein, for the full description of a flexible polypeptide one needs to consider both short- and long-range structural information.

Recently, Kallenbach and coworkers (56) suggested that PPII formation in alanine-based peptides is noncooperative, which lends support to the above analysis based on the assumption of residue independence. In addition, Rose and coworkers (18, 58) showed that Flory's isolated pair hypothesis (57) indeed holds in the PPII region of the Ramachandran map. Finally, in a recent theoretical study, Fitzkee and Rose (33) demonstrated how the global structure of a protein molecule can be significantly random-walk-like even though local secondary structure remains almost completely native-like. Our SAXS result is an experimental version of this “reconciliation problem” (11), and it is particularly intriguing because it is observed in such a short molecule.

Because the structural ensembles generated using the standard atomistic force fields did not match the experimental data well, we also have randomly generated several sets of ensembles (see Materials and Methods) having different PPII content using the absence of steric clash as the only criterion for accepting a given structure (Fig. 4B). Interestingly, for structures containing five or more PPII residues, even the most compact individual members of the ensembles exceed the measured R_gyr. In other words, if a given XAO molecule has five or more residues in the PPII configuration at once, its R_gyr will by necessity be greater than the value we measured. This fact further speaks in favor of the conformational model for XAO in which the molecule adopts a flexible, dynamic structure where the PPII configuration is never, or only rarely, adopted by all of the alanine residues at once. Close examination of the structures with low R_gyr and yet sizable PPII content reveals that in such structures most of the non-PPII residues occupy the broad α-helical part of the Ramachandran map. This result is expected, because if these residues were in the β-sheet region, the overall R_gyr would be reduced only negligibly.

The molecular dynamics simulations performed in this study are in disagreement with the experiments by Kallenbach and coworkers (22) in that they all predict little PPII structure in the XAO peptide. In particular, five of seven force fields used in this study predict extremely high levels of the α-helical configuration, which is experimentally not observed. It is possible that the main culprit for this failure is the fact that most force fields are tested against folded globular proteins and may therefore not be accurate enough to capture the structure and dynamics of the unfolded state. The force field that was found to perform the best in reproducing experimental helix-coil kinetics and thermodynamics for polyalanine-based 21-mer peptides, AMBER-99φ (32), predicts little PPII structure, as do most of the remaining AMBER force fields. Sorin and Pande (32) noted in their study that preferences for particular conformational states were dependent on peptide length. This study increases our understanding of this effect by adding a 7-mer polyalanine peptide to the di- and tripeptides studied by Zaman et al. (29) and the 21-mer studies of Sorin and Pande (32). It is intriguing to consider that moving from 3 to 7 to 21 Ala residues could yield such significant structural variation based solely on the length of the peptide. This observation adds another challenge to be tackled by the biosimulation community.

Our work suggests that the PPII structure is extremely flexible and that it persists over very short distances only. Based on our results, this persistence length is significantly less than seven residues. In fact, our results are not inconsistent with this persistence length being just two residues or so. For instance, the measured R_gyr (7.4 Å) is equivalent to the R_gyr of an ideal random-flight chain with 10 links and a persistence length of only 5.7 Å. Therefore, we believe that picturing the unfolded state of larger proteins as a chain of connected PPII rods may be misleading. Individual residues are likely to spend most of the time occupying the PPII region of the Ramachandran map, but even over very short stretches the unfolded structure deviates strongly from the extended PPII helix. Furthermore, if one accepts this explanation, one also must allow for a significantly higher entropy content in the unfolded state than what one gets under the assumption of a single dominant rod-like configuration. Finally, the compact nature of the XAO peptide as implied by our work presents a new challenge when it comes to describing the role of water in stabilizing the PPII structure. It is difficult to immediately see how such a compact structure could have a broad water-filled groove or channel postulated to be important for the stability of the PPII helix (18, 20, 23, 30, 59).

Finally, another factor that also should be considered is the effect of conformational averaging. The PPII values for backbone dihedral angles in alanine peptides were derived in a direct fashion by using three different experimental techniques, NMR vicinal J-coupling measurements (12, 22), vibrational spectroscopy, and Raman spectroscopy (28, 61, 62). In the case of all other experimental techniques, such as CD, the evidence is more indirect. All three of the above-mentioned techniques involve experimental readouts that are highly time- and ensemble-averaged. It would be interesting to see to what extent the final result is influenced by this averaging. It is possible that the backbone angles sample a significantly larger basin, but that experimental averaging pushes the observed values toward what is interpreted as the PPII value. This possibility also would be consistent with the model proposed above. Further study of the potential relevance of such averaging is needed.