Monte Carlo modeling of single-molecule cytoplasmic dynein

Abstract

Molecular motors are responsible for active transport and organization in the cell, underlying an enormous number of crucial biological processes. Dynein is more complicated in its structure and function than other motors. Recent experiments have found that, unlike other motors, dynein can take different size steps along microtubules depending on load and ATP concentration. We use Monte Carlo simulations to model the molecular motor function of cytoplasmic dynein at the single-molecule level. The theory relates dynein's enzymatic properties to its mechanical force production. Our simulations reproduce the main features of recent single-molecule experiments that found a discrete distribution of dynein step sizes, depending on load and ATP concentration. The model reproduces the large steps found experimentally under high ATP and no load by assuming that the ATP binding affinities at the secondary sites decrease as the number of ATP bound to these sites increases. Additionally, to capture the essential features of the step-size distribution at very low ATP concentration and no load, the ATP hydrolysis of the primary site must be dramatically reduced when none of the secondary sites have ATP bound to them. We make testable predictions that should guide future experiments related to dynein function.

Molecular motors are responsible for active transport and organization in the cell, underlying an enormous number of crucial biological processes (1). There are three classes of molecular motors, kinesin, myosin, and dynein. Myosins move along actin filaments, kinesin moves toward the plus end of a microtubule (MT), and dynein moves toward the MT minus end. To understand these motors better, experimental studies of the function of the motors at the single-molecule level have been conducted (2–9), and these quantitative measurements have then been modeled theoretically by using coupled differential rate equations (10–15).

Dynein is more complicated than kinesin or myosin. This complexity can be seen experimentally in the step-size distribution. The distribution of step sizes for kinesin and myosin are centered about a single value. For kinesin, the average step size is 8 nm (16), and for myosin-V it is 37 nm (17). Dynein, in contrast, displays four different step sizes (8, 16, 24, and 32 nm), depending on the load and ATP concentration (18). By “load” we mean an external backward force applied to a polystyrene bead by using an optical trap, when a dynein molecule is attached to the bead and hauls it along a microtubule. If there is no load, at low ATP the dynein moves with a mixture of 24- and 32-nm steps (18). When load is present, if sufficient ATP is available, the dynein can decrease its step size to 8 nm and produce force up to 1.1 pN. If the load is large enough so that the motor is no longer able to move the bead, we refer to the load as the stalling force. The stalling force increases linearly with ATP concentration before saturating at 1.1 pN (18). In this work, we use Monte Carlo simulations to investigate models of cytoplasmic dynein's function at the single-molecule level. Given certain hypotheses, we present a model that reproduces the experimental results. We compare the model's stalling force vs. ATP concentration curve with experiment as well as its predictions for the distributions of step sizes at different ATP concentrations. We also present the model's prediction of the dependence of velocity on force (load) and on ATP concentration.

On a molecular level, like kinesin, dynein has two heads that walk processively along a MT in discrete steps (see ref. 15 and references therein). This process is powered by converting the chemical energy released by hydrolyzing ATP into mechanical energy. In kinesin, each head has a single ATP binding site where ATP is hydrolyzed and released. However, each dynein head consists of six AAA domains, of which potentially four are ATP binding sites (see ref. 19 and references therein) (see Fig. 1). Although ATP hydrolysis predominantly happens at site 1, in principle it could occur at other sites as well. There is evidence that hydrolysis at site 1, and subsequent molecular function, can depend on the presence or absence of nucleotides at other secondary binding sites (20–22).

Fig. 1.

Sketch of the components of a single dynein head bound to a MT. The different AAA domains are shown as numbered spheres (1–6). The non-AAA C terminus domain (C) also is shown. ATP hydrolysis occurs primarily at AAA1. The dynein power stroke taking place in response to ADP release from AAA1 occurs in the direction shown by the thick curved arrow. AAA domains 2, 3, and 4 are proposed to play a regulatory role in force transmission through load-induced binding of nucleotides that can reduce the dynein step size (18).

Monte Carlo is an approach to computer simulations in which an event A occurs with a certain probability P_A where 0 ≤ P_A ≤ 1. In practice, during each time step, a random number x is generated with uniform probability between 0 and 1. If x ≤ P_A, event A occurs; if x > P_A, event A does not occur. To check the validity of the Monte Carlo approach, we show in Supporting Text, which is published as supporting information on the PNAS web site, that it reproduces previous experimental results obtained for kinesin (6).

Modeling Cytoplasmic Dynein

Our goal is to use modeling to clarify how dynein functions. To do so, we use Monte Carlo simulations to calculate experimentally measurable quantities such as the dependence of dynein's step-size distribution on ATP concentration and load, the dependence of stalling force on ATP concentration, and the force–velocity curve. Because many aspects of dynein are not yet explored experimentally, we start by indicating the basic hypotheses that we make about dynein function and then discuss the functional ramifications of each of them. We implemented these hypotheses to obtain agreement between the results of our Monte Carlo simulations and experimental observations. The legitimacy of such assumptions, which are effectively theoretical predictions, then can be tested independently by experiments. In addition, the theory as a whole can be tested by using it to make predictions about dynein function in currently unexplored parameter ranges, e.g., the motor's force–velocity relationship.

Our model focuses on a single dynein head even though cytoplasmic dynein has two heads. This approach makes sense for two reasons. First, modeling two heads requires significant additional assumptions and adjustable parameters that are not constrained by what is currently known experimentally. We are trying to limit the number of ad hoc assumptions as much as possible. Second, examination of electron micrographs in figure 4 of ref. 23 reveals that the power stroke of a single head can have a range of motion up to 43 nm. Thus, it would certainly be possible for a single head to dictate several step sizes. In the following assumptions and in Discussion, we will further explain why we believe this approach to be a reasonable one.

As we mentioned earlier, each dynein head consists of six AAA domains, of which potentially four are ATP binding sites. The ATP hydrolysis primarily responsible for the power stroke occurs at site 1. There is evidence that hydrolysis at site 1, and subsequent molecular function, could be altered by the presence or absence of nucleotides at other secondary binding sites, which are labeled as sites 2, 3, and 4 (20–22). In our Monte Carlo algorithm, we assume that ATP binding to site 1 has the highest priority, followed by binding at the secondary sites. If (n – 1) ATP are bound, the probability of binding the nth ATP to a secondary site is 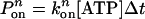, and the probability of the nth ATP unbinding from a secondary site is 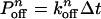where the time step Δt = 2 × 10^–4 s. In the following, we present the basic assumptions of our model (see Supporting Text for a more detailed description):

Assumption 1. Four distinct step sizes, determined by the nucleotide occupancy at the secondary sites.

The single-molecule experiments (18) indicate that cytoplasmic dynein can move on a MT with four different step sizes of 32, 24, 16, and 8 nm, all being multiples of 8 nm, the periodicity of a MT. The distributions of steps observed are a function of the available ATP, with only large steps observed at low ATP, so we propose a direct correlation between the molecule's instantaneous step size and the number of ATP molecules bound at the secondary sites of a single head. Here we are assuming that the step size is determined by the ATP-binding state of a single head. It is plausible that ATP binding compacts the head, which could determine the tilt of the stalk and stem, thus dictating the step size (24, 25) (see Discussion). Electron micrographs of dynein c have revealed that the tip of the stalk, which is the MT binding domain, has a distribution of positions ranging as high as 43 nm (see figure 4 in ref. 23). This range of positions is consistent with a single head dictating a variety of step sizes. Suppose that an ATP is bound at the site (AAA1) of primary hydrolysis. Then, we propose that if no ATPs are bound at the secondary sites, the molecule attempts to take a 32-nm step; if one ATP is bound at a secondary site, it takes a 24-nm step; if two are bound at secondary sites it tries to take a 16-nm step; and if all secondary sites are occupied it takes an 8-nm step. In principle, the actual step size could be modified by thermal noise, resulting in a distribution of step sizes centered about each of the four step sizes listed, as seen experimentally (18). We have not extensively evaluated this possibility but believe it does not fundamentally alter our findings.

Assumption 2. The binding affinities of the secondary sites decrease as the number of ATP bound to these sites increases. The highest affinity is associated with the site where primary hydrolysis occurs.

Kinetic studies have measured two ATP binding affinities in solution, obviously not under load, and found them to be different (26). The highest binding affinity K¹ is given by the ratio of the on-rate to the off-rate of the first ATP (26). (The superscript refers to the first ATP bound to the head.) We implement this observation by assuming that site 1 has the highest affinity because it is where primary hydrolysis occurs and is essential for dynein's motor activities (20). Experiment (26) finds that the binding affinity K² for the second ATP is about an order of magnitude lower than K¹, and this value is what we assume in our simulations. One can imagine that this second ATP binds to site 3 (see Assumption 5), but we do not use site assignments in our simulations. Binding a third and fourth ATP could not be observed in the kinetic measurements done in solution (26). In our simulations, we assume that the binding affinity of the two remaining secondary sites is very small. We can envision sites 2 and 4 as these remaining sites, but we do not specify this site assignment in the simulations. In the Monte Carlo simulations, the binding affinities without load F are ordered as follows: K¹(F = 0) > K²(F = 0) > K³(F = 0) > K⁴(F = 0). In implementing our simulation, we have assumed values for the on- and off-rates that are consistent with the binding affinities follows: and . The superscripts refer to the number of ATP bound, e.g., 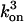refers to the on-rate of the third ATP, and refers to the off-rate of the third ATP from the dynein head. If site 1 becomes empty because of the motor taking a step, it always has highest priority for binding an ATP with an on-rate of . We require the assumption of decreasing binding affinities with increasing numbers of bound ATP to produce a detectable number of large steps at no load and high ATP (see Discussion). Experimental studies on both axonemal and cytoplasmic dynein suggest that such an assumption is reasonable (26, 27).

Assumption 3. The kinetics of ATP binding at the secondary sites are load dependent, with applied load increasing the ATP binding affinity.

Based on the solution kinetics measurements that suggest negligible ATP binding of the third and fourth ATP molecules (26), one might initially assume that ATP binding at the secondary sites, especially the third and fourth ATP, is irrelevant. However, experimental studies in vitro (20) and in vivo (21) demonstrate that the ability to bind ATP at secondary sites 2–4 is important for dynein function. One resolution of this apparent contradiction between the solution kinetic measurements and in vivo/in vitro studies is to propose that the ATP binding constants at these secondary sites are load dependent, that binding affinity increases with load, and that some function occurs at nonzero load. As we will see, assuming the increase in ATP affinity as a function of load is central to being able to reproduce the experimental dependence of stalling force on the available ATP concentration. In our Monte Carlo simulations, we implement the secondary site binding affinities dependence on load F with an exponential function: 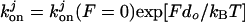, where j = 2, 3, or 4 is the number of ATP bound, d_o is an adjustable parameter with units of length, T is temperature, and k_B is the Boltzmann constant. We also have tried incorporating the load dependence in the off-rates rather than in the on-rates; we find that our results are unchanged when we take the error bars into account.

Assumption 4. The probability of ATP hydrolysis depends on the applied load.

Because dynein is a mechano-chemical enzyme, there must be a coupling between the applied load and its enzymatic cycle. In particular, we know that the motor “stalls” when subject to sufficient load, i.e., its enzymatic rate goes to zero (assuming that there is no futile hydrolysis). One way to implement this coupling to load, as has been done for kinesin, is to make a particular step in the enzymatic cycle load dependent so that it becomes rate limiting at loads close to the enzyme's stall force. We do that here, choosing ATP hydrolysis to be the load-dependent step, so that the probability P_cat of successful ATP hydrolysis decreases with increasing load. Thus, we set P_cat = k_catΔt with the load-dependent rate constant 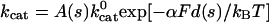, where d(s) is a linear function of the number of secondary sites binding ATP. It is equal to the size of the step that may be taken as explained in Assumption 1. α is the load distribution factor for hydrolysis. The factor A(s) will be explained in the next assumption.

Assumption 5. ATP hydrolysis at site 1 is highly enhanced if at least one secondary site binds ATP.

Initially, we needed to make this assumption to eliminate the excessive number of 32-nm steps at no load and low ATP (see Discussion). However, such an assumption is supported by independent experiments. Site 3 plays a crucial role in the MT-activated ATPase and motile activities of cytoplasmic dynein, either by ATP binding or ATP hydrolysis or both. The recent study of Kon et al. (20) shows that a mutation of site 3 that inhibits binding/hydrolysis of ATP leads to colocalization of dynein on a MT, independent of ATP levels. Hence, site 3 is critical in the ATP-induced release of a dynein head from the MT, which is needed to step along the MT. Similar conclusions also were drawn in refs. 21 and 22. Furthermore, as site 3 undergoes mutation, there is an ≈20-fold reduction in both the maximally activated ATPase activity at a saturating concentration of MT and the average speed of MT gliding (20). These experimental results require k_cat to strongly depend on whether or not a secondary site has an ATP molecule bound to it. So we set A(s) = 1 if site 1 and at least one secondary site is bound to ATP, and A = 0.01 otherwise.

Assumption 6. During the kinetic cycle of dynein, reversal of hydrolysis is possible.

ATP hydrolysis occurs through a series of chemical states (28–30). The technique of ¹⁸O exchange indicates that after ATP has been converted into ADP and P_i, but before the products ADP and P_i are released and before a step has occurred, reversal of hydrolysis (ADP·P_i → ATP) can occur (29). (This reversal cannot produce a backward step toward the plus end of the MT because that would violate the first law of thermodynamics.) This reversal of hydrolysis is more frequent in dynein than in kinesin (see the review in ref. 30). After hydrolysis occurs, the simulation allows reversal to occur with probability 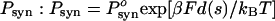, where β is the load distribution factor for reversal of hydrolysis [α + β = 1 (13, 14)]. The load dependence ensures that reversals are more likely to happen with increasing load, which may be the major cause of the motor stalling. If reversal does not occur in the Monte Carlo simulation, then ADP is released from site 1 and dynein takes a step. Experimentally, it is essentially the release of ADP that limits the rate of catalytic turnover (28–30) and, hence, the speed of the motor at saturating ATP levels.

Results

We let the model system evolve according to the Monte Carlo algorithm described above in Supporting Text. The load on motor is given by the restoring force F = k_trapx as it moves away from x = 0, the center of the trap. As it moves further away from the optical trap, it experiences a larger load and, hence, slower hydrolysis. This increase in load results in more frequent reversals of hydrolysis, thereby making the movement slower. This reduction in movement is clearly seen in the typical (simulated) trajectories of the system at different ATP concentrations as shown in Fig. 2.

Fig. 2.

Position vs. time from representative Monte Carlo simulations at [ATP] = 400 μM and [ATP] = 1 mM. For dynein, the following values were used in the simulations and apply to all of the dynein figures that follow. We take the optical trap stiffness k_trap = 0.007 pN·nm^–1 as in ref. 18. d₀ = 6 nm, α = 0.3, β = 0.7, and p_syn = 0.23. The rate constants have the values 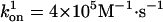, , 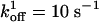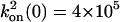M^–1·s^–1, , , 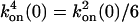, 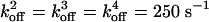and .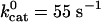

Tested Prediction of Stalling Forces. If the motor does not move for 1 s, then we terminate that particular run of the simulation, and the final position is used to calculate the stall force. This force is averaged over many runs to calculate the average stall force. In Fig. 3, we compare the simulation results for the stall force vs. ATP with the experimental observations (18). We find good qualitative agreement between experiment and theory. Note that both theory and experiment are in regimes where the concentrations of ATP, ADP, and P_i are all far from equilibrium, so stalling of the motor is not due to being near equilibrium. (See Discussion for a possible explanation for why the simulations find slightly higher values than seen experimentally.)

Fig. 3.

Average stalling force vs. ATP concentration from Monte Carlo simulations and experiment (18). The error bars represent standard deviation calculated from 5,000 samples. Increasing the sample size does not significantly alter the standard deviation.

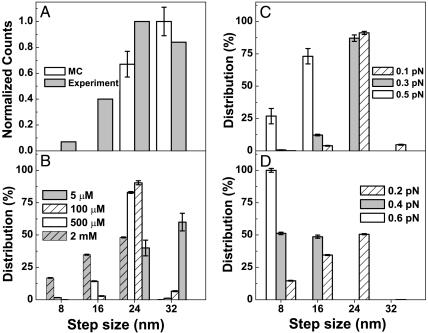
Tested Prediction of Step Size Distribution. We let the motor proceed for a long time without any load or under constant load and calculate the step size distribution for various ATP concentrations. We determined the value of the load-independent factor A(s) (for reduction in hydrolysis at site 1 due to the presence of ATP at secondary sites) by demanding that the 24- and 32-nm step sizes should be roughly equally probable at a very low ATP level (5 μM) as was seen experimentally (18) (see Discussion, too). A comparison between the calculated and experimental step distribution are shown for no load at low ATP level in Fig. 4A. We find good qualitative agreement between the experimental and theoretical distributions. As Fig. 4A shows, at low ATP and no load, small step sizes (8 and 16 nm) are seen experimentally but not in our simulations. These small steps could be the result of thermal noise, missteps, and steps in which dynein changes to another protofilament on the MT.

Fig. 4.

Step-size distribution of dynein for various values of load and ATP concentration. (A) Comparison of experimental step size distribution (18) with Monte Carlo simulations (MC) at [ATP] = 5 μM with no load. The experimental distribution of the step size was reproduced by using 8-nm bins for the sake of comparison with the simulation result. (B) Predicted step-size distribution with no load for various ATP concentrations. (C) Predicted step-size distribution for [ATP] = 100 μM for various loads. (D) Predicted step-size distribution for [ATP] = 1 mM for various loads. Simulation results are from 10 runs, each of 1,000-s duration. The error bars represent the standard deviation and are symmetrical about the average.

For no load and high ATP, the prediction is shown in Fig. 4B; as yet there is no experimental data. So this figure provides an experimental prediction that large step sizes should be observed at high ATP concentrations. Although the step distribution has not been measured at high ATP, there has been experimental observation of large 24-nm steps as zero load is approached (see figure 2 e and f in ref. 18).

Untested Predictions. One important validation of any model is the ability to predict function in previously uncharacterized parameter ranges. Here, we use our simulations to predict the following:

1. As Fig. 4B shows, at high ATP concentrations in the absence of load, small step sizes (8 and 16 nm) should constitute a substantial fraction of the step sizes along with 24-nm steps.

2. Fig. 4 C and D shows the step size distribution at different applied loads for a low ATP concentration of 100 μM and a high ATP concentration of 1 mM. Notice that the average step size decreases at larger loads.

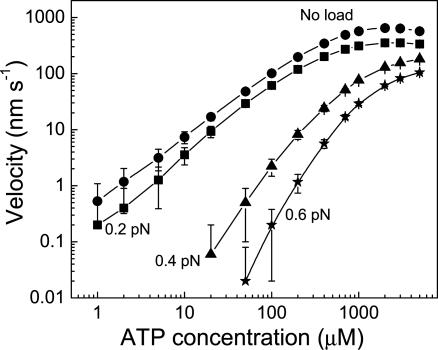
3. Fig. 5 shows the relationship between applied load and velocity at different ATP concentrations.

4. Fig. 6 shows the relationship between velocity and ATP concentration.

Fig. 5.

Predicted average velocity vs. load for dynein at ATP concentrations of 100 μM and 2 mM from Monte Carlo simulations. Error bars represent the standard deviation calculated from 10 samples of runs each lasting for 50 s.

Fig. 6.

Average velocity vs. ATP concentration for dynein for various values of load from Monte Carlo simulations. Error bars were calculated in the same way as in Fig. 5.

Figs. 5 and 6 show how the velocity is predicted to decrease with increasing load and decreasing ATP concentration.

Discussion

Our Monte Carlo-based approach provides experimentally testable predictions in the following two ways: (i) in the dependence of quantities such as the velocity and step size distribution on ATP concentration and load, and (ii) in the assumptions used. The biggest underlying assumption of the model is Assumption 1 that there is a direct correlation between the number of ATP molecules bound at secondary sites and the size of the step the motor takes. Experimentally, the stall force of dynein decreases upon lowering the ATP concentration, which was interpreted as a disruption of the proposed ATP-dependent gear mechanism of dynein (18). At low ATP, the lack of ATP available for binding at secondary sites in the head could prevent smaller step sizes under external load. Experimentally, the work done per step near stalling (W_s = step size d× stall force F_s) is approximately constant at all step sizes (see ref. 18). This relation links changes in the step size with changes in the stalling force. Theoretically, stalling arises when the probability P_syn of reversal of hydrolysis becomes high enough (see Assumption 6). Because P_syn increases exponentially with Fd(s), large loads will be associated with small d(s), i.e., with the binding of ATP at several secondary sites. It therefore seems likely that the effect of ATP binding at the secondary sites is indeed to change the motor's step size. Thus, it appears that the ability to take small steps (and hence increase force production) requires the presence of sufficient ATP. Consistent with the dependence of step size on ATP concentration is the experimental observation that at low ATP concentration with no load, dynein moves predominantly through a mixture of 24- and 32-nm steps (18). Under such no-load conditions, the primary site hydrolyzes ATP to generate motion; additional ATP binding at secondary sites is not required because small steps are not necessary.

The structural link between ATP binding and step size is not known because the tertiary structure of the AAA domains in dynein has not been determined. However, in other AAA-domain proteins such as N-ethylmaleimide-sensitive-factor (31), F1-ATPase (32, 33), and Hs1U (33), binding of ATP at the interface of AAA domains can induce the AAA ring to compact, and this scenario could be more generally applicable to other AAA proteins (24, 33, 34). For dynein, the part of the ring that compacts potentially acts as a lever arm transmitting strain from the site of primary hydrolysis to the MT-binding stalk (see Fig. 1), so the shorter lever arm could result in less amplification of the signal and smaller steps. Thus, there is a physical rationale connecting ATP binding to changes in step size. Assumption 3, that secondary-site ATP binding increases with load, is a corollary of Assumption 1: from solution biochemistry and kinetics (26) we know that the ATP binding affinity of the secondary sites in the absence of load is extraordinarily low (especially the third and fourth ATP). For secondary sites to play a significant role in molecular function [as indeed mutational experiments in vitro (20) and in vivo (21) suggest they do], it seems likely that under some circumstances they must bind ATP more strongly. Load-induced ATP binding is consistent with this idea.

Although Assumption 1 is not yet proven, it was required to reproduce the experimental relationship between stalling force and available ATP. Indeed, if we force dynein to take 8-nm steps irrespective of the number of ATP bound at additional binding sites, we end up getting an approximately constant value of stalling force throughout the range of ATP shown in Fig. 3. A similar result of approximately constant stalling force is obtained when we calculate the average stalling force for the model of kinesin by incorporating a load-dependent reversal probability. (The calculation of the velocity of kinesin shown in Supporting Text and in Figs. 7 and 8, which are published as supporting information on the PNAS web site, omits the very small reversal probability.) Note that the N state chemical kinetics model described in ref. 14 had to use an ad hoc ATP-dependent reversal rate to reproduce some of the features of the weak stall force variation as a function of ATP concentration in kinesin. These investigations thus suggest that the difference in the stalling force behavior of dynein and kinesin lies in dynein's ability to shift step size. Future single-molecule experiments with mutant dyneins (e.g., ones unable to bind ATP at sites 2 or 4 or both) should be able to directly test this hypothesis.

We observe from Fig. 3 that the values of average stalling force obtained from the simulation are consistently slightly higher than those reported in the experiment for ATP levels of <1 mM. It is possible that the difference results from one of the approximations we made in developing the theory. Although a number of possibilities could be considered, we believe that the most likely cause for the discrepancy is our ignoring the interaction between the two heads and simply approximating the result of the interaction by using an “effective” rate constant for ADP release. This approximation is certainly crude, and at low ATP levels the second (trailing) head might be slow to release the MT, providing drag on the first head and thus resulting in a lesser stall force than seen in our simulations. Such effects are not included in the simulations. However, it is worth pointing out that the experimental “low” ATP regime is not really that low (100 μM), so in principle there is abundant ATP available for the second head.

Three of the other assumptions came about in attempts to reproduce the step-size distribution. Originally, Assumptions 2 and 5 were not included in our model. However, each is required to reproduce certain aspects of motion. Assumption 5 states that ATP hydrolysis at site 1 is enhanced if a secondary site binds (or hydrolyzes) ATP. In the absence of Assumption 5, at low ATP and no load, the simulations predict that the motor takes almost entirely 32-nm steps. We needed something to suppress 32-nm steps in favor of the 24-nm steps seen experimentally and considered the possibility of increased probability of ATP hydrolysis at site 1 if an ATP was present at one of the secondary sites. Because step size depends on the presence of ATPs at the secondary sites, the preference to hydrolyze ATP at site 1 when an ATP was present at a secondary site favors 24-nm steps as opposed to 32-nm steps, which occur when no secondary sites are occupied. After making this assumption of motion occurring when ATP is bound to a secondary site, we discovered independent experimental evidence supporting this idea (20).

Assumption 2 is also important with regard to step size distributions but in a different regime. Assumption 2 states that ATP binding at secondary sites occurs with progressively smaller binding affinities. If this were not the case and all of the binding affinities at the secondary sites were identical, then at very high ATP but no load, all of the secondary sites would bind ATP, and the simulations would predict almost entirely 8-nm steps. However, experimentally, we observe large steps at high ATP under no load, although we do not yet know the exact distribution of step sizes (18). Assumption 2 prevents these secondary sites from filling up even in the presence of high ATP, as long as load is not present. The low binding affinities improve dynein's fuel economy by suppressing ATP binding at secondary sites (and subsequent small steps) when load is absent.

As described earlier, in running our simulations, we chose on- and off-rates consistent with the binding affinities. Experimental measurements of the interaction rates of monoclonal antibodies and various antigens have found that both the on- and off-rates vary. In some cases the association rates account for most of the variation in the binding affinities (35), whereas in other cases the variation of the binding affinities is determined primarily by the dissociation rate (35). So we have tried another choice with the same binding affinities but where the on-rates were all equal and only the off-rates varied. (See Supporting Text for exact values.) In this alternative choice, we also included all of the load dependence in the off-rates. Taking the error bars into account, we found that there is no change in any of our results.

Like the majority of the theoretical descriptions of kinesin, we model the kinetic cycle of one head of a two-headed molecule. This approach is obviously a significant simplification, and as for kinesin, we approximate the effect of the load from the other head by using effective rate constants, i.e., rate constants that reflect the way the head functions when receiving appropriate strain from the second (trailing) head. We believe this approach works for many aspects of the motor's function because the exact details of the head-to-head interactions and coupling may not be crucial; such a suggestion is strengthened by recent work showing that in a MT gliding assay (36), a recombinant cytoplasmic dynein fraction that functions as a monomer can drive efficient MT motion at speeds comparable with full-length motors. However, although such an approximation is a viable first model for dynein function, it likely leads to slight deviations between theory and experiment, such as the increasing deviation between theory and experiment of the stalling force with decreasing ATP levels as seen in Fig. 3. Future models will obviously need to investigate the nature of the coupling between the two heads (15, 37) and its specific ramifications.

Conclusion

The theoretical description we present here reproduces the major experimentally determined features of cytoplasmic dynein. Because it is based on a probabilistic Monte Carlo approach, it is easily generalizable to more complex situations, such as dynein functioning in the presence of regulatory cofactors like dynactin or Lis1. As single-molecule studies become more sophisticated and start to investigate more complex situations, e.g., the function of protein complexes as opposed to single proteins in isolation, we believe that such theoretical approaches will be increasingly valuable in clarifying the functional significance and ramifications of specific interactions.