Scoring schemes of palindrome clusters for more sensitive prediction of replication origins in herpesviruses

Abstract

Many empirical studies show that there are unusual clusters of palindromes, closely spaced direct and inverted repeats around the replication origins of herpesviruses. In this paper, we introduce two new scoring schemes to quantify the spatial abundance of palindromes in a genomic sequence. Based on these scoring schemes, a computational method to predict the locations of replication origins is developed. When our predictions are compared with 39 known or annotated replication origins in 19 herpesviruses, close to 80% of the replication origins are located within 2% of the genome length. A list of predicted locations of replication origins in all the known herpesviruses with complete genome sequences is reported.

INTRODUCTION

Early studies (1,2) have reported that the nucleotide sequences around replication origins of certain herpesviruses have complex repetitive structures of closely spaced direct and inverted repeats. A palindrome is a special case of inverted repeats where a segment of nucleotide bases is immediately followed by its reverse complement. A high concentration of palindromes around replication origins has been found in these herpesviruses.

Herpesviruses utilize two different types of replication origins during lytic and latent infections. For each type of origins, the count and locations in the genome vary from one kind of herpesvirus to another. Most herpesviruses have one to two copies of latent and lytic origins. Presence of palindromes around replication origins is prevalent in both latent and lytic types (1–5).

As the central step in the reproduction of herpesviruses, viral DNA replication has been the target for a number of anti-herpesvirus drugs (e.g. acyclovir). Understanding the molecular mechanisms involved in DNA replication is of great importance in further developing strategies to control the growth and spread of viruses (6–8). Since replication origins are regarded as major sites for regulating genome replication, labor-intensive laboratory procedures have been used to search for replication origins (9–11).

With the increasing availability of genomic DNA sequence data, one way that may save time and resources would be to scan the viral genome sequence for the expected sequence features by a computer program before an experimental search for replication origins is launched. Masse et al. (3) first used this computational approach to predict the replication origin oriLyt on the human cytomegalovirus (HCMV) and then confirmed it by experimentation. In that computational analysis, one of the sequence features being scanned for in the genome sequence is the presence of a high concentration of palindromes of length 10 or above clustering within a window of 1000 bases.

A palindrome reads exactly the same from the 5′ end to the 3′ end on both strands of DNA (see Figure 1 for example). More precisely, we can define a palindrome to be a word pattern of the form b₁…b_Lb_L′…b₁′, where b′ is the complement of base b and L is the half-length of the palindrome. We call the letter b_L the left-center and b_L′ the right-center of the palindrome. The length of the palindrome in Figure 1 is 10 and L = 5.

Figure 1.

A palindrome of length 10.

Palindromes play important roles as protein-binding sites in DNA replication processes [(12), Chapter 1]. The local 2-fold symmetry created by the palindrome provides a binding site for DNA-binding proteins which are often dimeric in structure. Such double binding markedly increases the strength and specificity of the binding interaction [(13), Chapter 8]. High concentration of palindromes around replication origins is generally attributed to the reason that the initiation of DNA replication typically requires the binding of an assembly of enzymes to these DNA sequences. Helicase is an example of these enzymes known to bind with the initiation site, locally unwind the DNA helical structure, and pull apart the two complementary strands. This explanation is consistent with the observation of AT-rich regions, believed to facilitate the unwinding, in replication origin domains of the genome (5).

Leung et al. (14) describe how an evaluation criterion, based on the scan statistics (15,16), is developed for assessing palindrome clusters by modeling the occurrences of palindromes in the genome as points randomly sampled from the unit interval according to the uniform distribution. By identifying windows on the genome sequence containing statistically significant clusters of palindromes, the scan statistics, in principle, provide a method to predict likely locations of replication origins. This criterion, however, essentially assesses a window of the genome by only the counts of palindrome contained in it, regardless of the actual extent of the palindrome lengths. This drawback has led to missing some replication origins which contain one extremely long palindrome rather than a cluster of moderately long ones. In the present paper, we propose two new schemes for evaluating palindrome clusters and use the rankings of these evaluation criteria to predict the replication origins in the herpesviruses. By checking with known replication origins reported either in published literature or GenBank annotations, we assess the accuracy of the new prediction schemes. These assessments demonstrate that there is a substantial improvement over the original scan statistics criterion.

In Methods section, we describe the main steps of the prediction method and three scoring schemes. The first scoring scheme, called the palindrome count scheme (PCS), is essentially the scan statistics method first described by Leung et al. (14), and further discussed in the articles of Leung and Yamashita (17), and Leung et al. (4). Two new scoring schemes, namely, the palindrome length scheme (PLS) and the base-pair weighted scheme (BWS) are introduced as measures of palindrome clusters. In Results and Discussion section, we report the results of applying these scoring schemes to predict the locations of replication origins for 39 fully sequenced herpesviruses, and compare the prediction accuracies in terms of sensitivity and positive predictive value. A few concluding remarks are given in the final section.

METHODS

We propose a computational method to identify regions of a genome which harbor unusual clusters of palindromes. This, in turn, becomes the basis of our method to predict replication origins for the herpesviruses. Table 1 presents the viruses to be analyzed. The data set comprises all complete genome sequences of the herpesvirus family downloaded from GenBank at the NCBI web site in April 2005. For each virus, we list its abbreviation, accession number, sequence length and the relative frequencies of the four nucleotide bases in the genome (see Table 1).

Table 1.

The list of herpesviruses to be analyzed

Virus	Abbreviation	Accession	Length	Base composition (A, C, G, T)
Alcelaphine herpesvirus 1	AlHV1	NC_002531	130 608	(0.27, 0.24, 0.22, 0.26)
Ateline herpesvirus 3	AtHV3	NC_001987	108 409	(0.32, 0.19, 0.17, 0.31)
Bovine herpesvirus 1	BoHV1	NC_001847	135 301	(0.14, 0.36, 0.37, 0.14)
Bovine herpesvirus 4	BoHV4	NC_002665	108 873	(0.30, 0.21, 0.20, 0.29)
Bovine herpesvirus 5	BoHV5	NC_005261	138 390	(0.12, 0.37, 0.38, 0.13)
Callitrichine herpesvirus 3	CalHV3	NC_004367	149 696	(0.26, 0.25, 0.25, 0.25)
Cercopithecine herpesvirus 1	CeHV1	NC_004812	156 789	(0.13, 0.37, 0.38, 0.13)
Cercopithecine herpesvirus 15	CeHV15	NC_006146	171 096	(0.18, 0.31, 0.31, 0.20)
Cercopithecine herpesvirus 17	MMRV	NC_003401	133 719	(0.24, 0.27, 0.26, 0.23)
Cercopithecine herpesvirus 2	CeHV2	NC_006560	150 715	(0.12, 0.38, 0.38, 0.12)
Cercopithecine herpesvirus 8	CeHV8	NC_006150	221 454	(0.26, 0.25, 0.24, 0.25)
Cercopithecine herpesvirus 9	CeHV7	NC_002686	124 138	(0.29, 0.21, 0.20, 0.30)
Equid herpesvirus 1	EHV1	NC_001491	150 224	(0.22, 0.29, 0.28, 0.22)
Equid herpesvirus 2	EHV2	NC_001650	184 427	(0.22, 0.29, 0.28, 0.21)
Equid herpesvirus 4	EHV4	NC_001844	145 597	(0.25, 0.25, 0.25, 0.25)
Gallid herpesvirus 1	GaHV1	NC_006623	148 687	(0.26, 0.24, 0.24, 0.26)
Gallid herpesvirus 2	GaHV2	NC_002229	174 077	(0.28, 0.22, 0.22, 0.28)
Gallid herpesvirus 3	GaHV3	NC_002577	164 270	(0.23, 0.27, 0.27, 0.23)
Human herpesvirus 1	HSV1	NC_001806	152 261	(0.16, 0.34, 0.34, 0.16)
Human herpesvirus 2	HSV2	NC_001798	154 746	(0.15, 0.35, 0.35, 0.15)
Human herpesvirus 3	VZV	NC_001348	124 884	(0.27, 0.23, 0.23, 0.27)
Human herpesvirus 4	EBV	NC_001345	172 281	(0.20, 0.30, 0.29, 0.20)
Human herpesvirus 5 strain AD169	HCMV	NC_001347	230 287	(0.22, 0.28, 0.29, 0.21)
Human herpesvirus 5 strain Merlin	HCMV-M	NC_006273	235 645	(0.21, 0.29, 0.29, 0.21)
Human herpesvirus 6	HHV6	NC_001664	159 321	(0.29, 0.22, 0.21, 0.29)
Human herpesvirus 6B	HHV6B	NC_000898	162 114	(0.29, 0.22, 0.21, 0.29)
Human herpesvirus 7	HHV7	NC_001716	153 080	(0.32, 0.20, 0.17, 0.31)
Human herpesvirus 8	HHV8	NC_003409	137 508	(0.24, 0.27, 0.26, 0.23)
Ictalurid herpesvirus 1	IcHV1	NC_001493	134 226	(0.21, 0.28, 0.28, 0.22)
Meleagrid herpesvirus 1	MeHV1	NC_002641	159 160	(0.26, 0.24, 0.24, 0.26)
Murid herpesvirus 1	MCMV	NC_004065	230 278	(0.20, 0.29, 0.30, 0.21)
Murid herpesvirus 2	RCMV	NC_002512	230 138	(0.19, 0.30, 0.31, 0.20)
Murid herpesvirus 4	MUHV4	NC_001826	119 450	(0.27, 0.24, 0.23, 0.26)
Ostreid herpesvirus 1	OsHV1	NC_005881	207 439	(0.31, 0.19, 0.19, 0.30)
Pongine herpesvirus 4	CCMV	NC_003521	241 087	(0.19, 0.31, 0.31, 0.19)
Psittacid herpesvirus 1	PSHV1	NC_005264	163 025	(0.19, 0.31, 0.30, 0.20)
Saimiriine herpesvirus 2	SaHV2	NC_001350	112 930	(0.33, 0.18, 0.16, 0.32)
Suid herpesvirus 1	SHV1	NC_006151	143 461	(0.13, 0.37, 0.37, 0.13)
Tupaiid herpesvirus 1	THV	NC_002794	195 859	(0.17, 0.33, 0.34, 0.17)

Our method for predicting replication origins consists of four basic steps: (i) locate palindromes at or above a prescribed length; (ii) choose a scoring scheme for palindromes; (iii) compute a score for each window of the genome according to the chosen scoring scheme; and (iv) select regions with high scores.

Step (i): Locating palindromes at or above a prescribed length

As very short palindromes occur frequently by chance, a parameter, L, needs to be chosen where palindromes of length below 2L will not be considered in the analysis. Leung et al. (4) propose a procedure, which is based on bench-marking with the well-studied HCMV virus, for the choice of L. This choice takes into account the length of the sequence, as well as the base frequencies in the genome. Using this criterion, L is chosen to be 6 for the BoHV1, BoHV5, CeHV1, HSV1, HSV2 and SHV1 sequences and 5 for the other sequences. Once the minimal palindrome length has been chosen, the sequences are run through the palindrome program, which is part of EMBOSS [European Molecular Biology Open Software Suite, (18)], to extract the palindrome positions and lengths. Each of these palindromes will be assigned a score according to a scoring scheme chosen in the next step. Note that although it is possible for one palindrome to contain a shorter one in it (e.g. the length 12 palindrome ACCGTGCACGGT contains the length 10 palindrome CCGTGCACGG), EMBOSS automatically discards the shorter redundant palindrome and report only the longest one.

Step (ii): Choosing a scoring scheme for palindromes

Three schemes for scoring palindromes are described. In all of them, any palindrome of length less than 2L will always get a score 0.

1. Palindrome count score (PCS): In this scoring scheme, a palindrome is given a score 1 when its length is at or above 2L.

2. Palindrome length score (PLS): A palindrome of length 2s ≥ 2L is given a score s/L. For example, if we let L = 5, a palindrome of length 10 will get a score of 1, while one of length 24 will get a score of 2.4.

3. Base-pair weighted score of order m (BWS_m).

The idea behind BWS is that a higher score should be given to rarer palindromes, namely those which have lower probabilities to occur by chance. We assess the probability of occurrence of a particular palindrome based on Markov type sequence models [(19),Chapter 3]. Here m denotes the order of the Markov chain. Then, we take the negative logarithm of the probability of a palindrome to give it a positive score which is higher when the probability is lower.

We give a simple example of calculating the BWS₀ score. In the Markov model with order m = 0, the letters in the sequence are independent of each other. A palindrome containing respectively n_A, n_C, n_G, n_T of A, C, G and T occurs with probability $p_A^{n_A}{p}_C^{n_C}{p}_G^{n_G}{p}_T^{n_T}$ where p_A, p_C, p_G, p_T are the relative base frequencies in the sequence. The BWS₀ score of such a palindrome will be the negative logarithm of this probability, which is equal to −(n_A log p_A + n_C log p_C + n_G log p_G + n_T log p_T). Consider two palindromes: CACGTACGTG and TTTTTAAAAA in a very CG-rich genome, say, with relative base frequencies p_A = p_T = 0.1 and p_C = p_G = 0.4. The latter palindrome is much less likely to occur than the former, and accordingly should receive a higher score to reflect its rarity compared with the former. Indeed, the calculated scores of the two palindromes turn out to be 14.7 for the former and 23.0 for the latter.

Step (iii): Computing the window score

The score of a window in the genome is simply the total of the scores of all the palindromes occurring in this window. A palindrome is considered in the window if its left-center is. By trying out a variety of window lengths with the method, we have found that it is best to choose the window length w at 0.5% of the genome length, rounded down to the nearest hundred bases for convenience. Also, we let consecutive windows overlap by half their lengths. That is, the first window spans the first through the wth bases, the second from the ($\frac{w}{2}+1$) to ($\frac{3w}{2}$)th bases and so on. Because of the way the sliding windows are constructed, the length of the last window is usually shorter than w.

Step (iv): Selecting regions with significant palindrome clusters

For the PCS, regions that harbor statistically significant clusters of palindromes are identified using the scan statistics criterion as described in Leung et al. (14). As the criteria for statistical significance for PLS and BWS have not yet been established, we use a non-parametric approach where a fixed number of top scoring windows are chosen as the predicted locations of replication origins. It is well known that herpesviruses have multiple replication origins. However, there does not appear to be any obvious rule to determine the number of top scoring windows that one should take. Based on sensitivity and positive predictive value consideration (defined below), we find that using the top 3–5 ranked windows for prediction works well for the herpesviruses.

RESULTS AND DISCUSSION

Scan statistics method versus the new scoring schemes

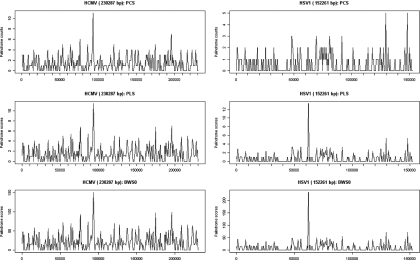
To compare and contrast the two new scoring schemes with the scan statistics method, now called PCS, the sliding window plots for HCMV and HSV1 using PCS, PLS and BWS₀ score schemes are displayed in Figure 2. In each plot, the scores of the windows are plotted against the position of the window. For HCMV, the highest scoring window is the same for all three schemes. This window corresponds to the oriLyt of the HCMV identified by Masse et al. (3). For HSV1, however, the plot of the PCS look rather different from those of the PLS and BWS. The highest scoring window in each of PLS and BWS corresponds to the oriL, and the two next highest peaks are close to the two oriS. In contrast, the PCS fails to locate any significant clusters of palindromes.

Figure 2.

Sliding window plots of HCMV and HSV1 using PCS, PLS and BWS₀. The first window spans the first through the wth bases, the second the ($\frac{w}{2}+1$)th to ($\frac{3w}{2}$)th bases, and so on. The score of a window is the total of the scores of all the palindromes occurring in this window according to PCS, PLS or BWS₀.

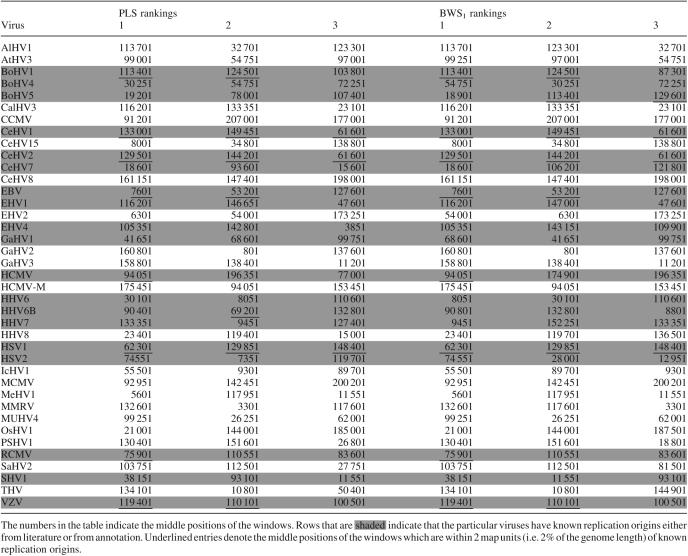
Table 2 shows the top 3 scoring windows for each of the 39 viruses under both the PLS and BWS schemes. The numbers in the table indicate the middle positions of the windows. In cases where two or more high scoring windows are close to one another, only one of them is picked to represent the region that gave the high scores. We adopt the practice that when a certain high scoring window is chosen, the neighboring 8 windows both to the left and to the right of it will not be considered subsequently. Rows that are shaded indicate that the particular viruses have known replication origins either from literature or from annotation. Underlined entries denote the middle positions of the windows which are within 2 map units (a map unit, abbreviated mu, is 1% of the genome length) of known replication origins. Shaded rows without any underlined entries show that the computational method fails to predict the known origins of replication. Finally, rows that are not shaded denote those viruses whose origins of replication are not known, as far as we know. Table 3 lists the regions with significant clusters of palindromes as found by the PCS scheme.

Table 2.

High scoring windows of PLS and BWS₁

Table 3.

Regions with significant clusters of palindromes as found by the PCS

Virus	Region
AlHV1	113 456–113 759
AtHV3	95 350–100 098
BoHV1	77 155–77 168, 102 895–106 948, 113 462–113 636, 124 582–124 756, 131 268–135 221
CalHv3	21 899–23 918, 115 406–117 660, 133 180–133 587
CCMV	88 376–93 659, 206 555–207 582
CeHV1	112 833–113 219
CeHV8	147 015–147 280, 158 953–164 225
CeHV15	5182–10 840, 32 483–36 810, 137 852–139 781, 150 277–152 289
EBV	6772–11 675, 49 460–54 858
EHV1	115 125–119 096, 144 064–148 035
EHV2	4911–9106, 147 228–147 250, 171 785–175 980
GaHV3	10 409–11 952, 104 965–105 067, 121 153–123 174, 138 321–138 935, 158 536–159 150
HCMV	90 515–95 115, 195 962–196 203
HCMV-M	90 881–96 835, 175 177–176 003, 201 246–201 487
HHV6b	88 469–94 716
HHV7	124 985–128 653
HHV8	21 913–23 705
MCMV	92 621–93 412, 142 118–142 186
MeHV1	116 644–116 667
MMRV	3464–3517, 130 148–132 723
MuHV4	96 755–105 094
PsHV1	128 677–131 155, 151 017–153 495
RCMV	74 134–76 485, 118 126–118 854
SHV1	36 683–41 606
THV	10 089–11 213

For example, for the virus EBV, the region 6772–11 675 bp (and 49 460–54 858 bp) is deemed to contain a high concentration of palindromes. BoHV4, BoHV5, CeHV2, CeHV7, EHV4, GaHV1, GaHV2, HHV6, HSV1, HSV2, IcHV1, OsHV1, SaHV2 and VZV have no significant clusters of palindromes.

Prediction accuracy

We next examine the correspondence between the locations of these high scoring windows and those of the known replication origins. From Genbank sequence entries, annotations and literature, we are able to compile a list of 39 known replication origins for some of the viruses in our dataset. Table 4 shows the distance between each known origin from the nearest significant palindrome cluster for PCS, or the nearest high scoring window for PLS and BWS₁ if the center of the cluster or window is within 2 mu of the origin. Otherwise a ‘—’ is entered. The distance is calculated from the mid-point of the window to the mid-point of the closest replication origin. Clearly, Table 4 shows that both PLS and BWS present a substantial improvement in the prediction accuracy of replication origins. For the PLS and BWS, we have used the top 3 scoring windows for each virus to construct this table.

Table 4.

Prediction performance of various scoring schemes, PLS and BWS, based on top 3 scoring windows

Virus	Known ORIs/Names		PCS	PLS	BWS1
BoHV1	111 080–111 300	(oriS)	1.75 mu	1.63 mu	1.63 mu
	126918–127 138	(oriS)	1.61 mu	1.87 mu	1.87 mu
BoHV4	97 143–98 850	(oriLyt)	—	—	—
BoHV5	113 206–113 418	(oriLyt)	—	—	0.06 mu
	129 595–129 807	(oriLyt)	—	—	0.07 mu
CeHV1	61 592–61 789	(oriL1)	—	0.057 mu	0.057 mu
	61 795–61 992	(oriL2)	—	0.18 mu	0.18 mu
	132 795–132 796	(oriS1)	—	0.13 mu	0.13 mu
	132 998–132 999	(oriS2)	—	0.0016 mu	0.0016 mu
	149 425–149 426	(oriS2)	—	0.016 mu	0.016 mu
	149 628–149 629	(oriS1)	—	0.11 mu	0.11 mu
CeHV2	61 445–61 542	(oriL)	—	0.07 mu	0.07 mu
	129 452–129 623	(oriS)	—	0.02 mu	0.02 mu
	144 386–144 557	(oriS)	—	0.17 mu	0.17 mu
CeHV7	109 627–109 646		—	—	—
	118 613–118 632		—	—	—
EBV	7315–9312	(oriP)	contains ori	0.41 mu	0.41 mu
	52 589–53 581	(oriLyt)	contains ori	0.067 mu	0.067 mu
EHV1	126 187–126 338		—	—	—
EHV4	73 900–73 919	(oriL)	—	—	—
	119 462–119 481	(oriS)	—	—	—
	138 568–138 587	(oriS)	—	—	—
GaHV1	24 738–25 005	(oriL)	—	—	—
HCMV	93 201–94 646	(oriLyt)	contains ori	0.055 mu	0.055 mu
HHV6	67 617–67 993	(oriLyt)	—	—	—
HHV6b	68 740–69 581	(oriLyt)	—	0.024 mu	—
HHV7	66 685–67 298		—	—	—
HSV1	62 475	(oriL)	—	0.11 mu	0.11 mu
	131 999	(oriS)	—	1.41 mu	1.41 mu
	146 235	(oriS)	—	1.42 mu	1.42 mu
HSV2	62 930	(oriL)	—	—	—
	132 760	(oriS)	—	—	—
	148 981	(oriS)	—	—	—
RCMV	75 666–78 970	(oriLyt)	overlaps ori	0.62 mu	0.62 mu
SHV1	63 848–63 908	(oriL)	—	—	—
	114 393–115 009	(oriS)	—	—	—
	129 593–130 209	(oriS)	—	—	—
VZV	110 087–110 350		—	0.094 mu	0.094 mu
	119 547–119 810		—	0.22 mu	0.22 mu

The table shows the distance between each known origin from the nearest significant palindrome cluster for PCS, or the nearest high scoring window for PLS and BWS₁ if the center of the cluster or window is within 2 mu of the origin. For example, one of the top 3 scoring windows under the PLS (and BWS) for RCMV is 0.62 map unit away from the RCMV oriLyt.

Prediction accuracy of the different schemes can be quantified by two commonly accepted measures: sensitivity and positive predictive value (PPV). In our context, sensitivity is the percentage of known origins that are close to the regions suggested by the prediction; and positive predictive value is the percentage of identified regions that are close to the known origins.

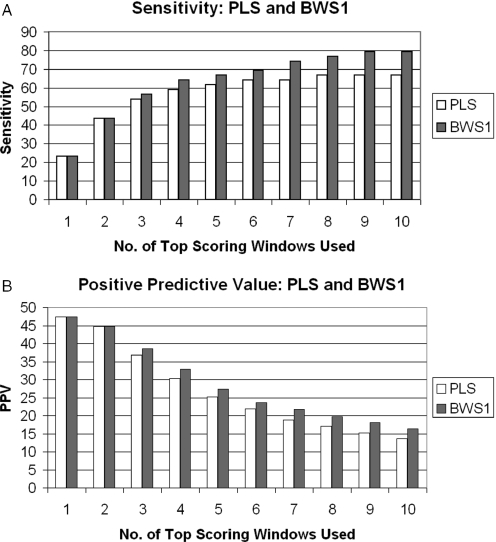
Figure 3 shows the performance of the various schemes. For the PLS and BWS₁, the sensitivity and positive predictive value using 1–10 top scoring windows are given in percentages. Results from BWS₀ and BWS₂ are also obtained (data not shown). Their prediction accuracies are close to but slightly less than that of BWS₁. Note that as the number of windows increases, we gain in sensitivity but at the same time lose in positive predictive value. The highest sensitivities attained by PLS and BWS₁ are 67 and 79%, respectively. The highest positive predictive values for both schemes are 47%.

Figure 3.

Sensitivity and positive predictive values of the PLS and BWS. In our context, sensitivity is the percentage of known origins that are close to the regions suggested by the prediction; and positive predictive value is the percentage of identified regions that are close to the known origins. The sensitivity and positive predictive values of the PCS are 15 and 25, respectively.

Difference between PLS and BWS

Note that both PLS and BWS take the length of the palindromes into account, as longer palindromes have lower probability of occurrence than shorter ones. Moreover, the BWS takes into account the base and word frequencies which affect the probability of occurrence of the palindrome. Consider, for example, the BWS₀ score

$$-(n_{A}log{p}_A+n_{C}log{p}_C+n_{G}log{p}_G+n_{T}log{p}_T)$$

can be viewed as a weighted sum, with weights according to the negative logarithms of the base frequencies. If the base probabilities are all equal, the BWS₀ will reduce to (log 4)(n_A + n_C + n_G + n_T) which is equal to (log 4) × Length of palindrome and hence is equivalent to the PLS.

In essence, the BWS includes more information about the sequence in its prediction and so we expect it to give better prediction accuracy. Our results show that this is indeed true. When we choose to use 3 or more top ranking windows, the BWS performs better than the PLS in terms of (higher) sensitivity and positive predictive value.

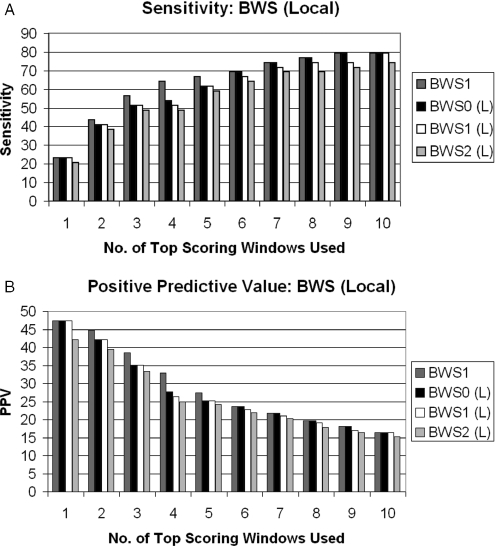
Suspecting that the probability of occurrence of palindromes might not be well estimated on the basis of a global base and word frequencies, we also try calculating palindrome probabilities using the base and word frequencies of those at the local window rather than those of the entire genome.

Figure 4 shows the sensitivity and positive predictive values of the local BWS of order 0, 1 and 2. We use BWS_m(Local) to represent the local version of BWS of order m. According to these results, the local version still does not perform any better than BWS₁.

Figure 4.

Sensitivity and positive predictive values of l ocal BWS.

Further improvement of the algorithm

While our results show that using PLS and BWS with the ranking approach clearly outperforms the PCS, we have to note that the PCS is the only scheme where a rigorous statistical significance criterion, based on the probability distribution of the scan statistics, is currently available. The probability distributions of the maximal window scores with PLS and BWS have yet to be established. We have some preliminary results on approximating the distributions of the window score under PLS by compound Poisson distribution. The compound Poisson distribution is motivated from a marked Poisson process point of view. The occurrence of a palindrome of length 2L and above is modeled by a Poisson process (4), and the actual length of this palindrome is modeled by a geometric distribution.

On closer examination of the known replication origins in this set of genome sequences, we notice that some of the origins missed by this prediction algorithm are actually rather long approximate palindromes. They are missed because we choose to consider only the perfect palindromes. For example, in HSV2, allowing just one error would have let us pick up a 136 base long approximate palindrome centered at 62 930, which is where the reported replication origin is located. If we include these approximate palindromes in our consideration, the sensitivity can be further increased.

CONCLUDING REMARKS

It is mentioned in the introduction that palindromes are merely one type of sequence features known to be associated with replication origins. Other frequently observed characteristics around replication origins include clustering of closely spaced direct and inverted repeats, as well as high AT content. We have actually examined each of these other types of sequence features and found that none of them, when used alone on our data set, reaches the same level of prediction accuracy offered by the BWS. However, it is likely that the prediction accuracy can be further improved by appropriately incorporating them in the prediction scheme. In fact, several replication origins in BoHV4, EHV4 and HSV2 which are not identified by any of PCS, PLS or BWS can be easily detected by the high local AT content around them. Exactly in what way all the different sequence features should be combined to produce the optimal prediction results is the subject of an ongoing investigation.

While it is encouraging to see that close to 80% of replication origins can be predicted using a palindrome-based scoring scheme like BWS, we have also noted that the positive predictive value is rather low whenever the corresponding sensitivity exceeds 50%. This means that a substantial percentage of the high-scoring windows do not correspond to confirmed replication origins. On closer examination of these high scoring windows which are not replication origins, some of them turn out to be regulatory sequences such as transcription factor binding sites. So far, we have not made use of palindromes to predict regulatory sites, but this would be an important area to explore.

Our prediction scheme is geared towards herpesviruses and still needs to be tested on other DNA viruses. There are a few other methods proposed for prediction of replication origins for bacterial, archaeal and yeast genomes (20–23). These methods, which are based on DNA asymmetry, flanking sequence similarity, z-curves, might be adapted to work on viral DNA as well.

Finally, we note that these endeavors to accurately predict replication origins has motivated several interesting and challenging mathematical problems about random letter sequences and probability distributions of patterns on them. We are now dealing with palindromes only but there will be a stream of similar problems about direct and inverted repeats that calls for efforts from the mathematical scientists.