Limitations and potentials of current motif discovery algorithms

Abstract

Computational methods for de novo identification of gene regulation elements, such as transcription factor binding sites, have proved to be useful for deciphering genetic regulatory networks. However, despite the availability of a large number of algorithms, their strengths and weaknesses are not sufficiently understood. Here, we designed a comprehensive set of performance measures and benchmarked five modern sequence-based motif discovery algorithms using large datasets generated from Escherichia coli RegulonDB. Factors that affect the prediction accuracy, scalability and reliability are characterized. It is revealed that the nucleotide and the binding site level accuracy are very low, while the motif level accuracy is relatively high, which indicates that the algorithms can usually capture at least one correct motif in an input sequence. To exploit diverse predictions from multiple runs of one or more algorithms, a consensus ensemble algorithm has been developed, which achieved 6–45% improvement over the base algorithms by increasing both the sensitivity and specificity. Our study illustrates limitations and potentials of existing sequence-based motif discovery algorithms. Taking advantage of the revealed potentials, several promising directions for further improvements are discussed. Since the sequence-based algorithms are the baseline of most of the modern motif discovery algorithms, this paper suggests substantial improvements would be possible for them.

INTRODUCTION

Computational identification of transcription factor binding sites from the upstream regions of genes has proved to be extremely valuable in functional genomics for deciphering the complex genetic regulatory networks (1–4). Correspondingly, there have emerged a large number of computational algorithms for identifying regulatory elements from DNA sequences with or without additional information, which have been classified and summarized in excellent reviews (1,2,5–8). Systems that integrate these tools for transcription regulation analysis are also available (9). Recently, however, it has been realized that current motif discovery algorithms are far from perfect. To improve the prediction accuracy, researchers incorporated other sources of information to complement the sequence information, such as phylogenetic trees and gene expression patterns (10–14).

On the other hand, despite the availability of dozens of motif discovery algorithms, there are few systematic comparative benchmarking that work to independently evaluate the prediction performance of existing motif discovery algorithms (15–19). Day and McMorris (15) compared consensus methods for motif discovery in terms of their appropriateness, basis, conformity, consistency, rationality and robustness. These measures are defined mostly from program users' point of view and thus are extremely valuable to guide users to make choice from consensus methods. However, since it is an early work, no widely used modern algorithms are evaluated. Benítez-Bellón et al. (20) evaluated one motif discovery algorithm, namely, Dyad-analysis and one pattern search/matching algorithm and suggested how to select optimal matching threshold to achieve better prediction results. Although the same RegulonDB datasets of the earlier stage were used as in this paper, no systematic comparison of multiple motif discovery algorithms has been carried out in this research. The influence of other factors, such as sequence number and scalability, is also not characterized. Sinha and Tompa (17) compared their YMF (21) with two other algorithms with synthetic data and real datasets from yeast. Recently, 13 motif discovery algorithms have been evaluated using a well-selected set of eukaryotic datasets (18).

The focus of this paper is to extend earlier works to prokaryotic datasets and to clarify the limitations and potentials of existing motif discovery algorithms. Complementary to the previous benchmarking work (18) in which algorithm developers were allowed to fine-tune the running parameters and reported the best results, we only allow minimal parameter-tuning during performance evaluation. Performance evaluation based only on the predictions with the highest score has the risk of penalizing some practically effective algorithms, since in many cases the predicted motifs with the highest score are not the motifs with the highest accuracy (19). Here, a predicted motif is defined as all the predicted binding sites for an input sequence set out of one prediction by a motif discovery algorithm. It should also be noted that no motif-search algorithms are included in this investigation as discussed by Benítez-Bellón et al. (20) and more extensively by Osada et al. (22). Although there are iterative alternating steps between pattern search and position-specific score matrix (PSSM) pattern summarization, there is no clear-cut two stages of pattern discovery and pattern search in our evaluated algorithms as in the case of Dyad-analysis (23).

We define a set of prediction performance indexes for motif discovery algorithms and conduct comparative evaluation of five motif discovery algorithms in terms of their prediction accuracy, scalability and the reliability of their significance scores with the RegulonDB, in which the real binding site information is available through experimental methods. We investigated how factors such as the width of a target motif, the number of input sequences and the information content of target motifs may influence the prediction accuracy. Based on these evaluations, we provide some guidelines for motif discovery algorithm users as well as algorithm developers for improving the prediction accuracy. Five algorithms, namely, AlignACE (24), MEME (25), BioProspector (26), MDScan (19) and MotifSampler (27) are evaluated. These are the motif discovery algorithms that only use DNA sequence information. There are several factors considered in choosing these algorithms. First, they are widely used in practice. Second, they are used as the base algorithms to develop more advanced algorithms, such as PhyME (13). Third, these algorithms are readily downloadable from Internet, allowing us to do large-scale local benchmarking runs. Since the average motif length of RegulonDB is 21, we do not include algorithms that can only handle short motifs (e.g. <10 nt), such as the oligonucleotide frequency counting method (28). Some of these algorithms turn out to be impractical due to their prohibitive demand for computational resources (29). We also pass by the algorithms that are only suitable for highly conserved motifs, such as some combinatorial or enumerative exact algorithms (12).

Our comprehensive large-scale benchmark experiments show that the performance of popular motif algorithms based only on DNA sequence information is still quite low, with ∼15–25% accuracy at the nucleotide level and 25–35% at the binding site level for sequences of 400 nt long. However, surprisingly, they are capable of predicting at least one binding site correctly in more than 90% of the time. Among the factors that affect the prediction accuracy, the sequence length is found to be the most critical. The performance of all algorithms degrades significantly as the sequence length increases. On the other hand, we find that if a certain number of sequences are available, using more sequences does not improve the prediction accuracy. Finally, we propose a simple ensemble algorithm for motif discovery by combining prediction results from multiple runs of three heuristic motif discovery algorithms. The ensemble algorithm can improve the prediction accuracy of their corresponding base algorithms by up to 45% in the case of sequence sets with lengths of 100 nt. The best ensemble algorithm achieves a better performance than the popular MEME algorithm by 52%. The improvement is achieved by both increasing the specificity and sensitivity. These results imply that we can take advantage of many choices of basic motif discovery algorithms to develop a strong ensemble algorithm. Results from different algorithms or algorithm runs can be used as a cross-validation between each other, suggesting that high consensus among multiple runs strongly indicates that a motif is found correctly.

MATERIALS AND METHODS

Datasets

To evaluate motif discovery algorithms, it is desirable to have diverse datasets to illuminate the effects of a variety of factors on prediction performance. We use the binding sites (motif) information of Escherichia coli K-12 stored in RegulonDB (30) to generate various types of input sequence sets. RegulonDB is selected based on the following considerations: it has been used by many other researchers for benchmark (25,27,31); it complements the latest benchmark study (18) in which only eukaryotic datasets were used; it has also been used by a comparative study of motif representation and motif search algorithms (22) and an early evaluation of a motif discovery and a motif search algorithm (20).

In this benchmarking, the test sequences are generated using a cleaned RegulonDB as well as the gene information and the whole genome sequence of E.coli. The raw data for generating input sequences include the following three files: ecoli.regulonDB (30), which stores experimentally determined binding sites information including transcription factors, start and end positions on the genome, and location on the forward or reverse sequence; ecoli.gene, which includes start and end positions of genes in the genome; ecoli.genome, which is the whole E.coli genome sequence taken from KEGG database (32).

Binding site records in RegulonDB are organized in groups which bind to the same transcription factor. From RegulonDB, the following binding sites records are discarded: any record that does not have positional information on the genome, any duplicated record, any record that differs with other binding site records only by a <5 nt shift. Finally, we remove binding site groups with only one sequence. We refer this cleaned dataset as ECRDB70. Note that our ECRDB70 is the source dataset from which a variety of input datasets are generated (see below). ECRDB70 is thus different from the input sequence datasets used in the previous benchmarking work (18).

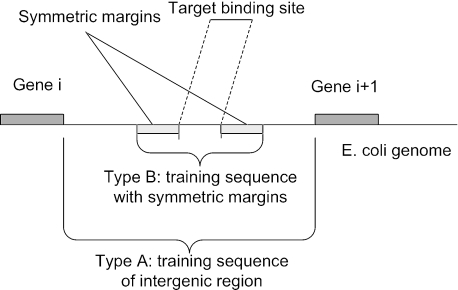
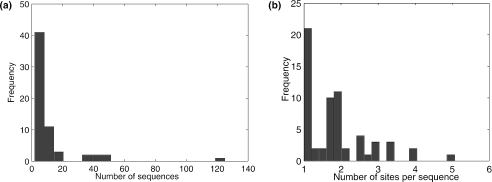
We generated two types of datasets (Type A and B) from ECRDB70 (Figure 1). Type A datasets are generated from the intergenic regions of E.coli genome. It is generated as follows: for each known binding site of a motif group, we align it to the E.coli genome, locating the adjacent genes to the binding site and extracting the intergenic region to generate one input sequence. If all the binding sites in a motif group are located in the same intergenic region thus only one intergenic sequence can be extracted, that motif group was discarded. The final screened dataset has 62 motif groups, which is termed ECRDB62A. It has the following characteristics: the average number of sequences per motif group: 12; the average number of sites per sequence: 1.85; the average sequence length: 300 nt; the average site width: 22.83. Figure 2 shows the distributions of the number of sequences per motif group and the number of sites per sequence.

Figure 1.

Two types of generated input sequences. Target binding site position information comes from ecoli.regulonDB, gene information from ecoli.genes, and genome information from ecoli.genome.

Figure 2.

Statistics of the ECRDB62A dataset. (a) Distribution of the number of sequences for a binding site group; (b) distribution of the number of sites per sequence.

Type B datasets include sequences with symmetric margins on both sides of known binding sites. They are generated as follows. For each binding site of a motif group, we align it with the E.coli genome and extend the binding site in both directions by adding symmetric margins of a given length along the genome. In this manner, we can define a series of datasets with increasing margin sizes to test the scalability of motif discovery algorithms. In some motif groups, multiple binding sites appear in a single sequence when the margin size is large. For instance, transcription factor XylR has binding sites at the positions 3728472, 3728492, 3728622 and 3728642 in the genome. Thus, when the margin size is >200, all the binding sites appear in each of the input sequences though these sequences are different. We kept these exceptional cases in the dataset because this case also happens in a real situation. Each Type B dataset (ECRDB70B-X) with margin size X has the following characteristics: there are 70 binding site groups, each with at least two sequences; the average number of sequences per motif group is 12 with the standard deviation of 21; the average number of sites per sequence is 1.62; the average site width is 21.70 with the standard deviation of 11.74. The high values of the standard deviations reflect the diversity and variation among input sequence sets. For type B datasets, we observe that when the margin sizes are larger (e.g. >500 nt), some part of the sequences are located in the coding regions. However, as to be shown in Results, no significant influence has been observed of these variations on the prediction accuracy. Type A dataset is suitable for analyzing motif discovery for co-expressed genes while B provides a good model for analyzing data from ChIP–chip experiments.

The ECRDB70, ECRDB62A (the intergenic dataset), ECRDB70B-X motif datasets and the generated sequence datasets used in our experiments are available at http://dragon.bio.purdue.edu/pmotif/.

Algorithms tested

Five tested motif discovery algorithms are briefly described below. We introduce the major characteristics of each algorithm as well as the running parameters used in our experiments. We also describe a random algorithm used to evaluate the statistical significance of the prediction accuracy of tested motif discovery algorithms.

Basically, most of the algorithm parameters are set as default values or are set based on very general biological facts rather than on the details of the RegulonDB datasets (See Supplementary Material for the list of parameters used). This is more realistic than the previous study (18), since in practice expert knowledge of using a specific algorithm is usually not available for ordinary users. Our minimal parameter-tuning policy ensures that the algorithm performance reported here is closer to that in real-world practice. The difficulty of tuning parameters is discussed in Results.

AlignACE

AlignACE (24) is a stochastic motif discovery algorithm based on the widely adopted Gibbs Sampling method (33). Compared with the original Gibbs Sampling method, it adds the following major features: both strands of sequences are searched; near-optimum sampling is improved; an iterative masking approach is used to search multiple motifs. Running parameters for AlignACE are set as default except that the gcback (the background GC content) is set as 0.5 and the expected motif width is set to 15 unless otherwise specified. We have investigated the effect of the motif width setting in Table 3.

Table 3.

Influence of estimated motif width on the nucleotide level prediction accuracy (nPC)

Algorithm motif width	5	10	15	20	25
AlignACE (10)	0.068	0.142	0.139	0.127	0.100
BioProspector (10)	0.041	0.136	0.205	0.230	0.222
MDScan	0.073	0.164	0.215	0.237	0.221
MEME	0.177	0.177	0.177	0.177	0.177
MotifSampler (10)	0.055	0.107	0.149	0.147	0.170

The major statistical score used by AlignACE, the MAP score, measures the degree to which a motif is over-represented relative to the expected random occurrence of such a motif in the sequence.

BioProspector

BioProspector (26) is another variant of the Gibbs Sampling algorithm. Compared with the Lawrence version (33), it added a Markov model estimated from all promoter sequences in the genome to model adjacent nucleotide dependency. It has 15 parameters. We use the default values for most of these parameters except for the motif width, which is set to 15, and the number of top motifs to report, which is set to 5. The background frequency model is generated using the whole E.coli genome, and the third-order Markov model is used unless otherwise specified. The order of the Markov model is chosen because it was the best among those tested (see Results).

MDScan

MDScan (19) is an enumerative deterministic greedy algorithm. It selects several top motif candidates according to the chip-array enhancement score to build motif models and then employs a greedy strategy to improve the models. We used the default parameter set except for the motif width, which is set to 15. The background frequency model is generated using the whole E.coli genome, and the third-order Markov model is used unless otherwise specified. MDScan uses a maximum a posterior (MAP) score to evaluate candidate motifs.

MEME

MEME (Multiple Expectation Maximization Estimation) (25) is based on the expectation maximization (EM) technique. With a given motif width w, MEME first decomposes original sequences into w-mers. Each w-mer could be a motif or a background subsequence to be determined by the motif and background model components. The search space increases significantly with increasing number of sequences and sequence lengths. It is the only algorithm in this evaluation that does not require a motif width parameter, which can be estimated by itself. We set the maximum dataset size in characters as 1 million, maximum running time as 3600 CPU seconds, maximal number of motifs to find as five, minimum number of sites for each motif as one. The rest of the parameters are used as default. The background frequency model is generated using the whole E.coli genome, and the third-order Markov model is used unless otherwise specified.

MotifSampler

MotifSampler (27) is another motif discovery algorithm based on Gibbs sampling. It extends the original Gibbs Sampling approach in two ways. First, it introduces a higher-order Markov background model. Second, it incorporates a Bayesian mechanism to estimate the number of motifs occurring in each sequence.

MotifSampler has seven major parameters. We made the following adjustments to the default parameter values. We only search input sequences without including its reverse complements because all known sites are aligned on the forward direction of the input sequences. We search five different motifs with width of 15 unless specified otherwise. The number of repeating runs is set to five. The background frequency model is generated using the intergenic region sequences of all E.coli genome, and the third-order Markov model is used unless otherwise specified.

Consensus ensemble algorithm

Stochastic motif discovery algorithms, such as AlignACE, BioProspector and MotifSampler, usually obtain different predictions for different running conditions, such as parameter settings or random seeds. However, it is observed that many such predictions tend to cluster together, which hints that summarizing these results may improve the prediction performance. In this section, we propose a simple consensus ensemble algorithm (CEA) to illustrate how ensemble algorithms could improve existing motif discovery algorithms.

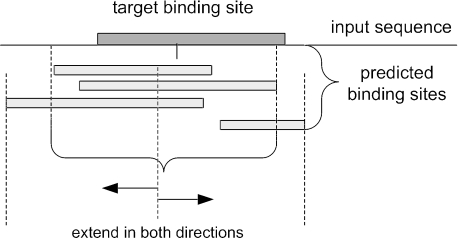
The CEA algorithm is composed of the following steps. (i) A base motif discovery algorithm such as AlignACE with different random seeds is run for N_r times (N_r = 10 in the current test). For each run, a predicted motif with the highest score and one more more binding sites is collected, thus resulting in total of motifs. (ii) For each input sequence, all the predicted binding sites on the input sequence from the motifs are aligned on the sequence (Figure 3). (iii) For each position of the input sequence, the number of times the position is included in predicted binding sites, or votes to the position, V_i, are counted. Then, it is normalized by the number of predicted motifs, N_r, to compute the consensus score of the position, V_i/N_r. (iv) Positions whose consensus score is smaller than a threshold parameter, θ_c, are discarded. Consecutive highly voted positions form a candidate of a binding site region as shown in Figure 3. But if the width of a candidate region is shorter than the binding site width specified by the parameter of the base algorithm (e.g. 15), that region is discarded. Multiple candidate regions may be generated. In case when no positions are left on the sequence by this discarding step, the position with the highest consensus score is kept. (v) Adjustment of the binding site width for each candidate region. Starting from the center of a candidate region, extend 1 nt in the direction of one of its two sides that has higher consensus score until the specified motif width is reached. Note that CEA only generates one binding site prediction per candidate region. Depending on the threshold, θ_c, zero or more (but at most two) binding sites will be reported from each input sequence. In Table 7, results with different threshold values are shown. A more sophisticated ensemble algorithm without ratio parameter has been developed and will be reported elsewhere.

Figure 3.

A simple consensus ensemble algorithm. Top predictions from multiple runs are aligned together to determine the boundary of the prospective motif based on over-representation. Then, a squeezing/expansion procedure will be applied to extract a motif prediction of a specified motif width starting from the center of the boundary region.

Table 7.

Comparison of nucleotide level prediction accuracy (nPC) of consensus ensemble algorithms to standard-alone base algorithms

Threshold (θc)	Margin size 50
	AlignACE	BioProspector	MotifSampler	MDScan	MEME
0.1	0.201	0.267	0.306
0.2	0.219	0.275	0.347	N/A	N/A
0.3	0.242	0.307	0.382
0.4	0.253	0.324	0.372
Best of ensemble	0.253	0.324	0.382
Base algorithm	0.182	0.304	0.263	0.294	0.252
Multi-restart	0.221	0.276	0.213	N/A	N/A

Random algorithm

To estimate the statistical significance of the prediction accuracy, a certain number of sites are randomly picked up as the predicted motifs. The number of sites picked up for each input sequence is determined as follows: 10 runs of AlignACE, BioProspector, and MotifSampler and one run of MEME are conducted to get the minimum and the maximum numbers of predicted sites for ith input sequence, nSiteMin_i and nSiteMax_i respectively. Then, the number of sites to be predicted for ith input sequence is randomly chosen between [nSiteMin_i, nSiteMax_i]. This random algorithm is run 1000 times for an input sequence set.

Measures of prediction accuracy

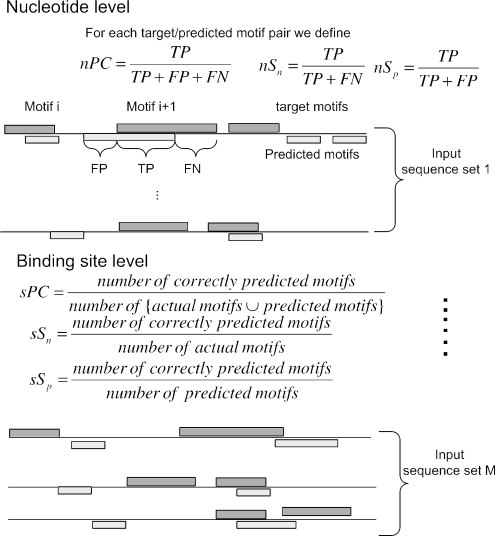
There are several prediction accuracy measures for evaluating motif discovery algorithms (13,17,19,27). Many of them are derived from the accuracy definitions for evaluating gene predictions (34,35). Here, we use three levels of performance criteria: nucleotide, binding site and motif levels.

Nucleotide level accuracy

First, for each target binding site with overlapping predicted binding sites in an input sequence, we define the following values for calculating accuracy metrics at the nucleotide level (Figure 4): nTP (true positive), the number of target binding site positions predicted as binding site positions; nTN (true negative), the number of non-target binding site positions predicted as non-binding site positions; nFP (false positive), the number of non-target binding site positions predicted as binding site positions; nFN (false negative), the number of target binding site positions predicted as non-binding site positions.

Figure 4.

Measures of prediction accuracy at the nucleotide and motif levels. Accuracy scores over an input sequence set are the average accuracy scores over all its sequences. The overall accuracy scores of a motif discovery algorithm are the average accuracy scores over all M input sequence sets.

The sensitivity over a pair of target/predicted binding sites is defined as:

$$n{\text{S}}_n=\frac{n\text{TP}}{n\text{TP}+n\text{FN}}$$ 1

and specificity is defined as:

$$n{\text{S}}_p=\frac{n\text{TP}}{n\text{TP}+n\text{FP}}.$$ 2

In order to capture both specificity and sensitivity in a single accuracy measurement, we use the nucleotide level performance coefficient (nPC) following Pevzner and Sze (16) and Tompa et al. (18):

$$n\text{PC}=\frac{n\text{TP}}{n\text{TP}+n\text{FP}+n\text{FN}}$$ 3

According to this definition, the nPC value ranges over (0, 1) with the perfect prediction being the value of 1. Compared with the correlation coefficient (CC) (34,35), nPC has several benefits: it is straightforward to interpret, and practically, it also tells the experimental biologists the probable range that the true binding sites are located around the predicted positions. We also used the F-measure or Harmonic mean (36) as the overall accuracy measurement. Compared with geometric or arithmetic mean, it tends to penalize more the imbalance of sensitivity and specificity. The F-measure is defined as:

$$F=\frac{2\ast \text{Sn}\ast \text{Sp}}{\text{Sn}+\text{Sp}}.$$ 4

In the case that Sn and Sp are equal to 0, F-value is defined as 0.

In addition to accuracy scores for target binding sites with overlapping predictions, we need to address the cases of target binding sites which do not overlap predictions or predictions which do not overlap with any target binding sites. Suppose MT is the number of missing targets and MP the number of wrong predictions. We define the number of non-overlapping target and predicted binding site pairs as the larger number of MT and MP. The accuracy scores of these non-overlapping pairs are set to zero. This definition will penalize algorithms that report either too many or too few binding site predictions.

Based on the scores defined for the binding site pairs, the accuracy scores of a motif discovery algorithm are calculated as:

$$\begin{array}{c}\frac{1}{(\#\text{-}\text{motifgroup})}{\displaystyle \sum _{\text{motifgroup}}}\frac{1}{(\#\text{-}\text{sequences})}\\ \times {\displaystyle \sum _{\text{sequences}}}\frac{1}{(\#\text{-}\text{sitepairs})}{\displaystyle \sum _{\text{sitepairs}}}n\text{PC}\left(\text{or }n\text{ SP or }n\text{Sn}\right)\end{array}$$ 5

Thus, the score is first averaged over all binding site pairs in a sequence, followed by averaging over all sequences in a motif groups, then averaged over all the motif groups. Note that we allow multiple binding sites on a sequence as target sites.

Binding site level accuracy

The binding site level accuracy indicates whether predicted binding sites overlap with true binding sites by one or more nucleotide position. We define, sTP, sFP and sFN as follows: sTP, the number of predicted binding sites which overlaps with the true binding sites by at least 1 nt; sFP, the number of predicted binding sites which have no overlaps with the true binding sites; sFN, the number of true binding sites that have no overlaps with any predicted binding sites.

For each input sequence, we define the following accuracy metrics at the binding site level:

Performance coefficient:

$$\text{sPC}=\frac{\text{sTP}}{\text{sTP}+\text{sFP}+\text{sFN}}$$ 6

Sensitivity:

$$\text{sSn}=\frac{\text{sTP}}{\text{sTP}+\text{sFN}}.$$ 7

Specificity:

$$\text{sSp}=\frac{\text{sTP}}{\text{sTP}+\text{sFP}}.$$ 8

The binding site level accuracy score of an input sequence set (e.g. ArcA) is the average of the scores over all its sequences. The binding site level accuracy score of the entire benchmark dataset is the average of the scores for all input sequence sets.

Sequence and motif level accuracy

To evaluate the capability to find at least one binding site in an input sequence, we define the sequence level success rate as the number of sequences N_s that have at least one correctly predicted motif divided by the total number N of sequences in an input sequence set:

$$\text{sSr}=\frac{N_s}{N}$$ 9

The overall sequence success rate of an algorithm is thus the average of sSr over all the input sequence sets.

We introduce the motif level success rate score mSr, a sensitivity measure, to evaluate the adaptability of an algorithm to different types of motifs. is defined as the number of target motif groups N_p, which have at least one correctly predicted binding site divided by the total number of target motifs (M = 70). A prediction is regarded as correct when the predicted motif overlaps with the target motif by at least 1 nt.

$${\text{mS}}_{\text{r}}=\frac{Np}{M}.$$ 10

Alignment of annotated binding sites in RegulonDB

We use the experimentally determined binding sites information as the targets of prediction. Since the binding site sequences listed in RegulonDB are collected from literature of different experiments, initially they are not aligned to see the consensus motif patterns. Qin et al. (37) mentioned one such example in which by shifting the experimentally determined binding sites, more consistent motif patterns can be obtained. Here, we performed a systematic alignment of motif sequences in RegulonDB. Starting from a set of unaligned binding sites, we obtain an alignment which will show the conservation of each residue at each position of the binding site. Figure 5 shows an example in RegulonDB, where the number of consensus positions increased from 2 to 15 by shifting the sequences back-and-forth. Increasing the number of consensus positions in a motif sequence alignment is critical for motif searching algorithms since most of them use a PSSM (8) to create a motif model, which is highly sensitive to consensus patterns of aligned sequences.

Figure 5.

An example of binding site misalignment in a motif in RegulonDB. The shaded columns are those with at least 80% dominance of a certain nucleotide. (a) Original binding sites of motif TrpR; (b) the shifted binding site with maximum shift of four positions to maximize the number of consensus positions.

To evaluate improvement of consensus patterns of aligned motif sequences, we compare the information contents (38) of motifs before and after the alignment operation:

$$I_{\text{seq}}={\displaystyle \sum _{j=1}^L}{\displaystyle \sum _{i=1}^A}{f}_{i,j}ln\frac{f_{i,j}}{p_i}$$ 11

where A is the alphabet of nucleotides (A, C, G, T). L is the length of the sequences; p_i is the a priori probability of letter i, is the frequency that letter i occurs at position j; I_seq is the information content of the sequences.

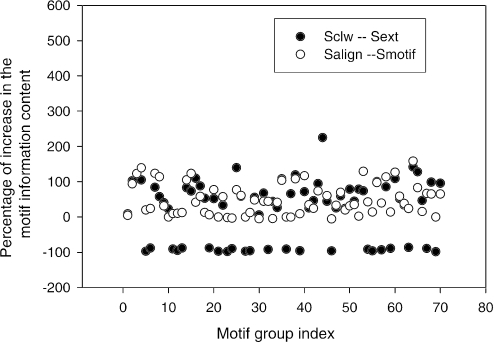
To align a motif sequence set, first, we extend each known binding site in a motif group S_motif in both directions by 20 nt to create an extended sequence set S_ext. Then, we apply the multiple sequence alignment tool clustalW (39) to S_ext with a high penalty for gaps (essentially not allowing any gap in a multiple sequence alignment), which generates a new aligned sequence set, S_clw. To reconstruct a new motif set S_align, we trim each sequence in the S_clw to a new sequence with length equal to the original motif length as follows: starting from the center position of the sequence in S_clw, we check the information content of the nucleotides in the two columns in both directions and extend the motifs in the direction with a higher information content or randomly pick a direction if both directions have an equal information content. This procedure proceeds until the total length is equal to the original motif length. Finally, for all these aligned sequence sets, S_motif, S_ext, S_clw and S_align, we calculate their information contents to compare the conservation level of the sequence patterns.

RESULTS

Prediction performance on ECRDB62A set

Table 1 shows the prediction performance at the nucleotide, binding site and motif levels for the five motif discovery algorithms as well as the random algorithm. The accuracy scores of AlignACE, BioProspector, MDScan and MotifSampler are averaged over 100 runs. The random algorithm is repeated for 1000 runs.

Table 1.

Prediction accuracy on the E.coli intergenic region dataset at nucleotide, binding site and motif levels

Algorithms	Nucleotide level				BindingSite level				Motif level
	nPC	nSn	nSp	nF	sPC	sSn	sSp	nF	mSr	sSr
AlignACE	0.128	0.198	0.152	0.172	0.234	0.355	0.335	0.345	0.903	0.537
BioProspector	0.174	0.205	0.270	0.233	0.294	0.424	0.374	0.397	0.952	0.642
MDScan	0.149	0.177	0.230	0.200	0.240	0.328	0.355	0.341	0.935	0.531
MEME	0.158	0.259	0.199	0.225	0.295	0.461	0.436	0.448	1.000	0.590
MotifSampler	0.153	0.179	0.237	0.204	0.302	0.331	0.476	0.390	0.919	0.524
Random	0.050	0.061	0.083	0.070	0.100	0.161	0.146	0.153	0.730	0.342

First, we found that at the nucleotide level, the prediction accuracy of all algorithms is relatively low: the maximum sensitivity, specificity and performance coefficient are only 0.259, 0.270 and 0.174, respectively. The accuracy levels are higher than the performance scores reported previously on eukaryotic data (18). This is due to their longer sequences ranging from 500 to 3000 nt, while the sequence lengths in ECRDB62A vary from 86 to 676 nt (average: 289 nt). BioProspector achieved the highest performance coefficient and specificity while MEME has the best sensitivity, partly due to its capability to estimate motif lengths. We find that all algorithms are significantly better than the random algorithm at the nucleotide level. Comparing the nPC and nF, we also found that both measures generate the identical ranking orders for the algorithms' performances. Therefore, below only PC/Sp/Sn accuracy scores are presented.

The prediction performance at the binding site level is better than the nucleotide level. The maximum specificity reaches 0.476 for MotifSampler and the maximum performance coefficient reaches 0.302 for MotifSampler. These accuracy scores are higher than what was reported before (18) because we regard overlaps with one or more nucleotides as sufficient to qualify as a correct prediction, while at least 4 nt overlaps were needed in the previous work (18). The justification is that when a predicted binding site overlaps with the true site with at least 1 nt, it is not difficult for experimental biologists to locate the true binding site position around the predicted anchor position since the motif width is only 10–20 nt on average. This higher prediction accuracy at binding sites level implies that at least these algorithms can locate rough positions of binding sites. At the binding site level, BioProspector and MEME are comparable with MotifSampler in terms of performance coefficient scores, all of which are better than AlignACE. This means that BioProspector and MotifSampler indeed improve the prediction performance of the simple Gibbs Sampling method. We also found that MEME is the best in terms of sensitivity and BioProspector best in terms of sequence level success rate, sSr while MEME is the second.

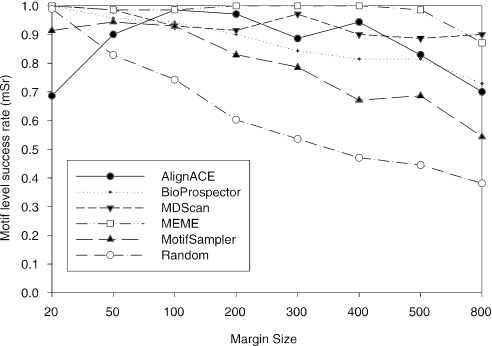
What is unexpected is the motif level success rate mS_r. We found that the motif level success rates of all five algorithms are >0.90, which is much higher than 0.73, the average performance of 1000 runs of the random algorithm. The P-value for the random algorithm to achieve an accuracy score of >0.900 is 0.000015, which shows the significance of the motif level success rate of the tested algorithms. The P-value is calculated from 1000 runs of the random algorithm. The maximum accuracy in the population is 0.839 with the standard deviation of 0.04. This comparison demonstrates that the algorithms are able to reliably predict at least one correct binding site from all motif groups. This fact could be potentially exploited to improve existing algorithms. We also found the motif level success rate, mSr, of MEME is the highest among the five algorithms, showing that MEME can handle more diverse input sequences.

Another interesting observation is that the prediction accuracy of stochastic algorithms, such as AlignACE, BioProspector and MotifSampler, are very stable over multiple runs. For the mean nPC scores of AlignACE, BioProspector and MotifSampler, the standard deviation is <0.01 for 100 runs. Because we did not observe a significant difference in different runs, all forthcoming experiment results for these three algorithms are from only one run.

It would be interesting to compare our results on prokaryotic datasets with what reported on eukaryotic datasets (18) since both studies evaluated AlignACE, MotifSampler and MEME and used the statistics nPC in the evaluation. However, note that this comparison is not straightforward because of the following reasons. First, the previous work allowed the developers of each algorithm to tune its parameter sets specifically to individual input data and also human intervention to the outputs as pre- and post-processing including literature survey, while we adopt the minimal parameter-tuning principle to simulate the motif discovery situation in practice by biologists. The level of human intervention allowed in the previous work is not feasible for the current large benchmark study. Second, the datasets are significantly different, which strongly affects the prediction performance. For example, the sequence length used in the previous work (18) varies from 500 to 3000 bp, while it varies from 86 to 676 in ECRDB62A. This explains that even though experts tuned their algorithms for the eukaryotic datasets, the maximum nPC score for all three algorithms is <0.05, which is much lower than 0.158 as reported here on ECRDB62A datasets and 0.10 on ECRDB70B-800 whose sequence length is ∼1600 bp.

In this study, we evaluated the accuracy of the best prediction out of top five scoring predictions. This is because in practice biologists can test five candidate motifs by experiments if they know the correct sites are included in the top five predictions with a reasonably high probability (accuracy). But for comparison, we also reported the statistics of the accuracy of the top-scoring motifs in Table 2.

Table 2.

The statistics of the top five predictions in terms of nPC on ECRDB62A set

Algorithm	Best	Worst	Mean	Standard deviation	Top-scored
AlignACE	0.128	0.029	0.072	0.045	0.083
BioProspector	0.174	0.097	0.124	0.041	0.130
MDScan	0.149	0.068	0.106	0.034	0.099
MEME	0.158	0.002	0.054	0.069	0.116
MotifSampler	0.153	0.010	0.062	0.065	0.069

First, it is evident that on average the top-scoring motif is not the best prediction. For example, in the case of MotifSampler the top-scoring motif corresponds to the best prediction in only 45% of the cases. Second, the discrepancy of the accuracy between the best and the worst prediction is relatively larger for AlignACE, MEME and MotifSampler, and the mean accuracy of them are lower than the other two algorithms. We found that this is resulted from the way these three algorithms find the next best-scoring motifs: once the top-scoring motif is found, its positions are masked out so that no subsequent sites are overlapped with them. Therefore, averaging the accuracy of the multiple top-scoring motifs is disadvantageous for the three algorithms.

Scalability

The scalability concerns how the algorithm performance changes with the increase of the number of sequences, the motif width and the sequence length.

We generated eight types of datasets with different margin sizes (extending on both sides of target motifs) of 20, 50, 100, 200, 300, 400, 500 and 800. Hence, the total sequence length is the target motif width plus twice the margin size. Each type has 70 motif groups with at least two sequences in a dataset. We run the five algorithms with the same parameter settings as in the previous section.

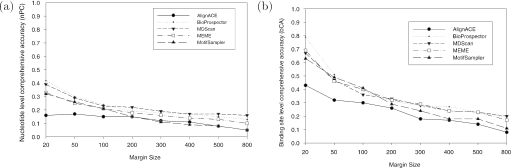
Figure 6 shows the prediction accuracy at the nucleotide and binding site levels. First at the nucleotide level, the performance of all the algorithms decreases significantly as the sequence length increases (Figure 6a). When the margin size is <200 nt, all algorithms except for AlignACE showed a similar performance. What is interesting is that when the margin size becomes larger than 400 nt, BioProspector, MDScan and MEME become the best algorithms, while MotifSampler and AlignACE become quite ineffective. Note that AlignACE and MotifSampler are all based on Gibbs sampling strategy while MEME and MDScan have an enumerative component in their search strategy. This performance discrepancy shows that for long input sequences, Gibbs sampling strategy tends to become too inefficient to identify the binding sites correctly.

Figure 6.

Scalability in terms of Performance coefficient (PC) with respect to the input sequence length (margin size). (a) nPC at nucleotide level; (b) sPC at binding site level.

At the binding site level, BioProspector, MDScan and MEME are the best algorithms, especially when the sequence length (double margin size) becomes >300 nt (Figure 6b). Figure 7 shows the motif level success rates with respect to different margin sizes. Here, MEME is the best with its capability to locate at least one correct binding site for a given dataset. In this test, AlignACE also has a high success rate. We also find all algorithms are significantly better than the random algorithm in terms of the motif level success rate.

Figure 7.

Motif level success rate (mSr) with respect to the sequence length (margin size).

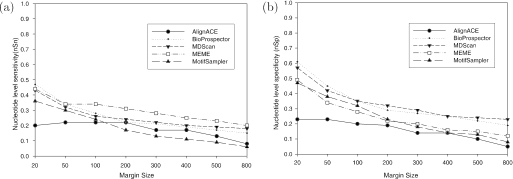
To examine why MEME has the highest motif level success rate, we compare the sensitivity (nSn) and the specificity (nSp) of these algorithms (Figure 8). It is illuminating that MEME has a dominant sensitivity, contributing to its high success rate mSr. One possible explanation of MEME's high sensitivity is that it is the only algorithm that has an exhaustive enumerative component while all other algorithms have a local search component. Another possible factor is that MEME can automatically adjust the motif widths while other algorithms use a fixed motif width.

Figure 8.

The nucleotide level prediction accuracy in terms of sensitivity (nSn) and specificity (nSp) with respect to the sequence lengths (margin sizes). (a) nSn at nucleotide level; (b) nSp at nucleotide level.

Effect of different parameters for the expected width and numbers of motifs

Motif discovery algorithms have several parameters to tune its prediction performance. Here, we examined the effect of two of the most critical parameters of the algorithms. One is the expected motif width W_e, and the other is the expected number N_bs of binding sites for a sequence or dataset. To evaluate how the parameter W_e affects the performance, we run the algorithms on the ECRDB70B-200 dataset using different W_e ranging from 5 to 25 with step of 5. For stochastic algorithms, such as AlignACE, BioProspector and MotifSampler, the experiments are repeated for 10 times and the average scores are reported. Since MEME can adaptively estimate the best motif width, we only conducted a single run using the parameter setting specified in the Method Section.

Table 3 shows how the nucleotide level accuracy varies with the different parameter of estimated motif width, W_e. Generally speaking, if W_e is too small, the algorithms will be penalized in sensitivity. If W_e is too large, they will be penalized in specificity. We found that for both BioProspector and MDScan, the best performance is achieved at W_e of 20, which is closest to the average target motif width of 21.9, while AlignACE and MotifSampler work best with W_e of 10 and 25, respectively.

We have chosen 15 as the expected motif width, which is approximately the average between the default value of the algorithms (which is 10 expect for MEME) and the average size of the binding sites in the benchmark set. The results in Table 3 clarified that the optimal value for the motif width differs from algorithm to algorithm even for the same benchmark dataset. The value 15 we used performed better or equal (MEME) for four of the algorithms than using the default value of 10. These results illustrate the difficulty for biologists to tune good parameters when they use these algorithms.

Another parameter we have examined is the number of expected binding sites in an input dataset. AlignACE and MEME have the parameter and MotifSampler also has it as the maximal number of expected binding sites for a sequence. MDScan and BioProspector do not have the parameter which user can tune. For both ECRDB62A and ECRDB70B-X datasets, there are cases that multiple binding sites of a motif exist on a single sequence. We run AlignACE, MEME and MotifSampler on the ECRDB70B-200 dataset with a different value of the estimated sites per sequence (nSite) ranging from 1 to 5. We conduct one run for MEME and 10 runs for AlignACE and MotifSampler, and the average accuracy scores are reported. All other parameters are set as described in Materials and Methods. In Table 4, the rightmost column shows the results with the default nSite value (AlignACE: 10, MEME and MotifSampler: Unset). Both AlignACE and MotifSamper achieve the highest accuracy with the default setting. However, MEME works best with nSite of 1. This is a little surprising since for the ECRDB70B-200 dataset, the average number of site per sequence is 1.78 with the standard deviation of 0.8.

Table 4.

Influence of estimated number of sites per sequence on the nucleotide level prediction accuracy (nPC)

Site no/seq	1	2	3	4	5	Default
AlignACE	0.144	0.141	0.134	0.126	0.121	0.144
MEME	0.194	0.186	0.167	0.142	0.114	0.177
MotifSampler	0.126	0.136	0.142	0.148	0.143	0.149

The analysis above on the effect of changing two parameters illustrates the difficulty of users to tune parameters. A different algorithm has a different optimal parameter even for the same dataset. Moreover, the optimal parameter does not always correspond to the average value of that parameter in the dataset, so that making a good guess of the optimal parameter value is even difficult. In practice, it is also difficult to obtain the data to make an estimation of the parameter values.

Effect of the background Markov models

Another factor that affects the prediction accuracy of some motif discovery algorithms is the background Markov models generated from background sequences. To evaluate their effects, we generated two types of background Markov models for BioProspector, MotifSampler and MEME: the first type is generated from the whole E.coli genome; the second type is created using only the intergenic regions. We generated six Markov background models with the order ranging from 0th to 5th for each model type except that BioProspector, which has only 0th to 3rd order background models. We run the algorithms over the intergenic dataset (Table 5).

Table 5.

Influence of background Markov models on the nucleotide level prediction accuracy (nPC)

Background sequences	Markov order	0	1	2	3	4	5	Mean
Whole genome	BioProspector	0.174	0.173	0.172	0.174	N/A	N/A	0.173
	MEME	0.152	0.158	0.149	0.157	0.141	0.156	0.152
	MotifSampler	0.146	0.140	0.139	0.143	0.144	0.146	0.143
Intergenic region	BioProspector	0.168	0.173	0.170	0.158	N/A	N/A	0.167
	MEME	0.137	0.136	0.140	0.140	0.141	0.146	0.140
	MotifSampler	0.144	0.151	0.145	0.152	0.150	0.152	0.149

Unexpectedly, the order of the background Markov models does not have a significant impact on the performance. For example, MEME achieves similar performances with 1st, 2nd and 3rd order models generated from the whole E.coli genome. This is also true for other two algorithms. We also found background models from the whole genome or intergenic regions lead to different prediction accuracy for the algorithms. Both BioProspector and MEME achieve a better accuracy for the whole genome background models while MotifSampler works better with background models from intergenic regions. Based on these observations, we use the third-order Markov models from whole genome for BioProspector and MEME and the third-order Markov models from intergenic regions for MotifSampler throughout this study.

Effect of the number of input sequences

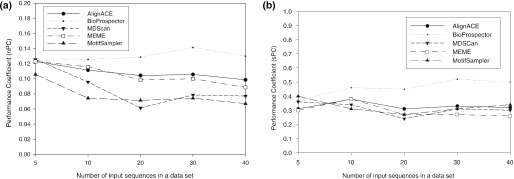
In this section, we investigate how the number of sequences in a given input sequence set affects the prediction accuracy because it is a dominant factor that determines the time complexity of motif discovery algorithms. For this study, input sets with K (=5, 10, 20, 30, 40) number of sequences are generated as follows: first, we select the following seven motif groups, CRP.txt (286 sequences), Lrp (150 sequences), FIS(138 sequences), IHF (126 sequences), FNR (102 sequences), NarL (84 sequences) and ArcA (80 sequences). These motif groups are the only ones with at least 40 sequences. For each motif group, we extend each binding site with 200 nt on both sides to create raw input sequences. Then, from each such set of raw input sequences, we randomly select K sequences without duplicates. Ten such sequence sets are created for each K. We then run the motif discovery algorithms on all 70 (=7*10) datasets. The prediction accuracy scores are then averaged for all the input sequence sets with the same number of (K) sequences (Figure 9). It is observed that when the number of sequences becomes >10, the performance coefficient at nucleotide level becomes stable (Figure 9a). More input sequences do not improve the prediction accuracy. Figure 9b even shows that the binding site level accuracy are almost independent of the number of sequences except that BioProspector seems to benefit from more input sequences. Therefore, for a large input sequence set, it is recommended to use an algorithm which has a good scalability to the number of sequences, such as BioProspector. If a user insists to use a computationally demanding algorithm, such as MEME, this observation suggests a novel approach: namely, one can input only partial input sequences to a motif discovery algorithm to obtain a motif model (e.g. PSSM) and then use this model to find motifs in the remaining sequences. In this manner, a significant reduction in the running time can be achieved without sacrificing the prediction accuracy.

Figure 9.

Comparison of prediction performance in terms of the number of input sequences in a dataset. The margin size is 200. (a) Nucleotide site level accuracy (nPC); (b) Binding site level accuracy (sPC).

Effect of the motif length

The target motif length is another factor that influences the prediction accuracy. For a given margin size on both sides, the conserved motif length along with the conservation level determines the signal-to-noise ratio. In the ECRDB70B-200, the motif length varies from 5 to 61 nt with the mean of 22.8 (the standard deviation is 11.92). To evaluate the effect of the motif length on the prediction accuracy, ideally, we need to remove other factors, such as the number of sequences in the input sequence set. However, from the previous section, we know that the influence of the number of sequence on the prediction accuracy is limited. Therefore, we used the same results from the previous section, reorganizing them to examine how motif length affects algorithm performance. Specifically, we extract the prediction accuracy scores of all the algorithms on the input sequence sets with the margin size of 200 nt on both sides. The motifs are grouped into four motif length groups, namely, {mL≤9}, {10<mL≤15}, {16<mL≤20}, {21<mL≤25}, {26<mL}. Then, the accuracy score is averaged within the length groups.

The results are summarized in Table 6. We found that AlignACE and MEME achieve higher prediction accuracy on datasets with longer motif width. For Mdscan, motif width barely affects the performance (between 0.2 and 0.23), and in addition, the maximum (0.23) is obtained for motifs of 21–25 nt. On the other hand, BioProspector and MotifSampler have no simple relationships between the motif length and the performance; they achieved the highest accuracy on datasets with intermediate motif lengths. One possible reason for this difference is that only AlignACE and MEME has the capability to adjust motif model length in a single run. Since the average motif length is 21.70, when the motif length becomes bigger, those algorithms with fixed-length motif models will be increasingly penalized due to the inappropriate parameter setting of the motif length. In practice, the real motif length of an input sequence set is usually unknown and usually users have to specify an estimated motif length for AlignACE, MDScan, MotifSampler and BioProspector. It is thus suggested to run these algorithms multiple times with different motif widths to get the best result.

Table 6.

Nucleotide level prediction accuracy versus motif widths

Motif width	(1,9)	(10–15)	(16–20)	(21–25)	(26–)
No. of targets	3	13	22	16	16
Algorithm	Performance coefficient (nPC)
Alignace	0.077	0.126	0.130	0.155	0.200
Bioprospector	0.145	0.216	0.208	0.166	0.174
MDScan	0.210	0.218	0.221	0.226	0.196
MEME	0.050	0.151	0.176	0.180	0.220
MotifSampler	0.148	0.107	0.225	0.090	0.145

Correlation between the significance scores and the accuracy

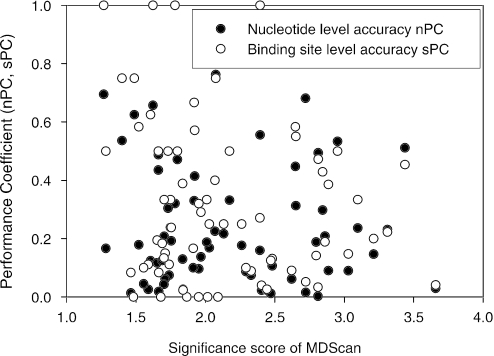
Most of motif discovery algorithms provide a score which evaluate the statistical significance of predicted binding sites. As investigated by Liu et al. (19) the binding site with the highest significance scores are not necessarily the best prediction of the target motifs. They calculated the average ranks of the correct binding sites when in the top five reported binding sites by MDScan, BioProspector, CONSENSUS (40) and AlignACE. They found that MDScan and BioProspector usually report the most accurate predictions with the top score while the most accurate predictions of the other two algorithms are within top 1 to 3 on average. However, their study did not show the consistency between the significance scores and the accuracy scores.

Here, we examined whether motif significance scores are correlated with prediction accuracy using ECRDB70B-200. Figure 10 shows results of MDScan. The performance coefficient scores (nPC and sPC) of the binding sites with the top score are plotted relative to their MAP scores. However, no clear correlation between these two scores is found. For each significance score range, the variation of accuracy is large. This lack of correlation between the significance scores and the accuracy scores also applies to other four algorithms, showing that high significance score does not necessarily indicate high prediction accuracy. We also found that motif significance scores from different input sequence sets are not comparable in general. In other words, one cannot judge the quality of a prediction simply by looking at its significance score.

Figure 10.

Correlation between motif significance scores and performance coefficient scores of MDScan.

Ensemble algorithms

In the pioneering study of gene-prediction algorithm evaluation, Burset and Guigo (34) showed that combining the outputs of several algorithms can be beneficial to improve the specificity, which means that coincidence of several algorithms can reinforce a given prediction. These combining algorithms are called ensemble algorithms in the machine learning field and have proven to be extremely successful (41). In the domain of protein structure prediction, ensemble algorithms or meta-server approaches are also very successful, as reported in CASP5 (42). Despite these encouraging results, to the best of our knowledge, there is no report of ensemble algorithms for motif discovery problems. Here, we show the first result for a simple ensemble algorithm for motif discovery. The datasets used here are the same as used in previous experiments with margin size 50. We have tested ensemble algorithms based on multiple runs of three stochastic algorithms, AlignACE, BioProspector and MotifSampler.

Table 7 shows the nucleotide level performance coefficient (nPC) of the three ensemble algorithms tested on the ECRDB70B-50. For comparison, it also shows the results of the base algorithms as well as MDScan and MEME. For each base algorithm, we tested four different consensus threshold values and summarize the best results (the fifth row of Table 7). The score in the bracket shows the highest accuracy among all. First, we find that ensemble algorithms have improved the accuracy over their corresponding base algorithms. Ensemble AlignACE, BioProspector and MotifSampler show improved performance by 39, 6 and 45%, respectively. The best ensemble algorithm (based on MotifSampler) outperforms the best standalone algorithm (BioProspector) by 26.5% with the accuracy score of 0.382 versus 0.302. The ensemble algorithm can also improve the performance of AlignACE to the level of MEME. These results show that a high degree of consensus among multiple predictions is a good indication of the quality of the predicted binding sites.

A remaining question about ensemble algorithms is whether its increased accuracy comes from synergetic effects of multiple predictions or simply because multiple runs have a better chance of getting a site with a higher accuracy. We developed a simple multi-restart algorithm in which a base algorithm is repeated for 10 times, each run reporting five predictions. We sort 50 predictions by their statistical score and report the top five scoring predictions as the final results of the multi-restart algorithm (the last row of Table 7). While the multi-restart algorithm improves AlignACE, it works worse than the base algorithms for BioProspector and MotifSampler. We found that reporting the top five scoring predictions out of 10 runs can make the final results worse because the score does not correlates well with the accuracy as shown by Table 2, Figure 10 and by Liu et al. (10). For MotifSampler, we used the consensus score, because it correlates better with the accuracy than the other two scores provided (but still not good: the correlation coefficient between nPC and the consensus score is 0.21, 0.21 with the information content, and −0.049 with the log-likelihood score, all with a P-value of >0.05). It confirms that ensemble algorithms distinguish themselves from the multiple-restarting strategy by exploiting synergetic effects among multiple predictions.

We also tested the simple ensemble algorithm on sequences with larger margin sizes. We found that when the margin size is increased to 200, our simple ensemble algorithm achieved similar or worse performance than corresponding base algorithms. After close examination, we found that this failure is caused by the divergence of the predictions of the base algorithms for long input sequences. To address this divergent prediction issue, we are developing more sophisticated clustering-based ensemble algorithms. The ensemble algorithms shown here are based on multiple runs of a single standalone algorithm. It is natural to combine results of multiple algorithms to achieve synergetic effect, which we have observed their benefits in our preliminary experiments. This research will be reported elsewhere.

DISCUSSION

We have developed a comprehensive set of performance measures at the nucleotide, binding site and motif levels and systematically evaluated five motif discovery algorithms using a prokaryotic motif dataset, ECRDB70. We selected algorithms which solely use input sequences for finding motifs, because this is the baseline of any of the recent algorithms which will also incorporate additional information. Special attention is paid to carefully examine factors that affect the prediction accuracy, which have not been carried out in the previous studies. We found that the prediction accuracy at the nucleotide and binding site levels is relatively low while the motif level prediction accuracy is surprisingly high. These conclusions complement the evaluation work reported for eukaryotic datasets (18). We compared the scalability of these algorithms and found that Gibbs Sampling based algorithms tend to fail for long sequences. Other algorithms also show significant degradation when the sequence lengths increase. These results suggest a need for improving scalability of motif discovery algorithms, which is particularly important when motifs are sought from an increasing number of complete genome sequences. We also found that the capability of adapting motif length is important which partially contributes to the dominance of MEME's high prediction sensitivity. Interestingly, it is observed that increasing the number of input sequences does not always improve the prediction accuracy once it reaches a threshold level, which can be exploited to reduce computational complexity of some algorithms. Another observation is that for noisy real datasets, no strong correlation between significance scores and prediction accuracy is observed for all motif discovery algorithms across all datasets. Finally, we developed a simple ensemble motif discovery algorithm that showed promising results for input sequence datasets of moderate length, showing that the available diverse motif discovery algorithms can be exploited to our advantage. It also implies that the high degree of consensus among multiple predictions of one or more algorithms may indicate their correctness.

Alignment of motif sequences in RegulonDB

In Figure 5, we have shown one example of alignment with increased consensus positions. We systematically checked the differences of the information content for the prealigned motif sets in ECRDB70 S_motif and for the aligned motif sets S_align. The same comparison is also applied to the extended sequence sets S_ext and aligned sequence sets S_clw (Figure 11). We found that multiple sequence alignment can increase the information content of a motif group with an average gain of 95.7%. The aligned sequences S_clw increase the information content of S_ext by ∼65%. There are some degradation of information content from S_ext to S_ckw due to the inherent divergence in the region of outside of motifs. The significant increase of information content suggests that shifting binding sites in a motif group using a multiple alignment procedure can greatly improve the motif models, thus improve the subsequent motif search performance.

Figure 11.

Difference of the information content between two sequence sets. Aligned sequences S_clw and the expanded sequences S_ext; realigned motifs S_align and the original motifs S_motif.

The alignment procedure could be further improved if the following fact of the annotated binding sites in RegulonDB is considered. It is known that some transcription factors are not sensitive to the strands of the DNA, which means that for some binding sites, either one of the two strands may be annotated in RegulonDB. It is thus possible that the opposite strand of an annotated binding site can be used to generate an alignment with more consensus position. For a set of K binding sites there are 2^K combinations of strand selections in total. For small K, one can simply enumerate all of them and pick out the one with highest information content. For a very large K, it is computationally prohibitive to test all the possible combinations of strands of K sequences. For such a large K, after we do a coarse alignment as described above, for each binding site sequence, we could test whether a replacement with the opposite strand can improve the information content. If true, we include its opposite strand rather than the annotated site to build the motif model. These algorithms are to be tested in a future work.

Limitations of current motif discovery algorithms

Despite the long-time effort for the motif discovery problem, our benchmarking results show that current sequence-based motif discovery algorithms have several fundamental limitations. First, the nucleotide level and binding site level prediction accuracy are still very low (i.e. nPC and sPC) (Figure 6) even on the prokaryotic motifs, which are supposed to be easier to be captured than eukaryotic ones. Therefore, in the current situation users should be aware of the limitations and be extremely careful in interpreting computational predictions. It should be also noticed that the significance score of algorithms do not necessarily corresponds directly to the accuracy of found motifs (Figure 10). The lack of scalability is another problem for all the evaluated algorithms. Below we list three technical difficulties which cause these limitations.

The first one is the inherent low signal/noise ratio in only-sequence-based motif discovery problems. As shown in Figure 6b, prediction performance decreases significantly as the length of sequences increases for all five algorithms. Several strategies have been proposed to increase the signal-to-noise ratio. Wang et al. (43) proposed an iterative refinement approach to this problem. Phylogenetic trees and structural information can be incorporated to increase signal-to-noise ratio (10–13,44–47).

The limitation also comes from the pattern model used to capture the regularity among the binding sites for transaction factors. The PSSM model is used for all five algorithms, with a slight variation. This model, however, has difficulty in modeling gapped motifs and assumes that the nucleotide positions are independent of each other, which is not true in reality. The syntactic deterministic motif models, such as consensus sequence models, suffer from their applicability only to short, highly conserved sequences (48). Several methods have been proposed to incorporate position-dependence information, including a novel hidden Markov model method (48), which tries to capture dependency between non-adjacent positions using a position re-ordering method. Osada et al. (22) introduced per-position information content as well as local pairwise nucleotide dependencies to improve the motif search performance. However, such more advanced motif models have not been incorporated into current motif discovery algorithms.

The local optima phenomena in optimization algorithms should be also mentioned here. Many popular motif discovery algorithms are based on heuristic search algorithms such as greedy search (13), Gibbs sampling (24,27) and Expectation Maximization (13,25). The performances of these methods are subject to potential suboptimal solutions in the search space. While usually 10–20 starting points are evaluated to find the most potential search direction, the effectiveness of this simple approach is usually limited for large multi-modal search spaces found in datasets with long sequences. Extensive experiments are needed to evaluate how severe the local optima issue could limit the performance of existing heuristic-based methods and whether stronger global optimization techniques, such as genetic algorithms and others (49), could be used to improve it.

Potentials of motif discovery algorithms

Although the low prediction performance has been revealed on the nucleotide and the binding site level accuracy, we believe that sequence-based motif discovery still has room for improvement. First, we could take advantage of the high motif-level success rate (mSr ≥ 0.92), a capability to identify at least one binding site correctly for a motif group in ECRDB70 (i.e. mSr, Figure 7).

A remarkable characteristic of the motif level success rate is the better tolerance to a longer input sequence size, i.e. a better scalability (Figure 7). Based on this observation, one natural idea of searching motifs in a set of long sequences is to perform the motif search in two steps, namely, to perform the second search just in the vicinity of motifs identified in the initial search. In this manner, the search space could be greatly reduced.

Two additional approaches we propose here are the ensemble algorithms and the hybrid algorithms. This is to take advantage of the high motif-level success rate and the stochastic nature of some motif discovery algorithms.

Ensemble algorithms are compound algorithms that combine the results of multiple predictions from multiple runs of a single or multiple algorithms. Ensemble algorithms have been shown to be able to build strong algorithms based on simple weak algorithms in both gene-finding (35), protein structure prediction (42) and machine learning (41). Our simple consensus ensemble algorithm provides the first proof of the promise of ensemble algorithms in motif discovery problems. Therefore, it is expected that ensemble algorithms are able to improve the accuracy of motif discovery. First, it is found that coincidence of the predictions of multiple algorithms usually could indicate the confidence of the predictions. Second, since all five evaluated algorithms achieved very high motif-level success rates, a set of diverse predictions from multiple algorithms thus has a high probability to cover all binding sites. There are several ways to exploit this property using ensemble algorithms. One way is to apply a motif discovery algorithm in two steps as described above, and another way is to apply a clustering algorithm on the multiple predictions to identify consensus predicted regions. As dozens of motif discovery algorithms are available today, the ensemble approach is especially promising to use them to our advantage.

So-called hybrid algorithms assemble the complementary components of multiple algorithms to build a stronger algorithm. This is different from assembling multiple predictions in an ensemble algorithm. Many algorithms have been proposed to address the motif discovery problems, from early algorithms based on consensus strings or regular expressions to the popular PSSM-based heuristic algorithms and the latest algorithms that exploit phylogenetic information. As shown by Sinha and Tompa (17), each type of algorithms have their own strengths. It is thus natural to combine characteristics to develop better algorithms. For example, heuristic algorithms have an advantage in their flexible representation of motif models while statistical algorithms usually run much faster than heuristic search methods (19). A hybrid algorithm can then be designed by first applying statistic algorithms to find potential sequence segments and then applying heuristic algorithms to locate the final motif positions.

The second interesting characteristic observed in this study is that increasing the number of sequences does not necessarily improve the prediction accuracy once the minimum number is reached. There are several ways to exploit this characteristic. First, it can be used to significantly reduce the running time of some time-consuming motif discovery algorithms by only feed a portion of the input sequences and then use the extracted motif model to find the binding sites on the remaining sequences. Second, we can divide the input sequences into multiple groups and apply different algorithms on each group. We then use the ensemble algorithms to summarize the predictions.

A trend of recent motif discovery algorithms is to incorporate additional information, such as phylogenetic trees or family sequences, to improve the predication accuracy (13,14). This strategy can effectively increase the signal/noise ratio, thus greatly improve both the specificity and sensitivity. In contrast, in our study, we have carefully revealed limitations and potentials of current sequence-based algorithms, and indicated ways to take advantage of the potentials for improvement. Since sequence-based approach is the baseline of any modern algorithms, our finding will surely benefit to improve almost all the algorithms.