A thermodynamic approach to designing structure-free combinatorial DNA word sets

Abstract

An algorithm is presented for the generation of sets of non-interacting DNA sequences, employing existing thermodynamic models for the prediction of duplex stabilities and secondary structures. A DNA ‘word’ structure is employed in which individual DNA ‘words’ of a given length (e.g. 12mer and 16mer) may be concatenated into longer sequences (e.g. four tandem words and six tandem words). This approach, where multiple word variants are used at each tandem word position, allows very large sets of non-interacting DNA strands to be assembled from combinations of the individual words. Word sets were generated and their figures of merit are compared to sets as described previously in the literature (e.g. 4, 8, 12, 15 and 16mer). The predicted hybridization behavior was experimentally verified on selected members of the sets using standard UV hyperchromism measurements of duplex melting temperatures (T_ms). Additional experimental validation was obtained by using the sequences in formulating and solving a small example of a DNA computing problem.

INTRODUCTION

In the half-century that has elapsed since the discovery of the DNA double helix (1), the basic understanding provided by the crystal structure has served as the foundation for the development of an increasingly detailed and powerful set of rules describing its formation, stability and properties. The first set of empirical models developed in the early '60 s, which parameterized duplex stabilities as a general function of GC content and salt concentration (2,3), were followed by detailed thermodynamic models based on the measurements of nearest neighbor effects (4–8). These widely-used models provide reliable predictions of the stability of DNA and RNA duplexes, and served in turn as the foundation for the development of excellent thermodynamic models for the prediction of RNA and DNA secondary structures (9–14). These models make possible the deterministic design of nucleic acid molecules with desired secondary and tertiary structure (15,16). There is no other class of chemical compounds for which any predictive model of comparable power exists. This fact, coupled with the widespread ability to chemically or biologically synthesize DNA or RNA molecules of any desired sequence virtually at will, has made nucleic acids the material of choice for ‘designer chemistry’, and nucleic acids have thus become the de facto standard for a myriad of emerging problems in molecular design (17–19).

One general problem that has emerged in this area is the design of ‘structure-free’ sets of DNA molecules (20–22). A brief historical perspective on the topic is provided in the accompanying manuscript (23). There are many situations in which one wishes to have access to a large family of ‘independent’ DNA molecules: i.e. sets of single-stranded DNA molecules which can be targeted independently in DNA hybridization reactions with their complements, in such a manner that there is a strong discrimination between hybridization and different members of the set. The molecules are single-stranded so that their sequences are available for binding to their complements; by the same logic, they need to be devoid of intramolecular secondary structures that would render their sequences unavailable for hybridization. Areas in which such families of molecules are important include the design and construction of nanostructures (24–26), nanodevices (18,27–29), DNA directed organic synthesis (30), addressed targeting of particular components of complex arrays (27,28,31,32) and DNA computing approaches (33–38).

Although in principle the power of the predictive models for DNA design should make such work straightforward, a significant issue does arise in the case where a large number of non-interacting molecules are needed. The size of the set of all possible DNA sequences of a given length grows exponentially with length. The sets of interactions between the elements of the set also grow exponentially. This daunting complexity is nonetheless small compared to the combinatorial explosion that occurs when modelling the secondary structure of these molecules rather than simply assessing their pairwise interactions (13,39). Overall, the problem of designing sets of non-interacting DNA or RNA molecules is extremely challenging from a computational standpoint. Problems of this type arise frequently in computer science, and the study and design of algorithms to address them is an active area of research.

In the present work an algorithm is presented for the generation of sets of non-interacting DNA sequences, employing existing thermodynamic models for the prediction of duplex stabilities and secondary structures (see Figure 1). A DNA ‘word’ structure is employed in which individual DNA ‘words’ of a given length (e.g. 12mer and 16mer) may be concatenated into longer sequences (e.g. four tandem words and six tandem words). While long strands may be formed by concatenation of individual words, complements cannot be simultaneously concatenated to one another. This approach, where multiple word variants are used at each tandem word position, allows very large sets of non-interacting DNA strands to be assembled from combinations of the individual words. There is a fundamental trade-off between the size of the non-interacting word sets that can be obtained, and the degree of hybridization discrimination between members of the sets. Example word sets were generated (Table 1 and Supplementary Material 1), with the general properties of two example sets (12mer and 16mer) summarized in Table 2. Words sets created with this algorithm compare favorably to previously published word sets (Table 3) (22,36,40,41). The predicted hybridization behavior was experimentally verified on selected members of one of the new sets using standard UV hyperchromism measurements of duplex melting temperatures (T_ms). Additional experimental validation was obtained by using the sequences in formulating and solving a small example of a DNA computing problem.

Figure 1.

The algorithm used for the generation of a set of 65 536 non-interacting DNA sequences using a 4 × 16 structure (four tandem words, with 16 variants at each position). The algorithm employs existing thermodynamic models for the prediction of duplex stabilities and secondary structures.

Table 1.

Examples of 64 member sets of 12mer and 16mer

Example 12mer set
A1–16	CACCATCTACAT	ACCAATTCTCTC	TTCCTTCTCTTC	TCCTATCTCACT
	TTCATACCTCAC	CTCTTCACTACA	ACACATTTTCAC	CAACACTTTCAA
	TTTCTTTCACCA	ACCACTAAACAA	TCCACAAATCAA	TCCTATACCACA
	TCACAATTCCAA	TTCACATTTCCT	CACCTACATCTT	CAATCCACATTC
B1–16	AACACCTCAATT	CACCTTTATCCT	CACCAAATTTCA	AACCAACATCAT
	AAAACCTCCTTT	CACCATATTCCT	ACCAATTCCATT	CACTCAATACCT
	AACCACTTTCAT	CAACCATTCCTA	ACCTTTTCATCA	ACCTTTTTCTCA
	CACCAAAATCAA	CACAACATTTCA	CAAACCTTCCTA	CACTCATCTCTT
C1–16	ACACCATTCATT	ACCAAAATTCCT	ACACACTAACAT	CTCCATACATCA
	CTCCTTCTCATT	CTCCAAATACCT	AACCATCATCAA	ACAACTCTACTC
	ACAATCTCACAT	ACACCATAAACA	AACTCAATCCTC	ACTCTATCACCT
	CTCCATAACCTT	ACAAAATCTCCA	ACACAAATCCTT	ACAATCCATCAA
D1–16	ACCATACAAACA	ACACAATAACCA	ACTAACCTTCAC	ACACACTTCTTT
	ACTTACTCCTCT	ACCTATCTACCA	AACCAATCACAT	ACCATACTCTCT
	AACCATTTACCA	AACAATCACCAT	ACCATAACAACA	ACAATCTCTCTC
	ATCATCCAAACA	ACTATACCTCCA	ACCAATACAACA	ACCAATAACACA
Example 16mer set
A1–8	ACTCACAAATTATCTC	TCTCTCTTAAATCACA	ACATCAATCTCTAAAC	ACATTCCTAAAAACAA
	ACTAATCTTTCCAAAC	TTTTTTCTCTCTACAC	ATTTTCTTCTTTTCCA	CACAAAATCTTCTTCT
B1–8	ACCATTAATTTCCATC	TTATTAATCCTCACCA	CTCTCCATCAAATATC	ACCTAATCACCTAAAT
	ACATTCATTCAATTCA	AACTACTTATTCCTCA	CAATATATCCTTCCAC	CTTTTTAACTTCCTCA
C1–8	TCTCTTCTCCAATTAA	ACCTAATACTTCATCA	TCACACATCAAAATTA	CACACCTTCTTATATC
	ACCTATTTTTTACCAC	TTCCTTTTATCCTTTC	TTCTTTCTCATATCCA	TCTTATCATCTACCTC
D1–8	TCCAACATCCTAATAT	CTACAATCACTTCTAC	ACCTATTATTCAACAC	CAACCAATCATAAAAC
	ACCTACACTTAATACT	TTCTTACTAACCATCA	ACACCATAATTCCTAT	TTCAAACTCAATCAAT
E1–8	TCAATTTTCCATTCTT	ACCATTTCATATCTCT	CTTTCCTCCTATAAAC	CAAAAATACATCACCT
	AACTCATACTTTTCAC	TACCTCTCTATTTCAA	ACCAAACTAACATATC	AACATTCTACATCAAC
F1–8	ACAACTAAAACATTCA	ACCTTAAAATAACCAC	CTCAATAACCTCATTT	CAACATTACTCTACTC
	ACCATACAATAAACAC	AACACTAATAACACAC	TATTACCTCTTCCAAA	ACAATACCTACAAATC
G1–8	CACTCATCTAACAAAT	TCTATACTCACTTTCA	CACTACATTTTCTCAA	CACACTATCCTTAAAC
	TCTTTATTCTCCTTCA	TCTTCCATATTAACCA	CACAAAAAAAAAACCA	CACTCCACATAATTTT
H1–8	ACCTTCAACTACTATT	CAAACAATCCTATTCA	ACCTTCATTTTAAACA	ACAATTATCAACTCTC
	CTCCAACTTTCTTATC	CATACAACTCCATTTT	TACCATTTACCTAACA	CAAAAATTTTTCCACA

Tandem word sequences are made by joining words into longer sequences according to the structure A_iB_jC_kD_l for 12mers or A_i-B_j…H_p for 16mers. Numbering of the word sequences proceeds down the columns and then across the rows.

Table 2.

Properties of example word sets

Properties of example word sets
Word length (nt)	12	16
Total words in set	64	64
Number of tandem words	4	8
Combinatorial complexity	216 (65 536)	2124 (16 777 216)
Perfect complement Tm range (°C)a	43.4–43.5	51.8–52.8
Closest mismatch Tm (°C)b	34.4	24.8

^aMelting temperatures were calculated using the formula of Allawi and SantaLucia Jr (8) with an oligonucleotide concentration of 10⁻⁸ M and a salt concentration of 1 M NaCl.

^bT_ms calculated for the most stable mismatched duplexes (see Table 3).

Table 3.

Comparisons with literature sets

Set name	Word number length	PM ΔG (T1)		MM ΔG (T2) min	Tm range (T5)		ρ	δ	δ*	Δ	CombFold	τ	τ*	Match		Mismatch
		Min	Max		Min	Max
S1Braich	40	−16.80	−13.57	−9.29	46.64	55.75	9.11	6.25	4.28	354.33	−1.25	4.10	1.84	w14	c14	w14	c4
S1 Shortreed	15mers	−15.22	−13.71	−7.29	47.01	49.98	2.97	7.20	6.42	5418.59	−2.47	7.03	5.81	w8	c8	w38	c8
S2 Brenner	8	−1.97	−1.01	−1.86	−67.19	−48.07	19.12	−0.19	−0.85	0.73				w1	c1	w1	c3
S2 Shortreed	4mers	−1.51	−1.01	−0.67	−67.19	−49.66	17.53	0.39	0.34	1.88				w6	c6	w6	c8
S4 Frutos	108	−8.95	−6.50	−8.72	17.06	27.34	10.28	−0.33	−2.22	0.61				w4	c4	w3	w4
S4 Shortreed	8mers	−8.59	−6.50	−6.70	17.06	25.78	8.72	1.35	−0.20	8.90				w59	c59	w12	c59
S5 Penchovsky	24	−17.94	−16.84	−8.72	55.15	58.65	3.50	8.79	8.12	3570.05	0.00	6.88	5.78	w22	c22	w22	c11
S5 Shortreed	16mers	−17.75	−17.05	−7.91	56.07	57.41	1.34	9.34	9.14	10842.11	−0.77	8.32	8.06	w16	c16	w16	c19
S7 Tulpan	64	−13.24	−12.54	−8.89	42.41	43.48	1.07	3.72	3.65	95.59	0.00	0.23	−0.64	w54	c54	w54	c64
S7 Shortreed	12mers	−12.66	−11.78	−8.94	42.38	43.50	1.12	2.87	2.84	23.20	−1.03	2.91	2.76	w14	c14	w14	c19
S8 Tulpan	64	−16.98	−15.70	−7.61	51.81	52.75	0.94	8.15	8.09	9816.31	−2.52	3.55	3.49	w56	c56	w3	c56
S8 Shortreed	16mers	−16.42	−15.45	−7.62	51.81	52.77	0.96	8.11	7.83	4740.07	−5.50	5.59	5.25	w12	c12	w12	c36
S8 Tulpan (10 C)	64	−25.45	−24.19	−14.30	51.81	52.75	0.94	10.04	9.89	10606.99	−16.93	4.17	3.75	w64	c64	w64	c13
S8 Shortreed (10 C)	16mers	−25.22	−24.12	−11.65	51.81	52.77	0.96	13.02	12.47	106597.39	−12.07	9.21	8.37	w11	c11	w19	c11

Six pairwise comparisons were made between sets created using the algorithm described here and sets created using other published algorithms. Sets were named according to the first author of the work and also by (S1–S8) to match nomenclature used in the accompanying manuscript. All free energies are in kcal/mol and all temperatures are in °C. T1 contains values for the minimum and maximum free energy for perfectly complementary duplexes w_ic_i; T2 contains the free energy of the most stable mismatch between words and complements (w_ic_j or w_jc_i); T5 contains values for the minimum and maximum melting temperatures for all perfectly complementary duplexes in the set; ρ is the width of the melting temperature range; δ and δ* refer to free energy differences between perfect matches and mismatches (see Equation 1 and the accompanying text); Δ refers to the discrimination factor (Equation 8); CombFold is the minimum free energy for the most stable secondary structure, which is formed when individual words are concatenated together for the formation of the combinatorial library; τ and τ* refer to free energies associated with mishybridization between word complements and word-word junctions (see Equation 10 and the accompanying text). Vacant table entries for the Brenner and Frutos sets are because words in these sets were not designed with concatenation in mind. The columns with the headings ‘match’ and ‘mismatch’ contain the identities of the sequences with the narrowest gap in free energy between a perfect match hybridization and a mismatch hybridization.

MATERIALS AND METHODS

Reagents

Oligonucleotides for the melting temperature studies were purchased from Integrated DNA Technologies. They were obtained in PAGE purified form and used as received. The buffer for the melting temperature studies was a solution of 1.0 M NaCl (Aldrich, Milwaukee, WI), 10 mM sodium cacodylate (pH 7.0) (Hampton Research, Aliso Viejo, CA) and 0.5 mM EDTA (Sigma, Milwaukee, WI). Oligonucleotides were mixed with buffer to a concentration of 1 μM. All other oligonucleotides were synthesized at the DNA Synthesis Laboratory, UW Madison Biotechnology Center. Single-stranded 84mer target sequences (Table 4) and PCR primers were obtained in column-purified form and thiol modified probe oligomers (Table 2) were purified immediately preceding use. Concentrations were calculated from the UV-absorbance at 260 nm. DTT was obtained from (Aldrich, Milwaukee, WI) and triethanolamine (TEA) was obtained from (Sigma, Milwaukee, WI).

Table 4.

DNA sequences employed in illustrative DNA computation

	Forward primer (Pf)—Ai-Bj-C-D-reverse primer (Pr)
PfA1B1CDPr	ATAATACCCTCCCACCCA-ATTTCCACCATT-ACCACCCTATAT-ATTCCTCACAAA-AACCATAAACCA-CACCCACCTCCCATAATA
PfA1B2CDPr	ATAATACCCTCCCACCCA-ATTTCCACCATT-CACACCTTATCT-ATTCCTCACAAA-AACCATAAACCA-CACCCACCTCCCATAATA
PfA2B1CDPr	ATAATACCCTCCCACCCA-AACACAACTCTT-ACCACCCTATAT-ATTCCTCACAAA-AACCATAAACCA-CACCCACCTCCCATAATA
PfA2B2CDPr	ATAATACCCTCCCACCCA-AACACAACTCTT-CACACCTTATCT-ATTCCTCACAAA-AACCATAAACCA-CACCCACCTCCCATAATA

Each target for the DNA computation is listed starting from the 5′ end. Forward (Pf) and reverse (Pr) primers, 18 bases long, bracket the four 12 nt word sequences, ABCD. The two sequences for A (A₁ = ATTTCCACCATT and A₂ = AACACAACTCTT) are in boldface. The two sequences for B (B₁ = ACCACCCTATAT and B₂ = CACACCTTATCT) are in italics. The third and forth words, C and D are the underlined sequence, serve as place holders in this computation. The sequences of words used in the computation were generated by a second equivalent DNA library selection.

Melting temperature studies

The experimental parameters were based on the work of Allawi and SantaLucia Jr (8). Melting points were determined by identification of the 50% melting point in plots of UV-absorbance at 260 nm versus temperature. The instrument employed for the absorbance measurements was an HP 845 UV-Visible absorption spectrophotometer, equipped with a temperature programmable thermostatted cuvette holder. Before measuring the melting temperature, the oligonucleotide solutions were elevated to a temperature of 85°C for 5 min. Annealing was performed by slowly dropping the temperature from 85°C to 0°C at a rate of 3°C per min. The temperature was maintained at 0°C until the onset of the melting measurement. Each step consisted of raising the temperature by 0.8°C and then holding at that temperature for 1 min prior to measuring the absorbance at 260 nm. The measurement range was from 15°C to 75°C. Liquid wax (Chill-Out 14, MJ Research, Boston, MA) was added to the surface of the DNA solution to prevent evaporation that would have otherwise occurred during the long heating cycles of the melting temperature studies.

Probe purification

Prior to surface attachment, the disulfide bonds of the thiol modified probes were cleaved with DTT. The dried oligonucleotide was resuspended to 33 μg/ml and 10 μl of DNA was combined in an high-performance liquid chromatography (HPLC) injection vial with 10 μl of 0.2 M DTT (pH 8.3–8.5). This solution was allowed to sit at room temperature for 30 min before injection. The oligonucleotide solution was separated by binary gradient reverse-phase HPLC. Collected fractions, which contained the pure oligonucleotide, were lyophilized and then resuspended in 10 μl of 100 mM TEA (pH 7.0).

Probe attachment

Thiol modified probes were attached to the surface using previously reported chemistries (42). Briefly, 18 × 18 × 1 mm gold (1000 Å) over chromium (50 Å) glass slides (EMF Corp., Ithaca, NY) were washed with dH2O (∼500 ml/chip) followed by ethanol (∼500 ml/chip) and dried before being submerged in 1 mM ethanolic 11-amino-1-undecanethiol hydrochloride (Dojindo Molecular Technologies, Inc. Gaithersburg, MD) for 24–48 h. The chips were washed again with ethanol followed by deionized water and dried under a stream of nitrogen gas. The gold surface was covered with 500 μl of 0.4 mg/ml Sulfo-SSMCC (Pierce Biotechnology, Inc., Rockford, IL) in 0.1 M TEA (pH 7.0) buffer in a humid chamber and incubated at room temperature for 25 min.

To attach the probe to the modified surface, 30 μl of 100 μM purified probe was sandwiched between two functionalized gold-coated chips. These were allowed to react for ∼20 h in a humid chamber at room temperature in the dark. Excess probe was then washed away with ∼250 ml deionized water. Chips were dried under a stream of nitrogen before immersion in 8 M urea for 30 min. The chips were subsequently washed with ∼200 ml deionized water and incubated in 1.0 M NaCl for 60 min at 58.5°C.

DNA computation experiments (overview)

A small example DNA computation (Figure 2) was performed using words from the 12mer DNA word set (Table 1). Full length strands were constructed using four tandem words and both forward and reverse primer sequences (see Table 4). Four 84mer sequences, encoding two bits of information, form the combinatorial library for this prototype surface-based DNA computation. The first bit of information is encoded by means of two different sequences for the first word (A₁ and A₂), and the second bit of information is encoded by two different sequences for the second word (B₁ and B₂). In this experiment only a single sequence was employed for each of words C and D, hence these words did not encode information. In the first round of the computation, the oligonucleotide mixture is applied to two separate chips. One chip has probe immobilized on the surface that is complementary to A₁ (Table 5). The other chip has probe immobilized to the surface that is complementary to A₂. Each chip captures two of the four original library members. Probes on the first chip hybridize to sequences containing A₁ and probes on the second chip hybridize to sequences containing A₂. Targets eluted from each chip are collected and divided into two equal aliquots. Each of these solutions is applied to a chip modified either with the complement to B₁ or the complement to B₂. Each of the four final chips is expected to uniquely yield one of the four sequences present in the original library. The identities of the eluted sequences were determined by PCR amplification and DNA sequencing.

Figure 2.

DNA computation schematic diagram. See DNA computation experiments (overview) in the Materials and Methods.

Table 5.

Capture probe sequences

A1-complement	5′-AATGGTGGAAATTTTTTTTTTTTTTTTSH-3′
A2-complement	5′-AAGAGTTGTGTTTTTTTTTTTTTTTTTSH-3′
B1-complement	5′-ATATAGGGTGGTTTTTTTTTTTTTTTTSH-3′
B2-complement	5′-AGATAAGGTGTGTTTTTTTTTTTTTTTSH-3′

Capture probe sequences complementary to each of the four different word sequences of the combinatorial library were synthesized with 15 nt T-spacers and a thiol modifier at the 3′ end.

DNA computation (first round)

Prior to the first computational hybridization, the chip's surface was pretreated with 30 μl of 2 μM solution containing all four target oligonucleotides. Target oligonucleotides were allowed to hybridize to the immobilized probes for 30 min. These were subsequently denatured in 8 M urea for 30 min, rinsed and dried. The immobilized probes were rehydrated by soaking the chips in 1 M NaCl. Later, 30 μl of the same target solution at a concentration of 2 μM was sandwiched between two chips, and allowed to hybridize for ∼20 h.

The solution containing unbound oligonucleotides was removed with a brief 10 ml of 1 M NaCl wash followed by a brief 10 min incubation of the chip in 10 ml of 1 M NaCl at 37°C. Hybridized oligonucleotides were eluted by placing the chip on a hot-block (94°C) and covering it with 300 μl of deionized water. Every 30–40 s, over a period of 8 min, 100 μl of solution was removed to a sample collection vial and replaced with an equal volume of water. The combined solution aliquots were reduced to dryness by rotary evaporation and resuspended in 30 μl of 1 M NaCl.

DNA computation (second round)

In the second round four separate chips were employed for hybridization. Two chips were functionalized with complement to B₁ and two chips were functionalized with complement to B₂. The target DNA molecules recovered from the chip with complement to A₁ (in the first round) were divided into equivalent portions. One portion was placed on the chip with complement to B₁ and the other portion was placed on the chip with complement to B₂. The target DNA molecules recovered from the chip with complement to A₂ (in the first round) were treated similarly. A cover slip was applied to each of the four chips to aid in the even distribution of target solution and to help reduce evaporation. Chips with cover slips were placed in humid chambers, and target molecules were allowed to hybridize to immobilized complements overnight. Following hybridization, excess target solution was removed with a brief 10 ml of 1 M NaCl rinse. Hybridized oligonucleotides were eluted as done previously, and reduced to dryness by rotary evaporation prior to resuspension in 100 μl of water.

Readout

Eluted oligonucleotides were amplified by PCR using HotStart Micro 100 reaction tubes (Molecular Bio-Products, San Diego, CA). Amplifications were carried out with a final volume of 50 μl containing 10 μl of oligonucleotide solution as template, 10× Easy-A reaction buffer (Stratagene, La Jolla, CA), 8 mM of each dNTP, 1 mM of each primer and 2 U Easy-A polymerase (Stratagene, La Jolla, CA). The PCR was performed with a DNA Engine (PTC-200 Peltier Thermal Cycler, MJ Research, Waltham, MA). An initial denaturation at 94°C for 2 min was followed by 35 cycles of amplification at 94°C for 40 s (denaturation), 45°C for 30 s (annealing) and 72°C for 30 s (elongation) and ending with a final extension step lasting 6 min at 72°C. Amplification products were visualized in a 3% agarose gel (Bio-Rad, Hercules, CA) with SYBR Green I nucleic acid gel stain (Molecular Probes, Inc., Eugene, OR). All gels were imaged using a Molecular Dynamics FluorImager 575 instrument.

PCR amplified DNA was extracted with a QIAquick Gel Extraction Kit (Qiagen, Valencia, CA) using a microcentrifuge following the manufacturer's protocol. Extracted DNA was subsequently cloned, following the manufacturer's protocol, with a TOPO TA Cloning Kit with PCR 2.1 TOPO vector (Invitrogen, Carlsbad, CA) and One Shot TOP10 Chemically Competent Escherichia Coli. Plasmid DNA was then purified with QIAprep Spin Miniprep Kit (Qiagen). Following an EcoRI digest (New England Biolabs, Beverly, MA) to determine the presence of the 84mer insert, purified DNA was submitted to the DNA Sequencing Laboratory, UW Madison Biotechnology Center.

PairFold and CombFold

In order to design words so that the stability of mismatched duplexes is low relative to the stability of perfect duplexes, we use the PairFold v1.1 program of Andronescu et al. (43,44). This program computes the minimum free energy (MFE) of secondary structures formed by each mismatched duplex (at standard conditions). PairFold incorporates the thermodynamic parameters of SantaLucia Jr (45) for stacked pairs and loops. PairFold employs a dynamic programming algorithm that is very similar to the Mfold server (46) for prediction of the MFE secondary structure of single RNA molecules, but is extended to handle pairs of molecules by including an initiation penalty for intermolecular interaction, as is done in the OligoWalk program of Mathews et al. (47). We also use PairFold to build a junction mismatch hybridization database (described later). To test whether long strands composed by concatenating several words do not form unwanted secondary structure, we use the CombFold v1.0 program of Andronescu et al. (48). This tool can efficiently find the minimum free energy secondary structure formed by any strand in a large combinatorial set (at standard conditions). If this structure has no base pairs, then it follows that all strands in the combinatorial set are predicted to have no unwanted secondary structure. The source code and precompiled libraries are available upon request from the authors (PairFold is publicly available at www.rnasoft.ca).

RESULTS AND DISCUSSION

Word length

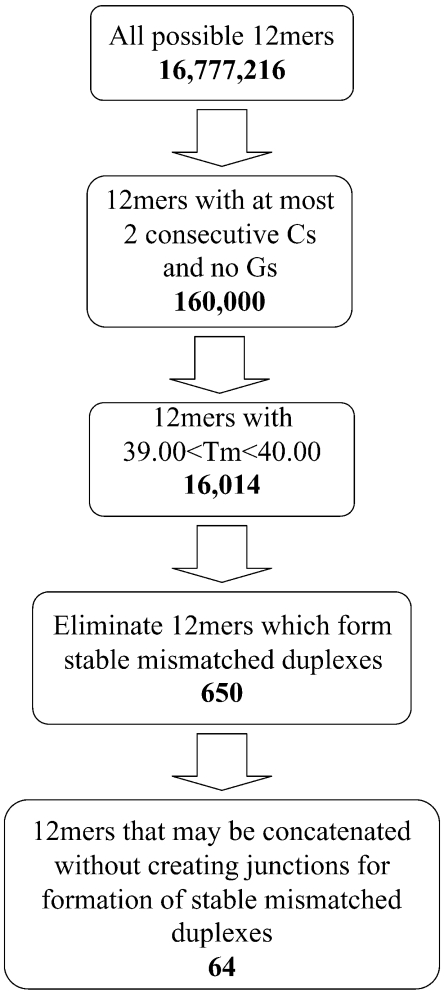
A schematic diagram of the algorithm employed here for word set design (Figure 1) illustrates the process used for the production of a combinatorial library of 65 536 unique DNA sequences. This library was formed by combining 64 individual 12mer DNA words (Table 1) into sequences of four tandem words. The choice of word length is based upon consideration of four major factors. First, it is desirable for the hybridization conditions to be within a practical range for experimental work. Second, if the total length of the DNA strands is less than ∼100 nt, it is reasonably straightforward to synthesize the strands by direct chemical synthesis, thereby avoiding the need for either enzymatic [e.g. ligation (36) or PCR (49)] or biological (e.g. cloning) methods. Third, the longer the word length the greater the number of possible sequences of that length, which provides a correspondingly greater pool from which to choose suitable word sequences. Finally, the size of the computational problem increases dramatically as word length increases, necessitating greatly increased computation time [the algorithm described in the accompanying manuscript overcomes the challenge of scaling by use of an efficient conflict-driven local search approach (23)]. The choice of word length thus involves careful consideration of all these facets of library design. The example 12mer and 16mer sets described here offer a reasonable balance between these conflicting factors. In the case of the 12mer set there are a total of 4¹² ≈ 17 million possible words. The algorithm is presented and discussed below for the case of 12mer; essentially the same approach was employed for generation of the 16mer word sets and is applicable, if desired, to other word lengths.

Eliminating Gs and limiting Cs

Once the choice of word length has been made, the algorithm consists of four successive steps of winnowing down the initial set of all possible sequences to a small final set of words. The first step is to eliminate all sequences with any Gs or more than two consecutive Cs. The decision to exclude the guanine nucleotide, G, was based on our inability to successfully generate (in silico) a combinatorial library that was free of secondary structure when G was allowed. Because of the tremendous loss of complexity that results by excluding G altogether, we first performed a systematic investigation of how we might include G. Using the nearest neighbor stabilities of Allawi and SantaLucia Jr (8), we created word sets where, certain nearest neighbor pairs were excluded. The stability of base pairs with specific nearest neighbors are as follows: GC > CG > GG > GA, GT, CA > CT > AA > AT > TA. We created three different types of sets. In the first set, we excluded words containing GC, CG or GG but allowed words containing GA and GT. We further eliminated GA in the second set and GT in the third set. The last set was essentially free of G except that some words were terminated in G. From these we created combinatorial libraries (using the methods described here) and analysed their secondary structure with the software program CombFold (50). In terms of free energy of secondary structure, each group of sets improved (more positive free energy for the most stable occurrence of secondary structure in a tandem word sequence) as the G-containing nearest neighbor pairs were eliminated. Only the final group of sets lacked significant secondary structure in the concatenated sequences since the only remaining sources of secondary structure emanate from short runs of As and Ts separated by Cs. We decided to also eliminate even the single terminal G from the sets as it added little to the available combinatorial diversity and simplified the word design problem. Similar conclusions have been reached by a number of other groups interested in the word design problem (51).

The need to eliminate words having more than two consecutive Cs stems from issues relating to the performance of robust hybridization reactions

There is ample evidence in the literature for formation of structures known as G-quartets (52) between oligonucleotides with multiple consecutive guanine nucleotides. Specifically, oligonucleotides with more than two consecutive Gs readily form these structures. Cs present in the word sets are mirrored by Gs in the word set complements, which are employed in all solution-phase and surface-based hybridization reactions. Oligonucleotides tied up in a G-quartet may then not be available for hybridization. In surface-based hybridization reactions, where complementary word sequences are immobilized on solid-supports in close proximity to one-another, this design aspect takes on special significance. In order to eliminate word-complements with more than two consecutive Gs, it was thus necessary to eliminate words with more than two consecutive Cs. This design criterion was also maintained at junctions between words. After these sequence elimination steps the set of possible sequences is decreased by approximately two orders of magnitude to ∼160 000 sequences.

Selection of T_m range

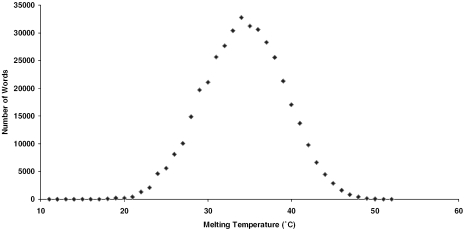
The remaining 160 000 DNA word sequences have a fairly broad range of melting temperatures that covers the approximate range from 10°C to 50°C (Figure 3). A one degree window centered near the peak of the distribution was selected in order that the sequences will hybridize similarly at a fixed temperature. For the 12mer set this yielded 16 014 words with melting temperatures in the range of 42.4–43.5°C.

Figure 3.

This distribution was generated by calculating the melting temperatures of all possible 12mer duplexes where each word was composed of only A, C or T and also where a maximum of two consecutive Cs is allowed. Temperature calculations were performed using the nearest neighbor parameters of Allawi and SantaLucia (8) with an oligo concentration of 10 nM and the concentration of salt set at 1 M NaCl.

Elimination of words that form stable mismatched duplexes

From this set of 16 014 possible word candidates we wished to find a subset of words none of which form stable mismatched duplexes with any other member of the subset or their complements. There are three types of mismatched duplexes to consider: word to word; word to word-complement; and word-complement to word-complement. Of the three types, the word to word-complement mismatched duplex type is the most stable and therefore the most important to avoid. The reduced alphabet {A,T,C} for words and {A,T,G} for complements significantly reduces unwanted word-word and complement-complement mismatch hybridizations. The task of identifying word sets where word to complement mismatch hybridizations are minimized is the heart of the problem in DNA word design. We will present below one heuristic approach to the development of the necessary word sets, and the accompanying paper presents an alternative route (23).

In order to develop the word sets it is necessary to define what difference in stability between the perfectly matched duplexes and the mismatched duplexes is acceptable. Ideally, one wishes to form only the desired perfectly matched duplexes and none of the mismatched duplexes under a given set of hybridization conditions. In reality one will not have a perfect discrimination between the two, but will have to accept some degree of cross-hybridization, with the acceptability thereby being dependent on the application. A related issue is the extent to which the desired hybridization reaction goes to completion, which is determined by the equilibrium constant for the reaction. An analysis of this problem is as follows:

Free energy gap

The free energy gap, δ, between perfect complements and mismatched duplexes is an excellent metric for describing the quality of a combinatorial library. The definition of δ employed here is essentially the same as the accompanying manuscript and somewhat more specific than the related measure δ* (23). Let w_i be a single-stranded DNA word sequence with perfect complement c_i. Here, δ describes the minimum free energy gap between a perfectly complementary duplex w_ic_i and the most stable mismatched duplexes involving w_i and c_i.

$$\begin{array}{c}\delta =\underset{1\le i\ne j\le N}{min}\{min[\Delta G°(w_i,c_j),\Delta G°(w_i,w_j),\Delta G°(w_i,w_i),\\ \Delta G°(w_j,c_i),\Delta G°(c_i,c_j),\Delta G°(c_i,c_i)]-\Delta G°(w_i,c_i\left)\right\}\end{array}$$ 1

Frequently, complements are immobilized on surfaces, which prevent them from interacting with one another with respect to mismatch duplex formation. In such cases, the free energies of formation between complements [ΔG°(c_i, c_j) and ΔG°(c_i, c_i)] can be neglected and Equation 1 reduces to

$$\begin{array}{c}\delta ={\displaystyle \underset{1\le i\ne j\le N}{min}}\{min[\Delta G°(w_i,c_j),\Delta G°(w_i,w_j),\Delta G°(w_i,w_i),\\ \Delta G°(w_j,c_i)]-\Delta G°(w_i,c_i\left)\right\}\end{array}$$ 2

Hybridization discrimination

A certain amount of mismatch hybridization will naturally accompany specific hybridization in systems where large numbers of different oligonucleotide sequences are mixed together. The term discrimination factor, D, used here is to describe the ratio of desired hybridization events (matched duplexes) to mismatch hybridization events (mismatched duplexes) in a competitive hybridization reaction where two different sequences are competing to bind with a third sequence. This value, in the context of a set of words and complements, represents the worst-case hybridization discrimination and can be used as a metric for comparison of expected hybridization performance among different word sets. Brackets [] in the following equations indicate equilibrium concentrations and N is the number of unique word sequences in the set.

$$D\equiv \frac{\left[\text{matched duplexes}\right]}{\left[\text{mismatched duplexes}\right]}.$$ 3

A systematic evaluation of all such competitive hybridization reactions in a word set is performed to identify the group of three sequences that have the minimum discrimination factor. The discrimination factor for the competitive hybridization of any two members of a DNA word set and a single word-complement can be calculated when the individual equilibrium expressions are coupled together as described below. Let w_i be a DNA word that is the perfect complement of c_i. Let w_j be a second DNA word that forms a mismatched duplex with c_i. The discrimination factor for c_i is D_ci, the ratio of correctly formed duplexes, w_ic_i, to mismatched duplexes, w_jc_i.

$$D_{c_i}={\displaystyle \underset{1\le i\le N}{min}}\left\{{\displaystyle \underset{1\le j\le N,j\ne i}{min}}\left[\frac{\left[w_i{c}_i\right]}{\left[w_j{c}_i\right]}\right]\right\}$$ 4

The equilibrium expression for duplex formation between the DNA word, w_i, and its perfect complement, c_i, is:

$$w_i+c_i{\displaystyle \stackrel{K(w_i,c_i)}{\iff }}{w}_i{c}_i.$$ 5

The equilibrium constant for that reaction is K(w_i,c_i). Analogously, the equilibrium expression for the formation of a mismatched duplex between an undesired DNA word, w_j, and the same complement, c_i, is:

$$w_j+c_i{\displaystyle \stackrel{K(w_j,c_i)}{\iff }}{w}_j{c}_i.$$ 6

The equilibrium constant for that reaction is K(w_j,c_i). The equilibrium constant K is related to free energy by the well known expression ΔG° = −RTlnK. Upon substitution of Equations 5 and 6 into the definition above (Equation 4) we arrive at a useful expression for D_ci that is a function of temperature, equilibrium concentration and free energy. Any interaction between w_i and w_j is assumed to be negligible because of the reduced alphabet {A,C,T} (23).

$$D_{c_i}={\displaystyle \underset{1\le i\le N}{min}}\left\{{\displaystyle \underset{1\le j\le N,j\ne i}{min}}\left[{\text{e}}^{[-\Delta G(w_i,c_i)+\Delta G(w_j,c_i\left)\right]/RT}·\frac{\left[w_i\right]}{\left[w_j\right]}\right]\right\}$$ 7

There is an analogous term, D_wi, that describes the discrimination in competitive hybridization of two complements, c_i and c_j, to a single word, w_i.

$$D_{w_i}={\displaystyle \underset{1\le i\le N}{min}}\left\{{\displaystyle \underset{1\le j\le N,j\ne i}{min}}\left[e^{[-\Delta G(w_i,c_i)+\Delta G(w_i,c_j\left)\right]/RT}·\frac{\left[c_i\right]}{\left[c_j\right]}\right]\right\}$$ 8

Thus, for the entire set of words and complements, the discrimination factor, Δ, is

$$\Delta ={\displaystyle \underset{1\le i\le N}{min}}\{D_{w_i},D_{c_i}\}$$ 9

This term, Δ, is used for comparison with other word sets.

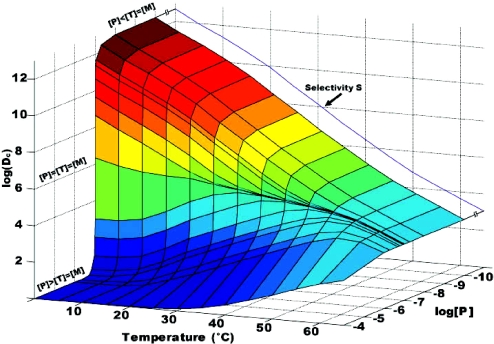
It is conventional to discuss competitive equilibria in terms of selectivity. The formal definition of selectivity, S, is the ratio of the temperature dependent equilibrium constants [i.e. S = K(w_i, c_i)/K(w_j, c_i)] (53). However, this parameter does not adequately reveal the impact that the relative concentrations of the reactive species have on the formation of the desired product. In reactions where the reactive species have similar concentrations, discrimination is often far from ideal. Two DNA words from the set of 16mer (Table 1) were chosen to aid in illustrating this point. Let w_i = TCT TAA TCA TAC CTT C, w_j = CAC TCT ATC AAT CAT A and c_i = G AAG GTA TGA TTA AGA. Also, let the concentrations of the two competing oligos be equal [w_i] = [w_j] = 1 × 10⁻⁷ M and let the concentration of the perfect complement of w_i, [c_i], vary around that value. These words were chosen because they have the smallest free energy gap between the perfectly complementary pair, w_ic_i and the mismatched duplex, w_jc_i. The graph of Equation 6 under these circumstances (Figure 4) reveals that the discrimination, D_ci, is highest (approaching the maximum selectivity) when c_i is the limiting reagent and lowest when c_i is present in excess. Any c_i that is not consumed in a reaction with w_i will be available to react with w_j and form the mismatched duplex, w_jc_i. This is the reason for the low discrimination where c_i is in excess.

Figure 4.

Discrimination, D_ci, (Equation 8) was calculated for the system of three oligonucleotides undergoing competitive hybridization with one another. Two oligonucleotides T = TCTTAATCATACCTTC and M = CACTCTATCAATCATA compete for hybridization to P = GAAGGTATGATTAAGA. The oligonucleotide P is perfectly complementary to T and forms a mismatched duplex with M. In this example, [T] = [M] = 1 × 10⁻⁷ M and [P] varies between 10⁻⁴ M and 10⁻¹⁰ M. Free energy calculations were performed with the assumption that hybridizations would be performed in 1 M NaCl. For reference, the temperature dependent selectivity, S, is shown as the blue line and is highlighted with an arrow. Discrimination, D_ci, is highest (approaching the maximum selectivity) when P is the limiting reagent ([P] < [T] = [M]) and lowest when P is present in excess ([P] > [T] = [M]). Any P that is not consumed in a reaction with T will be available to react with M and form the mismatched duplex, MP. This is the reason for the low discrimination.

Hybridization efficiency

Hybridization efficiency can be a critical factor when working with DNA word sets. Some applications that employ DNA word sets perform repetitive hybridization assays on the set. In such cases, a low hybridization yield can significantly limit the number of consecutive hybridizations that can be performed. In single step hybridization experiments, it is possible to drive the equilibrium forward by increasing either the DNA word concentration or DNA complement concentration. A useful working definition for hybridization efficiency is:

$$\text{Efficiency}\equiv E=\frac{\left[w_i{c}_i\right]}{\left[w_i\right]+\left[w_i{c}_i\right]}$$ 10

Heuristic Algorithm—the following section outlines an iterative process for winnowing down a large set of words to a smaller set, which has an acceptable free energy gap between perfectly complementary sequences and stable mismatches. Working oligonucleotide concentrations and hybridization temperature are required inputs for the winnowing process. For reasons having to do with an application of particular interest to our group, DNA concentrations of 10⁻⁷ M were selected, and the hybridization temperature was taken as T = 37°C. After several iterations, the original list of 16 014 words was reduced to 650, with δ = 2.87 kcal/mol and Δ = 23.2.

The heuristic employed to develop word sets is as follows:

1. The list of 16 014 word candidates is randomly shuffled.

2. The word that appears first in the randomly shuffled group of word candidates is selected as the first member of the word set and is denoted w₁.

3. The stability (free energy of formation) of the mismatched duplexes formed between w₁ and the remaining 16 013 words and 16 013 complements are calculated. A similar calculation is performed for c₁. Any word/complement that forms a mismatched duplex with either w₁ or c₁ having a free energy that differs from the free energy of the perfectly matched duplex w₁c₁ {ΔG°(w₁, c₁) − min[ΔG°(w₁, c_k), ΔG°(w_k, c₁)]} smaller than an arbitrary cut-off is eliminated. This leaves a set of word candidates somewhat reduced in size. Note, choosing a cut-off value is an iterative process with the goal being to increase the value as much as possible while retaining the requisite number of words in the final set.

4. The second word (w₂) is removed from the candidate list and placed in the word set.

5. Step 3 is repeated using w₂ and c₂ in place of w₁ and c₁ and the values for k adjusted for the smaller number of possible word candidates.

6. This process is continued until the initial list of word candidates is exhausted and the word set is complete. The size of the word sets produced in this manner depends in large part on the choice of a cut-off value. If the size of the set produced is unsatisfactory, the process may be repeated using a different cut-off value. In addition, the initial randomization and choice of the first word moderately influences the ultimate set size, albeit in an indeterminate manner.

Selection of words that may be concatenated without creating junctions for formation of stable mismatched duplexes

The junctions that are created when two words are concatenated together provide new sites for mismatch hybridization. Therefore, the set produced by the winnowing process just described is intentionally oversized compared to the number of unique words needed for formation of the combinatorial library. In that way, those words that produce junctions that are likely sources of mismatch hybridization can be avoided. The final stage in this example set design process is to reduce the set of 650 words to a set of 64 that can be concatenated without significant mismatch hybridization at junctions.

There are nine different varieties of mismatch hybridization in a combinatorial library that have the potential to compromise discrimination and overall hybridization efficiency (Figure 5). Possible mismatch hybridization Types A, B and C were addressed in the section above and will not be revisited here. Type D, in which a complement can potentially bind to a word junction, is the most significant possible junction-related mismatch hybridization. This reflects the fact that the complements contain stronger-binding G nucleotides that can potentially hybridize to the C-containing word junction sequences. The bimolecular interactions Types E and F do not involve word-complements, therefore do not possess the more stable G:C base pairs and thus are of lesser concern. The unimolecular interactions Types G, H and I also do not involve G:C base pairs and thus are also of less concern. Accordingly, the primary focus of the analysis of hybridization issues caused by junctions was on Type D interactions. It is necessary to point out that, for the sets described, complements are not permitted to be concatenated with one another to avoid having to consider the mismatch hybridizations that would occur as a result of creating complement-complement junctions.

Figure 5.

This is a schematic diagram that illustrates several of the most likely varieties of mishybridization. Mishybridization can occur between a set word (shown as a blue line) and word complement (red line) or any combination thereof. The thin black line connecting the word sequences (blue lines) indicates a junction. In practice, there is no special separation between words at the junction. Rather, there is one continuous sequence of nucleotides. The junction break is shown here for convenience. The short black vertical lines indicate hypothetical base pairings.

In analogy to the term δ, which is used to describe the free energy difference between hybridization and mismatch hybridization of individual words to their complements, the term τ is used to describe mismatch hybridization at junctions. Let w_iw_j be the concatenation of the two words w_i and w_j. Let c_k be the complement to w_k ≠ w_i, w_j. The free energy of mismatch hybridization between c_k and w_iw_j is ΔG°(w_iw_j, c_k). Then, for the set of all concatenated word pairs, w_iw_j, τ is

$$\tau ={\displaystyle \underset{1\le i,j,k\le N;i\ne j\ne k}{min}}\{\Delta G°(w_i{w}_j,c_k)-\Delta G°(w_k,c_k\left)\right\}$$ 11

The guiding principle for the organization of words into sets that can be concatenated into large combinatorial libraries is to maintain as large a value for τ as possible. This ensures that hybridization among perfectly complementary sequences is energetically favored compared with other pairwise interactions (mismatch hybridizations).

Junction mismatch hybridization database

There are 421 850 different possible junctions that can be formed between any two words chosen from a group of 650 [given by n(n − 1)] which is the case where concatenated word sequences cannot be among identical words, with n = 650). Determining the mismatch hybridization stability between these junctions and all of the 650 word-complements is a large but tractable problem that takes about two days to complete on a Pentium IV desktop computer. This was done, and for each word-junction the number of word complements that hybridized with stability above an arbitrary cut-off value was recorded along with the numerical identifier for each of the mishybridizing word-complements. (Note: On the first pass, the cut-off value is set equal to δ. On subsequent passes, it is adjusted up or down depending on the success of generating a combinatorial library of the requisite size.) The words were then placed in a ranked list ordered by the number of junction mismatch hybridizations in which they participated. Words that participated in the fewest number of junction mismatch hybridizations were ranked higher than words that participated in larger numbers of junction mismatch hybridizations. This information was stored in a searchable database and used as described below for the organization of the set into tandem word sequences.

The use of a junction interaction database is a distinguishing feature of this DNA word-set design algorithm. Its use allows a fixed number of words to be rapidly and efficiently organized into a tandem word set, the formation of which produces no junctions that are expected to participate in junction mismatch hybridizations. The process for selection and organization of a subset of words (64 out of 650) into a combinatorial library and which uses the junction interaction database is given below. The time required for this process is ∼1 s. In contrast, an exhaustive search through all possibilities (all sets of 64 words from a group of 650) would require 3.4 × 10⁸⁹ analyses.

Creating a combinatorial library

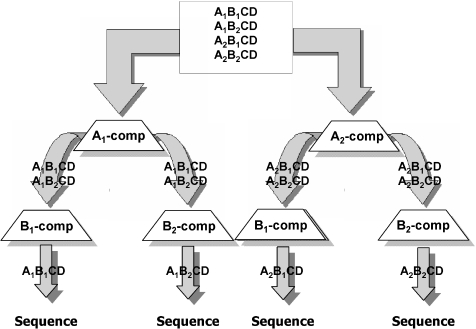
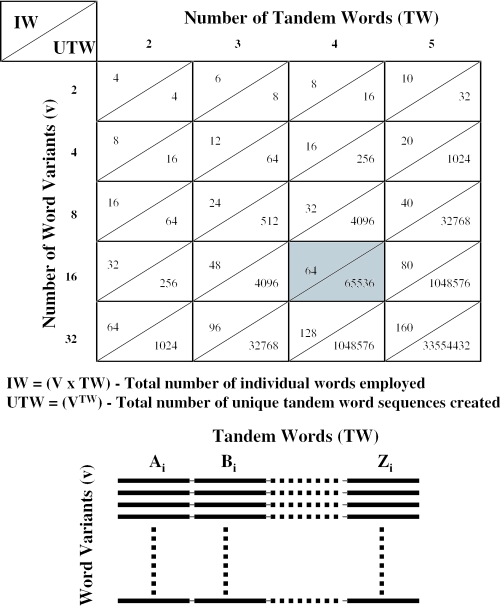
The final stage in the set creation was organization of the set into groups of words. The nature of the application will determine the degree of combinatorial complexity needed. Figure 6 shows different ways in which a large number of tandem word sequences can be created from a fairly small number of individual words, and Figure 6B shows the manner in which combinatorial sets of tandem words can be constructed. For illustrative purposes we will focus here on the development of a set of tandem word sequences using a 4 × 16 structure (four tandem words, with 16 variants at each position, producing 16⁴ = 65 536 different tandem word sequences from 64 individual words—see the panel of Figure 6A shaded in gray). There is a further restriction that all 64 words are unique. The following scheme produced sets (Table 1) with high hybridization discrimination and negligible secondary structure.

1. Choose A₁–A₁₆ randomly from the word candidate list (650 possibilities in this example).

2. Choose B₁ by finding the first word in the ranked junction mismatch hybridization database that does not create an A_i-B₁ junction (for all i) that hybridizes with stability above the cut-off value to any of the ‘A’ words or their complements. The complement of B₁ must also not hybridize with stability above the cut-off value to the A_i-B₁ junctions.

3. Choose B₂ similarly with the additional constraint that neither B₂ nor B2-complement hybridizes with stability above the cut-off value to the junctions of A_i-B₁ or A_i-B₂ for all i. B₁ and B1-complement are checked again to ensure that they do not hybridize with stability above the cut-off value to any junction formed by A_i-B₂.

4. Continue step three in an analogous fashion until all 16 words of group B are chosen.

5. The 16 words in group C are chosen next considering the interactions of C_i and C_i complement with both the junction A_i-B_j and the junction B_i-C_j for all i and j.

6. The 16 words in group D are chosen last, considering the interactions of D_i and D_i complement with the junctions A_i-B_j, B_i-C_j and C_i-D_j for all i and j.

In the above step 1, the decision to choose the first 16 words at random was motivated by the fact that each unique group would ultimately lead to a unique set of 64 words, the properties of which could be compared to all sets generated in that fashion. Sets created in this way were found to be superior to other previously published word sets (see discussion below). It is probable that selection of the first group of 16 by some other heuristic may be more effective and thus, this point remains as a subject for future investigations.

Figure 6.

Large combinatorial libraries of structure-free DNA sequences are constructed by linking small numbers of words together in a combinatorial fashion. The table above illustrates the number of tandem word sequences that can be created (lower right triangle in each table box) from a small number of words (upper left triangle in each table box). For each box, the number of tandem words linked together to form each sequence variant is listed across the top of the table whereas the number of word variants at each tandem word position is listed down the rows.

Designing primers for a combinatorial library

The details of primer creation are provided in Supplementary Material 2.

Comparison against published words sets

The potential for mismatch hybridization at junctions is significantly greater than at individual words. Therefore, the most challenging aspect in creating a combinatorial word library is the selection and organization of words into groups following the initial winnow down stages. Four word sets were created using the algorithm described above, and compared to four published word sets (22,36,40,41). The properties of these new sets are tabulated along with the properties of the published sets in Table 3. The free energy gap between perfect matches and mismatch hybridizations, δ, the width of the melting temperature distribution, ρ and the discrimination factor, Δ, were improved in all four cases. Two of the four published sets were originally designed to be used in combinatorial libraries. The analysis of the potential for mismatch hybridization at junctions revealed an improved value for τ in the newly created sets. Again, this is the most challenging aspect and it required a slight reduction of δ to achieve such high values for τ.

In addition, two new sets were created for direct comparison to the algorithm that is presented in the accompanying manuscript (23). The free energy gap between perfect matches and mismatch hybridizations, δ, the width of the melting temperature distribution, ρ and the discrimination factor, Δ, were slightly better in the Tulpan sets. However, the value for τ is better for the sets created with the algorithm presented above. A comparison of the values of δ and τ indicate that mismatch hybridization at junctions is more limiting than that between individual words and complements. Therefore, the sets with greater value for τ can be expected to outperform sets with lower value for τ. Large values for τ were obtained at the expense of the free energy gap between perfect matches and mismatch hybridizations, the width of the melting temperature distribution, and the discrimination factor. This is the natural consequence when a large intermediate set of words is maintained for use in the final combinatorial library assembly.

Our companion paper presents a method of obtaining large sets of non-interacting DNA sequences that emphasizes speed, an advantage as larger and larger sets become needed. The data in Table 2 support the nearly equivalent effectiveness of both algorithms at producing excellent word sets as determined by the figures of merit. With that said, the algorithm described here provides important insights into the thermodynamic factors that govern selection of non-interacting sets. These insights should serve as the foundation of new algorithms for word set creation.

Temperature dependence of discrimination factor

Discrimination in competitive hybridization can be enhanced by proper choice of hybridization reaction temperature. At 37°C, Δ for the 16mer S8 set (Table 1B) has a modest value of 4740. However, when the hybridization temperature is reduced to 10°C, Δ increases more than 20 times to a value of 107 597. This is based on the assumption that the number of perfectly complementary target molecules is the same as the number of complements. When this assumption is valid, lowering the hybridization temperature results in a significant reduction in false hybridization events and improved hybridization efficiency. However, when the number of perfectly complementary target molecules is smaller than the number of complements, raising the hybridization reaction temperature can provide increased discrimination at the expense of lower hybridization efficiency.

Experimental validations

The predicted hybridization behavior was experimentally verified on selected members of the sets using standard UV hyperchromism measurements of T_ms. Additional experimental validation was obtained by using the sequences in formulating and solving a small example of a DNA computing problem.

When you have two perfectly matched complementary oligonucleotides whose concentrations are not equal, the oligonucleotide in excess are available to bind with mismatched complements present in the solution, which can lead to a significant loss of hybridization discrimination. In contrast, the oligonucleotide present at a lower concentration will be bound to its perfectly matched complement almost quantitatively, thus exhibiting a high degree of hybridization discrimination. It is therefore essential, when designing specific hybridization reactions, to closely control the relevant oligonucleotide concentrations.

T_m measurements

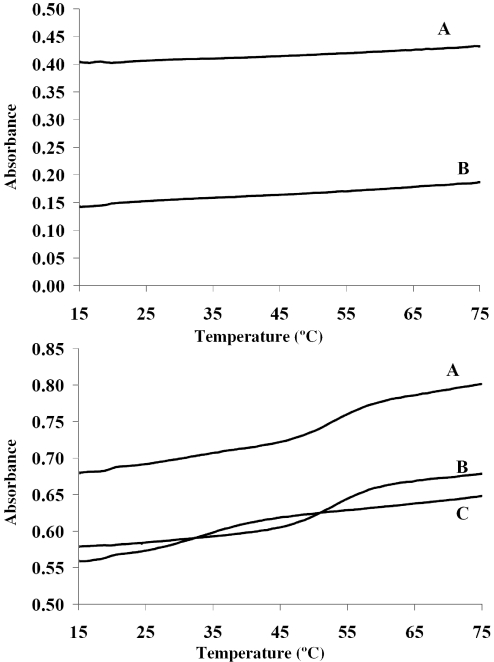
The PairFold software was used to screen the entire 64 word 12mer set to identify the word and word-complement pair that is most likely to non-specifically hybridize to one another (the worst-case mismatch hybridization in the entire word set). The worst performing pair identified in the 12mer set shown in Table 1 was the C₂ word and the A₉ word-complement, which is denoted as A_9C. Three additional words were chosen randomly (A₁₂, B₄ and D₄). These four words were used to construct the A₁₂C₂B₄D₄ 48mer tandem word sequence. Three melting curve determinations were performed along with two control experiments (Figure 7). In the first experiment, the melting temperature of the duplex formed between the 48mer target and the perfectly complementary 12mer, C_2C, was measured (Figure 7 top panel B). In the second experiment, the melting temperature of the duplex formed between the 48mer and the non-complementary 12mer, A_9C was measured (Figure 7 top panel C). In the third experiment, the melting behavior of the 48mer in an equimolar mixture with both the complementary and non-complementary 12mers was analysed (Figure 7 top panel A). Control melting experiments were performed on solutions of each complementary oligonucleotide and tandem word sequence in isolation (Figure 7 bottom panel). The sample words and concatenated word sequence performed in accordance with our expectations based upon the calculated melting temperatures. Control experiments displayed no evidence of secondary structure or intermolecular mismatch hybridization. Namely, absorbance versus temperature curves for the various sequences in isolation were flat throughout the evaluated temperature range. For the perfectly complementary duplex, the experimental data yielded a melting temperature of 55°C (50% melted based on linear fits to double-stranded and single-stranded lines), in accordance with the calculated melting temperature of 55°C. The melting temperature of the duplex formed between the 48mer and the mishybridizing 12mer was 35°C, also in agreement with our calculations. That 20°C difference is expected to be the narrowest gap between any perfectly complementary sequence and any mishybridizing sequence. In the final experiment, both 12mers were mixed with the 48mer at equimolar concentrations to set up a competitive hybridization as would be found under many normal experimental situations. The melting behavior showed no signs that the mishybridizing duplex had occupied any of the available binding sites on the 48mer. The melting behavior of this mixed solution closely matched that of the solution containing only 48mer and perfectly complementary 12mer. This demonstrates a high degree of discrimination for this set.

Figure 7.

Top Panel: Melting Temperature Experiments. A. Competitive Hybridization—the melting behavior of the 48mer in an equimolar mixture with both the complementary and non-complementary 12mer; B. Perfect match—the melting temperature of the duplex formed between the 48mer target and the perfectly complementary 12mer, C2C; and C. Mismatch—melting temperature of the duplex formed between the 48mer and the non-complementary 12mer, A9C. Bottom Panel: Control melting experiments were performed on solutions of each oligonucleotide in isolation (A, 48mer; B, 12mer).

Illustrative DNA computation

A small example DNA computation was performed using words chosen randomly from one of the created DNA word libraries (see Materials and Methods for an explanation of the DNA computing experiment Figure 1). In the first round of the computation, the complete library mixture was applied to two separate chips. One chip had a word-complement (Table 4) to A₁ immobilized on the surface. The other chip had a word-complement (Table 4) complementary to A₂ immobilized on the surface. Each chip captures two of the four original library members. Chip one probes anneal to sequences containing A₁ and chip two probes anneal to sequences containing A₂. Targets that hybridized to each chip were collected and divided into two separate but equivalent sub-populations. These in turn were placed on one of two different chips that were modified either with the complement to B₁ or the complement to B₂. Each of the four final chips was expected to yield one of the four species present in the original library. The oligonucleotides collected from the four chips were PCR amplified and sequenced in duplicate. In each case, the DNA sequence obtained matched the expected sequence, thus yielding the correct result.

CONCLUSION

We have demonstrated a completely thermodynamic approach to combinatorial DNA word library design. Elements from a library that was created using this approach were shown to perform well in experimental tests of melting behavior and in a small example of a DNA computing problem.

SUPPLEMENTARY MATERIAL

Supplementary Material is available at NAR Online.