Abstract
We describe a new algorithm for design of strand sets, for use in DNA computations or universal microarrays. Our algorithm can design sets that satisfy any of several thermodynamic and combinatorial constraints, which aim to maximize desired hybridizations between strands and their complements, while minimizing undesired cross-hybridizations. To heuristically search for good strand sets, our algorithm uses a conflict-driven stochastic local search approach, which is known to be effective in solving comparable search problems. The PairFold program of Andronescu et al. [M. Andronescu, Z. C. Zhang and A. Condon (2005) J. Mol. Biol., 345, 987–1001; M. Andronescu, R. Aguirre-Hernandez, A. Condon, and H. Hoos (2003) Nucleic Acids Res., 31, 3416–3422.] is used to calculate the minimum free energy of hybridization between two mismatched strands. We describe new thermodynamic measures of the quality of strand sets. With respect to these measures of quality, our algorithm consistently finds, within reasonable time, sets that are significantly better than previously published sets in the literature.
INTRODUCTION
The design of DNA and RNA sequences is a key step in many biotechnological applications. Uses of DNA microarrays rely on accurate design for probes that are immobilized on a surface and bind specifically to complementary targets in a complex solution. In the case of universal DNA microarrays, probes are not designed to bind to a genomic sequence or product, but instead probe complements are ligated to the genomic sequences, and the ligated product is captured on the array via specific hybridization between the probe and its complement (1). DNA strands are also designed for use in DNA-templated organic synthesis and DNA display, whereby the ‘template’ DNA strands direct the production of a library of small polymers (2,3). In DNA computing experiments (4), short oligonucleotides, called words, are units of information storage. Words are concatenated into long strands which store several bits of information. In a surface-based computation (5), words, or their complements, are typically immobilized on a planar surface—just like oligonucleotide probes on a DNA microarray chip. In this paper, we consider the problem of designing moderate-sized, high-quality sets of strands for such applications. For notational consistency with the accompanying paper (6), in the context of microarray applications, we use word to mean a probe and word complement to mean a target, and strand design may refer to design of words or word complements. In what follows, we will focus on design of words, and they are meant to be attached to a surface.
Specific hybridization between a word and its complement is the means for reading bits of information in a DNA computation and for attaching data to a microarray. Therefore, it is important that the word oligonucleotides are designed so as to (i) maximize desired hybridization, i.e. specific hybridization between a word and its perfect complement, and (ii) minimize undesired hybridization, i.e. non-specific cross-hybridization between a word and the complement of a distinct word, or between two complements under fixed environmental conditions such as temperature. In this work, we assume that words are immobilized on a surface and cannot hybridize to each other.
To design good strand sets computationally, it is important to have a reliable predictor of the quality of a set—that is, how well the set meets goals (i) and (ii) experimentally. With respect to a given measure of quality, a key algorithmic challenge is to design a high-quality strand set, when the length of the strands and the size of the set are specified. An alternative formulation of the challenge is to design a set of strands of a given length whose quality meets a certain threshold, and which is as large as possible.
This strand design problem is computationally difficult because the size of the solution space—all possible sets of strands of the specified length and size—can be enormous (e.g. for strands of length 10, there are more than 10370 strand sets of size 100), and there is no known efficient procedure that is guaranteed to find optimal strand sets even for the simplest design criteria. As a result, heuristic algorithms are used for strand design.
Combinatorial criteria have been widely used in the design of word sets (7–12); criteria include uniform GC-content across words (so that desired hybridization between words and their complements have similar melting temperature) and a large number of mismatches between two words. In addition, heuristic algorithms which search for word sets satisfying such combinatorial criteria have been proposed. Of these, Tulpan et al. (13) did an empirical evaluation of a stochastic local search algorithm and showed that the algorithm could find sets whose quality (measured using the combinatorial criteria) matched or exceeded previously reported constructions.
However, combinatorial criteria alone can be a poor measure of the quality of a set. Garzon et al. (14) and Rose et al. (15) proposed thermodynamically based measures of quality that are based on statistical mechanics principles. But it is difficult to computationally measure the quality of a set using their criteria for many reasons. First, the evaluation of all possible structural configurations of the reactants and products present in a reaction is computationally intractable. Second, even if the sets of thermodynamic parameters for all possible nearest-neighbor interactions (including all sizes of internal and multi-loops) would be completely known, the direct calculation of the ‘computational incoherence’ measure introduced by Garzon et al. requires the computation of the concentrations of all possible reactants and products of a reaction. To obtain the values of all concentrations in a generalized hybridization reaction, where all products, reactants and their alternate states coexist, it is necessary to solve massive systems of coupled quadratic equations, which is still a challenge nowadays.
Fan et al. (1) used thermodynamic criteria for design of probes for universal microarrays, but provided little detail of their method or design criteria. Penchovsky and Ackermann (16) combined combinatorial and thermodynamic criteria to design sets of sequences for molecular computations. They required that the melting temperature of words in a set lie within a small range, in order to maximize desired hybridization. In addition, they introduced a new ‘free energy gap’ measure of the quality of a set, which is denoted by δ* throughout our paper: to avoid undesired hybridization, the gap between the largest MFE (minimum free energy) of any duplex formed from a word and its complement, and the smallest MFE of any mismatch duplex formed from a word and the complement of a distinct word, should be as large as possible (δ* is defined precisely in Materials and Methods). They also developed a heuristic algorithm to design word sets. A weakness of their algorithm is that their means for measuring the free energy of a duplex secondary structure with mismatches relies on a program for measuring the free energy of a single-stranded molecule, requiring the linking of the strands with an artificial hairpin structure. Another weakness of their random search algorithm lies in the search strategy, which works as a generate-and-test mechanism (a simplification of hill climbing)—this type of simple search mechanism is generally known to achieve poorer results than more advanced stochastic local search methods, such as the one underlying the strand design algorithm presented here (17). Also, Penchovsky and Ackermann do not provide comparisons of the quality of sets obtained using their algorithm with those constructed using previous methods.
The main contribution of this paper is a new algorithm for design of strand sets, which produces high-quality sets within a reasonable running time. The algorithm builds on that of Tulpan et al. (13), but takes thermodynamic as well as combinatorial quality criteria into account in a flexible way. The PairFold software of Andronescu et al. (18,19) is used to calculate the minimum free energy of a duplex, in a manner that is more accurate than the approach of Penchovsky and Ackermann. Our algorithm uses a stochastic local search approach to heuristically search for good sets, which is known to be effective in solving comparable complex search problems (17).
To test the quality of our algorithm, we compare sets produced by our algorithm with seven sets from the literature, in the following referred to as ‘control sets’. Braich et al. (20) found the solution of an NP-complete problem on a DNA computer, using a set of 40 15mers. Brenner et al. (21) used a set of 8 4mers as a DNA vocabulary that helps to build a larger library of longer strands (∼17 million 32mers), which in turn were used to identify and extract genes that are differentially expressed. Faulhammer et al. (22) used an RNA library of 20 15mers to solve an instance of a computationally hard problem (‘Knights Problem’). Frutos et al. (23) developed a DNA set of 108 8mers, which can be used to store and manipulate information in DNA molecules attached on surfaces. Penchovsky and Ackermann (16) developed a set of 24 16mers, which can be used to encode binary information in DNA molecules. Shortreed et al. (6) developed two sets of 64 12mers and 16mers, which can be used to encode large amounts of information using DNA strands.
We used our algorithm to design both sets of the same size and satisfying the same constraints, but of higher quality as the seven control sets, and also to design sets of the same quality but of larger size than the control sets. We incorporated the combinatorial, melting temperature and other thermodynamic design criteria used in the design of the control sets. To compare the quality of the sets generated by our algorithm with the control sets, we use a variant of the free energy gap criterion proposed by Penchovsky and Ackermann (Materials and Methods for details), as well as new measures, introduced in this paper [and in the accompanying paper (6)], of the pairwise sensitivity, specificity and discrimination of pairs of words or complements.
We consider a system with one word wi and two competing complements ci and cj, which reaches equilibrium. We use a notion of pairwise sensitivity to measure the degree to which, when in competition with cj, the complement ci properly hybridizes to the word wi, and a notion of pairwise specificity to measure the degree to which the complements cj remain unhybridized (and thus free to bind with wj). We also use a notion of pairwise discrimination that is the ratio [wici]/[wicj] of concentrations of desired versus undesired hybridizations to the word wi.
We obtain sets that are at least as good as the respective control sets in all cases, and significantly better in most cases. For example, Ackermann and Penchovsky reported a set of 24 words of length 16, with a free energy gap δ* of 8.12 kcal/mol, whereas our algorithm produced a set of 24 oligos of length 16 satisfying the same combinatorial constraints as that of Penchovsky and Ackermann, but having a narrower melting temperature range, a free energy gap δ* of 9.2 kcal/mol, and a pairwise discrimination that is 1.6 times better. Also, our algorithm produced a set of 44 strands of roughly the same quality as the Penchovsky and Ackermann set, yet whose pairwise discrimination is 1.2 times bigger. Overall, we obtained sets that improve on the free energy gap δ* from 0.77 kcal/mol for the set by Brenner et al. (21), to 4.81 kcal/mol for the set by Faulhammer et al. (22).
Although our algorithm and analysis focus on the design of word sets when the measure of quality is based on interactions between pairs of words and/or complements, in DNA computing applications, it is also important that when the words are concatenated to store several bits of information, complements are unlikely to hybridize anywhere on the longer strands (including junctions between pairs of words), and that the longer strands do not form undesired secondary structure. We developed a heuristic approach for arranging strands in a set, and also report on additional measures of the quality of sets of concatenated strands. In some, but not all, cases, we were able to obtain improved partitionings of the control sets using our algorithm. In Discussion, we suggest ways in which better partitionings might be possible.
In the following section, we describe our algorithm, the combinatorial and thermodynamic design criteria that are incorporated into our algorithm, and our measures of quality of word sets. We then provide a detailed analysis of our results, compared with sets previously reported in the literature.
MATERIALS AND METHODS
Throughout the paper, we use symbols w1,w2, …, wk to denote words and c1,c2, …, ck to denote the corresponding complements. Thus, word wi and complement ci form a perfect match (duplex), whereas word wi and complement cj, where j ≠ i, and complements ci and cj, form mismatches. In this paper, we design for strands attached to surfaces, and we call them words, thus being consistent with the accompanying paper (6).
Design constraints
Our algorithm can design a set S of equally long DNA strands, being either words or complements, where S is of specified set size N. In this section, we list the combinatorial and thermodynamic constraints that are supported by our algorithm. The user of the algorithm may choose which constraints should be used in the design of a set. Table 1 (see ‘In silico experimental protocols’) summarizes which of these constraints have been previously used in the design of control sets.
Table 1.
Control sets used as a basis for comparison with the results obtained from our algorithm
| S1 Braich et al. (20) | S2 Brenner et al. (21) | S3 Faulhammer et al. (22) | S4 Frutos et al. (23) | S5 Penchovsky and Ackermann (16) | S6 Random | S7 Shortreed et al. 1(6) | S8 Shortreed et al. 2(6) | |
|---|---|---|---|---|---|---|---|---|
| Control set: original constraints | ||||||||
| Word length | 15 | 4 | 15 | 8 | 16 | 16 | 12 | 16 |
| No. of words | 40 | 8 | 20 | 108 | 24 | 24 | 64 | 64 |
| C1 | ✓ | ✓ | ✓ | ✓ | ||||
| ≥4 mismatches | ≥3 mismatches | maximize mismatches | ≥4 mismatches | |||||
| C2 | ✓ | ✓ | ||||||
| ≥4 mismatches | ≥4 mismatches | |||||||
| C3 | ✓ | |||||||
| ≤7 matches | ||||||||
| C4 | ✓ | |||||||
| ≤7 matches | ||||||||
| C5 | ✓ | ✓ | ||||||
| 35.33% | 25.00% | |||||||
| C6 | ✓ | ✓ | ✓ | ✓ | ||||
| CCC | CCC | |||||||
| 5H | CCC (5′,3′ ends) | CC (5′,3′ ends) | CC (5′,3′ ends) | |||||
| C7 | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | ✓ | |
| A,C,T | A,C,T | A,C,T | A,C,T | A,C,T | A,C,T | A,C,T | ||
| T1 | ✓ | |||||||
| Implicit | ✓ | ✓ | ||||||
| T2 | ✓ | ✓ | ✓ | |||||
| T3 | min value: −6.46 ≥ −8.24 | min value: −2.62 ≥ −2.79 | min value: −4.50 ≥ −5.48 | ✓ | ✓ | |||
| Implicit | max value: −0.07 ≥ 0.00 | |||||||
| T5 | ✓ | ✓ | ✓ | ✓ | ||||
| average = 45°C | range of ±1.5°C | 1°C range | 1°C range | |||||
| Control sets: extrapolated constraints | ||||||||
| T1 range (kcal/mol) | [−16.80, −13.57] | [−1.96, −1.01] | [−17.56, −11.63] | [−8.95, −6.50] | [−17.94, −16.84] | [−19.31, −12.74] | [−12.66, −11.78] | [−16.42, −15.45] |
| T2 range (kcal/mol) | [−9.29, −0.22] | [−1.86, 0.00] | [−7.98, −1.29] | [−6.83, 0.00] | [−8.72, −2.26] | [−8.35, −0.86] | [−8.94, −0.93] | [−7.62, −1.10] |
| T3 range (kcal/mol) | [−4.48, 0.00] | [−0.64, 0.00] | [−5.02, 0.00] | [−8.24, 0.00] | [−2.79, 0.00] | [−5.48, −0.00] | [−5.06, 0.00] | [−9.06, 0.00] |
| T5 range (°C) | [46.64, 55.75] | [−67.19, −48.07] | [40.87, 58.20] | [17.06, 27.34] | [55.15, 58.65] | [43.56, 62.23] | [42.38, 43.50] | [51.81, 52.77] |
Each column of the table, other than the leftmost, corresponds to one set. Each column header gives a set ID and, for all but set S6, a reference to the paper in which the set was published. The next two rows report the strand length and the number of strands in each set. Following these, there is one row per type of combinatorial or thermodynamic constraint C1 to T5 (except for T4—see Materials and Methods for details). A check mark in a column indicates that a constraint of the column's type was enforced when designing the set, and further information about the composition of the strands is given where available. The second part of the table describes thermodynamic properties of control sets. For each set, the rows of the table give the free energy ranges corresponding to constraints T1 (desired word–complement interactions), T2 (undesired word–complement interactions) and T3 (undesired complement–complement interactions), respectively and the melting temperature range corresponding to constraint T5. Note that these thermodynamic constraints were not used as design constraints for the control sets, other than those of the accompanying paper of Shortreed et al. (6).
Combinatorial constraints
C1: Direct mismatches
The number of mismatches in a perfect alignment of two strands must be above a given threshold. Here, in a perfect alignment of bases from two strands, the ith base of the first strand is aligned with the ith base of the second strand, and a mismatch is an alignment of two distinct bases. For example, G aligned with A, C, or T is a mismatch whereas G aligned with G is a match. (This constraint can be applied to pairs of words only, to pairs of complements only or to both pairs of words and complements.)
C2: Complement mismatches
The number of mismatches in a perfect alignment of a strand and a complement of a strand must be above a given threshold.
C3: Slide mismatches
The number of mismatches in a slide of one strand over another must be above a given threshold. A slide of strand S over another strand S′ (both of equal length) is an alignment of S and S′, in which, for some i, the first base of S is aligned with the ith base of S′, the second base of S is aligned with the (i+1)th base of S′, and so on, so that the first i−1 bases of S′ and the last i−1 bases of S are unaligned. For example, the strands S = 5′-ACC-3′ and S′ = 5′-TGC-3′ can overlap in three, two, one or zero positions. If i = 2 (we start counting from zero, i.e. no slides), base ‘A’ of strand S is aligned with base ‘C’ from strand S′.
C4: Consecutive matches
The maximum number of consecutive matches between all slides of one strand over the other must be in a given range.
C5: GC content
The number of Gs and/or Cs in a word must be in a given range. For example, all words presented in (24) have 4, 5 or 6 Cs.
C6: Forbidden subsequences
Each strand must not contain given undesired subsequences either along the whole strand, at the 5′ and 3′ ends and/or in the middle of the strand, as required.
C7: Alphabet size
All strands must contain bases belonging to a given non-empty subset of the alphabet {A,C,G,T}. It is a common practice to design DNA strands over the {A,C,T} alphabet in order to minimize undesired structures, such as G-quartets, that can be caused by the presence of Gs.
Constraint C5 can be used to attain desired hybridization (goal 1). Roughly, the stability of a word–complement pair increases as the content of Gs and Cs within sequences increases. Constraint C5 is also used to ensure uniform melting temperatures across desired word–complement pairings. Constraints C1–C4, C6 and C7 can be used in various combinations to avoid undesired hybridization (goal 2). As is widely known, the strength of hybridization between two sequences (or between bases of the same sequence) depends roughly on the number of nucleotide bonds formed (longer stems are more stable than shorter ones; this is modeled by C1–C4 and C6), and on the types of nucleotides involved in bonding (Cs and Gs bind more strongly than As and Ts, due to an extra hydrogen bond; this is modeled by C7).
Thermodynamic constraints
These constraints rely on the thermodynamic nearest-neighbor model introduced by Crothers and Zimm (25) and Tinoco and coworkers (26) in the 1960s. We use the DNA parameters of SantaLucia (27) (some parameters are unpublished) and the PairFold v1.1 implementation of Andronescu et al. (18) to calculate minimum free energies of duplexes. We use the parameters and equation (3) of SantaLucia and Hicks (28) to calculate melting temperature, assuming a 1 M salt concentration and 1 × 10−7 M concentration of both words and complements (for a total concentration of 2 × 10−7 M). The melting temperature is only calculated for perfectly matched duplexes.
Throughout, we use the following notation. T denotes the temperature of the reaction, R = 1.98717 cal/(mol K) is the gas constant, ΔG0(x,y) is the minimum free energy of the duplex xy at standard conditions, and TMi denotes the melting temperature of word wi.
T1: Perfect match free energy
The free energy of a word and its complement must be in a given range: for any i,
T2: Complement mismatch free energy
The free energy of a word and the complement of a distinct word must be in a given range: for any i, j ≠ i,
T3: Complement–complement mismatch free energy
The free energy of a complement–complement duplex must be in a given range: for any i, j,
T4: Word–word mismatch free energy
The free energy of a pair of words must be in a given range: for any i, j,
T5: Melting temperatures
The melting temperature for each word and its complement must be in a given range: for any i,
Constraint T5 can be used to select words with uniform melting temperatures, with a higher degree of accuracy than by using GC content (C5), by choosing TMmax5 − TMmin5 to be small. Constraint T1 can further help in selecting sequences by measuring the strength of the bonds (free energy) that form between each sequence and its perfect match, regardless of the number of matches or the individual nucleotides that take part in bonding (16).
Constraints T2, T3 and T4 are used to restrict undesired hybridization, which can occur between a word and the complement of a different word (T2), or between two distinct complements (T3) or words (T4). Typically, the given ranges should not overlap with the range for T1. (Because in this work, we focus on applications where words are affixed to a surface, we do not consider constraint T4 for the set designs used in our empirical study, but the current version of our set design software supports its use.)
Evaluation criteria
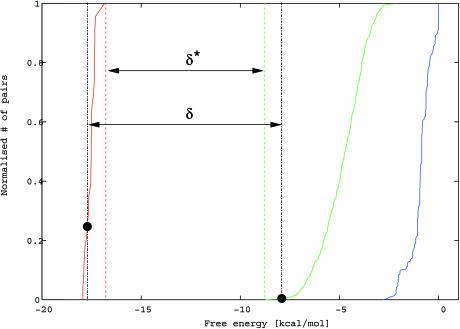
We use several measures to gauge the quality of a word set. Two of them account for the free energy gaps, denoted by δ and δ*. δ represents the free energy gap between perfect matches and imperfect matches of a word (see Figure 1). For every word wi in the set, we consider the difference between the perfect match free energy, ΔG0(wi, ci), and the minimum free energy of a mismatch involving wi or ci. The minimum such difference, over all wi in the set, is denoted by δ:
| 1 |
Figure 1.
Positive free energy gaps of correct and incorrect word–complement pairs for set S5 Penchovsky. The three curves represent (from left to right) the cumulative distribution of the free energy values of all correct word–complement hybrids, of all incorrect word–complement hybrids and of all (incorrect) complement–complement hybrids. The two dots represent the specific values of i and j that determine the free energy gap as defined in Equation 1.
Note that the rightmost min takes into account three types of mismatches, namely mismatches between ci and a word wj with j ≠ i, between cj and a word wi with j ≠ i, and also mismatches between a complement ci and itself or another complement cj.
A related quantity of interest, previously proposed by Penchovsky and Ackermann (16), is δ*, defined as follows. Let
| 2 |
| 3 |
| 4 |
Then
| 5 |
The value δ* is of interest because the thermodynamic constraints T1–T3 allow one to directly design a set for which δ* is above a certain threshold. Moreover, since δ ≥ δ*, it follows that δ* provides a useful lower bound on the (true) energy gap δ between competing desired and undesired hybridizations. Penchovsky and Ackermann (16) use δ* as a measure of the quality of their set. Roughly speaking, the larger δ and δ* are, the larger the gap between the free energy of desired and undesired hybridizations, and thus the better the set is.
Then, we measure the melting temperature interval width, ρ, for perfect matches (word–complement duplexes), which is defined as the difference between the highest and the lowest melting temperature values of all word–complement duplexes.
| 6 |
The third type of measure that we use provides insight on the relative abundance of desired versus undesired interactions. To define these measures, which are pairwise specificity, sensitivity and discrimination, we consider the following interactions, which can occur between words and complements in a set:
I1: wi + ci ⇌ wici
A word wi perfectly matches the corresponding complement ci (desired hybridization).
I2: wi + cj ⇌ wicj
A word wi imperfectly matches a complement cj, where i ≠ j (undesired hybridization).
I3: ci + cj ⇌ cicj
A complement ci imperfectly hybridizes with a complement cj, where i ≠ j (undesired hybridization).
I4: wi + wj ⇌ wiwj
A word wi imperfectly hybridizes with a word wj, where i ≠ j (undesired hybridization).
I5: c ⇌ cfolded
The MFE structure for a complement contains base pairs, i.e. a subsequence of a complement c hybridizes with another subsequence belonging to the same complement (undesired hybridization).
I6: w ⇌ wfolded
The MFE structure for a word contains base pairs, i.e. a subsequence of a word w hybridizes with another subsequence belonging to the same word (undesired hybridization).
For simplicity, we ignore interactions among three or more strands. (A limited form of interaction between three strands will be discussed later, in Discussion). In the following analysis, we will also ignore interactions of type I4, as in a surface-based application, words are fixed on surfaces and so cannot interact with each other. However, the method of analysis could be extended to model such interactions if needed. (We note that our algorithm can design strand sets so that undesired interactions between words are unlikely; it is just in the modeling step that such interactions are ignored.) We will also ignore for now undesired hybridization of types I5 and I6, and address these separately in Discussion.
Therefore, to model competition between a word wi and two distinct complements ci and cj, we consider a 6-phase model:
| 7 |
| 8 |
| 9 |
Equations 7–9 describe desired (I1) and undesired (I2, I3) hybridization between words and complements.
Let [wi]0, [ci]0 and [cj]0 represent the initial strand concentrations (which are known quantities, i.e. 1 × 10−7 M each in our case), and let [wi], [ci] and [cj] represent the equilibrium strand concentrations (unknown quantities). Let [wici], [wicj] and [cicj] be the equilibrium concentrations for the hybridization products wici, wicj and cicj. The following system of equilibrium equations describes the relationships between concentrations, free energies and reaction temperature for single strands and hybrids.
| 10 |
| 11 |
| 12 |
| 13 |
| 14 |
| 15 |
In our software, the system of Equations 10–15 is implemented and solved using Maple v9.
We are interested in maximizing the number of complements ci that are properly hybridized to wi, as opposed to being unhybridized or hybridized to another cj. In this context, we consider duplexes wici to be true positives, and single strands ci and duplexes cicj to be false negatives (since in these, ci is not hybridized as desired), and so we define the pairwise sensitivity as follows:
| 16 |
Similarly, we are interested in maximizing the number of complements cj that are not hybridized. In this context, we consider single strands cj to be true negatives, while duplexes wicj and cicj are considered false positives (since in these cases, there is undesired hybridization involving cj). Thus, we define the pairwise specificity as follows:
| 17 |
Clearly, pairwise sensitivity and specificity values are always between 0 and 1; the closer these values are to 1, the better the quality of the set, at least with respect to competition between ci and cj for wi.
We are also interested in maximizing the ratio of correctly formed duplexes, i.e. true positives to incorrect duplexes, i.e. false positives. Thus, we define the pairwise discrimination as follows:
| 18 |
For each of our strand sets, we measure the pairwise sensitivity, specificity and discrimination assuming that initial concentration of words and complements is 1 × 10−7 M each.
The DNA design algorithm
Our DNA design algorithm is based on a stochastic local search approach described in greater detail in Tulpan et al. (13). It takes as input the desired strand length l and set size N, along with a specification of which constraints the set must satisfy (see algorithm outline in Figure 5 for further details), and attempts to find a set that meets these requirements. The algorithm performs a search in a space of DNA strand sets of fixed size that may violate the given constraints, using a search strategy that combines randomized iterative improvement and random walk.
Figure 5.
Outline of the stochastic local search procedure for DNA strand design.
The algorithm is initialized with a randomly selected set of N DNA strands, all of which are selected to fulfill any combination of single-strand constraints (C5, C6, C7, T1, T5). Our implementation also provides the possibility to initialize the algorithm with a given set of strands, obtained using other methods. If such a set has less than N strands, it is expanded with randomly generated strands such that a set of N strands is always obtained. Then, repeatedly, a conflict—that is, a pair of strands, x,y, that violates one or more constraints—is selected and the conflict is resolved by replacing one of the conflicting strands, e.g. x, with a new strand, say x′. The replacement is done so that all constraints of type C5, C6, C7, T1 and T5 are satisfied by the strand x′, and with a probabilistic bias towards maximally reducing the overall number of violated constraints (conflict-driven search). In each search step, the conflict to be resolved is performed uniformly at random, and the new strand, x′, is selected as follows, from a larger pool of strands M (generated uniformly at random) that fulfills all single-strand constraints. With a fixed probability, θ, x′ is selected from M uniformly at random, regardless of the number of other constraint violations that will result from it. In the remaining cases, each replacement strand in M is assigned a score, defined as the net decrease in the number of constraint violations caused by it, and a strand with maximal score is selected. (If there are multiple replacement strands with the same score, one of them is chosen uniformly at random.) The parameter θ, also called the noise parameter, controls the balance between the greediness and the randomness of the search process; the optimal value for θ when using relatively large random neighbor sets M was shown to be close to zero (29). The algorithm terminates when a set of DNA strands that satisfies all given constraints has been found, or after a specified number of search steps (cutoff) have been completed.
Our algorithm has been implemented in C/C++ and has been compiled and run under SuSe Linux 9.1, kernel version 2.6.5. Since no system-specific libraries are used, the algorithm should compile on most operating systems supporting standard C/C++ language compilers. Academic users can obtain our software from http://www.cs.ubc.ca/labs/beta/Software/DnaCodeDesign. The source code and precompiled libraries for PairFold v1.1 have been made publicly available at http://www.rnasoft.ca. Since for this paper, we used some unpublished parameters of John SantaLucia Jr., the online version contains a complete set of publicly available DNA nearest-neighbor parameters kindly provided by David Mathews.
In silico experimental protocols
The results presented in this paper were obtained by in silico DNA design. Our software was run on a PC with dual 2 GHz Intel Xeon CPU (only one of which was used in our experiments), 512 KB cache and 4 GB RAM, running SuSe Linux 9.1 (kernel 2.6.5). To test the ability of our algorithm to design DNA sets with various sizes and properties, we first selected seven representative sets from the literature as controls (these are denoted by S1 … S5, S7 and S8 in our tables). We evaluated each control set using the measures discussed in this paper. All values are presented in Table 1.
We used the following general protocol to design improved and enlarged sets. For each set, we used constraints C6, C7, T1–T3 and T5. Constraints C6 and C7 have been set to match the original constraints used in the design of the controls (see Table 1). Constraints T1–T3 and T5 have been initialized as described at the bottom of Table 1. A detailed description of the design protocol follows next.
To design sets of the same size, but higher quality than the respective control set, we used the following protocol. For each set, we performed 20 independent runs with specific parameter settings, and with a maximum cutoff of 12 CPU hours per run. For the first run, the algorithm was initialized with the maximum and minimum values of T1, T2, T3 and T5 of the control sets. Then, in any consecutive run, we set to a very small value, and we decremented the value of in steps of 0.25 kcal/mol, thus increasing the free energy gap δ*. We reported the best of the sets obtained from these 20 runs (these are the sets S1-1, S2-1, …, S8-1 in our tables). We reported also the CPU time required to design the best sets as being the sum of all independent CPU times spent by the algorithm to obtain incrementally improved sets up to the one reported in Table 2. The reported run time does not include the time to evaluate the quality of the designed sets.
Table 2.
Comparison of the quality of the control sets and our improved and enlarged sets
| Sets comparison | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Set | Word length | No. of words | δ [δ*] (kcal/mol) | ρ (°C) | Pairwise sensitivity | Pairwise specificity | Pairwise discrimination | CombFold MFE (kcal/mol) | τ [τ*] (kcal/mol) | Run time (CPU s/m/h) |
| S1 Braich | 15 | 40 | 6.25 [4.28] | 9.11 | 0.95 | 1.00 | 354.36 | −1.25 | 4.10 [1.84] | |
| S1-opt | 15 | 40 | 4.97 [3.78] | |||||||
| S1-1 | 15 | 40 | 7.57 [7.55] | 1.79 | 1.00 | 1.00 | 939.63 | −0.09 | 1.72 [1.36] | 2.6 h |
| S1-1-opt | 15 | 40 | 3.93 [3.79] | |||||||
| S1-2 | 15 | 114 | 6.42 [6.33] | 5.20 | 0.99 | 1.00 | 377.32 | −0.64 | 1.53 [1.53] | 1.8 h |
| S1-2-opt | 15 | 114 | 2.44 [2.12] | |||||||
| S2 Brenner | 4 | 8 | −0.19 [−0.85] | 19.12 | 0.00 | 1.00 | 0.73 | −3.19 | ||
| S2-1 | 4 | 8 | −0.08 [−0.08] | 13.49 | 0.00 | 1.00 | 1.30 | 0.00 | 4 s | |
| S2-2 | 4 | 13 | −0.47 [−0.67] | 17.23 | 0.00 | 1.00 | 0.82 | −3.04 | 12 s | |
| S3 Faulhammer | 15 | 20 | 6.13 [3.65] | 17.33 | 0.78 | 1.00 | 968.14 | −0.46 | 3.93 [−0.06] | |
| S3-opt | 15 | 20 | 5.43 [0.94] | |||||||
| S3-1 | 15 | 20 | 8.59 [8.46] | 3.81 | 0.99 | 1.00 | 5324.62 | −1.63 | 5.84 [5.32] | 15.6 min |
| S3-1-opt | 15 | 20 | 6.24 [6.16] | |||||||
| S3-2 | 15 | 110 | 6.25 [6.13] | 11.56 | 0.97 | 1.00 | 986.16 | −4.28 | 2.28 [1.80] | 4.7 h |
| S3-2-opt | 15 | 110 | 3.33 [2.47] | |||||||
| S4 Frutos | 8 | 108 | −0.21 [−2.22] | 10.28 | 0.00 | 0.95 | 6.25 | −11.19 | ||
| S4-1 | 8 | 108 | 1.28 [0.89] | 6.67 | 0.04 | 0.99 | 7.70 | −11.58 | 4 min | |
| S4-2 | 8 | 173 | 1.59 [0.73] | 5.71 | 0.06 | 0.99 | 15.67 | −13.07 | 1 h | |
| S5 Penchovsky | 16 | 24 | 8.79 [8.12] | 3.50 | 1.00 | 1.00 | 3569.76 | 0.00 | 6.88 [5.78] | |
| S5-opt | 16 | 24 | 7.09 [6.14] | |||||||
| S5-1 | 16 | 24 | 9.27 [9.20] | 1.95 | 1.00 | 1.00 | 5704.45 | 0.00 | 5.83 [5.79] | 1.5 h |
| S5-1-opt | 16 | 24 | 6.14 [6.08] | |||||||
| S5-2 | 16 | 44 | 8.90 [8.82] | 3.45 | 1.00 | 1.00 | 4163.51 | 0.00 | 4.57 [4.16] | 17 h |
| S5-2-opt | 16 | 44 | 5.61 [5.20] | |||||||
| S6 Random | 16 | 24 | 6.10 [4.39] | 18.67 | 0.90 | 1.00 | 522.73 | −2.34 | 3.74 [1.90] | 0.01 s |
| S7 Shortreed1 | 12 | 64 | 2.87 [2.84] | 1.11 | 0.79 | 0.97 | 23.20 | −1.03 | 2.91 [2.76] | |
| S7-opt | 12 | 64 | 2.91 [2.76] | |||||||
| S7-1 | 12 | 64 | 3.72 [3.65] | 1.07 | 0.88 | 0.98 | 49.59 | 0.00 | 0.23 [−0.64] | 1.9 h |
| S7-1-opt | 12 | 64 | 0.23 [−0.64] | |||||||
| S7-2 | 12 | 144 | 3.01 [2.85] | 1.11 | 0.79 | 0.97 | 27.74 | −3.94 | 0.00 [−1.83] | 2.7 h |
| S7-2-opt | 12 | 144 | 0.00 [−1.83] | |||||||
| S8 Shortreed2 | 16 | 64 | 6.77 [6.39] | 0.96 | 0.99 | 1.00 | 4739.83 | −5.50 | 5.59 [5.25] | |
| S8-opt | 16 | 64 | 5.59 [5.25] | |||||||
| S8-1 | 16 | 64 | 8.15 [8.09] | 0.94 | 0.99 | 1.00 | 5057.76 | −2.52 | 2.78 [2.74] | 1.7 h |
| S8-1-opt | 16 | 64 | 3.55 [3.49] | |||||||
| S8-2 | 16 | 80 | 7.91 [7.85] | 0.95 | 0.99 | 1.00 | 4093.02 | −4.32 | 3.69 [3.50] | 8.2 h |
| S8-2-opt | 16 | 80 | 3.69 [3.50] | |||||||
Each pair of rows (between delimiting lines) corresponds to one set, and lists quality measures for the control set, the improved set (indicated by the suffix ‘−1’) and the enlarged set (indicated by the suffix ‘−2’). Improvements over the control set are highlighted in boldface. The columns, from the left, give (i) set ID, (ii) the strand length for the set, (iii) the number of strands in the set, (iv) the free energy gaps δ and δ*, (v) the melting temperature interval width, (vi) the pairwise sensitivity, (vii) the pairwise specificity, (vii) the pairwise discrimination, (ix) the minimum free energy value as computed with CombFold v1.0 (19), (x) the minimum free energy gaps τ and τ* for junctions, and (xi) the run time, measured as total CPU time on our reference machine for running the respective experimental protocol until the given set was obtained. (See Materials and Methods for details). In the melting temperature column, the measurements were obtained using a function of the PairFold v1.1 package (18). Si-opt MFE values for junctions have been obtained after optimizing the arrangement of strands in subsets such that τ* is maximized (where τ* is the free energy gap that accounts for junctions, as defined in Equation 20).
To obtain bigger sets (which we denote by S1-2, S2-2, …, S8-2 in our tables) with approximately the same quality as the control sets, we used a slightly different protocol. For each set, we performed 20 independent runs; starting with the size of the control set, we incremented the size of the target set by 5 in each run. For sets S1-2, S3-2, S4-2, S5-2, S7-2 and S8-2, we initialized the T2, T3 and T5 range values with the ones corresponding to control sets S1, S3, S4, S5, S7 and S8, respectively. The T1 constraint values have been initialized as follows. The minimum perfect match free energy was initialized with , and the maximum was initialized with where X = δ − δ*. In this manner, we enforced δ* of the newly designed set to be bigger than δ of the control set, thus using a much harder constraint than for the design of better sets. For S2-2, the method described above did not provide bigger sets in <12 CPU hours on our reference machine, so we followed the same strategy as the one used to design better sets, i.e. initialized and with the corresponding values for the control set. One minor modification of this protocol was needed in the context of set S2-2. In this case, due to range overlaps in T1 and T3 in the control set, the constraints T1, T2, T3, and T5 (initialized with the values from the control set) were insufficient to ensure the uniqueness of the strands in the set. Thus, we removed any strands that occurred more than once in S2-2, trimming the set from 43 strands (with duplicates) to only 13 unique strands. We note that the duplication of strands could also be prevented in the stochastic local search (SLS) algorithm, e.g. by using Hamming distance constraints.
In addition, we generated 10 random sets using only the C7 constraint. We reported the best random set (S6) out of 10; this set is used as an additional control in our experiments. Table 1 provides references for these control sets and summarizes which constraints were originally used in their design.
RESULTS
The results of the two computational experiments described in the previous section are summarized in Table 2. As can be seen from Table 2, our algorithm is effective in designing sets of the same size as the control sets but with larger free energy gaps, δ*, between correct and incorrect word–complement pairs. Note that larger δ* values imposed as design constraints when generating the new sets using our algorithm induce larger δ values, as well as improved pairwise specificity, sensitivity and discrimination values. The actual free energy gaps, δ, are positive for all of these improved sets, except for the set S2-1, indicating that for every word complement, the hybrid formed with its correct word is more stable than the hybrid with any incorrect word, while in some cases (notably, for control sets S2 and S4), the bounds on the gap, δ*, are negative. Also, pairwise specificity is always at least as high, and often higher, as sensitivity, which indicates that (under the conditions studied here, in which all initial concentrations are equal) instability of correct word–complement hybrids tends to pose more of a problem than the stability of incorrect hybrids.
We also note that for all sets shown in the table, the melting temperature range ρ for correct word–complement pairs is at least as narrow for our new sets as for the control sets. In two cases, the melting temperature range for each of our improved sets is more than four times narrower than for the respective control sets, although such a reduction was not explicitly specified as a design constraint.
The results from our second experiment, in which we used our algorithm to design larger sets with thermodynamic properties comparable with the control sets, are also shown in Table 2. Note that in all cases, we were able to obtain substantially larger sets without any loss of quality (except for S8-2, whose pairwise discrimination is slightly lower), as measured by δ, ρ, pairwise sensitivity, specificity and discrimination.
It may be noted that the CPU time required for finding our improved sets varies substantially between the different sets, but is in most cases substantially <10 CPU hours, and always <20 CPU hours on our reference machine. Due to the highly randomized nature of our SLS algorithm, its run-time over multiple runs on exactly the same input data is quite variable (with standard deviation values in the same order as the run-times shown here)—this is typical for SLS algorithms in general and does not impact their ability to consistently solve hard combinatorial problems such as the strand design problems studied here (17).
DISCUSSION
The computational results reported in the previous section clearly demonstrate the ability of our SLS algorithm to design high quality DNA strand sets, where quality is assessed using a variety of measures.
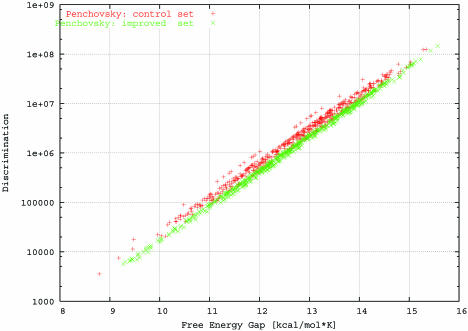
As previously noted, in our algorithm we only control the location and minimal size of the free energy gaps between correct and incorrect word–complement hybrids and the free energy range for correct hybrids, but not for the pairwise specificity, sensitivity or discrimination. However, considering the nature of Equations 10–15, there is a tight correlation between δ (and likewise, δ*) and the relative concentrations of correct versus incorrect hybrids, as directly measured by pairwise discrimination (see Equation 18). Figure 2 shows this correlation for sets S5 and S5-1; every point in this correlation plot corresponds to a positive solution of the equilibrium Equations 10–15 for one combination of a word, its correct complement and a distinct complement. The discrimination values within both sets vary over several orders of magnitude, and the overall pairwise discrimination is determined by a small number of relatively stable undesired hybrids.
Figure 2.
Correlation between pairwise discrimination values and duplex free energy gaps for sets S5 Penchovsky (control) and S5-1 (improved); each point in the plot corresponds to the discrimination and free energy gap values of a given word and an incorrect complement.
Our accompanying paper (6), introduces Δ, a variant of our notion of pairwise discrimination. We did not compute Δ for the sets reported in this paper since we did not model interactions involving more than one word, but the results in the accompanying paper indicate that Δ and our pairwise discrimination measure are quite similar.
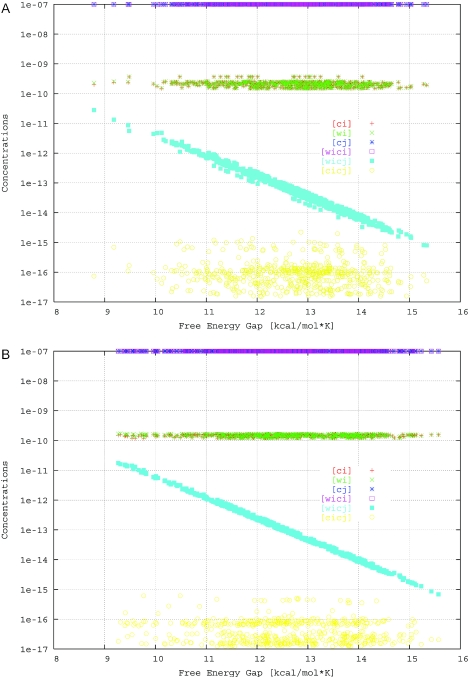
To further investigate how our quality measures depend on the free energy gap δ, we studied, for pairs of words wi and complements cj, the dependence of the equilibrium concentrations of the single DNA strands and hybrids, as determined by Equations 10–15, on the respective free energy gap values. Figure 3 illustrates the results of this analysis for sets S5 (top) and S5-1 (bottom). Clearly, the concentrations of the desired products, namely the correct hybrid, [wici], and the unbound incorrect complement, [ci], are consistently several orders of magnitude higher than the concentrations of any undesired products ([wi], [ci], [wicj] and [cicj]). Interestingly, undesired hybridization between complements is insignificant compared with the impact of incorrect word–complement hybrids. This means that for our sets, the competitive reactions wi + ci ⇌ wici and wi + ci ⇌ wicj dominate the more complex equilibria considered in our model; in particular, as clearly illustrated in Figure 3, the difference δij in free energy between correct and incorrect hybrids, wici and wicj, mostly determines the relative concentrations of correct versus incorrect hybrids, and hence the pairwise discrimination measure. This justifies the approach of Shortreed et al. (6) to ignore such interactions. However, there are cases where the product cicj can become significant, such as when the initial complement concentrations are significantly greater than the word concentrations, or when words are designed over a 4-base, rather than a 3-base, alphabet.
Figure 3.
Concentration of words, complements, perfect and imperfect matches as a function of duplex free energy gaps for sets (a) S5 Penchovsky (control), and (b) S5-1 (improved); each point in the plot corresponds to the equilibrium concentration of one single strand or duplex.
As can be seen from Figures 2 and 3, the improved set generated by our algorithm has higher pairwise discrimination because the relative concentrations of the worst (i.e. most stable) undesired hybrids have been reduced, as a result of the respective increased free energy gaps. At the same time, as a side effect, the concentrations of the most stable (undesired) complement–complement hybrids are also reduced. It may also be noted that compared with the reference sets, our new sets show more even distributions of the free energy gaps and pairwise discrimination values, as well as reduced variations in the concentrations of the words and complements obtained from our equilibria analyses. Although our model makes a number of simplifying assumptions, in particular, equal initial concentrations and independence of the individual equilibria, we expect to find similar differences in more realistic models, whose analysis is currently beyond our reach.
It may be noted that given these observations, pairwise sensitivity mainly depends on the stability of the correct word–complement hybrids. This is clearly reflected in the results from Table 2 which show that pairwise sensitivity correlates strongly with the melting temperature of the correct hybrids, TM. Note that in the case of S4 and the corresponding new sets, the relatively low TM values are a consequence of the small strand length and recall that in the original application, these strands are concatenated with strand labels, which effectively increases their length and the stability of the correct duplexes. Pairwise specificity, on the other hand, mainly depends on the concentration of incorrect word–complement duplexes, and hence improves as a result of increasing the free energy gap δ.
While these observations confirm the effectiveness of the free energy gap as a design constraint, it may be noted that highly constrained designs may not always be required in order to obtain good strand sets according to our quality measures. For example, we generated a set S6 of 24 strands of length 16 under the sole constraint that only the bases A,T and C may be used (C7), and found it to be quite reasonable with respect to our quality measures and as compared with some of our other sets (see Table 2). Constraint C7 is widely used in the design of DNA and RNA strand sets; this constraint substantially reduces the potential for forming stable incorrect complement–complement (or word–word duplexes, if word interaction is not precluded by immobilization on a surface), since such duplexes cannot contain any energetically favorable G–C pairs. Our results suggest that while simple combinatorial constraints such as C7, or similarly C4, may be sometimes sufficient for obtaining strand sets of reasonable quality (particularly, when only relatively small sets of reasonably long strands are required), better and larger strand sets can be found using high-performance algorithms that directly support thermodynamical design constraints.
As previously described, in DNA computing applications (as well as in the context of biomolecular tagging), words are not used in isolation, but words or their complements are rather concatenated to form longer strands. These concatemers represent strings of data, and the values that may occur at each position of such a string are encoded by a group of DNA words. For example, Braich et al. (20) used bit strings of length 20 in their DNA computation. These were represented as concatemers of 20 DNA words, where a different word was used for each bit at each of the 20 positions. Hence, they partitioned their set of 40 words of length 15 (S1 in Table 1) into 20 groups of two words each, and used the 220 strands of length 300 obtained by concatenation of one word from each group to represent the 220 bit strings of length 20. Similarly, the sets of Faulhammer et al. and Penchovsky et al. (S3 and S4) are partitioned into ten and twelve groups respectively, each consisting of two words, yielding a total of 210 and 212 long strands which encode bit strings of length 10 and 12, respectively.
The concatemers thus obtained need to satisfy two additional constraints. First, concatemers that can form stable secondary structures should be avoided as much as possible, because such secondary structure within a long strand may interfere with desired hybridizations between words and their complements. Second, undesired hybridizations between complements and any region between two adjacent words (or vice versa) on a long strand should also be avoided. Neither of these constraints is explicitly enforced in our design algorithm, although the slide mismatches constraint (C3) can help reduce hybridization of complements between words.
To evaluate our new sets with respect to the first additional constraint, we used the CombFold v1.0 algorithm (the software CombFold v1.0 is available upon request from the authors) by Andronescu et al. (19) to find the minimum free energy secondary structure over all concatemers that can be formed based on a given partitioning into groups. For the control sets, we considered the original partitionings reported in the literature, while for our new sets, we considered random partitionings with the same number and size of groups as used for the respective control sets. The results from the CombFold analysis of these sets and partitionings are shown in Table 2; they clearly demonstrate that for our improved and enlarged sets, the potential for concatemers with undesired stable secondary structures is not significantly higher than for the control sets. The worst values from the CombFold analysis are for the S4 sets (Frutos et al.), and these are the only sets which are designed over a 4-letter ({A,C,G,T}), rather than a 3-letter ({A,C,T}) alphabet; this suggests that a 3-letter alphabet is preferable.
The second additional constraint, on undesired hybridizations between complements and junctions of two concatenated words, can be formalized in two ways, as follows (analogous to δ and δ* defined earlier): for a given set whose words are partitioned into ordered groups, if words wi and wj are adjacent on a long strand (obtained by concatenating one word per group in order), we let wiwj denote the strand obtained by concatenating wi and wj. Let T be the set of triples (i, j, k) such that i, j and k are distinct, and the sequence wiwj appears on some long strand. We let
| 19 |
Let τ* be the gap between the free energy of desired hybridizations and undesired hybridizations at junctions, which now is as follows:
| 20 |
where is as defined in ‘Evaluation criteria’.
Also, we let τ be the gap between the free energy of desired hybridizations and undesired hybridizations at junctions, defined as follows:
| 21 |
Just as for δ and δ*, τ* is a lower bound for τ. Table 2 shows measurements of τ and τ* for sets S1, S3, S5, S7 and S8 and our respective improved and enlarged sets, using the same partitioning into groups as in the original references (for the control sets) or random partitionings into the same number of groups as for the control sets (for our new sets).
The partitioning of strands into groups can have a substantial impact on τ and τ*, and hence the potential for incorrect word–complement junction hybridizations. In order to find improved word partitionings, we developed a simple stochastic local search algorithm that takes as input a set of words, a desired group size and a value v, and partitions words into ordered groups of the desired size so that the value of τ* for the set with respect to these ordered groups is at least v (or if not, as close to v as possible). The algorithm starts with an initial arbitrary partitioning of words into groups. Then, the algorithm repeatedly swaps two strands from different groups, so as to ultimately reduce the value of τ*. Details are given in Figure 4; in our use of the algorithm, we chose the value 0.2 for the probability ψ, which controls whether a ‘worse’ partitioning P′ replaces the current partitioning P at an iteration of the algorithm. The value 0.2 was inferred from multiple runs of the algorithm on different strand sets. We simply selected the probability value that allows the algorithm to find a solution in the lowest number of iterations. Using this algorithm, we organized the words in sets S1, S3, S5, S7, S8 and our corresponding improved and enlarged designed sets—into ordered groups of size 2. For each set, over several runs, we gradually increased the input value v in increments of 1 kcal/mol, six times or until the algorithm did not succeed in finding a grouping for which τ* ≥ ν.
Figure 4.
Outline of the stochastic local search procedure used to partition strands into groups for use in DNA computations. A ‘bad junction’ is a junction with MFE lower than v.
In Table 2, we report the τ and τ* values obtained by optimizing the control sets as well as our respective new sets using this algorithm. We exclude the S2 [Brenner et al. (21)] and S4 [Frutos et al. (23)] sets, since these sets were not designed with the goal of concatenating strands in the sets. For three of the five sets, we were able to find new partitionings of the control sets which have improved τ and τ* values. Additionally, for these three sets, our new sets have τ* values that are better than those of the control sets, although in just one of these cases was the τ value of our new set better than that of the control set. We note that our algorithm optimized for τ* rather than τ; we expect that we would obtain further improvements on the τ values if our algorithm optimized for τ. However, our new sets S7 and S8 have poorer τ and τ* values than the control sets of Shortreed et al. (6). An important feature of the Shortreed et al. approach to grouping words in order to form concatemers is that the concatemers are formed from a pool of words that is larger than needed. This technique could be incorporated into the approach of this paper, and may yield better values of τ. Alternatively, our SLS algorithm for strand design (see Figure 5) could be adapted to take partitioning into account, although this would add to the complexity of that algorithm.
Overall, compared with the algorithm presented in the accompanying paper [Shortreed et al. (6)], the SLS-based design algorithm presented here is conceptually more complex, but based on a comparison between the S7 and S8 sets, produces sets with better free energy gap (δ), and pairwise discrimination, sensitivity and specificity. Moreover, it has better scaling behavior (particularly with respect to the memory requirements for longer words and the incorporation of additional constraints) and so it can be applied to a wider range of DNA word design problems. The approach of Shortreed et al. to partitioning strands in order to form concatemers has some strong features, such as the use of a pool of words that is larger than needed, which results in partitioned sets of the highest quality in many cases.
CONCLUSIONS
In this work, we introduced a new approach for DNA strand design that integrates thermodynamic as well as combinatorial constraints and uses a stochastic local search strategy that is effective at finding sets that satisfy these constraints. Furthermore, we showed that our design constraints are well correlated with measures of quality of a set, such as pairwise sensitivity, specificity and discrimination.
The current algorithm can easily be adapted to design strands for universal microarrays or molecular beacons with specific capture-probe capabilities. Constraints on interactions between strands that are immobilized on a surface, as well as between those in solution, are supported by the algorithm and can be integrated into our model in a straightforward way. Our model for evaluating quality of sets can support analysis when the initial concentrations of words and complements are not equal; particularly in the context of iterative DNA computations during which target concentrations vary, it would be useful to consider the quality of sets under uneven and varying word and complement concentrations.
In future work, we will investigate how our algorithm can be further adapted so that much larger sets, such as used in microarray applications, can be designed efficiently. In a preliminary study, we were able to design sets of 1000 20mers with a melting temperature range of 5°C and a free energy gap δ* of 5 kcal/mol in 2.7 CPU hours on our reference machine (averaged >10 independent runs). To design even larger sets, the memory requirements of our present algorithm need to be reduced; this can be achieved by using optimized or partial representations of the constraints between pairs of DNA strands during the search process. Alternatively, by using a slightly different approach, based on the local optimization of subsets of strands, it should be possible to obtain sets of tens of thousands of strands. We have also performed preliminary tests on the scaling of our algorithm's performance with strand length and sets of 50 50mers and 60mers with free energy gaps δ* ≥ 3.00 kcal/mol in 6 and 10 CPU minutes, respectively, on our reference machine (averaged >10 independent runs).
A relatively straightforward extension of our approach would be to additionally model interactions of type I4, in which words interact with each other. In this context, it would be particularly interesting to use a model that applies to the situation of densely packed surfaces, as encountered in DNA microarray and surface-based DNA computing applications; unfortunately, we are currently unaware of such a model.
Another direction for future work is to use the ensemble free energy, as given by the partition function, instead of the MFE calculations (provided by PairFold) in our approach. In this context, a reasonably efficient algorithm for calculating the partition function on pairs of strands is needed; to our best knowledge, no such algorithm is currently publicly available, but in principle, as soon as this situation changes, it will be easy to integrate such a procedure into our software.
Finally, it may be noted that our current thermodynamic model is limited to interactions between one word and two complements, and makes the simplifying assumption that the equilibria between any such triplet of strands are independent of each other. In future work, we intend to extend this model to more complex equilibria, which may, for example, capture competitive hybridization within a set comprising several words and complements. Ultimately, our goal is to devise a model that is accurate enough to allow quantitative predictions of the desired and undesired hybridizations within a given set of words and complements, and to support the computational design of DNA codes based on that model. We believe that the work presented in this paper represents a first important step towards achieving this larger and more ambitious goal.
Acknowledgments
We thank Igor Naverniouk for valuable help with Maple. Furthermore, we gratefully acknowledge Erik Winfree and David Mathews, who provided valuable feedback on ideas and concepts underlying this work. This work was supported by the US National Science Foundation through Grant Nos 0203892 and 0130108, and by the Canadian Natural Sciences and Engineering Research Council. Funding to pay the Open Access publication charges for this article was provided by The Natural Sciences and Engineering Research Council of Canada (NSERC).
Conflict of interest statement. None declared.
REFERENCES
- 1.Fan J., Chen X., Halushka M.K., Berno A., Huang X., Ryder T., Lipshutz R.J., Lockhart D.J., Chakravarti A. Parallel genotyping of Human SNPs using generic high-density oligonucleotide tag arrays. Genome Res. 2000;10:853–860. doi: 10.1101/gr.10.6.853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Gartner Z.J., Tse B.N., Grubina R., Doyon J.B., Snyder T.M., Liu D.R. DNA-templated organic synthesis and selection of a library of macrocycles. Science. 2004;305:1601–1605. doi: 10.1126/science.1102629. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Halpin D.R., Harbury P.B. DNA Display I. Sequence-encoded routing of DNA populations. PLoS Biol. 2004;2:e173. doi: 10.1371/journal.pbio.0020173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Adleman L.M. Molecular computation of solutions to combinatorial problem. Science. 1994;266:1021–1024. doi: 10.1126/science.7973651. [DOI] [PubMed] [Google Scholar]
- 5.Liu Q., Frutos A.G., Wang L., Condon A., Corn R.M., Smith L.M. DNA computations on surfaces. Nature. 2000;403:175–179. doi: 10.1038/35003155. [DOI] [PubMed] [Google Scholar]
- 6.Shortreed M.R., Chang S.B., Hong D., Phillips M., Campion B., Tulpan D.C., Andronescu M., Condon A., Hoos H.H., Smith L.M. A thermodynamic approach to designing structure-free combinatorial DNA word sets. Nucleic Acids Res. 2005;33:4965–4977. doi: 10.1093/nar/gki812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Arita M., Nishikawa A., Hagiya M., Komiya K., Gouzu H., Sakamoto K. Improving sequence design for DNA computing. Proc. Genetic and Evolutionary Computation Conference, GECCO 2000; 2000. pp. 875–882. [Google Scholar]
- 8.Ben-Dor A., Karp R., Schwikowski B., Yakhini Z. Universal DNA tag systems: a combinatorial design scheme. Proc. Fourth Annual International Conference on Computational Molecular Biology, RECOMB 2000; ACM; 2000. pp. 65–75. [DOI] [PubMed] [Google Scholar]
- 9.Deaton R., Murphy R.C., Garzon M., Franceschetti D.R., Stevens S.E., Jr Good encodings for DNA-based solutions to combinatorial problems. In: Landweber L.F., Baum E.B., editors. Proc. DNA Based Computers II, DIMACS Workshop; June 10–12; 1996. pp. 247–258. DIMACS Series in Discrete Mathematics and Theoretical Computer Science. [Google Scholar]
- 10.Deaton R., Garzon M., Murphy R.C., Rose J.A., Franceschetti D.R., Stevens S.E., Jr Genetic search of reliable encodings for DNA-based Computation. In: Koza J.R., Goldberg D.E., Fogel D.B., Riolo R.L., editors. Proc. First Annual Conference on Genetic Programming.1996. [Google Scholar]
- 11.Zhang B.T., Shin S.Y. Molecular algorithms for efficient and reliable DNA computing. In: Koza J.R., Deb K., Dorigo M., Fogel D.B., Garzon M., Iba H., Riolo R.L., editors. Proc. Third Annual Genetic Programming Conference, GP 1998; San Mateo, CA: Morgan Kaufmann; 1998. pp. 735–742. [Google Scholar]
- 12.Zhang B.T., Shin S.Y. Advances in Soft Computing—Engineering Design and Manufacturing. Springer-Verlag; 1998. Code optimization for DNA computing of maximal cliques. [Google Scholar]
- 13.Tulpan D.C., Hoos H.H., Condon A. Stochastic local search algorithms for DNA word design. Proc. Eighth International Workshop on DNA Based Computers; June 2002; Hokkaido, Japan. Springer-Verlag, 2003; 2002. pp. 229–241. Lecture Notes in Computer Science. [Google Scholar]
- 14.Garzon M., Deaton R.J., Rose J.A., Franceschetti D.R. Soft molecular computing. Proc. Fifth International Meeting on DNA Based Computers; June 14–15; MIT; 1999. pp. 89–98. [Google Scholar]
- 15.Rose J.A., Deaton R., Franceschetti D.R., Garzon M., Stevens S.E., Jr A statistical mechanical treatment of error in the annealing biostep of DNA computation. Special program in DNA and Molecular Computing at the Genetic and Evolutionary Computation Conference, GECCO 1999; Orlando FL: Morgan Kaufmann; 1999. [Google Scholar]
- 16.Penchovsky R., Ackermann J. DNA library design for molecular computation. J. Comp. Biol. 2003;10:215–229. doi: 10.1089/106652703321825973. [DOI] [PubMed] [Google Scholar]
- 17.Hoos H.H., Stützle T. Stochastic Local Search-Foundations and Applications. San Francisco, CA, USA: Morgan Kaufmann; 2004. [Google Scholar]
- 18.Andronescu M., Zhang Z.C., Condon A. Secondary structure prediction of interacting RNA molecules. J. Mol. Biol. 2005;345:987–1001. doi: 10.1016/j.jmb.2004.10.082. [DOI] [PubMed] [Google Scholar]
- 19.Andronescu M., Aguirre-Hernandez R., Condon A., Hoos H.H. RNAsoft: a suite of RNA secondary structure prediction and design software tools. Nucleic Acids Res. 2003;31:3416–3422. doi: 10.1093/nar/gkg612. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Braich R.S., Chelyapov N., Johnson C., Rothemund P.W., Adleman L. Solution of a 20-variable 3-SAT problem on a DNA computer. Science. 2002;296:478–479. doi: 10.1126/science.1069528. [DOI] [PubMed] [Google Scholar]
- 21.Brenner S., Williams S.R., Vermaas E.H., Storck T., Moon K., McCollum C., Mao J.I., Luo S., Kirchner J.J., Eletr S., et al. In vitro cloning of complex mixtures of DNA on microbeads: physical separation of differentially expressed cDNAs. Proc. Natl Acad. Sci. USA. 2000;97:1665–1670. doi: 10.1073/pnas.97.4.1665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Faulhammer D., Cukras A.R., Lipton R.J., Landweber L.F. Molecular computation: RNA solutions to chess problems. Proc. Natl Acad. Sci. USA. 2000;97:1385–1389. doi: 10.1073/pnas.97.4.1385. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Frutos A.G., Liu Q., Thiel A.J., Sanner A.M.W., Condon A.E., Smith L.M., Corn R.M. Demonstration of a Word Design Strategy for DNA Computing on Surfaces. Nucleic Acids Res. 1997;25:4748–4757. doi: 10.1093/nar/25.23.4748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Braich R.S., Johnson C., Rothemund P.W.K., Hwang D., Chelyapov N., Adleman L.M. Solution of a satisfiability problem on a gel-based DNA computer. Proc. Sixth International Workshop on DNA-Based Computers: DNA Computing, Lecture Notes in Computer Science; 2001. pp. 27–42. [Google Scholar]
- 25.Crothers D.M., Zimm B.H. Theory of the melting transition of synthetic polynucleotides: evaluation of the stacking free energy. J. Mol. Biol. 1964;116:1–9. doi: 10.1016/s0022-2836(64)80086-3. [DOI] [PubMed] [Google Scholar]
- 26.DeVoe H., Tinoco L., Jr The stability of helical polynucleotides: base contributions. J. Mol. Biol. 1962;4:500–517. doi: 10.1016/s0022-2836(62)80105-3. [DOI] [PubMed] [Google Scholar]
- 27.SantaLucia J., Jr A unified view of polymer, dumbbell, and oligonucleotide DNA nearest-neighbor thermodynamics. Proc. Natl Acad. Sci. USA. 1998;95:1460–1465. doi: 10.1073/pnas.95.4.1460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.SantaLucia J., Jr, Hicks D. The thermodynamics of DNA structural motifs. Annu. Rev. Biophys. Biomol. Struct. 2004;33:415–440. doi: 10.1146/annurev.biophys.32.110601.141800. [DOI] [PubMed] [Google Scholar]
- 29.Tulpan D.C., Hoos H.H. Hybrid randomised neighbourhoods improve stochastic local search for DNA Code Design. Canadian Conference on Artificial Intelligence 2003, Lecture Notes in Computer Science; Springer-Verlag; 2003. pp. 418–433. [Google Scholar]