Orthogonal arrangement of rhythm-generating microcircuits in the hippocampus

Abstract

As a structure involved in learning and memory, the hippocampus functions as a network. The functional differentiation along the longitudinal axis of the hippocampus is poorly demarcated in comparison with the transverse axis. Using patch clamp recordings in conjunction with post hoc anatomy, we have examined the pattern of connectivity and the functional differentiation along the long axis of the hippocampus. Here, we provide anatomical and physiological evidence that the prominent rhythmic network activities of the hippocampus, the behavior-specific gamma and theta oscillations, are seen predominantly along the transverse and longitudinal axes respectively. This orthogonal relationship is the result of the axonal field trajectories and the consequential interaction of the principal cells and major interneuron subtypes involved in generating each rhythm. Thus, the axonal arborization patterns of hippocampal inhibitory cells may represent a structural framework for the spatiotemporal distribution of activity observed within the hippocampus.

The hippocampus is required for the encoding of new information and for retrieving information shortly after acquisition (1). Spatial information is coded at theta frequencies (2) by clusters of neurons segmentally distributed along the longitudinal axis of the hippocampus (3). Gamma oscillations are also generated by the hippocampus nested within these theta rhythms and are thought to be involved in transient neuronal assembly formation (4), information transmission, and storage (5).

As previous observation has shown, the hippocampus is made up of multiple lamellae organized in parallel across the long axis, in which each lamella contains a functionally independent transverse circuit (6). The well defined connections between subregions along the transverse axis facilitates the investigation of crucial neurobiological processes such as network oscillatory activity in the in vitro preparation. Although the functionally segregated subregions of the long axis of the hippocampal formation may cooperate with each other during memory formation (for review, see ref. 7), morphological evidence about their interconnectivity is sparse. Although CA3 neurons connect to other CA3 neurons (8, 9), and excitation of interneurons occurs along the longitudinal axis (10), the involvement of hippocampal interneurons in the functional circuit along the longitudinal axis of hippocampus is still unclear.

Interneurons serve a wide variety of functions in the brain, amongst them generating and maintaining local or large scale coherent activity (for review, see ref. 11). They also have a particularly pivotal role in driving inhibition-based rhythms, such as gamma and theta frequency network oscillations (12–16). Theta rhythms are seen as a major operational mode of the hippocampus (for review, see ref. 17), and clusters of neurons that encode information required to perform spatial and non-spatial short-term memory tasks during theta rhythms are distributed in distinct segments along the length of the hippocampus (3). The circuit analysis of functional neuronal networks along the long axis may therefore provide a unique insight into the role played by the hippocampus in cortical information processing and memory formation.

Using whole-cell patch-clamp recordings in conjunction with post hoc anatomy, we investigated the three-dimensional axonal arborization patterns of different hippocampal CA3 interneurons. In contrast to all other recorded CA3 interneurons single distal dendrite targeting oriens lacunosum-moleculare (O-LM) cells arborized most extensively in the longitudinal axis as revealed by 3D reconstruction of these cells. Therefore, the axon plexus of this cell type innervates distal dendrites of pyramidal CA3 cells that are distributed in distinct segments along the length of the hippocampus. The experimental (electrophysiological) results and computational models suggest that these morphological features may underlie the observed orthogonal arrangement of rhythm-generating microcircuits in the hippocampus.

Materials and Methods

Slice Preparation. Transverse, coronal, and longitudinal slices (450-μm thickness) obtained from ventral, middle, and whole hippocampus, respectively (see Ai in Figs. 1, 2, 3), were prepared from C57 mice (P 18–25) in accordance with the United Kingdom Animals Scientific Procedures Act. Perisomatic interneurons were studied by using transgenic mice that expressed enhanced fluorescent protein under the control of the parvalbumin promoter. Slices were incubated at room temperature for at least 1 h in a holding chamber and then transferred to the recording chamber. The solution used during incubation and recording contained 126 mM NaCl, 3 mM KCl, 1.25 mM NaH₂PO₄, 2 mM CaCl₂, 2 mM MgSO₄, 24 mM NaHCO₃, and 10 mM glucose, saturated with 95% O₂ and 5% CO₂.

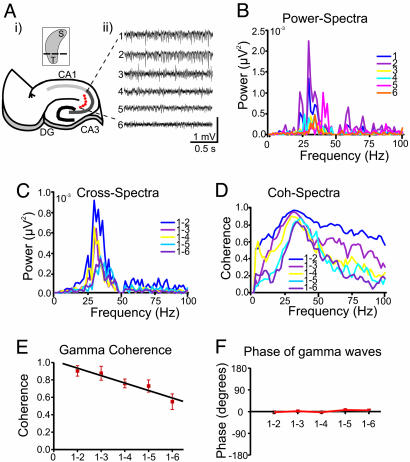
Fig. 1.

Properties of KA-induced gamma oscillations in transverse hippocampal slices. (Ai) Schematic illustration of location of field electrodes (1–6) along the transverse axis of the hippocampal CA3 region. (Ai Inset) Three-dimensional sketch of the hippocampus with the cutting planes in transverse direction. (Aii) Example of gamma frequency oscillations recorded from the two FP electrodes, one serving as a reference, whereas the second electrode was moved from a closer site (≈100 μm) to six consecutively more distant sites in ≈100-μm steps (as illustrated in Aii). (B–D) Power (B) and cross-spectral (C) density plots and coherence spectra (D) for the gamma activity from all recording sites (data are obtained from 1-min recordings). Peak gamma power for this slice was 33 Hz. (E) Mean gamma coherence as a function of interelectrode distance (n = 4). (F) Phase of KA-induced gamma waves in the transverse slices. In contrast to coherence, there was no clear phase shift of gamma waves in these slices.

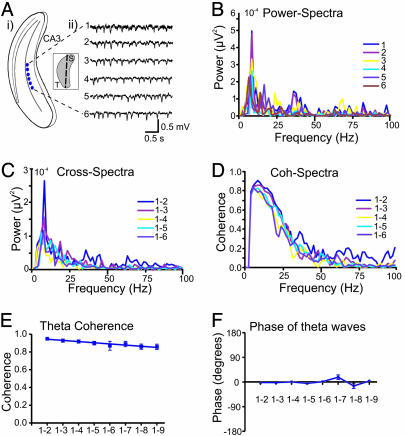
Fig. 2.

KA-induced theta-like network oscillations in longitudinal slices. (Ai) Schematic illustration showing the placement of recording electrodes (1–6) within the area CA3 of the longitudinal hippocampal slice. (Ai Inset) Three-dimensional sketch of the hippocampus with the cutting planes in longitudinal direction. (Aii) Representative extracellular recordings following bath-applied KA shows a theta-like activity. The oscillatory activity does not substantially change across the long axis of the hippocampus. (B–D) Power (B) and cross-spectral (C) density plots and coherence spectra (D) for the theta-like activity from all recording sites. The power spectrum shows a distinct peak at 8 Hz. (E and F) Mean theta coherence and phase in the longitudinal axis as a function of interelectrode distance (n = 7). The theta-like oscillatory activity showed no clear differences in both coherence (E) and phase (F) for different distance between the recording electrodes (1-2 to 1-9).

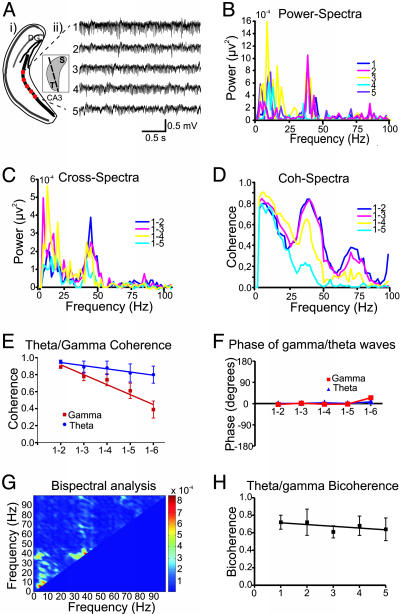
Fig. 3.

Simultaneous expression of gamma and theta frequency oscillations in the coronal slices. (A) Schematic illustration of the coronal slices with the recording sites (i) and the representative FP recordings of the oscillatory activity (ii) after bath-applied KA. (Ai Inset) Three-dimensional sketch of the hippocampus with the cutting planes in coronal direction. The power spectral (B) and cross-spectral (C) density plots demonstrates two clear peaks at theta (8 Hz) and gamma (38 Hz) frequency range. (D) Representative example of coherence spectra obtained from different recording sites along the coronal slices. Note a strong dependence of values of coherence on the recording distance for gamma waves but not for theta waves. Mean coherence (E) and phase (F) of theta and gamma waves in the coronal slices. In contrast to coherence, phase of theta and gamma oscillations were little changed as function of the recording distance. (G) Two-dimensional graph of the results of bispectral analysis. The (theta/gamma) peak indicates that theta and gamma power wax and wane in a correlated way. (H) Averaged theta/gamma bicoherence pattern during the network oscillations in the coronal slices (n = 5). High values of bicoherence indicates the strong functional interaction between the generators of theta and gamma oscillations.

Extracellular Field Recordings. Experiments were performed in an interface [at 34°C, dual channel field potential (FP) recordings] or in a submerged-type (at 29°C, patch clamp recordings) chamber. Kainate (KA) was applied either by bath (400 nM in the interface chamber) or by pressure pulse [1 mM, 60 psi (1 psi = 6.89 kPa), and duration 10–60 ms in an submerged chamber] to get a network oscillations. We used a pharmacological gamma-induction paradigm to study network oscillations in submerged slices (16). Ejected volume was generally correlated with oscillatory peak power and duration, whereas the peak frequency remained constant for any given slice. Single or dual (up to 8 recording sites separated by ≈100 μm) channel FP recordings and pressure application of KA were done in the stratum radiatum of the CA3 by using patch pipettes. FPs from dual channel were low pass filtered at 1 kHz with a custom-made Bessel filter, digitized at 4 kHz by using an ITC-16 A/D board (Instrutech, Mineola, NY) and analyzed by using wintida software (Heka, Lambrecht/Pfalz, Germany). Oscillatory peak frequency was determined by averaging several consecutive Fourier transforms, contained within a 2- to 30-s epoch. The spectral analysis of the FP recordings was conducted off-line by using matlab (Mathworks, Natick, MA). To exclude noise, the signal was digitally filtered by using an infinite impulse response notch filter at 50 Hz. The power spectral density, cross-spectral density, phases, and coherence spectra were computed for all signals and signal pairs. The power spectra were calculated by Fourier Transformation. Coherence (between 0 and 1) estimates the degree to which phases at the frequency of interest are dispersed. To compare the relation between frequencies in one recording site, bispectrum and bicoherence was computed (18). Bispectral analysis quantifies the degree of phase coupling between the frequencies of a signal. Bicoherence provides information about the phase-coupling at different frequencies independent of the amplitude obtainable from the power spectrum (see Supporting Text, which is published as supporting information on the PNAS web site). For further analysis, parameters for both theta (4–12 Hz) and gamma (25–45 Hz) bands (maximal and mean values) were extracted from the spectral and bispectral/bicoherence analysis. Student's t test was used for statistical comparisons, differences were considered statistically significant if P < 0.05. Average values are expressed as the mean ± SEM.

Whole-Cell Recordings. Concomitant with the extracellular FP whole-cell patch-clamp recordings in current clamp mode were obtained from stratum oriens/pyramidale interneurons and pyramidal cells of area CA3 visualized by infrared differential interference contrast videomicroscopy (Zeiss Axioskop). Whole-cell recording pipettes (3–5 MΩ) were filled with a solution containing 135 mM K-gluconate, 5 mM KCl, 2 mM ATP-Mg, 0.3 mM GTP-Na, 10 mM Hepes, plus 0.5% biocytin, pH 7.3 and 280 mOsm. An Axopatch 1D or Multiclamp 700B amplifier (Axon Instruments) was used for current-clamp recordings. The holding potential was -60 mV unless indicated otherwise. The seal resistance before establishing whole-cell mode was ≥2 GΩ. The series resistance (range 12–18 MΩ) was monitored repeatedly during the experiment by measuring the amplitude of the capacitive current in response to a -10-mV pulse.

Signals were filtered at 5 kHz (whole-cell recording) or 0.002–1 kHz (extracellular FP recording in submerged conditions) with an external eight-pole Bessel filter (Applegarth Electronics, Oxford) and digitized at 10 kHz by using an ITC-16 A/D board.

Anatomical Identification of Interneurons. Slices with a biocytin-filled interneuron were processed as have been described in ref. 16. Subsequently, the cells were reconstructed with the aid of a Neurolucida 3D reconstruction system. The absolute extension of axonal collaterals within and between adjacent axonal clusters was measured by using a neuroexplorer program (Neurolucida, MicroBrightField, Williston, VT).

Modeling and Simulations. The minimal network model studied in this paper consists of two O-LM (O) cells, two fast spiking interneurons (I), and a population of pyramidal cells represented by one somatic (E) and one dendritic (D) compartment that are electrically coupled. The O and I cells are modeled as a single compartment. All cells are modeled by using the Hodgkin-Huxley (HH) formalism. In what follows, we will refer to the somatic and dendritic compartments as E and D cells, respectively. The I, E, and D cells are modeled by using the standard HH (19–21) currents (transient sodium, delayed rectifier potassium, and leak) with the same equations as in ref. 22. The I, E, and D cells differ only in the applied bias current; i.e., in their natural frequency. The O cells have, in addition to the standard HH currents, an A current and a hyperpolarization-activated (h) current. We use a model adapted from a multicompartmental model proposed in ref. 23. Because the spiking E cell represents the output of all of the pyramids, we use the subthreshold behavior of the D cell to compare with measured variations in voltage of nonspiking E cells (see Results).

In the network, the cells are connected as schematically shown in Fig. 5D. The decay time of the I inhibitory postsynaptic potentials (IPSPs) are chosen to be 10 ms (24). The IPSPs originating from the O cells onto pyramidal cells was taken to be 20 ms (25). The decay time of the excitatory postsynaptic potentials onto O and I cells was taken to be 4 ms. In experiments, gap junctions have been shown to be important for generating theta and gamma rhythms. However, their proposed role in propagating excitatory and inhibitory signals in large networks (26) is not directly applicable to the small-scale models used in the present study, so we are not including them in our simulations. The simulations have been performed by using the xpp package (cvode method, tolerance = 10^-5, Δt = 0.02; ref. 27).

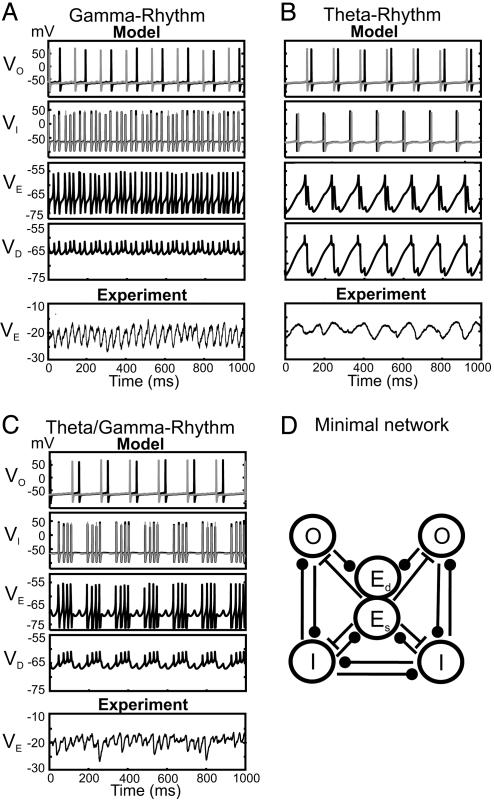
Fig. 5.

Models of gamma, theta, and theta/gamma network activity. (A–C Model) The network contains two O-LM cells (O), two fast spiking perisomatic targeting basket cells (I), and one pyramidal cell (E) representing a population. The pyramidal cell has two compartments: soma (E_s) and dendrite (E_d). To get from theta (B) to theta/gamma (C) to gamma (A) the OI and OD connections are decreased, whereas the EI and EO connections are increased. (A–C) In V_E, action potentials and afterhyperpolarizations are truncated for clarity. (A–C Experiment) Whole cell patch-clamp recordings from pyramidal cell soma (V_E) illustrate IPSPs (from a membrane potential of -20 mV) during kainite induced network oscillations. (D) Minimal network for investigating of gamma, theta, and theta/gamma rhythms.

The purpose of the simulations is to show that the switches in rhythms associated with changes in orientation of the slice can be replicated in a simple network model in which the change of orientation is reflected in the conductances of the synapses. We model the transverse “slice” as having a larger E-X conductance (where X represents O or I) than the longitudinal slice to reflect the predominantly transverse trajectory of E cell axon collaterals. The O-Z conductance (where Z is I or E) is larger in the longitudinal slice than in the transverse slice to reflect the predominantly longitudinal distribution of O-LM axon collaterals (see Fig. 4 B and C). The coronal slices have values that are in between. All other parameters are unchanged among simulations (see Supporting Text). In the absence of synaptic connections, each O cell fires at ≈10 Hz, each I cell fires at ≈30 Hz, the E cell (population) fires at 65 Hz, and the dendritic compartment (D) is silent.

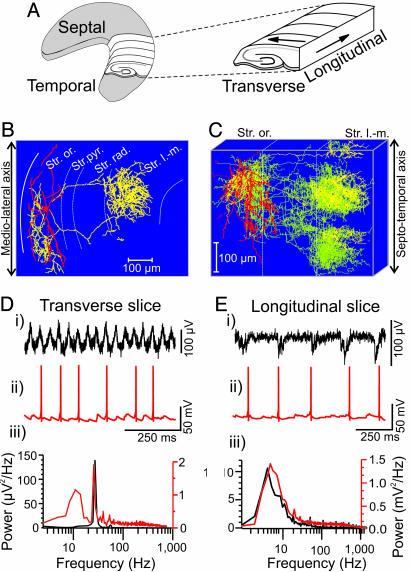
Fig. 4.

Morphological and electrophysiological characterization of O-LM interneurons in hippocampal slices. (A) Three-dimensional representation of the hippocampus illustrating the orientation of the transverse and longitudinal axis. (B) Neurolucida reconstruction of biocytin-filled O-LM cell in area CA3 from transverse slice. The soma and dendrites are drawn in red, whereas the axon is in yellow. (C) Superimposed neurolucida reconstruction of six rotated O-LM interneurons from transverse slices showing the axonal arborization in the longitudinal direction (axons of cell in B are yellow, and axons of all other O-LM cells are superimposed in green). (D) Typical example of extracellular FP (i) and concomitant current clamp recordings (ii) in an O-LM cell after induction of oscillatory activity with KA in the transverse slice. (iii) Corresponding power spectra (60-s epoch) from field (black) and current clamp (red) recordings. (E) Corresponding recordings from longitudinal slice after KA.

We note that we are using one E cell to represent the population, whereas, in vitro, the E cells fire very sparsely. Therefore, we cannot compare the somatic traces in the experiment with the behavior of the somatic compartment (E) in the model. However, the “subthreshold” behavior seen in the experimental traces shown in Fig. 5 A–C is captured in the nonspiking dendritic compartment (D cell) of the model. In the experiments, the voltage variations arise from the inhibition from interneurons, which fire when population of pyramids spikes. Because the interneurons are excited by the population of pyramidal cells, we expect the D cell voltage to covary with the somatic variation shown in the experimental recordings but with reversed signs. This finding is indeed what we see in Fig. 5.

Results

Bath application of KA (400 nM) in hippocampal transverse slices induced gamma frequency field oscillations in area CA3 (mean frequency 36.7 ± 2.0 Hz, n = 7, Fig. 1 A–C; see also ref. 28). To characterize the spatial distribution and synchronization of gamma activity across the horizontal extent of area CA3, dual extracellular recordings were performed in the present study. Recordings were conducted with two FP electrodes, one serving as a reference and the second electrode was moved from a closer site (≈100 μm) to six consecutively more distant sites in ≈100-μm steps (Fig. 1 A). When a close distance (100–200 μm) separated the electrodes, the coherence of the gamma signals across both was high (≈0.9). When the separation between the electrodes increased, the coherence of gamma activity decreased substantially (Fig. 1 D and E). Because gamma frequency power was variable along the recording sites (Fig. 1 A and B) and this variation may have had an effect on the coherence measurements, a regression analysis was conducted between the cross-spectral amplitude and coherence for each of the signal pairs. No significant linear relationship between these two parameters was found (P > 0.05; n = 4, data not shown), suggesting that changes in coherence are independent of the gamma amplitude. In contrast to coherence, the phase shift of gamma waves in the transverse slices was very low (within ± 10°) and remained unchanged in all distances measured (Fig. 1F).

To characterize the dynamics of network activity along the longitudinal axis, similar spectral analysis was undertaken in longitudinal hippocampal slices (Fig. 2). In contrast to transverse slices, the dominant field network activity in the longitudinal slices was in the theta frequency range (Fig. 2 Aii and B). This activity remained highly coherent along all distances measured (Fig. 2E). Similarly, low phase shift of theta waves, observed in the longitudinal axis, remain unchanged across all recording sites (Fig. 2F).

Selective manifestation of theta and gamma frequency activity, in the longitudinal and transverse axes, respectively, suggested an orthogonal relationship between the local circuits responsible for the generation of the two rhythms. We therefore tested the possibility that intermediate orientations of a hippocampal slice may contain sufficient local circuitry to support both gamma and theta rhythms concurrently. Using coronal slice preparations in which pseudotransverse sections of the hippocampus can be seen extended in the longitudinal plane by 30–60°, we investigated KA-induced network activity (Fig. 3A). Both theta and gamma population rhythms were manifest in this preparation with power spectra and cross spectra demonstrating two clear peaks, one in each frequency band (Fig. 3 B and C). The coherence values for gamma band reduced strongly as the interelectrode distance was increased, whereas the theta coherence values changed significantly less (Fig. 3 D and E). In contrast, phase coupling showed little variance (<25°) in both frequency bands (Fig. 3F). To investigate the correlation (phase coupling) between FP frequency components in the coronal slice, we performed bispectral and bicoherence analyses. When bispectral analysis was used, we found clear peaks in the theta and gamma frequency band, suggesting the high coupling powers in the same (theta/gamma) frequency (Fig. 3G). A further peak in the bispectral analysis indicates strong coupling tendency also between theta and gamma frequencies (Fig. 3G). Similarly, bicoherence analysis showed a high level of phase coupling between these two frequencies across all recording distances (Fig. 3H). This result indicates a strong functional interaction between the generators of theta and gamma frequency oscillations in slices with intermediate orientation.

To elucidate the cellular and synaptic mechanisms underlying field network activity in the transverse and longitudinal axes of the hippocampus, we further analyzed the pattern of connectivity and the functional differentiation along the long axis of the hippocampus. In particular, we focused on the morphological and physiological properties of O-LM interneurons, shown previously to generate theta rhythms as part of a local circuit (14). Using whole-cell patch-clamp recordings in conjunction with post hoc anatomy, we investigated the three-dimensional axonal arborization patterns of different hippocampal CA3 interneurons recorded in transverse slices. Parvalbumin containing perisomatic targeting interneurons, along with trilaminar and bistratified cells (16), show a clear tendency to arborize widely within the transverse plane (the maximal extensions of the projections of perisomatic targeting cells in transverse and longitudinal planes were 727.5 ± 54.4 μm and 310.0 ± 18.3 μm, n = 5, data not shown). However, distal dendrite targeting O-LM cells arborized most extensively in the longitudinal plane (the maximal axonal spread was 223.7 ± 12.2 μm and 430.3 ± 4.4 μm in transverse and longitudinal directions, respectively, n = 6) forming two (four of six cells) or three (two of six cells) clusters in this direction (Fig. 4 B and C). The axon branches of O-LM interneurons (n = 6) in the stratum lacunosum-moleculare tended to cluster in narrow bands both in the plane containing the cell soma (cluster width 125.9 ± 11.2 μm, n = 6) and also further along the longitudinal direction (width 118.7 ± 10.9 μm, n = 6). The longitudinal intercluster interval (between adjacent edges) was 92.2 ± 17.1 μm (n = 6). Therefore, the axon plexus of this cell type innervates distal dendrites of pyramidal CA3 cells that are distributed in distinct segments along the length of the hippocampus. In contrast to axonal arborizations in stratum lacunosum-moleculare, the axon branches of O-LM cells in stratum oriens form a single cluster at the level of their somata (Fig. 4C).

We further examined the intrinsic and synaptic properties of O-LM interneurons in transversal hippocampal slices. During depolarizing current injection O-LM cells show subthreshold membrane potential oscillations in the theta frequency range between 4.9 Hz and 11.9 Hz (mean frequency 8.1 ± 1.8 Hz, n = 7, data not shown). In addition, during KA-induced field gamma oscillations, these interneurons discharged with firing rates in the theta frequency range (8.2 ± 2.1 Hz, n = 9, Fig. 4D, see also ref. 16). The gamma frequency field oscillation was no longer present in the longitudinal slices. Instead, a low frequency oscillation in the theta frequency range (mean frequency 8.1 ± 2.0 Hz, n = 14) was the dominant activity in this preparation. Similar to the transverse slices, O-LM interneurons continued to fire at theta frequency during KA application in the longitudinal slices (Fig. 4Eii and iii). However, significant decreases in the frequency and amplitude of KA-induced excitatory postsynaptic potentials were observed in comparison with the transverse slice (Fig. 4 D ii and iii and E ii and iii). O-LM cells are likely to provide a theta-frequency patterned output to distal dendritic regions of pyramidal cells along the long axis of hippocampus.

Simulations. The results of our simulations are given in Fig. 5. Fig. 5A (Model) corresponds to the transverse slice by using parameter set I of Supporting Text. Here, the E and I cells generate a synchronized pattern at gamma frequencies, whereas the O cells fire at theta. The O → I, D connections prevent the E-I pattern from being completely periodic; the bottom graph shows that the gamma field is slightly modulated at theta frequencies. In the experiments, application of KA resulted in IPSPs at gamma frequency in pyramidal cells (Fig. 5A, Experiment). Fig. 5B (Model) corresponds to the longitudinal slice by using parameter set II of Supporting Text. Here all cells fire at theta frequencies, although not in a synchronous manner, and the FP shows a clear theta rhythm. Experimental recordings from pyramidal cells in longitudinal slices demonstrate rhythmic trains of IPSPs at theta frequency (Fig. 5B, Experiment). Fig. 5C (Model) corresponds to the coronal slice by using parameter set III of Supporting Text. Here the E and I cells generate a synchronous gamma pattern with periodic interruptions at theta frequencies. These interruptions are stronger than in Fig. 5A because of the greater strength of the O → I, D connections. The FP now displays a clear gamma rhythm modulated at theta frequencies. Whole cell patch-clamp recordings from pyramidal cells show the gamma frequency IPSPs modulated at theta frequency (Fig. 5C, Experiment).

Comparing Fig. 5 A–C, it is apparent that an increase in I cell frequency from theta to gamma does not necessarily suppress the O cells firing in our “minimal network” model (Fig. 5D). Because of the presence of an h current, the inhibitory interaction between fast spiking interneurons and O-LM cells has a dual inhibitory and excitatory effect that helps maintain the rhythm (22). For higher I cell frequencies and/or larger values of the maximal synaptic conductances, the O cells are effectively suppressed. The value of the frequency at which this suppression occurs is model dependent (22).

Discussion

Our experiments and model indicate an orthogonal arrangement of gamma and theta rhythm-generating microcircuits in hippocampal area CA3. Theta frequency oscillations are the dominant network activity along the long axis of the hippocampus interconnected through CA3 pyramidal cells and O-LM interneurons. In contrast, gamma-band oscillations are observed predominantly within the transverse axis of the hippocampus.

Local gamma generating microcircuits have been seen in vitro in transverse sections of hippocampus involving both recurrent inhibition (12) and heterogeneous networks of interneurons and principal cells (13, 16). In vivo area CA3, particularly subregion CA3a-b, has been suggested to be the principal source of intrahippocampal gamma rhythms (29). These gamma oscillations project to area CA1 along the transverse axis of the hippocampal slice (13, 14), albeit with a relatively steep drop-off in coherence even within area CA3 (ref. 30; see Fig. 1), suggesting that they may conform functionally to the lamellar organization originally proposed for the hippocampal formation (6).

In contrast, neurons in area CA3c of the hippocampus project in the longitudinal direction (9) and, in this study, we demonstrate that axonal projections from O-LM interneurons, capable of sustaining a field theta rhythm with tonic excitation (14), also project in this direction. In longitudinal slices, the preservation of these projections facilitated the generation of theta rhythms with robust coherence over large distances (see Fig. 2). This pattern of theta coherence has also been reported in the freely moving rat in vivo (30, 31). Generally, slower oscillations in vivo are spatially more extended (32). The almost complete absence of power in the gamma band in the horizontal section strongly suggests an orthogonal arrangement of the local hippocampal circuits responsible for the generation of the two rhythms. It should be noted that CA1 O-LM interneurons have been shown to extend up to 800 μm in both transverse and longitudinal planes (33), suggesting that this orthogonal arrangement, as described here, is specific for area CA3.

In the intact hippocampal formation, gamma activity is nested within the theta rhythm and is larger during theta-associated behaviors than during immobility (30, 34). Thus, we took advantage of the selective orientation possible with hippocampal slices to investigate the interplay between these two rhythms with orientations intermediate between the transverse and horizontal axis. Using coronal sections, it was possible to elicit both persistent gamma and theta rhythms. Bispectral and bicoherence analyses of these simultaneously expressed oscillations showed strong coupling in the theta-gamma wave bands. The field recordings still lacked the overt, large amplitude theta waves seen in vivo (see above), but this conclusion was not surprising given the absence of medial septum-diagonal band of Broca input (35). However, the phase locking of spatially distributed regions of hippocampus can occur in the absence of this input.

On the basis of morphological, electrophysiological, and computational analyses, we suggest that at least two factors are responsible for the orthogonal arrangement of rhythms in the hippocampus. First, most pyramidal cells of the CA3 region participate in the strong “gamma-generating” recurrent system in the transverse as opposed to longitudinal axis. The significantly lower amplitude and frequency of interneuron-excitatory postsynaptic potentials in longitudinal slice than those in the transverse slice during KA-induced network activity (see Fig. 4) support this notion. Second, “theta-generating” O-LM interneurons show at least a 2-fold larger axonal spread in the longitudinal rather than transverse plane. They may therefore provide much stronger (at least by a factor of 2) theta frequency patterned output to the distal parts of the pyramidal cells and to the interneurons in the longitudinal plane.

Coexistent gamma and theta rhythms may, therefore, represent a two-dimensional strategy for processing hippocampal inputs. The apparent orthogonal arrangement of theta and gamma generating microcircuits within the hippocampal network may allow activity within functional lamellae, along the classical trisynaptic circuit, to be temporally coordinated at gamma frequencies, whereas activity distributed between distinct lamellaes (e.g., see ref. 3) is temporally coordinated at theta frequencies.