Mutation, specialization, and hypersensitivity in highly optimized tolerance

Abstract

We introduce a model of evolution in which competing organisms are represented by percolation lattice models. Fitness is based on the number of occupied sites remaining after removing a cluster connected to a randomly selected site. High-fitness individuals arising through mutation and selection must trade off density versus robustness to loss, and are characterized by cellular barrier patterns that prevent large cascading losses to common disturbances. This model shows that Highly Optimized Tolerance (HOT), which links complexity to robustness in designed systems, arises naturally through Darwinian mechanisms. Although the model is a severe abstraction of biology, it produces a surprisingly wide variety of micro- and macroevolutionary features strikingly similar to real biological evolution.

In biological evolution, new species continually arise through mutation as natural selection determines the survival of the resulting organisms amidst fluctuating environmental conditions (1–4). The phrase “survival of the fittest” broadly encompasses an extensive collection of competitive and cooperative relationships between species and their environments (5). Evolutionary biologists aim to identify the patterns in this process through a combination of paleontological studies of phenotypic traits in the fossil record and genetic mapping and phenotypic studies of existing species in both natural and laboratory environments. Despite enormous progress on all fronts, there are many controversies regarding even the most basic questions, due in great part to the sheer complexity of organisms and ecosystems. In this paper we introduce a model which we hope will contribute to ongoing debates regarding the relationship between micro- and macroevolution, and perhaps stimulate new questions. We particularly focus on evolution and large-scale patterns such as extinction, necessity versus contingency, and phenotypic convergence versus genotypic divergence.

Any discussion of evolution and biology deals with multiple hierarchical classifications, with perhaps the most fundamental being the layered representation of genotype, phenotype, and fitness. Even these concepts are not without controversy, but generally phenotype refers to the expressed traits, which are observed through interaction with a specific environment. This formulation leads to fitness as a measure of the phenotypic success in reproduction and competition, subject to the environmental conditions experienced. Genotype refers to the heritable features that characterize individuals and are largely independent of the environment. Models for evolution where genotype, phenotype, and fitness are present and connected are bounded by two accepted descriptions. Darwinian evolution by random mutation and natural selection provides a broadly encompassing phenomenological starting point for discussing change, whereas molecular biology describes in detail the experimentally deduced physical, chemical, and biological pathways involved in evolution.

Many theoretical studies aimed at explaining extinction patterns and statistics in the fossil record (6) have focused on exclusively macroscopic definitions of fitness. In these models species lack genotypic and phenotypic notions of structure, heredity, and expression, and instead are represented in terms of scalar fitness variables obeying dynamical rules, whereby the system self-organizes to a critical point (SOC) or the “edge of chaos” (EOC) (4, 7, 8, 33). Here we introduce a model with concrete and distinct concepts of genotype, phenotype and fitness that are severe but hopefully meaningful abstractions from biology. Our model is motivated by a recently developed theoretical framework for understanding complexity, referred to as Highly Optimized Tolerance (HOT) (9–13). While the importance of robustness in biology has long been recognized (14), it is receiving renewed attention. Studies include robustness tradeoffs as a mechanism that drives complexity in biology (15, 16), and the relationship of robustness with evolvability (17).

A key signature of a HOT system is that it is simultaneously robust, yet fragile: robust to common disturbances the system is designed to handle, yet fragile to rare events and flaws in the design. Such structured sensitivity is a central property of biological systems over a broad range of scales (from individual cells and organisms to ecosystems), and is naturally associated with the ability to sustain a wide range of environmental conditions (weather, nutrients, etc.), yet have extreme sensitivity to certain small perturbations (mutation of a single gene, introduction of an exotic species, etc.). Initial papers on HOT focused primarily on percolation lattice models (18), representing “toy forests” subject to external “sparks.” This facilitated direct comparisons with SOC versions of the same model. Studies have focused on individual lattices deliberately optimized for a prescribed distribution of sparks. Here we explore this framework in a biological context: a community of lattice models subject to Darwinian evolution. We illustrate that HOT can arise through such evolution, and we explore the consequences of competition between different lattice “species” that are subject to selection based on fitness evaluated over different time horizons. While this model is simple, the behavior it exhibits is surprisingly rich. In the concluding sections we present an extensive discussion of its biological relevance.

The Model

Our model consists of a population of N × N square lattices. Each site is occupied or vacant, and the layout defines the lattice genotype. Contiguous nearest-neighbor occupied sites define connected clusters. External perturbations are modeled by “sparks,” which impact sites (i, j) based on a probability distribution P(i, j). If (i, j) is vacant nothing happens. However, if (i, j) is occupied the connected cluster of occupied sites containing (i, j) “burns” and is lost. For our numerical simulations we take P(i, j) ∝ exp(−(i + j)/ξ), where ξ is 1/6 of the lattice size. Our basic conclusions and the features of the resulting design [including sensitivity to changes in the P(i, j)] do not depend on the specific form of the nominal P(i, j), aside from the fact that the distribution is skewed. A skewed distribution reflects the fact that different perturbations have different frequencies, like external uncertainties in biology.

The phenotype is the list of possible event sizes l_n (number of sites in the nth connected cluster divided by the system size) along with the corresponding probabilities f_n (the sum of the P(i, j) values in the nth cluster). The list {f_n, l_n} includes l_n = 0 corresponding to the vacancies. The definition of phenotype is not unique, but our choice conveniently reduces the information contained in the genotype to the set of traits that can be observed through interaction with the environment, and contains sufficient information for subsequent evaluation of fitness.

The fitness reduces the phenotype of the lattice to a number. Because fitness depends on history and experience, the definition must take into account relevant time scales. These include the time scale of large-scale change in the environment, which corresponds to changes in P(i, j) (13). We assume P(i, j) remains fixed, so this time scale is effectively infinite. There is also a time scale for selection based on the relative fitness of individuals. This defines the time axis for mutation, reproduction, and determination of survival, represented as a discrete sequence of generations. Finally, there is the time scale over which fitness is evaluated. We consider two extreme cases, describing different “types”—one in which mutation and selection occurs at the same rate as individual environmental perturbations, and another in which the fitness accounts for the full spectrum of possible disturbances. (Here “type” describes organisms that share a common fitness evaluation mechanism.)

For both types, fitness is related to yield Y, the density of occupied sites surviving a single spark drawn from P(i, j). For a lattice of initial density ρ, Y = ρ − 〈l〉, where 〈l〉 is the density loss (or average loss) in one fire. The two types differ in how 〈l〉 is computed. For one, fitness is defined to be the yield Y_∞ = ρ − 〈l_n〉_fn averaged over the full set of possible events (the phenotype) weighted by the corresponding probabilities. For the other, the fitness Y₁ is evaluated stochastically based on a single spark applied to all members of the type: Y₁ = ρ − l_n. We refer to the Y₁ type as “hares” because they evolve rapidly, over-specialize for common disturbances, win in the short term, but are vulnerable to extinction in rare events (as shown in the next section). We refer to the Y_∞ type as “tortoises.” The effectively infinite time horizon on which tortoises base their evaluation of fitness ultimately leads to a better design for long-term survival.

We begin with 1,000 randomly generated lattices with N = 16, divided equally between the tortoise and hare types. Each subsequent generation consists of two offspring from each parent lattice, each with a finite probability of mutation. Here mutation corresponds to inverting the occupation of a site. The mutation probability is equal for each site, and taken sufficiently small that on average only one site mutates on one of the two offspring. Each resulting generation of offspring is then subject to natural selection based on fitness Y. We define an upper bound of 1,000 on the total population S. Competition based on fitness occurs among all of the lattices for this limited space in the community. Any lattice with Y < Y_d is considered “dead” and automatically discarded, along with the lowest overall performers from the tortoise and hare types considered jointly until the total size S of the community is S ≤ 1,000. The results shown have Y_d = 0.4.

Although our model is a severe abstraction from real biology and ecology, and emphasizes pure competition for space in the community, ignoring many other important types of interactions, the lattice layout makes the relationship between adaptation and fitness simple and transparent, and it allows direct comparison with familiar percolation models that have been used in an attempt to connect critical phenomena with biology and ecology. It is sufficiently general that it could be equally well motivated by competition and evolution in other settings, such as between technologies and companies in an economic setting. However, in the spirit of biological evolution, adaptation is accomplished through purposeless mutations and discriminating selection.

The resulting model has rich and illustrative dynamics, yet intuitively clear outcomes, contrasting differences in evolution and adaptation between organisms characterized by identical internal interactions and the same environmental conditions, but distinct time horizons for evaluating fitness. We focus on one particularly simple version of this model to introduce the basic concepts and results, but compare it with a variety of related models with alternative assumptions. This version maintains diversity with niches for each type that preserve the 50 most fit organisms, regardless of their fitness relative to the overall population and viability threshold (death rule). Each niche has only intratype competition, but we continue to allow intertype competition in the remaining pool of 900 organisms outside the niches.

Numerical Results

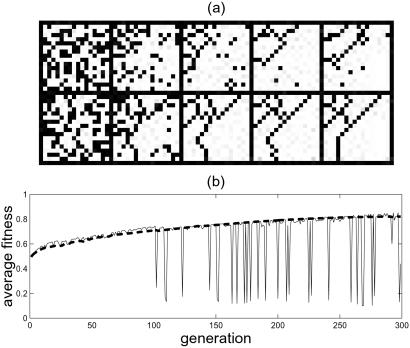
We begin with 1,000 randomly generated lattice organisms, equally divided between the two types, and with niches of size 50 allocated to each. We take P(i, j) ∝ exp(−(i + j)/ξ), where ξ = N/6, N = 16, and i = j = 1 in the upper left corner of the lattice. Fig. 1 illustrates the progressive stages of evolution. In both types, the original random parent lattice evolves toward patterns of increasing density and nongeneric spatial structure. Mutation and selection create order from the random homogeneous beginnings and lead to sharply defined, linear barriers of vacant sites, separating compact cellular clusters of occupied sites. Even at the relatively early stages of evolution the tortoises and hares begin to develop barrier patterns that are characteristic of their respective types. The tortoises sacrifice density to retain a higher concentration of barriers in regions that have less frequent sparks. For the hares, the configurations are noisier with some stray vacancies, and barriers in low-risk regions are lost because of the short-term competition. As illustrated in Fig. 1b, in early stages of the evolution the average fitness of each type is increasing. The average fitness of the hares typically exceeds that of the tortoises, although the hares' average fitness exhibits much more significant fluctuations attributable to the stochastic sampling of P(i, j).

Figure 1.

Early stages of evolution. (a) Sample lattices drawn randomly from generations 0 (left), 100, 300, 700, and 1,500 (right) for the hares (Upper) and tortoises (Lower). Black sites are vacant, and white sites are occupied. (b) Average fitness over the first 300 generations for the tortoises (smooth broken line) and hares (noisy solid line).

The last snapshot in Fig. 1a illustrates a representative configuration after 1,500 generations, when the average fitness has leveled off significantly compared with the increasing values in Fig. 1b. By that time, in a given run within each type organisms are nearly identical, and can be thought of as constituting a single species. For both the tortoise and hare types, different initial conditions consistently show convergent evolution from random layouts to qualitatively similar phenotypes (list of cell sizes and probabilities {f_n, l_n}), although the detailed location of barriers varies significantly between runs.

For both types, the long time patterns are similar to those observed previously for HOT systems constructed by deliberate optimal design (9, 10). These configurations illustrate the yield tradeoff that occurs between maximizing the density and constructing barriers to prevent loss from spreading. High yield states are associated with efficient, linear barriers concentrated in regions where P(i, j) is greatest (the upper left hand corner in Fig. 1a), in systems that are otherwise densely occupied. A primitive division of labor evolves between regions with large cells and high densities, and regions of small cells, lower occupation densities, and more barriers that protect the cells from sparks. The main distinction between the types is apparent in comparing the lower right portion of the lattices in Fig. 1a. The tortoises have a diagonal barrier cutting across the lattice that lies closer to the lower right corner of the lattice, where P(i, j) is relatively low. In comparison, hares have higher average initial density, and barriers only in the high-probability, upper left corner of the lattice because their evolution does not emphasize rare events.

Without niches, competition leads rapidly to the selection of a single type, and every remaining individual is the offspring of a single fortunately configured ancestor. This effect decays algebraically with population size, and would be irrelevant in systems which are large enough that the time associated with collapse to a single ancestor exceeds the times scale for evolution and extinction. However, in the community of 1,000 lattices, the collapse occurs within roughly 10 generations, when no significant evolution occurs, so success in this early competition is due primarily to yield variations in the initial configurations. Because these configurations are random, the two types behave similarly, and on average neither has an advantage. If the tortoises win this initial competition, they persist forever at the maximum population of 1,000. This result is not surprising because they are “optimized” for long-term yield. In contrast, if the hares survive, the organisms on average evolve more rapidly and to higher densities because they do not sacrifice density to protect against rare events. However, eventually they evolve to the point where a rare event causes death of all of the organisms (i.e., extinction) because a single spark in the lower right corner of a highly evolved member of this species drops the instantaneous yield below Y_d. It is the relative rapidity of evolutionary change and the ultimate extinction versus survival that led us to refer to the Y₁ type as hares and the Y_∞ type as tortoises.

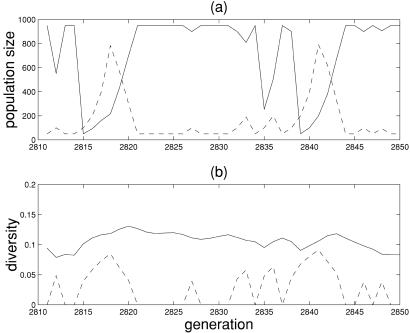
When niches are included both populations persist (by definition the niches retain the top 50 of each type), and we observe the irregular cyclic fluctuations illustrated in Fig. 2. Because they do not sacrifice density to protect against rare disturbances, the hares perform better on shorter time scales. For long periods when no rare events happen, the hares have higher fitness and thus dominate. Nearly all of the available 1,000 spaces belong to the hares, while the tortoise population is sustained at the minimum of 50. Thus the hares, with their short-term high fitness, dominate the community on shorter time scales. When a rare spark impacts the lower right portion of the lattice, the hares die when their yields drop below Y_d = 0.4. This leads to near extinction in which the hares are now pushed entirely back into their niche. Such dramatic events are shown in Fig. 2a as steep drops of the hare population to the minimum of 50. In contrast, the tortoises are broadly robust to the full spectrum of disturbances, and do not die in a rare event. Because the extinction of hares makes room for growth, the tortoise population begins to expand rapidly in the period just after a rare disturbance. Hares, the “fitter” species in the short term, face episodic near-extinctions in the long term, whereas the tortoises, which are more nearly optimal for the full spectrum of events, survive on long time scales, but lose out in short-term competition.

Figure 2.

Hare (solid line) and tortoise (broken line) population size (a) and diversity (b) versus time. Diversity corresponds to the root-mean-square deviation of the organisms within a type from the ensemble average configuration (Fig. 1), averaged over sites.

In the period just after a rare event, the overall size S of the community falls well below the upper bound of 1,000. This is a fertile time for growth and diversification (see Fig. 2b). Nearly all of the living spaces are available. All of the offspring survive, so that the acceptance rate of mutation is 100%, which is much higher than the background level, as the populations of both species simply double in each generation. The tortoises are one step ahead because they did not suffer during the rare event, so their population is roughly twice that of the hares. Such periods of growth are relatively brief, and they end when the saturation level is reached. Shortly thereafter, competition again becomes important. Because the hares outperform the tortoises in the short term, they dominate and squeeze the tortoise population back to their niche 50, which completes the cycle. This picture of peaceful periods with intermittent bursts of activity is an extremely simplified example of punctuated equilibrium (19).

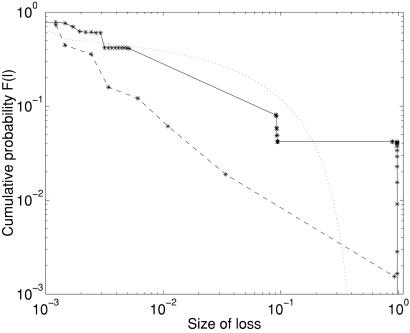
The two populations also differ in the overall statistics associated with the size distributions of losses f_i(l_i). In Fig. 3 we compare the cumulative probability distributions F(l_i) = ∑_lj≥li f_j(l_j) for the two species on a simulation using 64 × 64 lattice organisms for better statistics. All other parameters of the model remain fixed. For the hares the tail of the distribution is heavier than the power law tail associated with the tortoises. The probability density f_i(l_i) has a bump, which corresponds to the almost vertical steps of discrete losses of nearly identical size in the cumulative distribution, indicative of excess large events relative to an extrapolation of the rate of smaller events. The excess large events capture the hypersensitivity of a robust system when facing perturbations not incorporated in the design.

Figure 3.

The cumulative distributions of losses F(l) for the hares (solid line) and tortoises (broken line), plotted for 20,000 generations (after allowing for an initial transient of 10,000 steps) on 64 × 64 lattices. Discrete points represent the actual event sizes, with lines drawn between them to guide the eye. The dotted line is the corresponding statistics for a “critical” lattice.

Microevolutionary Features

In this paper we present an abstract model of evolution that has a simple and transparent connection between genotype, phenotype, environment, and fitness. Despite its extreme abstraction and simplicity, our model provides a clear mechanism whereby microscopic processes of mutation and selection at the organism level (“microevolution”) are linked through competition and interaction with an uncertain environment, to large-scale “macroevolutionary” patterns, such as extinction events. It further captures how intrinsic robust design tradeoffs interact with and constrain natural selection to generate highly ordered structure from randomness. It is the model's biological relevance that is the most serious question, and we will focus on two aspects, the plausibility of the basic assumptions in the model and the realism of the resulting “emergent” properties seen in the numerical studies.

We have investigated variants of the model to evaluate the importance of parameter values and assumptions. The extinction yield Y_d = 0.4 was varied with predictable results. The overall pattern was qualitatively retained, with relatively lower Y_d producing relatively longer periods between large “extinctions” of hares. The tortoises can be replaced by organisms that compute yield as the hares do, but with slow mutation rates. This too produces qualitatively similar results but of course the tortoises take longer to develop their structured barriers. A simplification using the PLR (Probability/Loss/Resource) formulation of HOT (12) replaces the concrete barrier patterns created by empty sites with macroscopic phenomenological resource/loss tradeoffs, and this too produces qualitatively similar dynamics. The PLR genotype is thus an abstract resource allocation making the PLR model more tractable and allowing for both computation with more organisms and niches and some analytic results.

Perhaps the most interesting variant we have studied involves creating habitats with different spark distributions P(i, j) (unpublished work). Competition occurs within each habitat and organisms can migrate between habits, but there are no protected niches. Lattices in a habitat with skewed distributions as in this paper become “specialists” and evolve like the hares, developing barriers concentrated in regions where sparks are frequent. Lattices in a habitat with a spatially uniform distribution of sparks become “generalists” by developing a roughly uniform grid of barriers, which is optimal in their habitat. The generalists essentially never suffer large extinction events and are safe but suboptimal in habitats with skewed distributions. The specialists eventually suffer total extinction caused by rare sparks because they lack the protected niche included in this paper. When this occurs, generalists who have migrated into the skewed habitat flourish and eventually evolve into specialists, and the cycle repeats (20). Adding a variable mutation rate that is itself subject to mutation and selection leads to generalist tortoises and specialist hares, and qualitatively similar cycles. This model has additional rich behavior.

The notion of genotype as an N² length bit string that is subject to random mutation by bit flips is neither novel nor remarkable. It is the phenotype of lattices in an uncertain environment and the resulting fitness that are most novel and most in need of justification. The fitness defined in terms of yield Y = ρ − 〈l〉 has two contributions, density and loss. The benefit of high density can be thought of as an abstraction of the throughput of tightly coupled and finely tuned metabolic and reproductive networks. In an ideal environment an organism would evolve to simply maximize throughput or density, wasting little energy or material on protecting its metabolic networks or reproductive mechanisms from perturbations. In our model without sparks, all of our organisms will eventually evolve to unit density lattices without vacancies or barriers. However, realistic environments include perturbations, and purely maximizing density would be catastrophic, because these perturbations would lead to cascading failures in an unprotected organism. This behavior is reflected in the loss contribution to yield, which forces organisms to make a tradeoff between high densities and potentially high losses versus lower densities and losses. Sparks are abstractions of the real uncertainties in the environment and in components, which include biochemical stochastics as well as fluctuations from temperature, oxygen, nutrients, predation, and parasites, to climate and weather, geophysical phenomena, and meteoroid impacts. Perturbations can vary enormously in their frequency, which is reflected in our model in the nonuniform (exponential) P(i, j).

Most damage in cells, organisms, and ecosystems, such as infections, epidemics, organ failure, cancer, starvation, forest fires, and takeover by exotic species, typically involves small initiating perturbations that cascade into network and system-wide events. For example, at the cellular level, when the temperature in a cell's environment rises above physiologically normal levels it can initiate a cascading failure event. First, the cell's internal temperature rises, which can cause proteins to denature, and then form aggregates, eventually losing functionality. This chain of events leads to failure of intracellular networks and ultimately cell death. At the other extreme of scale are the meteoroid impacts thought to be responsible for large extinctions. While there is certainly widespread death from the immediate blast, far greater losses are thought to occur from atmospheric dust particles blocking photosynthesis, leading to cascading failures of the food chain (34).

Our model focuses attention on a single, and we believe fundamental, abstraction of biological complexity: building barriers to cascading failures. Because this is not a familiar abstraction, it requires careful justification. Some robustness barriers are obvious from an organism's external physiology. Bacteria have cell walls to protect intracellular processes, and under extreme conditions may create hardened spores that can survive even boiling or the vacuum of space. Higher organisms develop exoskeletons, shells, horns, and thick and tough skins, or seek out and sometimes even construct protective barriers by using materials in their environment. Similarly, the cascading failure events that these mechanisms protect against are often obvious and transparent, such as trauma from physical attack. Even mechanisms conferring mobility often are used to put space and time barriers between organisms and their predators or parasites, or potentially damaging environmental perturbations

Neither our model nor molecular biology has such barriers “built in,” and they “emerge” only through evolution in an uncertain environment. Thus only a few hundred genes are required for minimal life in an idealized laboratory environment, but free-living bacteria often have many thousands of genes, most of whose knockout mutations are not lethal in laboratory conditions. This is because most genes code for sensors, actuators, and the complex regulatory networks that control them, and thus confer to the cell robustness to variations rather than the mere basic functionality required for survival in ideal circumstances. The central claim from our model is that the essence of this robustness, and hence of biological complexity, is the elaboration of highly structured mechanisms that create barriers to cascading failure events.

Most robustness barriers are far from obvious, and involve complex regulatory feedback and dynamics, to stop cascading failures that are themselves often cryptic and complex. There is no simple identification directly with external physiological features. The abstraction of barriers continues to hold nonetheless, but now we must consider them as occurring in the state space of an organism's dynamics. Bacteria both use chemotaxis and regulate metabolic pathways to utilize available nutrients and avoid starvation, and have a variety of sporulation strategies under extreme conditions. Higher organisms have even more sophisticated barrier mechanisms. Immune systems mount elaborate defenses to block infections, the route to cancer has multiple barriers, and damaged organs can regenerate. Much of the battle between parasites and hosts and between predators and prey can be viewed as the creation of ever more elaborate barriers in a joint state space. Even ecosystems exhibit sophisticated collective barrier behavior, although here the connection between genotype and overall fitness is least well understood. The succession patterns of vegetation after forest fires effectively build barriers to fires recurring too frequently. The global ecosystem apparently finely regulates oxygen levels far from equilibrium (21). Too much oxygen and huge fires would constantly sweep the planet, and too little would kill aerobic organisms.

Consider again the cascading failure effects of high temperature, which can be blocked by building barriers at a variety of levels. Mammals use complex feedback regulation and insulation to create a barrier protecting cells from external temperature changes. Bacteria exhibit thermotaxis, thus creating a spatial barrier to heat. Key proteins can have energy barriers for temperature stability, or have multiple (allelic or paralogous) variants. Regulated multiple gene loci allow individuals to respond to changing environments, whereas allelic variants allow populations to adapt on reproductive time scales. Finally, elaborate heat shock responses up-regulate chaperones, which refold denatured proteins. If we think of heat shock as a cascading failure event in the state space of the cell's dynamics, these protective measures can be thought of as building barriers in this state space. Note, however, that it is primarily fluctuations in temperature rather than absolute levels that require barriers. Microbes have been found at almost all temperatures and pressures where water is liquid, but none come close to surviving throughout this entire range. Thus both boiling and freezing reduce microbial growth.

We have aimed for the simplest model with an explicit genotype and phenotype that captures what we believe is the essential mechanism that drives the evolution of complexity in organisms and ecosystems, which is the emergence of robustness barriers to cascading failures through evolution and natural selection. In doing so, we have focused on primitive representations and have sacrificed the rich behavior and complexity of fitness, loss, and barrier formation in real organisms and ecosystems. Natural extensions to this model could include genetic transfer and recombination and interactions beyond direct competition, which could lead to food chains, various types of symbiosis, predation, and parasitism. However, this simplest model not only captures essential emergent feature of organisms at the microevolutionary level but also has interesting emergent macroevolutionary patterns, as we discuss next.

Macroevolutionary Consequences

In the fossil record, extinction “events” can be characterized in terms of “size,” a measure of the rate at which distinct species become extinct. Large events are associated with strong temporal clustering in the disappearance of individual species. It has been argued that overall the distribution of event sizes may have moderately heavy tails (22), and a variety of models have been studied in this context (4). In our model we sacrifice diversity of species to retain detailed internal structures. With only two types, and with each type converging to almost identical genotypes, the only nontrivial extinction statistics are associated with organisms. However, the model does capture the belief widely held within the paleontology community, that initiation of large extinction events is typically associated with rare or anomalous external causes, such as meteoroid impacts and large-scale geological change, whereas more frequent, smaller events are typically associated with a mixture of competition between species, as well as more commonplace variability in the habitat and other environmental conditions (1–4). Note that in our model, as in nature, this is a macroevolutionary pattern that is an entirely emergent property of the microevolutionary dynamics.

A recent review (23) argues that extinction is a “highly deterministic process” (24) in the sense that extinction-promoting traits are correlated both within an event and across events with similar initiating perturbations. In particular, many extinction-promoting traits are associated with “specialization.” Under common circumstances more specialized organisms can dominate in competition with organisms that are more robust for the full spectrum of the environmental uncertainty, but specialization also leads to hypersensitivity to rare disturbances. In our model, the internal structure of HOT systems corresponds to robust high-fitness states relative to the environment to which they are coupled. If the environment changes unexpectedly, or rare perturbations occur that are not taken into account in the evolutionary history of an organism, then the consequences may be especially severe. The hares become successfully specialized but systematically experience large extinctions.

A quite different view than HOT comes from advocates of self-organized criticality (SOC) (25–27) and the edge of chaos (EOC) (23). There is a large literature with a variety of models [see recent reviews (4, 8)], but they share some common themes. In broad terms, these groups suggest that the heavy tails are described by power laws and focus on claims of statistical self-similarity in the fossil record to argue that evolution naturally drives ecosystems to the neighborhood of a critical phase transition or bifurcation point. In this view, it is sufficient to explain large events as avalanche-like and arising from coevolutionary internal dynamics. Thus there is no need to invoke external abiotic forcing or model the highly structured complexity that is the focus of much of biological research. The SOC/EOC point of view has largely been rejected by the paleontology community precisely because it avoids both the highly structured, largely deterministic features that evolve in organisms and ecosystems and the large events that are attributed to abiotic perturbations in their environment.

We can reveal the flaws in the SOC/EOC argument by applying it to our lattice model, where it superficially appears to offer an attractive explanation for the macroevolutionary features of power laws and punctuated equilibrium. The SOC/EOC argument rests on two points, the first trivially true, and the second obviously false. First, note that at low densities ρ where the lattices are sparsely populated, the yield is also low because Y = ρ − 〈l〉 ≤ ρ. At sufficiently high densities, high losses 〈l〉 are unavoidable, and thus yield is also low. Thus the maximum yield must necessarily, and trivially, occur at some intermediate density. Second, for purely random lattices, this maximum occurs at the critical density, which provides one mechanism for power laws. The mistake in applying this argument to our model is attributing the maximum yield and the power law behavior to criticality. In fact, our lattices, whether tortoises or hares, generalists or specialists, evolve to a highly structured HOT state completely unlike criticality with much higher densities and yields. If we initialize the model with a set of random lattices at the percolation critical point, they evolve away from it. If we begin with completely empty lattices, the density necessarily passes through the critical density on the way to a high density state. However, even at the critical density, the community of evolved lattices will be completely unlike familiar critical lattices. The evolution process quickly leads to highly nongeneric, structured configurations, completely unlike criticality.

To create a variant of our model that does evolve to a critical point, we must assume that the genome consists of only a single number, the density ρ, and that the lattices are redrawn each time from an otherwise random ensemble, rather than inheriting any other features from their parent. Such evolution seems distinctly abiological, and the “order for free” (7) that emerges at criticality is completely unlike the order of either our lattice models or known biological organisms. Furthermore, the power laws at criticality have exponents much smaller than either our lattice models or the fossil record (4). In Fig. 3, the HOT power laws are steeper and extend to larger event sizes than the critical power laws, which are very flat. Large events at criticality are fractal, resulting in no macroscopic losses in the limit of large lattices. This is in contrast to both our model and the fossil record, which show losses that are a large fraction of the total organisms or species. Similar sharp contrasts between HOT and critical models in capturing the observed statistics and features of other real-world systems has been noted elsewhere (28). Newman and Palmer (4) have introduced a series of models that do produce more realistic statistics, driven by abiotic perturbations, unlike SOC. These models were inspired by the SOC/EOC models, but do not appear to be critical. Unlike our model, these models all lack a distinction between genotype and phenotype, relying on phenomenological fitness parameters.

Chance and necessity play out in our models in ways that are strikingly reminiscent of real biology. Our lattice models exhibit both genotypic divergence and phenotypic convergence in response to the environment. In all variants of our model, organisms consistently cycle through similar phenotypes, but even identical phenotypes can have genotypes that differ substantially in their defining bit strings. Nevertheless, the process of purposeless mutation and selection in our model, like biology, creates the impression of a clear direction in evolution, with results very similar to what would arise from purposeful engineering design for high yield. High-fitness genotypes must produce highly structured phenotypes, no matter whether the “design” process is deliberate or random. In short, the environment and necessity largely determine the gross phenotype, whereas chance dominates the details of the genotype. An engineer asked to design a high-fitness lattice might use a local search process that was essentially the tortoise evolution, although presumably an engineer would choose a more computationally efficient implementation. Even a hare-like lattice could arise if the engineer chose to risk disaster in favor of better short-term performance. Examples of such engineered systems abound (29), and certain technologies involve inherently high risk (30).

In our model, the rarity of an initiating spark site is more important than the spark's intrinsic severity in contributing to large extinctions. Although it may initially appear highly counterintuitive, this may also be true for the fossil record, even for large meteor impacts and other major geophysical phenomena. It has been argued that both early life and most of the earth's current biomass and genetic diversity are part of a “deep, hot biosphere” of methane-eating and “rock-eating” (lithotrophic) hyperthermophiles (31, 32). This underground biosphere has extreme but relatively constant conditions, is largely independent of surface life, and is protected from the harsh ionizing radiation and meteor strikes that bombard the surface. Organisms here may even benefit from the crustal damage caused by large impacts and other geophysical phenomena, which can increase the flow of methane fuel from greater depths. Once large impacts became rare, specialists could exploit this rarity to create a diverse but fragile surface ecosystem. Thus large geophysical events and meteor impacts are not intrinsically damaging to all or even most life on earth, but become so when their rarity allows for the evolution of vulnerable specialists. Even the large extinction event currently in progress and attributed to human impact threatens only a small subset of the biosphere, although it may be a subset essential to human survival.

Abbreviations

SOC

self-organized criticality

EOC

edge of chaos

HOT

Highly Optimized Tolerance