Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 1996 Jun;70(6):2950–2958. doi: 10.1016/S0006-3495(96)79865-X

Anomalous diffusion of water in biological tissues.

M Köpf 1, C Corinth 1, O Haferkamp 1, T F Nonnenmacher 1
PMCID: PMC1225275  PMID: 8744333

Abstract

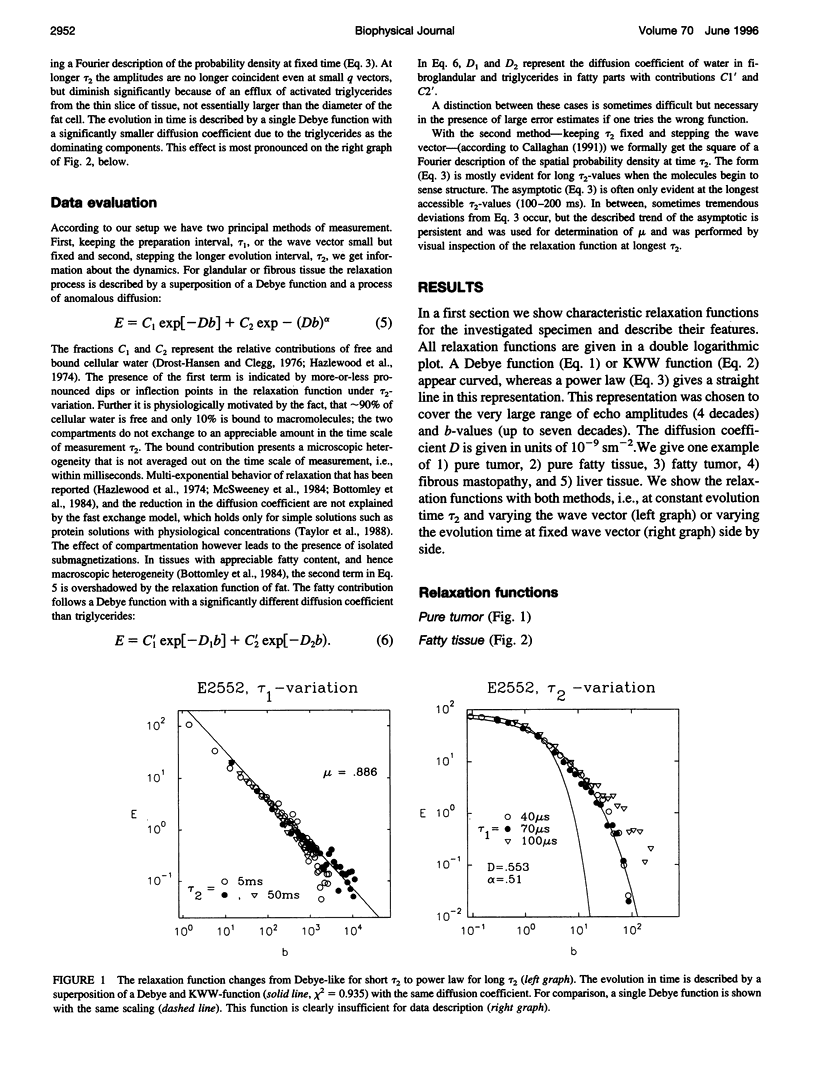
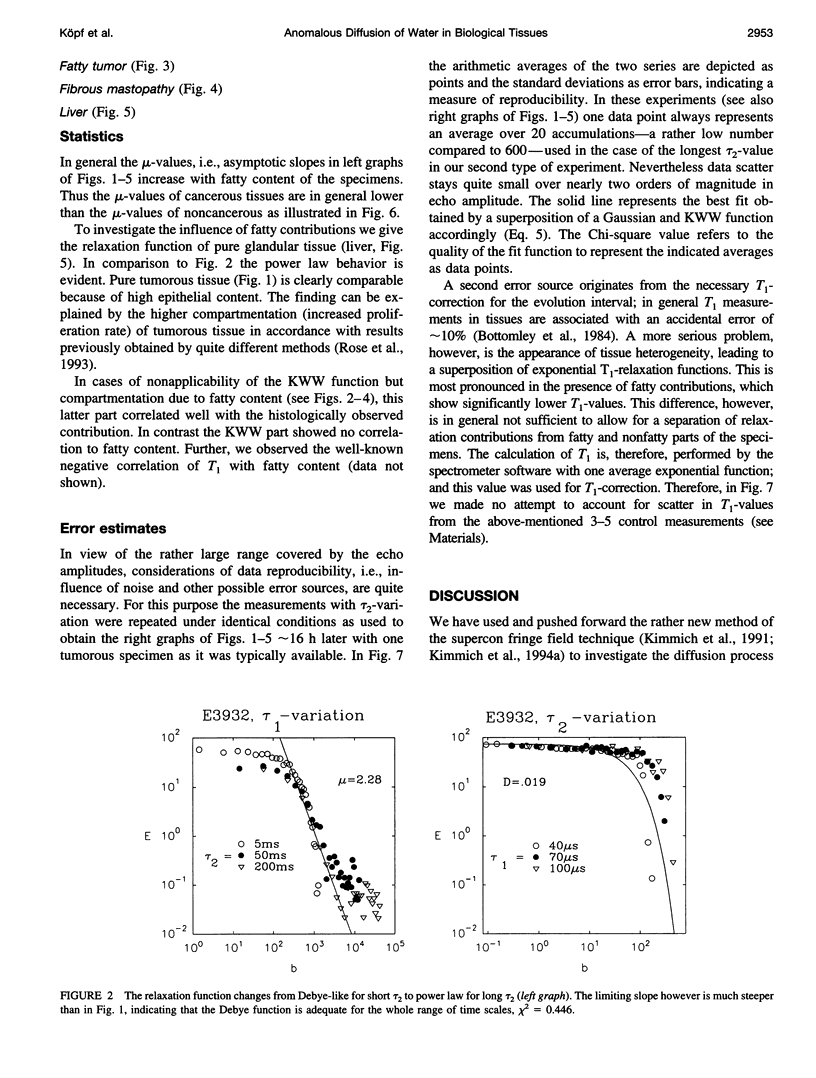
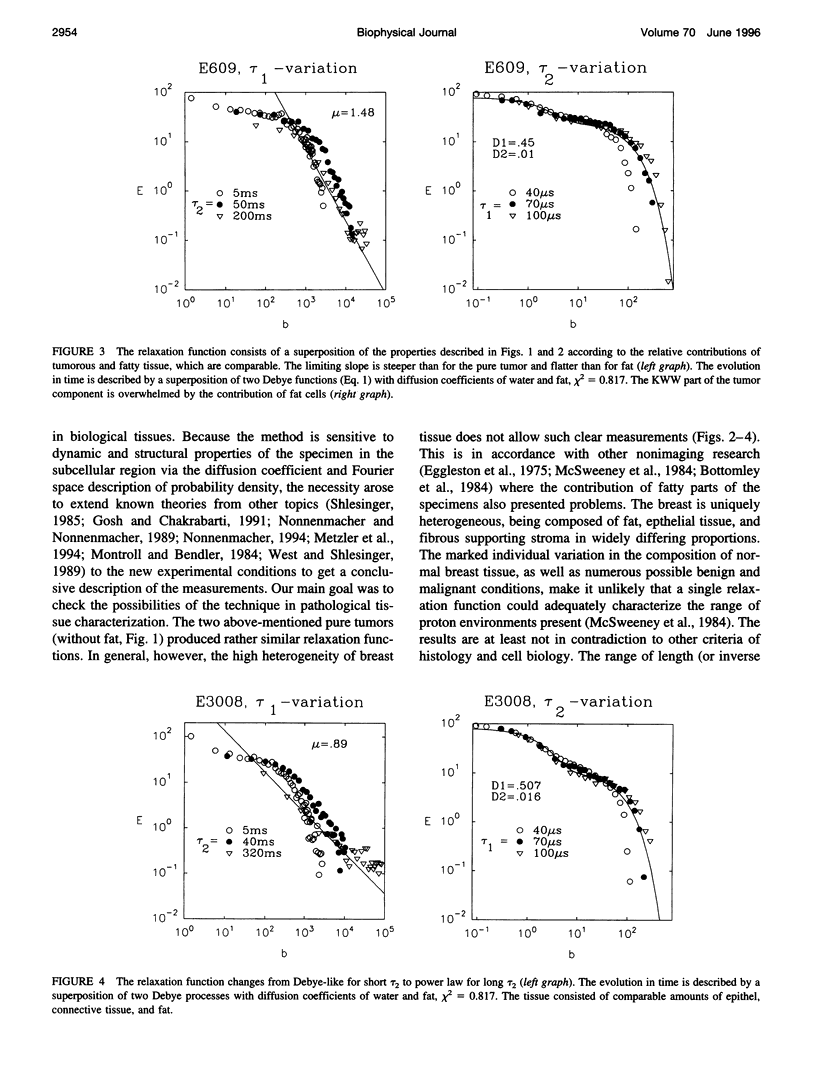
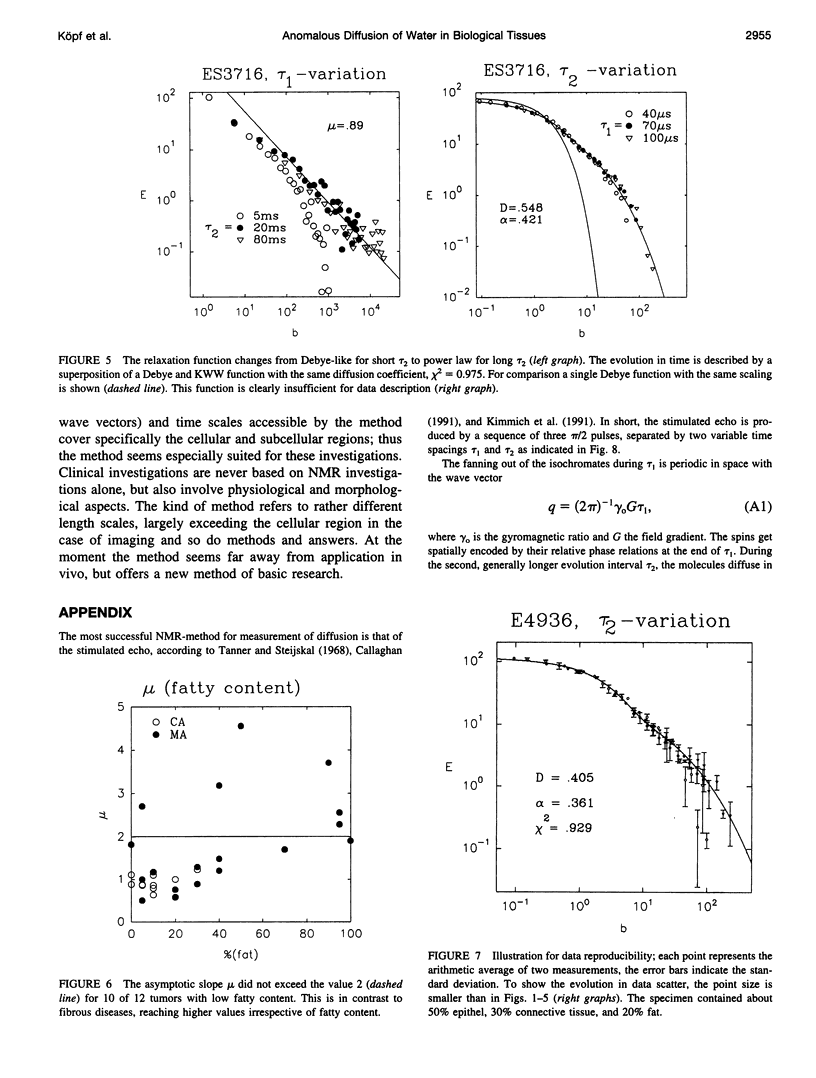
This article deals with the characterization of biological tissues and their pathological alterations. For this purpose, diffusion is measured by NMR in the fringe field of a large superconductor with a field gradient of 50 T/m, which is rather homogenous and stable. It is due to the unprecedented properties of the gradient that we are able not only to determine the usual diffusion coefficient, but also to observe the pronounced Non-Debye feature of the relaxation function due to cellular structure. The dynamics of the probability density follow a stretched exponential or Kohlrausch-Williams-Watts function. In the long time limit the Fourier transform of the probability density follows a long-tail Lévy function, whose asymptotic is related to the fractal dimension of the underlying cellular structure. Some of the properties of Lévy walk statistics are discussed and its potential importance in understanding certain biophysical phenomena like diffusion processes in biological tissues are pointed out. We present and discuss for the first time NMR data giving evidence for Lévy processes that capture the essential features of the observed power law (scaling) dynamics of water diffusion in fresh tissue specimens: carcinomas, fibrous mastopathies, adipose and liver tissues.

Full text

PDF
2951

Selected References

These references are in PubMed. This may not be the complete list of references from this article.

  1. Bottomley P. A., Foster T. H., Argersinger R. E., Pfeifer L. M. A review of normal tissue hydrogen NMR relaxation times and relaxation mechanisms from 1-100 MHz: dependence on tissue type, NMR frequency, temperature, species, excision, and age. Med Phys. 1984 Jul-Aug;11(4):425–448. doi: 10.1118/1.595535. [DOI] [PubMed] [Google Scholar]
  2. Cheng K. H. Quantitation of non-Einstein diffusion behavior of water in biological tissues by proton MR diffusion imaging: synthetic image calculations. Magn Reson Imaging. 1993;11(4):569–583. doi: 10.1016/0730-725x(93)90476-t. [DOI] [PubMed] [Google Scholar]
  3. Eggleston J. C., Saryan L. A., Hollis D. P. Nuclear magnetic resonance investigations of human neoplastic and abnormal nonneoplastic tissues. Cancer Res. 1975 May;35(5):1326–1332. [PubMed] [Google Scholar]
  4. Fujara F., Ilyina E., Nienstaedt H., Sillescu H., Spohr R., Trautmann C. Anisotropic diffusion in etched particle tracks studied by field gradient NMR. Magn Reson Imaging. 1994;12(2):245–246. doi: 10.1016/0730-725x(94)91527-x. [DOI] [PubMed] [Google Scholar]
  5. Glöckle W. G., Nonnenmacher T. F. A fractional calculus approach to self-similar protein dynamics. Biophys J. 1995 Jan;68(1):46–53. doi: 10.1016/S0006-3495(95)80157-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Hazlewood C. F., Chang D. C., Nichols B. L., Woessner D. E. Nuclear magnetic resonance transverse relaxation times of water protons in skeletal muscle. Biophys J. 1974 Aug;14(8):583–606. doi: 10.1016/S0006-3495(74)85937-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Hazlewood C. F., Rorschach H. E., Lin C. Diffusion of water in tissues and MRI. Magn Reson Med. 1991 Jun;19(2):214–216. doi: 10.1002/mrm.1910190204. [DOI] [PubMed] [Google Scholar]
  8. Ishida N., Ogawa H., Kano H. Diffusion of cell-associated water in ripening barley seeds. Magn Reson Imaging. 1995;13(5):745–751. doi: 10.1016/0730-725x(95)00028-f. [DOI] [PubMed] [Google Scholar]
  9. Kimmich R., Stapf S., Callaghan P., Coy A. Microstructure of porous media probed by NMR techniques in sub-micrometer length scales. Magn Reson Imaging. 1994;12(2):339–343. doi: 10.1016/0730-725x(94)91552-0. [DOI] [PubMed] [Google Scholar]
  10. Le Bihan D., Breton E., Lallemand D., Grenier P., Cabanis E., Laval-Jeantet M. MR imaging of intravoxel incoherent motions: application to diffusion and perfusion in neurologic disorders. Radiology. 1986 Nov;161(2):401–407. doi: 10.1148/radiology.161.2.3763909. [DOI] [PubMed] [Google Scholar]
  11. McSweeney M. B., Small W. C., Cerny V., Sewell W., Powell R. W., Goldstein J. H. Magnetic resonance imaging in the diagnosis of breast disease: use of transverse relaxation times. Radiology. 1984 Dec;153(3):741–744. doi: 10.1148/radiology.153.3.6093191. [DOI] [PubMed] [Google Scholar]
  12. Norris D. G., Niendorf T., Hoehn-Berlage M., Kohno K., Schneider E. J., Hainz P., Hropot M., Leibfritz D. Incidence of apparent restricted diffusion in three different models of cerebral infarction. Magn Reson Imaging. 1994;12(8):1175–1182. doi: 10.1016/0730-725x(94)90083-4. [DOI] [PubMed] [Google Scholar]
  13. Taylor D. G., Inamdar R., Bushell M. C. NMR imaging in theory and in practice. Phys Med Biol. 1988 Jun;33(6):635–670. doi: 10.1088/0031-9155/33/6/001. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES