Abstract
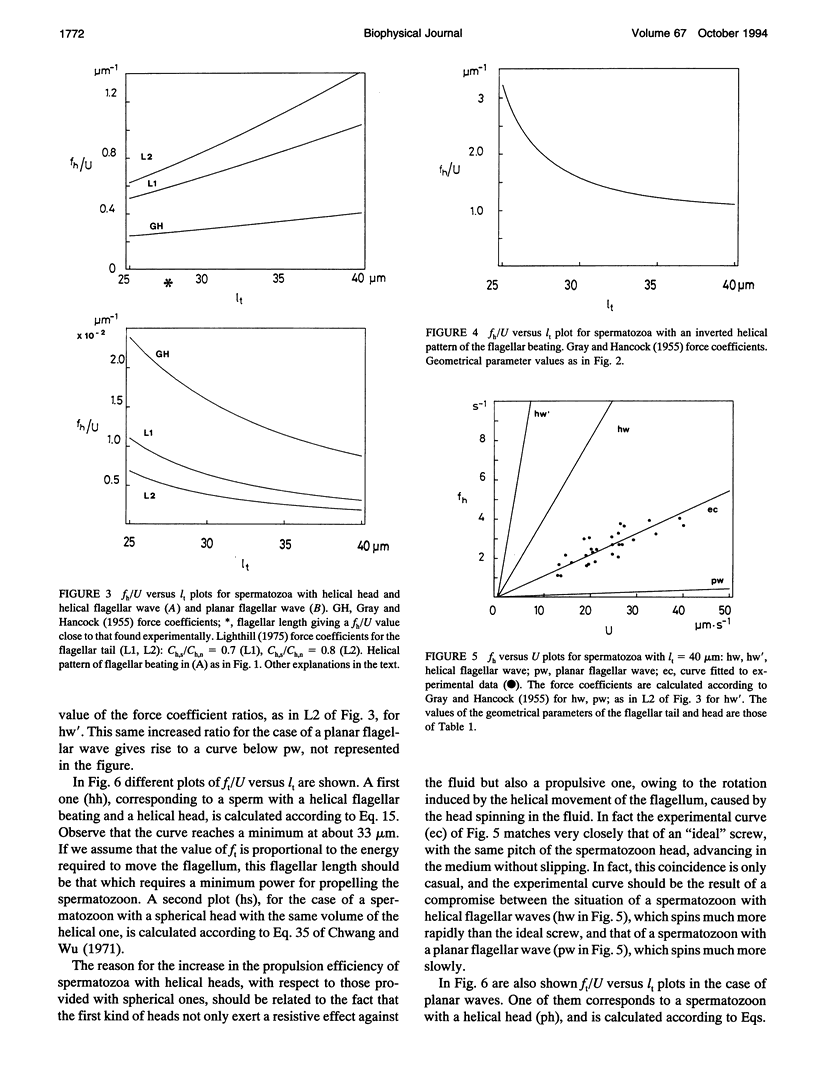
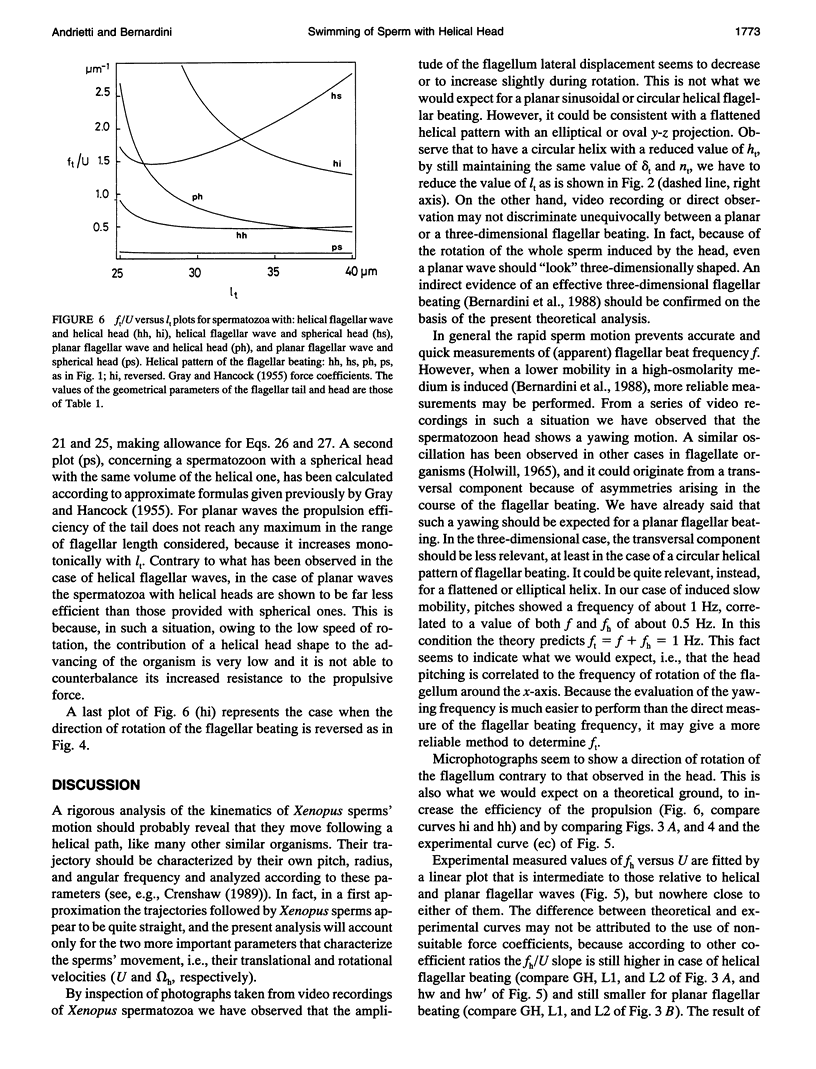
The present work is concerned with the study of the swimming of flagellated microscopic organisms with a helical head and a helical pattern of flagellar beating, such as Xenopus sperms. The theoretical approach is similar to that taken by Chang and Wu (1971) in the study of helical flagellar movement. The model used in the present study allows us to determine the velocity of propulsion (U) and the frequency of rotation of the sperm head (fh) as a function of the frequency of the wave of motion (ft) traveling along the tail. The results relative to the case of helical and planar flagellar waves are compared. Our main finding is that the helical shape of the head seems to increase the efficiency of propulsion of the spermatozoon when compared with the more commonly shaped spherical head. Experimentally measured values of fh versus U may be fitted by a linear plot whose slope is much higher than that corresponding to the case of planar flagellar beating. This fact is consistent with an effectively three-dimensional (nonplanar) movement of the flagellar tail. However, the results do not fit those predicted from a circular helix, suggesting that a different shape of the flagellar beating should be considered.
Full text
PDF





Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Bernardini G., Andrietti F., Camantini M., Cosson M. P. Xenopus spermatozoon: correlation between shape and motility. Gamete Res. 1988 Jun;20(2):165–175. doi: 10.1002/mrd.1120200207. [DOI] [PubMed] [Google Scholar]
- Brokaw C. J. Bending moments in free-swimming flagella. J Exp Biol. 1970 Oct;53(2):445–464. doi: 10.1242/jeb.53.2.445. [DOI] [PubMed] [Google Scholar]
- Chwang A. T., Wu T. Y. A note on the helical movement of micro-organisms. Proc R Soc Lond B Biol Sci. 1971 Aug 3;178(1052):327–346. doi: 10.1098/rspb.1971.0068. [DOI] [PubMed] [Google Scholar]
- Chwang A. T., Wu T. Y., Winet H. Locomotion of Spirilla. Biophys J. 1972 Nov;12(11):1549–1561. doi: 10.1016/S0006-3495(72)86181-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crenshaw H. C. Kinematics of helical motion of microorganisms capable of motion with four degrees of freedom. Biophys J. 1989 Nov;56(5):1029–1035. doi: 10.1016/S0006-3495(89)82748-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holwill M. E. The motion of Euglena viridis: the role of flagella. J Exp Biol. 1966 Jun;44(3):579–588. doi: 10.1242/jeb.44.3.579. [DOI] [PubMed] [Google Scholar]
- Myerscough M. R., Swan M. A. A model for swimming unipolar spirilla. J Theor Biol. 1989 Jul 21;139(2):201–218. doi: 10.1016/s0022-5193(89)80100-6. [DOI] [PubMed] [Google Scholar]


