Fold prediction of helical proteins using torsion angle dynamics and predicted restraints

Abstract

We describe a procedure for predicting the tertiary folds of α-helical proteins from their primary sequences. The central component of the procedure is a method for predicting interhelical contacts that is based on a helix-packing model. Instead of predicting the individual contacts, our method attempts to identify the entire patch of contacts that involve residues regularly spaced in the sequences. We use this component to glue together two powerful existing methods: a secondary structure prediction program, whose output serves as the input to the contact prediction algorithm, and the tortion angle dynamics program, which uses the predicted tertiary contacts and secondary structural states to assemble three-dimensional structures. In the final step, the procedure uses the initial set of simulated structures to refine the predicted contacts for a new round of structure calculation. When tested against 24 small to medium-sized proteins representing a wide range of helical folds, the completely automated procedure is able to generate native-like models within a limited number of trials consistently.

Prediction of protein structure based on sequence information is of great value for the interpretation of protein sequence data. The development of such methods will significantly reduce the number of protein structures that must be determined experimentally to obtain a structural complement for an organism (1). The main obstacles for ab initio protein structure prediction come from the immense number of possible conformations accessible to a polypeptide chain and the complex details of interatomic interactions. One way to partially overcome these difficulties is to introduce restraints into the structure calculation. In the most general form, such restraints may be expressed as Euclidean distances between spatially proximate atoms in a protein. Building structures consistent with distance restraints is a well-developed technique that has been used extensively in the construction of structural models based on NMR data (2). Torsion angle dynamics (TAD) (3, 4), the most recent addition to the inventory of distance-based methods, provides at present the most efficient way to calculate NMR structures of biomolecules (2).

Without experimental distance information, distance restraints have to be derived from prediction. Secondary structure prediction can be considered equivalent to the prediction of local or short-range residue–residue distances (i.e., distances between residues close in the sequence). Although the knowledge of secondary structural preferences alone does not entirely eliminate competing answers, it greatly reduces the number of tertiary restraints required to specify a unique fold. Currently, the most popular approach for predicting nonlocal contacts (i.e., contacts between residues distant in the sequence) in a protein is the correlated mutation analysis of multiply aligned sequences (5–10). Although correlated mutations have some predictive power, the results are not yet sufficient for the tertiary structure prediction (9, 10).

In this study we explore an alternative approach to contact prediction that is based directly on the amino acid types of the residues and their secondary structural environments. Different pairs of amino acids show differing propensities to be close in a folded protein; in the literature, such propensities often are represented by knowledge-based pair potentials (11). The main drawback of using pair preferences to predict contacts is that a particular pair of amino acids, regardless of its sequence or structural context, is always predicted with the same outcome (12). One possible way to overcome this problem is to combine residue pair specific effects with predicted local structural environments. Because secondary structure prediction is most accurate for α-helices, we focus on the prediction of tertiary contacts in helical proteins. The idea put to test here is based on the observation that helix packing interfaces in globular proteins consist of patches of contacts that involve residues regularly spaced in the sequence. Instead of predicting the individual contacts we attempt to identify the contact patches directly by using a scoring scheme that takes into account the contributions of all residue–residue contacts in a patch.

The feasibility of using the predicted contacts to assemble the globular fold of helical proteins was tested on a set of 24 proteins representing a wide range of small to medium-sized helical folds. For each protein, 500 independent TAD runs were carried out with the program dyana (3) and the predicted restraints, and the results were compared with the crystallographic or NMR structures. We found that for a majority of the targets native-like folds were among the 500 models thus generated. Models within a rms deviation (rmsd) of 4.5 Å were obtained for all nine small helical proteins (50–80 residues long), and structures within 6.5 Å rmsd were obtained for 14 of the 15 medium-sized proteins (80–100 residues long). The results were further improved by using a bootstrapping strategy that used half of the predicted contacts, based on the frequencies of their co-occurrences in the 500 models, to produce a new set of models. The bootstrapping strategy enriched the population of native-like models and enabled us to generate at least one native-like model for all proteins in the test set.

Methods

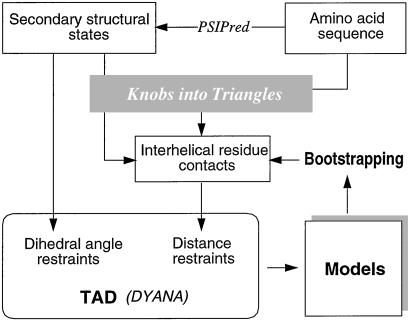
The proposed structure calculation procedure contains four stages: secondary structure prediction, interhelical contact prediction, tertiary structure assembly, and bootstrapping. The information flow among the four stages is summarized in Fig. 1.

Figure 1.

Schematic overview of the structure prediction procedure for α-helical proteins.

Secondary Structure Prediction.

The secondary structural states of each protein were predicted by using David Jone's psipred program (13). This program uses multiple sequence information and takes the position-specific scoring matrices generated by psi-blast (14) as input. To prepare for these matrices, we performed a psi-blast search for each target protein against the National Center for Biotechnology Information nonredundant sequence database (ftp://ncbi.nlm.nih.gov/blast/db/). The default E-value cutoff (0.001) was used, and the maximum number of iterations was set to five.

Interhelical Contacts.

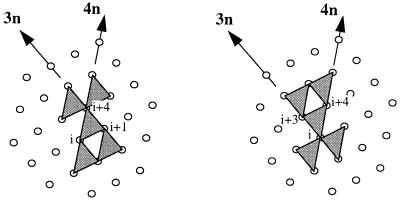
The surface of a helix can be described as a tessellation of two types of triangles: triangles formed by residues i, i+1, and i+4, and triangles formed by residues i, i+3, and i+4 (Fig. 2). When two helices pack against each other, a side chain from one of the helices can contact a triangular element (i.e., three side chains) from the second helix. This “knobs into triangles” (KIT) model differs from the popular “knobs into holes” model (15) in that the latter has one side chain from one helix interacting with four side chains (i, i+3, i+4, and i+7) from the other. Although the knobs into holes model elegantly describes the helix packing in ideal coiled–coil structures, it is too restricted to describe the helix packing in globular proteins where the knobs and holes frequently drift away from their ideal positions in the helix lattice (16). We consider two residues are in contact if the distance between the centroids of their side chains (C^α in the case of Gly) is less than 7 Å. An analysis of the 670 pairs of helices taken from a set of representative protein structures indicated that more than 85% of the interhelical residue–reside contacts could be described by the KIT model, whereas only 40% obeyed the knobs into holes rule.

Figure 2.

Triangle elements on the surface of a helix represented on a helix lattice. The helix lattice is created by projecting a regular helix cylindrically onto a plane (15). The two vectors, labeled 3n and 4n, correspond to the base vectors for the lattice where sequence separations are three and four, respectively. There are two types of triangles, one formed by residues i, i+1, and i+4 (Left), the other formed by residues i, i+3, and i+4 (Right). When two helices interact, two neighboring triangles on the first helix pack against two neighboring residues on a base vector of the second helix. Each triangle has four neighbors, represented here by the four shaded triangles surrounding the central triangle; these neighbors can be obtained by repeating the central triangle along the two base vectors in two opposite directions.

A single knob-triangle pair only partially restrains the configuration of two helices; the two helices can still rotate relative to each other, adopting different packing angles. We examine whether the combination of two spatially adjacent knob-triangle pairs provides sufficient restraints to both the translational and rotational degrees of freedom. Residues (or knobs) separated by three or four residues in the sequence are adjacent on the surface of a helix. Similarly, two triangles on a helix separated by three or four residues are also adjacent (Fig. 2). Considering that there are two types of triangles and that two helices can interact in two opposite orientations, there are 16 distinct ways to pack two adjacent knobs from one helix against two adjacent triangles from the other (Table 1). For convenience, we call the patches of contacts thus formed KIT patches. By definition, each KIT patch consists of two knob-triangle pairs making six residue–residue contacts.

Table 1.

KIT patches and helix packing angles

	k−3		k+3		k−4		k+4
	N	Ω	N	Ω	N	Ω	N	Ω
(i, i + 1, i + 4)3	42	−66.7 (25.1)	41	111.2 (22.2)	98	−151.4 (19.4)	23	27.5 (19.3)
(i, i + 3, i + 4)3	33	−77.8 (29.3)	35	115.2 (22.2)	100	−154.8 (15.5)	25	23.7 (23.2)
(i, i + 1, i + 4)4	88	−165.0 (18.0)	33	8.7 (34.9)	94	132.6 (18.5)	92	−50.2 (14.2)
(i, i + 3, i + 4)4	115	−163.4 (18.9)	34	4.7 (25.9)	121	136.0 (17.8)	152	−43.5 (14.7)

 A KIT patch is defined as two knob-triangle pairs making six interhelical residue–residue contacts. The two knobs on one helix are represented by k with a subscript indicating the sequence separation between the two knobs and their orientation relative to the two triangles. The two knobs interact with two triangles on the second helix. There are two types of triangles, represented here by (i, i + 1, i + 4) and (i, i + 3, i + 4), respectively. Triangle pairs separated by three and four residues are distinguished by the subscript. The combination of the different knobs and triangles give rise to 16 distinct types of KIT patches. N is the number of times the given type of KIT patch was observed in the 670 helix pairs taken from a set of nonredundant protein structures, and Ω is the mean helix packing angle averaged over the N observations (values in parentheses indicate the SDs). 

Using the database of 670 helix pairs, we calculated the mean and SD of helix packing angle (Ω) for each of the 16 KIT-patch types. The results (Table 1) show that the residual variation in Ω (i.e., the SD) is relatively small once a KIT-patch type is specified. Thus, if a KIT patch could be predicted, the main features of the helix packing would have been obtained.

For each pair of helices in the protein whose fold is to be predicted, we identified all possible KIT patches based on the 16 contact patterns listed in Table 1. The interaction energy of each patch was calculated as the sum over contributions from all six residue–residue contacts, with individual contribution estimated by using the Miyazawa–Jernigan contact energy table (17). For each pair of helices, the three KIT patches with the lowest interaction energies were selected. These patches were used as distance restraints only when all three had energies lower than a predefined cutoff that corresponded to −1 SD unit from the mean interaction energy of all possible KIT patches between every pair of helices in the protein. If this condition was not met, no distance restraints were assigned between the two helices.

Fold Assembly.

We used the dyana program (3) to generate three-dimensional structures consistent with the predicted restraints. dyana uses a fast recursive implementation of TAD that was originally developed for spacecraft dynamics and robotics (18). The input to dyana consisted of a set of dihedral angle restraints to enforce the predicted helical secondary structures and a set of distance restraints derived from the predicted tertiary contacts. To improve the computational efficiency, we converted all residues except for glycine and proline to alanine. The Φ and Ψ angles of the predicted helical residues were restrained to be between −58° and −56° and between −48° and −46°, respectively. The relative weight of the restraint (W) was taken as a function of the psipred prediction accuracy (c): W(c) = 2^c−3. Thus, a residue predicted with a confidence of 3 was assigned with the default weight of 1, and a residue with confidence 9 had the maximum weight of 64. Such a scheme maintains the overall rigidity of the helix but allows for more flexibility at lower confidence regions. An upper distance bound of 8 Å was specified between each pair of contact residues in a predicted KIT patch. With the exception of glycine, all distance restraints were placed on the C^β atoms; C^α was used as the representative atom for glycine. All distance restraints were weighted equally. No explicit lower bounds were assigned to the distance restraints; the dyana's internal van der Waals force field was used to remove unphysical clashes between atoms.

For structure calculation, we used the standard simulated annealing protocol of dyana, which consisted of 4,000 TAD steps. One-fifth of these were performed at an initial high temperature, followed by slow cooling during the rest of the schedule. An ensemble of 500 structures were calculated for each protein target, all starting from random conformations.

Bootstrapping.

Because the KIT patches were independently predicted, some of the predicted contacts may not be compatible with one another in three dimensions. We examined the possibilities of using the modeled structures to detect such incompatibility, thereby, to remove some of the falsely predicted contacts. If two predicted contacts were present in a modeled structure, we considered that the two contacts were coexpressed in that model. For a given contact, we counted the number of instances of its coexpressions with other predicted contacts in the 500 structures and used this number as a measure of the compatibility of the contact. The predicted contacts were ordered by compatibility, from the highest to the lowest. Contacts at the high compatibility end are retained in a new round of structure calculation that follows the same protocol described above. As we show later, this bootstrapping technique, which relies on the information that is already available in the structural models, does lead to a noticeable improvement in the performance.

Protein Targets.

To select a set of nonhomologous helical proteins (or protein domains) as targets, we started with the protein domain set provided by the scop (19) database (version 1.48), which contained a representative for each sequence family, and selected all single chain protein domains in the all-α structural class. From this list, we removed protein domains that fell into any of the following seven categories: (i) those with fewer than 50 residues or more than 100 residues, (ii) those made of a single helix or a helix hairpin, (iii) those missing coordinates for more than four consecutive residues, (iv) those containing a significant number of residues in the β conformation, (v) those with a nonglobular fold, (vi) those with the N and C termini restrained by another part of the protein, and (vii) those having a large buried surface in the intact protein. Of the remaining protein domains, a single representative was randomly selected from each scop fold. The final list contains 24 targets (Table 2), including nine small helical proteins (50–80 residues long) and 15 medium-sized helical proteins (80–100 residues long).

Table 2.

Results of structure calculation for the 24 test proteins

Protein	Fold	NRes	HDSSP	HPred	Q3	Initial 500 structures			After bootstrapping
						rmsdmin	<4.5 Å	<6.5 Å	rmsdmin	<4.5 Å	<6.5 Å
Small
1gab	1.8	53	3	3	83.0	2.6	108	171	2.2	112	184
1c5a	1.52	66	4	4	90.9	3.7	13	163	2.9	31	114
1a04A150–216	1.37	67	4	4	98.5	4.3	5	47	4.0	7	83
1b0nA1–68	1.36	68	5	4	91.2	4.0	3	12	3.4	1	12
1cktA	1.22	71	3	3	88.7	4.0	6	102	4.0	5	254
1lea	1.4	72	3	3	86.1	4.2	17	147	3.8	42	257
1b0xA	1.61	72	5	5	90.3	3.7	10	150	3.4	13	95
1nkl	1.65	78	4	4	92.3	4.0	10	56	4.0	3	112
2occH	1.53	79	3	3	89.9	3.6	21	219	3.1	117	283
Medium-sized
1lre	1.13	81	3	3	93.8	3.8	3	139	3.7	11	175
1kdxA	1.12	81	3	3	82.7	5.2	0	14	4.9	0	41
1lbu1–83	1.21	83	3	3	94.0	4.1	2	128	3.0	22	142
1ngr	1.76	85	6	6	88.2	4.7	0	23	4.5	1	29
2abd	1.11	86	4	4	88.4	5.7	0	10	6.3	0	3
1unkA	1.29	87	4	3	83.9	5.7	0	10	4.9	0	26
1ffh2–88	1.30	87	4	4	97.7	4.3	3	21	3.3	22	73
1a6s	1.62	87	4	5	85.1	4.8	0	10	5.2	0	27
1ctj	1.3	89	5	4	92.1	5.1	0	7	4.4	1	13
2ezyA	1.38	89	5	5	77.5	6.3	0	3	6.0	0	4
1bmtA651–740	1.49	90	5	4	91.1	5.6	0	17	5.6	0	29
1rzl	1.54	91	6	5	90.1	5.6	0	21	5.3	0	61
1aisB1108–1205	1.73	98	5	5	95.9	7.2	0	0	5.7	0	4
1bxm	1.124	99	6	4	68.7	5.8	0	2	6.1	0	6
1qc7A	1.79	100	5	6	82.2	5.1	0	29	4.1	7	43

 Protein, the Protein Data Bank code followed by chain identifier (uppercase), and if applicable, domain identifier (subscript); Fold, fold assignment according to the scop database (release 1.48). N_res, number of residues in the protein or protein domain. H_DSSP, number of helices according to dssp. H_Pred, number of helices predicted by psipred. Q3, percentage of correctly predicted secondary structure. rmsd_min, lowest rmsd in Å from the native structure. <4.5 Å, the number of structures within 4.5 Å rmsd from the native structure. <6.5 Å, the number of structures within 6.5 Å rmsd from the native structure. 

Results

The target proteins contained from three to seven helices and represented a variety of topologies. Table 2 shows the accuracy of the secondary structure prediction for these proteins. For a majority of the targets, the positions of the native helical segments were correctly predicted by psipred. The three state accuracy (Q3) of the prediction as compared with the secondary structure assignment of the native structure by dssp (20) ranged from 68.7% to 97.7%, with an overall accuracy of 86.9%. There were eight targets for which the number of predicted helices did not match the number of actual helices. In four cases, the disagreement was caused either by the omission of a small helix (1b0nA_1–68 and 1unkA) or by the overprediction of a small helix (1a6s and 1qc7A). In three cases (1ctj, 1bmtA_651−741, and 1rzl), two adjacent helices separated by one residue were replaced by a single continuous helix. The most significant discrepancy between dssp and the psipred prediction occurred in 1bxm. The native structure contains six α-helices, but the psipred prediction merges the third and fourth helices and misses entirely the second helix.

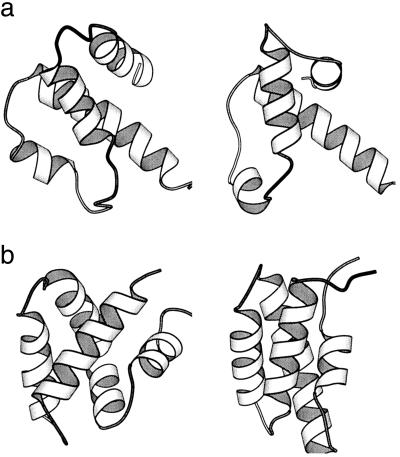
An ensemble of 500 structural models was generated for each target by using TAD and the predicted secondary structures and tertiary contacts (see Methods). Table 2 shows the C^α rmsd of the most native-like model of the 500 trials. Note that because our primary goal was to predict the helix packing in a protein, loop regions in the native structure were omitted from the rmsd calculation. To describe the frequency with which native-like models were generated, Table 2 also shows the number of models with less than 4.5 Å and the number of models with less than 6.5 Å rmsd from the native structure. Overall, the rate of success correlated with the size of the protein. Structure models within 4.5 Å rmsd from the native structure were readily obtained for the nine small helical proteins. The helix packing in the native structure was closely imitated by the simulated structures (see Fig. 3 for two examples).

Figure 3.

The experimental (Left) and the best predicted (Right) structures of 1c5a (a) and 1nkl (b).

In contrast, models with low rmsd from the native structures were relatively rare for medium-sized targets; only three targets (1lre, 1lbu₁₋₈₃, and 1ffh₂₋₈₈) had such good models. As protein size increases, the probability of obtaining models within a given rmsd decreases exponentially. Reva et al. (21) have suggested an rmsd of 6 Å as a reasonable upper limit for assessing the structural similarity between 60–80 residue proteins in the context of structure prediction. Here, we relax this cutoff slightly and consider a model within an rmsd of 6.5 Å (excluding loops) from the native structure to be quite successful for a medium-sized protein (>80 residues). Judged by this criterion, reasonable models were obtained for 14 of the 15 medium-sized targets (Table 2), including seven proteins that contained five or more helices.

We applied a bootstrapping technique described in Methods to select, among the predicted contacts, those with high compatibilities with other contacts, and used the selected contacts to generate new models. For each target, the threshold for selection was set such that half of the initially predicted contacts were used. The results for individual proteins are listed in Table 2. Note that in a majority of the cases, the population density of the near native (rmsd <4.5) and native-like (rmsd <6.5 Å) models increased. The improvement was especially noticeable for medium-sized proteins. All 15 proteins had native-like models, including five that had near native models.

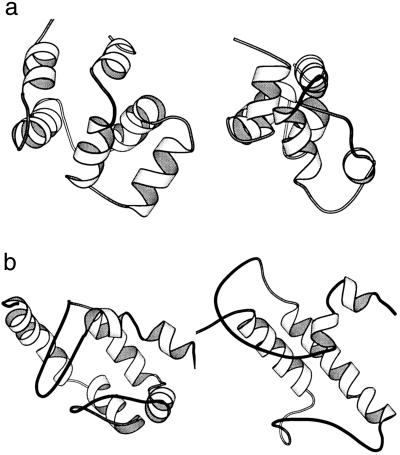
Previous ab initio folding simulations seldom used proteins with more than four helices (10, 22–24). With structural possibilities multiplied, such proteins are considerably more challenging for structure prediction. The consistent generation of native-like folds for these proteins within a limited number of trials is, therefore, a very encouraging result. For example, the best simulated model of target 1ngr was 4.5 Å from the native structure. As shown in Fig. 4a, the unusual Greek key topology of the six-helix bundle structure can be clearly recognized in the 4.5-Å rmsd model, although the simulated structure appears to be more compact than the native structure. Another interesting example is target 1bxm for which the quality of secondary structure prediction was poor. As illustrated in Fig. 4b, the essential topological features of the six-helix protein were well approximated by a four-helix model. This result suggests that the procedure is robust enough to handle some of the errors in secondary structure prediction.

Figure 4.

The experimental (Left) and the best predicted (Right) structures of 1ngr (a) and 1bxm (b).

To reduce the rate of false positives, we used a small number of statistically most probable contacts to specify tertiary distance restraints. With the full three-dimensional model constructed, a complete energy evaluation that includes contributions from all residue contacts becomes feasible. Ideally, such an energy evaluation would pick out the most native-like structure as the most favorable model. We tested the ability of current residue pair potentials to distinguish native-like from non-native-like models in the set of structures produced in this work. Three potentials were chosen: the classic Miyazawa–Jernigan contact energies (17), an updated pair contact potential developed by Skolnick and coworkers (25), and the secondary structural environment-dependent residue contact energies (ERCE) (26). These potentials were compared by the number of targets with at least one acceptable model (<6.5 Å rmsd from the native structure) among the 10 most preferred structures selected by each potential. The best result was obtained with ERCE, which selected reasonable models for 17 targets. In comparison, the Miyazawa–Jernigan contact energies succeeded in 12 cases, and the Skolnick contact energies in 11. Overall, although the use of residue pair potentials clearly increases the chance of finding native-like folds, the discriminatory power of these potentials remains very modest.

Discussion

A successful prediction of contacts between amino acids in a protein is a crucial step toward applying distance-based methods in ab initio protein structure prediction. We have shown a way to predict critical contacts between α-helices that focuses on patches of contacts defined by a helix-packing model (the KIT model). A procedure has been developed that combines the restraints predicted by the KIT model and predicted secondary structures to fold α-helical proteins. Despite the simplicity of this procedure, we were able to generate native-like models for a majority of the testing proteins within 500 trials. For small helical proteins, many near-native folds were generated.

In our calculation, the distance restraints were deliberately underdetermined to avoid false positives. However, the predicted contacts are approximate and noisy by nature. The successful generation of native-like folds for a majority of the targets depends critically on the semirigid nature of the α-helices. The regular geometry of helices helps to resolve some of the inconsistency in the predicted contacts. In fact, by prescribing a fixed distance restraint to all pairs of helices, Huang et al. (24) were able to generate native-like models for small helical proteins. However, their procedure is clearly insufficient in folding larger proteins with more helices and complex topologies. Methods such as the one presented here are needed to provide more specific distance restraints.

We have shown that TAD, which is gaining increasing popularity in NMR structure calculation, can be directly useful for ab initio folding. Earlier studies (2–4) have established that TAD is a more efficient conformational search procedure than other distance-based methods, including metric matrix distance geometry (27–30), which has been used by several authors to fold helical proteins (23, 24). TAD profits from a 10-fold reduction in the number of degrees of freedom and allows larger time steps and more adequate sampling of the conformation space (31). The complete analysis of a 100-residue protein costs less than 1 h of computer time on a DEC alpha workstation.

There is considerable room for improvement to our current approach. Although the procedure has yielded valid models for a number of small and medium-sized targets, including some with complex topologies, the success rate for medium-sized proteins is in general lower than that for small helical proteins (Table 2). Furthermore, the simulated models of medium-sized proteins tended to be more compact than the native structures. The overcompactness was caused mostly by the wrongly predicted contacts between helices that do not interact in the native structure. In many cases, knowing whether two helices interact is more important than knowing how they interact. The current procedure implements only a simple strategy, i.e., no distance restraints are assigned to any helix pairs that do not have KIT patches with significant interaction energies. Still to be examined are more sophisticated ways to scrutinize spurious helix–helix contacts, including placing a limit on the maximum number of helices with which a helix can interact. Also sought are better ways to optimize scoring functions for better discrimination between native-like and non-native-like structural models.

Abbreviations

KIT

knobs-into-triangles

TAD

torsion angle dynamics

rmsd

rms deviation