Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 1993 Jul;65(1):253–269. doi: 10.1016/S0006-3495(93)81034-8

Transition modes in Ising networks: an approximate theory for macromolecular recognition.

S Keating 1, E Di Cera 1
PMCID: PMC1225721  PMID: 8369436

Abstract

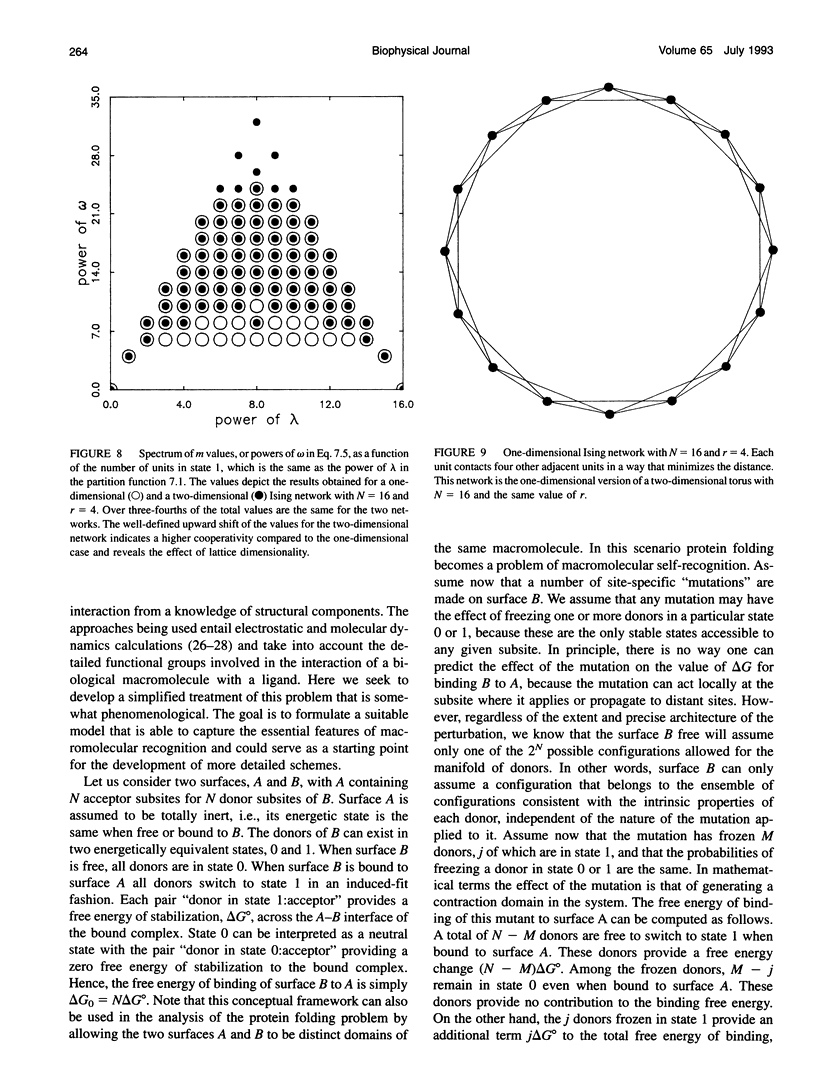
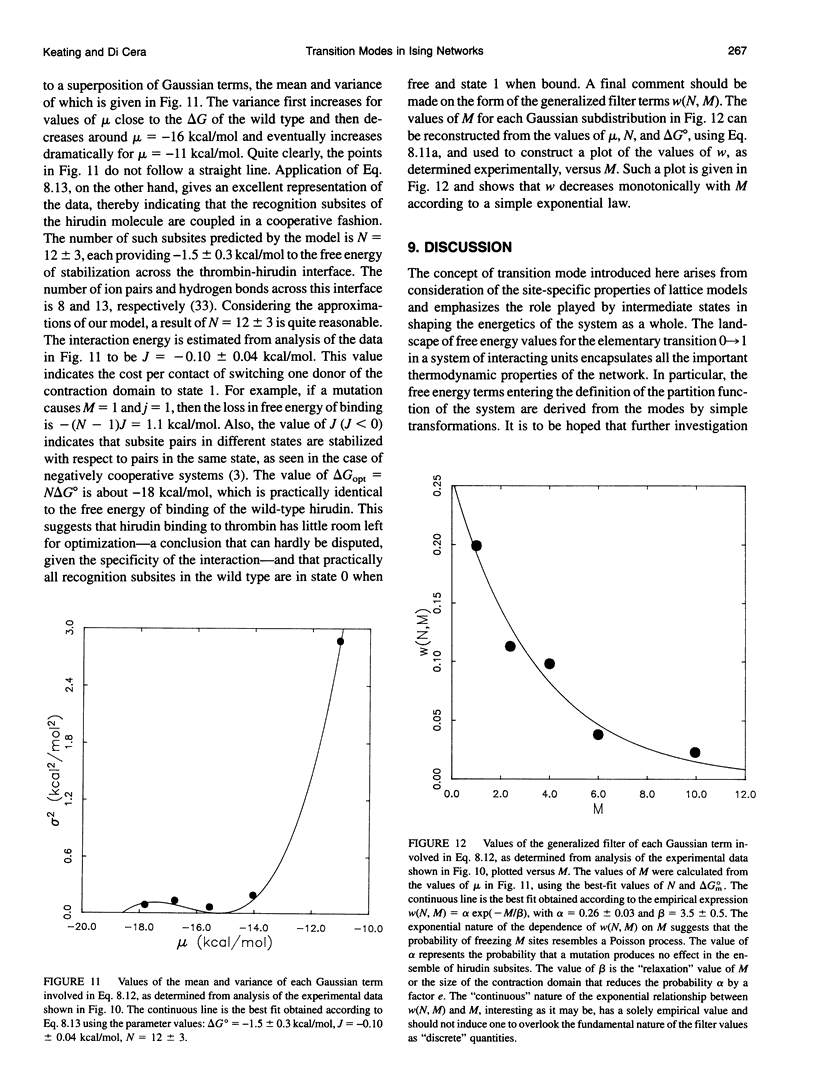
For a statistical lattice, or Ising network, composed of N identical units existing in two possible states, 0 and 1, and interacting according to a given geometry, a set of values can be found for the mean free energy of the 0-->1 transition of a single unit. Each value defines a transition mode in an ensemble of nu N = 3N - 2N possible values and reflects the role played by intermediate states in shaping the energetics of the system as a whole. The distribution of transition modes has a number of intriguing properties. Some of them apply quite generally to any Ising network, regardless of its dimension, while others are specific for each interaction geometry and dimensional embedding and bear on fundamental aspects of analytical number theory. The landscape of transition modes encapsulates all of the important thermodynamic properties of the network. The free energy terms defining the partition function of the system can be derived from the modes by simple transformations. Classical mean-field expressions can be obtained from consideration of the properties of transition modes in a rather straightforward way. The results obtained in the analysis of the transition mode distributions have been used to develop an approximate treatment of the problem of macromolecular recognition. This phenomenon is modeled as a cooperative process that involves a number of recognition subsites across an interface generated by the binding of two macromolecular components. The distribution of allowed binding free energies for the system is shown to be a superposition of Gaussian terms with mean and variance determined a priori by the theory. Application to the analysis of the biologically interaction of thrombin with hirudin has provided some useful information on basic aspects of the interaction, such as the number of recognition subsites involved and the energy balance for binding and cooperative coupling among them. Our results agree quite well with information derived independently from analysis of the crystal structure of the thrombin-hirudin complex.

Full text

PDF
256

Selected References

These references are in PubMed. This may not be the complete list of references from this article.

  1. Ackers G. K., Doyle M. L., Myers D., Daugherty M. A. Molecular code for cooperativity in hemoglobin. Science. 1992 Jan 3;255(5040):54–63. doi: 10.1126/science.1553532. [DOI] [PubMed] [Google Scholar]
  2. Beroza P., Fredkin D. R., Okamura M. Y., Feher G. Protonation of interacting residues in a protein by a Monte Carlo method: application to lysozyme and the photosynthetic reaction center of Rhodobacter sphaeroides. Proc Natl Acad Sci U S A. 1991 Jul 1;88(13):5804–5808. doi: 10.1073/pnas.88.13.5804. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Betz A., Hofsteenge J., Stone S. R. Ionic interactions in the formation of the thrombin-hirudin complex. Biochem J. 1991 May 1;275(Pt 3):801–803. doi: 10.1042/bj2750801. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. De Cristofaro R., Fenton J. W., 2nd, Di Cera E. Modulation of thrombin-hirudin interaction by specific ion effects. J Mol Biol. 1992 Jul 5;226(1):263–269. doi: 10.1016/0022-2836(92)90138-a. [DOI] [PubMed] [Google Scholar]
  5. Di Cera E., Chen Z. Q. The binding capacity is a probability density function. Biophys J. 1993 Jul;65(1):164–170. doi: 10.1016/S0006-3495(93)81033-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Di Cera E., Hopfner K. P., Wyman J. Symmetry conditions for binding processes. Proc Natl Acad Sci U S A. 1992 Apr 1;89(7):2727–2731. doi: 10.1073/pnas.89.7.2727. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Di Cera E. Thermodynamics of local linkage effects. Contracted partition functions and the analysis of site-specific energetics. Biophys Chem. 1990 Aug 31;37(1-3):147–164. doi: 10.1016/0301-4622(90)88015-k. [DOI] [PubMed] [Google Scholar]
  8. Freire E., Murphy K. P. Molecular basis of co-operativity in protein folding. J Mol Biol. 1991 Dec 5;222(3):687–698. doi: 10.1016/0022-2836(91)90505-z. [DOI] [PubMed] [Google Scholar]
  9. Gilson M. K., Honig B. H. Energetics of charge-charge interactions in proteins. Proteins. 1988;3(1):32–52. doi: 10.1002/prot.340030104. [DOI] [PubMed] [Google Scholar]
  10. Lewis P. N., Go N., Go M., Kotelchuck D., Scheraga H. A. Helix probability profiles of denatured proteins and their correlation with native structures. Proc Natl Acad Sci U S A. 1970 Apr;65(4):810–815. doi: 10.1073/pnas.65.4.810. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Matthew J. B., Gurd F. R. Calculation of electrostatic interactions in proteins. Methods Enzymol. 1986;130:413–436. doi: 10.1016/0076-6879(86)30019-3. [DOI] [PubMed] [Google Scholar]
  12. Rydel T. J., Tulinsky A., Bode W., Huber R. Refined structure of the hirudin-thrombin complex. J Mol Biol. 1991 Sep 20;221(2):583–601. doi: 10.1016/0022-2836(91)80074-5. [DOI] [PubMed] [Google Scholar]
  13. Stone S. R., Hofsteenge J. Kinetics of the inhibition of thrombin by hirudin. Biochemistry. 1986 Aug 12;25(16):4622–4628. doi: 10.1021/bi00364a025. [DOI] [PubMed] [Google Scholar]
  14. WYMAN J., Jr LINKED FUNCTIONS AND RECIPROCAL EFFECTS IN HEMOGLOBIN: A SECOND LOOK. Adv Protein Chem. 1964;19:223–286. doi: 10.1016/s0065-3233(08)60190-4. [DOI] [PubMed] [Google Scholar]
  15. Wallace A., Dennis S., Hofsteenge J., Stone S. R. Contribution of the N-terminal region of hirudin to its interaction with thrombin. Biochemistry. 1989 Dec 26;28(26):10079–10084. doi: 10.1021/bi00452a030. [DOI] [PubMed] [Google Scholar]

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES