Abstract
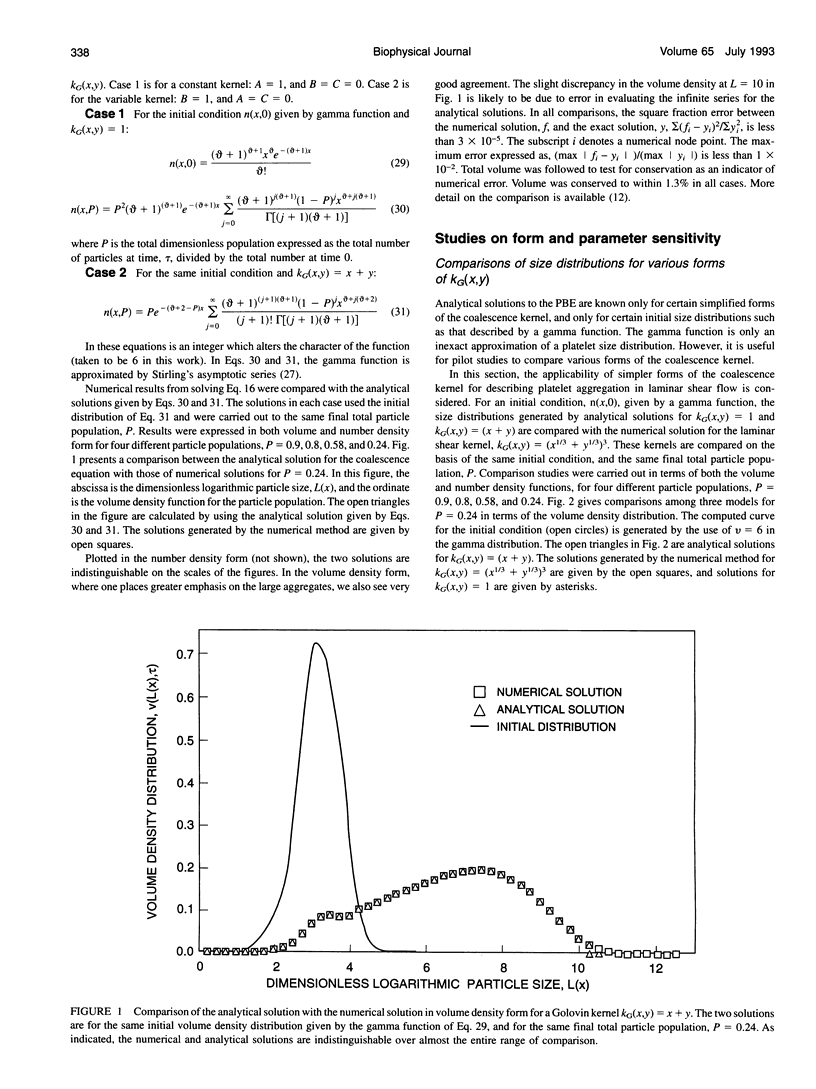
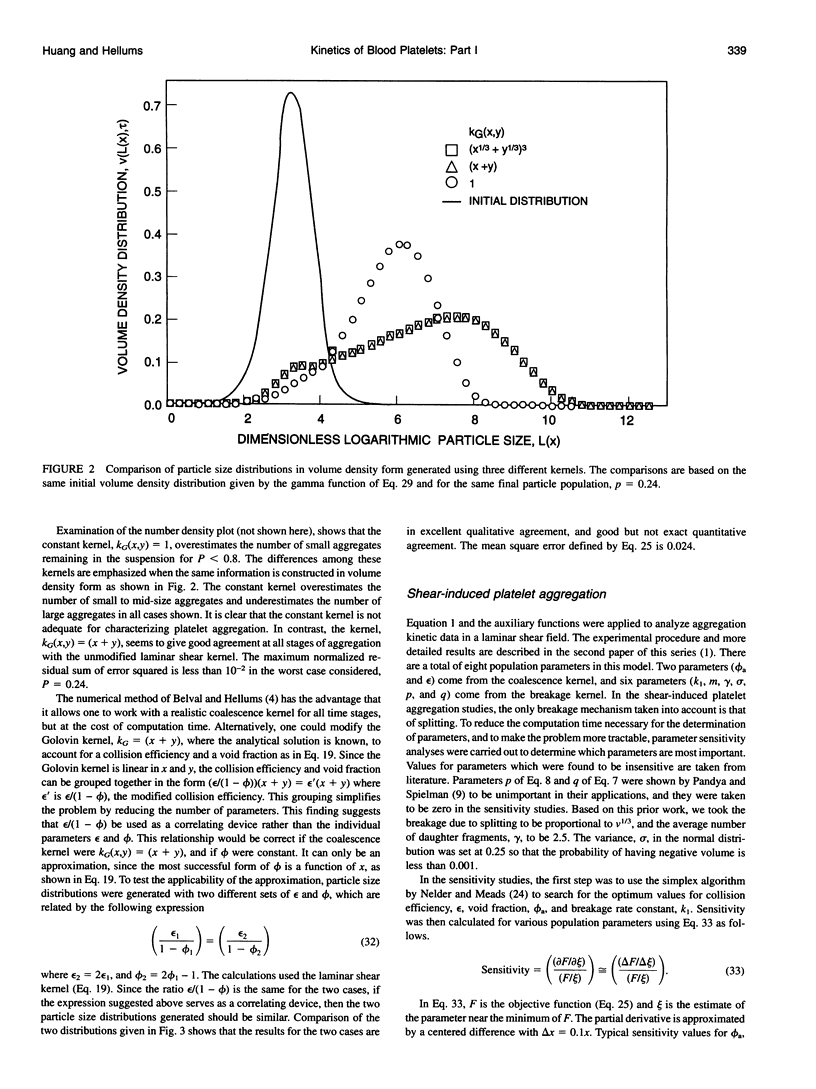
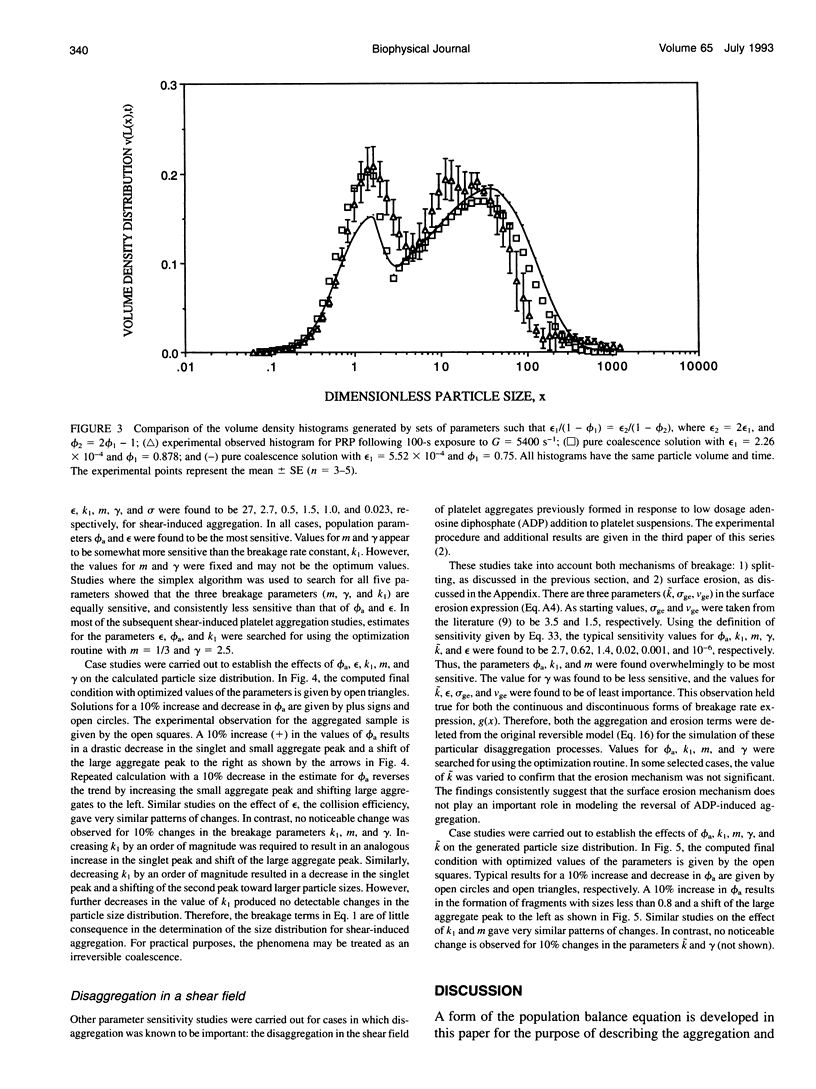
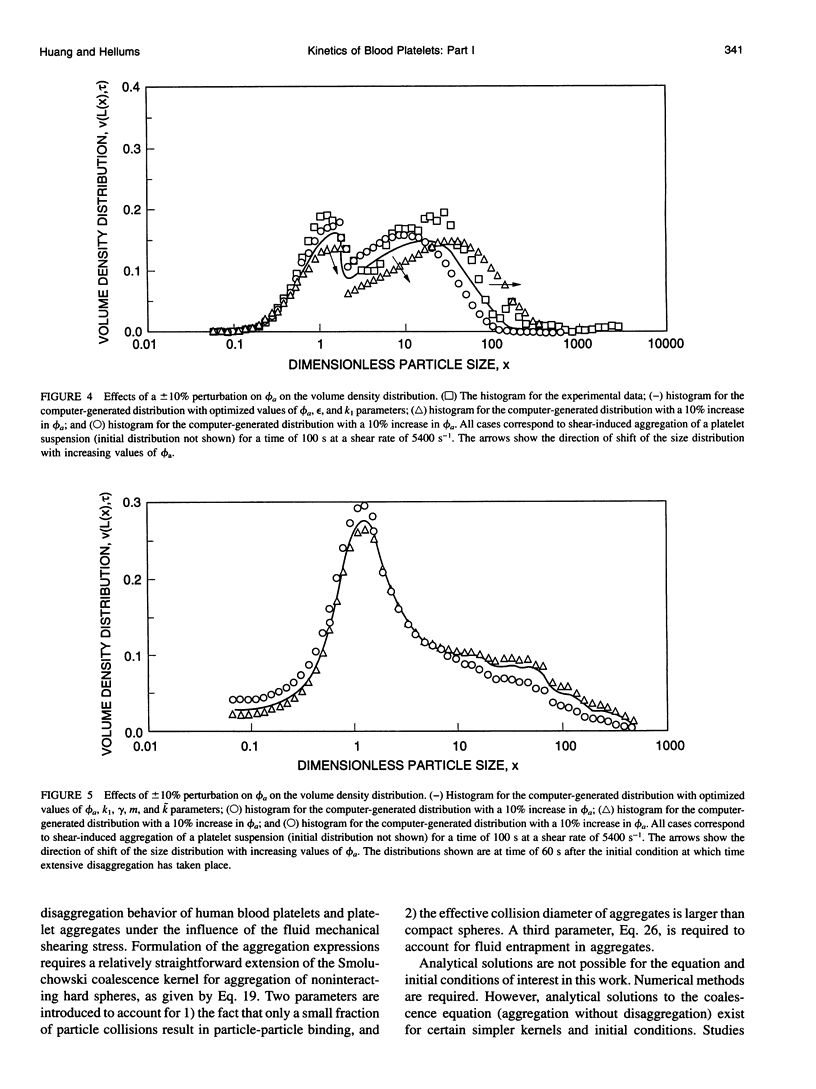
Hydrodynamic shear stress of sufficient intensity is known to cause platelet activation and aggregation and to alter the effects of biochemical platelet agonists and antagonists. In this work, a population balance equation (PBE) model is developed for analysis of platelet aggregation and disaggregation kinetics under the influence of a shear field. The model incorporates both aggregation and disaggregation by splitting and/or erosion mechanisms. This paper, the first of a series of three, deals with the formulation, simplification, and validation of the PBE and with the estimation of parameters involved in the PBE. These population parameters include collision efficiency, void fraction (related to the particle collision diameter), and the breakage rate coefficient. The platelet particle size distribution is determined experimentally, both initially and at some later times. The PBE can then be used to match satisfactorily the observed particle histograms, by appropriate choice of parameters of the model as functions of time, platelet size, and magnitude of physical or chemical stimuli. Besides providing information on adhesive forces and on the rates of aggregation and disaggregation, these parameters infer the physical properties of platelets and platelet aggregates. These properties are of potential value in increasing our understanding of the processes involved in thrombotic disease and/or therapy. A numerical procedure for solving the PBE is validated by application to simple cases for which analytical solutions are available. The model is applied to analysis of experiments, and parameter sensitivity studies are used to order the importance of the parameters and to reduce the complexity of the model. The simplified model is shown to give good agreement with experimental observations.
Full text
PDF





Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Bell D. N., Goldsmith H. L. Platelet aggregation in poiseuille flow: II. Effect of shear rate. Microvasc Res. 1984 May;27(3):316–330. doi: 10.1016/0026-2862(84)90063-3. [DOI] [PubMed] [Google Scholar]
- Belval T. K., Hellums J. D. Analysis of shear-induced platelet aggregation with population balance mathematics. Biophys J. 1986 Sep;50(3):479–487. doi: 10.1016/S0006-3495(86)83485-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Born G. V., Hume M. Effects of the numbers and sizes of platelet aggregates on the optical density of plasma. Nature. 1967 Sep 2;215(5105):1027–1029. doi: 10.1038/2151027a0. [DOI] [PubMed] [Google Scholar]
- Chang H. N., Robertson C. R. Platelet aggregation by laminar shear and Brownian motion. Ann Biomed Eng. 1976 Jun;4(2):151–183. doi: 10.1007/BF02363645. [DOI] [PubMed] [Google Scholar]
- Frojmovic M. M., Newton M., Goldsmith H. L. The microrheology of mammalian platelets: studies of rheo-optical transients and flow in tubes. Microvasc Res. 1976 Mar;11(2):203–215. doi: 10.1016/0026-2862(76)90052-2. [DOI] [PubMed] [Google Scholar]
- Huang P. Y., Hellums J. D. Aggregation and disaggregation kinetics of human blood platelets: Part II. Shear-induced platelet aggregation. Biophys J. 1993 Jul;65(1):344–353. doi: 10.1016/S0006-3495(93)81079-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang P. Y., Hellums J. D. Aggregation and disaggregation kinetics of human blood platelets: Part III. The disaggregation under shear stress of platelet aggregates. Biophys J. 1993 Jul;65(1):354–361. doi: 10.1016/S0006-3495(93)81080-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karino T., Goldsmith H. L. Aggregation of human platelets in an annular vortex distal to a tubular expansion. Microvasc Res. 1979 May;17(3 Pt 1):217–237. doi: 10.1016/s0026-2862(79)80001-1. [DOI] [PubMed] [Google Scholar]


