Gene Conversion and Different Population Histories May Explain the Contrast between Polymorphism and Linkage Disequilibrium Levels

Abstract

To characterize linkage disequilibrium (LD) levels in human populations, we have analyzed 10 independent noncoding segments in three population samples from the major ethnic groups—that is, Africans, Asians, and Europeans. Descriptive statistics show that LD decays much faster in the African samples than in the non-African ones. With the assumption of an equilibrium model, we estimated the population crossing-over parameter (4N_er_bp, where N_e is the effective population size and r_bp is the crossing-over rate per generation between adjacent base pairs) in the presence of gene conversion. In the African sample, LD and polymorphism levels lead to similar estimates of effective population size, as expected under an equilibrium model. Conversely, in both non-African samples, LD levels suggest a smaller effective population size than that implied by polymorphism levels. This observation is paralleled by significant departures from an equilibrium model in the spectrum of allele frequencies of the non-African samples. Besides ruling out the possibility that non-African populations are at equilibrium, these results suggest different demographic history (temporal and spatial) of these groups. Interestingly, the African sample fits the expectations of an equilibrium model based on polymorphism and divergence levels and on frequency spectrum. For this sample, the estimated ratio of gene conversion to crossing-over rates is 7.3 for a mean tract length of 500 bp, suggesting that gene conversion may be more frequent than previously thought. These findings imply that disease-association studies will require a much denser map of polymorphic sites in African than in non-African populations.

Introduction

Linkage disequilibrium (LD), the nonrandom association of alleles at linked sites, is a fundamental aspect of genetic variation. As such, LD has been of great interest to population geneticists, because it is thought to be informative with regard to the evolutionary forces shaping variation, including a variety of models of population history and natural selection (Hudson et al. 1994; Tishkoff et al. 1996). Owing to the recent emphasis on genomewide association studies, the characterization of LD in humans has become a key prerequisite for the design of such studies and the development of maps of single-nucleotide polymorphisms (SNPs) of adequate density (Jorde 1995; Risch and Merikangas 1996; Collins et al. 1997). Furthermore, analysis of LD may add to our knowledge of the mechanisms that determine recombination rates, for example, by allowing estimation of gene conversion and cross-over rates and their variation across the genome (Chakravarti et al. 1984; Andolfatto and Nordborg 1998; Przeworski and Wall 2001).

So far, two main approaches have been used to characterize the decay of LD between biallelic markers in humans. The descriptive approach relies on the collection of polymorphism data at linked sites (usually by genotyping previously ascertained SNPs) and summarizing LD by means of conventional summary statistics, typically D′ or the statistical significance of the association (namely, the P value from a Fisher’s exact test) (Jorde et al. 1993, 1994; Taillon-Miller et al. 2000; Reich et al. 2001). The modeling approach analyzes simplified models of human population history, using population parameters (i.e., the population mutation and crossing-over rates) that are estimated from different sources of data, such as polymorphism levels in resequencing surveys and the average crossing-over rate determined in pedigrees (Kruglyak 1999; Pritchard and Przeworski 2001). These approaches have led to contrasting results. On one hand, the descriptive studies show a great deal of variation in observed LD levels (Taillon-Miller et al. 2000). This may be partially accounted for by variation in recombination rates across the genome (fig. 2 in Reich et al. 2001). Furthermore, it is well known that the processes generating LD are highly stochastic (Pritchard and Przeworski 2001 and references therein); thus, variation in LD levels across studies examining different genomic regions is expected to occur simply by chance. Perhaps more interestingly, discrepancies are observed also between descriptive and modeling studies. In population samples of European origin, the observed LD levels are higher than predicted by modeling of population history (Kruglyak 1999; Pritchard and Przeworski 2001; Reich et al. 2001). On the other hand, a reanalysis of sequence-variation data in pooled worldwide samples found evidence of lower levels of LD than would be expected on the basis of estimates of crossing-over rate from pedigrees and models of constant and exponentially growing population size (Przeworski and Wall 2001). Models that included the effect of gene conversion occurring at a rate as much as two times higher than the crossing-over rate improved the fit of the data only partially. Likewise, multiple hits at CpG sites could not explain the data.

In the study reported here, we focused on the empirical characterization of LD, by means of an efficient multilocus data-collection scheme, in ethnically distinct population samples. When analyzed by application of widely used descriptive statistics, our results show that the decay of LD is faster in the African samples than in both the European and the Asian ones. However, conventional descriptive statistics have several drawbacks, such as sensitivity to sample size and to allele frequencies. As an alternative, we estimated the population crossing-over parameter, 4N_er_bp, for each population sample by use of a composite likelihood approach that provides better estimates than other ad hoc methods (Hudson 2001). By using an unbiased estimator of this parameter, we overcome the shortcomings of descriptive statistics of LD. Because over short distances gene conversion is likely to be the major factor contributing to the decay of LD, we assumed an equilibrium model that included crossing-over as well as gene conversion. The equilibrium model assumes a population of constant size, in which mating occurs at random; in addition, polymorphisms are neutral and always result from a single mutation event (infinite-sites model). Our study did not rely on previously ascertained SNPs; rather, every individual in the sample, as well as a chimpanzee outgroup, was resequenced. This allowed us to compare estimates of the effective population size that are based on polymorphism and interspecific divergence levels, on one hand, with those based on LD levels, on the other, for the same genomic regions and population samples. These data show that both non-African samples do not fit the expectations of an equilibrium model, yet all aspects of the African data are consistent with such a model. In conjunction with higher LD levels observed in the non-African samples, these results suggest different demographic histories outside Africa. Furthermore, substantial levels of gene conversion must be invoked to account for both single-site polymorphism and LD data.

Material and Methods

DNA Samples

Sequence variation was surveyed in DNA samples from three human populations: 15 Hausa from Yaounde (Cameroon), 15 individuals from central Italy, and 15 Han Chinese from Taiwan. The institutional review board of the University of Chicago approved this study. The same genomic regions were also sequenced in one common chimpanzee.

Selection of Genomic Regions

In choosing the genomic regions to be surveyed, we attempted to find sequence segments that (1) did not contain and were not tightly linked to coding regions and (2) were contained in regions with similar and nearly average crossing-over rates and percent G+C content. The GenBank database was searched for human BAC clone sequence entries >50 kb. An approximate local crossing-over rate was estimated for each region by comparing the genetic and physical maps as follows. For each sequence entry, sequence-tagged sites (STS) were identified by BLAST searches and were used to place each region on the physical and genetic maps, using National Center for Biotechnology Information MapViewer. The local centimorgan:megabase (cM:Mb) ratio for each region was determined by identifying all STS sites ⩽5 cM on either side of the region in both the Généthon genetic map and the GeneBridge 4 Radiation Hybrid map. For each marker, RH map positions were converted to base pairs, using chromosome-specific conversion rates obtained from Hudson et al. (1995). The average cM:Mb ratio was calculated across the distance of 10 cM. In addition, a local cM:Mb average was calculated using the two markers that most closely flank the region. The values obtained by this method have been compared with those obtained by Yu et al. (2001), when the latter were available, and were found to be similar (see table 1). Regions were selected within a limited range of 35%–45% G+C. BAC clone sequences that did not contain annotated genes and proteins were subjected to a series of BLAST searches against the GenBank nonredundant, SWISSPROT, and expressed-sequence-tag databases to identify potential similarities to other expressed sequences. Sequences were also subjected to gene-prediction searches, using Genefinder, F-genes, and Grail, to identify putative coding sequences. Only regions that had no significant BLAST hits to known genes or expressed sequences and that did not contain strongly predicted genes were selected for further study. Ten regions were selected from different chromosomes or different arms of the same chromosome (table 1). Within each of these regions, we defined a 10-kb segment to be surveyed in the population samples.

Table 1.

Genomic Regions Included in Resequencing Survey

Region(Accession Number)	Locus	%G+C	Forward Primera	Reverse Primera	cM/MbRHb	cM/MbMc
1 (AC003670)	12q13.1	40.6	52491–53671	61918–62143, 62161–63179	.96	1.13
2 (AL008731)	6p22.3-24.3	43.6	40993–42218	49842–51169	1.86	1.63
3 (AC002479)	5p15.2	40.6	17995–19385	26428–27830	1.45	1.44
4 (AL031653)	20p12	36.2	46230–47380	55320–56730	1.30	1.90
5 (AC004038)	5q23	36.1	42300–43980	51075–52445	1.14	NA
6 (AC007128)	7p11	39.2	13118–14180, 14360–14717	22200–23263, 23295–23733	1.21	1.37
7 (AC011507)	19q	43.2	41000–41214, 41450–42591	49728–50134, 50222–50669, 50713–51336	.87	NA
8 (AC004097)	16p	41.5	43127–43286, 43352–44115	52096–52867, 52953–53294	1.80	NA
9 (AC005659)	10q25	45.0	58310–58670, 58830–59250	67358–68369	1.08	1.18
10 (AC004047)	4q25	35.4	39169–40324	48988–49943	1.23	1.36
Average		40.1			1.29	1.43

^aForward and reverse refer to the two 1–2-kb segments in each locus pair in arbitrary order.

^bCrossing-over rate calculated by comparing the genetic and radiation hybrid maps.

^cCrossing-over rate calculated on the basis of the analysis carried out in Yu et al. 2001. NA = not applicable.

PCR Amplification

Primers for amplifications and sequencing were designed using Oligo 5 (Molecular Biology Insights) or Primer 3. All primers were designed on the basis of the GenBank sequence entry containing each region (table 1). All nucleotide positions mentioned in this article refer to these sequences. For regions 1–5, PCR primers were designed to amplify a segment of ∼10 kb from 200 ng of genomic DNA. The condition of the 10-kb amplification was as follows: initial denaturation at 92°C for 2 min, 10 cycles of 92°C for 10 s, annealing for 30 s, 68°C for 8 min, remaining cycles: 92°C for 10 s, annealing for 30 s, 68°C for 8 min plus an additional 20 s per cycle, final elongation at 68°C for 7 min. Primers were then designed to amplify 1–2 kb (arbitrarily labeled Forward and Reverse), at each end of the 10-kb segment, using 1 ml of the initial 10-kb amplification product as the template. Allele-specific PCR was found to have occurred in region 4. Thus, PCR primers were redesigned to amplify the areas around the amplification primers. In addition, the 1–2-kb segments were reamplified from 40 ng of genomic DNA, to determine diploid sequence. For regions 6–10, PCR primers were designed to amplify only the 1–2 kb at each end of the 10-kb segment directly from 40 ng of genomic DNA. The amplification conditions were as follows: initial denaturation at 94°C, 25–40 cycles at 92°C for 10 s, annealing for 30 s, 72°C for 90 s, and final elongation at 72°C for 2 min. Sequencing primers were designed to anneal every 400–500 bp, for complete coverage in both orientations of each locus pair.

Sequence Determination

PCR products were prepared for sequence analysis, either by using the Qiaquick PCR purification kit (Qiagen), according to the manufacturer's recommendation, or by treatment with a combination of shrimp alkaline phosphatase and exonuclease I (USB). Dye-terminator sequencing was performed with the ABI BigDye terminator cycle-sequencing kit, and products were analyzed on an ABI 377 or ABI 3700 automated sequencer (Applied Biosystems). Chromatograms were imported into Sequencher 3.1.1 (Gene Codes), for assembly into contigs and identification of polymorphic sites. Diploid sequence was determined, on both strands, for all individuals by visual inspection of each nucleotide position in high-quality chromatograms. The sequence data are available on the Di Rienzo Laboratory home page.

Statistical Analysis

The program DNAsp, version 3.50 (Rozas and Rozas 1999), was used to calculate nucleotide diversity, Tajima’s D, and interspecies sequence divergence. Arlequin, version 2.00, was used to test for Hardy-Weinberg equilibrium (Schneider et al. 2000). The multilocus Hudson-Kreitman-Aguadé (HKA) and Tajima’s D tests (Hudson et al. 1987; Tajima 1989) were done using the program HKA, kindly provided by Jody Hey (Rutgers University). LD was measured using both D′ and r², which were estimated from our diploid data by use of maximum likelihood (Hill 1974).

The Model and Parameter Estimation

The population crossing-over parameter and the gene conversion parameter were estimated under a standard infinite-sites Wright-Fisher model with both crossing-over and gene conversion. We assume no geographic structure and constant population size (N_e). Gene conversion was assumed to follow a model, as described by Wiuf and Hein (2000), with geometrically distributed conversion-tract length. We denote the mean tract length by L (which corresponds to 1/q in Wiuf and Hein), and the probability of a conversion tract initiating between two specified base pairs per generation as g. The probability of crossing-over per generation between two adjacent base pairs is denoted r_bp, and 4N_er_bp will be denoted ρ. (The crossing-over and gene-conversion rates are assumed to be the same at all sites in all 10 regions surveyed.) Our analysis considers the polymorphic sites in a pairwise manner. Under the assumed model, the sample configuration for a specified pair of sites depends on 4N_eμ (≅θ) and 4N_er_e, where μ is the neutral mutation rate and r_e is the “effective” recombination rate between the two sites. The effective recombination rate between two sites is the probability that a random gamete produced by a double heterozygote would be a recombinant gamete by either crossing-over or gene conversion. If the two sites are separated by d base pairs, the effective recombination rate between the two sites is assumed to be

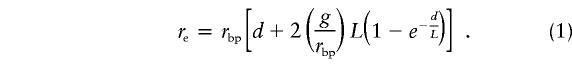We denote the ratio of gene conversion to crossing-over rate (g/r_bp) by f. In the rest of the present report, the crossing-over and conversion model is characterized by the three parameters r, f, and L. This model was also considered by Langley et al. (2000), who derived equation (1) and used it for estimation purposes. (In Langley et al. 2000, the parameter r_bp is denoted c, and L is denoted t.) The model is also similar to that of Andolfatto and Nordborg (1998), whose equation 1 gives the effective recombination rate for a model with fixed conversion-tract length. Their parameter γ corresponds approximately to the product gL in our model.)

Considering a pair of biallelic polymorphic sites, there are only four possible haplotypes. With phase-unknown diploid data, there are nine possible two-site genotypes. Thus, a sample of diploids can be characterized at two polymorphic sites by a nine-vector, the elements of which are the counts of each of the nine possible diploid genotypes in the sample. This nine-vector is denoted n. Under the equilibrium model, the probability of any two-site sample configuration, either haploid or diploid, is a function of θ and 4N_er_e. For small values of θ (and conditional on polymorphism at the two sites), the configuration probabilities are approximately independent of θ and thus are functions of only one unknown parameter, 4N_er_e. All possible haploid sample configuration probabilities were estimated for our sample sizes for a set of 4N_er_e values with Monte Carlo simulations (Hudson 1985, 2001). Hudson (2001) shows how to obtain diploid sample probabilities from the haploid probabilities. From equation (1), 4N_er_e is itself a function of d, ρ, and f, and, thus, for any pair of polymorphic sites in our data, the conditional probability of the two-site configuration can be obtained from the tabulated configuration probabilities as functions of ρ and f. We denote the probability of a two-site configuration conditional on polymorphism at both sites by q_c(n; ρ, f, d). To estimate ρ and f, we fix L and maximize the product:

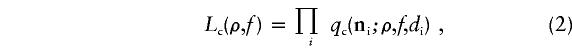where n_i is the two-site configuration for the ith pair of sites, d_i is the distance in base pairs between the ith pair of sites, and the product is over all pairs of polymorphic sites. The maximum composite-likelihood estimates of ρ and f will be designated with hats. Because of the statistical dependence between the n_i, the product, L_c, is not a true likelihood but will be referred to as the “pairwise composite likelihood.” In our case, we do not attempt to estimate tract length, L, but fixed its value at 500 bp or 1,000 bp. Similarly, in addition to estimating f and ρ, we consider estimating ρ with fixed values of f. Hudson (2001) describes properties of this estimator of ρ for the case where there is no gene conversion.

To obtain approximate confidence intervals (CIs), data sets analogous to ours were generated by coalescent methods with crossing-over and gene conversion. With these computer-generated data sets, the distribution of 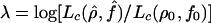was characterized. (In this expression, ρ₀ and f₀ are the values of the parameters used to generate the samples with a simulation program.) In particular, the 95th percentile of the distribution, denoted λ₉₅, was estimated for a range of parameter values and used to obtain approximate 95% CIs or confidence regions. The value of λ₉₅ depends on the unknown value of ρ. In particular this critical value is larger for smaller values of ρ. We used ρ values one-half the estimated values to get a conservative value of λ₉₅. Nevertheless, these CIs should be regarded as rough estimates only. Similarly, we tested the hypothesis of no gene conversion, by comparing the observed value of 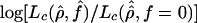(where the composite likelihood in the denominator is the maximum composite likelihood with f=0) with the 95th percentile of the distribution of this quantity in simulations with f=0. To obtain a 95% CI for ρ, given a fixed value of f, we estimated the 95th percentile of the distribution of 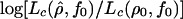for samples generated with ρ₀ equal to one-half the estimated value of ρ with f=f₀.

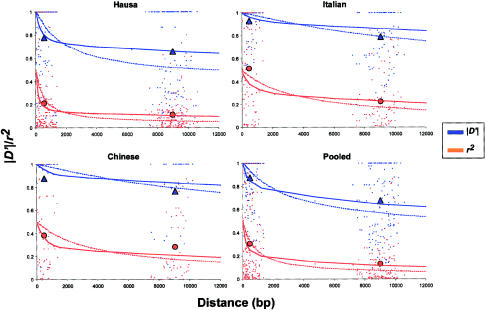
The two-site haploid sample configuration probabilities were also used to calculate the expected value of |D′| and r² for the sample sizes and allele frequencies used in this study. This was done by using the estimated ρ and f values and summing over all sample configurations with the required marginal allele frequencies (Hudson 2001). These results are shown in figure 1. The same procedure was used for different sample sizes and allele frequencies.

Figure 1.

Decay of pairwise linkage disequilibrium with distance. Symbols in red indicate r² values, and symbols in blue indicate |D′| values. The dots indicate the observed values for each pair of polymorphic sites. The solid triangles and circles indicate, respectively, the average values of |D′| and r² within and between 1-kb segments. The solid lines indicate the decay of LD expected under a model of crossing-over and gene conversion for L = 500 bp and f = 8. The dashed lines indicate the decay of LD expected under a model of crossing-over only. For each population sample, the expected LD decay was calculated based on the corresponding estimates of ρ from table 4.

Results

Scheme for Data Collection

In order to survey sequence variation and LD most efficiently, we resequenced a segment of ∼1 kb at each end of an ∼10-kb segment in all individuals from three population samples. Each of these two-segment units will be referred to as a “locus pair.” Ten such locus pairs, selected from different chromosomes or different arms of the same chromosome, were surveyed (table 1). In an attempt to characterize “typical” LD levels in the human genome, genomic regions were chosen according to a fixed set of criteria. The first one was that crossing-over rates were close to the genomewide average, as determined by comparing the physical and genetic maps. The average crossing-over rate for the selected regions was 1.29 cM/Mb (table 1). Because percent G+C content is related to sequence divergence and mutation rate (Wolfe et al. 1989), as well as crossing-over rate (Fullerton et al. 2001), the second criterion was that G+C content was 35%–45%. Furthermore, in an attempt to reduce the probability that the observed patterns of LD were affected by natural selection, we chose regions that do not contain or flank known coding regions. The ten locus pairs were resequenced in all individuals of samples drawn from three large populations from the major ethnic groups: Hausa of Cameroon (Sub-Saharan Africa), Italians (Europe), and Han Chinese (Asia). Unlike many other studies of LD, the present study is based on resequencing every individual in each sample. Thus, LD and levels of polymorphism can be assessed and contrasted for the same genomic regions and population samples, allowing more-precise inferences about population and genetic factors that affect the decay of LD.

Descriptive Summary of Sequence Variation and LD

The average divergence between human and chimpanzee sequences at the 10 locus pairs is 1.19%. We tested for heterogeneity of sequence divergence across the surveyed genomic regions by using the average number of sequence differences between all human and the chimpanzee sequences and averaging that over all regions. The expected numbers were then calculated for each region, with its length taken into account. The difference between observed and expected numbers was evaluated by a global χ² test that rejected the hypothesis of homogeneous divergence rates. Region 3 made the greatest contribution to the global χ², showing significantly higher interspecies divergence than the other regions. Once region 3 was removed, the remaining nine regions showed no significant global χ². This suggests that the mutation rate is higher in region 3, even though its percent G+C and CpG content are not correspondingly higher. Heterogeneity of polymorphism levels was assessed in the same way. No significant heterogeneity in polymorphism level across regions was found. (This test of heterogeneity of polymorphism levels assumes no linkage between sites. However, because linkage between sites increases the variance of the numbers of polymorphic sites, our conclusion of no heterogeneity would be the same if linkage were taken into account.)

As shown in table 2, nucleotide diversity over all loci is 0.11% in the Hausa sample. This is ∼10% and 50% higher than in the Italian and Chinese samples, respectively. The number of segregating sites in the African sample is ∼50% greater than either the Italian or the Chinese sample. Given these differences between populations, it is important to interpret analysis of pooled samples with caution.

Table 2.

Summary Statistics of Sequence Variation

		Hausa				Italians				Chinese
Region	La	Sb	πc(%)	TDd	De(%)	Sb	πc(%)	TDd	De(%)	Sb	πc(%)	TDd	De(%)
1	2,423 (2,049)	12	.08	−1.27	1.05	6	.08	−.16	1.08	3	.03	−.37	1.04
2	2,552	15	.18	.73	1.29	11	.06	−1.47	1.24	9	.04	−1.69	1.23
3	2,792	17	.15	−.03	1.97	13	.16	1.31	1.95	9	.11	1.00	1.97
4	2,560 (2,431)	10	.12	.74	1.41	7	.11	1.72	1.44	8	.08	.03	1.45
5	3,050	9	.08	.29	1.10	10	.11	.88	1.07	9	.05	−.99	1.11
6	2,920 (2,902)	16	.10	−.93	1.23	8	.06	−.53	1.21	9	.04	−1.45	1.20
7	2,811	11	.07	−.96	.94	7	.12	2.70	.94	10	.10	.37	.96
8	2,034	9	.09	−.69	.96	5	.07	.46	.94	8	.09	−.27	.93
9	1,791	6	.08	−.22	1.16	4	.08	1.10	1.17	3	.09	2.43	1.17
10	2,110	15	.15	−.52	.75	9	.13	.63	.80	8	.14	1.53	.79
Overall	25,043	120	.11	−.33	1.19	80	.10	.74	1.18	76	.07	−.12	1.19
Ne			11,555				10,504				7,353

^aLength (in bp) of sequenced segment. Numbers in parentheses indicate the length of the segment sequenced in the chimpanzee, if shorter than that sequenced in human samples.

^bNumber of polymorphic sites.

^cNucleotide diversity per base pair.

^dTajima’s D statistic (Tajima 1989).

^eSequence divergence per base pair from the orthologous regions in the chimpanzee.

Using the diploid phase-unknown sequence data, we calculated the maximum-likelihood estimate of the summary statistics of LD r² and |D′| for all pairs of polymorphic sites in the 10 locus pairs; this was done for each population sample separately and for the pooled sample (Hill 1974). (This estimation procedure relies on the assumption of Hardy-Weinberg equilibrium. Tests of Hardy-Weinberg equilibrium did not show significant departures after Bonferroni correction.) Because estimates of LD for low-frequency alleles in small samples are not very informative, only alleles with frequencies in the range 0.1–0.9 were included in this analysis. As shown in figure 1, in the Italians, mean r² for sites separated by <1 kb is 0.53, whereas, for sites separated by 8–10 kb, the average is 0.23. The Chinese result is similar, with average r² value of 0.38 for sites separated by <1 kb and an average r² of 0.28 for sites separated by 8–10 kb. In the Hausa, sites separated by <1 kb have an average r² of 0.21, considerably less than in Italians and Chinese, and for sites 8–10 kb apart, r² has dropped to an average of 0.11. Likewise, |D′| declines with distance more rapidly in the Hausa than in the other two population samples. The values of |D′| and r² are sensitive to the allele frequencies and sample sizes, and comparison of results between studies should take this into account. This issue is considered in more detail in the Discussion section.

Testing the Equilibrium Model

In the next section, the parameters of the equilibrium model will be estimated. Before proceeding with estimation, we tested the data for compatibility with this model. Because the polymorphism assay is based on a random sample in which all individuals are fully sequenced and because sequence from a chimpanzee outgroup was obtained, a variety of tests of the equilibrium model are available.

The HKA test is used to determine whether the levels of intraspecific polymorphism and interspecific divergence at a set of loci are consistent with the equilibrium model (Hudson et al. 1987). A multilocus version of the original HKA test was applied to all 10 regions in each population sample. No significant departures from the equilibrium model were detected (table 3).

Table 3.

Results of Multilocus HKA and Tajima’s D Tests

Population	Pa	Mean D	% Largerb	Variance D	% Largerb
Hausa	.71	−.285	76.6	.504	84.9
Italians	.94	.663	.90	1.399	11.4
Chinese	.75	.057	33.9	1.720	3.0

^aHKA test probability.

^bPercent of simulated values larger than observed.

Tajima’s D statistic, which summarizes information about the spectrum of allele frequency, was calculated for each region in each population sample (Tajima 1989). These values, as well as their averages and variances, are shown in tables 2 and 3. We tested whether the observed average and variance of Tajima’s D across loci was consistent with the equilibrium model by estimating the critical values of these distributions from Monte Carlo simulations (software kindly provided by J. Hey). (The mutation parameters used in the simulations were estimated in the HKA test, using both the polymorphism and divergence data.) In these simulations, the regions were assumed to be unlinked and to have no recombination occurring within them. As shown in table 3, the Italian sample has a positive average Tajima’s D that is significantly different from the equilibrium expectations. Less than 1% of the simulated samples had an average value of Tajima’s D that was as large or larger than the observed average value. The Chinese sample shows a marginally significant variance of Tajima’s D. If realistic levels of recombination were incorporated in the simulations, the P value for this observed variance would be smaller (as would the P value of the observed average Tajima’s D in Italians.) Although the African sample shows a negative overall Tajima’s D, the observation is far from statistically significant. The departures of the Italian and Chinese samples from the equilibrium model suggest that estimates of parameters based on this model should be interpreted with caution.

Estimating the Neutral Mutation Rate and the Effective Population Size

On the basis of the observed divergence (D) between human and chimpanzee sequences—and assuming a divergence time (t) of 5 million years—we can estimate the substitution rate for these regions as μ_y=D/2t=0.0119/[2×(5×10⁶)]=1.19×10^-9/year. Under the equilibrium model, this substitution rate is an estimate of the average neutral mutation rate per site at these loci. Note that no correction for multiple hits has been applied.

Under the equilibrium model, the expected nucleotide diversity (π) is 4N_eμ, where μ here is the neutral mutation rate per generation. This suggests estimating the effective population size (N_e) by π/4μ. The estimates of N_e shown in table 2 were obtained in this way, using the overall nucleotide diversity for each population sample and μ=20μ_y=2.38×10^-8, where we have assumed a generation time of 20 years. Similarly, estimates of effective population size can be obtained using the number of polymorphic sites. Because of the observed departures from the expectations of the equilibrium model, different estimates would be obtained for some samples using nucleotide diversity and number of polymorphic sites. As shown in table 2, the estimate of effective population size for the African sample is larger than that for the non-African ones, in line with previous studies (Przeworski et al. 2000). We emphasize however, that the data show significant departures from the simple equilibrium model in the non-African populations; thus, the meaning of these estimated values is unclear.

Estimating the Population Crossing-Over Parameter

Under a simple two-locus Wright-Fisher equilibrium model, the level of LD depends on the composite parameter, ρ=4N_er_bp, where N_e is the effective population size and r_bp is the crossing-over rate per generation between adjacent nucleotide positions, and the rate and tract length of gene conversion. The ratio of gene conversion to crossing-over rate is denoted by f (see Material and Methods section). We have used a pairwise composite likelihood method to estimate ρ and f for fixed values of mean conversion-tract length (L). By this method, the CIs for estimates of ρ and f based on a single locus pair are very large and make interpretation of individual estimates difficult (simulation results not shown). However, when the data from all 10 locus pairs are combined, good estimates can be obtained.

Although relatively little is known about gene conversion in mammals, studies in yeast and fruit flies suggest that the conversion-tract length is 300–2,000 bp (Hilliker et al. 1994; Paques and Haber 1999) and that f is ∼2–4 (Fogel et al. 1983; Foss et al. 1993; Hilliker et al. 1991). We restricted our attention to models with L=500 bp or 1,000 bp. We focused initially on the African sample, because it did not show departures from the equilibrium model assumed in the estimation procedure. For L=500 bp, the maximum composite-likelihood estimate of ρ and f in the African sample are 0.00089 and 7.3, respectively. Assuming the crossing-over rate per generation is 1.29 cM/Mb, the effective population size estimate for the African sample is ∼17,000, that is, 0.00089/(4^*1.29^*10^-8). This is roughly consistent with, but somewhat larger than, estimates of effective population size based on polymorphism levels described above.

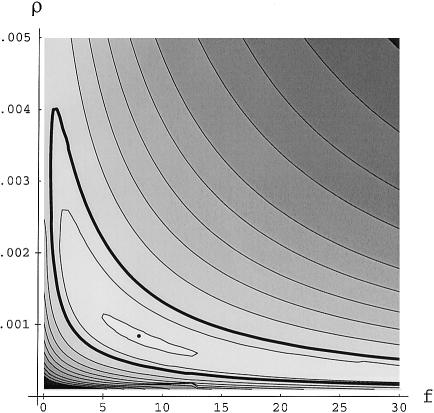
Figure 2 shows a 95% confidence region for ρ and f based on the African data. From the figure, it is clear that small values of f imply large values of ρ. Also, f<0.8 is incompatible with the data. In addition, for f<1, the plot in figure 2 suggests that ρ is likely to be >0.002, which in turn implies an implausibly large effective population size.

Figure 2.

Pairwise composite likelihood surface for the African sample. The heavy contour line indicates an approximate 95% confidence region based on simulations (see Material and Methods section). The other contour lines are at arbitrary intervals to depict the shape of the surface. The dot indicates the maximum at f=7.3 and r=.00089.

If we assume that N_e=12,000, as estimated from the levels of polymorphism in the African sample, and that r_bp=1.29 cM/Mb, as direct estimates of crossing-over rates suggest, then ρ=6.2×10^-4. Fixing this value of ρ and assuming L=500 bp, the maximum composite-likelihood estimate of f is 11 (approximate 95% confidenceregion=4.5–25). For smaller values of L, even larger values of f are estimated. The point, f=11, ρ=6.2×10^-4 is within the highest contour interval shown in figure 2, thus, is well within the 95% confidence region for f and ρ.

It is well known that admixture may increase LD levels, even at unlinked sites. This raises the possibility that unrecognized admixture might affect the estimates of the population cross-over and gene conversion parameters. To investigate this issue, we estimated |D′| and r² for pairs of unlinked sites for the Hausa and the pooled samples. The Hausa sample was chosen because it is used for estimating the gene conversion parameters, and the pooled sample was examined because it is artificially admixed. The significance of the observed mean |D′| and r² values was evaluated by a test in which diploid genotypes for each entire locus pair were randomly permuted across individuals. In the Hausa sample, the observed mean |D′| and r² were not significantly different from random expectations: the observed mean |D^′|=0.52 and r²=0.064, and the mean of the corresponding quantities from permutations are 0.55 and 0.071 (top and bottom 2.5th percentiles: 0.51–0.60 and 0.060–0.085, respectively). Conversely, the results for the pooled sample are consistent with some level of admixture: the observed mean of |D^′|=0.37 and r²=0.032, and the mean of the corresponding quantities from permutations are 0.30 and 0.022 (top and bottom 2.5th percentiles: 0.27–0.34 and 0.018–0.026, respectively). Thus, estimates of gene-conversion parameters that we obtain from the Hausa sample are unlikely to be inflated as a result of unrecognized admixture.

Estimates of ρ for the Italian and Chinese samples are shown in table 4. Because the equilibrium model is not compatible with the data from these populations, the estimates of ρ may not accurately estimate 4N_er_bp, but they may nonetheless provide useful indices of the rate of decay of LD with distance. From these estimates, it appears that LD decays at a rate roughly four times slower in the two non-African populations than in the African population. In agreement with the above results indicating a departure from the equilibrium model, the effective population sizes that these decay rates imply are not compatible with those estimated on the basis of polymorphism levels in these populations (see tables 2 and 4).

Table 4.

Estimates of the Population Crossing-Over Rate and 95% CIs (× 10⁻⁴)

		Hausa		Italians		Chinese
L(bp)	f		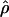Nea		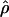Nea		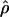Nea
…	0	45	87,209	5.6	10,853	6.0	11,628
500	4	13 (7.1–23)	25,194	2.9 (1.2–5.7)	5,620	3.4 (1.5–6.8)	6,589
1,000	4	11 (5.7–19)	21,318	2.2 (1.0–4.4)	4,264	2.6 (1.0–6.0)	5,039
500	8	8.4 (4.7–14)	16,279	1.9 (.9–3.7)	3,682	2.3 (.9–4.9)	4,457
1,000	8	6.0 (3.4–11)	11,628	1.4 (.6–2.8)	2,713	1.6 (.7–3.5)	3,101

^aN_e estimates are based on the average crossing-over rate of 1.29 cM/Mb shown in table 1.

The estimated population crossing-over and gene conversion rates can be used to calculate the expected values of the descriptive statistics of LD, r² and |D′|. Figure 1 shows the observed decay of LD with distance and the decay expected on the basis of a crossing-over model with and without gene conversion for our data. In agreement with the expectation that gene conversion affects mainly the decay of LD over short distances, the crossing-over/gene-conversion model shows a sharp decline within 1 kb. As shown in table 4, when gene conversion is included in the model, the estimate of the population crossing-over parameter for any given sample decreases. As a consequence, over longer distances, the expected LD is greater if gene conversion is taken into account than in a model including only the effect of crossing-over (as can be seen by comparing the dashed and solid lines in fig. 1). Because |D′| is sensitive to both allele frequencies and sample size, the results in figure 1 cannot be readily compared to those obtained from other studies. To facilitate comparisons, we calculated the distance at which the expected |D′| reaches half its maximum value on the basis of our estimates of the population crossing-over parameter and for different sample sizes and ranges of allele frequencies (table 5). For any given set of population parameters, the distance at which |D^′|=0.5 differs as much as fourfold for the sample sizes considered in table 5 and even more for the allele frequencies of 0.1–0.9 versus 0.3–0.7. These results underscore the difficulty of comparing LD levels across studies. On the basis of the estimates of the population crossing-over parameter and gene-conversion rate for the non-African samples, the expected |D′| for allele frequencies 0.1–0.9 equals one half the |D′|at 55–103 kb in samples of 90 chromosomes. On the basis of the corresponding estimates for the African sample, the expected |D′| for allele frequencies 0.1–0.9 halves at 11–16 kb in samples of 90 chromosomes.

Table 5.

Distance (in Kilobases) at which Expected |D′| = .5^[Note]

		Hausa		Italians		Chinese
SampleSizea	AlleleFrequency	f = 4	f = 8	f = 4	f = 8	f = 4	f = 8
30	.1–.9	42	63	210	325	172	265
60	.1–.9	14	20	79	117	65	98
90	.1–.9	11	16	67	103	55	83
90	.3–.7	1.9	1.4	23	34	18	26

Note.— Distance was calculated using the population-specific 4N_er_bp estimates in table 2 based on L = 500 bp.

^aNumber of chromosomes.

Discussion

The present survey of variation shows that LD decays much faster in the African sample than in both non-African samples. Because gene conversion is likely to play an important role in breaking down allelic association over short distances, we estimated the population crossing-over parameter, 4N_er_bp, for various gene conversion rates and tract lengths. This analysis shows that the LD data are not compatible with absence of gene conversion. When gene conversion is incorporated, we obtain estimates of the effective population size in the African sample that are consistent with those obtained from the observed levels of polymorphism and between-species divergence. Conversely, there is substantial disagreement between the estimates of effective population size based on LD and polymorphism data, respectively, for both non-African samples. Furthermore, by considering the effect of gene conversion, we show that the decay of LD is faster over short distances (but slower over large distances) than expected under previous models that did not include gene conversion.

Although it is difficult to compare precisely LD levels across empirical studies, it is clear that our findings agree with a substantial body of data indicating that LD decays at a faster rate in African than in non-African populations (Tishkoff et al. 1996, 1998, 2000; Kidd et al. 1998, 2000; Mateu et al. 2001; Reich et al. 2001). This finding is paralleled by the long-standing observation, confirmed in the present study, that African populations harbor more variation than non-African ones. Both findings are consistent with the idea that African populations maintained a larger long-term effective population size than did non-African ones. However, it had not been determined whether the extent of the differences in polymorphism and LD levels across populations were consistent with each other, that is, whether both aspects of the data implied similar estimates of effective size for any given population sample. To investigate this question, we chose (a) to collect polymorphism data by resequencing every individual in each population sample and (b) to sequence divergence data from an out-group. This scheme of data collection allowed us to use polymorphism and divergence data, on one hand, and LD data, on the other, to estimate the effective population size for exactly the same samples and genomic regions. The contrast between these estimates for the non-African samples (but not for the African sample) argues against the idea that non-African populations are at equilibrium. This conclusion is also corroborated by the observed departures from equilibrium in the average and variance of the spectrum of allele frequency across loci for the Italian and Chinese samples, respectively.

Different LD levels across populations can also be explained by different histories of ancient population structure or by a bottleneck in a subset of the populations. At present, it is impossible to discriminate between these competing scenarios. Demographic scenarios that included a bottleneck were previously tested based on microsatellite data. These analyses showed evidence of a bottleneck in non-African populations, but the results of analyses of African populations were consistent with an equilibrium model (Kimmel et al. 1998). Other studies of microsatellite data focused on testing either equilibrium models or models of exponential growth that lead to a star-shaped genealogy (Di Rienzo et al. 1998; Reich and Goldstein 1998; Gonser et al. 2000) and do not directly bear on the question of a bottleneck during the history of human populations. Wall and Przeworski (2000) noted that the frequency spectrum in non-African populations tends to show a deficit of rarer variants in comparison to the same locus in African populations. This can be quantified by calculating the difference between the Tajima’s D value for African and non-African samples at any given locus, and a sign test can be used to assess the significance of this pattern over a set of loci. It was proposed that this pattern of frequency spectrum could be more easily reconciled with a history of bottleneck in the non-African populations. In our data, a significant deficit of rare variants is observed only when the Italian sample is compared with the Hausa sample (two-tailed sign test P=.021). When the Italian sample is compared with the Chinese sample, we observe a deficit of rarer variants that approaches significance (P=.109). These results further support the notion of a departure from an equilibrium model for the Italian population. Furthermore, the different patterns observed for the Italian and Chinese samples suggest that more-complicated scenarios of demographic change will have to be developed and tested to account for all the non-African data.

A demographic model that includes a bottleneck was also considered by Reich et al. (2001) in the analysis of LD data for a Yoruban and a Swedish sample. It was shown that the LD data for the Swedish sample was consistent with a bottleneck. To compare our results to those of Reich et al., we calculated the distance at which expected |D^′|=0.5 on the basis of our estimates of the population crossing-over parameter (4N_er_bp) for similar sample sizes and range of allele frequencies (see table 5). Our results are in approximate agreement with those of Reich et al. (2001) for the African samples. However, it is possible that other African populations will show different rates of LD decay. In the non-African samples, LD decays faster in our data set (expected |D^′|=0.5 at 18–34 kb for allele frequencies 0.3–0.7) than in the data of Reich et al. 2001 (|D^′|=0.5 at 60 kb for allele frequencies 0.35–0.65). This difference may reflect different histories of northern and southern European populations. However, it should be pointed out that our estimates of the expected |D′| are based on the assumption of an equilibrium model that does not apply to the non-African samples in our data set. It is possible that the distance at which the expected |D^′|=0.5 would be greater (and possibly match the empirical estimate obtained by Reich et al. 2001) if the appropriate demographic model for these populations was employed.

Despite the fact that gene conversion is a well-documented phenomenon in eukaryotic genomes and an important mechanism in the breaking down of allelic associations over short distances, it has received little attention in modeling the decay of LD in humans (Wiehe et al. 2000; Wiuf and Hein 2000; Przeworski and Wall 2001). In agreement with this expectation, we show that our LD data are not consistent with a model that includes only cross-over (see fig. 2). This finding is further corroborated by the contrast between estimates of 4N_er_bp (and the corresponding estimates of the effective population size) assuming only cross-over (f=0) and those including gene conversion (f>0). In the absence of gene conversion, the effective population size estimate for the African sample is approximately seven times greater than that obtained on the basis of levels of polymorphism and divergence. Because the African sample fits the expectations of the equilibrium model for all other aspects of the data, we attribute this discrepancy to the inadequate consideration of all factors contributing to the decay of LD, in particular, of gene conversion. This observation also suggests that short-range LD data may lead to invalid inferences about population histories if gene conversion is not taken into account. In this regard, it is interesting to note that the estimates of effective population size based on the population crossing-over parameter for the non-African samples are substantially smaller if gene conversion is allowed.

Interestingly, our estimates of the frequency of gene conversion relative to cross-over (f) are higher than those obtained from experimental studies in other organisms. For example, typical results for meiotic recombination in yeast and fruit flies point toward a conversion rate two and four times greater, respectively, than the cross-over rate and a tract length of 350–2,000 bp (Fogel et al. 1983; Hilliker et al. 1991, 1994; Paques and Haber 1999). In our data, if the average tract length is fixed at 500 bp, the highest likelihood is observed for f=7.3, although the CIs include values typical for yeast. Single-sperm analysis of the HLA-DPB1 locus in humans detected gene-conversion events of smaller tract length (maximum tract length 54–132 bp) suggesting that tract length in mammalian and yeast cells may differ substantially (Zangenberg et al. 1995). Furthermore, the gene-conversion rates implied by the HLA-DPB1 results are quite large and suggest that f in this region is >20 (analysis not shown).

Recurrent mutations can inflate the apparent level of recombination. In particular, because their effect on patterns of variation may mimic that of gene conversion, recurrent mutations might result in upwardly biased estimates of the gene-conversion parameter, f. Because CpG sites are known to have roughly 10-fold higher rates of mutation than other sites (Savatier et al. 1985; Sved and Bird 1990; Cooper et al. 1995; Yang et al. 1996; Krawczak et al. 1998), such sites may contribute substantially to this effect (Templeton et al. 2000). To check for this effect, we removed all polymorphisms at CpG sites from our data set and re-estimated ρ and f. With the Hausa data, the estimate of r with f=0 is ∼7.5% lower than the estimate of ρ with all sites included. This is a small and statistically insignificant effect. In addition, the estimate of f is larger when the CpG sites are removed. Thus, there is no indication that the inclusion of CpG sites in our data results in upwardly biased estimates of ρ or f.

The extent of LD, together with its variability across different populations and genomic regions, is a critical parameter for the design of whole-genome disease-association studies. A question of particular interest regards the density of markers necessary to detect allelic associations and whether this density differs across ethnic groups. Our study agrees with other reports in showing that a sparser map will be sufficient in non-African populations. However, disease-association studies in populations of African origin—for example, African Americans—will require a much denser map. The extent of LD in the human genome had initially been characterized through computer simulations that yielded estimates of “useful” LD extending no farther than 3 kb (Kruglyak 1999). These simulations were based on a number of assumptions about population histories and population parameter values—for example, the assumption of exponential growth from an initial population size of 10,000. More recently, Pritchard and Przeworski (2001) simulated the decay of LD for an equilibrium population of effective size 10,000 (Pritchard and Przeworski 2001) and compared it with that expected under the model of Kruglyak (1999). Their results show that the equilibrium model predicts a somewhat slower decay of LD. The African data in the present study are likely to be consistent with the latter predictions, in that our estimates, based on either polymorphism or LD data, of effective population size consistently suggest an effective population size of ∼10,000. However, because the contribution of gene conversion had not been previously considered, the extent of LD over short distances in Africans may be lower than that predicted by Pritchard and Przeworski (2001). In fact, our estimates, based on gene conversion, of the population crossing-over parameter can now be used to obtain a more accurate characterization of the expected genomewide pattern of LD by computer simulations for African populations.

Conversely, our non-African data are in broad agreement with the conclusions of Reich et al. (2001) in showing that LD decays much more slowly than previously predicted in European populations, although it is not clear if the estimated rate of decay is the same in both studies. Furthermore, thanks to the inclusion of an Asian sample in our survey, we can extend similar conclusions beyond European populations. Additional polymorphism and LD data from more genomic regions and human populations are necessary to elucidate the details of LD decay in the human genome and human history.