Amyloid fibers are water-filled nanotubes

Abstract

A study of papers on amyloid fibers suggested to us that cylindrical β-sheets are the only structures consistent with some of the x-ray and electron microscope data. We then found that our own 7-year-old and hitherto enigmatic x-ray diagram of poly-l-glutamine fits a cylindrical sheet of 31 Å diameter made of β-strands with 20 residues per helical turn. Successive turns are linked by hydrogen bonds between both the main chain and side chain amides, and side chains point alternately into and out of the cylinder. Fibers of the exon-1 peptide of huntingtin and of the glutamine- and asparagine-rich region of the yeast prion Sup35 give the same underlying x-ray diagrams, which show that they have the same structure. Electron micrographs show that the 100-Å-thick fibers of the Sup35 peptide are ropes made of three protofibrils a little over 30 Å thick. They have a measured mass of 1,450 Da/Å, compared with 1,426 Da/Å for a calculated mass of three protofibrils each with 20 residues per helical turn wound around each other with a helical pitch of 510 Å. Published x-ray diagrams and electron micrographs show that fibers of synuclein, the protein that forms the aggregates of Parkinson disease, consist of single cylindrical β-sheets. Fibers of Alzheimer Aβ fragments and variants are probably made of either two or three concentric cylindrical β-sheets. Our structure of poly-l-glutamine fibers may explain why, in all but one of the neurodegenerative diseases resulting from extension of glutamine repeats, disease occurs when the number of repeats exceeds 37–40. A single helical turn with 20 residues would be unstable, because there is nothing to hold it in place, but two turns with 40 residues are stabilized by the hydrogen bonds between their amides and can act as nuclei for further helical growth. The Aβ peptide of Alzheimer's disease contains 42 residues, the best number for nucleating further growth. All these structures are very stable; the best hope for therapies lies in preventing their growth.

In the early 1930s W. T. Astbury discovered that x-ray fiber pictures of wool gave only two reflections, a meridional one at 5.1 Å and an equatorial one at 10 Å. When Astbury stretched wool under steam to twice its length, he got a different pattern, with a meridional reflection at 3.4 Å and equatorial ones at 4.8 and 10 Å. Astbury attributed the meridional reflection to the periodic repeat of the amino acid residues along the length of the polypeptide chains, the 4.-Å reflection to the backbone separation of neighboring main chains, and the 10-Å reflection to the separation of neighboring main chains by their side chains. He called the unstretched wool the α- and the stretched wool the β-pattern. In 1935, Astbury wondered whether stretched polypeptide chains of denatured globular proteins would also give a β-pattern, but he found that the 3.4-Å meridional reflection was now replaced by the 4.8-Å reflection that was no longer on the equator. Astbury called this result the cross-β-pattern, because it implied that the chains ran across rather than along the fiber axes (1). In 1951, Linus Pauling showed that the α-pattern was given by α-helices and the β-pattern by pleated sheets, but the structure underlying the cross-β-pattern has remained enigmatic. Astbury's observation lay dormant until its rediscovery in x-ray diffraction pictures of amyloid fibers brought it to new prominence.

Derivation of the Structure

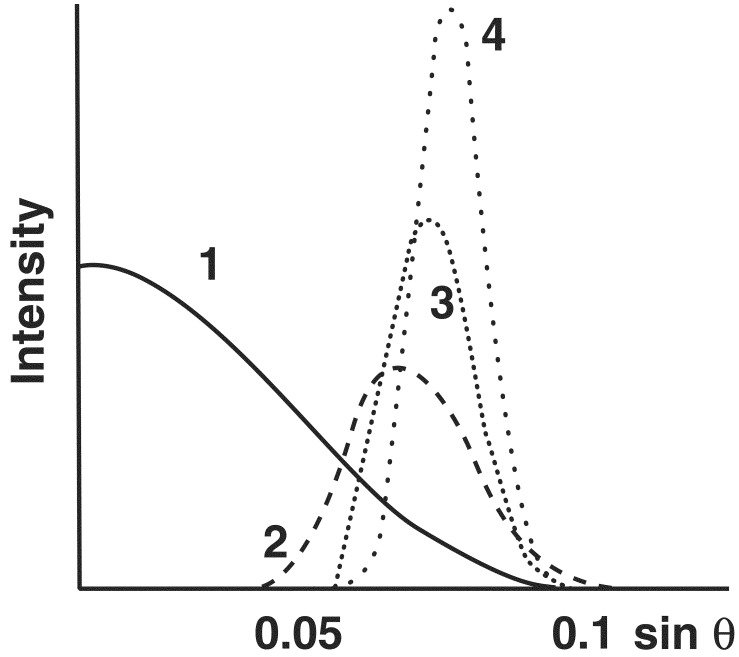
The fiber patterns of many amyloids show both the meridional 4.75-Å and the equatorial 10-Å reflection, but the 10-Å reflection is missing from fiber patterns of the poly-l-glutamine peptide D₂Q₁₅K₂, of the exon-1 peptide of huntingtin, and very weak in the pattern from the synuclein fibers of Parkinson's disease (2); it is also invisible on the published reproduction of the x-ray fiber pattern of the Alzheimer Aβ peptide (residues 22–35, figure 1N of reference 3). In all these fiber patterns, the meridional reflection at 4.75 Å remains very strong. What the absence of the 10-Å reflection is telling us can be understood if we calculate the Fourier transforms of one or more β-sheets, because the Fourier transform of any object is the mathematical analogue of its diffraction pattern (4). The transform of any molecular structure can be calculated from its atomic coordinates. In β-sheets, the side chains extend alternately on either side of the main chain, which makes them 10 Å wide. Fig. 1 shows the transforms of one, two, three, and four such β-sheets along a line normal to the plane of the sheets, representing the analogues of x-ray reflections from the plane of the sheets. A single sheet gives only a central maximum flanked by much weaker sets of fringes, not shown here. Two sheets 10 Å apart give a broad, weak reflection at 10 Å⁻¹ spacing. Addition of more sheets makes that reflection sharper and stronger. The number of sheets can be gauged by comparing the half-width of the maximum in the transform with that of the corresponding reflection in the diffraction pattern. Inverting the argument, only structures made of single sheets give no 10-Å reflection.

Figure 1.

Calculated Fourier transforms of a single 10-Å-wide β-sheet and of one, two, and three sheets spaced 10 Å apart.

Fibers of D₂Q₁₅K₂ show a broad low angle reflection at about 31 Å spacing as expected from cylindrical protofibrils approximately that distance apart. Supposing the fibrils themselves consisted of stacks of β-strands forming planar zigzags 10 Å apart normal to the fiber axis, then the transforms show that they would give a distinct 10-Å equatorial reflection. A structure that would fail to give that reflection is one forming a single cylindrical β-sheet made of hydrogen-bonded β-strands wound around the fiber axis in a circle or helix.

We found such a model to account for the x-ray diffraction patterns of poly-l-glutamine, of the exon-1 peptide of huntingtin, and of a peptide corresponding to the glutamine/asparagine rich region of the yeast prion Sup35 (13). It also accounts satisfactorily for the published structural data on other amyloid fibers that react with congo red and give the meridional 4.75-Å x-ray reflection. Suppose the external diameter of cylindrical D₂Q₁₅K₂ fibers is 30 Å; then the diameter of the circular main chain would be 10 Å less or 20 Å and its circumference 20π = 62.8 Å. Because the repeat per residue in a parallel β-sheet is 3.2 Å, there would be 63/3.2 = 19.6 or 20 residues per turn. The D₂Q₁₅K₂ peptide contains 19 residues. It would fit a circular model if a saltbridge between the terminal lysines and aspartates occupied about the same space as an additional 20th residue. There cannot be 19 residues per turn, because hydrogen bonds between the main chain amides of successive turns essential for stability are possible only if the number of residues per turn is even. If we take account of the 3-Å-wide layer of water that adheres to the surface of proteins and is therefore unavailable as a solvent to diffusible electrolytes (5), then the central cylindrical cavity is only 6 Å wide; it would be hard for large stains such as phosphotungstate or uranylacetate to diffuse into this narrow channel, but water and small ions could do so.

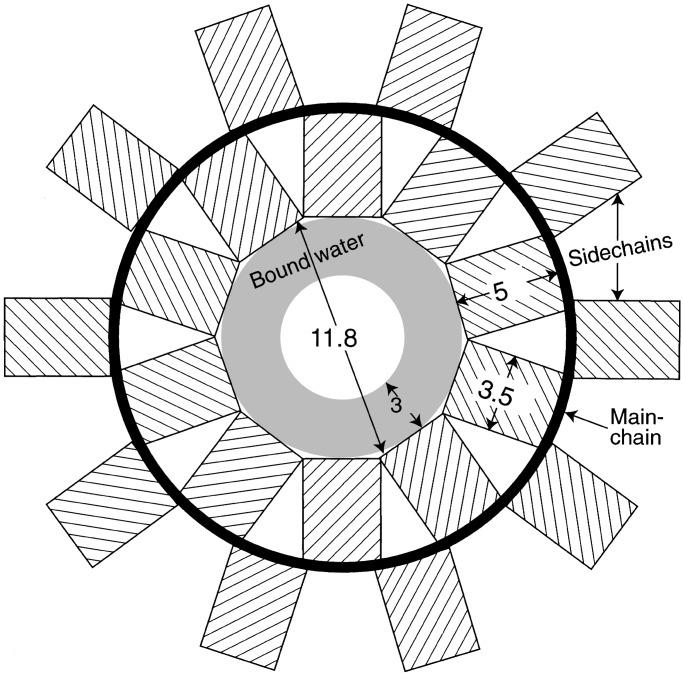
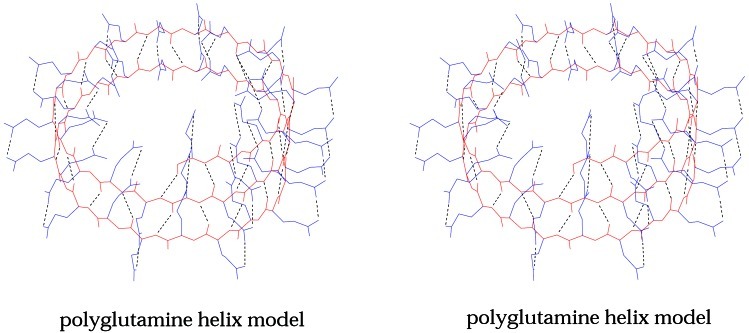
Fig. 2 shows a diagrammatic projection of this structure normal to the fiber axis. The main chain is represented by the heavy circle, and the side chains by rectangular boxes 5 Å long and 3.5 Å across. In a helix of 20 residues per turn, the terminal atoms of side chains of average length would be at the correct van der Waals distance of 3.6 Å from each other. With 18 residues per turn, this value shrinks to 3.2 Å, a little short; with 22 residues per turn, it expands to 3.9 Å, so that contact is lost. Twenty residues per turn may be the most stable structure for any sequence of residues. Fig. 3 shows a computer-generated model of helical poly-l-glutamine with 20 residues per turn. Residues in neighboring turns are linked by hydrogen bonds between both their main chain and side chain amides, with every CO in one helical turn being linked to an NH or NH₂ in the next turn, forming polar zippers (6) that make the structure very stable, indeed.

Figure 2.

Diagrammatic projection of a helical fiber with 20 residues per turn on a plane normal to the fiber axis.

Figure 3.

Computer-generated model of a poly-l-glutamine helix with 20 residues per turn (stereo pair). The main chain is black and the side chains are red. Hydrogen bonds are broken lines. The main chain conformational angles of this model are all in or near allowed regions of the Ramachandran plot.

Fig. 4 shows the x-ray diffraction pattern of fibers of the poly-l-glutamine peptide D₂Q₁₅K₂. The equator contains reflections at 3.2 Å and 3.6 Å. The value of 3.2 Å corresponds to the repeat of amino acids in a parallel β-sheet and 3.6 Å to the repeat of the side chain amides in the circle facing the internal cavity. In addition to the 31-Å reflection already mentioned, there is a dominant meridional reflection 4.75 Å together with its second order at 2.38 Å, and a weak one at 8.3 Å, together with its stronger second order at 4.15 Å and its weak third order at 2.8 Å. This picture was taken with the x-ray beam parallel to a thin film on which the fibers had been deposited, so that only fibers parallel to the film would have contributed. An electron diffraction picture taken with the beam normal to the plane of the film (not shown) had the 4.75-Å reflection and the 8.3-Å reflection and their higher orders at right angles to each other, indicating that they came from different, mutually perpendicular fibers. The glutamine- and asparagine-rich Sup35 peptide showed a similar x-ray diffraction pattern. It is not clear what structure the pattern with the 8.3-Å repeat represents, and we shall discuss it no further. The x-ray diffraction pattern shows that our sample also contains a very small fraction of α-helices. It seems that glutamine polymers can assume more than one structure similar in energy. We shall consider the fibers that give only the 4.75-Å reflection and its second order.

Figure 4.

X-ray diagram of D₂Q₁₅K₂ taken with the beam normal to the fiber axis.

On electron micrographs, only bundles of the D₂Q₁₅K₂ fibers were visible, but the Sup35 peptide yielded the clear picture of Fig. 5A. It contains single, straight fibers about 100 Å across, flanked by dark streaks on alternate sides at intervals of 85 Å along the fiber axis, signs of a rope composed of more than one protofibril that overlap alternately on either side. Fig. 5B shows models of bundles of plastic tubes wound around each other and representing the protofibrils. Two tubes wound around each other overlap at regular intervals along the center. Three tubes overlap alternately on either side, whereas four (not shown) overlap alternately on both sides and in the center. The electron micrograph says that there must be three, with a pitch of 6 × 85 Å = 510 Å.

Figure 5.

(Upper) Electron micrograph of fibers made of the glutamine- and asparagine-rich region of Sup35. Note the repeat of 3 × 170 Å along the fiber axis. Our peptide has the sequence: H-AspAspAsnAsnGlnGlnAsnTyrGlnGlnTyrSerGlnAsnGlyAsnGlnGlnGlnGlyLysLys-QH. (Lower) Twisted ropes made of two or three overlapping plastic tubes to show overlaps.

The 4.75-Å reflection is characteristic of the distance between the main chains in a β-sheet and is compatible with a cylindrical net made of β-strands running either normal to the fiber axis or wound helically around it at an angle of 85.8° (4.75/20 × 3.2 = 0.0742 = sin 4.2°). If we take 510 Å as the pitch p of the triple helix, then the angle of inclination of the individual fibrils relative to the fiber axis is given by sin α = (2πr/p) = (2π15/510) = 0.184, which makes α = 10.6°.

As a check of this structure, we measured the mass per unit length of our fibers by comparing their electron scattering at 40 keV out of a 10-mrad aperture with that of tobacco mosaic and fd virus standards. This measurement yielded 1,450 (±145) Da/Å. The average molecular mass of the amino acids in our peptide is 120; this result makes the calculated mass 3 × 2,400/4.75 = 1,516 Da/Å if the cylinders were straight, but their inclination raises this to 1,516/cos10.6 = 1,542. On the other hand, the intervals between chain termini joined by a saltbridge is 5.3 Å or 8.3% of the circumference of 64 Å. In our peptide, these intervals come after every 22 rather than 20 residues, which reduce the mass deficiency to 7.5%, giving a mass of 1,426 Da/Å, in good agreement with the observed value.

Our approach to the amyloid problem was inspired by Pauling's approach to α-keratin. Pauling argued that, in a polymer made of identical monomers such as peptides, the monomers must take up structurally equivalent positions, which is possible only in a helix. He then found the only steroechemically satisfactory one to be the α-helix. We have applied the same argument to amyloid fibers. If they are made of β-strands running normal to the fiber axis, then the only structure that puts them into equivalent positions is a helix wound around a cylinder. We then found that stereochemistry does not allow fewer than 20 residues per turn.

Implications of the Structure

The poly-l-glutamine fibers provide a stereochemical reason why, in all but one of the neurodegenerative diseases resulting from extension of glutamine repeats, no one gets the disease if the number of repeats is fewer than 37, and no one is free from it if the number exceeds 40 (9), and also why exon-1 peptides with variable numbers of glutamine repeats synthesized in Escherichia coli start to aggregate when the number of repeats exceeds 35–40 (10). The number of repeats per turn in poly-l-glutamine fibers is 20, but a single helical turn has nothing to stabilize it. The first structure stable enough to form a nucleus for the growth of a helical fiber would consist of two turns with 40 residues held together by hydrogen bonds between the amides of successive turns. If there were only 30 residues, then a tail of 10 residues would still hang loose. Occasionally, structures lacking a few residues to complete the second turn might act as nuclei, but these would be increasingly improbable and therefore rarer events. These rules hold whatever the protein of which the glutamine repeat forms a part.

The growth of the fibers is also governed by two opposing entropic factors. The random coil state is stabilized with respect to a folded state by a much higher entropy arising from the large number of possible conformations associated with internal degrees of freedom. On the other hand, the greater exposure of polar groups to solvent tends to lower the entropy of the random coil state, because the free amides bind water molecules. As the number of bonds between the two chains rises, the freedom lost with each additional hydrogen bond diminishes until it becomes negligible compared with the positive entropy gained by the freed water. This result is an important factor contributing to the formation of amyloid fibers.

It is difficult to guess the structure of naturally occurring full-length huntingtin fibers, because only electron micrographs of huntingtin aggregates in tissue sections have been published on which the structure of individual fibers cannot be discerned. Formation of a β-sheet by a single huntingtin molecule cannot proceed beyond the proline repeats that follow the glutamine repeat, because prolines are misfit in β-sheets. Helical cylinders could grow either if the proline repeats branched out, leaving the remaining chain to continue the helix or, more probably, by the glutamine repeats of many huntingtin molecules being joined in a single cylindrical β-sheet, forming the trunks of a tree from which the remainder of the molecules branched out in all sides, screening it from reaction with congo red.

The age of onset of Huntington's disease is inversely related to an exponential function of the number of glutamine repeats (12), but the refolding of the glutamines into helical cylinders would take only fractions of a second and therefore cannot be the rate-determining step. According to the theory of nucleation of aggregates (12), the probability of nucleation would be an exponential function of the free energy of formation of the nucleus. Because the addition of each glutamine stabilizes the helix by the formation of another three or four hydrogen bonds, that probability is likely to rise exponentially with the number of repeats.

Thicker amyloid fibers may consist of two or more concentric cylindrical β-sheets or of two or more single cylindrical sheet fibers wound around each other. The published evidence on the structure of different amyloid fibers and our suggested interpretations are summarized in Table 1. None of this evidence is inconsistent with the model proposed here, but only poly-l-glutamine yielded a diffraction pattern sufficiently detailed and distinct to yield a model. The complete Aβ peptide contains 42 residues, just the right number to nucleate a cylindrical shell; this finding and the many possible strong electrostatic interactions in β-sheets made of the Aβ peptide shown in the accompanying paper (13) and the absence of prolines account for the propensity of the Aβ peptide to form the extracellular amyloid plaques found in Alzheimer patients.

Table 1.

Interpretation of amyloid structures

Protein fiber	Experimental method	Experimental findings	Suggested interpretation	Reference
Alzheimer extracellular Aβ plaques, residues 11–25 fragment	X-ray diffraction and computed reconstruction from electron micrographs	All fibers give a strong 4.75-Å meridional x-ray reflection. Small angle reflections were not recorded. Optical reconstruction shows cylinders of 57 Å diameter with 37-Å-thick walls surrounding a central hole of 19.5 Å diameter. It also shows β-strands clearly stacked 4.75 Å apart with their length normal to the fiber axis	Two concentric cylinders of β-sheets, the chains run normal to the fiber axis as in the reconstruction; calculated fiber diameter 60 Å	7
Alzheimer extracellular Aβ variant, residues 11–25 with Asp-23 → Lys substitution	Electron microscopy and x-ray diffraction	Fibers of 35–40 Å diameter. Strong 4.75-meridional and extremely weak 10-Å equatorial reflexions	Single cylindrical β-sheet made of two 14-residue peptides arranged in tandem in a circle, giving a calculated fiber diameter of 40 Å	8
Synuclein deposits in Parkinson's disease and synthetic fibers of wild-type synuclein	Electron microscopy and electron diffraction	Filaments 60–90 Å wide that give only the strong 4.75-Å meridional reflexion and its second order, and a very weak equatorial 10-Å reflexion	Rods made of single cylindrical shells of helically wound β-strands forming dimers or trimers	2
Human transthyretin variant Val-30 → Met	X-ray diffraction	Meridional reflections indexed as orders of 115 Å; very strong reflexion at 4.83 Å, strong reflexion at 4.65 Å, suggesting sampling of transform with peak at 4.75 Å. Strong equatorial reflexion at 64 Å, medium ones at 12.6 and 10.1 Å, suggesting sampling of peak at 10.9 Å	Possibly two protofibrils of 32 Å diameter wound around each other with a 115-Å repeat	17

If this interpretation is correct, amyloids consist of narrow tubes (nanotubes) with a central water-filled cavity. Cyclic peptides made of alternate D and L residues form such nanotubes that kill bacteria by inserting themselves into membranes and depolarizing them (14). M. Stewart (personal communication) suggested to us that some amyloid fibers might be conductors and kill cells by the same mechanism. The structures described here also suggest a possible mechanism for the propagation of the yeast prions. Assuming that their structure is similar to that of Sup35, it is conceivable that single nanotubes dissociating from a cluster could act as seeds for the growth of more of their own kind, for example, by acting as templates for the coiling of daughter chains. Too little is known about the structures of animal prions to guess how they might form. What hopes for therapy? Formation of amyloids and of huntingtin aggregates is reversible (15, 16). Aromatic compounds such as congo red that can insert themselves into gaps between helical turns might destabilize the cylindrical shells and initiate this process, but prevention would be more effective and probably easier to achieve.

Intracellular inclusions are now recognized as the cause of diseases. Many of them have one important feature in common: they consist of normally soluble proteins with a variety of complex three-dimensional structures that are apparently stable, until some trigger converts them to bundles of fibers uniformly made up of β-pleated sheets with their strands running normal to the fiber axis. We suggest that the structure presented here is common to most and possibly all of them, because the absence of free non-hydrogen-bonded amides makes cylindrical β-sheets more stable than any alternative fiber structure made of zig-zag β-strands.