The concerted mechanism of photo-induced biprotonic transfer in 7-azaindole dimers: A model for the secondary evolution of the classic C_2h dimer and comparison of four mechanisms

Abstract

A mechanism is proposed for the formation in gas phase, during a short time, of the delicately symmetrical coplanar C_2h classic 7-azaindole (7AI) doubly hydrogen-bonded dimer. Of the five card-pack or otherwise random geometry structures most likely to be formed in the supersonic jet expansion molecular beam, none would be an obvious precursor to the C_2h dimer. One unstable dimer with dipole–dipole, van der Waals, and plane-to-plane hydrogen bonding is shown to be capable of unhinging about the hydrogen-bond pair as an axis, from 0° to 90° to 180°, yielding a deep minimum for the C_2h structure with its delicate geometry and symmetry. This relaxation mechanism is feasible in the 3-μs interval between the nozzle escape and the first laser pulse interception of the molecular beam. In the second part of the paper four published mechanisms are compared for concerted vs. two-step biprotonic phototransfer for the 7AI dimers. The dependence of the latter two models on H-atom instead of proton-transfer as an intermediate step negates the mechanism in a singlet (π,π*) electronic state by the valency repulsion, in the 3-electron orbital that would be generated. The concerted mechanism for biprotonic phototransfer is reaffirmed by the analysis of the quantum mechanical conditions set on the biprotonic transfer in the photo-excited molecular 7AI pair.

Molecular pairs in valency, H-bonding, or close van der Waals interaction upon excitation are subject to in-phase perturbation by the photon electromagnetic field, in most cases the electric-dipole component. The resultant excitation is perforce coherent. In a doubly H-bonded pair such as the classic C_2h dimer of 7-azaindole (7AI), the coherent excitation induces several simultaneity responses. The molecular pair exhibits (i) excitonic state splitting, (ii) a shift of electron density within the framework of each molecule, resulting in synchronous acid–base changes at opposite ends of the molecule, and (iii) intermolecular acceptance vs. ejection with respective coordinated ejection vs. acceptance of protons in the partner molecule. These simultaneity principles were presented in the companion paper (1). In the research on (7AI)₂ photo-induced biprotonic transfer, the final molecular (7AI) product appears as the classic C_2h 7AI tautomer pair. This is a structure of snowflake-like symmetric delicacy. It is coplanar, centrosymmetric, and is in the C_2h symmetry point group, the most symmetric of the set of dimers studied. Upon adiabatic expansion by means of a supersonic nozzle with carrier gas, cooling the warm reservoir vapor to 7 K or less, dimerization can occur. In the preceding paper (1) we have shown calculations of six stable dimers with significant binding energies; five of them are either card-pack structures or rather random geometry dimers easily formable upon supersonic expansion.

Although the calculations show the C_2h dimer to be the most stable of the six dimer structures considered, it seems most unlikely that the spatial orientation requirements of this rather symmetrical dimer structure could be met on the picosecond time scale of the supersonic jet. None of the other five dimers offer an easily accessible path to the C_2h dimer form, even with the nonequilibrium excitation of an optical transition.

One dimer that proved to be unstable does offer a pathway to the formation of the C_2h dimer as a secondary product on a delayed time scale. Scheme A shows a card-pack dimer of C₂ symmetry, which would exhibit a double-H-bond capacity plane to plane. At 0° for this C₂ dimer the binding energy is −10.1 kcal/mol, but it is not a stable minimum. The H bond, however, acts as a hinge and at 90° the binding energy increases to −14.2 kcal/mol. Finally, at 180° the dimer has unfolded to form the C_2h classic 7AI dimer, with its deep minimum of −20.3 kcal/mol in binding energy.

Obviously, the laser pulse excitation (and giant laser pulse of the coulomb-explosion) would provide the energy for the relaxation to the 180° minimum. This model suggests that the original 0° dimer → 180° dimer conversion would occur sometime between the picosecond time scale of the nozzle ejection and entry in the time-of-flight (TOF) mass spectrometer time scale detecting species on the microsecond scale.

Theoretical Methods

The method executed in a previous set of papers (2–6) and in the companion paper (1) allows us to propose an alternative mechanism for the double-proton transfer of the classic 7AI dimer (see below). The method used is based on the following theoretical levels of calculation. (i) The ground state with full geometry optimization is described by means of density functional theory (DFT) with the hybrid functional B3LYP and the 6-31G** basis set. The proton transfer (PT) potential energy curves, with geometry optimization at each point, for the ground electronic state of the classic 7AI dimer have been reported elsewhere (ref. 2 and references therein). These PT curves show that there does not exist a stable single PT intermediate in the ground state, neither by assuming a concerted process nor by assuming a stepwise (two PT steps) process. The normal and double PT tautomers of the classic 7AI dimer exhibit true minima with all of the frequencies positive. (ii) Full geometry optimization at the MP2 level is used for calculating the card-pack geometry (1) of the 7AI dimers in the ground electronic state. The MP2 level with the 6-31G** basis set yields excellent results, because it takes into account the van der Waals interaction between the two monomer units of the dimer. (iii) The PT potential energy curves for the first excited electronic state were calculated by concerted and stepwise mechanisms (3) by executing a single-excitation configuration interaction (CIS) method without geometry optimization to calculate the transition electronic energies, and subsequently these energies were added to the corresponding ground state DFT energies. The CIS method (with geometry optimization) and the complete active space (CAS) self-consistent field (SCF) method have been reported to misinterpret the PT energy curves (7–9), thereby adding spurious effects, as for example, unrealistic PT barriers, which disappear after dynamical electron correlation has been included. To implement dynamical electron correlation, two methods published in the literature have yielded good results—that is, the multiconfigurational second-order perturbation (CASPT2) method (7, 8) and the CIS method without geometry optimization over DFT optimized geometries of the ground state (3, 5, 9–13). In addition, some authors (14) have successfully used CIS (without geometry optimization) over the MP2 optimized geometries of the ground state, to thus construct the PT curve of the excited state of 1-amino-3-propenal. The CASPT2 method was not executed on the 7AI dimers because of the enormous computational cost involved. A first attempt to execute the CASPT2 method on the classic C_2h 7AI dimer has been recently reported (15) with frozen 1s core electrons, and very limited number of atomic functions on the C, N, and H atoms, by including excited-state geometry optimization at the CASSCF level, to reproduce experimental vertical electronic transitions of the monomer and dimer molecule. (iv) Time-dependent DFT calculations, which also include dynamical electron correlation (unpublished work), have been used for calculating the PT potential energy curve of the first electronic excited state of the classic C_2h 7AI dimer to the double-proton transfer tautomer.

The validity of the computational methods used is also provided by comparison of theoretical results (at B3LYP-DFT level with 6-31G** basis set) with experimental molecular structures and properties of the 7AI monomer, the C_2h classic 7AI dimer, and their respective PT tautomers. The calculations are very consistent with experiments. Relevant evidence on the reliability of the theoretical calculations used is reported in the companion paper (Theoretical Methods section of ref. 1). All of the calculations have been executed with the GAUSSIAN 98 program (16).

Mechanism of the 7AI Dimer Formation

On one hand, the most feasible way for the formation of the classic 7AI dimer and the remaining five 7AI dimers described in the accompanying paper (1) will be explained on the basis of collision cross sections and the geometry evolution observed with DFT and MP2 methods. The difference between PT and H-atom transfer is stressed. The problem is to deduce the mechanism of the 7AI dimer tautomerization. Four double PT mechanisms for the classic coplanar C_2h 7AI dimer molecule will be critically examined to achieve a better understanding of the subject. These are the four double PT mechanisms reported in the literature: the stepwise-type mechanism of Zewail and his colleagues (17–19), the stepwise-type mechanism of Castleman and his colleagues (20, 21), the concerted-type mechanism of Takeuchi and Tahara (22–24), and the concerted-type mechanism of Catalán, Valle, and Kasha (2–5).

Electron Density Mapping of the Classic C_2h 7AI Dimer Molecule.

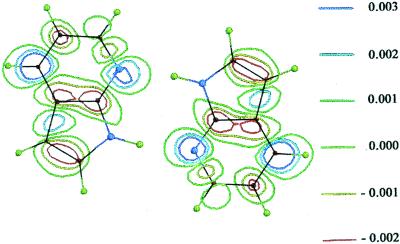
Fig. 1 gives the electron density difference map for S₀ → S₁ excitation, which now includes all electrons of the state configurations, not only the π → π* electronic excitation. This even more impressively shows the dramatic and simultaneous increase in acidity at the pyrrolo-N-(H) site and the increase in basicity at the pyridino-N: site upon photo-excitation. The pyrrolo-protons must jump across the hydrogen-bonding site to the (aza)-N: acceptor in a period within the excited state lifetime. The biprotonic-transfer barrier in the S₁ − S′₁ potential is calculated to be less than 4.8 kcal/mol, as shown by the time-dependent DFT calculated PT potentials for this classic 7AI dimer (unpublished work). The stability of this C_2h dimer is indicated by the S₀ energy of dimer formation, which is −17.2 kcal/mol [to −20.3 kcal/mol, in table 1 of the companion paper (1)].

Figure 1.

Quantum theoretical calculated electron density difference map, ρ(S₁) − ρ(S₀), for 7AI “classic” C_2h dimer (C_2h, doubly H-bonded, coplanar, centrosymmetric). Densities are given in units of point density charge of electrons.

Doubly H-Bonded Coplanar C_2h Dimer Formation Mechanism in the Adiabatic Nozzle.

If we subject one of the 7AI molecules of the dipole–dipole card-pack dimer to a C₂ (twofold) rotation about its long axis, we reach another card-pack dimer with fascinating new possibilities of intermolecular H-bonding, that is, the Doubly H-Bonded Card-Pack 7AI Dimer (Scheme A). This dimer may have dominant permanent dipole–dipole interaction, with some contribution of dispersion interaction, and weak double H bonding. The N⁷ (n,sp²) lone-pair orbitals have axial symmetry along the 7AI ring C⁴–N⁷ axis, with some extension in space, and the pyrrole N¹-H proton has a proton field that could distort the (n,sp²) lone-pair orbital of the N⁷-aza atoms. Out-of-plane (pyrrole)-N-H vibrations may favor simultaneous biprotonic transfer for the exciton S₁ state of this dimer. We may conclude that this dimer could show some fair tendency to undergo S₁–S′₁ tautomerization. However, our MP2 calculations show that this dimer does not possess a minimum of energy. When optimizing the molecular geometry, the initial geometry of the doubly H-bonded 7AI card-pack dimer evolves, by preserving the two hydrogen bonds intact, to the doubly H-bonded centrosymmetric C_2h 7AI dimer. Thus, it is fairly plausible that because of the larger collisional cross section presented by the doubly H-bonded card-pack dimer, it is primarily formed in the supersonic adiabatic expansion, and subsequently this card-pack dimer evolves to the corresponding classic C_2h dimer, thereby reaching a stable energy minimum. Upon excitation, during the evolution time from the card-pack dimer to the coplanar H-bonded dimer the proton transfer may occur.

It is estimated that at a supersonic velocity of Mach 3, the 3-cm distance between the nozzle and the first laser pulse interception corresponds to a transit time of 3 μs. Thus there is adequate time for the hinging relaxation mechanism that we picture for the conversion from the doubly-H-bonded card-pack to the classic centrosymmetric coplanar dimer.

The dipole moment of the optimized geometry for the classic C_2h 7AI dimer is 0, and the dipole moment of the doubly H-bonded card-pack 7AI dimer results in 1.4 debye (1 debye = 0.358 × 10⁻³⁰ C⋅m). A single point calculation on a doubly H-bonded T-shaped dimer (at ca. 90°) reveals a dipole moment of 1.1 debye. Thus, for the free-jet experiments, the carrier gas helium could stabilize in a greater extent, by means of van der Waals forces and instant dipole–dipole interactions, that molecular geometry with larger dipole moment, for instance, the doubly H-bonded card-pack 7AI dimer (Scheme A). Varying the pressure of the carrier gas could test this hypothesis. A sufficiently high stagnation pressure under supersonic adiabatic expansion conditions may stabilize the doubly H-bonded card-pack 7AI dimer, thus precluding the formation of the coplanar doubly H-bonded C_2h 7AI dimer. Evidence of the feasibility of this mechanism has been reported (20, 21): upon increasing the stagnation pressure the so-called nonreactive species develops and the coplanar doubly H-bonded C_2h 7AI dimer disappears.

The increase of the stagnation pressure of the carrier gas in the experiments by Castleman and co-workers (21) and Fuke and Kaya (25) can certainly induce a medium-enhanced energy barrier to the structural motion of the doubly H-bonded card-pack dimer on its evolution to the coplanar C_2h dimer. This phenomenon represents a cage effect, whose magnitude depends on the requirements of the geometry change, and on the pressure of the carrier gas.

The Problem of PT vs. H-Atom Transfer.

Many researchers have expressed a dilemma or demonstrate confusion in deciding whether a PT or an H-atom transfer occurs in such cases as the photo-induced biprotonic transfer in 7AI (17–21, 26, 27). Part of the origin of the confusion lies in not recognizing the electronic aspects of the hydrogen bond, and its involvement with the localized σ-orbital electron lone pair in the first excited electronic state (π,π*).

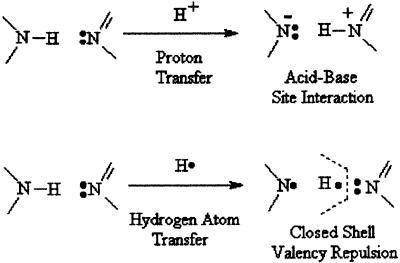
At the same time, in H-atom transfer, the radical H^⋅ is transferred, creating a special valence theory dilemma at the receptor atom. Fig. 2 traces the electronic reality of the H⁺ vs. H^⋅ transfer.

Figure 2.

PT vs. H-atom transfer electronic mechanism.

PT always involves an acidic proton—i.e., one bonded to a highly electronegative atom (N, O), “hydrogen-bonded” to an acceptor atom containing a σ-electron orbital lone pair (such as the sp²,n orbital of an aza-N atom); the electronegative atom then acts as a basic center. It has been assumed very generally that the “H-bond” is purely electrostatic in character, but recent work by Fulton and Perhacs (e.g., ref. 28) has shown that there is some covalent component in H bonding; no lone pair, no H bonding.

If the ground-state electronic distribution on the host molecules contributing the acid–base respective sites for the H atom suddenly changes, as in photo-excitation, then suddenly the hetero-atoms may reverse their roles, and the proton may be driven to reverse its tight-bonding (covalent bonding) site and its loose-bonding (H-bonding) site. In such acid/base site switching, it is definitively the H⁺ particle that is moved with natural facility (Fig. 2).

The H-atom or (H^⋅) transfer obviously differs enormously in bonding energy changes, but carries with it a dilemma: the acceptor atom (if it is a lone-pair-bearing hetero-atom) cannot accept the radical transfer. The Pauli principle of electron-pair limitation per (nondegenerate) electronic orbital would immediately be reflected in a closed-shell repulsion. Three-electron bonds are not stable. Without complete chemical reaction with irreversible radical species formation and decomposition, H-atom transfer does not occur, and it can play no part in the PT of interest to spectroscopists. The molecules retain their molecular electronic integrity before and after the PT, and the protonic or biprotonic transfer is highly reversible upon losing electronic excitation.

Models for the Photo-Induced Biprotonic Transfer in 7AI

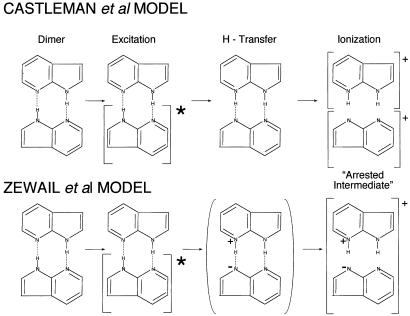
Four principal models have been proposed in the literature for the molecular electronic mechanism of the biprotonic phototransfer in 7AI. We have discussed them previously (2–5) with reference to the experimental techniques and details. Here we shall take the overview of the main features of the proposed mechanisms (Fig. 3).

Figure 3.

Proposed two-step 7AI biprotonic transfer mechanisms of Castleman and colleagues and Zewail and colleagues.

Proposed Two-Step Model for the 7AI Photon-Tautomerization.

Model of Castleman and colleagues.

This model makes two assumptions: First, the transfer is a two-step atom transfer process: first one atom is transferred, then the second, leading to the final tautomerized species. Spectroscopically, the excitation then must follow localized electronic excitation on moiety a of the dimer, then moiety b. We have demonstrated that such a supposition is inconsistent with the spectroscopic facts, and with basic quantum theory.

Second, these authors clearly use neutral (H^⋅)-atom radical transfer. This violates the valence theory basis of the conjectured intermediate species stability (Fig. 2).

The above steps are shown as involving no charged-species generation. Therefore, it is assumed that the second laser pulse yields the ionized species shown, (7AI)(H)⁺. We have argued (3, 4) that the two species suggested could be produced by the experimental procedure shown, and will discuss in the following section further points on the Coulomb-explosion, second (giant) laser pulse technique used.

Model of Zewail and colleagues.

Both Castleman and Zewail originally based their explanation of an intermediate species in the phototautomerization of 7AI on the basis of a calculated theoretical potential curve which seemed to show a deep potential minimum between the initial dimer normal tautomer and the final dimer tautomer in the classic 7AI dimer phototautomerization. It has been shown (3, 4) that the inadequate restricted Hartree–Fock (RHF) quantum-mechanical technique used gave rise to an illusory intermediate minimum.

In their first papers (17, 18) Zewail and his colleagues assumed that a first proton transfer would be a step to the intermediate, yielding a cationic/anionic nonseparated zwitterionic molecular pair (see Fig. 3). The experimental and theoretical study of the actual cation and anion of 7AI (4) indicates spectroscopic and energetic information inconsistent with this model. There is no direct spectroscopic evidence for the existence of such an intermediate cation–anion pair formation in the phototautomerization.

We conclude that the TOF kinetic and isotope effects observed by the Zewail group do not establish a two-step biprotonic phototautomerization, and the origin of their postexcitation, postionization kinetics must lie in the diversity of molecular dimers produced in the adiabatic nozzle molecular beam technique.

The One-Step 7AI Biprotonic Phototautomerization Model.

Takeuchi and Tahara one-step concerted mechanism.

These authors have proposed a plausible model based on femtosecond up-conversion kinetic experiments (22, 24). They demonstrate a significant excitation wavelength dependence for the fluorescence decay of the classic C_2h 7AI dimer in hexane, thus changing from a biexponential decay, with 0.2-ps and ca. 1.1-ps decay times, to single-exponential decay, with ca. 1.1-ps decay time. It is reported that there exists a significant change of the fluorescence biexponential decay amplitudes when the excitation wavelength is changed (from 280 to 313 nm). Also, the dimer fluorescence showed a single-exponential decay when excited at the red edge of the absorption of the 7AI dimer. These data do not conform to a stepwise (two-step) PT process, because such wavelength dependence would not have been measured. Therefore, on the basis of these observations Takeuchi and Tahara have interpreted the short decay time of 0.2 ps as ascribable to electronic relaxation (internal conversion) for the normal tautomer dimer between the S₂ (L_b) and S₁ (L_a) states, and the subsequent decay time of ca. 1.1 ps is ascribed to the single-step concerted PT of the 7AI dimer molecule.

Catalán–Valle–Kasha one-step concerted mechanism.

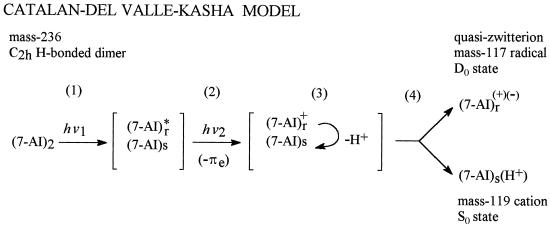
In our previous papers we have outlined by a three-aspect analysis the basis of the concerted one-step biprotonic transfer model (2–5). We have also attempted to explain what the Coulomb-explosion second step could do in the Castleman group researches. In Fig. 4 we show the steps by which we believe the ionic species detected in the TOF technique could be produced. The Castleman group believes that the second laser pulse (Coulomb-explosion) is simply a detection tool and does not influence the mechanism of production. Our analysis indicates, in contrast, that the Coulomb-explosion step creates the very species that those researchers think are involved in the first-step photo-excitation.

Figure 4.

Analysis of our proposed mechanism by which the ionic species are detected in the TOF mass spectrometer (r and s label the two molecules of the dimer; asterisk labels excitation).

In brief, we know the photo-excitation is excitonic—i.e., both moieties must be simultaneously excited (both the Zewail group and the Castleman group use the exact excitonic wavelength origin for their excitation laser pulse). In Fig. 4, step 1 shows a representation of one half of the molecular exciton wave function; the partner (7AI)_r(7AI)_s* with the 2nd moiety excited is considered necessarily present (3). Step 2 represents the second laser pulse π-electron photo-ionization of the Zewail group. In this step 2 it is also feasible that the π-ionized dimer could be broken off, thus resulting in monomeric fragments of different charge.

The removal of an integral electron forces localization determining which moiety of the pair is ionized. The π-electron cationic species (+ charge localizes dominantly at the pyrrole end in the 7AI monomer S₁ state), driving off the H⁺ (step 3), leading to separation of the (7AI)(H⁺) cation and the zwitterion (7AI⁺)⁻. This odd-configuration zwitterion is a π-electron radical cation yielding a doublet D₀ state, with a localized n-orbital pair on the pyrrole-N yielding a skeletal anionic character.

On Laser Coulomb-Explosion Experiments.

This type of experiment has been done to study the dynamics of the doubly H-bonded centrosymmetric C_2h 7AI dimer in the first singlet (π,π*) excited state. The method used involves a first-laser excitation of the sample at low intensities, and a subsequent high-intensity-laser coulomb-explosion, thereby causing field ionization of the sample. The ionic species, thereafter, are monitored by means of TOF mass spectrometry on the microsecond scale. The coulomb-explosion experimental conditions involve high laser intensity excitation and pulse widths of 120–200 fs. On laser coulomb-explosion imaging of proton motion, Bandrauk and Chelkowski (29) have recently published results on the bond-softening of the ground-state geometry by charge-resonance effects in both odd- and even-electron systems when pumped with femtosecond pulse lasers at high intensities. These authors emphasize that “these distortions produce movements of the nuclei in the ground state to larger internuclear distances, which can only be limited by using pulses shorter than 5 fs.” From exact non-Born-Oppenheimer simulations of the dissociative-ionization dynamics of H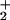 it is shown that wide femtosecond pulses, for example, a 12.8-fs pulse, cause nuclei displacement of 0.2 Å for the H–H distance. These observations lead to the conclusion that coulomb-explosion conditions applied to the doubly H-bonded 7AI dimer may, because of its invasive nature, change the double PT reaction mechanism from concerted to stepwise.

Conclusion

The experimental appearance of the centrosymmetric, coplanar doubly H-bonded C_2h dimer of 7AI is explainable as a secondary species deriving from the unusual card-pack dimer that has plane-to-plane double-H-bonding (Scheme A). Although the card-pack 0° configuration has significant net bonding energy (−10.1 kcal/mol), it does not represent a stable minimum, but can hinge about the (H-bond)–(H-bond) axis via a 90° configuration (−14.2 kcal/mol), to the C_2h classic dimer in the 180° coplanar configuration (−20.3 kcal/mol), which occurs at a deep true minimum.

The possibility of five other stable dimers formable at the picosecond time scale of the supersonic jet nozzle expansion suggests that those may result in kinetic measurements with picosecond probe pulses giving the illusion of intermediate steps in the biprotonic transfer. But none of the feasible stable dimers, described in the companion paper (1), could lead to the C_2h configuration without drastic rearrangement and high energy input. The required energy could come from the multiple laser pulse technique used, especially the giant laser pulse of the coulomb-expansion technique.

For the phototautomerization biprotonic transfer, double-step mechanisms have been proposed by two research groups (17–19, 20, 21). However, the interpretation based on an H-atom transfer intermediate would be negated by the valency repulsion illustrated in Fig. 2.

A concerted one-step biprotonic transfer model has been proposed by two research groups (2–5, 22, 24), in which simultaneity of the two-proton transfer is basic. The quantum theoretical analysis sets the necessary conditions (excitonic or coherent excitation) for a biprotonic transfer concerted mechanism, and this is shown to be consistent with quantum mechanical calculations (potential energy curves) and spectroscopic observations.

Scheme A.

Abbreviations

7AI

7-azaindole

TOF

time-of-flight

DFT

density functional theory

PT

proton transfer

CIS

single-excitation configuration interaction