Minimal principle for rotor filaments

Abstract

Three-dimensional rotors, or scroll waves, provide essential insight into the activity of excitable media. They also are a suspected cause in the formation and maintenance of ventricular fibrillation, whose lethality is well known. It is therefore of considerable interest to find out what configurations can be adopted by such pathologies. A scroll's behavior is embodied in its organizing center or filament, a largely quiescent tube about which the scroll rotates. Predicting filament shape has normally required computer-intensive simulations of the whole scroll in time. We have found a fast and robust principle that yields the prediction for stationary filaments on a purely geometrical basis, blind to the reaction parameters of the medium. The procedure is to calculate the filament shape as a minimal path. We work in singly diffusive media whose diffusivity tensor—and no other feature—varies spatially. Mathematical and numerical evidence is presented for the proposition that a stable filament is a geodesic in a three-dimensional space whose metric is given by the inverse diffusivity tensor of the medium. Away from the boundaries, a stable filament is unaffected by the reaction parameters. The algorithmic aspects of this work are subsidiary to our main purpose of drawing attention to the universal and unexpectedly exact fit of an elementary geodesic principle within reaction–diffusion theories.

The importance of scroll waves and their filament in understanding the behavior of excitable media has been consistently emphasized in the literature (1–6), and a good deal of study has focused on the filament itself (6). The relevance of these phenomena to ventricular fibrillation has been proposed by several authors (7–11).

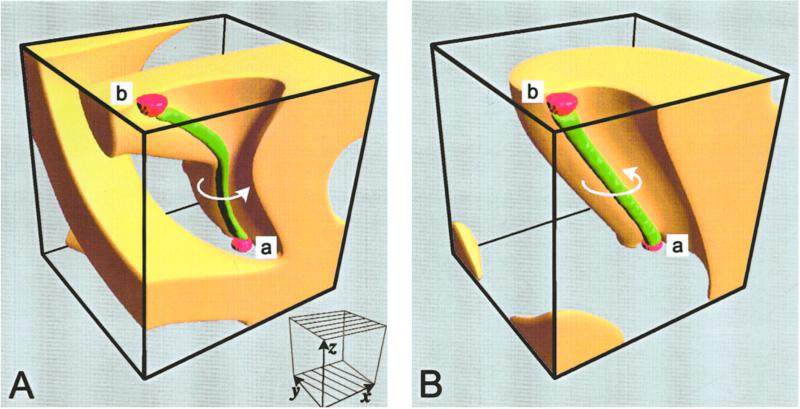
Anticipating our own analysis of that topic, we present Fig. 1 as an orientation to what follows. Fig. 1A depicts a steady-state scroll wave in a nonuniform diffusion–reaction environment. In this simulation, the shell-like structure is a snapshot of, for example, the electrical activity in the heart. It surrounds the unexcited filament, shown as a tube extending between the two anchor points, which help ensure filament stability (12). The complexity of its shape, as seen in Fig. 1, is what we aim to predict quantitatively. That complexity is due in this case to directions of maximum propagation speed (“fibers”) that gradually change their orientation between top and bottom surfaces, pretty much as in ventricular heart muscle; we refer to this configuration as “twisted anisotropy.” Generally speaking, we are concerned with how a rotating scroll, and especially its filament, is shaped by the geometry of the medium.

Figure 1.

(A) A steady-state scroll and filament under uniform left-handed twisted anisotropy. Near the top boundary, the fibers are parallel to the x axis; near the bottom they are rotated by 120° (although still parallel to the xy plane), as indicated in the small Inset. We take the anisotropic coupling ratio to be D_L/D_T = 9. The twist and anisotropy are comparable to observations in the human ventricular wall. The propagating potential is displayed here as a snapshot of the region (yellow) where it is above a cutoff value equal to 50% of maximum. The filament (green) is the tubular surface described over time by the locus of two independent propagating variables with fixed assigned values; the scroll rotates in the direction of the small elliptical arrow. The filament is anchored to a pair of small boundary protrusions (red) a and b. Note how the local anisotropy flattens the filament's cross section into approximately a small ellipse. The scroll results from a FitzHugh–Nagumo-type model and D tensor specified in ref. 18. Our choice of model, as well as of a cubic enclosure, is for illustrative purposes only and does not reflect in any way on the generality of the work. (B) For comparison, and as a guide to visualizing the scroll of A, we show a similarly pinned scroll, with the same membrane reaction parameters but in a uniformly isotropic medium. The boundaries have a remarkably weak effect on rectilinearity; this fact provides a further control on our results.

The Model

A reaction–diffusion model, in the standard (13–16) monodomain formulation with single diffusing variable, describes the space–time propagation of a set of variables (u, v₁, v₂, v₃, …) ≡ (u, v⃗) according to the parabolic partial differential equations

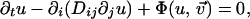1

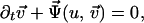2

D_ij being the diffusion tensor. For the three spatial coordinates, we use the notation (x₁, x₂, x₃) = (x, y, z), and in Eq. 1 we sum over repeated indices. The reaction functions Φ and Ψ⃗, which are in general nonlinear in u and v⃗, are considered given. In electrocardiology, these terms serve to represent the detailed ionic behavior of the cell membranes. For simplicity, we chose, in the preparation of Fig. 1A, a version of the FitzHugh–Nagumo theory (13, 14), whose complete specifications can be found in ref. 17; only two propagating variables are involved. The particular choice of model is, however, of no importance to the conclusions of this paper as long as it supports the existence of a scroll wave that is periodic in time, implying a stationary filament.

Returning to the form of Eq. 1, we choose to consider a diffusivity tensor D_ij that is entirely responsible for any inhomogeneity or anisotropy in the medium. At any point in space, the six independent components D_ij = D_ji govern, in magnitude and direction, the local propagation velocity of the excitation wave. In heart tissue, the D_ij tensor can be reduced to the diagonal form diag(D_L, D_T, D_T): D_L longitudinally and D_T transversely to the local muscle fiber. We have D_L/D_T≈9 in humans, corresponding to a ratio of about 3:1 for the speeds in those principal directions. The twisted anisotropy in Fig. 1 is specified in ref. 18. Thus, in our analysis, we need to know only one pair of characteristics: the fiber direction at every point and the ratio D_L/D_T. Here the fiber has no anatomical identity; in the mathematics, it refers only to the local direction of fastest propagation.

The Geodesic Hypothesis

So far, the only way to predict the shape of a steady-state filament has been to solve Eqs. 1 and 2 for the complete scroll over a long time interval, i.e., over many or at least several rotations of the scroll; appropriate boundary conditions are assumed in space and time. Here, in a totally different approach, we present a minimum-path principle that dispenses us from actually solving those partial differential equations; instead, they are replaced by a set of three ordinary differential equations. The only input we shall need is the diffusion part of the diffusion–reaction model.

The geodesic hypothesis arises naturally in uniform media. A scroll filament that equilibrates between two anchoring points in a uniform medium is known to do so along a straight line (12); see Fig. 1B. Although this observation is usually considered a trivial consequence of symmetry, the straight line is surely the most basic example of a geodesic (19). We know likewise that a large class of nonequilibrium filaments possess the analogue of positive mechanical tension (20), also suggesting a minimal principle. This intuition is somewhat curtailed by results found in nonuniformly anisotropic media. These typically reveal equilibrium filaments that do not adopt a rectilinear shape (17).

The actual configuration of the filament will be shown here to be a geodesic, or minimum path, given in differential form (21) by a set of three simultaneous ordinary differential equations

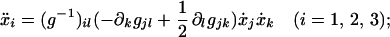3

each dot stands for ordinary differentiation with respect to a path length s. In this equation, g = g(x₁, x₂, x₃) is the metric, defined by the form of the path element,

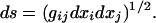4

If every element of the metric g_ij = g_ji is known, Eq. 3 is easy to solve numerically for a segment whose coordinates and direction are specified at one end. Eventually we want to identify the filament with one such geodesic. Although the filament is, strictly speaking, a tube, the geodesic is seen in ref. 17 to be a mathematical line contained within that tube.

As regards the solution to Eq. 3, its three components are not mutually independent, because they must satisfy

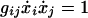5

by virtue of expression 4 for ds. In practice, however, we can solve for the three x_i independently and then integrate ds if we are interested in mapping s along the path. We see, incidentally, that the set of Eqs. 3 and 4 is invariant under a fixed arbitrary scaling by a factor k: g → kg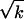, s →  s.

The generalities of this section are as far as we can go until we know the specific form of the metric g_ij(x). How can we establish that such a metric exists, and how do we determine its form? The exact answer has now become obtainable from a large class of media (17), described here in short as having a “deformed anisotropy.” Any such medium is characterized by mutually parallel-translated fibers of arbitrary planar but curved shape. Here the filament solution, although nontrivial, is known exactly. To find a metric that makes Eq. 3 valid, we use the following approach.

Starting with a family of diffusivity tensors D, we analytically derive (17) the exact form of the equilibrium filaments supported by any one of these tensors. Thus, the ẋ and ẍ that will be needed in Eq. 3 become known explicitly. If, perhaps by a lucky guess, the explicit form of the tensor g_ij could be written down, it would just be a matter of substitution in Eq. 3 to demonstrate the correctness of the guess. As shown below, that approach is quite feasible, and thus the geodesic principle can be proved analytically in a class of media.

The Metric

The procedure will now be outlined in more detail.

Step 1.

We construct a family of explicit diffusivity tensors that give rise to exactly known scroll wave filaments. If the direction of fastest propagation defines a local “fiber” direction, we take the prototype fiber to be, say, in the xz plane. Its z coordinate as a function of x is

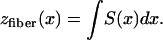6

The arbitrary constant in the indefinite integral, together with a constant value for y_fiber, define the choice of a specific fiber. The slope S is a finite single-valued function of x, but otherwise unspecified. All fibers in xyz space are copies of the prototype, parallel-translated, with the translation vector parallel to the yz plane. In short, the medium enjoys a wide, but not complete, generality. In terms of constant principal speeds D_L and D_T, the diffusivity D_ij has the components

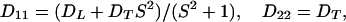7

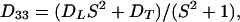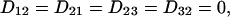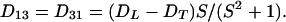Step 2.

The exact stationary filament solution of Eqs. 1 and 2 must be written down. The diffusivity is as in Eq. 7 and the reaction functions Φ, Ψ are arbitrary. With x playing the role of a parameter along the filament curve, the latter is found to be given in the xz plane by (17)

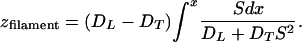8

Qualitatively speaking, the filament adopts a local slope intermediate between that of the fiber and the x axis. Although there is much freedom in the model, a few special assumptions were involved in obtaining solution 8:

(i) The propagating variable u obeys zero-flux (homogeneous Neumann) boundary conditions over two boundary planes perpendicular to the x axis;

(ii) an equilibrium filament exists and is unique under condition i; and

(iii) The medium is infinite (in practice, a few turns of the scroll wide) in the y and z directions.

The coordinates x_i in the prototypical geodesic, Eqs. 3 and 4, are now given by

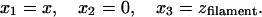9

Step 3.

We have obtained the metric directly by trying some likely candidates. A small number of trials soon pointed to the inverse diffusivity tensor, g_ij = (D⁻¹)_ij, whose diagonal form is D⁻¹ = diag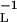(D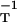, D, D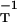). This fits Eqs. 3 and 4 exactly, in the following way.

Calculating D⁻¹ from Eq. 7, and using Eq. 9 for the x_i, as well as direct substitution in Eqs. 3 and 4, yields an identity. (With our choice of coordinates, i = 2 is automatic.) In locally diagonalized form, we have

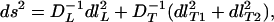10

where the orthogonal components of true distance are dl_L in the longitudinal direction and dl_T1, dl_T2 in the transverse directions. (In a cardiological context, D⁻¹ corresponds to a resistivity tensor, and therefore the minimization of ∫ds yields, loosely speaking, a path of least resistance.) To conclude: We have established that the D⁻¹ tensor is the metric seen by filaments under deformed anisotropies.

Simulations and Degree of Universality

In verifying an exactly derived result, simulations are for confirmation only, and indeed, in the large class of single-diffusion models where we have been able to conduct a mathematical analysis, the geodesic principle holds exactly. We are referring here to those media that support periodic scrolls and exhibit deformed anisotropy. Under more general kinds of diffusivities, however, the answer must rely on numerical simulations. So far, none has turned out an exception to our result.

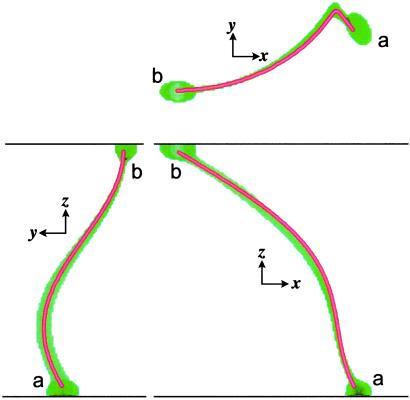
Twisted anisotropy, which we address in Figs. 1A and 2, is an important case that has defied analytic proof and therefore requires computational verification. Its nontriviality resides in the fact that successive layers of tissue consist of fibers whose direction changes from layer to layer, in contrast to deformed anisotropy. The importance of twisted anisotropy stems from its relevance to the heart. Fig. 1A shows a perspective of the scroll, simulated according to Eqs. 1 and 2, with its filament. Comparison between this simulation and the geodesic curve obtained from Eq. 3 is displayed in the Cartesian projections of Fig. 2. The agreement between simulation and theory is striking.

Figure 2.

Comparison between simulation and theory. We present the three orthogonal projections of both the filament (green) and the local geodesic (thin red–yellow curve); we calculated the geodesic by integrating Eq. 2, using as “initial conditions” the coordinates and direction cosines at the lower end, b, of the simulated filament. We see a clear agreement between theory and simulation.

In confirmation of the universality (i.e., reaction independence) of the geodesic result, we have recalculated the scroll of Fig. 1A with modified reaction parameters, resulting in a substantial change in the wave form. That is to say, the spiral cross sections of the scroll change shape and size according to these parameters; especially noteworthy is the near-doubling of the wave frequency. The filament nevertheless keeps its invariant configuration. The scroll's sense of rotation is likewise immaterial, as we have tested.

Discussion

Our conclusions can be summarized as follows: In media with nonuniform diffusivity, stable open-ended filaments coincide with geodesics; the metric is given by the inverse diffusivity tensor of the medium; filament shape is therefore unaffected by the reaction part of the reaction–diffusion model generating the scroll—the results are purely geometric. Stated more figuratively, only geometrical “forces” are responsible for positioning the filament at equilibrium, despite the fact that other forces (from the medium's reaction) are also known to be at work in moving the filament before equilibrium is reached.

For safe implementation of the geodesic principle, a few caveats should be kept in mind. We first recall that stability of the filament—meaning complete stationarity—is an essential prerequisite to our implementation of the geodesic principle. We have also had to assume that all and any medium nonuniformities are expressed in the diffusivity tensor rather than, for example, in the reaction parameters.

Our test cases are filaments anchored at both ends. How essential is that feature? Anchoring seems unrelated to the geodesic property, because the latter must apply locally to every segment of the filament through the agency of Eq. 3. The reason anchoring is often needed by open filaments is to enforce the stationarity under which the minimum principle applies. In general it is not needed, however. Our study of ref. 17 is an outstanding example of a stationary, nonrectilinear, nonanchored filament. The present work does not include consideration of closed filaments (scroll rings, knots, and links) (22–24). Such a study, which would be of considerable interest, requires a careful topological study, which we have not yet undertaken.

We note that experimental applications are conceivable. Today's developing technique of cardiac tissue transillumination (25, 26) allows some visualization of the filament; its data should become more accurately interpretable with the help of the method described here, possibly combined with known topological constraints (27). In actual heart tissue, the fiber architecture can often be considered given (28).

Looking to the future, we must hope that mathematical exactness will be supplemented by a more qualitative understanding of why the result is valid. In particular, the “least-resistance” rule seems mysterious when pertaining to a scroll-wave filament. Meandering scrolls should be interesting candidates for a future treatment using the minimal principle. Incentive for further research in the direction of the present work should be provided by the long and well-known history of variational principles, especially in geometric contexts.