Group-wise normalization in differential abundance analysis of microbiome samples

Abstract

Background

A key challenge in differential abundance analysis (DAA) of microbial sequencing data is that the counts for each sample are compositional, resulting in potentially biased comparisons of the absolute abundance across study groups. Normalization-based DAA methods rely on external normalization factors that account for compositionality by standardizing the counts onto a common numerical scale. However, existing normalization methods have struggled to maintain the false discovery rate in settings where the variance or compositional bias is large. This article proposes a novel framework for normalization that can reduce bias in DAA by re-conceptualizing normalization as a group-level task. We present two new normalization methods within the group-wise framework: group-wise relative log expression (G-RLE) and fold-truncated sum scaling (FTSS).

Results

G-RLE and FTSS achieve higher statistical power for identifying differentially abundant taxa than existing methods in model-based and synthetic data simulation settings. The two novel methods also maintain the false discovery rate in challenging scenarios where existing methods suffer. The best results are obtained from using FTSS normalization with the DAA method MetagenomeSeq.

Conclusion

Compared with other methods for normalizing compositional sequence count data prior to DAA, the proposed group-level normalization frameworks offer more robust statistical inference. With a solid mathematical foundation, validated performance in numerical studies, and publicly available software, these new methods can help improve rigor and reproducibility in microbiome research.

Introduction

Advancements in genetic sequencing technologies have enabled high-resolution cataloguing of the human microbiome, the microbial communities that collectively help modulate biological functions in the mouth, skin, reproductive tract, gastrointestinal tract and other sites [1, 2]. The role of the microbiome in human health has prompted research on finding specific microbes that differ in abundance according to site, exposures, disease status, or treatments, to name a few. In differential abundance analysis (DAA), microbes are analyzed in categories defined by clustering the sequencing reads into phylogenetic taxa.

One of the main challenges in DAA is that the microbial counts for each sample are typically compositional: across categories, the counts are constrained to sum to the total number of reads produced by the sequencing operation, referred to as that sample’s “library size" or “sequencing depth" [3, 4]. Thus, even when the goal is to compare the absolute abundance or quantity of microbes in the source, the data provide information only on the proportion of each taxon out of the whole ecosystem (the relative abundance). To ignore this compositional structure and apply standard statistical methods can—and often does—produce biased inference and inflated false discovery rates (FDRs), a phenomenon known as “compositional bias" [4–6].

Statistical methods for DAA that can account for compositional bias have generally fallen into two classes. The first class, which we call “normalization-based methods," requires normalizing the taxon counts to account for their compositional nature. In these approaches, a “normalization factor" is used to scale counts, enabling a meaningful comparison across samples. Normalization-based methods are generally required within or in conjunction with commonly used DAA software packages such as edgeR [7], DESeq2 [8], and MetagenomeSeq [9]. The normalization factor is computed separately from the DAA model using one of several available normalization methods [10]. The second class of DAA methods, which we call “compositional data analysis methods," uses advanced statistical de-biasing procedures to correct model estimates without the need for external normalization [6]. Examples of analysis frameworks employing this approach include LinDA [11], ANCOM-BC [5], ADAPT [12], and ALDEx2 [4].

This article focuses on normalization-based methods, presenting a novel framework for the external calculation of normalization factors. Although the use of compositional data analysis methods has been increasing, normalization-based methods remain widely used in microbiome applications. Indeed, using Google Scholar to search for the term “microbiome" in publications from January 1, 2021 to June 23, 2025 yielded 1,210 items citing the original MetagenomeSeq article, as well as 9,630 items citing the original DESeq2 article. Although these numbers may not reflect the relative popularity of normalization-based DAA methods compared with that of alternatives, they demonstrate the frequent, ongoing use of normalization-based methods for microbiome research.

Several methods for calculating normalization factors have appeared in the literature. An early representative example is the relative log expression (RLE), which computes the normalization factor for a given sample by taking the across-taxon median of that sample’s fold changes compared to the “average" sample [13]. The key assumption of this method is that most samples should have similar true abundance to the average sample for most taxa; thus, a sample with high log fold changes should be counter-balanced with a high normalization factor. Many alternatives to RLE have been proposed following similar themes to account for different aspects of the data, such as zero-inflation, and have been reviewed in detail by others [10, 14]. However, these methods have generally suffered from poor FDR control and inflated type I error rates when used for DAA of microbiome data, especially when the differences in absolute abundance across study groups are large [11, 15].

We present a normalization framework that reduces bias in DAA through its innovative use of group-level summary statistics of the subpopulations being compared. Several recent methods have been proposed in which compositional bias is quantified as a statistical parameter under different modeling assumptions, allowing for bias to be resolved by estimating this parameter [16, 17]. In a similar fashion, we present a mathematical derivation that formally quantifies the statistical bias under an assumed model. We show that this derivation leads to a novel view of normalization as a group-level rather than a sample-level task. The group-wise view of normalization motivates two novel methods for calculating normalization factors: group-wise relative log expression (G-RLE), which applies RLE at the group level instead of the sample level, and fold truncated sum scaling (FTSS), which uses group-level summary statistics to find reference taxa. By presenting two normalization methods that adopt a group-wise approach instead of only one, we aim to show that the overall idea of normalizing data at the group level, rather than any one group-wise method, offers better performance for DAA compared to the traditional approach. We demonstrate this by comparing G-RLE and FTSS to existing normalization methods in extensive simulations that vary signal-to-noise ratio, signal sparsity, and other factors. We also perform additional analyses of synthetic data based on two real-world microbiome datasets. Altogether, our results suggest the group-wise normalization framework offers higher power and more reliable FDR control than existing methods for normalization.

Methods

Group-wise normalization

Compositional bias as a statistical parameter

In this section, we derive a formal characterization of the statistical bias from performing DAA on the observed taxon counts under a simple multinomial model. Suppose we have n vectors of q taxon counts 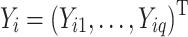, , each representing a microbiome sample of the 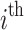subject in a study. Define the library size for sample i as 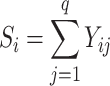, and let be a binary covariate indicating group membership. Finally, let denote the vector of the true absolute abundances corresponding to , and let denote the true relative abundances corresponding to . Neither nor is observed.

We view the taxon counts as arising from the hierarchical data-generating mechanism

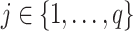, . Under this model, the absolute abundance () is represented as a deterministic function of two parameters: , the absolute abundance in the samples with , and , the log fold change in absolute abundance across covariate groups, the parameter of interest. Let Although, in reality, we do not believe the absolute abundance is equal for all samples within the same study group, this assumption provides mathematical convenience for developing a formal view of compositional bias.

Most normalization-based DAA methods are designed to estimate by fitting univariate models such as Poisson or negative binomial models. To illustrate the resulting bias, we consider the simple case of fitting q Poisson models of the form

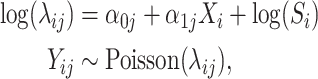for . Let

denote the “pooled" observed relative abundance of taxon j in in group 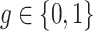. Then maximum likelihood estimator of is , which we will call the observed log fold change in contrast to 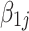, the true log fold change.

The statistical challenge with compositional data is that 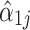is biased for estimating . Indeed, we show in the supplementary materials (Section 1) that

as , where denotes convergence in probability. Thus,

1

where is an additive bias term that results from the compositional setting. Since is identified only up to a constant, the bias term is not eliminated by fitting the multinomial model instead of the Poisson model. We provide additional details for this derivation in Section 1 of the Supplementary Materials.

A critical feature of is that it does not depend on the specific taxon. Indeed, can be exactly interpreted as the log-ratio of the average total absolute abundance in the samples compared to the samples—a summary measure of the difference in microbial content across groups. Motivated by this observation, our proposed methodology contrasts from existing normalization in using its focus on group-level rather than sample-level summary statistics.

Sample-wise versus group-wise normalization

Some commonly used normalization methods are RLE, cumulative sum scaling (CSS) [9], trimmed mean of M-values (TMM) [18], geometric mean of pairwise ratios (GMPR) [16], and Wrench [17] (Table 1). These methods involve the calculation of normalization factors, say , , that reduce compositional bias when substituted for 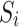in the model’s offset term. Using as in our derivation is called total sum scaling (TSS). The general approach for calculating is to divide each sample’s observed taxon counts or relative abundances by the corresponding values of some reference—which could be a single, pre-specified sample or a pooled version of the full dataset—then set as a summary statistic of these ratios. Ideally, under sparsity assumptions about the proportion of taxa that are differentially abundant, the normalization factors are proportional to the unknown sampling fractions, enabling inference on the absolute abundance scale [19].

Table 1.

Normalization methods

Method	Software	Normalization factor
TSS	N/A	Library size
CSS [9]	metagenomeSeq R package	Truncated library size to exclude outliers
RLE [13]	edgeR R package	Median of count ratios compared to the average sample
GMPR [16]	GMPR package on GitHub	Robust average of sample-to-sample comparisons to account for zero-inflation
TMM [18]	edgeR R package	Trimmed and weighted average of fold changes compared to a reference sample
Wrench [17]	Wrench R package	Robust average of model-regularized fold changes

The idea of the proposed normalization framework is to shift the focus from sample-to-sample comparisons to group-level comparisons. Specifically, for RLE, GMPR, TMM, and Wrench, the summary statistic underlying the normalization factor is computed at the sample level, summarizing the fold changes between that sample and the “typical" sample. However, as elucidated by in Equation 1, the compositional estimation bias reflects a difference at the level of the group: the ratio of the average total absolute abundance between study groups. The group-wise framework makes use of this observation by relying on summary statistics of the log fold changes between groups rather than samples—re-conceptualizing normalization as an intrinsically group-level task. Next, we present two new normalization methods that use this framework.

G-RLE: RLE normalization at the group level

The first proposed method is group-wise relative log expression (G-RLE): a modified version of RLE that depends on group-level instead of sample-level fold changes. Specifically, let be the geometric mean of the group-level relative abundances, . Now, for group , let . The normalization factors are calculated as .

In this definition, the group-level relative abundances , , 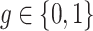are effectively treated as two microbiome samples, and the summary statistics () are computed as if the dataset contained only those samples. The normalization factors are then computed for each individual by their corresponding group-level statistic. The final normalization factors, , remain sample-specific, and their magnitudes depend on the summarized data across treatment groups. If the median true log fold change is zero, using as the offset eliminates from Equation 1 (Supplementary Material, Section 1).

FTSS: Scaling normalization based on reference taxa

The second proposed method is fold-truncated sum scaling (FTSS): a truncation-based normalization approach that uses “reference taxa" that are assumed to be equally abundant under the considered model. Identifying reference taxa is a common strategy in both normalization-based and compositional data analysis methods for DAA [6]. The notion of reference taxa has direct relevance to the compositional bias from Equation 1; indeed, if were restricted to exclude taxa that are differentially abundant, the bias term in would disappear (Supplementary Material, Section 1).

FTSS builds on the convergence established in Eq. 1, which implies that, in large samples, the log fold changes in the observed relative abundance (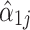) should approximate the true log fold changes of interest () up to the additive constant . We now make the additional assumption that only a minority of taxa are differentially abundant; thus, most of the s should be zero, and their corresponding 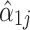s should be near .

In FTSS, the compositional bias is estimated as 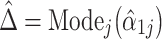using Gaussian kernel density estimation, and the library size is restricted so that it includes only taxa for which is within a pre-specified percentile of . Specifically, let be a function denoting the proportion of taxa whose 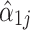is at most x, and let be the pre-specified proportion of taxa to be included in the truncated sum. Then

The logic of the procedure is that taxa whose observed log fold changes are close to 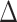should have true log fold changes equal to (or close to) zero; thus, taxa with observed log fold changes near should form a reasonable reference set.

We used a synthetic microbiome dataset to illustrate how FTSS uses the observed log fold changes. The true non-zero log fold changes were generated from a Normal(1, 1) distribution for only 10% of the taxa. The observed log fold changes of the equally abundant taxa form a tight, mound-shaped distribution that is off-center from zero (Fig. 1A). This clustering suggests that the reference taxa can be chosen based on the proximity of their log fold changes to the mode log fold change. When the observed log fold changes are compared to the true log fold changes (Fig. 1B), the trend in points lies directly below the line Y = X, suggesting a constant bias term as characterized by in Equation 1. The gray ribbon covers taxa that fall within a percentile interval around the mode log fold change; such taxa form the truncated library size. Moreover, although a differentially abundant taxon is mistakenly included in the reference set, this is unlikely to introduce bias since the true log fold change of that taxon is small.

Fig. 1.

Identification of reference taxa in FTSS. (A) Stacked histograms of the observed log fold changes from a synthetic microbiome dataset based on the MLVS/MBS data. The orange histogram shows equally abundant taxa and blue shows differentially abundant taxa. (B) A plot of the observed versus true log fold changes. The gray band shows a 40% interval around the estimated mode from the distribution shown in (A). Taxa that fall within the gray band form the truncated scaling factor in FTSS normalization

Model-based simulations

We compared the performance of the proposed FTSS and G-RLE normalization methods to that of TSS, TMM, RLE, GMPR, CSS, and Wrench in simulations using the DAA methods edgeR [7], DESeq2 [8], and metagenomeSeq [9] (summarized in Supplementary Material, Section 2). Every combination of normalization method and DAA method was evaluated by two metrics: the true positive rate (TPR) for detecting at fixed values of the false positive rate (FPR), and the TPR and false discovery rate (FDR) at a 0.05 nominal FDR after applying the Benjamini and Hochberg procedure [20]. TPR is defined as the average proportion of differentially abundant that are detected, whereas FPR is the average proportion of equally abundant that are detected. Since the primary objective of group-wise normalization is to mitigate the FDR inflation caused by compositional bias, no other comparison metrics were considered. We averaged these values over 1,000 replications in each of 18 simulation settings.

Data generation and settings

We generated data from a hierarchical multinomial model that incorporated subject-level variance and zero-inflation. Several methods for simulating microbiome data have appeared in the literature; our approach was based on the models presented by Lee et al. [21] and Chiquet et al. [22] to induce correlations among the positive- and zero-valued taxon counts. Specifically, for , we generated initial, positive absolute abundances of q taxa under the model , where the ’s are correlated error terms. was sampled from a multivariate normal distribution, MVN(, ), where is the variance and is a correlation matrix.

We incorporated zero-inflation with a multivariate probit distribution [23] by introducing latent variables, 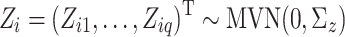, where the correlation matrix induces relationships in the presence and absence of taxa in each sample. Then , the final absolute abundance of taxon j in sample i, and , the corresponding relative abundance, are set to be

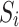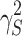where the parameter controls the degree of zero inflation. Finally, we sampled the library sizes from a negative binomial distribution with mean and variance and generated the final taxon counts as .

In these simulations, the number of taxa (q) was fixed at 300, and the parameter was chosen so that the marginal probability of each being zero was 0.50. The 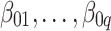values were sampled from a 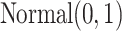distribution. The correlation matrix 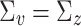was sampled from a Wishart distribution with 2q degrees of freedom and identity scale matrix. We set 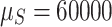and .

The following parameters were varied: , which were defined by sampling the first 10%, 20%, or 30% of the entries from a and setting the others to zero; , which was set to 1, 1.5, or 2 as “low", “medium", and “high" variance settings, respectively; and n, which was set to 200 or 500. The purpose of generating log fold changes from a Normal(1, 1) distribution was to introduce heavy compositional bias driven by a handful of taxa with large signals—settings in which existing normalization methods have struggled to control false positives [24]. Half the data were given 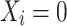and half . The combinations of , , and n produced 18 different settings in total.

Synthetic data simulations

Microbiome sequence data exhibit complicated correlation structures that are hard to replicate in simulations. Thus, we performed additional simulations based on synthetic data derived from two real-world microbiome datasets. The first dataset is from the Pediatric HIV/AIDS Cohort Study (PHACS), and the second dataset combines data from the Men’s Lifestyle Validation Study (MLVS) and the Mind-Body Study (MBS). We refer to the two datasets as simply “PHACS" or “MBS/MLVS", respectively. Since PHACS and MLVS/MBS contain samples from the oral and gut microbiome, respectively, the synthetic data encompassed two of the most common types of microbiome data analyzed. The datasets also differ in their sample sizes, numbers of taxa, library size distributions, and zero percentages, promoting a robust comparison of normalization methods across multiple realistic scenarios.

Datasets

The Adolescent Master Protocol is a prospective cohort study conducted by the PHACS network on the health effects of HIV infection among perinatally HIV-exposed youth. From September 2012 to January 2014, subgingival dental plaque samples were collected on 254 subjects ages 10–22 years [25–27]. Participants were excluded if they had antibiotic exposure in the prior 3 months. DNA was isolated from plaque specimens and sequenced in the V3/V4 region of the 16S rRNA gene [28, 29]. The sequencing reads were trimmed, filtered, and grouped using the DADA2 pipeline [30], and reads matched to the curated Human Oral Microbiome Database (99.9% of reads matched to the species or genus level) [31]. The final dataset included taxon counts for 344 OTUs on each of 254 samples. The samples averaged 62% zeros and 66.7 thousand reads (range: 1.31 thousand to 227 thousand).

MLVS was a one-year follow-up study of the Health Professionals Follow-Up Study (HPFS), an ongoing prospective cohort study that began in 1986 [32–34]. HPFS comprised 51,529 US male health professionals; of these, 307 participants were included in the MLVS and provided up to two pairs of self-collected stool samples from 2011 to 2013.

MBS was a one-year follow-up study of the Nurses’ Health Study II (NHSII), an ongoing prospective cohort study of female registered nurses that began in 1989 [35, 36]. From 2013 to 2014, 213 of the 116,429 NHSII participants were enrolled into MBS and had their gut microbiome sequenced based on two self-collected stool samples. For both MLVS and MBS, participants were free of coronary heart disease, stroke, cancer, and major neurological disease at the time of enrollment.

Sequencing procedures for MBS and MLVS were identical. Reads were processed through KneaData 0.3. High-quality reads were taxonomically profiled using MetaPhlAn 4 [37], resulting in 2201 species-levels taxa in the HPFS cohort and 1860 in the NHSII cohort. We kept taxa present in at least 10% of samples with a minimum relative abundance of 0.0001 and present in both cohorts. The initial number of taxa was 1,860 in the MBS and 2,201 in the MLVS; after filtering, 372 taxa remained. Following the approach used in other studies from the same cohorts, we combined the MLVS and MBS data into a single dataset [38, 39]. The combined data included 213 female and 307 male participants. The samples averaged 55% zeros and 14.4 million reads (range: 556 thousand to 54.0 million).

Data generation and settings

With either dataset, we perturbed the taxon counts to induce signals corresponding to a binary covariate while preserving the overall structure, i.e., while ensuring that the variance, correlations, zero-inflation and relative abundance of the synthetic data mirror those of the real data.

We generated the synthetic data with a re-sampling scheme similar to down-sampling [24]. Specifically, we began with the observed taxon count matrix from either PHACS or MLVS/MBS, with n observations and q OTUs. Let be a vector of q log fold changes. To generate a single synthetic dataset, we split in half at random to define , the subjects with , and , the subjects with . While remained unchanged, for each 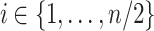, we re-sampled the taxon counts of the 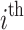subject in as , where is the library size and is a vector of probabilities such that . We generated in the same fashion as for the model-based settings described above, resulting in settings with 10%, 20%, or 30% signals.

For analysis, we used the same DAA methods, normalization methods, and evaluation metrics as for the model-based simulations. We evaluated methods’ performance in 1,000 replications.

Additional simulations

In addition to the primary simulation study described in Sects. 2.2 and 2.3, we considered alternative data-generating mechanisms in which certain aspects of the original settings were modified (for details, see Supplementary Materials, Section 3). Briefly, for the model-based simulations, we explored scenarios with (1) systematically different library sizes between groups or (2) adjustment for a single, continuous confounding variable. We also included a small number of simulations comparing LinDA—a compositional data analysis method which does not require external normalization—to MetagenomeSeq paired with G-RLE or FTSS. For the synthetic data simulations, we performed simulations in which (1) no taxa were differentially abundant (a global null setting), or (2) the signals of the differentially abundant taxa induced minimal compositional bias.

Application

To demonstrate how group-wise normalization can be implemented on real microbiome data, we performed DAA on the cohorts from PHACS and MBS/MLVS. For PHACS, the study groups under comparison were perinatally HIV-exposed youths who had been infected or not infected with HIV. In MBS/MLVS, the covariate was a binary variable indicating whether the participant had above or below median fiber intake. Dietary information was collected using semiquantitative food frequency questionnaires (FFQs) every four years, beginning in 1986 for HPFS and in 1991 for NHS2. Fiber intake was calculated by multiplying the reported frequency of consumption of each food by its nutrient content, primarily based on the USDA Nutrient Database corresponding to the time the FFQ was administered. We used average intake of fiber from baseline to the FFQ administered before fecal sample collection to reflect long-term dietary habit. The fiber consumption was further adjusted for total energy intake using the nutrient residual method.

We identified microbrial biomarkers for HIV exposure and fiber intake by performing DAA with MetagenomeSeq. We omitted edgeR and DESeq2 because they exhibited poor FDR calibration in synthetic datasets based on the PHACS data (Sect. 3.1). For simplicity, we limited our analysis to the normalization methods G-RLE, FTSS, GMPR, Wrench, and TSS. GMPR is an important comparator because it is a frequent choice for normalization in DAA studies. We included Wrench because it is the recommended normalization method in the MetagenomeSeq software. Finally, we included TSS as a baseline since it is analogous to perfoming DAA without normalizing. Since the application is intended to be comparative and since MetagenomeSeq does not accommodate confounding variables, we considered only simple, unadjusted comparisons of the relevant study groups. P-values were compared to a 5% nominal FDR level using the Benjamini and Hockberg procedure.

Results

Simulation results

Model-based simulations

For datasets with a “high" variance, 200 or 500 samples, and in which either DESeq2 or MetagenomeSeq were used for DAA, G-RLE and FTSS were more sensitive than existing normalization methods at every value of the FPR (Fig. 2). This improvement in TPR was slight when the signal percentage was 10% but increased to 10–15 percentage points higher than the best-performing existing method, GMPR, when the signal percentage was raised to 20% or 30%. We generally observed greater differences in TPR between normalization methods at larger signal percentages—settings where the compositional bias between groups was most severe. Comparing across DAA methods, we observed slightly better TPR at fixed levels of the FPR when using MetagenomeSeq instead of DESeq2. We also observed moderately better TPR with instead of . Results for the low and medium variance simulations were similar (Supplementary Material, Section 4).

Fig. 2.

True positive rate for detecting differentially abundant taxa for simulations with high variance. Value shown is the mean over 1000 replicates of each setting. Columns indicate sample size and DAA method while rows indicate the proportion of differentially abundant taxa out of 300. Confidence bands are not shown since the maximum band height was only 0.016

At a nominal FDR of 0.05 (Fig. 3), FTSS attained the highest TPR in every setting and G-RLE the second-highest in most settings, with FTSS often beating GMPR by more than 5 percentage points. Meanwhile, both FTSS and G-RLE either maintained the nominal FDR or close to it in settings where existing methods struggled, specifically, with 30% signals and a small sample size, or 20–30% signals and a larger sample size. In one of the more extreme cases—using MetagenomeSeq on datasets with 30% signals, high variance, and —FTSS achieved around 73% TPR and 3% FDR, whereas GMPR had only 64% TPR and 31% FDR. Results for the low and medium variance settings were similar and had better FDR control across the board (Supplementary Material, Section 4). Comparing across DAA methods, MetagenomeSeq exhibited better TPR and FDR than DESeq2 across the board. The combination of MetagenomeSeq with FTSS was the only pair to achieve lower FDR than the nominal level in every setting. FTSS paired with DESeq2 came close to doing so but had lower TPR. Finally, our additional results suggest the group-wise framework remains effective and outperforms existing methods (1) in analyses adjusted for a confounding variable or (2) when the library sizes are imbalanced between study groups (Supplementary Materials Section 3). In a limited set of simulations comparing LinDA, which does not require normalization, to MetagenomeSeq paired with FTSS or G-RLE, we found that all three approaches offered strong FDR calibration but LinDA had much lower TPR (Supplementary Materials, Section 3.4).

Fig. 3.

Performance of normalization methods at nominal false discovery rate for simulations with high variance. The true positive rate (blue) and observed false discovery rate (red) corresponding to a nominal false discovery rate of 0.05 (the dashed line). Value shown is the mean over 1000 replicates and 95% confidence interval for each setting. Columns indicate sample size and DAA method. Rows indicate the proportion of differentially abundant taxa out of 300 total

Synthetic data simulations

Analysis of synthetic data based on the MLVS/MBS data produced similar results to the model-based simulations, with both DESeq2 and MetagenomeSeq maintaining the FDR or close to it when paired with either FTSS or G-RLE (Fig. 4). In contrast, the competing normalization methods struggled in their FDR control when 20% or 30% of the taxa were differentially abundant. FTSS combined with MetagenomeSeq maintained the FDR near 0.05 and achieved the highest power in every setting. In settings where there were no differentially abundant taxa (Supplementary Materials, Section 3.1), the average number of false positives was fewer than 0.25 taxa for all normalization methods when paired with DESeq2 or MetagenomeSeq, with the exception of RLE-DESeq2 (mean: 0.88; 95% confidence interval: 0.72–1.0). In simulation settings with 20% differentially abundant taxa but minimal compositional bias, the normalization methods generally maintained the nominal FDR and had similar TPR (Supplementary Materials, Section 3.2).

Fig. 4.

Performance of normalization methods at nominal false discovery rate in synthetic data simulations. The true positive rate (blue) and observed false discovery rate (red) corresponding to a nominal false discovery rate of 0.05 using either the MLVS/MBS or PHACS dataset. Value shown is the mean over 1,000 replicates and 95% confidence interval for each setting. Rows indicate the proportion of differentially abundant taxa

Analysis of synthetic data based on the PHACS gave different results depending on the choice of DAA method. With MetagenomeSeq, comparisons across normalization methods gave similar results to those described above for the model-based simulations and the other synthetic dataset. In contrast, with DESeq2, no normalization method controlled the FDR, which often exceeded the TPR. Similarly, in situations with no differentially abundant taxa, the normalization methods averaged between 6 and 11 false positives when paired with DESeq2 but fewer than 0.85 false positives when paired with MetagenomeSeq (Supplementary Materials, Section 3.1).

Application results

With the PHACS data, no taxa out of 344 had a statistically significant log fold change with respect to HIV infection for any normalization method. Analysis of the MBS/MLVS data using MetagenomeSeq identified five to seven taxa out of 372 that were significantly associated with fiber consumption at the 5% FDR level, depending on the normalization method (Table 2). Each taxon that was identified when using a group-wise normalization method was also identified when using at least one sample-wise method, and vice versa. The point estimates of statistically significant log fold changes were similar across normalization methods. When using TSS, the log fold changes had a mean of  0.03 and an inter-quartile range of  0.24 to 0.16, indicative of a setting with little compositional bias where it is typical for normalization methods to perform similarly.

Table 2.

Statistically significant log fold changes with respect to fiber intake in MBS/MLVS

	Normalization method
Taxon	TSS	GMPR	Wrench	G-RLE	FTSS
Blautia luti	1.013	1.019	1.076	0.993	1.032
Clostridium sp. AM33-3	0.647	0.655	0.704	0.636	0.678
Ruminococcus torques	-0.440	-0.398	-0.413	-0.449	-0.405
Lacrimispora celerecrescens	-0.557	-0.511	-0.508	-0.567	-0.514
Mediterraneibacter glycyrrhizinilyticus	-0.923	-0.867	-0.897	-0.941	-0.906
UBA11774 sp003507655	X	0.527	0.546	X	0.523
Clostridium sp. AF20-17LB	X	0.665	0.722	X	0.697

Discussion

We presented a novel framework for normalization that exploits assumptions about group-level log fold changes, using normalization factors that directly target the compositional bias term across comparison groups. In numerical studies, the proposed G-RLE and FTSS normalization methods demonstrated substantial improvements in sensitivity and FDR control over existing techniques, especially in challenging scenarios involving a high proportion of differentially abundant taxa or high noise.

In general, we observed larger differences between normalization methods when there were many differentially abundant taxa, and the compositional bias was most severe. While the sample-wise normalization methods struggled to control the FDR and FPR in such settings, FTSS and G-RLE achieved reliable FDR and FPR control without sacrificing power, which attests to the relative strength of FTSS and G-RLE in high-bias settings. In settings with little to no compositional bias, all normalization methods performed similarly well in terms of their TPR and FPR. Therefore, the group-wise framework is especially useful when it is expected that many taxa may be differentially abundant, or that the differentially abundant taxa have large effect sizes.

The rationale for developing two methods was to show generally that group-wise normalization can outperform traditional methods in terms of FDR and TPR. The most direct comparison is between G-RLE and RLE, which are group-wise and samplewise versions of the same normalization method, respectively. The fact that G-RLE—a simple method that applies RLE to the group-pooled data—offers substantially better FDR calibration than RLE suggests that group-wise normalization is better-suited for high-bias DAA settings than the traditional, sample-wise approach. Between G-RLE and FTSS, the latter was more consistent in maintaining the FDR and achieved slightly higher power; thus, we see FTSS as the preferred group-wise method in general. The main drawback of FTSS compared to G-RLE is that it requires specifying the hyper-parameter , which controls the proportion of taxa included in the truncated library size. While we view setting , the value used in this article, to be a reasonable choice that should perform well in most settings, an alternative approach would be to optimize 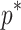for a given dataset by simulation. Another strategy would be to perform sensitivity analyses that explore how the signals change when different values of are used.

The performance gap between the group-wise normalization methods and existing approaches likely stems from their fundamental difference in approach. Traditional methods estimate sampling fractions using sample-level log fold changes, whereas the group-wise framework compares pooled group-level data to estimate a single mathematical bias term. Statistically, estimating one parameter—the bias term—may be easier than estimating multiple sampling fractions from potentially noisy comparisons of individual samples. This advantage may be especially pronounced in zero-inflated settings, since group-level pooled data remain strictly positive. As a result, the summary statistics used by the group-wise method may offer inherent robustness, unlike conventional approaches that can struggle with excessive zeros in individual samples.

Our simulations revealed a scenario in which all normalization methods, including the proposed frameworks, failed to control the FDR—namely, when edgeR or DESeq2 was applied to simulated data based on the PHACS data. This was likely due to challenges such as extremely high sparsity, as approximately 40% of taxa had fewer than 5 counts per sample on average. We obtained stronger FDR control on the PHACS data when pairing the group-wise framework with MetagenomeSeq, a tool specifically designed for zero-inflated datasets. When analyzing the real version of the PHACS data, no taxa out of 344 were identified as associated with HIV status. If any such associations exist, the challenging technical features of the PHACS data may partly explain why none were detected.

Our analysis of MLVS/MBS identified several taxa whose abundance was associated with fiber intake, including some that have previously been linked to human health. Taxa from the Blautia family have probiotic benefits, are potential biomarkers for inflammatory and metabolic diseases, and may play important roles in the maintenance of colonic mucus [40, 41]. Ruminococcus torques also influences intestinal mucus and is a potential biomarker for irritable bowel syndrome and Crohn’s disease [42, 43]. UBA11774 sp003507655 is a potential mediator between diet and triglycerides [44].

Recent methodological work has centered on compositional data analysis tools for DAA that do not require external normalization factors, such as LinDA [11], ANCOM-BC [5], ADAPT [12], and ALDEx2 [4], among others. We omitted these methods from our primary simulation study because the objective was to establish the relative performance of normalization methods, not DAA methods. In a limited set of simulations comparing LinDA’s performance to that of MetagenomeSeq paired with FTSS or G-RLE, all three approaches offered excellent FDR calibration in challenging settings, but LinDA had much lower sensitivity (Supplementary Materials, Section 3.4). The loss in power when using LinDA instead of MetagenomeSeq may result from differences in how the methods handle counts of zero. LinDA handles zeros via imputation, whereas MetagenomeSeq fits a zero-inflated model that accounts for structural zeros internally. Since the model-based simulated datasets have approximately 50% zeros, MetagenomeSeq may attain higher sensitivity because it captures the true data-generating process more accurately. Normalization-based and non-normalization based DAA methods are both popular in the microbiome literature, and performing a rigorous comparison of the group-wise normalization framework to non-normalization-based DAA methods is an important direction for future research.

We also note that the proposed group-wise framework is designed explicitly for settings in which the main covariate of interest is categorical, not continuous. Consequently, we view the group-wise normalization framework as primarily suited for DAA comparing study groups, exposure statuses, or subpopulations, which is a central task in microbiome data analysis. A key direction for further investigation is the development of methods to calculate normalization factors that can reduce compositional bias in more complex settings not considered in this study, especially those in which the main covariate of interest is continuous.

Conclusion

In conclusion, the proposed group-wise normalization framework, including two possible normalization approaches, enables more robust statistical analysis for investigating the association between the covariate of interest and taxon levels than existing tools. The mathematical derivation, based on the data-generating mechanism considered in this work, along with the publicly available software and findings from our simulation studies, will support rigor and reproducibility in microbiome research.

Author contributions

D.C., K.L., and H.T.R. developed the methodology; D.C. performed the analysis; D.C., J.R.S and K.L. conceptualized the project; K.L., J.R.S., and B.A.C. supervised the project; F.W. and Q.S. were responsible for data acquisition and cleaning; D.C. wrote the initial draft of the manuscript; all authors assisted in revising and reviewing the manuscript.

Funding

This project was supported by the National Institute of Dental and Craniofacial Research (R03DE027486) and the National Institute of General Medical Sciences (R01GM126257). D.C. was supported by the Predoctoral Training Grant (T32GM135117) provided by the National Institute of General Medical Sciences. B.A.C. was supported by the National Institute of Environmental Health Sciences (P30ES000002). The Pediatric HIV/AIDS Cohort Study (PHACS) network was supported by the Eunice Kennedy Shriver National Institute of Child Health & Human Development (NICHD) and other NIH institutes through grants to the Harvard T.H. Chan School of Public Health (P01HD103133 and HD052102) and with Tulane University School of Medicine (HD052104). The Health Professionals Follow-Up study (U01 CA 167552) and Nurse’s Health Study (U01 CA176726) are supported by the National Cancer Institute. The content of this manuscript is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.

Data availability

The data used in this study cannot be shared publicly for confidentiality reasons. To request data access, follow the instructions provided on the Pediatric HIV/AIDS Cohort Study, Nurse’s Health Study, or Health Professionals Follow-up Study websites. We provide computer code for replicating this study in the additional files and on our GitHub page.

Declarations

Ethics approval and consent to participate

Not applicable. This study does not involve human participants, identifiable human data, or animal subjects. The synthetic data were generated and analyzed using a re-sampling method applied to de-identified microbiome datasets. As no individual-level or personally identifiable data were used, formal ethics approval and informed consent were not required.

Consent for publication

Not applicable.

Competing interests

The authors have declared there are no competing interests.

Supplementary Information

The online version contains supplementary material available at 10.1186/s12859-025-06235-9.