Abstract
A typical protein structure is a compact packing of connected α-helices and/or β-strands. We have developed a method for generating the ensemble of compact structures a given set of helices and strands can form. The method is tested on structures composed of four α-helices connected by short turns. All such natural four-helix bundles that are connected by short turns seen in nature are reproduced to closer than 3.6 Å per residue within the ensemble. Because structures with no natural counterpart may be targets for ab initio structure design, the designability of each structure in the ensemble—defined as the number of sequences with that structure as their lowest-energy state—is evaluated using a hydrophobic energy. For the case of four α-helices, a small set of highly designable structures emerges, most of which have an analog among the known four-helix fold families; however, several packings and topologies with no analogs in protein database are identified.
The number of proteins with structures in the Protein Data Bank continues to grow at an exponential rate. There is a great diversity of amino acid sequences in these proteins, yet there is much less diversity in the structures themselves. Among currently known structures, only several hundred qualitatively distinct folds have been identified—indeed, it has been estimated that there are only about 1,000 distinct protein folds in nature (1–5). Has nature exhausted all possible folds? If not, how can we design proteins to adopt folds not seen in nature?
Important progress has been made in designing natural folds “from scratch” (6–9). Recently several attempts have been made to modify natural folds. Dahiyat and Mayo (10) were able to design a zinc finger that no longer depended on a zinc ion for stability. Harbury et al. (11) were able to design sequences of amino acids so that the superhelical twist of coiled coils was right handed, in contrast to the left-handed twist found in nature up to that time (12). Kortemme et al. successfully designed a three-stranded β-sheet protein (13).
Combinatorial experimental approaches to creating new protein structures are also possible. Studies of the folding of random amino acid sequences by Davidson and Sauer (14) identified some sequences that appear to fold. However, the conformations were not sufficiently rigid to allow structural determination by either x-ray crystallography or nuclear magnetic resonance techniques to see whether there were novel folds. Recently, Szostak and colleagues (15) were able to find folding proteins by in vitro evolution. This method can be used to identify proteins that bind to a particular substrate. It gives the ability to design for certain function but with no guarantee that the proteins found in this way will be novel folds. Another powerful method to evolve for novel functions (or potentially new folds) is in vitro DNA recombination (16). But again, it has not been applied to screening for new folds.
Theoretical approaches to the design of qualitatively new folds have followed two paths: searching within structure space for new folds (17, 18) and searching in sequence space for sequences that lead to new folds (19, 20, 21). The first approach has thus far relied on enumerating protein backbones using a finite set of dihedral-angle pairs (22). In this approach, enumerating all backbones for proteins of length greater than 30 is computationally intractable. Sampling methods can generate longer chains, but so far fail to achieve realistic secondary structures (18). The second approach has been attempted using several schemes. One involves enumerating helical structures by using sequence specific contacts (19). Another uses a library of sequences with known structure to assemble possible structures that a given sequence may adopt (20). However, searching the large space of sequences for potentially new folds is a huge computational challenge.
In this paper, we present a computational method for generating packings of secondary structures that, we believe, will facilitate the search for novel protein folds and complement the methods described above. Our method is motivated by the following observations: Most naturally occurring protein structures are composed of two fundamental building blocks, α-helices and β-strands (for a discussion of why secondary structure might arise in heteropolymers from a variational principle approach, see ref. 23). A typical protein structure is a packing of helices and strands connected by turns. The helices and strands are stabilized by hydrogen bonds, by tertiary interactions, and by the high propensity of some amino acids to form helices and of others to form strands (24). Because some residues are hydrophobic, the helices and strands pack together in a specific way to minimize the exposure of the hydrophobic regions to water.
The packing of secondary structural elements, with the connecting turns cut away, is generally known as a protein's “stack.” This stack, plus information about which elements are connected together by turns, yields the protein's fold (25). Our method for generating protein folds begins by first specifying a fixed number of α-helices and/or β-strands of fixed lengths, and second systematically enumerating all of the possible stacks of these elements. The great advantage of using fixed secondary structural elements is that one freezes many of the degrees of freedom of the chain. The freezing of these elements can be designed in by choosing amino acids with appropriate helical or strand propensities. [Loops can later be used to connect the secondary structures (26, 27).] To test our scheme for generating stacks, we apply it to the packing of four α-helices. Four helix bundles are a good test case as the natural bundles fall into a small number of fold families (28), and it has proven possible to design four-helix bundles through a careful selection of hydrophobic-polar sequences (7, 8). Our method is able to reproduce the four-helix-bundle families in the Structural Classification of Proteins (scop) database (25).
Within a set of stacks, those with no natural counterparts are potential candidates for the design of novel protein folds. To identify promising candidates, we consider their “designability.” The designability of a structure is defined as the number of amino acid sequences that have that structure as their lowest-energy conformation. In lattice models, it has been shown that the sequences associated with highly designable structures have protein-like properties: mutational stability, (29, 30) thermodynamic stability, (30, 31), fast folding kinetics (29, 32), and tertiary symmetry (33, 34). Recently, off-lattice studies of protein structures have also shown that certain backbone configurations are highly designable, and that the associated sequences have enhanced mutational and thermodynamic stability (17, 18). Hence, we aim to identify those stack configurations with high designability, and without natural counterparts, as targets for novel structure design.
Methods
Generation of Ensemble of Stacks.
The elements of the stack are chosen depending on the size and type of protein desired. These elements can be α-helices and/or β-strands. The number of each type of element is specified, as is the length in residues of each element. The sequential arrangement of the elements along the protein chain is also specified, along with the maximum length of the turns connecting elements.
Each element in the stack is assumed to be a rigid body, described by its center of mass and three Euler angles. The same simplifying assumption has been used previously by Erman, Bahar, and Jernigan in their work on the packing of pairs of α-helices (36). This method also compliments previous work that has looked at the packing of fixed secondary structure (37–40). An element, helix or strand, is specified by its backbone α-carbon-atom positions and its amino acid side-chain centroids, the latter taken to lie in the direction of the β-carbon at a distance of 2.1 Å from the α-carbon. Helices are constructed using a helical periodicity of 3.6 residues and a helical rise of 1.5 Å per residue. Strands are created by using a single backbone dihedral angle pair from the β-strand region of the Ramachandran plot. A stack is generated by first randomly selecting the center of mass and Euler angles for each element (if an element's center of mass and angles cause it to violate self-avoidance with one of the other elements, then its degrees of freedom are re-selected randomly). Then these variables are relaxed so as to minimize the packing energy (described in detail below). A local minimum of the packing energy is found by using a conjugate-gradient method, described in ref. 41. This yields a stack. With the centers of mass and angles determined, various symmetry operations are then performed to generate additional stacks. For α-helical elements these are screw operations that correspond to rotating the helix by ±100° and translating it by ±1.5 Å along the helix direction. For β-strands, slide operations correspond to translating each residue up or down by one residue along the strand direction. Each stack is then checked to see whether it satisfies a set of supplied constraints. For instance, stacks that exceed a specified total surface exposure or compactness measure, or have end-to-end distances of connected elements that exceed some cut-off, are excluded from the set. If a stack satisfies the constraints, it is added to the ensemble. Stacks are generated in this way until the ensemble of possible stacks for this model is complete, as discussed below.
The choice of packing energy Epacking is motivated by the hydrophobic force, which produces the compact stacks found in nature. The first term of the packing energy is
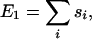 |
where si is the surface exposure to water of the ith residue along the chain. The surface exposure of each residue is calculated by approximating each side chain as a sphere with radius RS = 3.1 Å centered at a distance L = 2.1 Å from its α-carbon atom, in the direction of the β-carbon. The surface exposure si of each side-chain sphere is found using the method of Flower (42), with a water molecule represented as a sphere of radius RH2O = 1.4 Å.
We add to this hydrophobic energy a second term that represents the effect of excluded volume. This term, E2, is a pairwise repulsive energy among backbone α-carbon atoms and side-chain centroids on different elements. The excluded volume energy is given by,
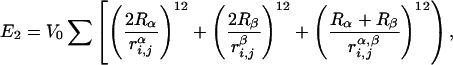 |
where Rα = 1.75 Å and Rβ = 2.25 Å are sphere sizes for the backbone α-carbon atoms and side-chain centroids, respectively, r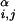 is the distance between backbone α-carbon atoms i and j, r
is the distance between backbone α-carbon atoms i and j, r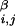 is the distance between centroids i and j, and r
is the distance between centroids i and j, and r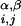 is the distance between backbone α-carbon atom i and centroid j. V0 sets the scale of the repulsive energy.
is the distance between backbone α-carbon atom i and centroid j. V0 sets the scale of the repulsive energy.
Lastly, we include a weak compression energy E3 and an energy E4 due to tethers between the ends of connected elements. These energies have the form,
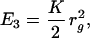 |
where rg is the radius of gyration of the entire stack,† and
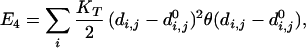 |
where di,j is the distance between the connected ends of tethered elements i and j, d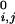 is a specified equilibrium length (for the case of the helices above we used 12 Å), and θ is a step function that is 0 if di,j < d
is a specified equilibrium length (for the case of the helices above we used 12 Å), and θ is a step function that is 0 if di,j < d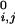 , and 1 otherwise. The spring constants, K and KT, are chosen to be small so that these terms act as weak perturbations.
, and 1 otherwise. The spring constants, K and KT, are chosen to be small so that these terms act as weak perturbations.
The actual minimization of the total energy Epacking = E1 + E2 + E3 + E4 using the conjugate-gradient method proceeds in steps, akin to annealing. The scheduled parameter is V0. Initially V0 is chosen to be large, so that there is a large repulsion between all of the elements. (The starting value of V0 varies depending on the number and size of the chosen elements. The initial V0 is chosen so as to generate a smooth collapse of the elements. For the case of four-helix bundles we chose a starting V0 of 35.0.) At a given V0, a minimum of Epacking is found for the full set of center of mass and angle variables. V0 is then reduced by a constant factor (90%) and a small random change is made to each degree of freedom. (The size of the random “kick” is also scaled along with V0, with the initial kick being 1 Å for the centers of mass and 15° for each Euler angle.) The V0 schedule is terminated when any two centroids are at a distance less than some specified contact distance, taken to be 2RS. At this point, E3 and E4 are set to zero, leaving only E1 and E2 to be minimized in the last conjugate gradient step. V0 is then set to its final value‡ and the last conjugate-gradient minimization is performed to yield final values of each rigid element's center of mass and orientation angles.
Flexible Elements.
The method described above can be generalized to allow flexibility of the secondary structural elements. In natural protein structures, α-helices are relatively rigid, whereas β-strands are more flexible. Hence, the extension of the method to include flexible elements is more important in the case of β-strands.
The flexural modes of rod-shaped objects are bending, stretching, and twisting. All these internal flexural modes can be included in the generation of stacks for both α-helices and β-strands. It is possible to determine the appropriate degree of flexibility for each internal mode by reference to known protein structures. A harmonic energy function Eflex for these flexural modes can then be added to the packing energy, with coefficients chosen to reproduce the degree of flexibility observed in natural proteins. For example, if the degree of bending of an α-helix is represented by the angle θ, then the additional term in Epacking representing this mode would be
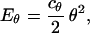 |
where the constant cθ can be chosen so that the average degree of bending 〈θ2〉 in the generated stacks matches that observed in natural structures. In the current work, however, we focus on α-helical proteins and only rigid elements are considered.
Hydrogen Bonding.
In natural proteins, β-strands are typically stabilized by the formation of hydrogen bonds between strands. To generate stack configurations that include strands it is therefore important to include an interstrand hydrogen-bonding energy Ehb in the packing energy Epacking. One form of a hydrogen-bonding energy function is given in ref. 43.
Completeness of Stack Ensemble.
Designability is determined via a competition for amino acid sequences within a complete set of stacks. Because the method for generating stacks is based on random sampling, a criterion must be specified for when to stop sampling. We stop the generation of structures when a specified fraction of newly generated stacks already occurs in the previously generated ensemble. If the fraction is not satisfied, the newly generated structures are added to the ensemble, and more stacks are randomly generated. We use crms (center-of-mass root mean square) to measure similarity between the ensemble and the newly generated structures, and consider two structures to be similar if their crms is less than 1.5 Å. The distance measure, crms, is defined as
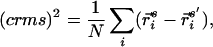 |
where r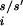 is the position of the ith α-carbon for the s/s′ stack and N is the number of backbone α-carbons. The stacks s and s′ are aligned by performing a least-squares fit using crms as the metric. We demand that 95% of the newly generated structures be similar to one of the structures in the ensemble before stopping the structure generation procedure.
is the position of the ith α-carbon for the s/s′ stack and N is the number of backbone α-carbons. The stacks s and s′ are aligned by performing a least-squares fit using crms as the metric. We demand that 95% of the newly generated structures be similar to one of the structures in the ensemble before stopping the structure generation procedure.
Clustering.
Many of the randomly generated stacks form clusters of closely related structures. It is computationally advantageous to reduce the sample by retaining only one member of each cluster. These representative structures are selected in the following way. The entire set of stacks is sorted according to total surface exposure—i.e., from most compact to least compact. Starting at the top of this list with the most compact stack, we eliminate all stacks that are closer to it than 1.5 Å crms. This process is repeated for the next most compact structure in the list until the end of the list is reached. We can typically compress the large ensemble of structures by a factor of three through five in this way.
Designabilities of Stacks.
The designabilities of the representative stacks, after clustering, are determined by allowing the structures to compete for a random sample of possible amino acid sequences. The designability of a stack is defined as the number of sequences for which that stack has the lowest energy. We assume that the hydrophobic energy is the dominant term contributing to the energy of a sequence on a given structure. This energy is given by
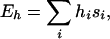 |
where hi is the hydrophobicity of the ith element of the sequence and si is the fractional surface exposure of the ith side-chain sphere in the particular stack. For each sequence considered, the lowest-energy stack in the representative ensemble is determined. By sampling a large number of randomly selected sequences, it is possible to reliably estimate the relative designabilities of different stacks.
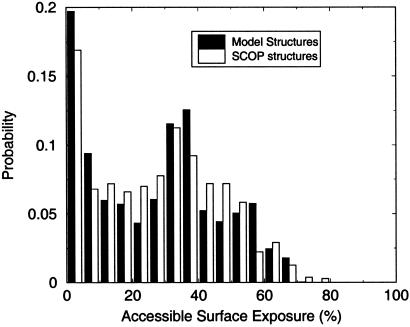
For the designability calculation, we used binary sequences consisting of only two types of amino acids. Such sequences are also known as “HP-sequences” for hydrophobic (H) and polar (P) amino acids. In previous studies, we found only minimal differences in the designabilities of top structures when binary sequences and sequences with a continuous distribution of hydrophobicities were used (17). The two hydrophobicity values can be written as hi = h0 ± δh, where h0 is a compactification energy, and δh measures the relative difference between hydrophobic and polar residues. From the Miyazawa–Jernigan matrix (44) of amino acid interaction energies, we infer a typical energy difference between hydrophobic and polar residues of 1.5kBT/contact. On average, a buried residue makes four noncovalent contacts; therefore, we take 2δh = 6.0kBT. The compactification energy h0 was determined by fitting the surface-area distribution of the set of eleven natural four-helix bundles given in Results to the surface-area distributions for the 100 most designable four-helix stacks, using different values of h0 to assess designability. The best fit is shown in Fig. 1, and this corresponded to h0 = 2kBT. Thus, in our model hydrophobic residues have a hydrophobicity of 5kBT and polar residues −1kBT.
Fig 1.
Best fit of surface distribution of the 11 scop proteins to top 100 designable structures found using h0 = 2kBT.
If flexible α-helices and/or β-strands are used in generating stacks, the energy Eflex associated with the flexural modes can be added to the hydrophobic energy Eh. Similarly, if interstrand hydrogen bonding is included, Ehb can be added as well. The energies Eflex and Ehb add a sequence independent contribution to each stack.
Results
We applied our structure generation method to the packing of four α-helices. We chose each helix to be 15 residues long§ (each helix has a periodicity of 3.6 residues and a rise of 1.5 Å per residue). The backbones of turns connecting the helices were not specified, but the turns were constrained to be short. Specifically, we discarded a stack if any of the end-to-end distances between connected helices exceeded 12 Å. The method generated a “complete” ensemble of four-helix stacks consisting of 1,297,808 structures (for a discussion of completeness, see Methods). This large ensemble of structures was then clustered, resulting in 188,538 representative structures.
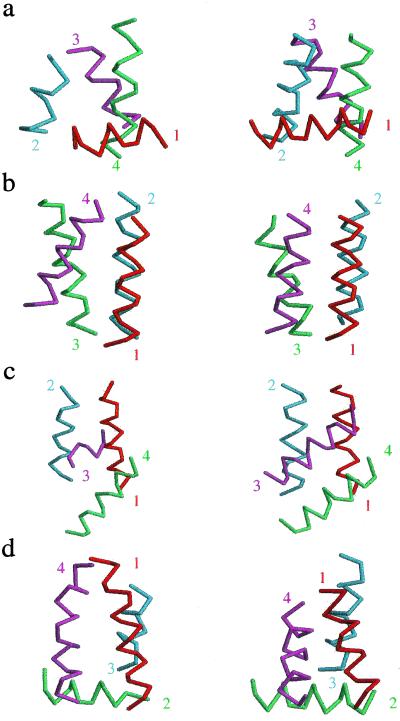
To test whether the method reproduced the natural four-helix bundles, we selected 11 proteins with short turns, from different scop families, and searched our representative structures for the best fits. To account for length differences between helices in the scop structures (the lengths ranged from 7–18 residues) and the 15-residue helices in our model, we chose the shorter length for each comparison. For the longer helix of each mismatched pair, we tried all possible truncations down to the shorter length. Thus, for each pairing of a scop structure with one of our representative structures, we computed the best fit among all possible combinations of truncations. Fig. 2 shows four overall best fits among all possible pairings. For the eleven natural four-helix bundles, the average crms to a representative structure was 2.86 Å. Table 1 summarizes the results of fitting the natural four-helix bundles to our representative structures. In all cases, the natural structure had a counterpart in the representative ensemble at a crms distance of less than 3.6 Å per residue.
Fig 2.
Representative fits for four scop proteins (left column) to model four-helix bundles (right column): (a) fit for 1EH2 (crms = 2.74 Å per residue), (b) fit for 1FFH (crms = 3.54 Å per residue), (c) fit for 1CEI (crms = 2.95 Å per residue), (d) fit for 1POU (crms = 2.81 Å per residue). Numbers indicate helix number and their location indicates the beginning of the given helix.
Table 1.
Results of fitting selected set of eleven proteins from scop database to ensemble of model four-helix bundles
| PDB ID | crms, Å |
|---|---|
| 2.96 | |
| 3.54 | |
| 2.85 | |
| 1.65 | |
| 2.95 | |
| 2.85 | |
| 2.81 | |
| 3.02 | |
| 2.74 | |
| 2.75 | |
| 3.44 |
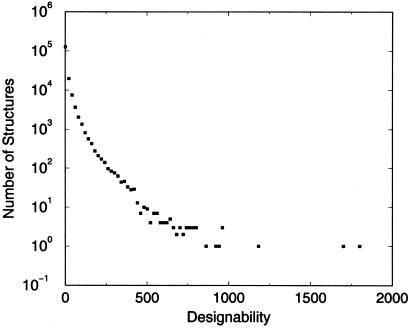
An important goal is to identify stacks with no natural counterparts as candidates for the design of novel protein folds. To identify which stacks might be promising candidates, we performed a designability calculation by using a hydrophobic energy (see Methods) on the ensemble of representatives of our four-helix structures. We used a random sample of 4,000,000 binary amino acid sequences. Fig. 3 shows the results of the designability calculation. The distribution of designabilities is consistent with previous results for both lattice (30) and off-lattice models (17, 18)—namely, there is a small set of highly designable structures with the great majority of structures poorly designable or undesignable. The average designability—i.e., the average number of sequences per stack—was 4,000,000/188,538 = 21. The most designable structure was the lowest-energy state of 1,813 sequences.
Fig 3.
Histogram of the number of structures with a given designability for the representative structures of the four-helix-bundle ensemble. Only a few of the structures are highly designable—i.e., are lowest-energy states of a large number of sequences. Most structures are lowest-energy states of few or no sequences.
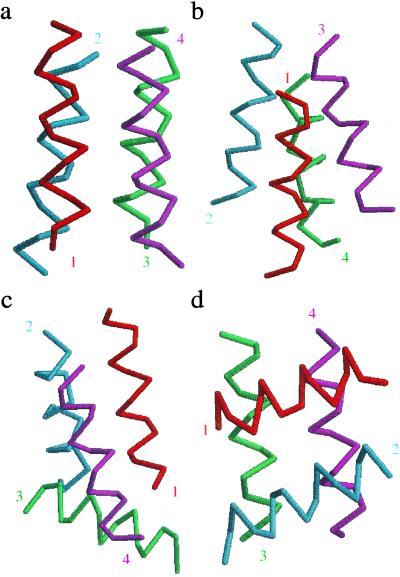
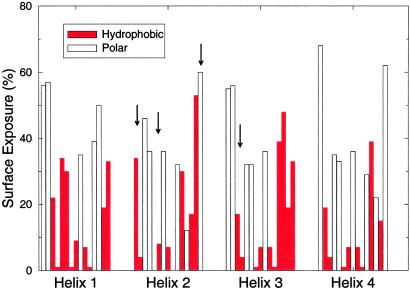
Almost all of the designable structures have an analog amongst the four-helix fold families. The four most designable distinct folds are shown in order of designability in Fig. 4. The topmost designable structure is an up-and-down four-helix bundle, the second most designable fold is a variant of the up-and-down fold except that there is a crossover connection, the third most designable fold falls within the λ-repressor DNA-binding-domain class and the last fold is an orthogonal array (25). Table 2 presents particular binary sequences that have these structures as lowest-energy folds. We obtained these sequences by matching them to the surface area pattern of each of the four folds and then introducing mutations to maximize the energy gap. The energy gap was defined as the smallest energy difference to a competing structure at a crms > 4 Å (i.e., a structure with a different fold type). Sequences were obtained by first calculating the mean surface-area exposure of each side chain for each structure, and assigning a hydrophobic residue to each site with surface exposure below the mean. Point and double mutations were randomly performed on the sequence by changing H (hydrophobic) to a P (polar) or a P to an H, and the mutation(s) was kept if the gap was made larger. This process of mutation was performed until a sequence was obtained where a mutation at any site made the gap smaller. The last column in Table 2 lists the resulting energy gaps. Fig. 5 shows the pattern of surface exposure along each helix for structure a of Fig. 4 along with the corresponding HP pattern (red for hydrophobic, open for polar). Notice that the HP pattern of the optimized sequence in Fig. 5 does not always follow the rule H at buried site, P at exposed site. For sites that depart from the rule—i.e., a hydrophobic residue on an exposed site—we found that the nearest competing structure was even more exposed on that site (e.g., site 14 of helix 2 and site 13 of helix 3). For the site that had a polar residue on a buried site (site 12 of helix 2), the nearest competing structure was less exposed on that site. Thus, it is sometimes beneficial to have hydrophobic residues exposed and/or polar residues buried to “design-out” competing structures (35).
Fig 4.
Four most designable distinct four-helix folds: (a) up-and-down fold, (b) up-and-down with a crossover connection fold, (c) λ-repressor-type fold, (d) orthogonal-array fold. Numbers indicate helix number and their location indicates the beginning of the given helix.
Table 2.
Results for the four most designable distinct folds for the model four-helix bundles shown in Fig. 4
| Structure | Sequence | Energy gap, kBT | Minimum mutations |
|---|---|---|---|
| a helix 1 | PPHHHHHHPHHPPHH | 6.65 | 4 |
| a helix 2 | HHPPHHPHHPHPHHP | ||
| a helix 3 | PPHHPPHHPHHHHHH | ||
| a helix 4 | PHHPPHHPHHPHPHP | ||
| b helix 1 | HHPPHHPHHPHHHHP | 5.85 | 3 |
| b helix 2 | HHHPPHHPHHHPHHP | ||
| b helix 3 | PPHHHHHPHPPPHHP | ||
| b helix 4 | HPHHHPHHPHHPHHH | ||
| c helix 1 | HHHHPPHPPPHPPHP | 8.3 | 5 |
| c helix 2 | PHPPHHPPPHPPHHP | ||
| c helix 3 | PHPPHHHPPHHPPPP | ||
| c helix 4 | PPPPHPPPHPPHHHH | ||
| d helix 1 | HPHHHPHHPPHHHPP | 4.70 | 3 |
| d helix 2 | PHHPHHHPHHPPPHP | ||
| d helix 3 | PHHPHHHPHHPHHPP | ||
| d helix 4 | PHHHPHHPHHHHHHH |
Column 2 gives the optimized hydrophobic-polar patterning of each of the length 15 helices. For these sequences, the third column gives the energy gap in kBT to the nearest distinct structural competitor. The last column gives the minimum number of point mutations necessary to reduce the energy gap to zero.
Fig 5.
Surface-area exposure for each of the four helices for structure a in Fig. 4 colored with the hydrophobic-polar pattern of the optimized sequence (red bar, hydrophobic; open bar, polar). All sites with <10% exposure are occupied by hydrophobic amino acids. Also shown are the four mutation sites (arrows) that reduce the energy gap between this structure and its competitor to zero (sites 2, 6, and 15 of helix 2, and site 3 of helix 3).
An important characteristic of natural proteins is their stability against mutations of individual amino acids. Generally, it requires several mutations to cause a natural protein to fail to fold. For our four most designable distinct folds, we have analyzed the mutational stability of the optimized sequences (Table 2). We find that a minimum of three to five mutations are required to reduce the energy gap to zero. For structure a of Fig. 4, four mutations are required to close the gap; the most effective sites for these mutations are shown by arrows in Fig. 5.
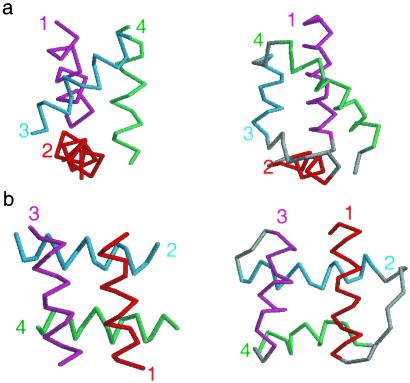
Not all of the highly designable structures identified by our method have close analogs among known natural folds. We used a vector-based alignment tool called “Mammoth” (A. R. Ortiz, C. E. M. Strauss, and O. Olmea, unpublished work) to align the top 1,000 designable structures against 4,188 α-helical proteins from the scop database. In Fig. 6, we show two of our designable structures (left) that had low alignment scores, along with their closest analogs in the databank (right). The first structure, shown in Fig. 6a, is similar to the POU binding domain. The model structure was the 15th most designable among the representative ensemble. Unlike the POU bundle, which has three helices coiled with a left-handed twist, the model structure has the same three helices coiled with a right-handed twist. We found no similar structure with a right-handed twist in the databank. The second structure, shown in Fig. 6b, is an orthogonal array, ranking it 80th among the representative ensemble. The model structure's closest natural analog 1AF7 has a long turn connecting helix 1 to helix 2. In the model fold, helix 1 is reversed allowing it to connect to helix 2 with a short turn. These structures, and others with no known natural counterparts, may be candidates for the design of novel folds.
Fig 6.
Two designable four-helix folds with no known natural analogs. On the right are the closest aligned naturally occurring folds (44), and on the left are the model structures. (a) 1POU has a left-handed twist of the top three helices. The model structure has a right-handed twist of these helices. (b) 1AF7 has a long turn connecting helix 1 to helix 2. The model structure has helix 1 reversed, allowing a short turn between helix 1 and helix 2.
Discussion and Conclusions
We have presented a method for generating protein stacks by packing together fixed secondary structural elements. The method was used to generate an ensemble of stacks of four α-helices. Each of eleven natural structures, stripped of turns, was matched to within 3.6 Å crms by a stack in the model ensemble, despite different helix lengths in the natural and model structures. The quantitative similarity between the model structures and the natural four-helix bundles suggests that the method is a reliable way of exploring the space of possible stacks.
The designabilities of the generated stacks followed the previously observed pattern (17, 30): a small set of structures were highly designable, being lowest-energy states of many more than their share of sequences, whereas the majority of structures were poorly designable. The universality of this distribution of designabilities in model studies suggests that it may apply to real protein structures as well—some structures may be intrinsically much more designable than others. Also consistent with previous model studies, sequences that fold into highly designable structures were typically thermodynamically stable and stable against mutations. We found that a minimum of three to five mutations were required to destabilize optimized sequences for our most designable structures. Interestingly, the hydrophobic-polar patterns of these optimized sequences depart significantly from the simple rule hydrophobic at buried sites, polar at exposed sites.
Almost all of the most designable four-helix stacks emerging from our model have analogs among the known four-helix-bundle folds. This finding suggests that nature has found all, or nearly all, designable four-helix bundles. However, several four-helix folds were identified by our method that have no analogs in protein database. These are now the target of design.
Acknowledgments
We thank Jonathan Miller, David Moroz, Ranjan Mukopadahay, and Chen Zeng for rewarding discussions.
This paper was submitted directly (Track II) to the PNAS office.
r = 1/NΣj(R
= 1/NΣj(R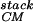 − r
− r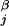 )2, where R
)2, where R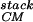 is the center of mass of the entire stack and r
is the center of mass of the entire stack and r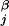 is the position of centroid j.
is the position of centroid j.
The final value of V0 is determined by a fitting procedure involving a naturally occurring stack composed of similar elements. Specifically, V0 is chosen to minimize the crms distance between the stack before and after a conjugate-gradient minimization, with fixed E1 and E2. For the four-helix bundle we found that a value of V0 = 0.05 produced the best fits to the chosen scop structures. V0 controls the interhelical separation, and thus changing it by a few percent only serves to increase or decrease the contact distances of helices. Making V0 significantly different from this makes the side-chain spheres unphysically small or large, which can lead to unreasonable packings.
The procedure was also tested on the packing of shorter (10 residues) and longer helices (20 residues), with the short helices producing highly variable packings and the longer helices tending to always pack into up and down configurations.
References
- 1.Chothia C. (1992) Nature (London) 357, 543-544. [DOI] [PubMed] [Google Scholar]
- 2.Orengo C. A., Jones, D. T. & Thornton, J. M. (1994) Nature (London) 372, 631-634. [DOI] [PubMed] [Google Scholar]
- 3.Brenner S. E., Chothia, C. & Hubbard, T. J. P. (1997) Curr. Opin. Struct. Biol. 7, 369-376. [DOI] [PubMed] [Google Scholar]
- 4.Wang Z. X. (1996) Proteins 26, 186-191. [DOI] [PubMed] [Google Scholar]
- 5.Govindarajan S., Recabarren, R. & Goldstein, R. A. (1999) Proteins 35, 408-414. [PubMed] [Google Scholar]
- 6.Richardson J. S., Richardson, D. C., Tweedy, N. B., Gernert, K. M., Quinn, T. P., Hecht, M. H., Erickson, B. W., Yan, Y., McClain, R. D. & Donlan, M. E. (1992) Biophys. J. 63, 1185-1209. [PMC free article] [PubMed] [Google Scholar]
- 7.Bryson J. W., Betz, S. F., Lu, H. S., Suich, D. J., Zhou, H. X., O'Neil, K. T. & DeGrado, W. F. (1995) Science 270, 935-941. [DOI] [PubMed] [Google Scholar]
- 8.Kamtekar S., Schiffer, J. M., Xiong, H., Babik, J. M. & Hecht, M. H. (1993) Science 262, 1680-1685. [DOI] [PubMed] [Google Scholar]
- 9.DeGrado W. F., Summa, C. M., Pavone, V., Nastri, F. & Lombardi, A. (1999) Annu. Rev. Biochem. 68, 779-819. [DOI] [PubMed] [Google Scholar]
- 10.Dahiyat B. I. & Mayo, S. L. (1997) Science 278, 82-87. [DOI] [PubMed] [Google Scholar]
- 11.Harbury P. B., Plecs, J. J., Tidor, B., Alber, T. & Kim, P. S. (1998) Science 282, 1462-1467. [DOI] [PubMed] [Google Scholar]
- 12.MacKenzie K. R., Prestegard, J. H. & Engelman, D. M. (1997) Science 276, 131-133. [DOI] [PubMed] [Google Scholar]
- 13.Kortemme T., Ramirez-Alvarado, M. & Serrano, L. (1998) Science 281, 253-256. [DOI] [PubMed] [Google Scholar]
- 14.Davidson A. R. & Sauer, R. T. (1994) Proc. Natl. Acad. Sci. USA 91, 2146-2150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Keefe A. D. & Szostak, J. W. (2001) Nature (London) 410, 715-718. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Giver L. & Arnold, F. H. (1998) Curr. Opin. Chem. Biol. 2, 335-338. [DOI] [PubMed] [Google Scholar]
- 17.Miller J., Zeng, C., Wingreen, N. S. & Tang, C. (2002) Proteins 47, 506-512. [DOI] [PubMed] [Google Scholar]
- 18.Emberly E., Miller, J., Zeng, C., Wingreen, N. S. & Tang, C. (2002) Proteins 47, 295-304. [DOI] [PubMed] [Google Scholar]
- 19.Fain B. & Levitt, M. (2001) J. Mol. Biol. 305, 191-201. [DOI] [PubMed] [Google Scholar]
- 20.Simons K. T., Bonneau, R., Ruczinski, I. & Baker, D. (1999) Proteins Suppl. 3, 171-176. [DOI] [PubMed] [Google Scholar]
- 21.Simons K. T., Strauss, C. & Baker, D. (2001) J. Mol. Biol. 306, 1191-1199. [DOI] [PubMed] [Google Scholar]
- 22.Park B. H. & Levitt, M. (1995) J. Mol. Biol. 249, 493-507. [DOI] [PubMed] [Google Scholar]
- 23.Banavar, J. R., Maritan, A., Cristian, M. & Seno, F. (2001) http://xxx.lanl.gov (accessible with cond-mat/0105209).
- 24.Munoz V. & Serrano, L. (1994) Proteins 20, 301-311. [DOI] [PubMed] [Google Scholar]
- 25.Murzin A. G., Brenner, S. E., Hubbard, T. & Chothia, C. (1995) J. Mol. Biol. 247, 536-540. [DOI] [PubMed] [Google Scholar]
- 26.Vita C., Drakopoulou, E., Vizzavona, J., Rochette, S., Martin, L., Menez, A., Roumestand, C., Yang, Y. S., Ylisastigui, L., Benjouad, A. & Gluckman, J. C. (1999) Proc. Natl. Acad. Sci. USA 96, 13091-13096. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Liang S. D., Liu, Z. J., Li, W. Z., Ni, L. S. & Lai, L. H. (2000) Biopolymers 54, 515-523. [DOI] [PubMed] [Google Scholar]
- 28.Harris N. L., Presnell, S. R. & Cohen, F. E. (1994) J. Mol. Biol. 236, 1356-1368. [DOI] [PubMed] [Google Scholar]
- 29.Govindarajan S. & Goldstein, R. A. (1995) Biopolymers 36, 43-51. [DOI] [PubMed] [Google Scholar]
- 30.Li H., Helling, R., Tang, C. & Wingreen, N. (1996) Science 273, 666-669. [DOI] [PubMed] [Google Scholar]
- 31.Li H., Tang, C. & Wingreen, N. S. (1998) Proc. Natl. Acad. Sci. USA 95, 4987-4990. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Mélin R., Li, H., Wingreen, N. S. & Tang, C. (1999) J. Chem. Phys. 110, 1252-1262. [Google Scholar]
- 33.Wang T., Miller, J., Wingreen, N. S., Tang, C. & Dill, K. A. (2000) J. Chem. Phys. 113, 8329-8336. [Google Scholar]
- 34.Wolynes P. G. (1996) Proc. Natl. Acad. Sci. USA 93, 14249-14255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.DeGrado W. F. (1997) Science 278, 80-81. [DOI] [PubMed] [Google Scholar]
- 36.Erman B., Bahar, I. & Jernigan, R. L. (1997) J. Chem. Phys. 107, 2046-2059. [Google Scholar]
- 37.Monge A., Friesner, R. A. & Honig, B. (1994) Proc. Natl. Acad. Sci. USA 91, 5027-5029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Monge A., Lathrop, E. J., Gunn, J. R., Shenkin, P. S. & Friesner, R. A. (1995) J. Mol. Biol. 247, 995-1012. [DOI] [PubMed] [Google Scholar]
- 39.Park B. & Levitt, M. (1996) J. Mol. Biol. 258, 367-392. [DOI] [PubMed] [Google Scholar]
- 40.Chou K. C., Maggiora, G. M., Nemethy, G. & Scheraga, H. A. (1988) Proc. Natl. Acad. Sci. USA 85, 4295-4299. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Press W. H., Teukolsky, S. A., Vellerling, W. T. & Flannery, B. P., (1992) Numerical Recipes in C (Cambridge Univ. Press, Cambridge, MA), pp. 420–425.
- 42.Flower D. R. (1997) J. Mol. Graph. 15, 238-244. [DOI] [PubMed] [Google Scholar]
- 43.Dahiyat B. I., Gordon, D. B. & Mayo, S. L. (1997) Protein Sci. 6, 1333-1337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Miyazawa S. & Jernigan, R. L. (1985) Macromolecules 18, 534-552. [Google Scholar]