The Discovery of Single-Nucleotide Polymorphisms—and Inferences about Human Demographic History

Abstract

A method of historical inference that accounts for ascertainment bias is developed and applied to single-nucleotide polymorphism (SNP) data in humans. The data consist of 84 short fragments of the genome that were selected, from three recent SNP surveys, to contain at least two polymorphisms in their respective ascertainment samples and that were then fully resequenced in 47 globally distributed individuals. Ascertainment bias is the deviation, from what would be observed in a random sample, caused either by discovery of polymorphisms in small samples or by locus selection based on levels or patterns of polymorphism. The three SNP surveys from which the present data were derived differ both in their protocols for ascertainment and in the size of the samples used for discovery. We implemented a Monte Carlo maximum-likelihood method to fit a subdivided-population model that includes a possible change in effective size at some time in the past. Incorrectly assuming that ascertainment bias does not exist causes errors in inference, affecting both estimates of migration rates and historical changes in size. Migration rates are overestimated when ascertainment bias is ignored. However, the direction of error in inferences about changes in effective population size (whether the population is inferred to be shrinking or growing) depends on whether either the numbers of SNPs per fragment or the SNP-allele frequencies are analyzed. We use the abbreviation “SDL,” for “SNP-discovered locus,” in recognition of the genomic-discovery context of SNPs. When ascertainment bias is modeled fully, both the number of SNPs per SDL and their allele frequencies support a scenario of growth in effective size in the context of a subdivided population. If subdivision is ignored, however, the hypothesis of constant effective population size cannot be rejected. An important conclusion of this work is that, in demographic or other studies, SNP data are useful only to the extent that their ascertainment can be modeled.

Introduction

Single-nucleotide polymorphisms (SNPs) are the markers of choice, both for studies of linkage and for studies of historical demography. This is due to (a) the relative abundance of SNPs in the human genome, compared with other types of polymorphisms, (b) the efficiency with which they can be assayed, and (c) the ease with which they can be analyzed by the tools of population genetics. It is typically assumed that each SNP is the result of a single mutation event and that different SNPs segregate independently of one another. These assumptions are probably correct much of the time. Then, it is the allele frequencies at SNPs, as well as the distribution of the polymorphisms among subpopulations, that can tell us about demographic history. However, SNPs are discovered—and, later, genotyped—by primer pairs that amplify short fragments of the genome rather than single sites. We refer to these SNP-discovered loci as “SDLs.” Some proportion of SDLs will be found to contain multiple SNPs, especially as the sample sizes from human populations increase. This represents an opportunity to garner more information from polymorphism data—namely, the number of SNPs per SDL, denoted by “S,” and their joint frequencies in a sample.

The SDL context of SNPs also has important implications for the correction of ascertainment bias. The data analyzed below are derived from SDLs discovered in three recent SNP surveys: those by Wang et al. (1998), Cargill et al. (1999), and Altshuler et al. (2000). The first two of these studies reported SDLs that had at least one SNP segregating in a relatively small, geographically restricted sample and in a relatively large, globally distributed sample, respectively; the third study found polymorphisms in a relatively small, globally distributed sample but also introduced a new SNP-discovery protocol, called “reduced representation shotgun sequencing,” in which it is necessary to impose an upper bound on S. A large fraction of the 1.42 million SNPs in the high-density SNP map reported recently were discovered by a modified version of this method (The International SNP Map Working Group 2001). In some applications, it will be necessary to model this discovery process. In addition, all of the SDLs studied herein contain multiple SNPs, because they were originally chosen, for a study of genomewide patterns of linkage disequilibrium (Ardlie et al. 2001), to have at least two SNPs segregating in their respective ascertainment samples. We show that, both in S and in the allele frequencies of SNPs, there is substantial information about population history. However, the mark of ascertainment bias is different for these two kinds of data. To correct properly for ascertainment bias, it is necessary to know the complete pattern of polymorphism discovered at an SDL, even if only a single SNP is typed in a later study.

We are concerned with two aspects of human historical demography: population subdivision and changes in effective population size, N_e, over time. Although the human population may be less structured than that of chimpanzees and other close relatives (Kaessmann et al. 1999), it is clear that subdivision has played a role in the shaping of human polymorphism. There is less agreement about the pattern of changes in the human N_e (Hawks et al. 2000). The early reports of mtDNA diversity seemed to indicate a recent large increase in N_e (Cann et al. 1987; Vigilant et al. 1991). When nuclear data became available, the first few data sets appeared to contradict this, showing instead a pattern consistent with a decrease in N_e, rather than an increase (Hey 1997). This conclusion was based in part on deviations from the expected frequency distribution of polymorphic sites. Deviations in the frequency spectrum are summarized by Tajima’s (1989) statistic, D, which tends to be negative when N_e increases and which tends to be positive when it decreases. A recent survey of available nuclear loci (Przeworski et al. 2000) showed a broad range of D values and concluded that neither a constant N_e nor long-term exponential growth could explain the pattern. Two more-recent reports have suggested a stronger signature of growth (Stephens et al. 2001; Yu et al. 2001). Although humans have certainly increased in number—and although we might expect to find genetic evidence of this—it is important to keep in mind that census size is not the only determinant of N_e. In a subdivided population, changes in the rate and pattern of migration can either mimic or obscure a signature of growth, because N_e is inversely proportional to the migration rate (Wright 1943; Nei and Takahata 1993) and depends on the pattern of migration across the population (Wakeley 2001).

Before we describe our model and the effects that ascertainment bias has on historical inference, some background for a simpler model will be helpful. Expectations about patterns of polymorphism are typically based on the coalescent (Kingman 1982; Hudson 1983b; Tajima 1983), a stochastic model that describes the genealogical history of a sample of DNA sequences. In this model, it is assumed that a sample of size n is taken without replacement and, importantly, without regard to variation in the population. It is also assumed that N_e has been constant over time and not subject to current or historical subdivision. Variation at the genetic locus under study is assumed not to be affected by selection, either directly or (through linkage to other loci) indirectly. The standard model also assumes that there is no intralocus recombination. If these assumptions hold for a sample of DNA sequences from some population, the genealogy of the sample will be a randomly bifurcating tree with exactly n-1 coalescent nodes, such as that shown in figure 1. Furthermore, the time during which there were exactly k lineages is exponentially distributed, with mean

Watterson 1975; (Kingman 1982). These times, t_k are measured in units of 2N_e generations, where N_e is the inbreeding effective size of the population. Equation (1) shows that the expected value of t_k is larger when k is smaller—that is, for the more ancient coalescent intervals in the genealogy. The relative branch lengths in the genealogy shown in figure 1 are those expected from equation (1).

Figure 1.

Example genealogy, drawn with branch lengths equal to the coalescent expectations, which shows the structure of the data analyzed here: “A,” “D,” and “O” are, respectively, samples that are only in the ascertainment set, samples that are only in the data set, and “overlap” samples (i.e., those which are in both the data set and the ascertainment set). Three types of branches are distinguished, corresponding to the three kinds of observable polymorphisms discussed in the text.

All the standard predictions of the coalescent—for example, those reported by Tavaré (1984)—follow from the two basic results described above: the randomly bifurcating structure of genealogies and the exponentially distributed times to common-ancestor events. However, predictions about what should be observed in a sample of genetic data are different, depending on the mutation process at the locus under consideration. When the rates of mutation and recombination per site are very low, the infinite-sites–mutation model without intralocus recombination is appropriate (Watterson 1975). We use this model below and exclude the SDLs that show direct evidence of either multiple mutations, recombination, or gene conversion (Ardlie et al. 2001). Under the infinite-sites–mutation model, there is a one-to-one correspondence between mutations and polymorphic sites in a sample. Considering the genealogy, this means that a polymorphic site that is segregating at frequency i/n in the sample must be the result of a mutation that occurred on a branch of the genealogy that partitions the tips of the tree into two sets: one of size i and one of size n-i. The number of mutations that occur on a branch of length T is Poisson distributed, with mean Tlθ/2, where l is the length (in base pairs) of the locus or SDL, θ=4N_eu, and u is the neutral mutation rate per base pair per generation.

Inferences about the demographic history of populations are often made by comparison of observed data, such as SNP data, to the following prediction of the standard coalescent model with infinite-sites mutation: the expected number of segregating sites at which one base is present in i copies and in which the other base is present in n-i copies in a sample is equal to

(Tajima 1989; Fu 1995). Because the ancestral state is typically unknown, i ranges from 1 to [n/2], where [n/2] is the largest integer that is ⩽n/2. Thus, E(η_i) is the sum of two terms, the expectation for a mutant-site pattern, i, and for its complement, n-i. To avoid counting the same pattern twice, we must correct for the case i=n-i, using Kronecker’s δ, which is 1 if i=n-i and which is 0 otherwise. Equation (2) specifies that singleton polymorphisms (i=1) should be the most abundant and that the numbers of other kinds of polymorphisms should fall off in a characteristic manner as i increases. If the polymorphic-site frequencies in a data set deviate significantly from this prediction, then one or more of the assumptions of the model must be incorrect. Tajima’s (1989) D, as well as the statistics proposed by Fu and Li (1993), will detect deviations in two directions: either too few low-frequency sites or too many. Figure 2 plots the distributions of Tajima's D among SDLs for the three data sets studied here and shows that D tends to be positive in two of them. This is the result of an excess of middle-frequency polymorphisms, which, here, we show to be due to ascertainment bias in these two data sets.

Figure 2.

Distribution of Tajima’s (1989) D among SDLs, in each of the three data sets.

Every SDL and SNP has an associated ascertainment sample, the sample in which it was originally discovered. In fact, this is true of any genetic marker. Subsequent genotyping of SNPs is done with different, typically much larger, data samples, which may or may not overlap with the ascertainment sample. There are three kinds of samples in this context: (1) “ascertainment-only” samples, which are included in the ascertainment study but not in a later data set, (2) “overlap” samples, which are included in both the ascertainment study and a later data set, and (3) “data-only” samples, which are included in a later data set but were not part of the original discovery study; we will refer to the numbers of these samples as “n_A,” “n_O,” and “n_D,” respectively. In total, the ascertainment sample is of size n_A+n_O, and the data sample is of size n_D+n_O. Because the chance that an SNP will be segregating in a small ascertainment sample is higher for middle-frequency polymorphisms than it is for low-frequency polymorphisms, the counts of the two bases segregating in later data samples will tend more toward the middle frequencies than toward the expectation for random sample given by equation (2). This effect will be exacerbated if a frequency cutoff is used before an SNP is recognized in the ascertainment sample. The bias in frequencies that results from initial screening in a small sample has been described before, in other contexts (Ewens et al. 1981; Sherry et al. 1997), and its importance for human SNPs has recently been emphasized (Kuhner et al. 2000; Nielsen 2000).

Here we describe two further aspects of ascertainment bias: the consequences of choosing uncharacteristically polymorphic loci and the effects that ascertainment bias has on the distribution of S. We are concerned with these phenomena both because the data considered here were selected to have S⩾2 in the ascertainment sample (Ardlie et al. 2001) and because some of our analyses depend on the distribution of S. Figures 3 and 4 display simulation results of ascertainment bias under the standard coalescent model. In both figure 3 and figure 4, we simulated SDLs that were l=400 bp long, with θ=.0005 per base pair and a data sample size of n_D=10. Using Watterson’s (1975) result, which is equivalent to the sum shown in equation (2) over all i, we find that the expected value of S is 0.566. Figure 3 shows that the SNP-allele frequencies are skewed toward the middle frequencies both (a) when SDLs are required to have SNPs segregating in small ascertainment samples and (b) when SDLs are selected to contain multiple SNPs. The effect is stronger in the former case than in the latter but should not be ignored in either case.

Figure 3.

Expected numbers of SNPs segregating in different frequencies, in a sample of size n_D+n_O=10, relative to the number of singleton polymorphisms; results are averages, over 100,000 simulated data sets, for a 400-bp-long SDL, with θ=.0005 per base pair. a, Effect of requiring an SDL to have at least one SNP in the first n_O samples drawn from the population. b, Effect of separating SDLs into classes with different numbers of SNPs, with n_D=0.

Figure 4.

Coefficient of variation of S, in a sample of size n_D+n_O=10; results are averages, over 100,000 simulated data sets, for a 400-bp-long SDL, with θ=.0005 per base pair. a, Effect of requiring SDLs to have at least k SNPs, under the assumption n_D=0. b, Effect of requiring an SDL to have at least one SNP that must be segregating in the first n_O samples drawn from the population.

The effect shown in figure 3a is fairly well known and follows directly from sampling considerations. It has important consequences for the mutation distribution over the genealogy of the sample. Mutations that occur during the most recent coalescent interval, t_n, can only be singletons, but mutations that occur on the earlier branches in the genealogy can be segregating at higher frequencies. Thus, by preferentially gathering middle-frequency SNPs, more or less directly, as in figure 3a, we are also selecting older mutations. The reason why this effect is also seen in figure 3b, when SDLs are chosen to be highly polymorphic, is that much of the variation in the total length of the genealogy—and, thus, in S—is attributable to variation in the length of the longest and most ancient coalescent interval, t₂. Mutations that occur during this interval can be segregating at any frequency in the sample and thus tend more toward the middle frequencies than do recent mutations.

Figure 4 shows the effects that these same ascertainment processes have on one aspect of the distribution of S: the coefficient of variation of S. Both (a) using smaller ascertainment samples for discovery and (b) imposing a cutoff for S cause the coefficient of variation to be smaller than that which would be observed in a random sample. Imposing a lower bound on S causes this directly, but it is less obvious why the same thing occurs when higher-frequency polymorphisms are selected. Again, the answer is in the mutations' placement on the genealogy. Using the exponential distribution with the mean shown in equation (1) and considering the Poisson (lθ/2) mutation process, we can easily show that the coefficient of variation of the number of segregating sites at a locus that descend from mutations that occurred during coalescent interval t_k is 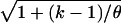and thus is smaller for more-ancient mutations. It is important to consider separately the effects that ascertainment has on S and on the allele frequencies, because the consequences for historical inference are different for the two types of data. For example, extreme population growth is known to make sample genealogies star shaped (Slatkin and Hudson 1991). This results in an excess of singleton polymorphisms, because of long external branches, but it also decreases variation in S, because most genealogies will tend to be the same size. The effects of milder growth are in this same direction. Population decline reverses these effects, producing both an excess of middle-frequency polymorphisms and increasing interlocus variation in S. If ascertainment bias is ignored, an analysis of frequency spectra would point toward a shrinking population, whereas an analysis of numbers of SNPs would point toward an expanding population, even though the truth may be that the size of the population has not changed.

Material and Methods

Ascertainment of SDLs

Ardlie et al. (2001) analyzed 106 SDLs chosen from three recent SNP surveys (Wang et al. 1998; Cargill et al. 1999; Altshuler et al. 2000). These were selected on the basis of their having at least two SNPs segregating in the samples used for discovery and were then fully resequenced in a sample of 47 globally distributed individuals; for a description of these samples, see the article by Ardlie et al. (2001). We refer here to the SDLs derived from studies by Wang et al. (1998), Cargill et al. (1999), and Altshuler et al. (2000), as “data set 1,” “data set 2,” and “data set 3,” respectively. Individuals were partitioned into demes, or subpopulations, mostly on the basis of geographic origin but with some attention to ethnic identity within localities. Table 1 lists these demes and gives the n_D, n_O, and n_A for each data set; sample sizes are numbers of chromosomes, rather than numbers of diploid individuals. The number of chromosomes listed for the CEPH Utah pedigree in data set 1 (Wang et al. 1998) is an odd number because the ascertainment sample in that study included a maternal grandmother and her son (GM07340 and GM07057, respectively), from family 1331.

Table 1.

Numbers of n_D, n_O, and n_A Chromosomes/Haplotypes Sampled from Each Deme

	Data Set 1			Data Set 2			Data Set 3
Deme	nD	nO	nA	nD	nO	nA	nD	nO	nA
Utah-CEPH	6	0	5	0	6	10	6	0	2
Venezuelan-CEPH	2	0	4	0	2	0	2	0	0
Irish	2	0	0	2	0	0	2	0	0
Russian/Adygei	6	0	0	0	6	4	6	0	0
Russian/Zuevsky	4	0	0	0	4	6	2	2	0
Chinese	8	0	0	0	8	2	6	2	0
Cambodian	6	0	0	0	6	0	6	0	0
Melanesian	8	0	0	6	2	0	6	2	0
Japanese	4	0	0	2	2	2	2	2	0
Taiwanese/Ami	6	0	0	6	0	0	6	0	0
Taiwanese/Atayal	4	0	0	4	0	0	4	0	0
South Indian	2	0	0	2	0	0	2	0	0
Amerindian	8	0	0	8	0	0	8	0	2
CAR/Pygmy	6	0	0	6	0	0	6	0	2
Zaire/Pygmy	4	0	0	4	0	0	4	0	0
Sudanese/Dinka	4	0	0	4	0	0	4	0	0
Sudanese/Shilluk	2	0	0	2	0	0	2	0	0
Sudanese/Arab	2	0	0	2	0	0	2	0	0
Ethiopian/Semitic	6	0	0	6	0	0	6	0	0
Libyan/Semitic	4	0	0	4	0	0	4	0	0
Amish-CEPH	0	0	6	0	0	0	0	0	2
African American	0	0	0	0	0	20	0	0	2
French-CEPH	0	0	0	0	0	0	0	0	2
Total	94	0	15	58	36	44	86	8	12

The 106 SDLs studied by Ardlie et al. (2001) included 41 from the study by Wang et al. (1998), 29 from the study by Cargill et al. (1999), and 36 from the study by Altshuler et al. (2000). We excluded four of these SDLs, all from data set 3, because, when they were resequenced, they were found to have fewer than two SNPs in the ascertainment sample and thus did not fit our model of ascertainment bias. In addition, 17 SDLs were removed—7, 4, and 6 from data sets 1, 2, and 3, respectively—because they showed direct evidence of either recombination or gene conversion (in the case of 6 SDLs) or of multiple mutations (in the case of 11 SDLs) (Ardlie et al. 2001). Finally, we excluded one SDL from data set 3 because it mapped to the X chromosome and thus has a different N_e and, possibly, a different migration pattern than do the autosomal SDLs. We also ran all of the analyses with these SDLs included, and the results were the same. In sum, data set 1 contains 34 SDLs, and data sets 2 and 3 each contain 25 SDLs, all of which appear to fit both our model for ascertainment and the infinite-sites–mutation model, without recombination or gene conversion.

The SDLs in data set 3, which were discovered by the method described by Altshuler et al. (2000), must be treated differently than those in data sets 1 and 2. In this case, the ascertainment sample for each SDL is not identical to the n_A+n_O samples listed in table 1 but, rather, is a random sample of these, taken with replacement. The sizes of these random samples are the “clique sizes” used by Altshuler et al. (2000); however, they are not the final sizes reported in that article, because the SDLs studied both by us and by Ardlie et al. (2001) were selected prior to the completion of Altshuler et al.'s (2000) study. These clique sizes differ among SDLs and range from two to six, with a mean of three. To exclude multicopy sequences, Altshuler et al. (2000) imposed an upper bound of no more than one SNP per 100 bp in an SDL. Thus, in addition to the lower bound of two SNPs, which is true for all three data sets, when we analyze data set 3 we must include an upper bound on S in the ascertainment sample and take into account the subsampling of the ascertainment sample, to form cliques.

A Model of Historical Demography

We used the subdivided-population model recently described by Wakeley (2001). This is a generalized version of Wright’s (1931) island model, in which the sizes of demes (N), the contributions of each deme to the migrant pool (α), and the fraction of each deme that is replaced by migrants every generation (m) vary across the population. It is assumed that the number of demes in the population is large relative to the size of the sample under study. Simulation results indicate that, for the large-number-of-demes approximations to hold, the number of demes need only be three or four times the sample size (Wakeley 1998). The parameters that determine the pattern of genetic variation in a sample are M=2Nm for each sampled deme and θ=4N_eu, where N_e is the effective size of the entire population and u is the neutral mutation rate at a locus. N_e depends both on the total number of demes and on the distributions of N, α, and m among demes. It is important to note that θ in this model is the expected number of nucleotide differences for a pair of sequences from different demes. This is a consequence of there being a large number of demes; a randomly chosen pair will almost never be from the same deme.

As in the study by Wakeley (1999), we allow for the possibility of a single, abrupt change in N_e at some time in the past. This could be the result of a change in the total population size, but it could also be caused by changes either in the relative sizes of demes, in the relative contributions to the migrant pool, or in the backward-migration rates (Wakeley 2001). The large-number-of-demes model is characterized by a short, recent “scattering” phase and a longer, more ancient “collecting” phase (Wakeley 1999). The scattering phase is a stochastic sample-size adjustment that accounts for the tendency of samples from the same deme to be more closely related than are samples from different demes. The collecting phase is a Kingman-type coalescent process with effective size N_e. The ancestry of a sample can be described analytically but is easily simulated, and we take this route in modeling ascertainment bias. Genealogies are simulated as follows. First, the scattering phase is performed for each deme’s sample, by the “Chinese-restaurant” process (Arratia et al. 1992). This is one of several stochastic processes known to produce Ewens’s (1972) distribution, which is the appropriate model for the numbers of descendants, of the lineages from each deme, that enter the collecting phase (Wakeley 1999). Then, conditional on this, the collecting phase for the remaining lineages is a coalescent process, but with a change in N_e at some time in the past. Observed data will depend both on M_i, 1⩽i⩽d, which are the values of 2Nm for each of the d sampled demes, and on θ. They will also depend on Q=N_eA/N_e, the ratio of the ancestral N_e to the current N_e, and on T=t/(2N_e), the time, in the past, at which the change in N_e occurred, measured in units of 2N_e generations.

Methods of Ancestral Inference

The data have the following structure at each SDL: There are some S_D and some S_O; S_A are not directly observed. However, we do have some information about these which we must take into account when we condition on ascertainment; namely, for the SDL to have been selected, the sum S_A+S_O must be ⩾2 (Ardlie et al. 2001). For data sets 1 and 2, S_A+S_O⩾2 must be true for the ascertainment sample of n_A+n_O chromosomes listed in table 1; for data set 3, it must be true in a randomly chosen ascertainment sample of some smaller size (“clique size”; see the “Ascertainment of SDLs” subsection, above). In addition, for data set 3, we must also impose the upper bound: S_A+S_O⩽Z, where Z=[l/100]—that is, there is no more than one SNP per 100 bp (Altshuler et al. 2000).

The three categories of SNPs—S_D, S_O, and S_A—are mutually exclusive. Thus, under the infinite-sites–mutation model, they are generated via mutation on nonoverlapping sets of branches in the genealogy of the sample. Figure 1 shows one possible realization of such a genealogy, with n_D=n_O=n_A=3, and distinguishes the three possible kinds of branches. In this genealogy, let T_D be the sum of all the solid branches, T_O be the sum of all the short-dashed branches, and T_A be the sum of all the long-dashed branches; every branch in the genealogy must fall into one of these three categories. Given these values, the numbers of polymorphisms—S_D, S_O, and S_A—are mutually independent and Poisson distributed, with parameters T_Dlθ/2, T_Olθ/2, and T_Alθ/2, respectively. Our analyses depend on this, because we calculate likelihoods and other quantities by conditioning on the genealogy of the sample and averaging values over many simulated genealogies.

In addition to S_D and S_O (and S_A), the complete data include the joint frequencies of SNPs among demes and the linkage patterns between SNPs within each SDL. We would like to use this information to make inferences about the parameters of the model: Ω={θ,Q,T,M}, where , where M is the set of demic migration parameters. We are most interested in inferences about Q and T and treat M and θ as nuisance parameters. Ideally, we would like to base our inferences on Pr{data|Ω,asc}, the likelihood for the complete data, given the ascertainment scheme. However, this is computationally infeasible. Instead, we first obtain moment-based estimates of 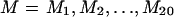for each of the three data sets, on the basis of the numbers of polymorphisms segregating within each deme. We then use the distribution of n_D and n_O to make inferences about θ. This step gives information about Q and T as well, because θ is estimated over a grid of (Q,T) values, by maximization of . Last, fixing both M and θ from these analyses, we use 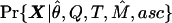to make inferences about Q and T, where X is a vector of the frequencies of the less-frequent bases segregating at each SNP on each SDL. We ignore the pattern of linkage between SNPs. These procedures are still computationally intensive. It takes several days on a fast workstation to perform all of the analyses described below.

Estimation of M

We estimate M by fitting the expected S segregating in each deme to the observed values, conditional on ascertainment. Let S_Dk and S_Ok be the numbers of segregating sites in deme k for some SDL, and let S^<k>_A be the number of SNPs discovered on that SDL that are not segregating in deme k; thus, S^<k>_A includes S_A and S_O that are not polymorphic in the data sample from deme k. The expected number of SNPs segregating in the data sample from deme k, given the parameters of the model and the ascertainment scheme, is

where Z=∞ for data sets 1 and 2 and where Z=[l/100] for data set 3. Appendix A describes how we compute equation (3), first by conditioning on the genealogy of the sample and then, using simulations, “integrating” over genealogies. We solve numerically for M and θ by minimizing the difference between the expectation presented by equation (3) and the observed values of S_Dk and S_Ok. We later discard these estimates of θ in favor of the maximum-likelihood estimate described below. However, these moment-based and maximum-likelihood estimates of θ were very similar for all three data sets.

The reason why Q and T do not appear in equation (3) is that we estimate M only for the case of no change in N_e, Q=1. The parameter T is meaningless in this case. This was done for computational reasons—namely, because it is too computationally expensive to estimate M for every value of Q and T. This introduces some error into the results: the likelihood is accurately estimated for Q=1 but will be underestimated for other values of Q (and T). Thus, the direction of error is conservative with respect to the null hypothesis of no change in N_e.

Estimation of θ

Once we have estimated the set of demic migration parameters M, they are fixed for the rest of the analysis. We calculate the likelihood based on S, conditional on M and on ascertainment:

Appendix B describes how this quantity is computed. We use equation (4) to optimize for θ over a grid of paired values of Q and T. The justification for doing this is that most of the information regarding θ is in S, not in their unrooted allele frequencies (Fu 1994). Thus, our likelihood function, presented in equation (6), below, is probably close to the true likelihood based on all the data. The values of θ obtained in this step are then fixed, together with the M from before, in the computation, using the frequency data, of the likelihood of Q and T.

Joint Maximum-Likelihood Surface Estimation for Q and T

If we take 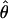to mean the estimates of θ over the grid of Q and T, then the analysis above yields

This is the joint likelihood for Q and T, based on the distribution of S. We can combine this information with the following likelihood analysis of the SNP frequencies, because the results are independent.

Let the count of the less-frequent base at data-only SNP i be X⁽ⁱ⁾_D, and let the count of the less-frequent base at overlap SNP i be X⁽ⁱ⁾_O. The frequency data at an SDL can be summarized as . Again, we do not keep track of linkage patterns between SNPs, partly because these are genotypic data but mostly to reduce the computational burden of calculating the likelihood. The frequency-based likelihood is computed conditional on the numbers of SNPs at an SDL:

Appendix C describes how this is done. We consider the two likelihoods, which are presented in equation (4) and equation (5), to be independent and calculate the overall likelihood of the data as

In fact, L_X(Q,T) and L_S(Q,T) are not strictly independent, because they are both conditional on the estimates of M and because L_X(Q,T) is conditional on the estimates of θ from the optimization of L_S(Q,T).

We also performed all of these analyses without conditioning on ascertainment. This was done by (a) fixing all the lower bounds above at 0 and fixing all the upper bounds at ∞, (b) making the ascertainment samples identical to the data samples, and (c) lumping all polymorphisms into one class: S=S_D+S_O+S_A. The next section describes the various effects that ignoring the ascertainment bias can have on historical inference. In addition, we ran the analyses under the assumption of no population subdivision, by setting every migration parameter equal to 10⁴, and compared these results to the more-general model.

Results

Our first result is not surprising: θ is overestimated if ascertainment bias is ignored. The values of θ before correction for ascertainment bias are .00224, .00122, and .0021 for data sets 1, 2, and 3, respectively; the corrected values are .0010, .0008, and .0019, respectively. For ease of interpretation, these are the values obtained when Q=1—that is, when N_e has been constant. Thus, they are not the global maximum-likelihood estimates for the complete model, although they do not differ much from them. It is important again to note that, under the demographic model used here, and with Q=1, these are equivalent to the expected number of differences per site when two sequences from separate demes are compared. This is different than the average number of pairwise differences in a sample, which would include both within-deme and between-deme comparisons and which thus would be smaller.

Estimates of M

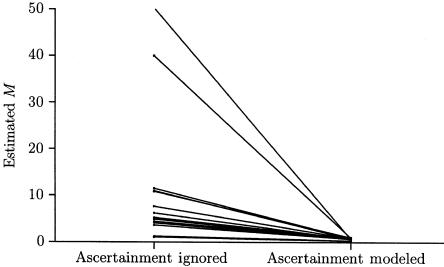
Figure 5 shows that demic migration parameters can be substantially overestimated when ascertainment bias is ignored. The results pictured are those for data set 2, but the results for data sets 1 and 3 are similar. When SDLs are chosen to be highly polymorphic, those obtained are more likely to contain migrants or to be descended from migrants than is a random sample. These values of M will remain fixed in most of the analyses below, the exception being the analysis assuming a panmictic population.

Figure 5.

Estimates of 2Nm, for data set 2, both when ascertainment is ignored and when it is modeled. For this data set, five demes had infinite-migration-rate estimates when ascertainment was ignored; these five demes are not plotted.

Analysis of S

Figure 6 plots the likelihood surface for Q and T, based on the distributions of n_D and n_O for each of the three data sets, both when ascertainment bias is ignored (fig. 6a) and when it is modeled (fig. 6b). The lightest area shown, bounded by the first contour, is the approximate joint 95% confidence region for Q and T—that is, 3 log-likelihood units from the maximum. Comparison of figure 6a to figure 6b shows that ignoring the ascertainment bias prevents some very unlikely values of Q and T from being rejected—those in the lower left of the panels, which are consistent with a recent increase in N_e. Figure 6 also shows that the differences between ignoring and modeling the ascertainment bias are similar for all three data sets when numbers of SNPs are analyzed.

Figure 6.

Likelihood surfaces for Q and T, based on the distribution of n_D and n_O for each of the three data sets, when ascertainment bias is ignored (a) and when it is modeled (b).

Because the results in figure 6 are so similar for all three data sets, we combined them, as shown in figure 7. When the data are analyzed together and ascertainment bias is ignored (fig. 7a), a model with constant N_e (Q=1) is rejected in favor of one in which the N_e has increased. Correction for ascertainment bias, presented in figure 7b, shows that this result is spurious and, instead, reveals a valley in the likelihood surface, over much of the same area as that encompassed by the peak in figure 7a. Thus, in the analysis of S only, we cannot reject the hypothesis of no change in N_e (Q=1). The difference between figures 7a and 7b can be understood by referring back to figure 4, which shows that ascertainment bias decreases variation in S, thus creating a false signal of population growth.

Figure 7.

Combined likelihood surfaces for Q and T, based on the distribution of n_D and n_O for all three data sets, when ascertainment bias is ignored (a) and when it is modeled (b).

Analysis of SNP Allele Frequencies

Figure 8 plots the likelihood surface for Q and T, based on the allele frequencies at data-only and overlap SNPs, for each of the three data sets, both when ascertainment bias is ignored (fig. 8a) and when it is modeled (fig. 8b). In contrast to the analysis of S, the analysis of the frequencies shows great differences, between the three data sets, in the effects of ascertainment. When ascertainment bias is ignored, data sets 1 and 3 both show a likelihood-surface peak consistent with a shrinking population. Both data set 1 and data set 3 have small ascertainment samples (see table 1; data set 2, which has a large ascertainment sample, shows no such peak). As with the tendency for Tajima’s D to be positive for data sets 1 and 3 (fig. 2), these peaks reflect the overrepresentation of middle-frequency polymorphisms expected from ascertainment bias (e.g., see fig. 3). When ascertainment bias is modeled properly, as in figure 8b, all three data sets show the same pattern, and none of them reject a constant N_e. This pattern is similar both to that found in the analysis of numbers of SNPs, shown in figures 6 and 7, and to the frequency-based surface for data set 2, as shown in figure 8a—that is, the correction of frequencies for ascertainment bias is minor for data set 2 but is quite striking for data sets 1 and 3.

Figure 8.

Likelihood surfaces for Q and T, based on the allele frequencies at data-only and overlap SNPs, conditioned on their numbers, for each of the three data sets, when ascertainment bias is ignored (a) and when it is modeled (b).

Combined Analysis with and without Subdivision

Encouraged by the similarity of the results for all three data sets, in both figure 6b and figure 8b, we combined the results of all the analyses, according to equation (6). This gives us our best estimate of the demographic history of humans and is shown in figure 9b. When either just the S or just the SNP-allele frequencies is used, it is not possible to reject the hypothesis of no change in N_e; however, when all the data are used, a significant signature of population growth emerges. Figure 9a shows the corresponding overall picture when it is assumed that the human population is not subdivided. Even if we model ascertainment bias, if we ignore population subdivision then we also ignore this apparent signal of population growth in the data. We call this signal “apparent” because its significance depends on our estimates of M, and we have not properly accounted for variation in these. However, we note that, in figure 9a, there is also a peak for Q<1, a peak that is not visible in the figure because the contours are drawn 3 log-likelihood units apart. Thus, regardless of our estimates of M, these data support a scenario of population growth; however, if we have underestimated M for some reason, then we may be wrong in calling it “significant.”

Figure 9.

Combined likelihood surfaces for Q and T, for all the data, (a) when the population is assumed to be panmictic and (b) fitting the subdivided-population model described in the text.

Discussion

Our analysis reveals two very different effects of ascertainment bias: a decrease in among-SDL variation in SNP number and an increase in heterozygosity (allele frequency) within SDLs. The second of these effects is fairly well known, but the first is not. We have also shown that these two kinds of bias have opposite effects on inferences about historical demography. This is illustrated in figures 3 and 4, for simulated data, and in figures 6 and 8, for polymorphism data from humans. Figure 6 shows close agreement between the three diverse data sets exactly where we expect the effects of ascertainment to be similar for all three. In this analysis of S, when results for the three data sets are pooled to produce figure 7, ascertainment bias introduces a false signal of population expansion. In contrast, figure 8 shows disagreement among data sets when we expect the magnitude of ascertainment bias to differ but shows close agreement when the ascertainment process is included in the likelihood model. In this case, when the frequencies of SNPs are analyzed (fig. 8a, data sets 1 and 3), ascertainment bias produces a false signal of population decline. Comparison of these results to figures 3 and 4, as well as the good agreement between data sets, lends support to the overall picture of human history suggested by figure 9b.

Wakeley (1999) fitted a restricted version of this same demographic model, in which it was assumed that all demes have the same migration parameter, to RFLP data from a worldwide sample of humans (Bowcock et al. 1987; Matullo et al. 1994; Poloni et al. 1995). A pattern like that in figure 8a, for data sets 1 and 3, was found. Although those RFLP data are known to be subject to ascertainment bias (Mountain and Cavalli-Sforza 1994), the latter's contribution to this pattern could not be assessed directly (Wakeley 1999). The present study suggests that the apparent signature of a decrease in N_e, observed, by Wakeley (1999), for the RFLP data, is probably the result of ascertainment bias.

In our computations, we have assumed that recombination and gene conversion do not occur in these short SDLs and that θ does not vary among loci. Both assumptions are false, and a more complete approach would account for this. Our approach was to delete the loci that showed direct evidence of either multiple mutations, recombination, or gene conversion. Recombination and gene conversion will certainly affect the distribution of S and could bias the results nonconservatively (Hudson 1983a; Kaplan and Hudson 1985), although the interaction between recombination, ascertainment, demography, and our deletion of recombinant SDLs is difficult to predict. Only 5% of SDLs showed evidence of either recombination or gene conversion (Ardlie et al. 2001). As for mutation, there could still be some θ variation among the SDLs that we analyzed. This would result in S variation greater than that which a constant-population-size model would predict; however, this would indicate population decline, which we did not observe (figs. 6b and 7b). The effects that these phenomena have on the allele frequencies at SNPs are difficult to predict, but the fact that identical results were obtained regardless of whether we deleted aberrant SDLs indicates that none of these effects are very strong.

Clearly, the effects that the polymorphism-discovery process has on later demographic inferences can be quite pronounced. Furthermore, the direction of the bias introduced is not always the same; it depends on which aspect of the data is used for inference. Caution in both the design of experiments and the choice of markers seems indicated. However, our results are also encouraging. If the discovery process is known, and if ascertainment bias is modeled, then accurate demographic inferences can be made. The present data suggest that both population subdivision and changes in N_e have been important in human history. Within the limits of our model and our methods of analysis, the data indicate a history of growth in N_e within the context of a subdivided population. The joint 95% confidence region for Q and T, enclosed by the first contour in figure 9b, is quite broad, which is consistent with the results of other recent studies (Wall and Przeworski 2000), despite the fact that the human population has increased dramatically in census size. Because N_e depends both on the census size and on the rates and pattern of migration across the population (Wright 1943; Nei and Takahata 1993; Wakeley 2001), studies of historical changes in N_e must also take subdivision into account. A comparison of figures 9a and 9b illustrates how population subdivision and growth can be conflated. When subdivision is ignored, the signal of growth in these data is missed. Furthermore, the unexpectedly small observable effect of growth in human genetic data may be due to changes in rates and/or in patterns of migration.

Appendix A

Let C_k represent the condition Z⩾S^<k>_A+S_Ok⩾2. Then, starting from equation (3) and using the rules for conditional probability, we have

In equation (A1) and below, we use “Ψ” to denote the set of all possible genealogies with branch lengths. This representation suggests that E[S_Dk+S_Ok|C_k,θ,M] can be estimated consistently as

where G_i is one of n genealogies simulated from P(G|θ,M).

For each simulated tree, we store T_Dk, T_Ok, and T^<k>_A; these are the total lengths of branches in the genealogy that could give rise to an SNP that is segregating in the data-only sample from deme k, in the overlap sample from deme k, and in the total ascertainment sample but not in deme k, respectively. Branch lengths are measured in units of 2N_e generations. Given T_Dk, T_Ok, and T^<k>_A, the numbers of mutations in each of these three classes are independent Poisson random variables with parameters T_Dklθ/2, T_Oklθ/2, and T^<k>_Alθ/2. Thus, we have

The second term in equation (A3) is calculated by further conditioning on the value of S^<k>_A:

The expectation on the right-hand side of the foregoing equation is given by

and P(S_Ok=x) and (S^<k>_A=j) are the appropriate Poisson probabilities. Similarly, the term P(C_k|θ,M,G_i) in equation (A2) is given by

and the sum, S^<k>_A+S_Ok, is Poisson distributed with parameter (T^<k>_A+T_Ok)lθ/2.

Appendix B

We compute the likelihood L_S(θ,Q,T) as follows:

where G_i is a genealogy simulated from . For each genealogy, we store the values of T_D, T_O, and T_A, which are the total branch lengths that contribute to S_D, S_O, and S_A, respectively. Given the genealogy and, therefore, these times, S_D, S_O, and S_A are independent Poisson random variables with parameters T_Dlθ/2, T_Olθ/2, and T_Alθ/2, respectively. Thus, we have

Because of independence, the term in the numerator of equation (B1) is given by

The first two terms on the right-hand side of equation (B2) are simple Poisson probabilities, and the third term is just the sum of these over a range of values:

Appendix C

To save space, let C represent the condition Z⩾S_A+S_O⩾2, and let . We compute the likelihood as follows:

where, again, Ψ denotes the set of all possible genealogies with branch lengths. The steps above rely on the fact that conditioning on the genealogy of the sample makes S_D, S_O, and S_A independent and Poisson distributed with respective parameters T_Dlθ/2, T_Olθ/2, and T_Alθ/2 defined by the genealogy. Again, G_i is a genealogy simulated from P(G|Ω^*). As above, we can compute each of the terms in equation (C1) easily; for example, P(S_D|Ω^*,G_i) and P(S_O|Ω^*,G_i) are again simply Poisson probabilities, with parameters T_Dlθ/2 and T_Olθ/2. Also, the term P(C|S_O,Ω^*,G_i) is identical to equation (B3).

Last, it follows from the Poisson mutation process that, given that a mutation occurs, the place where it occurs is uniformly distributed among the branches in the genealogy, in proportion to their lengths. Therefore, we have

where t⁽ⁱ⁾_D and t⁽ⁱ⁾_O are the total length of branches, in the genealogy, on which a mutation would produce polymorphic-site patterns X⁽ⁱ⁾_D and X⁽ⁱ⁾_O, respectively. The terms t⁽ⁱ⁾_D/T_D and t⁽ⁱ⁾_O/T_O in equation (C2) are the probabilities that a mutation that has occurred in the genealogy has occurred on a branch corresponding to the patterns X⁽ⁱ⁾_D and X⁽ⁱ⁾_O.