Molecular origin of time-dependent fluorescence shifts in proteins

Abstract

Time-resolved fluorescence spectroscopy is used increasingly to probe molecular motions at the aqueous interfaces of biological macromolecules and membranes. By recording the time variation of the fluorescence frequency, thermal atomic fluctuations in the vicinity of the chromophore can be probed. From such fluorescence Stokes shift (FSS) experiments, it has been inferred that water motions in the hydration layer are slowed down by 1–3 orders of magnitude. To provide a more secure foundation for the interpretation of FSS data, we use molecular dynamics simulations to examine the molecular origin of the FSS from a tryptophan residue in a protein. By using linear response theory to decompose the FSS into its water and protein components, we find that the water component dominates the static FSS but decays rapidly. Thus, after a few picoseconds, the FSS essentially reflects protein dynamics, including the self-motion of the chromophore. Because of its collective nature, the FSS response is insensitive to the motion of individual water molecules. Collective water displacement by slowly fluctuating protein groups introduces a long-time tail in the water autocorrelation function, but this dynamic coupling is hardly manifested in the observed FSS. Our analysis reconciles FSS data with the picture of a highly dynamic hydration layer, derived mainly from magnetic relaxation dispersion and simulation studies, and calls for a revision of previous interpretations of FSS decays in terms of slow hydration dynamics at biomolecular and other interfaces.

Time-resolved optical spectroscopy is a powerful tool for investigating chemical dynamics in condensed phases (1, 2). For example, fluorescence up-conversion spectroscopy (3) with subpicosecond resolution has provided detailed insights about polar solvent relaxation after electronic rearrangement in a solute chromophore (4, 5). In recent years, this dynamic fluorescence Stokes shift (FSS) technique and the related photon echo technique have been applied increasingly to proteins (6–8). The FSS essentially reports on the electrostatic potential sensed by the altered charge distribution. For a protein-bound chromophore, the sources of this potential are nearby water molecules and charged or polar protein groups. In general, the relative importance of the water and protein contributions is not known a priori, leading to ambiguity in the interpretation of FSS data.

Neglecting the protein contribution, some investigators have used the FSS as a probe of protein hydration dynamics (9–11). FSS data have thus been interpreted in terms of a model that relates the long-time decay of the collective FSS response to the mean residence time of individual water molecules in the hydration layer (11–13). The same approach has been used to study the hydration dynamics of nonnative proteins (14, 15), DNA (16), micelles, microemulsions, and membranes (17–20). The general conclusion from these FSS studies is that the diffusive motions of water molecules hydrating biological macromolecules or surfactant aggregates is dramatically slowed down as compared with bulk water, typically by 1–3 orders of magnitude. This conclusion is at variance with magnetic relaxation studies of the same types of system (21, 22). In particular, magnetic relaxation dispersion (MRD) measurements have shown that the vast majority of the water molecules interacting with a protein surface are slowed down in their diffusive motions by a mere factor of 2–3 as compared with bulk water, similar to the hydration of small organic molecules. The MRD results are consistent with molecular dynamics (MD) simulation studies of aqueous proteins (23–25).

The diverging pictures of protein hydration dynamics emerging from FSS studies on the one hand and from MRD and MD studies on the other hand led us to reconsider the molecular origin and interpretation of the dynamic FSS in proteins. We have thus performed nanosecond MD simulations of the protein monellin, the single Trp residue of which has recently been used as a FSS probe of hydration dynamics (10). The detailed information about interactions and dynamics provided by the MD trajectory allows us to unambiguously dissect and analyze the time correlation function probed by the FSS experiment.

Methods

Simulations. The program charmm (26) with the all-hydrogen parameter set (Version 22; ref. 27) was used for MD simulations at 300 K of the 95-residue, two-chain protein monellin, embedded in a 28-Å radius sphere of TIP3P (28) water. The spherical geometry was imposed by a stochastic deformable boundary potential (29). Water molecules in the 26- to 28-Å shell were propagated by using a Langevin integrator with a friction coefficient of 50 ps^–1 on the water oxygens. Bonds to hydrogens were constrained with the SHAKE algorithm (30), allowing a 2-fs time step in the leap-frog integration. Spherical force-shift truncation (31, 32) with 12-Å cutoff was applied. The nonbonded list was generated up to 14 Å and was updated whenever any atom had moved >1 Å. The initial configuration of the protein was taken from the crystal structure with Protein Data Bank ID code 4MON (33). Two trajectories were generated, 5.2 ns with ground-state charges for Trp-3 and 2.4 ns with excited-state charges. The analysis was based on 5.0 and 2.0 ns, respectively. For reference purposes, we also analyzed a 1.0-ns equilibrated trajectory of zwitterionic l-Trp in TIP3P water at 300 K, taken from a previous MD simulation (34).

Excited-State Charges for Trp-3. The ¹L_a excited state of the indole ring, which is the fluorescing state of Trp in proteins (35), is highly polarizable, with a dipole moment ranging from ≈5.6 D in nonpolar solvents or in gas phase to 7–12 D in polar environments (36–38). A minimal modification, similar to that proposed by Smolyar and Wong (36), of the ground-state partial charges in the charmm22 Trp model (27) involves four atoms, which in our representation of the ¹L_a electronic structure were assigned the following charges (in units of e, with ground-state charges within parentheses): C^γ, 0.10 (–0.03); N^ε1, –0.37 (–0.61); C^ε3, –0.44 (–0.115); C^ζ2, –0.16 (–0.115). These charges result in a dipole moment of 7.9 D for the indole ring in the direction of the ¹L_a transition moment.

Analysis. The relevant time correlation function (TCF), C(t) = 〈ΔE(t)ΔE(0)〉 – 〈ΔE〉², was computed from the MD trajectories with a resolution of 0.2 ps. We model ΔE as a sum of Coulomb interactions (39) between pairs of charges in the chromophore (index α) and in the environment: ΔE(t) = Σ_αΔq_αφ_α(t), where Δq_α is the change in the partial charge of chromophore atom α upon excitation and φ_α is the electrostatic potential at atomic site α, produced by all partial charges in the environment. The TCFs C₀(t) and C₁(t) were obtained in this way by using trajectories with Trp-3 ground-state and excited-state charges, respectively. The computed TCFs were subjected to Levenberg–Marquardt χ² minimization with the model function

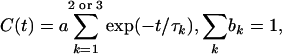[1]

with a = 1 for the reduced TCF C(t)/C(0). Parameter errors were propagated from standard deviations in C(t), estimated from the Zwanzig–Ailawadi formula (40), which was found to be consistent with errors deduced from 10 block averages.

Results and Discussion

Theory. The dynamic FSS, Δν(t), is defined as the difference in the frequency, ν(t), of the maximum in the fluorescence emission spectrum, measured a time t after excitation, and the same frequency measured at steady state (t → ∞)

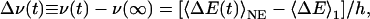[2]

where h is Planck's constant and ΔE = E₁ – E₀ is the difference between excited-state and ground-state chromophore–environment interaction energies, here assumed to be purely electrostatic. Further, 〈ΔE(t)〉_NE represents a nonequilibrium ensemble average, where the environment is initially equilibrated in the presence of ground-state charges and then (t > 0) evolves in the presence of excited-state charges. This time-dependent ensemble average evolves from the initial (t = 0) value 〈ΔE〉₀ to the final (t → ∞) value 〈ΔE〉₁, which are equilibrium ensemble averages with the chromophore in the ground (0) or excited (1) state, respectively. The static FSS, Δν(0) = ν(0) – ν(∞), is thus [〈ΔE〉₀ – 〈ΔE〉₁]/h. The dynamic FSS is usually reported in normalized form as (1, 2)

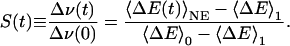[3]

The response function S(t) describes the collective relaxation of the environment after an initial charge rearrangement in the chromophore.

The use of the dynamic FSS for probing hydration dynamics (spontaneous equilibrium fluctuations) rests on the linear response approximation (LRA). The LRA links the nonequilibrium response function S(t) to the equilibrium TCF, C(t), of the fluctuation ΔE(t) – 〈ΔE〉 through the fluctuation-dissipation theorem (41–43)

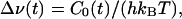[4]

where k_B is Boltzmann's constant and T the temperature. The TCF C₀(t) describes spontaneous fluctuations in an environment that is in equilibrium with ground-state chromophore charges. If the unperturbed reference state for the LR expansion is chosen as the excited (rather than ground) state, one obtains the fluctuation-dissipation theorem in an alternative form (43), with C₀(t) in Eq. 4 replaced by the excited-state TCF C₁(t). Combination of these two relations yields C₀(t) = C₁(t) to linear order in ΔE/(k_BT).

The electrostatic potential at chromophore site α is produced by partial charges on protein atoms (P) and water molecules (W). At any instant, it can therefore be decomposed uniquely as 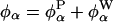. It follows from Eq. 2 that the dynamic FSS can be decomposed likewise as Δν(t) = Δν^P(t) + Δν^W(t), where (Z = P or W)

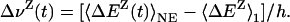[5]

By setting t = 0 and noting that 〈ΔE^Z(0)〉_NE = 〈ΔE^Z〉₀, this relation allows us to compute the protein and water components, Δν^P(0) and Δν^W(0), of the static FSS. To obtain the corresponding components of the dynamic FSS Δν(t) from our equilibrium MD trajectories, we must make use of the fluctuation-dissipation theorem, Eq. 4. The proper decomposition of the TCF C₀(t) follows from the generalized fluctuation-dissipation theorem for a composite perturbation (41). We thus find that

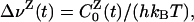[6]

where we have introduced the partial TCFs

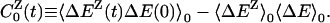[7]

Furthermore, we find that

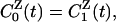[8]

with 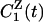defined in analogy with 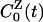. The protein and water components of the measured dynamic FSS thus are associated with the partial TCFs in Eq. 7, rather than with the autocorrelation functions 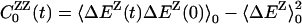. The latter do not obey a linear response relation like Eq. 8. Although essential for a correct decomposition of the FSS from equilibrium MD simulations, the relations in Eqs. 6–8 do not appear to have been used previously.

As demonstrated below, the LRA is valid to a good approximation for Trp-3 in monellin. We therefore can combine the ground-state and excited-state trajectories to obtain total and partial TCFs with less statistical noise. In the following, this additional averaging is indicated by omission of the 0/1 subscript. To simplify the notation, we use the same symbol, S(t), for the normalized response function as for the reduced TCF, C(t)/C(0). In the LRA, these quantities are equal. Thus, for example, the protein component of the reduced TCF computed from the ground-state trajectory, 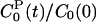, is denoted by .

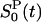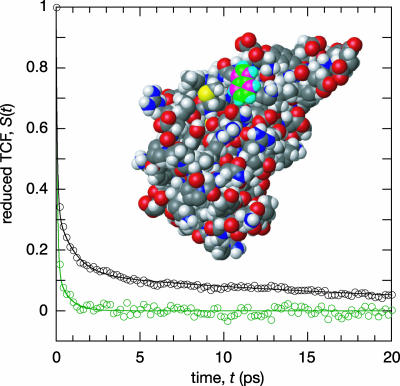
Total FSS Decay for Trp in Water and Protein Environments. Fig. 1 shows the reduced TCF, S(t), computed from MD trajectories for zwitterionic Trp and for Trp-3 in monellin. For free Trp, S(t) is well described by a biexponential decay function (see Eq. 1) with a major inertial component (b₁ = 0.86 ± 0.04; τ₁ = 70 ± 10 fs) and a minor diffusive component (b₂ = 0.14 ± 0.04; τ₂ = 0.7 ± 0.2 ps). Bearing in mind that the TIP3P water model yields somewhat too fast dynamics (44, 45), the diffusive correlation time agrees well with the experimental result, 1.2 ps, at pH 7.5 (5). As expected, a similar analysis of an MD trajectory for Trp in SPC/E water (34) yields the same τ₁ but a slightly longer τ₂ of 1.0 ± 0.1 ps (see Fig. 3, which is published as supporting information on the PNAS web site). If the excited chromophore is modeled as a point dipole in a spherical cavity embedded in a uniform dielectric medium, τ₂ becomes the dipolar longitudinal relaxation time (46), τ_μ = [(2ε_∞ + 1)/(2 ε₀ + 1)]τ_D, which is 0.6 ps for bulk water at 298 K. Compared with the 1.2-ps experimental decay time for free Trp, the 0.6-ps model estimate obtained with bulk water parameters indicates that the diffusive motions of water molecules interacting with Trp are about a factor of 2 slower than in bulk water. This conclusion is in agreement with ¹⁷O magnetic relaxation results for small organic solutes (ref. 21 and references therein). The ultrafast component of S(t), which is not fully resolved in dynamic FSS experiments (5), mainly reflects librational motions, and the initial (<0.2 ps) decay is expected to be Gaussian with superimposed damped oscillations (4). Because we focus on the diffusive processes here, we have not attempted to characterize in detail this inertial component.

Fig. 1.

Reduced TCF, S(t) = C(t)/C(0), for zwitterionic Trp (green symbols and curve) and for Trp-3 in monellin (black), both in aqueous solution at 300 K. The two curves represent a biexponential fit to the data range 0–2 ps (free Trp) and a triexponential fit to the data range 0–20 ps (monellin). The crystal structure with Protein Data Bank ID code 4MON of monellin (33) is shown with the atoms of the indole ring of Trp-3 color-coded as follows: green, C atoms; cyan, H atoms; magenta, atoms with modified partial charges in the excited state.

We now turn to the more slowly decaying TCF for Trp-3 in monellin (Fig. 1). Just as for free Trp, S(t) exhibits a dominant ultrafast decay (b₁ = 0.66 ± 0.02; τ₁ = 70 ± 10 fs), but the diffusive decay is now much slower. At least two diffusive correlation times are required, but their values depend to some extent on the data range included in the fit. From the data range 0–20 ps, we obtain b₂ = 0.22 ± 0.02, τ₂ = 1.0 ± 0.1 ps, and b₃ = 0.12 ± 0.01, τ₃ = 23 ± 2 ps, but an asymptotic analysis yields a longer correlation time (see below). The experimental S(t) for monellin was modeled by two exponential components of equal amplitude and with time constants of 2 and 16 ps (10), similar to our correlation times τ₂ and τ₃. Because of the finite instrumental response time, 0.5 ps in the monellin study (10), the true zero-time emission spectrum needed to obtain ν(0) in Eq. 3 cannot be measured directly (47). This limitation is particularly severe in aqueous solutions, where the inertial response is exceptionally fast (4). For this reason, the experimental amplitudes cannot be compared with the simulated ones. Nevertheless, both experiment and simulation exhibit a diffusive decay on the 10- to 100-ps time scale for Trp-3 in monellin.

In the experimental FSS study of monellin (10), and in similar studies of other proteins (11, 12, 15), the slow diffusive decay was attributed entirely to water dynamics. The profound implication of this interpretation is that water molecules interacting with protein surfaces are motionally retarded by 1–2 orders of magnitude as compared with bulk water. As noted above, this interpretation contradicts MRD (20, 21) and MD (23–25) studies, showing that the vast majority of water molecules in the protein hydration layer are dynamically similar to water molecules interacting with small solutes. To resolve this issue, we shall use the MD simulation to dissect the dynamic FSS from monellin. First, however, we consider the static FSS and the LRA.

Static FSS and Linear Response. The static FSS, Δν(0), can be obtained directly from equilibrium ensemble averages of ΔE, computed from ground-state and excited-state trajectories. These and other averages used in this section are collected in Table 1. For Trp-3 in monellin, we thus obtain Δν = 3,200 cm^–1. Because the experimental FSS response function misses most of the ultrafast inertial decay, the measured value, Δν(0) = 960 cm^–1 (10), is much smaller than the simulated one. Indeed, the experimental value agrees much better with the simulated diffusive FSS, Δν_diffusive(0) = (1 – b₁)Δν(0) = 1,090 cm^–1, obtained by subtracting the ultrafast contribution. This comparison should not be affected significantly by vibrational relaxation in the chromophore, because both the experimental (with 0.5-ps instrument response time) and the simulated static FSS refer to vibrationally relaxed states.

Table 1. Equilibrium ensemble averages for Trp-3 in monellin.

Quantity	Ground state	Excited state
〈ΔE〉	-6.15	-15.32
〈ΔEP〉	-4.38	-6.80
〈ΔEW〉	-1.77	-8.52
C(0)	5.39	5.08
CPP(0)	9.36	4.56
CWW(0)	11.38	7.06
CX(0)	-15.35	-6.54
CP(0)	1.68	1.29
CW(0)	3.71	3.79

These averages were computed with 0.4-ps resolution in the MD trajectories. The units are kcal·mol^-1 for ΔE and kcal²·mol^-2 for the initial TCFs.

The steady-state emission FSS (relative to the isolated chromophore), Δν_em = –〈ΔE〉₁/h, is readily accessible by experiment. The experimental wavelengths are λ₀ = 295 nm and λ(∞) = 342 nm (10, 38), corresponding to Δν_em = 4,660 cm^–1. With 〈ΔE〉₁ from the excited-state MD trajectory (Table 1), we obtain 5,360 cm^–1, 15% above the experimental value. This result indicates that our simple model for the excited-state charge distribution is sufficiently accurate for our purposes.

If the LRA is valid, the static FSS also can be computed from the initial value of the TCF (Eq. 4 with t = 0). By using the ground-state and excited-state trajectories, we thus obtain Δν(0) = 3,160 and 2,980 cm^–1, respectively (Table 1). These values are merely 1.4% and 7.1%, respectively, smaller than the static FSS computed directly from Eq. 2 (with t = 0), demonstrating that the LRA is an excellent approximation for Trp-3 in monellin. This result is in line with previous experience. Whereas significant deviations from LRA behavior have been documented for small solutes with sizeable variations in atomic charges (42, 43, 48), the LRA is expected to be more accurate for chromophores, like Trp, with relatively large size and modest charge variations (39, 49, 50).

Trp-3 resides at the protein surface with one face and one edge of the indole ring exposed to water (Fig. 1). The solvent-accessible area is reduced from 240 Ų for the free indole to 110 Ų in monellin. Hence, it is reasonable to suppose that a large part of the FSS is due to interactions between the chromophore and its highly polarizable hydration shell. Indeed, by using Eq. 5 with t = 0, we find that 74% of the static FSS, Δν(0) = 3,200 cm^–1, is due to interactions with water molecules. If the LRA is valid, the static FSS also can be decomposed with the aid of Eq. 6 with t = 0. This equation yields values for Δν^P(0) that are 16% larger (ground state) or 10% smaller (excited state) than the value computed directly from Eq. 5. For the water component the corresponding figures are 8% smaller (ground state) and 6% smaller (excited state). We therefore conclude that the LRA is a useful approximation, not only for the total FSS, but also for its protein and water components. This conclusion also can be drawn directly from Table 1. The total and partial zero-time TCFs C(0), 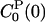, and 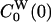satisfy the LRA relation, Eq. 8, to a good approximation. In contrast, the auto-TCFs 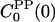and 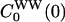as well as the cross-TCF 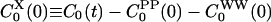differ greatly between the ground- and excited-state simulations.

With the aid of Eq. 6, we also can dissect the static FSS for free Trp. The protein component then refers to the interaction of the altered charges in the indole ring with the f lexible –CH₂CH(COO^–)NH⁺₃ moiety. In this way we find that the water contribution to the static FSS is 92% (or 94% for the SPC/E water model). As expected, interactions with water make a larger contribution for free Trp than for the partly exposed Trp-3 in monellin.

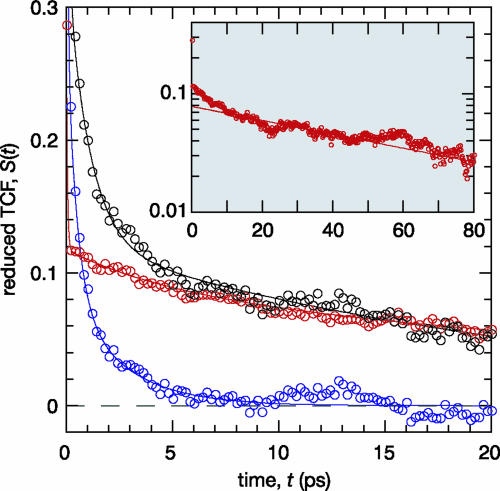
Decomposition of the Dynamic FSS. Fig. 2 shows the reduced TCF S(t) for Trp-3 in monellin along with its protein and water components, S^P(t) and S^W(t). Whereas the water component dominates the static FSS (71 ± 1% from the fit in Fig. 2), it decays much more rapidly than the protein component. As a result, S(t) essentially reports on chromophore–protein interactions after ≈5 ps. A triexponential fit to the water component S^W(t) in the range 0–8 ps yields a dominant inertial decay with b₁ = 0.59 ± 0.04 and τ₁ = 50 ± 20 fs. As compared with free Trp, the librational correlation time does not differ significantly, but the relative amplitude is smaller, indicating stronger orientational constraints on water molecules hydrating the protein-bound Trp. The diffusive decay is modeled by two components with b₂ = 0.29 ± 0.04, τ₂ = 0.5 ± 0.1 ps, and b₃ = 0.12 ± 0.02, τ₃ = 2.5 ± 0.3 ps. An amplitude-weighted average of the two diffusive components yields an effective (integral) correlation time of 1.5 ps, a factor of 2 longer than for free Trp. (A biexponential fit yields a diffusive correlation time of 1.6 ± 0.7 ps, but the reduced χ² is four times higher than for the triexponential fit.)

Fig. 2.

Decomposition of the total reduced TCF, S(t) (black symbols and curve), into partial TCFs corresponding to the protein, S^P(t) (red), and water, S^W(t) (blue), components of the FSS response function. The curves represent triexponential fits to the data range 0–8 ps (water) or 0–20 ps (protein and total). Inset shows a semilogarithmic plot of the protein component on a wider time scale, and the line corresponds to the longest decay time (74 ps) deduced from a biexponential fit to the data range 5–150 ps.

The protein component S^P(t) differs qualitatively from the water component (Fig. 2). The initial value is much smaller, accounting for only 29 ± 1% of the total FSS. Moreover, although the inertial decay is similar to that in S^W(t), the diffusive decay beyond 0.2 ps is much slower. A biexponential fit in the range 0–8 ps, as for S^W(t), yields b₁ = 0.60 ± 0.02, τ₁ = 50 ± 30 fs and b₂ = 0.40 ± 0.02, τ₂ = 20 ± 2 ps. However, when S^P(t) is analyzed over a wider time interval it becomes clear that the diffusive tail must be described by several correlation times. The shortest of these times is ≈5 ps and the longest, determined from a biexponential fit (see Fig. 2 Inset) to data in the range 5–150 ps, is 74 ± 4 ps. This correlation time must be attributed to protein conformational fluctuations in the neighborhood of Trp-3. As expected, the total S(t) exhibits a similarly slow asymptotic decay.

The energy fluctuations probed by the FSS experiment are caused by variations in the relative positions of chromophore atoms and surrounding atoms. It is therefore not possible to distinguish the motions of nearby water molecules or protein atoms from the motion of the chromophore itself. For example, a wobbling motion of the indole ring might produce large fluctuations in 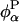without much effect on 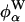(if the hydration shell on the exposed side is intact). If this type of self-motion contributes to the slow decay of S^P(t), then the fluorescence anisotropy, r(t), of Trp-3 should decay on a similar time scale. A single-exponential fit to the experimental r(t) for Trp-3 in monellin yields a decay time of 55 ps (10), whereas a triexponential fit to the simulated anisotropy decay yields correlation times of 0.6, 7, and 60 ps and a plateau value of 0.78 ± 0.01 (see Fig. 4, which is published as supporting information on the PNAS web site). The similarity of the longest correlation times in S^P(t) and r(t) raises the possibility, but does not prove, that self-motion of the indole ring makes a major contribution to the slow diffusive decay of the FSS response function S(t). Such a scenario was invoked in a recent MD simulation of the dynamic FSS for a coumarin dye at the aqueous interface of solid zirconia (50). In the experimental FSS study of monellin, the longest fitted decay time in the response function S(t) was 16 ps (10). However, a longer decay time would have been obtained in a triexponential fit or if S(t) were not forced to zero prematurely by equating ν(∞) with the observed ν(t) at t = 120 ps (10).

Hydration Dynamics. The present MD analysis demonstrates that, at least for Trp-3 in monellin, the long-time FSS decay reflects protein dynamics rather than motions of water molecules in the hydration layer. In contrast, Bagchi and coworkers (51) recently presented an MD analysis of a 36-residue protein fragment that was taken to support the hypothesis (10–16) that the long-time FSS decay reflects slow water motions. To understand why the two MD studies lead to different conclusions, two interrelated issues must be addressed, (i) the decomposition of the FSS into protein and water parts, and (ii) the interpretation of the water component in terms of molecular motions.

Regarding the first issue, we note that Bagchi et al. (51) focus on the auto-TCFs C^PP(t) and C^WW(t). However, as we have shown here, it is the partial TCFs C^P(t) and C^W(t) that correspond (in the LRA) to the protein and water components of the FSS. The water–water auto-TCF C^WW(t) also exhibits a long-time tail in our monellin simulation, but this fact does not imply a correspondingly slow motion of individual water molecules in the hydration layer. To understand the physical basis of this important distinction, consider the limiting case of infinitely fast hydration dynamics, where the hydration adjusts instantaneously during the slow diffusive motion of a solvent-exposed side chain or of the chromophore itself. If the water is described as a dielectric medium with relative permittivity ε_W, then φ^P_α = ε_Wφ_α and φ^W_α = (1 – ε_W)φ_α. It is readily shown that for this limiting model S^PP(t) = ε²_WS(t), S^WW(t) = (ε_W – 1)²S(t), and S^X(t) = –2ε_W(ε_W – 1)S(t). For ε_W ≫ 1, this model thus predicts that S^PP(t) ≈ S^WW(t) and that S^X(t) ≈–2S^PP(t). The simulation data conform surprisingly well to this crude model (see figure 3 of ref. 51, where the cross-TCF is displayed as S^X(t)/2), suggesting that the long-time decay of the simulated S^WW(t) results from collective water displacement by slowly moving protein residues rather than from slow motions of individual water molecules. It also should be noted that the simulation in ref. 51 involves a substantial perturbation: all partial charges of polar amino acids were switched from zero to their full values. Such a large perturbation may violate the LRA and does not necessarily provide a faithful model for the FSS of a real chromophore.

The second fundamental issue concerns the interpretation of the water component of the dynamic FSS. Experimental FSS data from proteins and other biomolecules (10–16) have been interpreted in terms of a model (11–13) that links the long-time FSS decay to the residence times (inverse exchange rates) of water molecules in the hydration layer. We refer to this model as the Bagchi–Zewail (BZ) model. In the development of the BZ model, the energy ΔE(t) is formally expressed as a space and orientation integral of a time-dependent density or propagator, ρ(r, Ω, t) (12). This quantity embodies the full complexity of the collective many-body dynamics in the system and its evolution involves pairwise and higher particle correlations that can only be handled approximately (52). In the BZ model, ρ(r, Ω, t) is replaced by the single-particle propagator, ρ_S(r, Ω, t). This approximation amounts to a complete neglect of correlations between different particles. The model then assigns the water molecules to two (or three) discrete states, in which case the single-particle propagator obeys an exchange-rotation equation of the stochastic Liouville type widely used in connection with magnetic relaxation (53, 54). If, as assumed in the BZ model, the “bound” water molecules are rotationally immobilized and if they exchange slowly with the other water molecules, then the two time constants of the two-state model correspond to the rotational correlation time of “nonbound” water molecules and to the mean residence time of bound water molecules (53). In the BZ model, these time constants are identified with the two decay times obtained from a biexponential fit to the measured FSS response function (10–16).

To see the problem with the BZ model, consider a hydration site with a long residence time, say 100 ps. According to the BZ model, exchange of bound water molecules out of such sites will give rise to a 100-ps decay time in the FSS response function, S(t). However, S(t) probes the collective response of the system (1, 42) and does not (like magnetic relaxation, for example) reflect the diffusional trajectories of individual water molecules (or protein atoms). In other words, S(t) depends on the probability [related to ρ(r, Ω, t)] of finding any bound water molecule in the hydration site at time t, rather than the probability [related to ρ_S(r, Ω, t)] that a particular water molecule remains in that site. Because the hydration site will nearly always be occupied by some water molecule (with reproducible mean orientation), except for the brief duration of the actual exchange event (assumed to be negligibly short in the BZ model), it follows that S(t) is virtually unaffected by the exchange. Dynamic FSS experiments therefore cannot furnish information about the exchange kinetics (or residence times) of water molecules at protein surfaces. The spurious prediction of the BZ model stems from the neglect of the particle correlations that maintain an essentially uniform water density in the space outside the protein. The same neglect underlies the inappropriate description of protein hydration as a thermodynamic binding equilibrium, where the free energy difference determines the relative populations of “free” and bound water (11, 12, 17, 18). As a result of strong intermolecular correlations, the transition of a water molecule from the bound to the free state is invariably accompanied by a reverse transition of another water molecule. In other words, we are dealing with a symmetric exchange process for which the equilibrium constant is trivially equal to one.

Concluding Remarks

Certain types of experiment, like ¹⁷O MRD (21, 22), furnish direct information about water dynamics because they probe the diffusional trajectories of individual water molecules by means of the single-particle TCF. In contrast, the energy relaxation probed by a dynamic FSS experiment reflects the collective fluctuations of the complete environment of the chromophore. It is therefore not straightforward to assign FSS decay times to particular modes of molecular motion. In the interfacial region, diffusive protein motions must be strongly coupled to water motions. The energy fluctuations probed by an interfacial probe therefore tend to be compensating in the sense that the protein and water contributions, 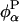and 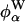, to the electrostatic potential fluctuate with larger amplitude and slower rate than does their sum. The dynamic coupling that results from water displacement by a diffusing part of the protein persists even if the water molecules move at infinite rate, as illustrated by the dielectric continuum model considered above. This dynamic coupling, which is ignored in the BZ model (11–13), introduces a trivial long-time decay in the water auto-TCF C^WW(t), which is absent, or strongly suppressed, in the water component C^W(t) of the dynamic FSS. This behavior is clearly evident in the initial values of the TCFs for Trp-3 in monellin (Table 1).

Our simulation-based decomposition of the dynamic FSS into its protein and water components indicates that the slow decay observed for Trp-3 in monellin (10) is due to protein, rather than water, motions. A similar MD analysis of the eight Trp residues in α-chymotrypsin (data not shown) fully supports the qualitative picture emerging from the monellin simulation. Because the hydration layer of proteins and a wide variety of other macromolecules and molecular aggregates has been found to be highly mobile (20, 21), it seems likely that, in all of these systems, the FSS will exhibit a rapidly decaying water component and long-time tail due to macromolecule dynamics. The interpretation of FSS decays in a wide range of systems in terms of slow water dynamics (9–20) therefore needs to be revised.

The present analysis reconciles the published FSS data with the picture of a highly mobile hydration layer that has emerged from recent MRD and MD studies. MRD experiments show that, at ambient temperature, nearly all water molecules in the hydration layer of a protein are dynamically similar to the hydration water of small organic molecules, being slowed down by about a factor of 2 as compared with bulk water (21, 22). Consistent with this finding, the water component of the simulated FSS for the protein-bound Trp has an effective diffusive correlation time of 1.5 ps, not much longer than the value of 0.7 ps found for free Trp. MD simulations of water molecules near protein surfaces have yielded similarly small rotational retardation factors (23–25) and our own MD results for monellin (data not shown) conform to this well-established picture. Rotational TCFs averaged over the complete hydration layer of a protein show a long-time (power-law) tail (23–25). The dominant contribution to this tail comes from translationally mediated rotation through exchange of a small number of more strongly retarded water molecules, typically located in surface pockets (21, 22), and from diffusive randomization of the local anisotropy induced by the protein surface (24). Such weak long-time tails should therefore not be taken as evidence for a large rotational retardation for the majority of water molecules in the hydration layer.

The FSS technique has been extensively used to study solvent relaxation in response to an abrupt charge rearrangement in a solute chromophore (1, 2). For this reason, the method itself has come to be known as “solvation dynamics.” This practice is misleading when the chromophore is attached to a protein, in which case some authors even refer to the response function S(t) as the “hydration correlation function.” The findings of the present study, which can be summarized as “solvation ≠ hydration,” suggest that a more neutral terminology is preferable. In fact, the broader implications of this work are that, even for solvent-exposed chromophores, the long-time decay of the FSS is a valuable probe of the collective conformational dynamics of proteins and other biological macromolecules.