Abstract
In response to charge separation or transfer, polar liquids respond in a simple linear fashion. A similar linear response for proteins might be expected from the central limit theorem and is postulated in widely used theories of protein electrostatics, including the Marcus electron transfer theory and dielectric continuum theories. Although these theories are supported by a variety of experimental data, the exact validity of a linear protein dielectric response has been difficult to determine. Molecular dynamics simulations are presented that establish a linear dielectric response of both protein and surrounding solvent over the course of a biologically relevant electron transfer reaction: oxido-reduction of yeast cytochrome c in solution. Using an umbrella-sampling free energy approach with long simulations, an accurate treatment of long-range electrostatics and both classical and quantum models of the heme, good agreement is obtained with experiment for the redox potential relative to a heme–octapeptide complex. We obtain a reorganization free energy that is only half that for heme–octapeptide and is reproduced with a dielectric continuum model where the heme vicinity has a dielectric constant of only 1.1. This value implies that the contribution of protein reorganization to the electron transfer free energy barrier is reduced almost to the theoretical limit (a dielectric of one), and that the fluctuations of the electrostatic potential on the heme have a simple harmonic form, in accord with Marcus theory, even though the fluctuations of many individual protein groups (especially at the protein surface) are anharmonic.
Chemical events in proteins often involve charge separation or transfer: enzyme reactions, photoexcitation of bound chromophores, proton binding and release, and electron transfer (1, 2). In response to such an event, the protein and solvent undergo dielectric relaxation, or reorganization, in the form of electronic polarization and displacement of atomic groups. Thus, enzyme reaction rates and driving forces are sensitive to the dielectric properties of the active site (3). An important goal in biophysics is to find models that can describe the dielectric properties of proteins (3–7). In the case of small molecules in aqueous solution, simple behavior is observed: the reorganization of the solvent is approximately a linear function of the solute charge rearrangement (8–12). This is consistent with simple models, like the dielectric continuum model (4, 13), or a model where the solvent fluctuations are assumed to be gaussian (14–16).
Proteins are much more complex. They are heterogeneous polymers, and fluctuations around their folded structure are governed by an anharmonic, rugged energy surface (17, 18). The average polarity and flexibility of a folded protein are much lower than those of water, so the dielectric properties vary strongly across the protein–solvent interface. Recent experimental studies have used spectroscopic probes (19–23) whose optical absorption and emission are sensitive to the dielectric properties of the environment. Reorganization energies for intra- and interprotein electron transfer have also been measured (1, 24). The validity of linear response models has been examined; thus, a gaussian density of electron donor states was observed in cytochrome c over a ∼1-eV energy range (25), whereas deviations from a linear response were observed in a calmodulin–coumarin complex, in the form of differences between ground and excited state dynamics (23). However, the experimental interpretation is rarely straightforward; for example, these approaches often involve chemical modifications of the protein or non-native probes that can produce structural or dynamical changes. It is also difficult to separate the protein response from the large solvent contribution and to detect nonlinearities in the former. Thus, photon echo spectroscopy data for lysozyme can be reproduced with several models that use very different descriptions of the protein dielectric properties (21).
Molecular dynamics (MD) simulations are an increasingly powerful complementary approach. Time-dependent relaxation (26–30), electron transfer rates (27, 31), reorganization free energies (32–36), and redox potentials (37) have been calculated. However, because of simulation costs, and because fully reliable treatments of long-range electrostatic interactions are relatively recent (3, 38–40), it has been difficult to study the dielectric response of fully solvated proteins to high accuracy and precision over long time periods. Thus, although pioneering early studies examined the shape of electron or proton transfer free energy curves (27, 41), these and other studies assumed the validity of linear response for all (5, 32–34, 42) or part (27, 35–37, 41) of the system (usually a spherical region surrounded by a dielectric continuum or a lattice of polarizable dipoles). Several relied on approximate electrostatic treatments (e.g., truncation) (32, 43). Only a few used a large explicit solvent region (>20-Å radius) (27, 40, 41) and/or tested the dependency of the results on model size (40, 44).
Here, simulations are reported that directly verify the linear response of a solvated protein over the course of a biologically meaningful charge transfer reaction, oxido-reduction of the electron transfer protein cytochrome c (Cyt c) from yeast. Cyt c plays an important role in respiration (45); it has potential applications in bioelectronics (46), and was recently shown to play a role in protein–protein signaling and apoptosis (47). It is the experimental standard for studies of biological electron transfer (24, 45) and has served as a model for studies of protein folding and dynamics. X-ray and NMR structures are available (48–52), along with a wealth of biochemical and biophysical information (45, 53).
Cyt c reduction is modeled here by gradually inserting a charge −e on the heme (in the form of atomic partial charges). Using an umbrella-sampling free energy technique (9, 41), a large model of the fully solvated protein, an accurate electrostatic treatment, long MD simulations (23 ns total), and both classical and path integral quantum mechanical (27, 43, 54, 55) treatments of the heme, it is shown that the free energy is a parabolic function of the inserted charge. This parabolic shape implies (see below) that the induced polarization is a linear function of the charge and that the fluctuations of the total electrostatic potential on the heme are gaussian, even though the fluctuations of many individual protein groups are strongly nongaussian (56, 57). The time dependency of the dielectric relaxation is also consistent with a linear response (see supporting information, which is published on the PNAS web site, www.pnas.org). These data lend support to interpretations of electrostatic effects in proteins with simple linear models such as continuum models (4–7, 3, 14). The reorganization free energy calculated here is low (−17.8 kcal/mol) and is reproduced with a dielectric continuum model where the heme vicinity has a dielectric constant of only 1.1, consistent with earlier work (32, 34, 37, 58). The calculated redox potential relative to a small microperoxidase-8 reference system is in good agreement with experiment (37, 59).
Methods
Linear Response Theory.
Dielectric susceptibility.
The dielectric response of a solvated protein to a perturbing charge, such as a redox electron, is related to the equilibrium fluctuations of the unperturbed system through linear response theory (60, 61), recalled briefly here (Eqs. 1–6). A perturbing charge density λρp contributes a term
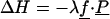 |
1 |
to the Hamiltonian,† where f is the field due to ρp, E = −4πP is the field due to the remaining charge density, and “⋅” represents the dot product between functions [∫ f(r)⋅P(r) dr, where the integration is over all space]. Let δP = P − 〈P〉0, where the brackets indicate a Boltzmann average over the unperturbed system. The Boltzmann average 〈δP〉λ over the perturbed system represents the mean microscopic density of polarization charge induced by the perturbing field λf (the “response”). From Eq. 1 and the definition of the Boltzmann average, one obtains (60, 61):
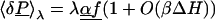 |
2 |
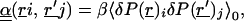 |
3 |
where β = 1/kT, k is Boltzmann's constant; T is the temperature; O(⋅⋅ ) represents quantities of first order or more in βΔH; i, j represent cartesian components x, y, or z; and α is a dielectric susceptibility operator that does not depend on λ. To lowest order in βΔH, the response scales linearly with the perturbation.
Gaussian fluctuations.
To the same order in βΔH, the free energy derivative is linear with respect to λf, and the free energy is parabolic:
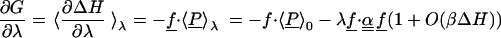 |
4 |
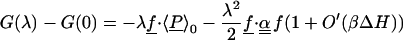 |
5 |
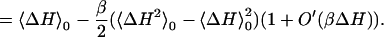 |
6 |
The last equation is the usual cumulant expansion of the free energy (63). Eqs. 1–6 are exact within classical statistical mechanics. A parabolic free energy [i.e., a negligible O′(βΔH) in Eqs. 5 and 6] implies that cumulants of ΔH of order >2 are negligible, i.e., ΔH, is a gaussian random variable, and also that 〈δP〉λ in Eq. 2 is linear. Conversely, if ΔH is gaussian, its higher cumulants are zero, and the free energy is a parabolic function of λ (15). Under these conditions, the free energy is also a parabolic function of ΔH itself, motivating the use of ΔH as a reaction coordinate to describe electron transfer (4, 8, 27, 29). Thus, a parabolic free energy, a linear free energy derivative, a gaussian ΔH, and the linearity of 〈δP〉λ are strictly equivalent properties, accurate to the same order in βΔH. A sufficient condition for them to hold is for the equilibrium fluctuations of the charge density to be gaussian at all points, as in the gaussian field model (14). However, this condition is not necessary, e.g., it is not verified for Cyt c [see below, refs. 56 and 57], even though ΔH is essentially gaussian.
Reorganization free energy.
Marcus introduced a decomposition of the free energy (13) that is physically illuminating and is used below to compare the microscopic simulations to a macroscopic continuum model. The first, static free energy component ΔGstat, corresponds to the introduction of the perturbing charge with the system constrained to stay in its unperturbed structure; more precisely, the Boltzmann weights of all conformational states are kept fixed in this step. (Imposing the weaker constraint ΔH = 〈ΔH〉0 in this step leads to the same free energy decomposition.) In a second step, the constraints are released, and the system is allowed to relax, yielding a relaxation or reorganization free energy ΔGrlx. The first step is adiabatic and has zero entropy change (e.g., equations 1.16–17 of ref. 64). Therefore,
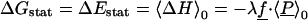 |
7 |
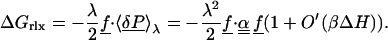 |
8 |
The static free energy measures the polarity of the system in the absence of the perturbation (through 〈P〉0); the reorganization free energy measures its polarizability.
Molecular Dynamics Setup and Free Energy Calculation.
Cyt c reduction was modeled as an insertion of point charges δqi = −0.25e on the four heme nitrogens coordinating the iron (37, 65). In the simulations, the following expression for ΔH was used (obtained by rearranging Eq. 1):
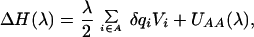 |
9 |
where A is the set of heme nitrogens, Vi is the Ewald electrostatic potential produced on atom i by atoms not in A, and UAA is the self energy of the set A, which is essentially a constant in this system (semirigid heme). The charging free energy was obtained by an umbrella-sampling approach (9, 41, 63) that gradually maps the energy function from that of the reactant state to that of the product, by varying λ (Eqs. 1 and 9) from 0 to 1. The mapping was performed in five steps or “windows,” i.e., a series of five simulations was performed (1.3–2.3 ns each; 7.7 ns total), with total inserted charges, respectively, of 0 (oxidized state), −0.25e, −0.5e, −0.75e, and −1e (reduced state). This series of simulations is referred to as “run 1.” Ionizable protein side chains were fixed in their most common protonation state at pH 7 (32); the absence of an H/D isotope effect on the electron transfer rate (66) suggests that coupling between oxido-reduction and proton binding/release is negligible (Cyt c is an electron carrier, not a proton pump). The heme propionates were assumed ionized, as in previous work (32, 34, 37). The first simulation window of run 1 was started from the crystal structure of the oxidized form (48), solvated by 6,345 water molecules (including 61 crystal waters), 5 chloride ions, and a crystal sulfate ion, placed in a 59-Å cubic box, and replicated periodically in all directions to avoid edge effects. Successive simulations were started from the configuration reached after 300–500 ps of the previous window. The charmm22 force field (protein, ions) (67) and tip3p water model (68) were used. Long-range electrostatic interactions were treated by Particle Mesh Ewald summation (38, 39); this work represents the first use of Ewald summation in a protein-charging free energy calculation. The system was maintained at room temperature and pressure by a Nosé–Hoover thermostat/barostat (69). A second series of simulations (“run 2”) was started from the endpoint of the first series and run “backwards” (red → ox). A third series (run 3) was started from the crystal structure of the reduced state and incrementally oxidized (7.7 ns total). Finally, another ox → red run (run 4) was done assuming the redox electron is entirely concentrated on the heme iron instead of on the coordinating nitrogens. Two ox → red mutation runs were also performed in the same conditions for a small reference system, a heme coordinated by an octapeptide fragment of Cyt c (MP-8) and methionine, solvated by a 59-Å box of water. The redox electron was inserted on either the heme nitrogens or the iron, as above.
Quantum Simulations.
The solvated MP-8/heme/Met complex was also simulated in its oxidized and reduced states (450 ps each) with the path integral method, which treats the nuclear degrees of freedom quantum mechanically (43, 54, 55). This technique maps the quantum system onto an equivalent classical one, where each solute atom is replicated n times, corresponding to a Trotter factorization of the system's density matrix into n equivalent pieces. The n copies of each atom (“beads”) are connected by springs and interact only with other atomic beads of the same rank. Here, only the solute was quantized, with n = 15 beads per atom; the solvent was treated classically [the effects of solvent quantization on dielectric relaxation have already been evaluated (43, 55, 70)]. Notice that electronic degrees of freedom, including inner-sphere contributions, are treated implicitly through atomic partial charges (43, 55, 67); quantum electronic contributions to heme reorganization have already been calculated and shown to be small (71). The charmm22 force field (67) and the flexible SPC water model (72) were used, with a periodic box size of 40 Å and a 0.2-fs timestep. Nonbonded interactions were truncated on a group basis at 12-Å separations. Classical simulations were done in the same conditions. Simulations were done with the x-plor program (73).
Results
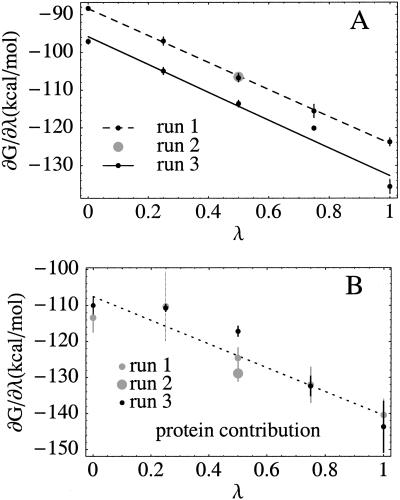
Fig. 1A shows the free energy derivative ∂G/∂λ for the solvated protein as a function of the “coupling” parameter λ (where −λe is the inserted charge). The linearity of ∂G/∂λ is almost perfect for run 1, and the “backwards” run 2 superimposes perfectly on run 1. Run 3 (prepared independently, using the reduced crystal structure) is also linear, with the same slope, but is offset with respect to runs 1 and 2, yielding a free energy difference of ΔGox→red = −113.7 kcal/mol, compared to −106.4 kcal/mol for runs 1 and 2. The protein's direct contribution to the free energy derivative (63, 74) is noisier but also linear within the estimated uncertainty (Fig. 1B) and corresponds to a −123.5 kcal/mol contribution to ΔGox→red; this estimate includes the contribution of three buried waters (see below). The remaining +17.1 kcal/mol of ΔGox→red are the contribution of the rest of the solvent. For MP-8 in solution, ΔGox→red = −100.8 kcal/mol, so that the Cyt c redox potential relative to MP-8 is ΔΔG = 8.0 kcal/mol [averaging runs 1–3 (76)],‡ or 5.6 kcal/mol (runs 1–2 only), compared to 6.9 kcal/mol from experiment (59). Run 4, with the redox electron concentrated on the heme iron [in agreement with recent molecular orbital calculations (65)] gave a ΔΔG of 7.9 kcal/mol. A similar ΔΔG was obtained earlier (37) with the much simpler (and intrinsically linear) Protein Dipole Langevin Dipole model.
Figure 1.
(A) Free energy derivative (kcal/mol) vs. the coupling parameter λ, which measures the proportion of the redox electron inserted into the structure. Each dot corresponds to a 1.3- to 2.3-ns simulation. Lines are least-squares linear fits to the dots. For run 2, only one simulation was done (with λ = 0.5; grey dot). Error bars are obtained as the dispersion of block averages, with the simulation divided into four equal blocks. (B) Protein contribution to ∂G/∂λ (from run 1).
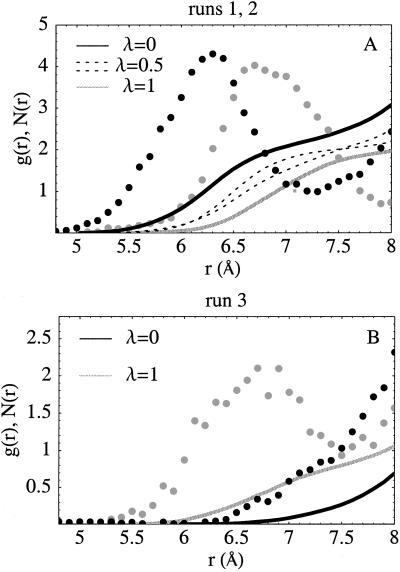
Experimental differences between the oxidized and reduced structures are very small (48) (0.4-Å mean backbone deviation). During the MD simulations, the backbone deviations from the ferri and ferro crystal structures are similar, typically about 1.2 Å for the inner half of the protein (and 1.5 Å overall) at the end of each simulation window [significantly better than in earlier work (32, 34, 58)]. Three buried water-molecules are conserved across eukaryotic Cyt c's (48–52); their positions are well reproduced throughout the simulations, with one difference (see below). One of these, W166 (48), hydrogen bonds to Asn-52, Tyr-67, and Thr-78 and shifts positions between the oxidized and reduced crystal structures: in yeast Cyt c, the iron-oxygen distance increases from 5.0 to 6.6 Å on reduction. In the homologous tuna Cyt c, the increase is from 6.1 to 6.6 Å (50). Fig. 2 illustrates the movement of W166 during the simulations. In run 1, the iron–oxygen distance increases (from 6.2 to 7.0 Å) on reduction, in agreement with experiment. In the midpoint simulation, λ = 0.5, the position is almost halfway between the endpoint positions, i.e., the shift is a linear function of λ. The reverse movement is seen in the backwards run 2, as it should be. In run 3 (Fig. 2B), W166 remains close to the experimental crystal position most of the time in the first (reduced state) simulation but moves toward the protein surface as oxidation proceeds. This behavior is seen experimentally in horse Cyt c (49) [which has the same reorganization energy as yeast Cyt c but a different redox potential (25)], but not in yeast (or tuna or rice) Cyt c (48, 50, 52). This movement accounts in part for the difference, or “hysteresis,” between the run 1 and 3 free energies.
Figure 2.
Position of the redox-sensitive buried crystal water W166 (see text) relative to the heme iron during the simulations. (A) Dots: radial distribution function g(r) of water oxygens around the heme iron (scaled arbitrarily for clarity); g(r) represents the probability of finding a water at the specified distance during the simulation. Black: λ = 0 (oxidized state); grey: λ = 1 (reduced state). Run 1 data. The peak is produced by W166; it shifts from 6.2 to 7.0 Å on reduction. Lines: mean number N(r) of waters within r of the iron; N(r) is the integral of g(r). The results for midpoint simulations from runs 1 and 2 (with λ = 0.5; both shown as dashed lines) are about midway between the endpoint curves. (B) Similar data for the endpoint simulations of run 3. In this run, the buried water moves towards the protein surface in the oxidized state (λ = 0).
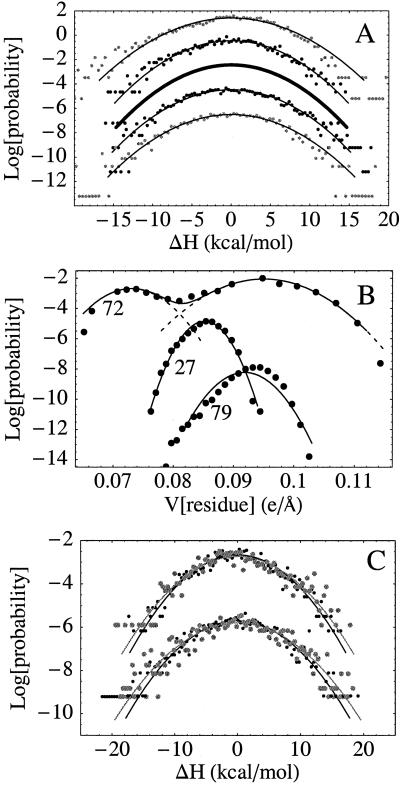
A linear free energy derivative implies gaussian fluctuations for the perturbing energy ΔH (see Methods) and an induced polarization that is proportional to λ (Eq. 2). Probability distributions of ΔH from the protein simulations are shown in Fig. 3A and are indeed highly gaussian in the ±10 kcal/mol range, with varying degrees of noise in their tails. The contributions of individual atomic groups are less harmonic (Fig. 3B). For example, 10% of the backbone and side chain groups within 10 Å of the heme, as well as 7 of 16 lysine side chains, have distinctly anharmonic motions (e.g., Lys-72 in Fig. 3B). Nevertheless, partly because the more anharmonic groups are at the protein surface, over 10 Å away from the iron, higher cumulants of all group contributions examined here are very small (<2% of their second cumulant).
Figure 3.
(A) Probability distribution of the perturbation energy ΔH from protein simulations (dots) with gaussian fits (lines). A constant offset is applied between simulations for clarity. From the top: run 3, reduced state; run 3, oxidized state; distribution derived from the slope of the free energy derivative; run 1, oxidized state; run 1, reduced state. The most accurate distribution, derived from the slope of ∂G/∂λ (thick, middle curve) is slightly narrower than those derived from the individual simulations (see text). (B) Probability distribution of the electrostatic potential (e/Å) produced on the heme iron by the three closest lysine side chains (Lys-27, -72, and -73), along with fits to one (Lys-27, -73) or two (Lys-72) gaussians. (C) Probability distribution of the perturbation energy ΔH from classical (grey) and path integral quantum (black) simulations of the MP-8/heme/Met complex in solution, showing a 10% narrowing due to quantum effects associated with nuclear tunneling. Upper curves, oxidized state; lower, reduced state.
For MP-8, probability distributions from both classical and path integral quantum simulations are shown in Fig. 3C. Nuclear tunneling, associated mainly with high-frequency heme motions, leads to a 10% narrowing of the probability distributions but does not change their shape. Narrowing is expected because of weaker correlations in the quantum description; a 10% narrowing of excitation energy distributions due to solvent quantization was found recently in simulations of tryptophan in solution (70).
The second derivative of the free energy determines the relaxation or reorganization free energy (Eq. 8): ΔGrlx = ½∂2G/∂λ2. From the slope of ∂G/∂λ in run 1, we obtain ∂2G/∂λ2 = −35.7 kcal/mol for 0 ≤ λ ≤ 1. Run 3 has essentially the same slope and gives the same result (Fig. 1A). An alternative estimate is obtained from the variance of ΔH: ∂2G/∂λ2 = −βVarλΔH (Eq. 6). In the five simulations of run 1, this estimate varies between −36.4 and −40.9 kcal/mol, with a mean of −38.7 kcal/mol. Thus, the variance of ΔH is overestimated by 2–15% when it is extracted from the individual simulations, despite their length (1.3–2.3 ns), presumably because of noise in the tails of the ΔH probability distribution.
The corresponding relaxation free energy (Eq. 8) is ΔGrlx = −17.8 kcal/mol, at the upper end of the range of values reported recently by Warshel and coworkers (34), who used a smaller model and much shorter simulations. It is less than half the relaxation free energy for MP-8/heme/Met, −38.0 kcal/mol [which is close to the Warshel estimate (34)], because the heme environment in the protein is only weakly polarizable, whereas in MP-8, the heme is largely exposed to polarizable solvent.
ΔGrlx can be used to calibrate a simple dielectric continuum model (32, 35, 36, 77), in which the inner part of the heme (nitrogens and iron) is treated as a cavity, the rest of the heme and the protein are treated as a homogeneous medium with dielectric constant ɛp, and the solvent has a dielectric ɛw = 80. In the context of the continuum model, the relaxation free energy is equal to the usual self energy of the perturbing charge (the redox electron) (32, 35). Using finite-difference solutions of the Poisson equation (78) and following the procedure introduced in refs. 32 and 35, we obtain ΔGrlx = −17.3 kcal/mol with ɛp = 1.1. Thus, the relaxation free energy and dielectric susceptibility from the MD simulations are consistent with a very low dielectric constant of ∼1.1 throughout the inner part of the protein. Introducing protein heterogeneity in the form of a second larger dielectric constant for the outer part of the protein was found (77) to increase ΔGrlx only slightly. Notice that the MD simulations do not include electronic polarizability explicitly; if they did, the continuum dielectric constant needed to reproduce ΔGrlx would presumably be closer to 2 (32).
Conclusion
The linear free energy derivative observed here for heme reduction implies that the induced polarization (the “response”) is linear, in accord with dielectric continuum models, and that the total electrostatic potential on the heme has simple gaussian fluctuations, even though the fluctuations of many of the individual protein groups are highly nongaussian. We believe this result could not have been easily anticipated, because the central limit theorem (60, 79) could have been violated for the present macromolecular system; indeed, the motions of many protein and solvent groups have strong mutual correlations that could introduce frustration.
The simulation model used here is semiquantitative. For example, the redox electron is treated classically as a set of atomic partial charges; electronic polarizability of the heme is not explicitly included; the force field parameters for the iron coordination sphere were not extensively optimized for both oxidation states (67); and reasonable but unproven assumptions were made concerning the protonation of the heme propionates and other groups. Nevertheless, we obtain fair agreement with experiment for both the redox potential relative to MP-8 (59) (using two different descriptions of the redox electron) and for the protein structure (including internal waters) and fluctuations (48) (measured by crystallographic B factors; not shown). Several factors suggest the agreement is meaningful. Compared to previous studies of Cyt c (32, 34, 37), the present simulation model is substantially larger; run times are longer (23 ns total; note, however, that the earlier smaller models may allow faster convergence); and none of the system is assumed to be linear, yet a similar redox potential difference is obtained (but a larger reorganization free energy). Recent molecular orbital calculations show that for the present, low-spin heme coordinated by imidazole and dimethylsulfide (His and Met analogues), the redox electron is mainly localized in the iron 3d orbitals (65), and inner-shell relaxation contributes about 1 kcal/mol to the reorganization energy (71). Nuclear tunneling does not change the nature of the electrostatic potential fluctuations (Fig. 3C). Muegge et al. (34) showed that the reorganization free energy and the redox potential relative to MP-8 are only moderately sensitive to propionate protonation. Comparison to that study also suggests that the present results do not depend significantly on the force field used. Finally, electrode voltammetry shows that the reorganization energy is a robust property, conserved across yeast, horse, and tuna Cyt c (all of which have different redox potentials) (25).
The reorganization free energy for Cyt c oxido-reduction is less than half that for MP-8/heme/Met in solution. To reproduce this result with a dielectric continuum model, a dielectric constant of only ɛp = 1.1 is needed for the heme vicinity. This is slightly lower than the polarizability deduced from Stokes shift measurements for a probe bound in the active site of the enzyme chymotrypsin in dehydrated films (22), from dielectric dispersion by dry protein powders (75), and from Stark shifts of chromophores in the photosynthetic reaction center (19). Together with Marcus theory (4), this shows that the heme pocket in Cyt c reduces almost to the theoretical limit (ɛp = 1) the contribution of protein reorganization to the electron transfer activation barrier.
The simulation techniques used here represent a “middle path” to study dielectric properties of proteins, between theory (14, 62) and experiment. They should prove increasingly useful for redox protein design, for understanding biological electron transfer, and for determining simple models to describe electrostatic effects in proteins.
Supplementary Material
Acknowledgments
Helpful discussions with Daniel Borgis are acknowledged, as well as financial support from the Centre National de la Recherche Scientifique and the Ministère de la Recherche. Some of the simulations were done at the Supercomputer Center of the Ministère de l'Education (CINES).
Abbreviations
- MD
molecular dynamics
- Cyt c
cytochrome c
Footnotes
This paper was submitted directly (Track II) to the PNAS office.
For a single perturbing charge q at the origin, ΔH = q ∫ 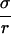 dr, where ρ is the charge density of the system, excluding q. Integrating by parts and using divE = 4πρ gives Eq. 1. For an arbitrary perturbing charge density, viewed as a set of infinitesimal point charges, the same result follows by superposition.
dr, where ρ is the charge density of the system, excluding q. Integrating by parts and using divE = 4πρ gives Eq. 1. For an arbitrary perturbing charge density, viewed as a set of infinitesimal point charges, the same result follows by superposition.
Recent work on irreversibility in MD free energy simulations suggests that the average of a forward and backward run is a good estimator of the free energy change, and that the associated uncertainty can be much smaller than the difference between the two runs (76).
References
- 1.Moser C, Keske J, Warncke K, Farid R, Dutton P. Nature (London) 1992;355:796–802. doi: 10.1038/355796a0. [DOI] [PubMed] [Google Scholar]
- 2.Nandi N, Battacharyya K, Bagchi B. Chem Rev. 2000;100:2013–2046. doi: 10.1021/cr980127v. [DOI] [PubMed] [Google Scholar]
- 3.Warshel A, Aqvist J. Annu Rev Biophys Biophys Chem. 1991;20:268–298. doi: 10.1146/annurev.bb.20.060191.001411. [DOI] [PubMed] [Google Scholar]
- 4.Marcus R. Annu Rev Phys Chem. 1964;15:155–196. [Google Scholar]
- 5.Honig B, Nicholls A. Science. 1995;268:1144–1149. doi: 10.1126/science.7761829. [DOI] [PubMed] [Google Scholar]
- 6.Schaefer M, Vlijmen H v, Karplus M. Adv Protein Chem. 1998;51:1–57. doi: 10.1016/s0065-3233(08)60650-6. [DOI] [PubMed] [Google Scholar]
- 7. Simonson, T. Curr. Opin. Struct. Biol. 11, 243–252. [DOI] [PubMed]
- 8.Warshel A. J Phys Chem. 1982;86:2218–2224. [Google Scholar]
- 9.Hwang J-K, Warshel A. J Am Chem Soc. 1987;109:715–720. [Google Scholar]
- 10.Maroncelli M, MacInnis J, Fleming G. Science. 1989;243:1674–1680. doi: 10.1126/science.243.4899.1674. [DOI] [PubMed] [Google Scholar]
- 11.Bader J, Chandler D. Chem Phys Lett. 1989;157:501–504. [Google Scholar]
- 12.Rossky P, Simon J. Nature (London) 1994;370:263–269. doi: 10.1038/370263a0. [DOI] [PubMed] [Google Scholar]
- 13.Marcus R. J Chem Phys. 1956;24:979–989. [Google Scholar]
- 14.Song X, Chandler D, Marcus R. J Phys Chem. 1996;100:11954–11959. [Google Scholar]
- 15.Levy R, Belhadj M, Kitchen D. J Chem Phys. 1991;95:3627–3633. [Google Scholar]
- 16.Hummer G, Pratt L, Garcia A. J Am Chem Soc. 1997;119:8523–8527. [Google Scholar]
- 17.Frauenfelder H, Sligar S, Wolynes P. Science. 1991;254:1598–1603. doi: 10.1126/science.1749933. [DOI] [PubMed] [Google Scholar]
- 18.Karplus M. J Phys Chem B. 2000;104:11–27. [Google Scholar]
- 19.Steffen M, Lao K, Boxer S. Science. 1994;264:810–816. doi: 10.1126/science.264.5160.810. [DOI] [PubMed] [Google Scholar]
- 20.Manas E, Vanderkooi J, Sharp K. J Phys Chem B. 1999;103:6334–6348. [Google Scholar]
- 21.Jordanides X, Lang M, Song X, Fleming G. J Phys Chem B. 1999;103:7995–8005. [Google Scholar]
- 22.Mertz E, Krishtalik L. Proc Natl Acad Sci USA. 2000;97:2081–2086. doi: 10.1073/pnas.050316997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Changenet-Barret P, Choma C, Gooding E, DeGrado W, Hochstrasser R. J Phys Chem B. 2000;104:9322–9329. [Google Scholar]
- 24.Winkler J, Gray H. Chem Rev. 1992;92:369–379. [Google Scholar]
- 25.Terrettaz S, Cheng J, Miller C. J Am Chem Soc. 1996;118:7857–7858. [Google Scholar]
- 26.Warshel A, Hwang J. J Chem Phys. 1986;84:4938–4946. [Google Scholar]
- 27.Warshel A, Chu Z, Parson W. Science. 1989;246:112–116. doi: 10.1126/science.2675313. [DOI] [PubMed] [Google Scholar]
- 28.Treutlein H, Schulten K, Brünger A, Karplus M, Deisenhofer J, Michel H. Proc Natl Acad Sci USA. 1992;89:75–79. doi: 10.1073/pnas.89.1.75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Gehlen J, Marchi M, Chandler D. Science. 1994;263:499–501. doi: 10.1126/science.263.5146.499. [DOI] [PubMed] [Google Scholar]
- 30.Xu D, Phillips C, Schulten K. J Phys Chem. 1996;100:12108–12121. [Google Scholar]
- 31.Ungar L, Newton M D, Voth G. J Phys Chem A. 1999;103:7367–7382. [Google Scholar]
- 32.Simonson T, Perahia D. J Am Chem Soc. 1995;117:7987–8000. [Google Scholar]
- 33.Basu G, Kitao A, Kuki A, Go N. J Phys Chem B. 1998;102:2076–2084. [Google Scholar]
- 34.Muegge I, Qi P, Wand A J, Chu Z, Warshel A. J Phys Chem B. 1997;101:825–836. [Google Scholar]
- 35.Simonson T, Archontis G, Karplus M. J Phys Chem B. 1999;103:6142–6156. [Google Scholar]
- 36.Archontis G, Simonson T. J Am Chem Soc. 2001;123:11047–11056. doi: 10.1021/ja010716+. [DOI] [PubMed] [Google Scholar]
- 37.Churg A, Warshel A. Biochemistry. 1986;25:1675–1681. doi: 10.1021/bi00355a035. [DOI] [PubMed] [Google Scholar]
- 38.Sagui C, Darden T. Annu Rev Biophys Biomol Struct. 1999;28:155–179. doi: 10.1146/annurev.biophys.28.1.155. [DOI] [PubMed] [Google Scholar]
- 39.Hummer G, Pratt L, Garcia A. J Phys Chem. 1996;100:1206–1215. [Google Scholar]
- 40. Simonson, T., Archontis, G. & Karplus, M. (2002) Acc. Chem. Res., in press. [DOI] [PubMed]
- 41.Yadav A, Jackson R, Holbrook J, Warshel A. J Am Chem Soc. 1991;113:4800–4805. [Google Scholar]
- 42.Del Buono G, Figueirido F, Levy R. Proteins. 1994;20:85–97. doi: 10.1002/prot.340200109. [DOI] [PubMed] [Google Scholar]
- 43.Zheng C, McCammon J, Wolynes P. Proc Natl Acad Sci USA. 1989;86:6441–6444. doi: 10.1073/pnas.86.17.6441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Alden R G, Warshel A. J Am Chem Soc. 1995;117:12284. [Google Scholar]
- 45.Moore G, Pettigrew G. Cytochromes c: Evolutionary, Structural and Physicochemical Aspects. Berlin: Springer; 1990. [Google Scholar]
- 46.Chupa J, McCauley J, Jr, Strongin R, Smith A, III, Blasie J, Petitcolas L, Bean J. Biophys J. 1994;67:336–358. doi: 10.1016/S0006-3495(94)80486-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Liu X, Kim C, Yang J, Jemmerson R, Wang X. Cell. 1996;86:147–157. doi: 10.1016/s0092-8674(00)80085-9. [DOI] [PubMed] [Google Scholar]
- 48.Berghuis A M, Brayer G D. J Mol Biol. 1992;223:959–976. doi: 10.1016/0022-2836(92)90255-i. [DOI] [PubMed] [Google Scholar]
- 49.Qi P, Beckman R, Wand A. Biochemistry. 1996;35:12275–12286. doi: 10.1021/bi961042w. [DOI] [PubMed] [Google Scholar]
- 50.Takano T, Dickerson R. Proc Nat Acad Sci USA. 1980;77:6371–6375. doi: 10.1073/pnas.77.11.6371. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Sanishvili R, Volz K, Westbrook E, Margoliash E. Structure (London) 1995;3:707–716. doi: 10.1016/s0969-2126(01)00205-2. [DOI] [PubMed] [Google Scholar]
- 52.Ochi H, Hata Y, Tanaka N, Kakudo M, Sakurai T, Aihara S, Morita Y. J Mol Biol. 1983;166:407–418. doi: 10.1016/s0022-2836(83)80092-8. [DOI] [PubMed] [Google Scholar]
- 53.Moore G. In: Protein Electron Transfer. Bendall D, editor. Oxford: BIOS; 1996. pp. 189–216. [Google Scholar]
- 54.Chandler D. J Phys Chem. 1984;88:3400–3407. [Google Scholar]
- 55.Straus J, Calhoun A, Voth G. J Chem Phys. 1995;102:529–539. [Google Scholar]
- 56.Simonson T, Perahia D. Far Disc. 1996;103:71–90. doi: 10.1039/fd9960300071. [DOI] [PubMed] [Google Scholar]
- 57.Garcia A, Hummer G. Proteins. 2000;38:261–272. [PubMed] [Google Scholar]
- 58.Simonson T. J Am Chem Soc. 1998;120:4875–4876. [Google Scholar]
- 59.Harbury H, Cronin J, Fanger M, Hettinger T, Murphy A, Myer Y, Vinogradov S. Proc Natl Acad Sci USA. 1965;54:1658–1664. doi: 10.1073/pnas.54.6.1658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Chandler D. Introduction to Modern Statistical Mechanics. Oxford: Oxford Univ. Press; 1987. [Google Scholar]
- 61.Hansen J P, McDonald I. Theory of Simple Liquids. New York: Academic; 1986. [Google Scholar]
- 62.Bone S, Pethig R. J Mol Biol. 1985;181:323–326. doi: 10.1016/0022-2836(85)90096-8. [DOI] [PubMed] [Google Scholar]
- 63.Simonson T. In: Computational Biochemistry and Biophysics. Becker O, Mackerell A Jr, Roux B, Watanabe M, editors. New York: Dekker; 2001. [Google Scholar]
- 64.Hill T. Introduction to Statistical Thermodynamics. Reading, MA: Addison-Wesley; 1962. [Google Scholar]
- 65.Rovira C, Carloni P, Parrinello M. J Phys Chem B. 1999;103:7031–7035. [Google Scholar]
- 66.Murgida D H, Hildebrandt P. J Am Chem Soc. 2001;123:4062–4068. doi: 10.1021/ja004165j. [DOI] [PubMed] [Google Scholar]
- 67.Mackerell A, Bashford D, Bellott M, Dunbrack R, Evanseck J, Field M, Fischer S, Gao J, Guo H, Ha S, et al. J Phys Chem B. 1998;102:3586–3616. doi: 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- 68.Jorgensen W, Chandrasekar J, Madura J, Impey R, Klein M. J Chem Phys. 1983;79:926–935. [Google Scholar]
- 69.Frenkel D, Smit B. Understanding Molecular Simulation. New York: Academic; 1996. [Google Scholar]
- 70.Simonson T, Wong C, Brünger A T. J Phys Chem A. 1997;101:1935–1945. [Google Scholar]
- 71.Sigfridsson E, Olsson M, Ryde U. J Phys Chem B. 2001;105:5546–5552. [Google Scholar]
- 72.Teleman O, Jonsson B, Engstrom S. Mol Phys. 1987;60:193–203. [Google Scholar]
- 73.Brünger A T. x-plor, ver. 3.1, A System for X-Ray Crystallography and NMR. New Haven, CT: Yale Univ. Press; 1992. [Google Scholar]
- 74.Gao J, Kuczera K, Tidor B, Karplus M. Science. 1989;244:1069–1072. doi: 10.1126/science.2727695. [DOI] [PubMed] [Google Scholar]
- 75.Song X, Chandler D. Phys Rev E. 1985;62:7949–7956. doi: 10.1103/physreve.62.7949. [DOI] [PubMed] [Google Scholar]
- 76.Hummer G. J Chem Phys. 2001;114:7330–7337. [Google Scholar]
- 77.Hoefinger S, Simonson T. J Comp Chem. 2001;22:290–305. [Google Scholar]
- 78.Madura J, Briggs J, Wade R, Davis M, Luty B, Ilin A, Antosiewicz J, Gilson M, Baheri B, Scott L, et al. Comp Phys Comm. 1995;91:57–95. [Google Scholar]
- 79.Khinchin A. Mathematical Foundations of Statistical Mechanics. New York: Dover; 1949. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.